Average protein density is a molecular-weight-dependent function

Abstract

The mass density of proteins is a relevant basic biophysical quantity. It is also a useful input parameter, for example, for three-dimensional structure determination by protein crystallography and studies of protein oligomers in solution by analytic ultracentrifugation. We have performed a critical analysis of published, theoretical, and experimental investigations about this issue and concluded that the average density of proteins is not a constant as often assumed. For proteins with a molecular weight below 20 kDa, the average density exhibits a positive deviation that increases for decreasing molecular weight. A simple molecular-weight-depending function is proposed that provides a more accurate estimate of the average protein density.

The mass density of proteins is an important basic biophysical quantity, which is directly related to the volume of a macromolecule of a given molecular weight. It is also a useful input parameter for macromolecular structure determination in X-ray single crystal crystallography. The practical application of the value of the average density of macromolecules for determination of the number of molecules per unit cell has been well known by protein crystallographers for a long time, this issue being first emphasized by Matthews (1968). In addition, estimates of the solvent content within the protein crystals is an important constraint in density modification procedures including solvent flattening (Wang 1985; Cowtan and Main 1996), histogram matching (Zhang and Main 1990), and solvent flipping (Abrahams and Leslie 1996). Furthermore, protein density, or rather the inverse of it, partial specific volume (v̄, the protein volume divided its molecular mass) is an important parameter in analytical ultracentrifugation experiments, particularly for studies of macromolecular oligomers in aqueous environment (Lebowitz et al. 2002). Partial specific volumes of proteins are not always easily determined experimentally and, therefore, their correct theoretical estimates might be very useful.

It is generally assumed that the spatial average of the density of proteins can be considered equal to 1.35 g/cm³ independent of the nature of the protein and particularly independent of its molecular weight.

More recently, Andersson and Hovmöller (1998^{, 2000}) stressed that every tool for speeding up three-dimensional protein structure determination is essential to bridge the gap between the high number of already sequenced proteins and the number of proteins whose high resolution structure is determined by protein crystallography techniques. They emphasized that the knowledge of the value of protein density as accurately as possible is essential for this purpose.

In this context, Andersson and Hovmöller (1998) claimed that the widely used average density value deduced from hydrodynamic and adiabatic compressibility experiments, ρ = 1.35 g/cm³, is not correct because of inherent errors in the measurements and stated that precise theoretical determinations would yield a more accurate estimate. Thus, they theoretically determined the average mass density of a number of proteins using the Voronoi construction, and obtained an overall density ρ = 1.22(2) g/cm³, this value being significantly lower than the previously accepted one (1.35 g/cm³).

Later on, Tsai et al. (1999) performed theoretical calculations using the average volume of buried residues to evaluate the proteins’ density and compare them with experimental data corresponding to 12 proteins taken from the compilation by Squire and Himmel (1979) and Gekko and Noguchi (1979). They obtained an average protein density estimate of 1.40(2) g/cm³, this value being higher than that reported by Andersson and Hovmöller (1998), and close to that currently used by protein crystallographers (1.35 g/cm³). These authors also reported previous experimental results compiled by Squire and Himmel (1979) and Gekko and Noguchi (1979), which yield an average density of 1.37(3) g/cm³.

Finally, Quillin and Matthews (2000) criticized the calculation procedure used by Andersson and Hovmöller (1998). Their main argument was that, in the procedure used by the latter authors, the contributions to the protein volume from the surface atoms were not properly accounted for. They selected 30 representative proteins of the set analyzed by Andersson and Hovmöller (1998), recalculated the protein volume using the Connolly (1993) algorithm, and determined the average density as 1.43(3) g/cm³.

All the density values mentioned above are listed in Table 1. The value 1.43(3) g/cm³ recalculated by Quillin and Matthews (2000) from the original determination by Andersson and Hovmöller (1998) is significantly higher than 1.22(2) g/cm³, approximately agrees with the calculations of Tsai et al. (1999), and is somewhat higher than, but close to, the experimental value of 1.35 g/cm³.

Table 1.

Reported molecular-weight-independent average mass density of proteins

Reference	Method	Density (g/cm3)
Andersson and Hovmöller (1998)	Theoretical	1.22 (2)
Tsai et al. (1999)	Theoretical	1.40 (2)
Quillin and Matthews (2000)	Theoretical	1.43 (3)
Squire and Himmel (1979) and Gekko and Noguchi (1979)	Experimental	1.37 (3)

The present note contains an analysis of the results reported by Quillin and Matthews (2000) and Tsai et al. (1999). The note aims at determining an eventual meaningful dependence of the mass densities of proteins on their molecular weight and explaining the observed differences between experimental and recent theoretical determinations.

Results and Discussion

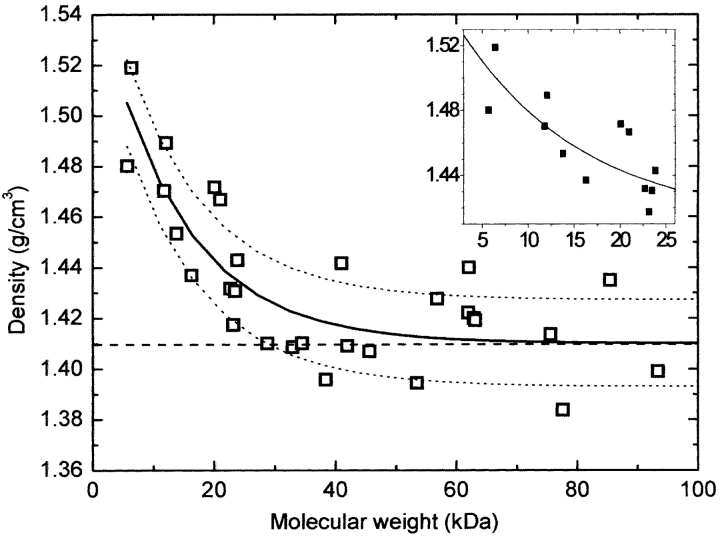
The first step of this investigation was to reanalyze the results obtained by Quillin and Matthews (2000). We have taken all the theoretical protein densities theoretically determined by them—reported in Table 1 of their article—and plotted them as a function of the molecular weight in Figure 1 ▶. At a first glance, a positive deviation of the density from a constant value is clearly apparent for low molecular weights. The trend of the observed variation can be well described by a simple exponential function:

Figure 1.

Square symbols correspond to the densities of a number of proteins calculated by Quillin and Matthews (2000). The solid line is the best fit of an exponential function (equation 1) to those values. Dotted lines are the limits associated to ±1 standard deviation (σ = 0.014 g/cm³). (Inset) An enlarged view of the low molecular weight part of the curve.

(1)

ρ_∞ being the asymptotic value of the mean density for high molecular weight (practically for M > 20 kDa), Δρ₀ the maximum deviation of the average density (for M approaching M = 0), and K a constant parameter. The exponential function that best fit to the calculated densities reported by Quillin and Matthews (2000) is plotted in Figure 1 ▶ as a continuous solid line. The deviation of the average density for small molecular weight starts to be apparent below M = 30 kDa and is statistically meaningful below M = 20 kDa.

Our fitting indicates that, for proteins with high molecular weight (say M > 30 kDa), a value ρ = 1.41(2) g/cm³ (instead of 1.43(3) g/cm³) represents well the average densities calculated by Quillin and Matthews (2000). On the other hand, for proteins with progressively decreasing molecular weight, the density is an increasing function, reaching a maximum value ρ = 1.50(2) g/cm³ for the smallest protein (M = 7 kDa).

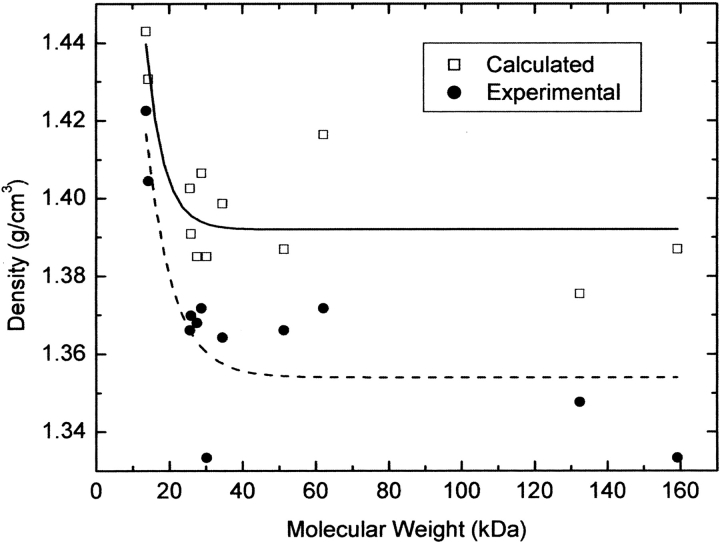
In Figure 2 ▶ the theoretical and experimental values of protein densities reported by Tsai et al. (1999) are plotted as a function of the molecular weight. Again, proteins with a molecular weight lower than 20 kDa clearly exhibit a density higher than those with molecular weight M > 20 kDa, thus providing further support to the mentioned conclusion derived from the data reported by Quillin and Matthews (2000).

Figure 2.

Experimental (filled circles) and theoretical (open squares) densities determined by Tsai et al. (1999) for a number of proteins. The solid line (above) and dashed line (below) correspond to the best fits of equation 1 to the calculated and experimental densities, respectively.

We also noticed in the curves plotted in Figure 2 ▶ from the results of Tsai et al. (1999) that the reported average densities of all the studied proteins, determined theoretically, are about 2.4% higher than those determined experimentally (Tsai et al. 1999). This difference can be qualitatively explained considering that the volume determined experimentally includes an ~3 Å thick water layer around the external surface (Svergun et al. 1998), this effect thus leading to an apparent decrease of the actual average density.

Moreover, in a recent article, Liang and Dill (2001) evaluated theoretically the internal packing of 636 proteins and concluded that large proteins are packed more loosely than small ones, thus demonstrating that the average density of small proteins is higher. This result explains the trends observed in Figures 1 ▶ and 2 ▶ and provides independent support to the theoretical determinations of Quillin and Matthews (2000) and Tsai et al. (1999).

Therefore, for a better estimate of the average density of proteins, we propose here the use of—instead of the constant value ρ = 1.35 g/cm³—the exponential function that best fit to the results reported by Quillin and Matthews (2000) plotted in Figure 1 ▶, that is,

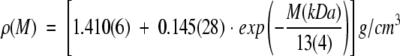(2)

Conclusion

We have noticed, based on previously published theoretical analysis and experimental results, a clear dependence of the average density of proteins on their molecular weight. The observed positive deviation at low molecular weight is clearly apparent both for theoretical (Tsai et al. 1999; Quillin and Matthews 2000) and experimental (Gekko and Noguchi 1979; Squire and Himmel 1979) data.

The deviation of the molecular-weight-dependent density, ρ(M), from the currently used average value (1.35 g/cm³) is particularly strong for proteins with M < 20 kDa. To obtain a better estimate of the density of these rather small proteins, instead of a molecular-weight-independent value, equation 2 should be used.

The difference between experimental and theoretical densities reported in the literature for all molecular weights (Fig. 2 ▶) is qualitatively justified by the existence of a structured water layer on the protein surface.

Proteins with a molecular weight below 30 kDa, being more amendable to protein crystallography and NMR, correspond to more than one-third of all the solved protein structures deposited in the Protein Data Bank (Berman et al. 2000). We propose here a more precise calculation of their density by using equation 2 instead of assuming a molecular-weight-independent value. Furthermore, the inverse of the protein density, the partial specific volumes of proteins, can be easily obtained from the same equation. The consequent improvement in the estimate of the protein density is expected to be particularly helpful in structural and biophysical studies regarding protein oligomers when accurate evaluation of the protein density might give a more precise value for the number of monomeric units composing an oligomer.

Article and publication are at http://www.proteinscience.org/cgi/doi/10.1110/ps.04688204.