Solvent effects on the conformational transition of a model polyalanine peptide

Abstract

We have investigated the folding of polyalanine by combining discontinuous molecular dynamics simulation with our newly developed off-lattice intermediate-resolution protein model. The thermodynamics of a system containing a single Ac-KA₁₄K-NH₂ molecule has been explored by using the replica exchange simulation method to map out the conformational transitions as a function of temperature. We have also explored the influence of solvent type on the folding process by varying the relative strength of the side-chain’s hydrophobic interactions and backbone hydrogen bonding interactions. The peptide in our simulations tends to mimic real polyalanine in that it can exist in three distinct structural states: α-helix, β-structures (including β-hairpin and β-sheet–like structures), and random coil, depending upon the solvent conditions. At low values of the hydrophobic interaction strength between nonpolar side-chains, the polyalanine peptide undergoes a relatively sharp transition between an α-helical conformation at low temperatures and a random-coil conformation at high temperatures. As the hydrophobic interaction strength increases, this transition shifts to higher temperatures. Increasing the hydrophobic interaction strength even further induces a second transition to a β-hairpin, resulting in an α-helical conformation at low temperatures, a β-hairpin at intermediate temperatures, and a random coil at high temperatures. At very high values of the hydrophobic interaction strength, polyalanines become β-hairpins and β-sheet–like structures at low temperatures and random coils at high temperatures. This study of the folding of a single polyalanine-based peptide sets the stage for a study of polyalanine aggregation in a forthcoming paper.

Small peptides undergo a spontaneous reversible disorder-to-order transition to a unique, three-dimensional equilibrium structure such as an α-helix or a β-structure when exposed to favorable physiological conditions. The information necessary to drive this folding transition is universally accepted to be encrypted solely within the linear amino acid sequence (Anfinsen 1973; Anfinsen and Scheraga 1975). However, experiments indicate that many peptides can be folded into alternative stable structures by changing the solution conditions (Rosenheck and Doty 1961; Kabsch and Sander 1984; Mutter and Hersperger 1990; Mutter et al. 1991; Zhong and Johnson 1992; Cohen et al. 1993; Waterhous and Johnson 1994). For example, many peptides are well known to undergo a sharp helix-coil transition as the temperature is increased (Poland and Scheraga 1970; Rohl and Baldwin 1998). Furthermore, the conformational transition between the α-helix and β-structure is greatly influenced by solvent conditions, including the pH (Mutter and Hersperger 1990; Cerpa et al. 1996; Tuchscherer et al. 1999), the temperature (Cerpa et al. 1996; Fukushima 1996; Zhang and Rich 1997), the salt or organic cosolvent concentration (Mutter and Hersperger 1990; Mutter et al. 1991; Reed and Kinzel 1991; Cerpa et al. 1996; Zhang and Rich 1997; Awasthi et al. 2001), the peptide concentration (Cerpa et al. 1996), and the redox state (Dado and Gellman 1993; Schenck et al. 1996). Despite the important role played by the solvent conditions in the α-β transition, our understanding of these effects is far from complete. Here computer simulations are performed in an attempt to examine the effect of solvent conditions on the α-β transition of model polyalanine peptides.

The effect of solvent conditions on the thermodynamics and kinetics of polyalanine and alanine-based peptides has been examined via computer simulations with atomistic models by a number of workers. One of the earliest simulations of the complete helix-coil transition was a study by Daggett and Levitt (1992), who performed molecular dynamics simulations of the denaturation of a 13-residue polyalanine α-helix using the force field by Levitt (1983) and the program ENCAD (Levitt 1990). They found that the helix is stable at all temperatures ranging from 5°C to 200°C in vacuum but only at low temperatures in solution. Vila et al. (2000) performed conformational Monte Carlo (MC) searches on ALA10 and ALA16. They observed that the helicity for both peptides was close to 0 when the model dielectric constant was 80, which corresponds to the value for pure water, and was >90% when the model dielectric constant was 2, which corresponds to the value within a protein environment without solvent polarization effects. Hansmann, Okamoto, and coworkers conducted multicanonical simulations by using the force field ECEPP/2 (Sippl et al. 1984) over a wide range of temperatures and found that the helix-coil transition of polyalanines of lengths 10 to 30 residues is a true thermodynamic phase transition in vacuum (Okamoto and Hansmann 1995; Hansmann and Okamoto 1999; Alves and Hansmann 2000 Alves and Hansmann 2001). The transition temperature was significantly lower in water, implying that presence of solvent tends to weaken helix formation (Mitsutake and Okamoto 2000; Peng and Hansmann 2002; Peng et al. 2003). Garcia and coworkers (Garcia and Sanbonmatsu 2002; Ghosh et al. 2003) investigated the thermodynamics of the helix-coil transition of a 21-residue polyalanine peptide in explicit water by conducting replica-exchange molecular dynamics (REMD) simulations with a modified AMBER force field. They found that the helix-coil transition is moderately cooperative over a broad temperature range. Ohkubo and Brooks III (2003) examined equilibrium helix-coil transitions of Ac-Ala_n-NMe (n = 3–20) as a function of temperature by using REMD with the CHARMm/GB implicit solvent force field. They found that the intrinsic helical propensity of alanine measured by the Zimm-Bragg parameters is independent of the chain length. Olivella et al. (2002) performed nanosecond molecular dynamics simulations by using the AMBER95 force field of Cornell et al. (1995) on polyalanine α-helices in polar and nonpolar solvents such as water and methane, respectively. They found that the intrahelical hydrogen bond is weaker in polar solvent than in nonpolar solvent. In contrast, a study by Mortenson et al. (2002), who performed all-atom simulations on ALA12 and ALA16 by using the same force field as Olivella et al. (2002), showed that changing the environment from in vacuo to aqueous conditions increases helicity.

All of the simulation studies mentioned above predict a transition between the α-helix and random coil but not the existence of a β-structure. Two recent studies, however, do predict the formation of a β-structure by polyalanines (Levy et al. 2001; Ding et al. 2003). Levy et al. (2001) performed molecular dynamics simulations by using the CHARMm program on polyalanine ALA12 at several temperatures and found that the native state is an α-helix in vacuum and a β-structure in aqueous solution. Ding et al. (2003) performed molecular dynamics simulations by applying a modified version of our implicit-solvent protein model (Smith and Hall 2001a,b) to Ho and DeGrado’s (1987) α_1B amphipathic α-helix peptide and observed the formation of a β-hairpin. Based on their calculation of the free energy of the β-hairpin, they concluded that the β-hairpin is a metastable intermediate. Because Ding et al. (2003) conducted constant-temperature simulations at low temperatures, their system might have been trapped in local minima, which would mean there was insufficient sampling of those parts of configurational space that are important in thermodynamic calculations.

In this article, we perform equilibrium simulations over a very wide range of solvent conditions to determine how these affect the formation of various peptide structures. The solvent conditions considered in this study are the temperature and the hydrophobic interaction strength between non-polar side-chains. We begin by simulating the folding of an isolated model polyalanine peptide over a wide range of temperatures in vacuum; in this case, the hydrophobic interaction is turned off. We examine the effect of temperature on the populations of the various structural states of the peptide and locate the conformational transitions between different structural states. The Zimm-Bragg equilibrium constants (Zimm and Bragg 1959) for propagation and nucleation of the helix are calculated to quantify specific preference for the α-helical state of each alanine residue on our model peptide. We then examine the effect of the hydrophobic interaction strength between nonpolar side-chains on the populations of the different structural states by varying the hydrophobic interaction strength from one-twelfth to one-half the hydrogen bonding interaction strength over a wide range of temperatures. At each value of the hydrophobic interaction strength and temperature, we calculate the conformational free energy of each structural state to determine which structure has the lowest free energy and hence locate the conformational transition between different structural states as a function of temperature.

The model peptide chosen for study is the polyalanine-based peptide Ac-KA₁₄K-NH₂. We focus on polyalanine-based peptides for three reasons. First, the small, uncharged, unbranched nature of alanine residues is amenable to simulation with the intermediate-resolution protein model that we developed previously (Smith and Hall 2001a,b). Second, polyalanine repeats have been implicated in human pathologies; in particular, they are responsible for the formation of anomalous filamentous intranuclear inclusions in oculopharyngeal muscular dystrophy patients (Brais et al. 1999). Third, synthetic polyalanine-based peptides have been shown by Blondelle and coworkers to undergo a transition from α-helical structures to β-sheet complexes at concentrated conditions in vitro (Forood et al. 1995; Blondelle et al. 1997), mimicking the structural transition believed to be a prerequisite for fibril nucleation and growth (Kirschner et al. 1986; Simmons et al. 1994; Horwich and Weissman 1997; Sunde and Blake 1997; Kusumoto et al. 1998; Harrison et al. 1999; Esler et al. 2000). Blondelle and coworkers observed that the α-helical structures were stabilized in part by intramolecular α-helical bonds and that the macromo-lecular β-sheet complex was stabilized by hydrophobic inter-sheet interactions. By using circular dichroism, Fourier-transform infrared spectroscopy, and reversed-phase high-performance liquid chromatography, they found that (1) β-sheet complex formation increased with increasing temperature, exhibiting an S-shaped dependence on temperature with a critical temperature of 45°C at a peptide concentration of 1.8 mM and an incubation time of 3 h, and (2) β-sheet complex formation increased with increasing peptide concentration above a critical concentration of 1 mM at 65°C.

The polyalanine-based peptide Ac-KA₁₄K-NH₂ is represented by using an off-lattice, implicit-solvent, intermediate-resolution protein model originally introduced by Smith and Hall (2001a^,b,c). In this article, we describe refinements to this model to make it more suitable for the study of aggregation phenomena in very large multiprotein systems. Three modifications have been made to the Smith/Hall model. First, the constraint on the fluctuation of the bond length between neighboring united atoms is relaxed by increasing its tolerance from ±2.0% about the ideal value to ±2.375% about the ideal value; this produces a more realistic Ramachandran plot than was previously obtained by extending the Φ-Ψ space explored to include Φ-Ψ angles that correspond to the lefthand α-helix and polyproline II (Voet and Voet 1990). Increasing the bond length fluctuation tolerance also increases the code’s speed because the united atoms move a greater distance between collisions. Second, the hydrogen bond formation algorithm was modified to include a penalty for breaking the bond when the hydrogen bond angle is too extreme. Third, the efficiency techniques that have been developed in our group for modeling polymer dynamics are implemented, which increases the code’s speed by a factor of 50. These modifications are discussed in greater detail in the Materials and Methods section.

Simulations are performed by using the discontinuous molecular dynamics (DMD) simulation algorithm (Alder and Wainwright 1959; Rapaport 1978 Rapaport 1979; Bellemans et al. 1980), which is an extremely fast alternative to traditional molecular dynamics and is applicable to systems of molecules interacting via discontinuous potentials, for example, hard-sphere and square-well potentials. Unlike soft potentials such as the Lennard-Jones potential, discontinuous potentials exert forces only when particles collide, enabling the exact (as opposed to numerical) solution of the collision dynamics. DMD simulations proceed by locating the next collision, advancing the system to that collision, and then calculating the collision dynamics. To ensure that our simulations have the capacity to effectively sample configurational space without getting trapped in local minima, we modify the replica-exchange method (Hukushima and Nemoto 1996) for use with our DMD algorithm simulation. Here we follow the approach of Sugita and Okamoto (1999), who originally formulated replica exchange as a combined molecular dynamics and Monte Carlo (MD/MC) method. In replica-exchange, multiple replicas of the same system are simulated over a wide range of temperatures. At set time intervals, replicas with temperatures that are nearest neighbors along the temperature spectrum are exchanged provided that a Metropolis criterion is satisfied. This procedure is repeated until all of the systems at different temperatures reach equilibrium. Once at equilibrium, the data collection phase begins, in which the probability of various energy levels and states are stored for use in a weighted histogram calculation (Ferrenberg and Swendsen 1989; Zhou et al. 1997) of the conformational free energy of the various peptide structures. This simulation procedure is discussed in greater detail in the Materials and Methods section.

Highlights of our simulation results are the following: We find that peptides in our simulations tend to mimic real polyalanines in that they can exist in three distinct structural states: α-helices, β-structure ensemble (including β-hairpin and β-sheet–like structures), and random coils, depending upon the solvent conditions. At low values of the hydrophobic interaction strength between nonpolar side-chains, the polyalanines undergo a relatively sharp transition between an α-helical conformation at low temperatures and a random-coil conformation at high temperatures. As the hydrophobic interaction strength increases, this transition shifts to higher temperatures. Increasing the hydrophobic interaction strength even further induces a second transition to a β-hairpin, resulting in an α-helical conformation at low temperatures, a β-hairpin at intermediate temperatures, and a random coil at high temperatures. At very high values of the hydrophobic interaction strength, polyalanines become β-hairpin and β-sheet–like structures at low temperatures and random coils at high temperatures. This study of the folding of a single polyalanine-based peptide sets the stage for a study of polyalanine aggregation in a forthcoming article.

This article is organized as follows: The next section presents the results obtained from simulations at various conditions. A further section contains a summary and discussion of our findings and a brief description of our future work on fibril formation in multipeptide systems based on the sequence studied in this article. The final section describes the methods used in this work, including the physical representation of the protein, its potential energy function, the DMD simulation technique, the replica-exchange method, and the weighted histogram method.

Results

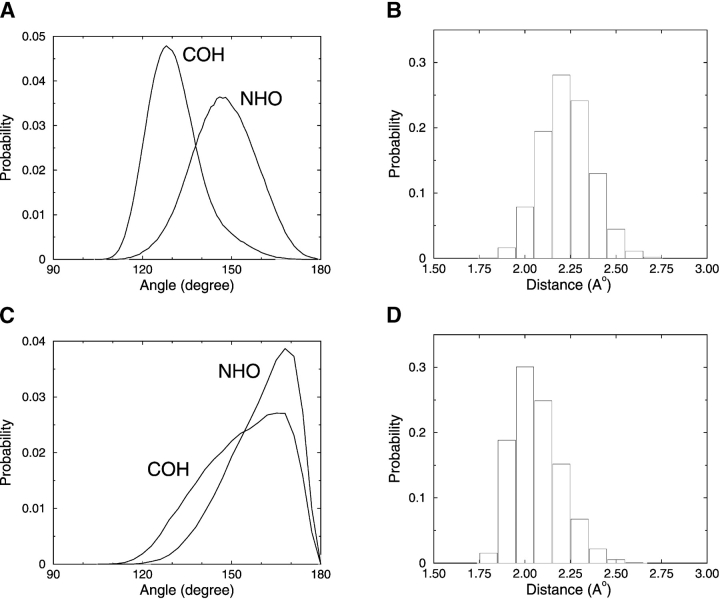
In this article, we modify the hydrogen-bonding potential of Smith and Hall (2001a^,b,c) by adapting an approach similar to that of Ding et al. (2003) as described in the Materials and Methods section. In our simulations, the new hydrogen-bonding criteria lead to hydrogen bonds with realistic OH distances and NHO angles as illustrated in Figure 1 ▶, which shows the distributions of the COH and NHO angles and the OH distances for both α-helices and β-structures. Snapshots of an α-helix and different β-structures are projected as Rasmol (Sayle and Milner-White 1995) renderings in Figure 2 ▶. The results in Figure 1 ▶ agree better with the hydrogen bond properties reported by Baker and Hubbard (1984) based on an extensive analysis of α-helices and β-structures in a high-resolution protein database than those reported in our previous study (Smith and Hall 2001a). For our α-helices, the NHO angle varies between 115° and 180° with a mean of 148°, and the COH angle varies between 110° and 170° with a mean of 131°. In comparison, Baker and Hubbard (1984) report a NHO angle ranging from 110° to 180° with a mean of ~157° and a COH angle ranging from 110° to 180° with a mean of ~147°. For our β-structures, the NHO angle varies between 120° and 180° with a mean of 160°, and the COH angle varies between 110° and 180° with a mean of 154°. In comparison, Baker and Hubbard (1984) report a NHO angle ranging from 120° to 180° with a mean of ~162° and a COH angle ranging from 120° to 180° with a mean of ~151°. For our α-helices, the hydrogen bond length (virtual hydrogen–to–virtual oxygen distance) varies between 1.8 and 2.8 Å with a mean of 2.23 Å. This distribution is somewhat different from the range (1.6–2.5 Å) and mean (2.04 Å) reported by Baker and Hubbard. For our β-structures, the hydrogen bond length varies between 1.8 and 2.9 Å with a mean of 2.06 Å. This distribution is also somewhat different from the range (1.6–2.5 Å) reported by Baker and Hubbard but in better agreement with their mean (1.94 Å).

Figure 1.

Distribution of hydrogen bond angles (A)and distances (B) for α-helices, and angles (C) and distances (D) for β-structures.

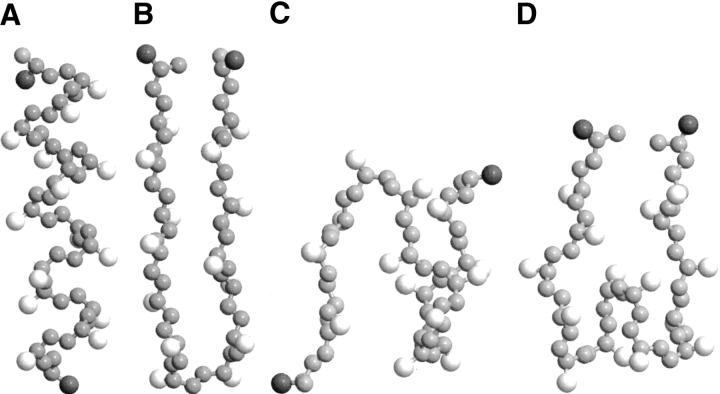
Figure 2.

Snapshots of the 16-residue peptide in an α-helix (A) and a β-hairpin (B). In addition to β-hairpins, other β-structures are β-sheet–like with two β-turns (C) and three β-turns (D). Hydrophobic side-chains are white, polar side-chains (at chain ends) are dark gray, and backbone atoms are light gray. Note that the united atoms are not shown full size for ease of viewing.

In this section, we present results from replica-exchange DMD/MC simulations on the structures formed by the isolated, 16-residue model KA14K peptide. One structure of interest is a full-length α-helix with four α-helical turns, 12 α-helical hydrogen bonds (defined as bonds between N_{i + 4} and C_i), and 10 hydrophobic contacts. Other structures of interest are those that have a significant number of β hydrogen bonds. A β hydrogen bond is defined to be a hydrogen bond between two residues with backbone angles that are in the β-region of the Ramachandran plot (0 ≤ Ψ ≤ 180 and −180 ≤ Φ ≤ −30). In this article, β-structures are defined to be structures having three or more β hydrogen bonds. Examples include β-hairpins and β-sheet–like structures. We focus particularly on the β-hairpin, which is defined to be a structure having one β-turn and six or more consecutive β hydrogen bonds that link one half of the peptide to the other half. β-Sheet–like structures are defined to be structures having two or more β-turns and three to five β hydrogen bonds. Snapshots of an α-helical structure, β-hairpin, and two β-sheet–like structures for the model peptide are shown in Figure 2 ▶, with hydrophobic residues colored white, polar residues colored dark gray, and backbone atoms colored light gray. Note that the united atoms are not shown full size for ease of viewing.

Intrinsic helical propensity of alanine

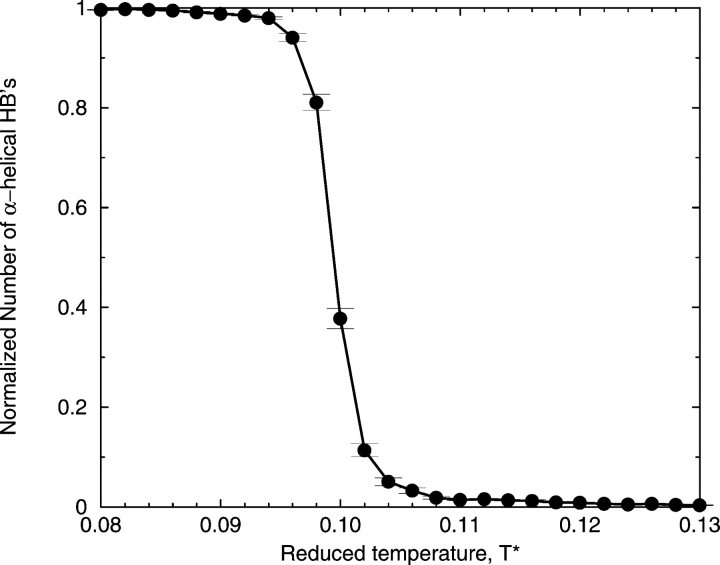
In the absence of hydrophobic interactions, model alanine residues on the KA14K peptide have a strong tendency to form α-helical hydrogen bonds. This is apparent from the high number of α-helical hydrogen bonds formed at low temperatures, as shown in Figure 3 ▶, which displays the normalized number of α-helical hydrogen bonds (relative to the perfect α-helix value of 12) at various reduced temperatures (T* = k_BT/ɛ_HB) averaged over a large ensemble of the peptide configurations at each temperature collected during the replica-exchange simulations when ɛ_{HP =} 0. Indeed, the specific preference of the alanine residue for the α-helical state is confirmed by calculating the parameters s (equilibrium constant for propagation of the helix) and σ_ZB (nucleation of the helix) in the Zimm-Bragg model (Zimm and Bragg 1959). According to this model, the propagation parameter, s, which is a measure of helix propensity, can have a value of 1 (the chain is 50% helical and the helix and coil are equally favored), greater than 1 (the helix is favored relative to a random coil), and less than 1 (the helix is disfavored relative to a random coil). An increase in s corresponds to increases in both the average number of helical residues (<n>) and the average length of a helical segment (<l_ZB>). The nucleation parameter, σ_ZB, which is a measure of the propensity for nucleating a helical segment, can have values between infinitely small (but not 0) and 1, with the infinitely small value corresponding to a large barrier to nucleation and a value of 1 corresponding to no barrier to nucleation. As σ_ZB increases toward a value of 1, the increased number of nucleation events corresponds to the creation of more helical segments, <n>, which has the effect of lowering the average segment length, <l_ZB>. For more details on the calculation of the Zimm-Bragg parameters, see our previous simulation study (Smith and Hall 2001a).

Figure 3.

Percentage of α-helical hydrogen bonds formed as a function of T* =k_BT/ɛ_HB in the absence of hydrophobicity.

Table 1 shows s and σ_ZB along with the average number of helical residues, <n>, and average length of a helical segment, <l_ZB>, observed in our simulations at different reduced temperatures, T*. At low temperatures, high values of s (1.80) indicate that the alanine residues on the model peptide have a strong preference to form helix over coil, which is in good agreement with preferences observed in experiment (Marqusee et al. 1989; Scholtz et al. 1991; Charkabartty et al. 1994; Chakrabartty and Baldwin 1995) and in the simulations of Okamoto and Hansmann (1995)^, Garcia and Sanbonmatsu (2002), and Ohkubo and Brooks III (2003).

Table 1.

Helix properties measured during simulations (average number of a-helical residues, <n>, and average length of an α-helical segment, <l_ZB>) and calculated Zimm-Bragg parameters (propagation parameter, s, and nucleation parameter, σ_ZB) for different values of reduced temperature

T*	<n>	< lZB>	s	σZB
0.0800	11.96 ± 0.01	11.95 ± 0.02	1.80	0.09
0.0940	11.73 ± 0.03	11.57 ± 0.06	1.65	0.08
0.0954	10.53 ± 0.32	10.31 ± 0.34	1.28	0.04
0.0970	10.35 ± 0.35	9.82 ± 0.40	1.26	0.05
0.0986	8.08 ± 0.54	7.85 ± 0.55	1.06	0.03
0.0994	6.15 ± 0.60	5.89 ± 0.59	0.96	0.03
0.1002	3.67 ± 0.58	3.60 ± 0.57	0.80	0.04
0.1026	3.23 ± 0.56	3.23 ± 0.56	0.76	0.05
0.1034	1.86 ± 0.45	1.78 ± 0.44	0.48	0.12
0.1042	1.34 ± 0.15	1.28 ± 0.15	0.24	0.32

The specific preference for the α-helical state of alanine residues by the model peptide depends on the temperature as indicated by Table 1. The propagation parameter, s, decreases with increasing temperature, ranging from its highest value of s = 1.80 at T* = 0.08, meaning that the helix is favored relative to a random coil, to its lowest value of s = 0.24 at T* = 0.1042, meaning that the helix is disfavored relative to a random coil. The transition temperature at which s = 1, where the chain is 50% helical, is between T* = 0.0986 and T* = 0.0994. The s values in our study are in good agreement with experimental results that yield estimates of s for alanine between 1.33 and 2.19 (Scholtz et al. 1991; Chakrabartty and Baldwin 1995; Spek et al. 1999) and with the simulation results from Okamoto and Hansmann (1995) (s = 1.1 to 1.7) and Garcia and Sanbonmatsu (2002) (s = 1.3 at 273K). The nucleation parameter, σ_ZB decreases with increasing temperature in the temperature range T* = 0.08 to the transition temperature. This indicates that nucleation is harder to accomplish at the transition temperature than at lower temperatures. However, as temperature is increased above the transition temperature, σ_ZB increases, indicating that nucleation is easier at higher temperatures. Our values of σ_ZB are all much larger than the experimental estimates (≈0.003 to 0.004) (Platzer et al. 1972; Scholtz et al. 1991; Chakrabartty et al. 1994) or the simulation estimate of Garcia and Sanbonmatsu (2002) (≈0.004), are in good agreement with other simulation estimates of Hansmann and coworkers (Okamoto and Hansmann 1995; Hansmann and Okamoto 1999) (≈0.07), Sung and Wu (1996) (≈0.056), and Ohkubo and Brooks III (2003) (≈0.05), and are smaller than simulation estimates (≈0.5) of Daggett et al. (1991) and Daggett and Levitt (1992). Our helical content of ~100% at T* < 0.10 (as displayed in Fig. 3 ▶) is significantly higher than the simulation estimate of ~34% by Garcia and Sanbonmatsu (2002) for the Ac-Ala21-methyl amide peptide (Ala21). Short polyalanine peptides such as Ala21 are not very good helix formers (Ingwall et al. 1968); such peptides can form better helices by substituting a few lysines (Williams et al. 1998), as is the case in our peptide Ac-KA₁₄K-NH₂.

Conformational transition as a function of temperature and hydrophobic interaction strength

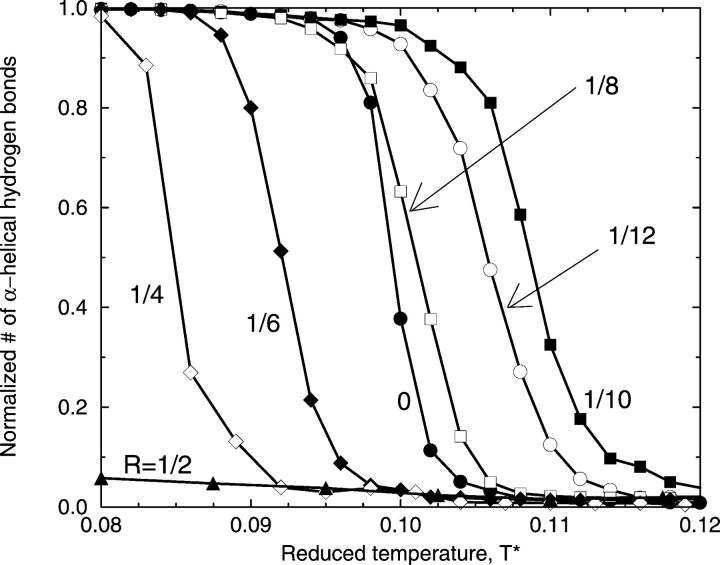
We now consider how the strength of the hydrophobic interaction between nonpolar side-chains affects the folding transition from the random coil to the native state. Figure 4 ▶ shows the percentage of α-helical hydrogen bonds formed (relative to the perfect α-helix value of 12) versus reduced temperature T* at different ratios R of the strength of the hydrophobic interaction (ɛ_HP) relative to that of the hydrogen bond, R ≡ɛ_HP/ɛ_HB. Notice that the reduced temperature T* measures not only temperature but also the strength of the hydrogen bond, ranging from strong hydrogen bonds at low T* (corresponding to deep N and C square wells) to weak bonds at high T* (corresponding to shallow N and C square wells). These results are average values calculated from a large ensemble of peptide configurations collected at each temperature during the replica-exchange simulations. Because the average errors, which are standard deviations from the average values at each temperature, are relatively small (on the order of those displayed in Fig. 3 ▶), we plot only the average values, omitting the error bars. When the hydrophobic interaction is absent (R = 0), which is equivalent to the vacuum condition, the midpoint of the folding transition (50% helicity) is at T* = 0.100, and the α-helical native state is the dominant conformation in the reduced temperature range of 0.080 to 0.095. When the hydrophobic interaction is present (equivalent to the presence of solution) at a low value (R = 1/12), the α-helical native state region expands to higher temperatures as the transition temperature shifts to T* = 0.106. In this case, turning on the hydrophobicity results in having 10 pairs of hydrophobic side-chains interact in the native α-helical structure, stabilizing an α-helical state that would otherwise be unstable in the absence of hydrophobicity. Increasing the level of hydrophobicity to R = 1/10 further stabilizes the α-helical state by increasing the midpoint of the folding transition to T* = 0.110. Increasing the level of the hydrophobic interaction further to R = 1/8, R = 1/6, and then R = 1/4 decreases the stability of the α-helical state as the midpoints of these folding transitions are at T* = 0.103, 0.092, and 0.085, respectively. Interestingly, the stability of the α-helical state at R = 1/8 is almost the same as that for the system without hydrophobicity because their folding transition midpoints are nearly the same. Increasing the level of the hydrophobic interaction further to R = 1/2 severely diminishes the ability of the peptide to form helices as indicated by the very low number of α-helical hydrogen bonds seen in the figure. In summary, the results in Figure 4 ▶ indicate that small amounts of hydrophobicity stabilize the α-helical native state of the model peptide, but large amounts of hydrophobicity prevent α-helix formation as the hydrophobic interactions overwhelm the system and trap the chain in nonnative structures.

Figure 4.

Percentage of α-helical hydrogen bonds formed as a function of T* at different ratios, R, of the strength of the hydrophobic interaction, ɛ_HP, relative to that of the hydrogen bond, ɛ_HB.

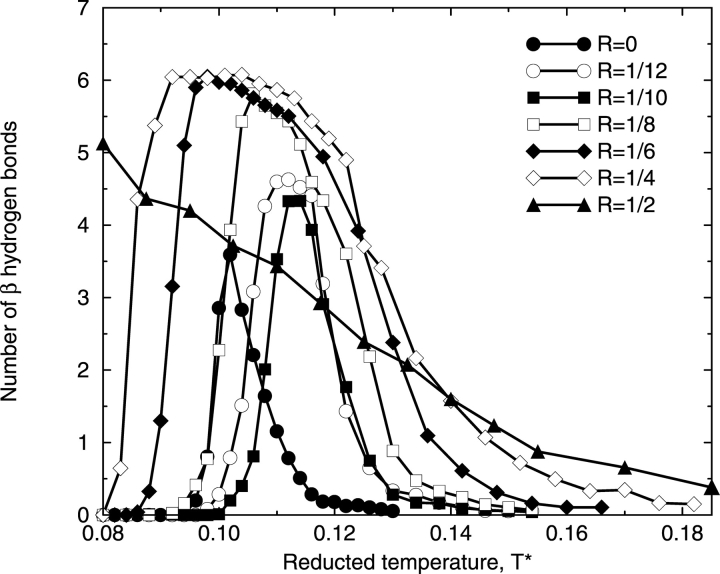
Increasing the hydrophobic interaction strength causes β hydrogen bonds to form at the expense of the α-helical hydrogen bonds. This is illustrated in Figure 5 ▶, which shows the number of β hydrogen bonds formed versus reduced temperature T* at different ratios R of the strength of the hydrophobic interaction (ɛ_HP) relative to that of the hydrogen bond (ɛ_HB). At low hydrophobic interaction strengths (R = 0, 1/12, and 1/10), the amplitude of each curve is less than five, meaning that most β-structures formed at these hydrophobic interaction strengths are not β-hairpins. As the hydrophobic interaction strength increases further to R = 1/8, 1/6, and then 1/4, the range of the β-structure temperature region expands and the amplitudes of the curves increase, indicating that the chains are likely to form even more β hydrogen bonds. The maximum number of β hydrogen bonds at these R values is well above the cut-off value for the β-hairpin structure, meaning that most β-structures formed over the β-structure temperature region at these hydrophobic interaction strengths are β-hairpins. As the hydrophobic interaction strength increases to R = 1/2, the trend with increasing R changes in that the β structures are no longer stable at intermediate temperatures but are instead stable at low temperatures. In addition to β-hairpins, β-sheet–like are formed at R = 1/2.

Figure 5.

Number of β-structure hydrogen bonds formed as a function of T* at different ratios, R, of the strength of the hydrophobic interaction, ɛ_HP, relative to that of the hydrogen bond, ɛ_HB.

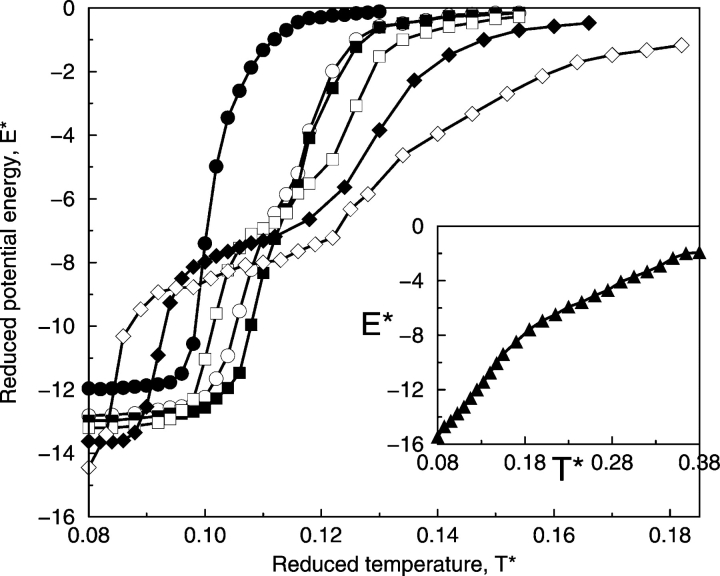
The strength of the hydrophobic interaction between side-chains affects the conformational transition between different states as can be seen in Figure 6 ▶, which shows the reduced potential energy of the system, E*, versus reduced temperature T* at different ratios of the strength of the hydrophobic interaction (ɛ_HP) relative to that of the hydrogen bond (ɛ_HB). The reduced potential energy of the system, E*, is the sum of the energy contributed by hydrogen bonds (the number of hydrogen bonds times ɛ_HB) and the energy contributed by hydrophobic interactions (the number of hydrophobic interactions times ɛ_HP) divided by ɛ_HB. At R < 1/2, the α-helical state is characterized by a reduced potential energy between −12.5 and −14.5 depending upon the value of R, the β-hairpin state is characterized by a reduced potential energy between −6.0 and −9.0, and the random-coil state is characterized by a reduced potential energy near 0. As indicated by Figure 6 ▶, when the hydrophobic interaction strength is weak (R = 0, 1/12, and 1/10), there is a relatively sharp transition from the random coil (E* = 0) at high temperatures to the α-helix at low temperatures. As the hydrophobic interaction strength increases up to R = 1/4, there is a significant expansion in the range of temperatures over which β-hairpins are found. In this case, the usual α-helix–random-coil transition is replaced by an α-helix–β-hairpin–random-coil transition. As the hydrophobic interaction strength increases up to R = 1/2, the potential energies of the α-helical and β-structure states, which include β-hairpins and β-sheet–like structures, are about the same at −16.0. However, as already discussed earlier with Figures 4 ▶ and 5 ▶, instead of forming an α-helix at low temperatures, the system forms β-hairpins and β-sheet–like structures (discussed below). In other words, as the hydrophobic interaction strength increases from R = 1/4 to R = 1/2, the potential energy of the β-structure states decreases, moving toward that of the α-helical state. Thus, the transition at R = 1/2 is between β-structure states at low temperatures and the random coil at high temperatures.

Figure 6.

Reduced potential energy of the system, E* = E/ɛ_HB as a function of T* at different ratios, R, of the strength of the hydrophobic interaction, ɛ_HB, relative to that of the hydrogen bond, ɛ_HB: R = 0 (filled circles), R = 1/12 (open circles), R = 1/10 (filled squares), R = 1/8 (open squares), R = 1/6 (filled diamonds), R = 1/4 (open diamonds), and R = 1/2 (filled triangles).

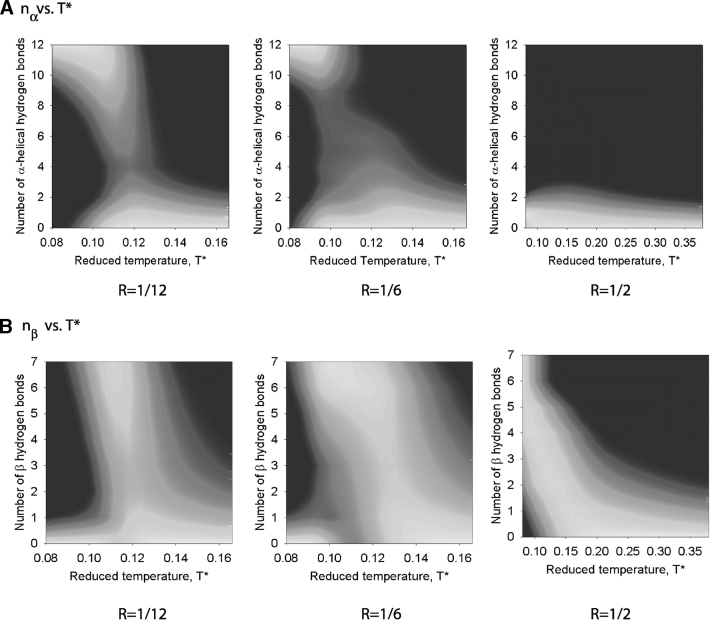
The conformational transitions found at different hydrophobic interaction strengths are displayed in Figure 7 ▶, which shows the probability of being in the different states as a function of the reduced temperature and (1) the number of α-helical hydrogen bonds (n_α) and (2) the number of β hydrogen bonds (n_β) at R = 1/12, 1/6, and 1/2. High values of the probability, P, correspond to the color white (P ≈e⁻¹), whereas low values of the probability correspond to the color black (P ≈e⁻⁵). At R = 1/12, Figure 7A ▶ indicates that there is a relatively broad region of low temperatures (T* = 0.08 to 0.10) over which the probability that n_α reaches its maximum value, n_α =12 in the α-helical state, is high. Figure 7B ▶ indicates that there is a relatively narrow range of intermediate temperatures (T* = 0.11 to 0.12) over which the probability that n_β reaches its maximum value, n_β =7 in the β-hairpin state, is high. When the hydrophobic interaction strength increases to R = 1/6, Figure 7A ▶ indicates that the low-temperature region over which n_α reaches its maximum value of n_α = 12 is considerably smaller (T* = 0.08 to 0.09) than that at R = 1/12. In contrast, Figure 7B ▶ indicates that the intermediate temperature region over which n_β reaches its maximum value of n_β = 7 is significantly larger (T* = 0.09–0.12) than that at R = 1/12. When the hydrophobic interaction strength increases further to R = 1/2, the probability that n_α is sizable is negligible as seen in Figure 7A ▶ over the whole temperature range. Instead of forming α-helical hydrogen bonds at low temperatures, high numbers, n_β = 7, of β hydrogen bonds are formed as seen in Figure 7B ▶.

Figure 7.

The conformational probability as a function of the number of α-helical hydrogen bonds n_α and T* (A) and the number of β hydrogen bonds n_β and T* (B) at R = 1/12, 1/6, and 1/2. High values of the probability, P, correspond to the color white (P ≈e⁻¹), whereas low values of the probability correspond to the color black (P ≈e⁻⁵)

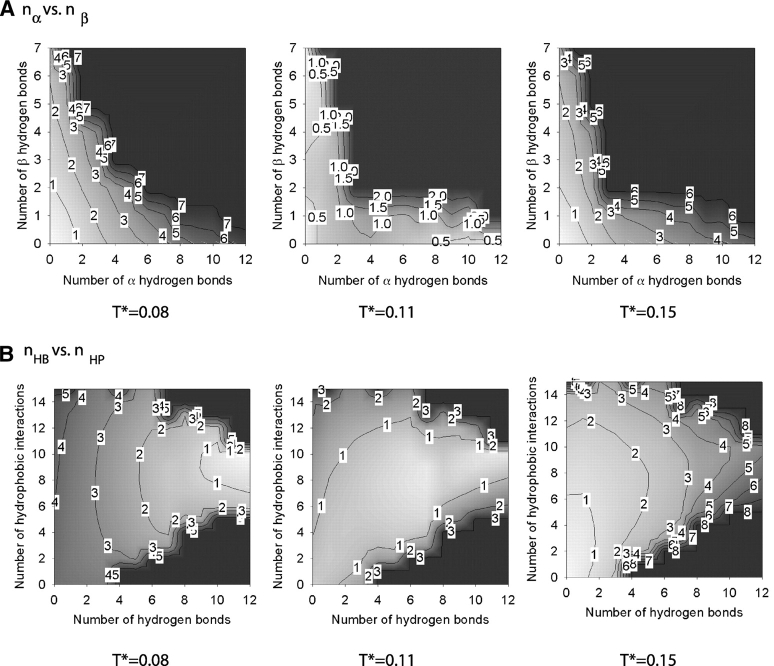
The free energy associated with the α-helix–random-coil transition at low hydrophobic interaction strengths, R = 1/12, has been calculated by using the weighted histogram method. The result is given in Figure 8 ▶, which shows iso-surface plots of (1) the free energy versus the number of α-helical (n_α) and β hydrogen (n_β) bonds, and (2) the free energy versus the total number of hydrogen bonds (n_HB) and the number of hydrophobic interactions (n_HP) at three temperatures T* = 0.08, 0.11, and 0.15. The colors white and black on these and subsequent graphs correspond to low values (starting from 0) and high values, respectively, of the free energy. Contour lines are labeled with a rounded-up value of the highest free energy in the enclosed region; for example, the lowest free energy region containing free energy values between 0 and 1 is labeled as 1. As previously seen in Figure 6 ▶, T* = 0.08 and 0.15 correspond to the lowest and highest temperatures at which the simulations at R = 1/12 were conducted, and T* = 0.11 corresponds to the transition temperature. The region in Figure 8A ▶ where n_α ≥ 8 and n_β ≤ 1 and the region in Figure 8B ▶ where n_HB ≥ 8 and 8 ≥ n_HP ≥ 10 belong to the α-helical state. The region where n_α < 1 and n_β > 5 in Figure 8A ▶ and the region where 5 < n_HB ≤ 7 and 8 ≤ n_HP ≤ 12 in Figure 8B ▶ belong to the β-hairpin structure. The region where n_α < 3 and n_β < 3 in Figure 8A ▶ and the region where n_HB < 3 and n_HP < 4 in Figure 8B ▶ belong to the random-coil state. At T* = 0.08, the α-helical state has the lowest free energy, which corresponds to the white region enclosed by a line with a free energy value of one, the β-hairpin state has the second lowest free energy, and the random-coil state has the highest free energy. At T* = 0.15, the random coil has the lowest free energy. In other words, at the two extreme temperatures, the system exhibits two distinct states. At the intermediate temperature, the third state—the β-hairpin—does exist as seen in plots at T* = 0.11 but does not dominate in that it has a similar free energy to that in the other two states.

Figure 8.

The Helmholz free energy of the system at R = 1/12 as a function of the number of α-helical hydrogen bonds n_α and the number of β hydrogen bonds n_β (A) and the total number of hydrogen bonds n_HB and the number of hydrophobic interactions n_HP (B) at three temperatures. The colors white and black correspond to low values (starting from 0) and high values, respectively, of the free energy. Contour lines are labeled with a rounded-up value of the highest free energy in the enclosed region.

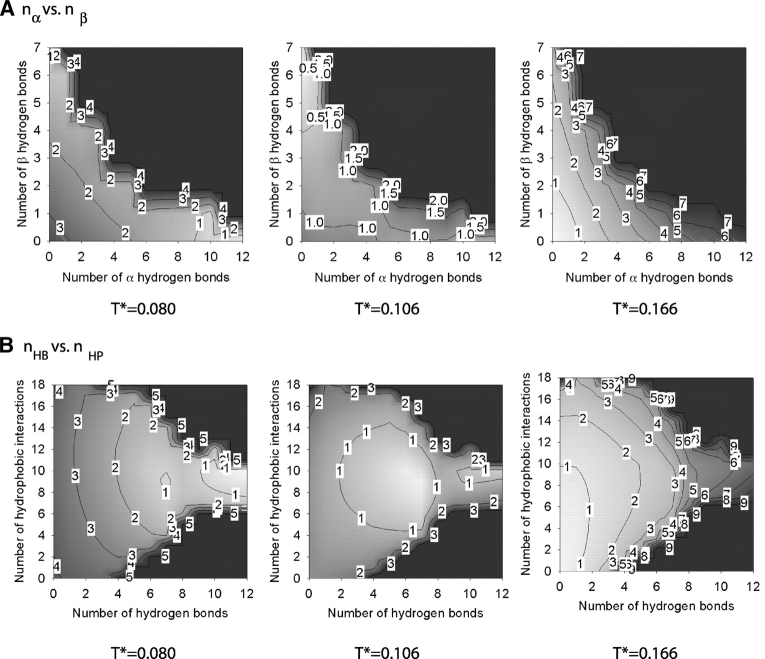
The free energy associated with the α-helix–β-hairpin–random-coil transition at intermediate hydrophobic interaction strengths, R = 1/6, is shown in Figure 9 ▶, which depicts isosurface plots of the free energy versus (1) the number of α-helical (n_α) and the number of β hydrogen bonds (n_β), and (2) the total number of hydrogen bonds (n_HB) and the number of hydrophobic interactions (n_HP) for the system at R = 1/6 at three temperatures, T* = 0.080, 0.106, and 0.166. As previously seen in Figure 6 ▶, T* = 0.080 and T* = 0.166 correspond to the lowest and highest temperatures at which the simulations at R = 1/6 were conducted; T* = 0.106 corresponds to an intermediate temperature. As indicated by Figure 9 ▶, the α-helical state is the most stable structure at T* = 0.080, whereas the random-coil state is the preferred structure at T* = 0.166. At T* = 0.106, the α-hairpin state has the lowest free energy as indicated by the red area in Figure 9 ▶. In other words, at the two extreme temperatures, the system exhibits two distinct states but at the intermediate temperature T* = 0.106, the third state—a β-hairpin—dominates.

Figure 9.

The Helmholz free energy of the system at R = 1/6 as a function of the number of α-helical hydrogen bonds n_α and the number of β hydrogen bonds n_β (A) and the total number of hydrogen bonds n_HB and the number of hydrophobic interactions n_HP (B) at three temperatures. The colors white and black correspond to low values (starting from 0) and high values, respectively, of the free energy. Contour lines are labeled with a rounded-up value of the highest free energy in the enclosed region.

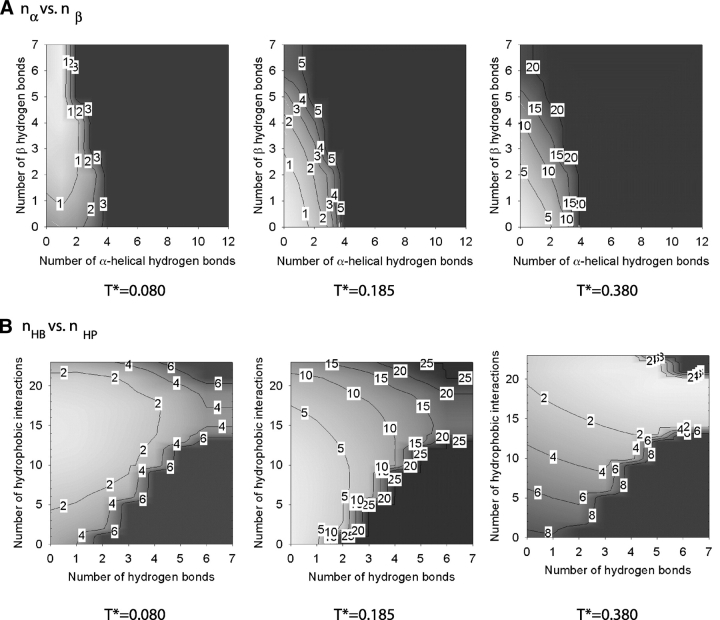
The free energy associated with the β-structure states—random-coil transition at high hydrophobic interaction strengths, R = 1/2, is shown in Figure 10 ▶, which depicts isosurface plots of the free energy versus (1) the number of α-helical (n_α) and the number of β hydrogen bonds (n_β), and (2) the total number of hydrogen bonds (n_HB) and the number of hydrophobic interactions (n_HP) for the system at R = 1/2 at three temperatures T* = 0.080, 0.185, and 0.380. At T* = 0.080, the polyalanine peptide is in multiple β-structure states with three to seven β hydrogen bonds and >13 hydrophobic interactions. In addition to β-hairpins, other β-like structures such as those shown in Figure 2 ▶ are observed. These structures have more than one β-turn with less β hydrogen bonds but more hydrophobic interactions than those found in a β-hairpin. Therefore, they are more compact than β-hairpins. At T* = 0.185, states with two or less β hydrogen bonds and eight to 20 hydrophobic interactions are found; these are amorphous without any secondary structure. At T* = 0.380, the polyalanine peptide is a random coil with no β hydrogen bonds and low numbers of hydrophobic interactions.

Figure 10.

The Helmholz free energy of the system at R = 1/2 as a function of the number of α-helical hydrogen bonds n_α and the number of β hydrogen bonds n_β (A) and the total number of hydrogen bonds n_HB and the number of hydrophobic interactions n_HP (B) at three temperatures. The colors white and black correspond to low values (starting from 0) and high values, respectively, of the free energy. Contour lines are labeled with a rounded-up value of the highest free energy in the enclosed region.

There are two factors that decide whether the polyalanine peptide will fold into an α-helix or a β-structure: enthalpy and entropy. Although the α-helix state has more intrapeptide hydrogen bonds than do the β-structure states (the maximum is 12 compared with seven), it has a fixed number of hydrophobic interactions that are specific between certain residues, whereas β-structures have a large ensemble of different states with different numbers of hydrophobic interactions that are relatively flexible. A measure of the number of states available to the system and hence the entropy is the size of the area occupied by these states in Figures 8 ▶, 9, ▶ and 10 ▶. For example, the area in Figures 8B ▶, 9B ▶, and 10B ▶ occupied by the β-structure states is noticeably larger than the area occupied by other states, which means that the entropy for the β-structure states is relatively large. As the hydrophobicity is increased, the enthalpies of both the α-helix and β-structure states decrease; however, the decrease in the enthalpy of the β-structure states is more significant than that of the α-helical state because the β-structure states can increase their number of hydrophobic interactions. In fact, the enthalpy of the β-structure states decreases toward that of the α-helical state as R increases (Fig. 6 ▶). At low-to-intermediate hydrophobic interaction strengths (R < 1/2) and low temperature, the α-helical state has the lowest enthalpy, which, because T* is low, is the most dominant contribution to the free energy; therefore, it is stable, having the lowest free energy at low temperatures. However, as the temperature increases toward intermediate temperatures, the entropy starts to play an important role in lowering the free energy and thus stabilizing the β-structure states, especially the β-hairpin state. As the hydrophobic interaction strength increases to R = 1/2, the enthalpy of the β-structure states decreases below that of the α-helical state, causing the β-structure states to have the lowest enthalpy, which, coupled with their high entropy, means that the β-structure states have the lowest free energy over a wide range of temperatures (both intermediate and low). In other words, increasing the hydrophobicity stabilizes the β-structure states and thus destabilizes the α-helical state.

Discussion

In this work, we presented a study of the folding thermodynamics of a model polyalanine peptide by using an improved version of our previously developed intermediate-resolution protein model in conjunction with DMD simulations. The focus was on how the solvent condition, as measured by the strength of the hydrophobic interaction between nonpolar side-chains and temperature, affects the conformational transitions of the peptide. We observe that the environment has a significant effect on the stability of the various structures, α-helix, β-structures (including β-hairpins and β-sheet–like structures), and random coil, at different temperatures. At low hydrophobic interaction strength, the peptide exhibits a two-state folding transition in which the α-helical state is the most stable structure at low temperatures and the random-coil state is the most stable state at high temperatures. At intermediate hydrophobic interaction strength, the β-hairpin state is introduced, resulting in an α-helical conformation at low temperatures, a β-hairpin at intermediate temperatures, and a random coil at high temperatures. At very high values of the hydrophobic interaction strength, the peptide folds via a two-state mechanism in which different types of β-structures, including β-hairpin and β-sheet–like structures, are the most stable structures at low temperatures and the random-coil state is the most stable state at high temperatures. Although there is no experimental evidence for the α-β transition in polyalanines as temperature changes, there are experiments that show that polyalanine adopts an α-helical conformation in hydrophobic environments such as the solid state or in nonpolar organic solutions and a β-structure conformation in polar aqueous solution (Ingwall et al. 1968; Platzer et al. 1972; Shoji et al. 1990; Blondell et al. 1997; Kimura et al. 1998^; Lee and Ramamoorthy 1999^; Warrass et al. 2000). This is also observed in experiments on many heterogeneous peptides that can be folded into alternative stable structures by changing the solution conditions such as the pH, salt, or organic cosolvent concentration; peptide concentration; and the redox state (Rosenheck and Doty 1961; Kabsch and Sander 1984; Mutter and Hersperger 1990; Mutter et al. 1991; Reed and Kinzel 1991; Zhong and Johnson 1992; Cohen et al. 1993; Dado and Gellman 1993; Waterhous and Johnson 1994; Cerpa et al. 1996; Fukushima 1996; Schenck et al. 1996; Zhang and Rich 1997; Tuchscherer et al. 1999; Awasthi et al. 2001; Wildman et al. 2002). Although there are many computer simulation studies in which the transition between α-helix and random coil of polyalanines is observed (Okamoto and Hansmann 1995; Vila et al. 1998; Hansmann and Okamoto 1999; Alves and Hansmann 2000; Mitsutake and Okamoto 2000; Alves and Hansmann 2001; Garcia and Sanbonmatsu 2002; Olivella et al. 2002; Peng and Hansmann 2002; Ghosh et al. 2003; Ohkubo and Brooks III 2003; Peng et al. 2003), there are only two studies thus far that predict the formation of both α-helix and β-structures (Levy et al. 2001; Ding et al. 2003). The vast majority of simulation studies by other investigators mentioned here are based on all-atom models, which prevents them from exploring transitions between different peptide structures over a wide range of solvent conditions and temperatures. Recently, simulations by Vila et al. (2000); Hansmann, Okamoto, and coworkers (Mitsutake and Okamoto 2000; Peng and Hansmann 2002; Peng et al. 2003); and Olivella et al. (2002) on polyalanines have been conducted over a wide range of temperatures but only in the presence and absence of the solvent. They showed that intrahelical hydrogen bonds are weakened in the presence of polar solvent, which might suggest that other non-helical interactions such as β hydrogen bonds are preferred. Recently, published experimental and simulation results (Shi et al. 2002; Gnanakaran and Garcia 2003) have showed that polyproline-II–like structures dominate over the α-helical structure at low temperatures for short alanine peptides up to seven residues. For longer alanine peptides, the α-helical structures dominate over polyproline II–like structures. In this work, polyproline-II–like structures were observed for the Ac-KA₁₄K-NH₂ peptide but at a quite low population (<1%).

It is important to point out that our model and analysis are subject to a number of limitations. Although the backbone of our model is detailed enough to display genuine protein character, the model side-chains are very simplified. Our model can account for the hydrophobic force by allowing side-chain beads to be either hydrophobic or polar but ignores other aspects of side-chain character including charge. Another shortcoming of the model is the lack of solvent. We incorporate solvent as a potential of mean force, which means that all chain beads are equally affected by “solvent” regardless of the chain conformation. Consequently, beads in the interior of a compact structure are just as affected by solvent as they would be if they were fully exposed in a random-coil structure. A more accurate solvation model would allow forces such as the hydrogen bonding force in the core of a collapsed chain to be different from those at the surface. It is unclear, however, that this shortcoming is critical in the work presented here because our peptides are so small that the concept of a “core” is hard to define. Despite these limitations, our model allows us to conduct simulations over a wide range of solvent conditions and temperatures because of its speed. Ongoing research in our group is aimed at using this simple protein model to study the effects of varying the temperature, peptide concentration and hydrophobic interaction strength on the formation of ordered aggregates, for example, fibrils, in multiprotein environments.

Materials and methods

Model peptide and forces

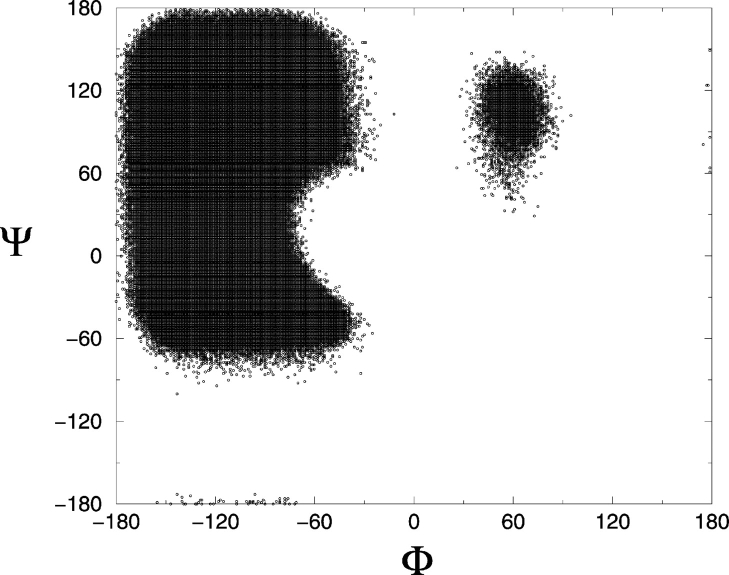
The model peptide is 16 residues long with the sequence PH14P, where H stands for a hydrophobic amino acid residue and P stands for a polar amino acid residue. This sequence was chosen to approximate Ac-KA₁₄K-NH₂ peptides, which have been shown by Blondelle and coworkers (Forood et al. 1995; Blondelle et al. 1997) to form stable, soluble β-sheet complexes. The peptide is represented at an intermediate level of resolution by using a model introduced by Smith and Hall (2001a^,b,c). Details of the model, including values for all parameters, are given in earlier articles. The model is based on a four-bead amino acid representation with realistic bond lengths and bond-angle constraints and has the ability to interact both intra- and intermolecularly via hydrogen bonding and hydrophobic interaction potentials. The geometry of the protein model is illustrated in Figure 11 ▶. Each amino acid residue is composed of four spheres, a three-sphere backbone comprised of united atom NH, C_αH, and C = O, and a single bead side-chain R (these are labeled N, C_α, C, and R, respectively in the figure). All backbone bond lengths and bond angles are fixed at their ideal values; the distance between consecutive C_α atoms is fixed so as to maintain the interpeptide bond in the trans configuration. The side-chains are held in positions relative to the backbone such that all residues are L-isomers. The solvent is modeled implicitly in the sense that its effect is factored into the energy function as a potential of mean force. All forces are modeled by either hard-sphere or square-well potentials. The excluded volumes of the four beads in each residue are modeled by using hard-sphere potentials with realistic diameters. Covalent bonds are maintained between adjacent spheres along the backbone by imposing hard sphere repulsions whenever the bond lengths attempt to move outside of the range between (l − δ) and (l + δ) where l is the bond length and δ is a tolerance. Ideal backbone bond angles, C_α-C_α distances, and residue L-isomerization are achieved by imposing pseudobonds as shown in Figure 11 ▶, which also fluctuate within a tolerance δ. In previous studies (Smith and Hall 2001a,b,c), the bond length and pseudobond tolerance δ were fixed at 2.0%, producing a relatively restricted region of sterically allowed Φ–Ψ space confined to the left side of the Ramachandran plot (Smith and Hall 2001a). In the present study, the bond length and pseudobond tolerance δ are relaxed to a value of 2.375%, producing a more realistic Ramachandran plot. This is seen in Figure 12 ▶, which shows a plot of Φ versus Ψ from our simulation on a peptide with small, alanine-sized side-chain residues. The sterically allowed region of Φ–Ψ space on the left side of the Ramachandran plot is larger than in our previous article. The shape of this region agrees better with standard, published data that describe the regions of sterically allowed Φ–Ψ space in real proteins (Voet and Voet 1990). All secondary structures including polyproline II and the lefthand α-helix (right side of plot) (Voet and Voet 1990) are observed in these simulations.

Figure 11.

Geometry of the intermediate resolution protein model for polyalanine. Covalent bonds are shown with narrow solid lines connecting beads. At least one of each type of pseudobond is shown with a thick disjointed line. Pseudobonds are used to maintain backbone bond angles, consecutive C_α distances, and residue L-isomerization. Note that the united atoms are not shown full size for ease of viewing.

Figure 12.

Ramachandran plots for simulations of alanine residues based on the bond length and pseudo-bond tolerance at 2.375%.

Hydrogen bonding between amide hydrogen atoms and carbonyl oxygen atoms on the same or neighboring chains is represented by a square-well attraction, the depth of which is ɛ_HB and range is 1.5σ_R where σ_R is the side-chain bead diameter between NH and C = O united atoms whenever (1) the virtual hydrogen and oxygen atoms (the location of which can be calculated at any time) are separated by 4.2 Å (the sum of the NH and C = O well widths), (2) the nitrogen-hydrogen and carbon-oxygen vectors point toward each other within a fairly generous tolerance, and (3) neither the NH nor the C = O is already involved in a hydrogen bond with a different partner. Smith and Hall (2001a^,b,c) satisfied the second requirement above by determining the locations of the virtual oxygen and hydrogen atoms based on the vector projections as shown by the arrow tips in Figure 13 ▶ and by stipulating that both the NHO and the COH angles be between 120° and 180°. In this article, we adopt an approach similar to that of Ding et al. (2003) and require that the four atom pairs N_i–C_α,j, N_i–N_{j + 1}, C_j–C_αi, C_j–C_{i − 1} shown connected by thick dashed lines in Figure 13 ▶ (hereafter referred to as auxiliary pairs), be separated by distances d that are chosen to maintain the hydrogen bond angle constraints; their values are given in Table 2. Upon the formation of a bond between N_i and C_j, these auxiliary pairs temporarily interact via a single-step square-shoulder potential:

Figure 13.

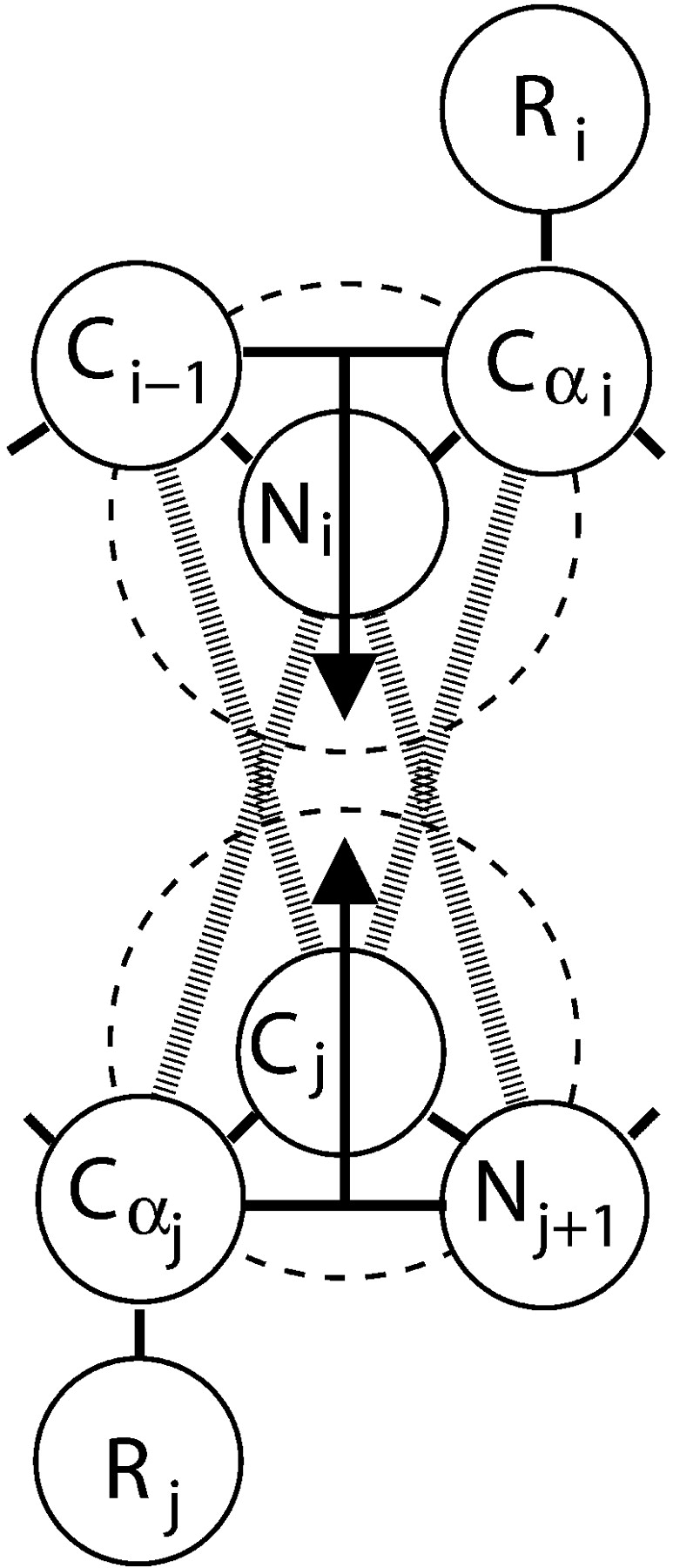
Backbone hydrogen bonding is achieved through a square-well interaction between N_i and C_j. The dashed circles symbolize the square-well attractive shells around N_i and C_j. The location of H_i can be determined by examining the geometry of C_i−1, N_i, and C_α,i and then projecting down through N_i as shown by the arrow. The location of O_j can be determined by examining the geometry of C_α,j, C_j, and N_j+1 and then projecting up through C_j as shown by the arrow. The thick disjointed lines symbolize the square-shoulder interactions between auxiliary pairs N_i - C_α,j, N_i - N_j+1, C_j - C_αi, and C_j - C_i−1.

Table 2.

Parameter d

Pairs	d(Å)
Ni–Cα,j	5.00
N i −Nj+1	4.74
Cj −Cα,j	4.86
C j–Ci−1	4.83

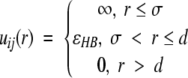where r is the distance between beads i and j; σ is the bead diameter; ɛ_HB is the shoulder height, which is equal to the well depth of the hydrogen bond between N_i and C_j; and d is the square-shoulder width. This interaction is more efficient computationally than that of Ding et al. (2003), who used a two-step square-shoulder potential to maintain hydrogen bond angles. In addition to preventing the hydrogen bond angles from straying outside of the desired values, the square-shoulder interaction within each auxiliary pair adds stability to the hydrogen bond by increasing the range of the repulsive forces between the beads that neighbor N_i and C_j as was done previously by Takada et al. (1999) and by Smith and Hall (2001a^,b,c). These auxiliary pairs return to their original interactions when the hydrogen bond is broken.

Interactions between hydrophobic side-chains are represented by a square-well potential of depth ɛ_HP and range 1.5σ_R, where σ_R is the side-chain bead diameter. Hydrophobic side-chains must be separated by at least three intervening residues in order to interact. The strengths of the hydrophobic contact, ɛ_HP, considered in this article are 0, 1/12, 1/10, 1/8, 1/6, 1/4, and 1/2 the strength of a hydrogen bond, ɛ_HB. Hydrogen bond strength and hydrophobic contact strength are independent of temperature, as has been assumed in previous simulation studies (Irback et al. 2000; Smith and Hall 2001b,c; Chen et al. 2003).

Discontinuous molecular dynamics

Simulations are performed by using the DMD simulation algorithm (Alder and Wainwright 1959; Rapaport 1978 Rapaport 1979; Bellemans et al. 1980), which is an extremely fast alternative to traditional molecular dynamics and is applicable to systems of molecules interacting via discontinuous potentials, for example, hard-sphere and square-well potentials. DMD simulations are conducted as follows. Each bead of the model protein chain is assigned a random initial position and a random initial velocity that do not violate any of the size constraints or assigned bond lengths and angles. The initial velocities are chosen at random from a Maxwell-Boltzmann distribution at a specified reduced temperature, T* = k_BT/ɛ_HB, where k_B is Boltzmann’s constant, T is temperature, and ɛ_HB is the strength of the hydrogen bond in the model as explained earlier. When a DMD simulation begins, each bead moves with its individual velocity. The simulation proceeds according to the following schedule: identify the first event, move forward in time until that event occurs, calculate new velocities for the pair of beads involved in the event and calculate any changes in system energy resulting from hydrogen bond events or hydrophobic interactions, find the second event, and so on. Types of events include excluded volume events, bond events, and square-well hydrogen bond and hydrophobic interaction events. An excluded volume event occurs when the surfaces of two hard-sphere beads collide and repel each other. A bond (or pseudobond) event occurs via a hard-sphere repulsion when two adjacent spheres attempt to move outside of their assigned bond length. Square-well events include well-capture, well-bounce, and well-dissociation “collisions” when a sphere enters, attempts to leave, or leaves the square well of another sphere. For more details on DMD simulations with square-well potentials, see articles by Alder and Wainwright (1959) and Smith et al. (1997).

Simulations are performed in the canonical ensemble, which means that the number of particles, volume, and temperature are held constant. Periodic boundary conditions are used to eliminate artifacts due to simulation box wall effects. The dimensions of the box are chosen to ensure that a chain cannot interact with more than one image of any other chain. For this study, we use a cubic box with sides 100 Å in length. Constant temperature is achieved by implementing the Andersen thermostat method (Andersen 1980) as was used previously (Zhou et al. 1997; Smith and Hall 2001a). With this procedure, all beads in the simulation are subject to random collisions with ghost particles. The postevent velocity of a bead colliding with a ghost particle is chosen randomly from a Maxwell-Boltzmann distribution at the simulation temperature.

Replica-exchange DMD/MC method

The replica-exchange method is implemented with 26 replica systems distributed over a broad interval of temperature ranging from T* = 0.08 to a high temperature at which the peptide is a total random coil. Each replica system is simulated at a different temperature, T, in the canonical ensemble by using the DMD method. The number of replicas and the distribution of temperatures are chosen to ensure that (1) there is a free random walk in temperature space, which means that every replica has the same probability of being switched to a neighboring temperature; (2) the number of replicas and hence temperatures sampled must be high enough to ensure that the probability of each replica being switched to a neighboring temperature is >10%; and (3) the highest temperature sampled must be high enough to prevent the system from becoming trapped in a local energy minimum. These requirements are the same as those stated by Sugita and Okamoto (1999). At fixed time intervals, replicas are sorted from lowest to highest temperature and subjected to the following temperature exchange MC procedure. Systems i and j, with neighboring temperatures T_i and T_j, respectively, can exchange configurations (system i changes to temperature T_i and system j to temperature T_j) with probability:

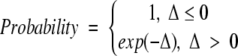Where Δ = [β_j - β_i](U_i - U_j), with β_{i =} 1/(k_BT_i) and U_i the potential energy of the system in state i. Initially, each system is in a random configuration obtained from an NVT simulation at high temperature. Exchange attempts occur every 20.0 reduced time units, where the reduced time is defined as t* ≡ t/σ (k_BT/m)^1/2, where t is the simulation time, and σ and m are the average bead diameter and mass; this corresponds to approximately five million collisions at each low temperature and six million collisions at each high temperature. Approximately 1000 replica-exchange attempts are made during our simulations before equilibrium is reached. Our equilibrium criteria require that the ensemble averages of the system’s total potential energy, which is collected at the end of each DMD run, vary by no >2.5% during the second half of all DMD runs at each temperature. Once equilibrium is reached, the data collection phase begins, in which 300 extra replica-exchange attempts are made. During the data collection phase, the properties of interest at each temperature are calculated throughout each DMD run. In addition, the probability of being in different energy levels and states is stored for conformational free energy calculations of the different thermodynamic properties of interest by using the weighted histogram method. At the end of the replica-exchange DMD/MC simulation, our data contain a large ensemble of peptide configurations at each temperature. Our simulations last for a long time, taking more than six billion collisions at each low temperature and eight billion collisions at each high temperature. A replica-exchange DMD/MC simulation at a single hydrophobic interaction strength requires 25 d on a single processor of an AMD Athlon MP 2200+ workstation.

Weighted histogram method

The conformational free energy of the various structures of the peptide is calculated by using the weighted histogram method (Ferrenberg and Swendsen 1989; Zhou et al. 1997) in order to determine the thermodynamic stability of each structure at different solvent conditions. The weighted histogram method is a least-squares optimization method that allows the calculation of degeneracy factors from simulations at several temperatures, which can then be used to calculate the thermodynamic properties of interest. In this method, each peptide conformation (state) is expressed in terms of the number of α-helical hydrogen bonds, i; the number of β-structure hydrogen bonds, j; and the number of hydrophobic interactions, k. The conformational free energy, A_i,j,k(T_l), in each energy state at temperature T_l can be calculated from the degeneracy factor g_i,j,k for the energy levels in energy state (i,j,k). For more details of our weighted histogram calculations, see an article by Zhou et al. (1997).

One can use the Helmholtz conformational free energy A_i,j,k(T_l) to compare the free energy of the various energy states. To facilitate the comparison, the conformational free energy A_i,j,k(T_l) in each energy state is broken down into two terms, A_i,j(T_l) and A_m,k(T_l). A_i,j(T_l) is the conformational free energy associated with the numbers of α-helical, i, and β-structure hydrogen bonds, j, regardless of the number of hydrophobic interactions, k. A_m,k(T_l) is the conformational free energy associated with the total number of hydrogen bonds, m, and the number of hydrophobic interactions, k. Here m is the sum of the number of α-helical and β hydrogen bonds (m = i + j), with the possible maximum number of hydrogen bonds being M = 12. In the Results section, A_i,j(T_l) and A_m,k(T_l) are presented in isosurface plots to compare the con-formational free energy of the various structures at different temperatures.