To be folded or to be unfolded?

Abstract

The lack of ordered structure in “natively unfolded” proteins raises a general question: Are there intrinsic properties of amino acid residues that are responsible for the absence of fixed structure at physiological conditions? In this article, we demonstrate that the competence of a protein to be folded or to be unfolded may be determined by the property of amino acid residues to form a sufficient number of contacts in a globular state. The expected average number of contacts per residue calculated from the amino acid sequence alone (using the average number of contacts for 20 amino acid residues in globular proteins) can be used as one of the simple indicators of natively unfolded proteins. The prediction accuracy for the sets of 80 folded and 90 natively unfolded proteins reaches 89% if the expected average number of contacts is used as a parameter and 83% in the case of hydrophobicity. An optimal set of artificial parameters for 20 amino acid residues obtained by Monte Carlo algorithm to maximally separate the sets of 90 natively unfolded and 80 folded proteins demonstrates the upper limit for prediction accuracy, which is 95%.

The goal of many studies is to find and define the structural and sequence features that are common to some class of proteins. The knowledge of such characteristics is of a paramount importance for comparative sequence analysis, for the de novo design of a protein, and for three-dimensional structure prediction methods. It is reasonable to suppose that proteins grouped together on the basis of a common architecture would reveal some commonality on the level of primary structure as well.

“Natively unfolded” proteins belong to the group of proteins lacking ordered structure under conditions of neutral pH in vitro. At this time, there are enough data on unstructured proteins possessing definite functional activity (Wright and Dyson 1999; Uversky et al. 2000; Uversky 2002). Understanding the reason why some proteins folded but others unfolded at physiological conditions is especially important, because for the de novo design of a protein, it is necessary to know what features of its primary structure define whether the protein will be folded or unfolded.

It was suggested that the lack of rigid globular structure under physiological conditions might represent a considerable functional advantage for natively unfolded proteins, as their large plasticity allows them to interact efficiently with several different targets, as compared to a folded protein with limited conformational flexibility (Wright and Dyson 1999; Dyson and Wright 2002). It was shown that a large portion of the sequences of natively unfolded proteins contains segments of low complexity and high predicted flexibility (Wootton 1994; Dunker et al. 1998; Romero et al. 1998, 1999; Galzitskaya et al. 2000; Obradovic et al. 2003; Vucetic et al. 2003; Radivojac et al. 2004). It was also indicated that a combination of low overall hydrophobicity and a large net charge represent a structural feature of natively unfolded proteins in comparison with small globular proteins (Uversky et al. 2000; Uversky 2002). However, it is not clear whether these parameters will be important for comparing natively unfolded proteins with a set of globular proteins without restriction on their length.

The structural uniqueness of native globular proteins is the result of the balance between the conformational entropy and the energy of residue interactions. It seems that natively unfolded proteins have no sufficient energetic interactions to compensate conformational entropy, resulting in the formation of globular state. Therefore, enhanced stabilization for them is achieved by additional interactions with other agents or by oligomerization.

In this work we suggest a simple indicator of natively unfolded proteins. It is the expected average number of contacts per residue calculated from the amino acid sequence alone. Here we have used the property of amino acid residues to form a sufficient number of contacts in a globular state to reduce conformational entropy. We have demonstrated that this parameter can define whether a protein will be folded or unfolded for the sets of 80 folded proteins and 90 natively unfolded ones with an accuracy of 89%, which exceeds that of hydrophobicity (83%). Moreover, we have obtained an optimal set of artificial parameters for 20 amino acid residues by using a Monte Carlo procedure to maximally separate natively unfolded and globular proteins. It is interesting that this set of parameters has a larger correlation with the number of contacts per residue than does the other set of structural parameters.

Results

The databases of proteins

We have created an “ideal” database of 80 globular X-ray-resolved proteins satisfying the general condition that the domain structure of protein is stable without additional interactions with other molecules or agents (for other additional conditions, see Materials and Methods) as a result of a fully exploited wealth of data available in the Protein Data Bank (PDB) (Bernstein et al. 1977) and SCOP (Murzin et al. 1995). The length of proteins in our database varies from 54 to 500 residues. The database of 80 globular X-ray structures is available at http://phys.protres.ru/~mlobanov/prot-base/ideal-base/.

The other set of structures has been obtained by inspection of the SCOP database (Murzin et al. 1995) 1.61 release, and 6626 domains have been found from seven general classes (a–g; see Materials and Methods). This database of structures has been used to calculate the average number of contacts per residue for 20 amino acid residues (see Table 1).

Table 1.

Properties of amino acid residues

Amino acid residue	G	P	A	D	E	K	S	N	Q	T	R	H	C	V	M	L	I	Y	F	W
No. of contacts	17.11	17.43	19.89	17.41	17.46	17.67	18.19	18.49	19.23	19.81	21.03	21.72	23.52	23.93	24.82	25.36	25.71	25.93	27.18	28.48
Artificial parameters	−7.73	−8.27	−2.37	−12.55	−8.96	−4.63	−5.03	0.18	−1.85	−8.15	−7.36	−8.13	−9.20	11.49	3.66	6.50	10.46	9.05	19.46	23.43

The database of 90 natively unfolded proteins was created using the names of natively unfolded proteins from the work of Uversky et al. (2000) and from the SWISS-PROT protein sequence data bank (Bairoch and Apweiler 2000).

The expected average number of contacts per residue for globular and unfolded proteins

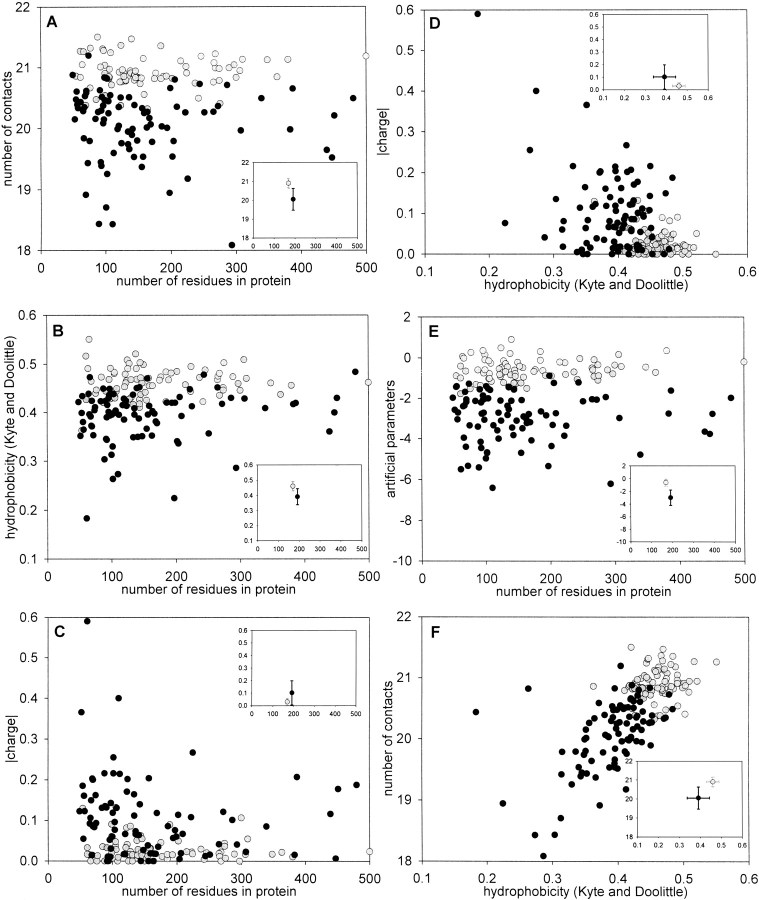
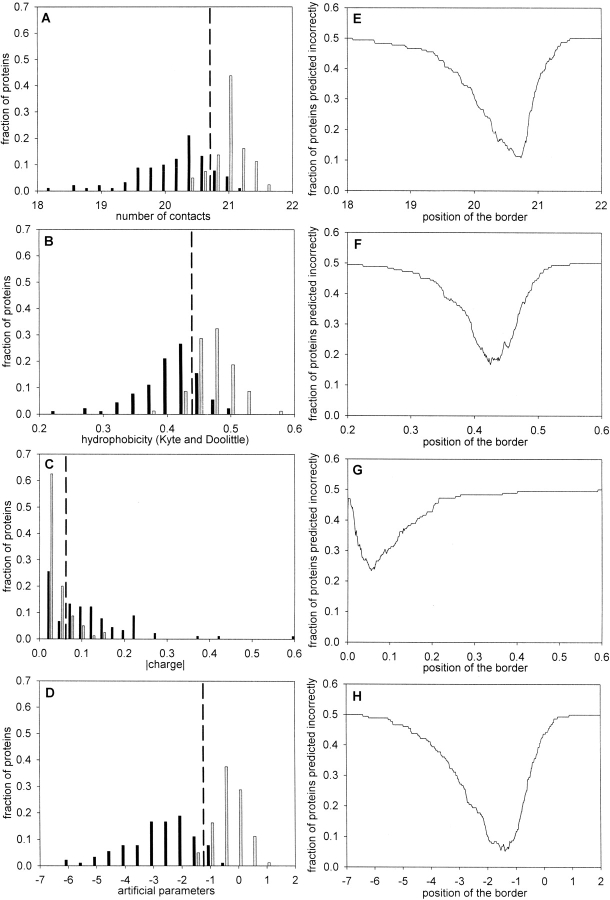
To examine whether the expected average number of contacts per residue has a correlation with the state of protein to be folded or unfolded, we analyzed proteins taken from our ideally folded database and from a paper by Uversky et al. (2000), in which their natively unfolded states are explained by low overall hydrophobicities and large net charges. Figure 1A ▶ demonstrates that statistically significant differences between the sets of 80 ideally folded proteins and 90 natively unfolded proteins are achieved if using the expected average number of contacts per residue calculated from amino acid sequence alone. Figure 2A ▶ shows a histogram representing the distribution of natively unfolded proteins and folded proteins as a function of the expected number of contacts per residue. Moreover, Figure 2E ▶ shows the dependence of the fraction of proteins predicted incorrectly on the border position of the expected average number of contacts per residues between two sets of proteins. The minimum value corresponding to 11% is achieved at 20.73 contacts per residue. This indicates that the average number of contacts per residue is a significant contributing factor in determining whether a protein will be folded or unfolded.

Figure 1.

Comparison of the mean values of different parameters computed from sequence alone for the set of 90 “natively unfolded” proteins (black circles) and for the set of 80 “ideally” folded proteins (gray circles). All parameters presented here are averaged per residue; one circle corresponds to one protein. Dependence of (A) expected number of contacts, (B) hydrophobicity in the Kyte and Doolittle (1982) scale, and (C) absolute magnitude of net charge on the number of residues in protein. (D) Dependence of net charge on hydrophobicity. (E) Dependence of the optimal set of artificial parameters on the number of residues in protein. (F) Dependence of expected number of contacts on hydrophobicity. Inset demonstrates the standard deviations for considered parameters.

Figure 2.

Histograms representing the distribution of 90 “natively unfolded” proteins (black bars) and 80 “ideally” folded proteins (gray bars) as a function of (A) expected number of contacts, (B) hydrophobicity on the Kyte and Doolittle (1982) scale, (C) absolute magnitude of net charge, and (D) optimal set of artificial parameters. The dashed line representing the optimal border between two groups of proteins is placed in the intersection of their distributions. The dependence of the fraction of proteins predicted incorrectly (i.e., native proteins predicted as natively unfolded and vice versa) on the border position of considered parameters between two sets of proteins: (E) for expected number of contacts, (F) for hydrophobicity, (G) for absolute magnitude of net charge, and (H) for optimal set of artificial parameters.

The average number of C and S atoms, hydrophobicity, and charge per residue for globular and unfolded proteins

We calculated several structural parameters such as volume, number of atoms, number of C and S atoms, hydrophobicity, and charge for ideally globular and natively unfolded proteins to answer the question of whether there is a significant difference between the average values of calculated parameters for unfolded and globular proteins. The results of these comparisons are presented in Table 2. A significant difference between two databases can be obtained considering such a structural parameter as hydrophobicity for both scales analyzed here.

Table 2.

Structural parameters calculated per residue for 90 “natively unfolded” and 80 “ideally” folded proteins

						Hydrophobicity
	Volume	No.of atoms	No. of C and S atoms	Charge	|Charge|	Kyte and Doolittle (1982)	Fauchere and Pliska (1983)	Expected no. of contacts	Artificial parameters
90 unfolded proteins	133 ± 8	7.7 ± 0.4	4.8 ± 0.3	−0.01 ± 0.14	0.10 ± 0.10	0.39 ± 0.05	−0.17 ± 0.24	20.05 ± 0.58	−3.0 ± 1.2
80 folded proteins	137 ± 5	7.9 ± 0.3	5.0 ± 0.2	−0.01 ± 0.04	0.03 ± 0.03	0.46 ± 0.03	−0.46 ± 0.11	20.91 ± 0.25	−0.6 ± 0.5

Figure 1, B and C ▶, presents the expected mean hydrophobicity and the mean net charge for the sets of 80 folded and 90 natively unfolded proteins. Moreover, no absolute separation is observed between the two databases of proteins if we consider two parameters simultaneously (Fig. 1D ▶), as in the work of Uversky et al. (2000). Statistical parameters for the mean hydrophobicity and the mean net charge demonstrate that consideration of these factors does not completely separate the natively unfolded proteins from native ones (see Table 2): The fraction of proteins predicted incorrectly for these two parameters is 11%. A better separation is achieved if the expected number of contacts and hydrophobicity space are taken into consideration (Fig. 1F ▶). The fraction of proteins predicted incorrectly for these parameters is 8%.

Figure 2, B and C ▶, shows a histogram representing the distribution of natively unfolded proteins and folded proteins as a function of mean hydrophobicity and mean net charge. Figure 2, F and G ▶, demonstrates the minimum value as a fraction of proteins predicted incorrectly for these parameters (17% and 24%, respectively).

An optimal set of artificial parameters for 20 amino acid residues for better separation between globular and unfolded proteins

To maximally separate the set of 80 ideally folded and 90 natively unfolded proteins, an optimal set of artificial parameters for 20 amino acid residues has been calculated by a Monte Carlo algorithm (see Materials and Methods). The obtained parameters are presented in Table 1. Figures 1E ▶ and 2D ▶ demonstrate the separation of two databases if artificial parameters are used. Figure 2H ▶ demonstrates that we cannot achieve full separation of two databases even if we consider the optimal set of artificial parameters (the fraction of proteins predicted incorrectly is 5%).

We calculated the coefficient of correlations for different structural parameters considered here. It is interesting that the largest coefficient of correlation is 0.84 between artificial parameters and the number of contacts per residue (see Table 3). At the same time, a high coefficient of correlation for structural parameters does not guarantee that both parameters will result in statistically significant separation between two databases. For example, the number of C and S atoms has a high correlation with the average number of contacts (0.76), but poor separation of the two sets of protein is obtained (see Table 2).

Table 3.

Correlation between structural parameters calculated for 20 amino acid residues

				Hydrophobicity
	Volume	No. of atoms	No. of C and S atoms	Kyte and Doolittle (1982)	Fauchere and Pliska (1983)	No. of contacts	Artificial parameters
Volume		0.92 ± 0.03	0.94 ± 0.03	−0.00 ± 0.22	−0.32 ± 0.20	0.69 ± 0.12	0.65 ± 0.13
Number of atoms			0.92 ± 0.04	−0.28 ± 0.21	−0.16 ± 0.22	0.54 ± 0.16	0.54 ± 0.16
Number of C and
S atoms				0.07 ± 0.22	−0.49 ± 0.17	0.76 ± 0.09	0.76 ± 0.09
Hydrophobicity
(Kyte and Doolittle)					−0.81 ± 0.08	0.62 ± 0.14	0.53 ± 0.16
Hydrophobicity
(Fauchere and Pliska)						−0.83 ± 0.07	−0.73 ± 0.10
Number of contacts							0.84 ± 0.07

Discussion

Because of the fully exploited wealth of available protein data, most analyses attempt to discover common structural and chemical properties. Natively unfolded proteins have extended unfolded regions and would require some additional agents for complete folding. Such proteins are common in nature, and their structure properties have biological importance.

The formation of sufficient residue–residue interactions is necessary to compensate for the conformational entropy during the protein folding process. Therefore, structural uniqueness of native proteins is a result of the balance between the conformational entropy and the energy of residue interactions. It seems that natively unfolded proteins have no sufficient energetic interactions to compensate for conformational entropy, resulting in the formation of a globular state. Therefore, the enhanced stabilization of these proteins is achieved by additional interactions with other agents or by oligomerization. In this work, we demonstrated that if the average number of contacts for 20 amino acid residues in globular proteins is calculated and then, using these parameters, the expected average number of contacts per residue from the sequence alone for folded and unfolded proteins is calculated, a significant difference between these parameters for two sets of folded and unfolded proteins will be obtained.

It has been shown previously that there are some features of amino acid sequences that are responsible for the lack of ordered structure in natively unfolded proteins: low overall hydrophobicity, and large net charge (Uversky et al. 2000). In this work, we demonstrate that full separation of these two groups of proteins was not achieved when both factors were considered simultaneously in comparison with the data of Uversky et al. (2000), where the set of “small” globular proteins are specifically localized within a unique region of the charge–hydrophobicity space. In this work, we suggest a simple indicator of natively unfolded proteins that separates two databases as effectively as the consideration of hydropohobicity and net charge simultaneously.

It is interesting to note that it is not possible to achieve full separation of these two databases even for the optimal set of artificial parameters, but it may be possible to ideally separate two databases of proteins considering several important structural properties simultaneously. Therefore, the search for the properties of amino acid residues affecting the protein folding process continues.

It is worth emphasizing that in the considered approach, our metrics, both the real and artificial ones, are sensitive to the sequence composition, but insensitive to the sequence itself. That is, the order of the residues might also play some role in predicting folded and unfolded states of proteins and might account for the imperfect ability of even an artificial, composition-alone metric to do this. Nevertheless, it is possible to take into account the order of the residues and also to predict unfolded regions for a whole protein if a contact profile of the complete sequence is constructed, using the average number of contacts for each amino acid residue in the globular state. Therefore, regions with low contact densities will probably correspond to unfolded regions. We use such an approach to predict unfolded regions for CASP6 targets.

In this work, we demonstrate that the competence of a protein to be folded or unfolded may be determined by the property of amino acid residues to form a sufficient number of contacts in globular state to reduce conformational entropy. This property, that is, the expected average number of contacts per residue, can be used to predict the state of protein with an unknown three-dimensional structure: either folded or unfolded.

Materials and methods

Database preparation

An ideal database of globular proteins was obtained by inspection of the SCOP database (Murzin et al. 1995) 1.63 release. We found 80 proteins whose three-dimensional structure was determined by X-ray methods satisfying reasonable quality criteria; there is only one chain in the PDB file (Bernstein et al. 1977). We consider only nonhomologous single-domain proteins without modified residues, without serious errors in connectivity, without disulfide bonds and ligands, and with all heavy atoms resolved, from the four general classes of SCOP (a, all α proteins; b, all β proteins; c, α/β proteins; d, α+β proteins). The length of proteins in our database varies from 54 to 500 residues.

The second set of structures was obtained by inspection of the SCOP database (Murzin et al. 1995) 1.61 release and 6626 domains from the seven general classes (a–g) with less than 80% sequence identity values were found: 1122 α proteins from class a, 1644 β proteins from class b, 1617 α/β proteins from class c, 1435 α+β proteins from class d, 142 multidomain proteins from class e, 127 membrane proteins from class f, and 528 small proteins from class g). This database of structures has been used to calculate the average number of contacts per residue.

The database of natively unfolded proteins was created using the names of natively unfolded proteins taken from the work of Uversky et al. (2000) and from the SWISS-PROT protein sequence data bank (Bairoch and Apweiler 2000). This set of 90 proteins described in the literature as natively unfolded, which at physiological conditions was reported to have the nuclear magnetic resonance chemical shifts of a random-coil, or lack significant ordered secondary structure (as determined by CD or Fourier transform infrared spectroscopy), or show hydrodynamic dimensions close to those typical of an unfolded polypeptide chain, is presented in the work of Uversky et al. (2000). The length of natively unfolded proteins ranges from 50 to 1827 residues.

Hydrophobicity

We consider two scales of hydrophobicity. The first one is calculated by using the Kyte and Doolittle (1982) scale (the same as in the work of Uversky et al. [2000]), and the second scale corresponds to more common hydrophobicity of side chains from Fauchere and Pliska (1983). The mean hydrophobicity is defined as a sum of the hydrophobicities of all residues divided by the number of residues in the amino acid sequence.

The average number of contacts per residue in globular state

Calculations of the average number of contacts for 20 amino acid residues in globular state were done using 6626 protein structures (see Table 2). In our case, two residues are considered to make contact if any pair of their heavy atoms is less than 8.0 Å. The expected average number of contacts per residue from the amino acid sequence alone is calculated as a sum of the average number of contacts of all residues divided by the number of residues in the amino acid sequence.

Charge

The mean net charge is defined as a net charge at pH 7.0 (total number of negatively charged Asp+Glu and positively charged Arg+Lys residues) divided by the total number of residues.

Monte Carlo search for an optimal set of artificial parameters for 20 amino acid residues

To maximally separate the set of 80 ideally folded and 90 natively unfolded proteins, a Monte Carlo algorithm was implemented. A random set of 20 parameters was generated. Starting from the random set of parameters (the mean value is equal to 1 and the standard deviation is equal to 10), we randomly changed a single parameter by adding a random number distributed in the range from −0.05 to 0.05. It is expected that the optimal set of parameters will produce a higher score,

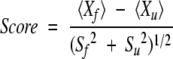where 〈X_f〉and 〈X_u〉are the mean values of adjustable parameters for the set of 80 ideally folded and 90 natively unfolded proteins, and S_f and S_u are the mean square deviations, respectively. No moves were considered that would result in a decrease in the score. After each step, we used linear transformation to obtain the same mean value and the same standard deviation. If for 1000 steps we did not observe the increase of the score we stopped our simulations. 40,000–60,000 Monte Carlo steps were performed in 10 optimization procedures, resulting in the same optimal set of artificial parameters for 20 amino acid residues (see Table 1).