Folding of a designed simple ankyrin repeat protein

Abstract

Ankyrin repeats (AR) are 33-residue motifs containing a β-turn, followed by two α-helices connected by a loop. AR occur in tandem arrangements and stack side-by-side to form elongated domains involved in very different cellular tasks. Recently, consensus libraries of AR repeats were constructed. Protein E1_5 represents a member of the shortest library, and consists of only a single consensus repeat flanked by designed N- and C-terminal capping repeats. Here we present a biophysical characterization of this AR domain. The protein is compactly folded, as judged from the heat capacity of the native state and from the specific unfolding enthalpy and entropy. From spectroscopic data, thermal and urea-induced unfolding can be modeled by a two-state transition. However, scanning calorimetry experiments reveal a deviation from the two-state behavior at elevated temperatures. Folding and unfolding at 5°C both follow monoexponential kinetics with k_folding = 28 sec⁻¹ and k_unfolding = 0.9 sec⁻¹. Kinetic and equilibrium unfolding parameters at 5°C agree very well. We conclude that E1_5 folds in a simple two-state manner at low temperatures while equilibrium intermediates become populated at higher temperatures. A chevron-plot analysis indicates that the protein traverses a very compact transition state along the folding/unfolding pathway. This work demonstrates that a designed minimal ankyrin repeat protein has the thermodynamic and kinetic properties of a compactly folded protein, and explains the favorable properties of the consensus framework.

A large number of protein classes are built on the modularity principle from homologous structural blocks (Marcotte et al. 1999; Letunic et al. 2002). Repeat proteins consist of a number of structurally identical motifs usually arranged in tandem, which stack to form elongated or supercoiled domains (Groves and Barford 1999). Repeating modules are typically 20–40 residues long, and contain secondary structure elements folding in a variety of topologies (Main et al. 2003). The linear assemblage of complementary repeats results in a relatively simple and robust scaffold, which is maintained by the regular repetition of hydrophobic contacts and hydrogen bonds. The architecture of stacked elements implies that stabilizing contacts are either within one repeat or between directly adjacent repeats, but there are no contacts between residues distant in sequence. Repeat proteins have adapted to different environments and promote ligand recognition through an array of variable functionalities in the side chains and sometimes in the main chain.

Ankyrin repeat proteins occur in virtually all species, even though the majority is found in eukaryots, and are involved in a wide range of cellular tasks, ranging from transcriptional regulation to cytoskeleton organization (Bork 1993). The ankyrin repeat (AR) is a 33-residue L-shaped motif, which contains two antiparallel α-helices connected by a short loop (Sedgwick and Smerdon 1999). The consecutive repeats stack in parallel and are joined by β-hairpins forming the base of the L. Four to six repeats are typical, but as many as 12 AR (Michaely et al. 2002) and 29 AR (Walker et al. 2000) in a single domain have been reported.

Due to their modular structure, repeat proteins in general, and AR in particular, are very attractive experimental objects both for testing our understanding about sequence–structure–stability–function relationships in proteins, and for developing molecular tools for biotechnological applications like, for example, specific molecular recognition (Binz et al. 2004; Forrer et al. 2004). Unlike the packing of globular protein domains, the linear packing of the repeat modules in AR proteins implies that local, regularly repeating packing interaction patterns are very important or even dominating the thermodynamic stability and folding mechanism (McDonald and Peters 1998). Indeed, the analysis of crystal structures has demonstrated that hydrophobic interactions between the helices within a single AR are not well optimized, while hydrophobic packing is tighter at interrepeat interfaces (Kohl et al. 2003). This peculiarity has prompted studies aimed at the elucidation of the thermodynamic stability as a function of the repeat number within a single AR domain consisting of several repeats (Zweifel and Barrick 2001b; Binz et al. 2003), the cooperative behavior and its limits (Bradley and Barrick 2002), the identification of minimal folding units (Zhang and Peng 2000; Mosavi et al. 2002), the thermodynamic consequences of mutations (Mosavi and Peng 2003; Zweifel et al. 2003), and the folding mechanism (Tang et al. 1999, 2003; Zeeb et al. 2002).

More recently, the design of novel AR has been reported (Mosavi et al. 2002; Binz et al. 2003, 2004). The two successful design strategies are both based on sequence data base analysis and identification of residues maintaining the AR fold. A multiple sequence alignment and statistical analysis was used to calculate the probability of amino acid usage at each position of AR (Mosavi et al. 2002). The successful application of a novel design strategy to construct combinatorial AR protein libraries to select specific binders was reported (Binz et al. 2003, 2004; Kohl et al. 2003). Sequence consensus analysis refined by structural considerations has led to the design of a 33 amino acid AR module in which seven positions are randomized to obtain AR libraries (Binz et al. 2003; Forrer et al. 2003; Kohl et al. 2003). To render repeat proteins soluble and monomeric the exposed hydrophobic faces of the terminal repeats are shielded by capping repeats. Library members containing two to four internal repeats flanked by N- and C-terminal capping motifs are soluble, do not oligomerize and display high thermodynamic stability (Binz et al. 2003). To characterize the behavior of the “idealized” consensus AR that are used in the library, here we investigate the stability and folding of one randomly chosen member of the smallest library consisting of a single consensus AR flanked by terminal capping repeats.

Results

The simplest AR library proteins consist of a single central consensus repeat flanked by N-terminal and C-terminal capping repeats (Fig. 1 ▶). Protein E1_5 was expressed in soluble form in the cytoplasm of Escherichia coli at high yield (80 mg purified protein per one liter of culture). The purified protein is monomeric at the concentrations and under the experimental conditions used in this study, as evidenced by gel filtration and multiangle light scattering (not shown). The far-UV CD spectrum has the typical spectral signature of naturally occurring and designed AR (not shown).

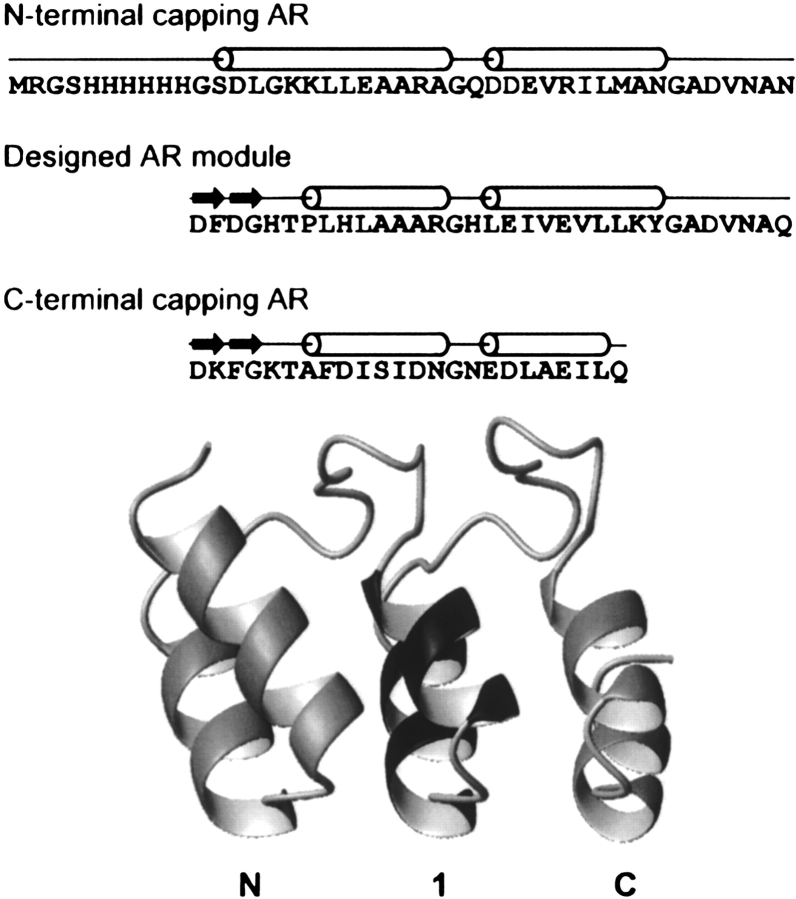
Figure 1.

The E_5 protein. After the N-terminal His tag, the sequence of the three ankyrin repeats are shown on separate lines. For orientation, the secondary structure elements are indicated above the sequence. Cylinders, α-helices; arrows, β-turns. In the structural model, the flanking capping repeats are shown in light gray, while the central consensus repeat is in dark gray. The N1C AR protein model was generated using homology modeling with Insight II (Accelrys) and the crystal structures of GABPb1 (PDB ID: 1AWC; Batchelor et al. 1998), E3_5 (1MJ0; Kohl et al. 2003), 3ANK (1N0Q; Mosavi et al. 2002), and 4ANK (1N0R; Mosavi et al. 2002) as templates. The picture was created using MOLMOL (Koradi et al. 1996).

Thermal unfolding

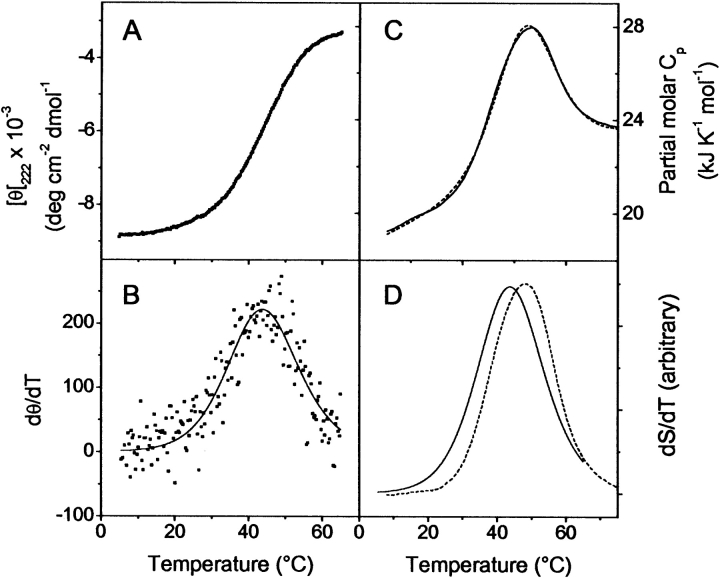
Unfolding of E1_5 at pH 7.0 was monitored by following the temperature-induced changes in ellipticity at 222 nm. The melting traces were superimposable with protein concentrations between 10 and 150 μM, thus demonstrating that no aggregation takes place in the temperature range studied. Thermal unfolding was reversible to >95% when the protein was heated to 65°C. Heating above that temperature reduced the reversibility due to a time-dependent process, possibly asparagine deamidation occurring at elevated temperatures in the deamidation-prone Asn-Ala and Asn-Gly sequences (Robinson and Robinson 2001). Therefore, CD data were analyzed only between 3°C and 65°C. The unfolding transition is sigmoidal, without indication for consecutive unfolding steps, yet it is quite broad (Fig. 2A ▶). Because the posttransitional portion of the signal change is not well defined if heating proceeds to 65°C only, the data were analyzed in the differential mode by the combined equations 1–3 (Fig. 2B ▶; John and Weeks 2000). The melting curves are compatible with a two-state unfolding transition with midpoint T_m = 44.2°C and van’t Hoff enthalpy Δ H_vH,CD = 130 ± 10 kJ mole⁻¹.

Figure 2.

Thermal melting of E1_5 at pH 7.0, followed by CD spectroscopy and DSC. Temperature-induced changes in MRE₂₂₂ are shown in A. Protein concentration was 30 μM. (B) The same data in the derivative mode (symbols). The best fit according to equations 1–3 with T_m = 44.2°C and ΔH_vH,CD = 130 ± 10 kJ mole⁻¹ is visualized by the continuous line. (C) Partial molar heat capacity changes upon heating at 1° min⁻¹. Protein concentration was 150 μM. The experimental data are shown as a continuous line. The broken line is the best fit for a two-state unfolding model determined with T_m = 48°C, ΔH_fit = 136 ± 5 kJ mole⁻¹ and ΔC_p = 2.0 ± 0.2 kJ K⁻¹ mole⁻¹. (D) Superposition of the excess heat capacity obtained by calorimetry (dashed line) and the temperature derivative of MRE₂₂₂ (continuous line) is shown. To facilitate the comparison, both functions were arbitrarily scaled.

The thermal stability and unfolding of E1_5 were further characterized by differential scanning calorimetry. In the native region between 5° and 25°C, the partial specific heat capacity is a linear function of temperature and increases with a ∂C_p/∂T = (6.8 ± 1.0) × 10⁻³ J K⁻² g⁻¹. Overall, the temperature dependence of the partial molar heat capacity can be reasonably modeled by a two-state conformational transition (Fig. 2C ▶). However, closer analysis reveals a small but significant deviation from the two-state model. Notably, the maximum of the heat capacity function appears at 48°C, higher than the T_m detected by CD spectroscopy (44°C; Fig. 2D ▶), although the best fit of the two-state unfolding model to the data was obtained with ΔH_fit,DSC = 136 ± 7 kJ mole⁻¹, which is identical within error with ΔH_vH,CD. The calorimetric, model-independent enthalpy, ΔH_cal,, amounts to 145 ± 5 kJ mole⁻¹, while the effective van’t Hoff enthalpy, ΔH_vH,DSC, obtained by analysis of the shape of the heat absorption peak, is 129 ± 10 kJ mole⁻¹. Thus, the ratio ΔH_vH,DSC/ΔH_cal is 0.89, indicative of a population of intermediate states in the transition zone. The data are best described by an unfolding heat capacity increment ΔC_p = 2.0 ± 0.2 kJ K⁻¹mole⁻¹. From thermal melting data, according to the Gibbs-Helmholtz equation, the free energy of unfolding of E1_5 at 5°C is Δ G_th = 11 ± 1 kJ mole⁻¹, higher than ΔG from urea induced unfolding (see below).

Urea-induced unfolding

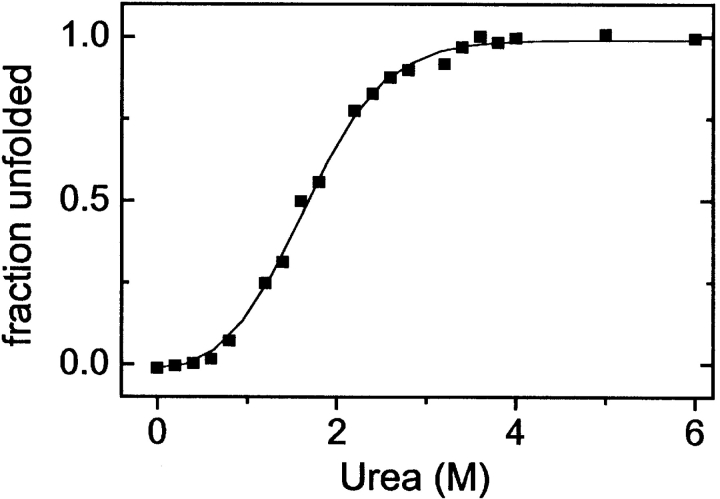
The stability of E1_5 at 5°C was assessed from isothermal urea-induced unfolding experiments by following the change in ellipticity at 222 nm. As in thermal unfolding, the unfolding curve is rather broad, but the data can be modeled with a two-state transition between native and unfolded protein with a midpoint at 1.8 M urea (Fig. 3 ▶). The linear extrapolation procedure yields Δ G_{ur,H20 =} 7.7 ± 0.8 kJ mole⁻¹ at 5°C and 0 urea. The urea dependence of ΔG,m_eq = −∂Δ G_urea/∂[urea], is 5.7 ± 0.5 kJ mole⁻¹ M⁻¹. Experiments were performed also at higher temperatures. The midpoint of unfolding shifts to slightly lower denaturant concentrations. Unfortunately, the pretransition portion of the unfolding curve is not well defined above 5°C, which precluded accurate determination of ΔG_unf at higher temperatures. However, according to our semiquantitative estimates, the combination of [urea]_1/2 and m_eq is such that the decrease in stability is less than 1 kJ mole⁻¹ between 5° and 20°C.

Figure 3.

Equilibrium urea-induced unfolding of E1_5 at 5°C followed by CD spectroscopy. The symbols are the experimental data presented as fraction unfolded protein. The continuous line is calculated by the linear extrapolation model for a two-state transition. Protein concentration was 25 μM.

Folding/unfolding kinetics

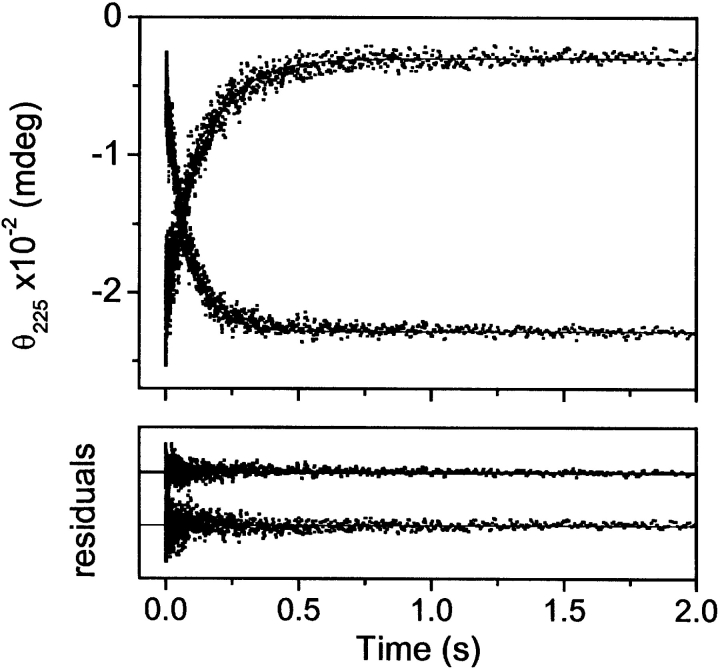
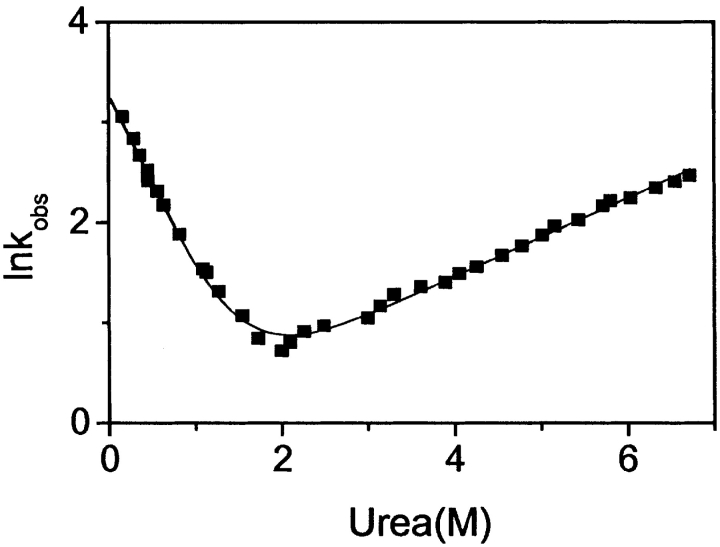
The rate of folding and unfolding of E1_5 was studied by following the time course of secondary structure formation/disruption after rapid dilution from or into urea at 5°C. Representative kinetic traces are shown in Figure 4 ▶. Folding and unfolding are both described precisely by single exponential phases at all urea concentrations tested. Throughout the entire range of urea concentrations the amplitudes of the kinetic traces account for >95% of the spectral differences between the folded and unfolded state measured at equilibrium. It follows that there are no kinetic phases observable by CD that are hidden in the dead time of the measurement. No curvature in the refolding and unfolding limbs of the Chevron plot is detected in the range of urea concentrations studied (Fig. 5 ▶). According to equation 4, the data set is consistent with k_f,H2O = 28 ± 2 sec⁻¹ and k_unf,H2O = 0.9 ± 0.1 sec⁻¹. The vertex of the Chevron plot is at 1.9 M urea. From kinetic data, the free energy of unfolding at 5°C is ΔG_kin,H2O = −RTln(k_unf,H2O/k_f,H2O) = 7.9 ± 0.9 kJ mole⁻¹, m_f = −1.85 ± 0.2 M⁻¹, m_unf = 0.43 ± 0.04 M⁻¹ and m_kin = RT(|m_f| + |m_unf|) = 5.3 ± 0.5 kJ mole⁻¹ M⁻¹.

Figure 4.

Representative kinetic traces describing refolding and unfolding of E1_5 at 5°C followed by CD stopped-flow. The lines are best fits according to a single exponential function. The residuals of the fits are shown in the lower panels. Final protein concentration was 25 μM. Final urea concentration was 0.45 M for refolding (downward trace) and 5.3 M for unfolding (upward trace), respectively.

Figure 5.

Urea dependence of the rate constants for refolding (left limb) and unfolding (right limb). The observed relaxation constants are presented as symbols. The continuous line was calculated according to equation 4.

Discussion

Peptides corresponding to the length of a single AR and being compactly packed and stable have not been reported so far. The reason for the intrinsic instabiliy of an isolated AR is that it is too small to form a well-developed hydrophobic core and cooperative accumulation of interrepeat contacts provides substantial stabilization in a folded domain of several AR. Two repeats can be sufficient to form a stable folding unit. It was demonstrated that the third and fourth AR of the tumor supressor p16^INK4 fold autonomously and cooperatively (Zhang and Peng 2000). Nevertheless, naturally occurring proteins very rarely contain less than three AR. Cooperative folding into parallel stacks of only a few repeats faces the problem of how to shield the hydrophobic core from the solvent, because the complementary surface of the tandem repeats is largely hydrophobic. In nature, specialized terminal repeats exposing one predominantly hydrophilic face to the solvent are often found to terminate the internal hydrophobic stack of AR domains. In the present design of consensus AR libraries (Binz et al. 2003; Forrer et al. 2003; Kohl et al. 2003) special capping repeats are used facilitating the correct folding of library members with a varying number of internal repeats. The success of this strategy has been demonstrated by proteins containing two to four AR between the caps (Binz et al. 2003; Forrer et al. 2003; Kohl et al. 2003). In contrast, the two-repeat consensus construct originally designed by Mosavi et al. (2ANK) is partially folded under some conditions but is not monomeric (Mosavi et al. 2002). Leucine to arginine substitutions on the surface of 2ANK allowed the partially folded protein to assume a fully folded conformation (Mosavi and Peng 2003), yet at the expense of thermodynamic stability, possibly due to local repulsions between like charges.

In the present study we show that the simplest possible library member containing a single internal repeat and two capping repeats is stably folded. The E1_5 protein is soluble and monomeric. MRE₂₂₂ (mean residue ellipticity at 222 nm) is −8700° cm⁻² dmole⁻¹. This helical content is slightly lower than what has been observed for library members containing two to four internal repeats, but it is comparable with the very stable four-repeat domain designed by Mosavi et al. (2000) and the Drosophila Notch protein containing five, six, or seven repeats (Zweifel and Barrick 2001a). Calorimetric data provide strong support that the protein is compactly folded. The specific unfolding enthalpy, 1.6 kJ (mole res)⁻¹, the specific unfolding entropy, 5.1 J K⁻¹ (mole res)⁻¹ at 48°C, as well as the temperature slope of the heat capacity of the folded protein are typical for globular proteins domains (Gomez et al. 1995; Makhatadze and Privalov 1995). (In the calculation, the N-terminal his-tag 12 residues [Fig. 1 ▶] are not taken into consideration, because they are unfolded and influence only negligibly the measured thermodynamic parameters.) These observations indicate that the enthalpy and entropy factors determining E1_5 stability are balanced similarly to globular proteins.

The unfolding transitions induced by heat and urea are relatively broad, implying that the cooperativity of tertiary structure consolidation/disruption is low, as is usual for proteins of small size (Fig. 2 ▶). Because the effective unfolding enthalpies measured by CD spectroscopy and calorimetry are lower than the model-independent calorimetric estimate, intermediate(s) become(s) populated at higher temperatures. The midpoint of thermal unfolding is shifted to higher temperatures when the transition is monitored by the changes in partial molar heat capacity (Fig. 2D ▶). Therefore, it is likely that melting of the α-helices precedes disruption of gross packing interactions upon temperature increase, and the intermediate(s) represent(s) a relatively compact species without pronounced helical content. A folding intermediate with the same overall structural features has been detected in folding of the tumor supressor p16 at 25°C (Tang et al. 1999). Statistical thermodynamic modeling of the heat capacity function to obtain the thermodynamic characteristics of the intermediate state(s) was not possible because the population of that state(s) is relatively low. Interestingly, the combined data collected at 5°C are consistent with a two-state behavior. Refolding and unfolding are both mono-exponential (Fig. 4 ▶). There is no evidence for a “roll-over” at strongly native conditions (Fig. 5 ▶). The free energy of unfolding measured at equilibrium using the two-state approximation is identical within error with the free energy calculated from kinetic data. Kinetic and equilibrium m-values also agree well. Possibly, there is a subtle, temperature-dependent change in the folding mechanism from simple two-state at low temperatures to a more complicated mechanism involving intermediate(s) at higher temperatures. Alternatively, the intermediary state(s) escape(s) detection at low temperatures.

In view of the slight differences in the unfolding at low and high temperatures, the different estimates of ΔG_unf of E1_5 obtained from thermal and isothermal unfolding data come as no surprise. Possibly, the stability measured directly at 5°C, ΔG_ur,H2O, is more reliable than ΔG_th extrapolated according to the Gibbs-Helmholtz equation using thermal melting data, because extrapolation is over a large temperature range and neglects the presence of intermediates. On the other hand, if significant tertiary contacts are retained in the absence of α-helical structure, stability might have been underestimated from both equilibrium and kinetic CD data collected at 5°C.

The protein is marginally stable, 8–11 kJ mole⁻¹. However, construct E2_5 having two internal repeats of the same sequence as E1_5 is dramatically more stable, displaying an increase in T_m of ~30°C, and a sixfold increase in stability compared to E1_5 (Binz et al. 2003). In comparison, the autonomously folded two-repeat fragment of p16^INK4 has a ΔG = 7.1 ± 1.7 kJ mole⁻¹ (Zhang and Peng 2000), while the full-length four repeat long p16^INK4 has a ΔG ~13 kJ mole⁻¹ (Tang et al. 1999) and the Drosophila Notch protein with 6 repeats has ΔG = 10 ± 1.5 kJ mole⁻¹ (Zweifel and Barrick 2001b). Taken together, these observations strengthen the contention that engineered consensus AR proteins are more stable than AR proteins occurring in nature, as recently discussed (Main et al. 2003; Forrer et al. 2004).

E1_5 unfolds and refolds following a single exponential phase when observing the changes in ellipticity at 225 nm. Within the precision of the measurements, both lnk_f and lnk_unf are linear functions of the urea concentration. Down to 0.15 M urea we do not observe “roll-over” in the refolding limb of the Chevron plot, which would be indicative of a urea-sensitive folding intermediate. This is consistent with an apparent reversible two-state folding of the “idealized” small AR protein. In contrast, the human CDK inhibitor p19INK4d and the tumor supressor p16 exhibit multiphasic folding kinetics in CD and fluorescence stopped-flow experiments (Tang et al. 1999; Zeeb et al. 2002). An intermediate has been postulated for the tumor supressor p16 (Tang et al. 1999). For E1_5, the existence of a folding intermediate accumulating at urea concentrations below 0.15 M, or appearing even at higher urea concentrations, yet not detectable by CD, cannot be completely ruled out. However, the good correspondence between equilibrium and kinetic ΔG and m-values argues against this possibility.

Despite its small size, some kinetic properties of E1_5 are very similar to those of the tumor supressor protein p16 containing four AR (Tang et al. 1999). The refolding rate of E1_5 extrapolated to zero urea is 28 sec⁻¹ at 5°C. Refolding of p16 proceeds through an intermediate which accumulates very rapidly and interconverts to the native state in the rate-limiting step with a rate constant of 33 sec⁻¹ at 25°C. These rates are relatively slow. Also, the unfolding rates are very similar: 0.9 sec⁻¹ at 5°C for E1_5 and 0.8 sec⁻¹ at 25°C for p16, indicating that the proteins unfold by crossing a similar energy barrier. Furthermore, both proteins exhibit a shallow unfolding limb in their Chevron plots. From the Tanford’s ratio, β_T = m_unf/(|m_ref| + |m_unf|), it can be concluded that E1_5 and p16 traverse a very compact rate-limiting high-energy state along the refolding/unfolding pathway. This transition state is 89% and 84% native-like with respect to its overall surface exposure for p16 and E1_5, respectively. At least some of these common biophysical features may be the consequence of the AR architecture and the similar thermodynamic stabilities of the two proteins.

In conclusion, the presented data demonstrate that E1_5, containing a central consensus AR flanked by capping repeats is an autonomously folding domain. Folding appears to be a simple two-state process at low temperatures, while equilibrium intermediates become populated at higher temperatures. The protein folds via a very compact transition state. The kinetic stability is low but equilibrium experiments predict a marked increase with the increasing number of repeats (Binz et al. 2003). With the characterization of the smallest library member the stage is now set for systematic studies of the biophysical properties of AR domains consisting of identical internal repeats as a function of the repeat number.

Materials and methods

Protein expression and purification

The construction and cloning of designed AR protein libraries is described in detail elsewhere (Binz et al. 2003). The sequence of the library member E1_5 is shown in Figure 1 ▶. The protein was expressed in the soluble form in XL1-Blue E. coli at 37°C after induction with 1 mM IPTG. After 4 h, the cells were harvested by centrifugation, resuspended in 50 mM Tris-HCl, 500 mM NaCl (pH 8.0) and sonicated. The lysate was centrifuged and glycerol (10% final concentration) and imidazole (20 mM final concentration) were added to the resulting supernatant. The protein was purified over a Ni-nitrilotriacetic acid column (2.5 mL column volume) according to the manufacturer’s instructions (Qiagen). The purity was checked by SDS-PAGE, and the identity of the protein was verified by mass spectroscopy. The protein was extensively dialyzed against the working buffer (see below) and protein concentrations were determined by UV spectroscopy using ɛ₂₈₀ =1280 cm⁻¹ M⁻¹ (Edelhoch 1967).

Buffers and chemicals

All chemicals were of the highest grade available, and were used without further purification. All experiments were performed in a buffer cocktail containing 7.5 mM each of boric acid, citric acid, and phosphoric acid, 100 mM KCl (pH 7.0). For experiments in urea, the denaturant was added before the pH adjustment. Urea concentrations were determined by measuring the refractive index.

Circular dichroism (CD) spectroscopy

Experiments were performed on a J-715 instrument (Jasco Ltd.) equipped with a computer-controlled water bath, using cylindrical jacketed cuvettes of 1 mm optical path length. Spectra were recorded three times between 200 and 250 nm at scanning rate of 5 nm min⁻¹. Thermal melting curves were recorded by continuous heating at 1° min⁻¹. Data points (ellipticity at 222 nm) were collected every 10 sec. Reversibility was determined from the recovery of the mean residue ellipticity (MRE₂₂₂) after cooling. Thermal melting curves were analyzed according to (John and Weeks 2000):

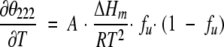(1)

where A is a scaling constant, R is the gas constant, and ΔH_m is the van’t Hoff enthalpy at T_m. The fraction of unfolded protein, f_u, is given by:

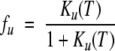(2)

and the equilibrium unfolding constant, K_u(T) is calculated with the van’t Hoff expression:

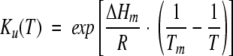(3)

For measuring of urea melting curves, 25 μM protein was incubated overnight at the corresponding urea concentrations. The signal was averaged over 3 min after thermal equilibration. Urea-induced equilibrium unfolding experiments were analyzed by nonlinear least-squares regression according to well-established procedures (Milev et al. 2003).

Differential scanning calorimetry (DSC)

The temperature dependence of the heat capacity was determined with the VP-DSC calorimeter (MicroCal LLC) at heating rate of 1° min⁻¹. Details on the performance of the instrument are given elsewhere (Plotnikov et al. 1997). After subtraction of the buffer versus buffer baseline, the data were transformed to partial specific heat capacity using a partial specific volume of 0.715 cm⁻³ g⁻¹ calculated from the amino acid sequence (Makhatadze et al. 1997). The data were analyzed by nonlinear least-squares regression using the program CpCalc 2.1 (Applied Thermodynamics) or in-house scripts written for NLREG (Phillip Sherod) utilizing thermodynamic modeling as described previously (Milev et al. 2003).

Stopped-flow kinetics

Kinetic experiments were performed with the π*-180 instrument (Applied Photophysics). The dead time was 1–2 msec, and the optical path length was 10 mm. Refolding was initiated by mixing one volume of buffered protein solution (250 μM) containing 4–5 M urea with 10 or 25 volumes of buffer, or with buffer containing various concentrations of the denaturant. Unfolding rates were measured by 1:10 dilution of the protein into solutions containing final urea concentrations >2.5 M. The detection wavelength was 225 nm and the slits were set to 4 mm. Ten to 15 firings were averaged for each kinetic trace. The data were analyzed with the software provided by the manufacturer. The Chevron plot was analyzed by the following equation (Fersht 1999):

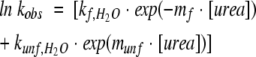(4)

k_obs is the relaxation constant at a given concentration of urea, k_f,H2O and k_unf,H2O are the refolding and unfolding rate constants, respectively, in the absence of urea. Coefficients m_f and m_unf describe the urea dependence of k_f,H2O and k_unf,H2O, respectively.