Automated selection of positions determining functional specificity of proteins by comparative analysis of orthologous groups in protein families

Abstract

The increasing volume of genomic data opens new possibilities for analysis of protein function. We introduce a method for automated selection of residues that determine the functional specificity of proteins with a common general function (the specificity-determining positions [SDP] prediction method). Such residues are assumed to be conserved within groups of orthologs (that may be assumed to have the same specificity) and to vary between paralogs. Thus, considering a multiple sequence alignment of a protein family divided into orthologous groups, one can select positions where the distribution of amino acids correlates with this division. Unlike previously published techniques, the introduced method directly takes into account nonuniformity of amino acid substitution frequencies. In addition, it does not require setting arbitrary thresholds. Instead, a formal procedure for threshold selection using the Bernoulli estimator is implemented. We tested the SDP prediction method on the LacI family of bacterial transcription factors and a sample of bacterial water and glycerol transporters belonging to the major intrinsic protein (MIP) family. In both cases, the comparison with available experimental and structural data strongly supported our predictions.

The exponential growth of genomic data strongly exceeds the capacity of experimental analysis of the protein function. On the other hand, intelligent use of the genomic data may save the experimentalists’ effort. A standard technique of the functional protein annotation is the similarity database search. However, in many cases it allows one to assign a general function to a protein of interest (e.g., “transcriptional regulator of the LacI family”), but cannot resolve the protein’s specificity (say, “purine or ribose repressor”). More detailed genomic analysis, using identification of orthologs, positional genomic analysis, metabolic reconstruction, analysis of regulation and other comparative techniques strongly improves the resolution of prediction (Koonin and Galperin 2003). In many cases, the comparative techniques allow one to tentatively assign common (often unknown) specificity to groups of proteins, and thus provide data for analysis of specificity-determining residues in protein sequences. An overview of some of these methods is given in Hannenhalli and Russell (2000). Some of them, in particular the evolutionary trace analysis (Lichtarge et al. 1996, 1997), and the structure-based approach to prediction of protein function (Johnson and Church 2000), rely strongly on the known protein structure or information about protein functional sites. However, in many cases the structural data are not available, and there are methods that use purely genomic data in the form of aligned protein sequences: hierarchical analysis (Livingstone and Barton 1993), evolutionary rate-based prediction (Gaucher et al. 2002), principal component analysis in the sequence space (Casari et al. 1995), prediction of functional subtypes (Hannenhalli and Russell 2000), and identification of specificity-determining residues using orthologs and paralogs (Mirny and Gelfand 2002).

We developed the specificity-determining positions (SDP) prediction method, a method for identification of specificity-determining residues that does not rely on any information about the protein family except its multiple sequence alignment (MSA) and specificity of some members of the family. It extends the technique developed in Mirny and Gelfand (2002) and incorporates some features from Hannenhalli and Russell 2000), but has significant differences from both. First, our algorithm takes into account the nonuniformity of amino acid substitution frequencies. The use of amino acid substitution matrices allows us to apply a uniform procedure to proteins of varying evolutionary divergence. Second, the algorithm incorporates an automated procedure for setting the recognition cutoff. It is based on the Bernoulli estimator. Positions scoring higher than this cutoff are predicted to determine the specificity. This procedure does not rely on any prior knowledge about the score distribution, in contrast to existing approaches that involve ad hoc settings.

By definition, orthologous and paralogous proteins have a common ancestor and thus almost always have the same general biochemical function. Orthologs, which diverge after speciation, normally have the same specificity. Thus a protein family can be divided into ortholog groups. Proteins from one group have the same functional specificity, whereas different groups generally have different specificities. We will assume that a “specificity group” is a group of orthologous proteins having the same specificity. Specificity of some groups may coincide or be unknown. The union of the derived groups should not necessarily cover the entire protein family. A set of positions of the MSA, which can best discriminate between these specificity groups, we call SDP. In brief, we search for positions that are well conserved within the specificity groups but differ between these groups. Using a set of SDP, one can build profiles for prediction of the specificity of a protein that belongs to the same family but whose specificity is unknown.

We tested our method on two protein families, the LacI family of bacterial transcription factors and the MIP family of membrane transporters. The LacI and MIP families were chosen because a large volume of structural and experimental data is available. In addition, the LacI family allows for direct comparison with the results of Mirny and Gelfand (2002), whereas the MIP family shows how the technique works when applied to transmembrane proteins consisting of segments with different statistical properties. The obtained results indicate that in both cases the derived sets of SDP seem reasonable when compared with known protein structures from the Protein Data Bank (PDB). The results obtained for the LacI family are in good agreement with the results of Mirny and Gelfand (2002). However, modifications of the algorithm led to the identification of several new positions that seem to be functionally important.

Results

Two different functions, the mutual information and the relative entropy, were used for identification of SDP, defined as positions whose Z-scores exceed the Bernoulli estimator threshold (see Materials and Methods). We describe only the results obtained with the mutual information formalism, because in tests we have not observed any significant difference in results produced by the mutual information and the relative entropy formalisms (data not shown). The obtained sets of SDP are also robust as regards the algorithm parameters.

Generation of test sets

We considered two protein families, the MIP family of membrane transporters and the LacI family of bacterial transcription factors.

The major intrinsic protein (MIP) family is a large and diverse family of transmembrane channels whose members are found in eubacteria, archaea, and eukaryotes. The MIP family can be divided into six major subfamilies (Zardoya and Villalba 2001). We considered two subfamilies with bacterial members: glycerol-transporting channel proteins (GLP) and aquaporins (AQPs), water-transporting channel proteins. All bacterial proteins from SWISS-PROT and TrEMBL databases that belong to the MIP family (entry IPR000425 in the InterPro database; Mulder et al. 2003) were considered. Incomplete sequences and sequences containing additional domains were excluded. From each pair of sequences that were more than 96% identical, only one sequence was retained. The obtained set contained 61 proteins from 43 genomes.

To test the quality of our predictions, we used the published 3D structure of a well-characterized GLP protein, GlpF from Escherichia coli (Fu et al. 2000, PDB identifier 1FX8). In the case of the AQP group, only 3D structures of almost identical eukaryotic proteins, bovine AQP1 (Sui et al. 2001) and human AQP1 (Murata et al. 2000) are resolved (PDB identifiers 1J4N and 1FQY, respectively). Therefore, we have supplemented the full set with these proteins and two of their paralogs from the GLP group, rat and human AQP7.

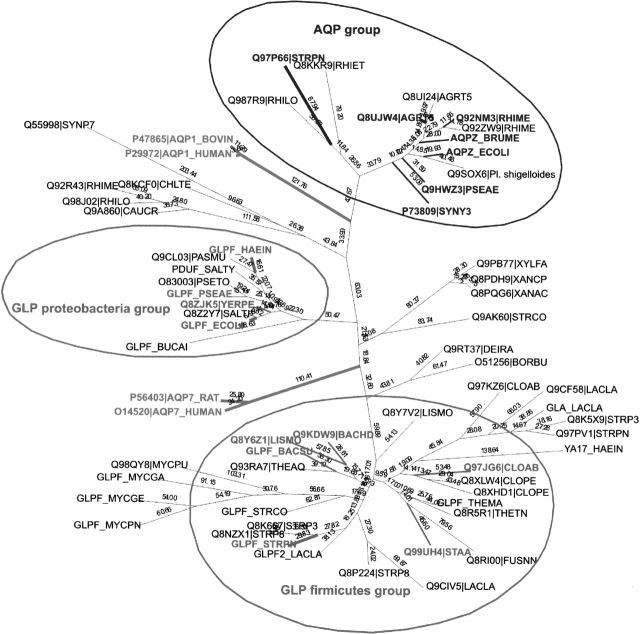
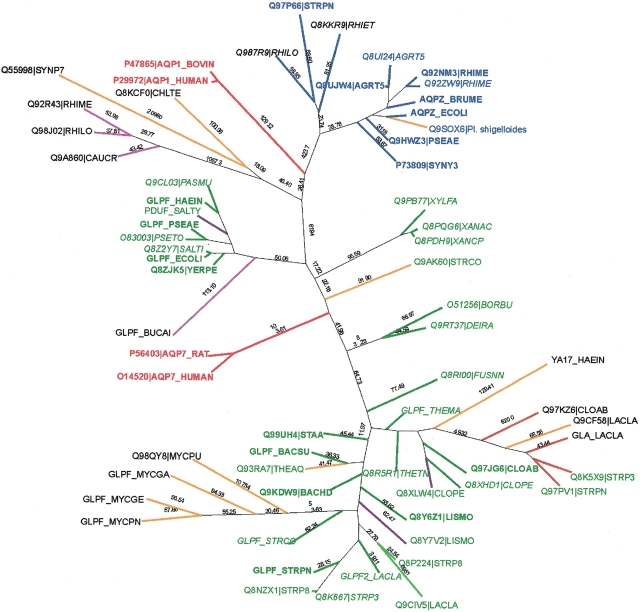
Transmembrane segments were predicted using the comparative technique of Sutormin et al. (2003). Testing demonstrated that the sets of identified SDP did not depend on minor changes of the transmembrane segment boundaries. All 65 proteins were aligned by CLUSTALX (Thompson et al. 1997) and the maximum likelihood tree was constructed by PHYLIP (Fig. 1 ▶; Felsenstein 1996).

Figure 1.

The phylogenetic tree of the analyzed proteins from the MIP family. Proteins of the AQP and the GLP training sets are in bold. Eukaryotic members of the MIP family are in bold and underlined.

As a training set for the SDP prediction, we selected 17 bacterial proteins that form compact clusters in the derived tree (labeled bold in Fig. 1 ▶): 7 orthologous proteins from the AQP group (average identity 59 ± 14%), and 10 orthologous proteins of the GLP group (average identity 48 ± 14%), the latter including four proteins from gram-negative gamma-proteobacteria and six proteins from gram-positive bacteria (Firmicutes). The orthology relationships for them were verified using GenomeExplorer (Mironov et al. 2000). The remaining 48 proteins were used as the test set.

In order to avoid spurious gaps arising from alignment of eukaryotic and bacterial proteins, we realigned all sequences as follows. The training sets for AQP and GLP from proteobacteria and GLP from firmicutes were aligned separately. Proteins that belonged to the same branches with either the AQP training set, the proteobacterial GLP training set, or the firmicute GLP training set were aligned to the derived profiles. Then two profiles for the proteobacterial and firmicute GLP were aligned to each other and proteins that belonged to the intermediate branches in the tree were aligned to the resulting profile in order to form the profile for the entire GLP group. Then the profiles for the AQP and GLP groups were aligned to each other. The remaining proteins of the full set and the eukaryotic proteins were aligned to the obtained profile.

The alignment of the LacI family was taken from Mirny and Gelfand (2002). It contained 15 specificity groups: AraR, KdgR, CcpA, DegA, YjmH, RbsR, PurR, CytR, GalSR, AscG, LacI, TreR, GntR, IdnR, and FruR. The resulting set of SDP was mapped to resolved 3D structures: the complex of the purine repressor with guanine and DNA (PDB identifier 1WET), the dimeric purine repressor (1JHZ), the complex of the dimeric Lac repressor with its anti-inducer ONPF (orthonitrophenyl-beta-D-fucopyranoside) and DNA (1JWL), and the complex of the dimeric trehalose repressor with its inducer trehalose-6-phosphate (1BYK), all from E. coli.

When comparing the predicted SDP with 3D structures, possible contacts between ligand molecules (substrate in the case of the MIP family, effector and DNA in the case of the LacI family) and amino acid residues or between amino acid residues of different subunits were characterized by the minimal distance between the atoms of the amino acid residue and the atoms of the ligand (or of the residues from the other subunit).

SDP for the LacI family

The Bernoulli estimator selected 40 SDP in the LacI family (Table 1, Fig. 2 ▶). Twelve of these positions were previously identified and described in Mirny and Gelfand (2002). Among the remaining candidates, new interesting positions could be observed. For example, residues in positions corresponding to 73Y and 74F of PurR from E. coli contact the effector in all three structures of the analyzed LacI repressors.

Table 1.

Specificity-determining positions in the LacI family

Residue description	Position (numbering as in PurR from E. coli)
Contacting DNA	15*, 16*, 55*, 56, 57
Other located in the DNA-binding domain	4, 21, 25
Contacting effector	73, 74, 122*, 160*, 192, 193, 221*, 246, 249*
Other located near the effector-binding pocket	66, 81, 85, 121, 123, 126, 145, 146*, 147*, 185, 186, 302
Contacting subunit	50*, 53, 69, 78, 91, 95, 98*, 114*
No obvious function (possible overprediction)	166, 233, 280

Contact criteria/DNA closer than 5 Å in PurR from E. coli; effector or subunit closer than 5 Å in at least one of the three proteins with resolved 3D structure (see the text) and closer than 7 Å in the other two proteins.

Asterisk (*): SDP according to Mirny and Gelfand (2000).

Figure 2.

Candidate SDP for the LacI (A) and TreR (B) repressors. Effector molecules are shown by space filling and colored yellow; SDP are shown by space filling and colored by function: red, residues in close contact with DNA; green, residues in close contact with effectors; blue, residues in close contact with the other subunit; white, residues near the DNA-binding or effector-binding region but not satisfying the contact criteria (see the legend to Table 1); gray, overprediction (residues with no obvious function).

Analyzing contacts in the available structures, one could easily assign a clear function to 22 of 40 predicted SDP (Table 1). Three more candidate SDP, namely, 4, 21, 25 (here and following the numbering is according to PurR of E. coli), are located in the DNA-binding domain but do not contact the DNA in PurR from E. coli according to our strong criterion (the minimal distance between the residue and DNA is <5 Å). It must be noted that the structural data about the DNA-binding domain are incomplete in all available 3D structures of LacI family proteins: this domain is absent in 1BYK and in 1JHZ, in 1JWL not all residues are resolved, and in 1WET only one DNA chain is presented. Therefore, we cannot exclude that these three SDP can be critical for binding DNA in other proteins of the LacI family (cp. following).

An interesting group comprises 12 SDP located behind the effector-binding pocket (Fig. 2 ▶). Closer analysis reveals that at least four of these SDP do not satisfy the contact criterion (the minimal distance between the residue atoms and the effector atom <5 Å in one of the three structures and <7 Å in the other two), but still contact the effector tightly in one of proteins analyzed (Fig. 3 ▶). For example, residues in SDP 145 and 146 do not contact the effector in PurR (1WET) and in TreR (1BYK), but the minimal distance to the effector in LacI (1JWL) is <5 Å. In general, the differences between three SDP sets, involved in strong contacts with effectors (Fig. 3 ▶), may reflect the difference in the size of effector molecules: guanine crystallized with PurR is significantly smaller than ONPF or threhalose-6-phosphate crystallized with LacI and TreR, respectively. This indicates that all SDP located near the substrate-binding pocket may be involved in identification of various effectors.

Figure 3.

Residues making close contacts with the effector (minimal distance <5 Å) in PurR, LacI, and TreR repressors (numbering as in PurR from E. coli).

SDP for the MIP family

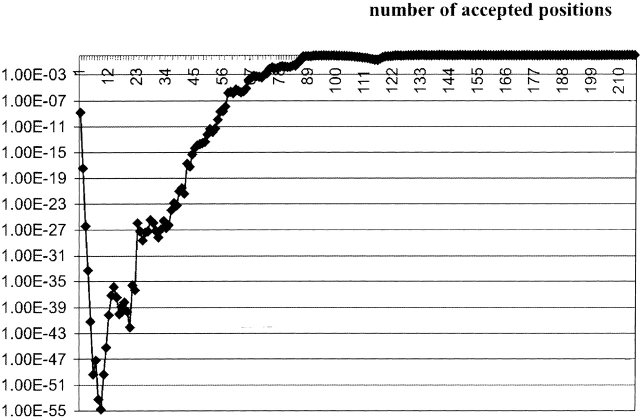
In this case, the Bernoulli estimator has two pronounced local minima with close values that produce 9 and 21 best Z-scores, respectively (Fig. 4 ▶). The list of these positions is given in Table 2. All SDP were mapped to the 3D structures of GlpF from E. coli and bovine AQP1 (Fig. 5 ▶).

Figure 4.

The Bernoulli estimator for the training set (17 bacterial MIP proteins). Horizontal axis: k, the number of accepted positions. Vertical axis: probability that there are at least k Z-scores Z ≥ Z_k.

Table 2.

Specificity-determining positions in water and glycerol transport proteins from the MIP family

Position		Amino acid residues in proteins of the training set			Description of the position
GlpF (E. coli)	AQP1 (bovine)	AQP group	GLP group	Z-scores	Water contacts, Å	AQP1 channel side	Glycerol contacts, Å	GlpF channel side	Interhelical interactions
207	198	SSSSSSS	DDDDDDDDDD	7.65E–12	5–7	Channel ?	5–7	Channel
236	214	FFFFFFF	PPPPPPPPPP	1.25E–11	5–7	Channel	7–10	Channel
48	58	FFFFFFF	WWWWWWWWWW	1.33E–11	<5*	Channel	<5*	Channel
135	127	GGGGGNG	FFFFFFFFFF	4.95E–11	7–10	Not helix	5–7	Not helix
159	151	FFFFFFF	LLLLLLLLLL	7.08E–11	<5*	Channel	<5*	Channel ?
187	178	LLLLLLL	IIIIIIIIII	8.33E–11	<5*	Channel	<5*	Channel
22	25	VVVVVVV	IIIIIIIIII	2.84E–09	5–7	Channel ?	7–10	Channel ?
195	186	IIIIILI	GGGGGGGGGG	3.88E–09	7–10	Channel ?	<5*	Channel ?
191	182	HHHHHIH	GGGGGGGGGG	1.60E–08	<5*	Channel	7–10	Channel
201	192	WSSSSSS	AAAAAAAAAA	2.48E–07	<5*	Not helix	<5*	Not helix
108	118	AAAAALA	YYYYYFYYYY	1.80E–06		Channel ?		Channel	+
137	131	LHHHHLH	TTTTTTTTTT	1.12E–05	5–7	Not helix	<5*	Not helix
211	202	AAAAAAA	KKKKRRRRRR	3.74E–05		Not channel	7–10	Channel ?
43	53	GGGGGGG	EEEEVVVVVV	7.92E–05		Not channel	7–10	Not helix	+
136	135	EEDEEEE	SSSSSSCSAS	9.77E–05		Not helix	5–7	Not helix
195	190	NNNNNGN	GGGGGGGGGG	1.02E–04	5–7*	Not channel	<5*	Not channel
194	185	SSSSSGS	MMMMLLLLLL	1.78E–04	7–10	Channel	7–10	Channel
24	27	GGGGGVG	FFFFFLLFLL	2.74E–04		Not channel	7–10	Not channel	+
20	23	WWWWWMW	LLLLLILIII	3.14E–04		Not channel	7–10	Not channel	+
200	191	TTTTTLT	FFFFYYYYYY	3.17E–04	<5*	Not helix	<5*	Not helix
193	184	VIIVIVI	SAASSSSSSS	8.53E–04		Not channel		Not channel	+

Asterisk (*): residues contacting the substrate (Fu et al. 2000; Sui et al. 2001).

Contacts: the minimal distance between the atoms of the current amino acid residue and the atoms of the substrate.

Channel side: orientation of the residues with respect to the channel, identified as follows: a vector perpendicular to the helix axis and pointing to the most exposed surface of the helix is calculated based on the residues solvent accessibility data published in the DSSP database (www.sander.ebi.ac.uk/dssp); the channel vector of a transmembrane helix is defined as the one opposite to the above defined vector; then for each residue the radius vector is computed as the vector perpendicular to the helix axis and pointing to Cα; finally, if the angle between the radius vector and the channel vector is smaller than 45°, the residue is labeled “channel”; if the angle is larger than 45° but smaller than 90°, “channel?”; in all other cases, “not channel.”

Not helix: residues not belonging to TM helices according to the secondary structure description in the corresponding PBD file.

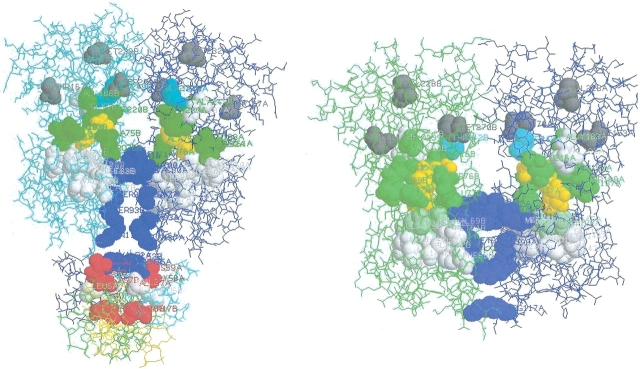
Figure 5.

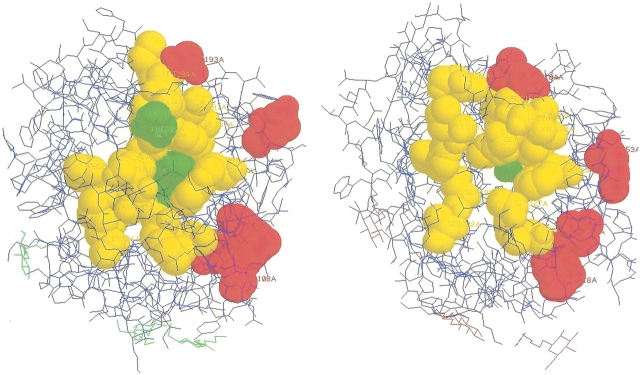
Candidate SDP for GlpF from E. coli and for bovine AQP1. (A) Structure of GlpF from E. coli with three glycerol molecules (top). (B) Structure of bovine AQP1 with several water molecules in the channel (top). Substrate molecules are shown by space filling and colored green. Candidate SDP are shown by space filling and colored yellow if they form the channel and red if they may establish subunit interactions (see the text for discussion).

Among the candidate SDP, there are positions 48W, 200F in GlpF (corresponding to 58F, 191C in bovine AQP1), which are described as forming the narrowest constriction region of the pore, possibly critical for the pore selectivity (Fu et al. 2000; Sui et al. 2001). The third residue that forms this constriction region, 206R of GlpF (197R of bovine AQP1) is conserved in both groups of the MIP family. Another residue critical for the water transport in AQP1, 182H, also was selected as an SDP.

Twelve residues, namely, 48W, 52V, 66H, 67L, 68N, 159L, 187I, 199G, 200F, 201A, 203N, and 206R, interact with glycerol in GlpF of E. coli (Fu et al. 2000). In bovine AQP1, the channel hydrophobic face is formed by 58F, 74G, 75A, 76H, 77L, 78N, 182H, 190G, 191G, 192G, 193I, 194N, 197R (Sui et al. 2001). Among the twelve residues interacting with glycerol, five residues, namely, 52V, 66H, 68N, 203N, and 206R, are conserved in both groups, and six residues (48W, 159L, 187I, 201A, 199G, 200F) are among predicted SDP. The majority of the 13 positions that form the hydrophobic face of the channel in bovine AQP1 are either conserved (74G, 76H, 78N, 194N, 197R) or predicted to be specificity determining (58F, 182H, 190G, 191G, 192G). Moreover, we identified two additional positions, namely, 195G and 137T in GlpF from E. coli (186I, 131L in bovine AQP1) that form a close contact with the substrate (see Table 2).

Generally, most candidate SDP either form a close contact with the heteroatoms (glycerol for GlpF of E. coli and water inside the conducting channel for bovine AQP1 [Fu et al. 2000; Sui et al. 2001)] or lie on the channel side of the alpha helices that form the channel (Fig. 5 ▶).

Most of the remaining candidate SDP, namely, 108Y, 43E, 20L, 24F, 193S in GlpF of E. coli, are possibly involved in formation of the tetrameric structure. They are located on the surface of the proteins and form two planes with the right angle between them (Fig. 5 ▶). Moreover, they are shown either to belong to helices contacting the neighboring monomer or to establish the helix–helix interactions (Table 2; Murata et al. 2000). Unfortunately, this cannot be confirmed by detailed structural analysis, as there are no known structures of MIP proteins involving more than one monomeric subunit.

A procedure for identification of new members of specificity groups

Twenty-four SDP predicted for bacterial proteins from the MIP family, which comprise ~10% of the MSA length, were used to score 44 bacterial proteins of this family. A protein was considered as recognized by a profile if the profile score (W_profile) of this protein exceeded 3.0. The results are shown in Figures 6 ▶ and 7 ▶.

Figure 6.

The phylogenetic tree of the proteins from MIP family (after the realignment, both training and test sets are included). The branch colors indicate orthology relationships: blue, bidirectional best hits (BETs) of AqpZ E. coli AQPZ_ECOLI); green, true GlpF orthologs, that is, BETs of GlpF from E. coli for gram-negative bacteria and BETs of GlpF from Bacillus subtilis for gram-positive bacteria if their genes lie in operons related to the glycerol metabolism; light green, recent GlpF paralogs whose genes lie in operons involved in the glycerol metabolism; purple, proteins homologous to PduF from Salmonella typhimurium whose genes are located in the gene cluster related to the propanediol degradation; brown, glyceroaquaporins, that is, BETs of GLA from Lactococcus lactis; magenta, true paralogs, that is, GlpF homologs whose genes lie in operons with functions other than glycerol metabolism; orange, proteins with unresolved orthology relationships. The colors of the protein names indicate the protein specificity assigned by SDP profiles: blue, proteins selected by the AQP SDP profile (W_AQP3); green, proteins selected by the GLP SDP profile (W_GLP3). The names of the proteins from the training sets for AQP and GLP groups are in bold. Bold red, eukaryotic MIP proteins.

Figure 7.

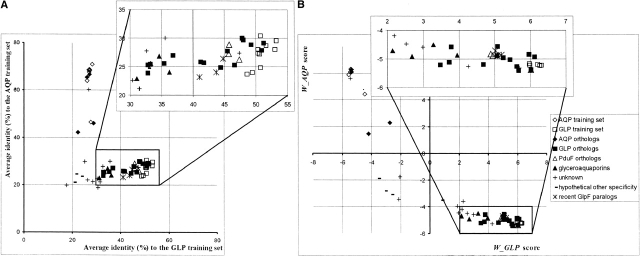
The protein function predicted by the SDP profile score. (A) Average identity of the test proteins to the proteins from the AQP and GLP training sets. (B) Scores of the proteins from the test set computed using the AQP and GLP profiles. For the interpretation of colors, see the legend to Figure 6 ▶.

All fifteen true orthologs and three recent paralogs (probably having the same function) of the GLP group were recognized correctly. Note that true GlpF orthologs from genomes Xylella fastidiosa, Xanthomonas campestris, Deinococcus radiodurans, and Borrelia burgdorferi were recognized correctly. These proteins have relatively weak similarity to the training set (average identity 33%–37%) and form separate branches in the phylogenetic tree (Fig. 6 ▶). But if only the SDP are considered, these proteins are 65%–72% identical to the proteins from the GLP training set. It is interesting that two examples of eukaryotic GLP proteins (human and rat AQP7) included in the MSA also are well recognized by the bacterial GLP profile (W_GLP = 4.3, W_AQP = −4.4), whereas eukaryotic AQPs differed significantly from both the bacterial GLP profile (W_GLP = −3.2 and 3.5 for the human and rat AQP7, respectively) and the bacterial AQP profile (W_AQP = 0.5 and 1.1, respectively).

On the other hand, two glyceroaquaporins are not recognized by either profile and two more glyceroaquaporins have relatively weak scores (see Fig. 7B ▶). These proteins are known to transport both water and glycerol (Froger et al. 2001). A detailed analysis shows that four amino acid residues differ systematically in glyceroaquaporins from those in glycerol facilitators and aquaporins, namely, 48W→Y, 187I→V, 191G→V, 200F/Y→P (the numbering as in GlpF from E. coli). In three of the four cases, the amino acid residues are substituted to smaller and less hydrophobic ones, probably making the channel permeable for water.

The specificity of the MIP family members from all mycoplasmas could not be identified. Although described as essential both in the glycerol and water transport mechanisms, the position corresponding to 200F of GlpF from E. coli can be occupied by a variety of amino acid residues (Y, C, S, T) in mycoplasmas. Moreover, of the five positions probably involved in subunit contacts, only one is conserved. This indicates that in mycoplasmal proteins, the interactions between the subunits are significantly different from those in all other studied GLP proteins.

PduF from Salmonella typhimurium and its orthologs are recognized by the GLP group profile. PduF is annotated as the propanediol diffusion facilitator (Daniel et al. 1999), and its gene is located divergently to the pdu operon that contains genes involved in the propanediol degradation. To the best of our knowledge, there are no experimental data about specificity of this protein to either propanediol or glycerol, which differ by only one hydroxyl group.

The SDP profiles do not accept true distant paralogs, for example, three orthologous proteins from alpha-proteobacteria, namely, Q92R43 from Sinorhizobium meliloti, Q98J02 from Mesorhizobium loti, and Q9A860 from Caulobacter crescentus. All three corresponding genes are located in one operon with putative arsenate reductase and a transcriptional regulator from the ArsR family. It is quite likely that these proteins mediate transport of arsenite/arsenate or other ions.

Discussion

We developed and implemented a technique for identification of SDP in protein families. Although obvious in small and evolutionary compact protein families, these positions are not easy to find without numerical analysis in large and complicated families that contain many specificity groups. Our method requires a multiple alignment and information about specificity of some members of a protein family. On the other hand, it does not rely on data about the 3D structure of the proteins. Instead, we used resolved 3D structures to test the obtained predictions. The SDP prediction method is based on the assumptions made in Mirny and Gelfand (2002): (1) Specificity groups in large protein families of homologous proteins are formed by orthologs; (2) the MSA is consistent with the structural alignment—that is, the aligned residues have similar spatial location; (3) specificity-determining residues have similar location in paralogous proteins. These assumptions, though not self-evident, seem to be strongly supported by available experimental data. For some families of enzymes, it was shown that positions of catalytic residues in the protein structure are conserved, although their identities and role in catalysis vary (Hasson et al. 1998).

The proposed method identifies positions for which the amino acid distribution is closely associated with functional grouping. We propose two different measures of association: the relative entropy and the mutual information. Until now we have not observed any substantial difference in results obtained using these measures. Further investigation may lead to deeper understanding of this issue.

The method identifies positions that are conserved within specificity groups but vary between the groups. Thus, it does not accept as SDP positions that may be essential for the protein function but are well conserved in the whole family. Generally, the residues that lie in the regions of contact and are likely to be functionally important are either absolutely conserved or specificity determining. Table 3 presents contacting residues of GlpF from E. coli. One can observe that the ratio of tightly contacting residues in SDP and in the set of absolutely conserved positions is much higher than in the protein on average (~¼ in both cases versus 1/10). No standard performance measures can be applied to these predictions, as there is no standard definition of a specificity-determining residue, and the experimental data are insufficient. However, there are contacting residues whose function is unclear. For example, although 138Y of GlpF is <5 Å away from the substrate in the resolved 3D structure, this position in orthologous proteins can be occupied by Y, G, D, A, and V residues with significantly different physical properties.

Table 3.

Statistics of the residues in the GlpF from E. coli (1FX8) that are in contact with cocrystallized glycerol molecules

		The number of contacting positions in different subsets
		SDPs	Absolutely conserved in all sequences from the training set	Other	Total MSA
Residues contacting the glycerol molecule	Tight contacts, Dmin ≤ 5 Å	6	10	11	27
	Medium contacts, 5<Dmin ≤ 7 Å	4	4	9	17
	Weak contacts, 7<Dmin ≤ 10 Å	4	18	40	62
	Total	27	41	181	249

The method was tested on two protein families of very different function. In both cases, the obtained results are consistent with the available data about the protein spatial structures and the experimental data about the protein function and the functional role of particular residues.

The set of SDP predicted for the LacI family includes positions described in Mirny and Gelfand (2002) and thus our results generally agree with the results of that study. Structural analysis of the SDP reveals that they mainly belong to three spatial groups: the DNA-binding region, the effector-binding pocket, and the surface of contact between subunits. As discussed in Mirny and Gelfand (2002), residues 15T, 16T, and 55K were shown to be critical for the DNA-binding specificity by a series of mutant experiments (Lehming et al. 1990; Sartorius et al. 1991; Glasfeld et al. 1997). These positions are among the predicted SDP. Twenty-four of 40 candidate SDP contact DNA, effector, or the other subunit of the dimer in the analyzed 3D structures under a very strict criterion of contact. Some of the remaining SDP contact the effector in one protein only and thus do not satisfy the criterion. They are located near the effector-binding pocket and possibly contribute to the effector recognition, but their exact function is unclear. 147W is an example of such position. It was predicted to be specificity determining in Mirny and Gelfand (2002). Although it does not contact guanine in the structure of PurR, this residue is essential for binding the corepressor (Huffman et al. 2002). Notably, this position is variable in four specificity groups. The same holds for position 55K, which is also not conserved in four groups, but is essential for binding. One more such position is 126Y, which is conserved in 10 groups and variable in 5 groups. These examples demonstrate that the SDP prediction method is capable of identifying such positions, which may be important when some substrates are much smaller than others. Another interesting example is 145M. It contacts ONPF in LacI (PDB identifier 1JWL), but does not contact guanine in the PurR (1WET). It would be interesting to test the importance of this residue for the purine binding.

The predicted SDP for the MIP family are mainly located in two spatial regions. They either form the conducting channel or participate in establishing the tetrameric structure. Two of three residues that are critical for the pore selectivity (Fu et al. 2000; Sui et al. 2001), namely, 48W and 200F of GlpF from E. coli, are among predicted SDP, and the third one, 206R, is strictly conserved in both considered groups. All residues that were described as interacting with the substrate and that are not conserved in both groups also are among the predicted SDP. Moreover, we identified as SDP some new residues that contact the substrate tightly (195G, 137T) or lie on the channel side of the channel-forming alpha helices. The remaining candidate SDP lie on the surface of the protein and likely form the tetrameric structure. Candidate SDP 236P, 207D, and 211K were experimentally shown to be critical for function (Lagrée et al. 1999). Mutations in positions corresponding to 207D and 211K in aquaporin 1 from Cicadella viridis to amino acids characteristic for the glycerol channel lead to the loss of ability to transport water. Similar joint mutations in positions corresponding to 236P and 237L lead to a change of function in glycerol transport.

Additionally, we present a simple and natural method for the specificity assignment. A recognition profile is constructed using only the SDP. Such profiles identify members of specificity groups better than the average protein similarity. This is additional evidence that SDP better discriminate between the specificity groups than do complete protein sequences.

Thus, we suggest the following scheme for analysis of a protein family. It does not require any assumptions about the biochemical function of the proteins, and thus can be applied to any family of homologous proteins.

First, preliminary specificity groups are identified by comparative genomic techniques (database similarity search, analysis of positional clusters and phylogenetic profiles, prediction of regulation, identification of protein functional signatures, etc.). These groups should be formed only by unambiguously orthologous proteins having the same specificity, although it is not required that proteins from different groups have different specificities. These groups constitute the training set. The union of the groups in the training set should not necessarily cover the entire family.

Second, all proteins in the training set are aligned and the SDP are identified. This procedure is completely formal and does not require any additional knowledge about the protein family. The predicted set of SDP can already be used for planning experiments on functional analysis or protein redesign.

Third, the remaining proteins are aligned to the training MSA and scored using the SDP profiles. This procedure may identify proteins whose specificity coincides with the specificity of one of the groups in the training set. The degree of certainty of this prediction can be higher than that of prediction based on the average protein similarity. In addition, the initially identified specificity groups can be scored using these profiles. This might identify paralogous groups that have the same specificity.

Similar approaches were described in Mirny and Gelfand (2002) and Hannenhalli and Russell (2000). The new features of the SDP prediction method are that: (1) It incorporates information about evolutionary distance within and between groups; (2) amino acid substitutions within specificity groups are weighted using a suitable amino acid substitution matrix, and thus substitutions of residues having similar physical properties are only weakly penalized; (3) the procedure for separation of SDP, B-cutoff, is absolutely formal and does not depend on specific properties of the protein family under analysis. Thus, the SDP prediction method does not contain any ad hoc parameters and can be applied to any family of homologous proteins in a standard way.

Materials and methods

Position score: Relative entropy and mutual information

As a measure of the association of the amino acid distribution with the specificity, we use the relative entropy and the mutual information. Both concepts were previously used for similar purposes (Hannenhalli and Russell 2000; Mirny and Gelfand 2002).

Consider position p of an MSA. Let α = 1,. . .,20 be a residue type and let i = 1,. . .,N denote a specificity group, where N is the total number of specificity groups. Then the relative entropy S_p at position p is defined by:

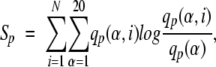where q_p(α,i) is the ratio of the count of residue α at position p in group i to the size of group i, q_p(α) is the frequency of residue α in whole alignment column p. The relative entropy is also known as the Kullback-Leibler distance (Cover and Thomas 1991) and can be considered as a distance between two distributions, the distribution of the residue frequencies in group i and the distribution of the residue frequencies in the whole alignment column. Particularly, S_pis always nonnegative, and S_p = 0 if and only if two distributions are identical.

The mutual information I_p (Cover and Thomas 1991) at position p is defined by:

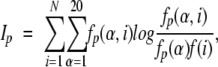where f_p(α,I) is the ratio of the number of occurrences of residue α in group i at position p to the length of the whole alignment column, f_p(α) is the frequency of residue α in the whole alignment column, f(i)is the fraction of proteins belonging to group i. The mutual information reflects the statistical association between two discrete random variables α and i. I_p is always nonnegative, I_p = 0 if and only if α and i are statistically independent. The larger I_p is, the stronger α and i are associated in position p of the MSA.

Unfortunately, the small sample size and the biased composition of each column strongly distort both S and I. Thus, we have to compute the statistical significance of these values (see following).

Further formalism for S and I is the same; therefore, following it is carried out only for the mutual information.

Modification of the amino acid frequencies using amino acid substitution matrices

Both the relative entropy and the mutual information are designed for probability distributions. However, the considered amino acid frequencies arise from a small and probably biased sample. To smooth these frequencies, we used the amino acid substitution matrices corresponding to the average evolutionary distance within a group or between the groups of the MSA. This approach has the following additional advantages: First, the amino acid substitutions are treated according to their probabilities, so that substitutions of residues having similar physical properties are only weakly penalized. It is possible to use different matrices for protein segments with different amino acid composition and statistical properties, for example, transmembrane segments and globular domains (see following). Second, the difference of the evolutionary distance within different specificity groups and between these groups is taken into account. Additionally, zero frequencies are avoided automatically, and thus the necessary pseudocounts are introduced in a natural way. As usual, the pseudocounts are proportional to the square root of the sample size (Lawrence et al. 1993). Thus the added sequences will not influence large samples much but will probably correct the composition of small ones.

Thus, instead of using f(α,i) = n(α,i)/n(i), where n(α,i) is the number of occurrences of residue α in group i, n(i) is the size of group i (i can be a single group or the whole alignment), we use “smoothed frequencies”:

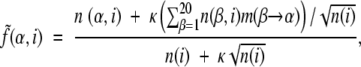where m(β→α) is the probability of amino acid substitution β→α according to the matrix chosen for group i, 0 ≤ κ ≤ 1 is a smoothing parameter. When calculating q(αi), n(i) is the size of groupi. When calculating q(α), f(αi), or f(α), n(i) is the size of the whole alignment column. Testing demonstrated that the obtained SDP set is robust as regards the exact choice of κ, 0.5 ≤ κ ≤ 1. The presented results were obtained for κ = 0.5.

We use the BATMAS series (Sutormin et al. 2003) as the amino acid substitution matrix for positions within transmembrane segments of transporters from the MIP family, and the BLOSUM series (Henikoff and Henikoff 1992) for position within loops of the transporters and for all positions in globular proteins from the LacI family. In all cases, we use the matrix for the evolutionary distance corresponding to that in the given specificity group or the protein family. For instance, BATMAS30 is used for groups with average identity between 30% and 40%, BATMAS40 in case of average identity between 40% and 50%, and so forth. Because the publicly available BLOSUM matrices correspond to the identities not exceeding ~60%, we derived matrices for groups with average identity >60% using the technique described in Sutormin et al. (2003).

A well-known problem is the interpretation of columns of the MSA that contain gaps. Here gap positions were treated as follows. A column of the MSA was ignored if either >30% of its constituents were gaps, or if only one group contained nongap constituents. If the i-th group contained only gaps in MSA position p, we assumed I(p,i) = 0. In the remaining cases, gaps were considered as an additional amino acid that was treated specifically when computing I: we assumed n(gap,i) = 0, m(α→gap) = m(gap→α) = 0.

Statistical significance

Following Mirny and Gelfand (2002), we compute the statistical significance of the observed values of the relative entropy or the mutual information using a procedure of random shuffling (Good 1994).

Consider a position of the MSA and compute I as described earlier. Then shuffle the column 10,000 times, that is, randomly change the content of the groups but retain their size and the column’s amino acid composition, and derive the distributions of the relative entropy and the mutual information F(I^sh) for the shuffled column. The I^sh values are systematically lower than those for an unshuffled column. This is a consequence of the fact that evolutionary distances within orthologous groups are systematically lower than between the groups.

The expected relative entropy and the expected mutual information are computed using a linear transformation:

I^exp = aI^sh + b,

where a and b do not depend on the position, that is, are the same for every position of the alignment. We calculate them by minimizing the difference between the observed values and the average expected value:

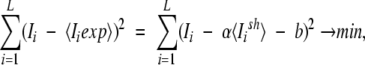where L is the total length of the alignment, I_i is the observed mutual information for the i-th column.

Z-scores are calculated as:

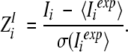High Z-scores 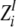indicate that for this position the residue distribution is much stronger associated with the grouping than for an average position of the MSA.

The Bernoulli estimator (B-cutoff)

Given a series of Z-scores corresponding to every position of an MSA, one needs to evaluate the significance of the Z-scores in order to tell whether the observed Z-score is sufficiently high to indicate an SDP. We developed an automated procedure for setting the thresholds based on computation of the Bernoulli estimator that has been applied in another context in (Vinogradov and Mironov 2002). This procedure does not rely on any properties of the considered protein family and thus the cutoff is selected automatically, in contrast to ad hoc setting in all previous studies. The idea of this procedure is to select those positions that are the least probable to arise by chance, assuming the Gaussian distribution of Z-scores.

Order the observed Z-scores by decrease: Z₁,Z₂,. . ., and find k such that

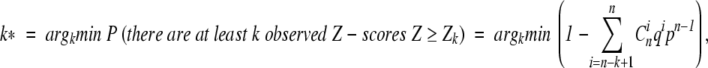where n is the total number of considered positions,

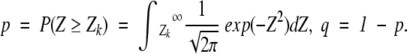Thus, as a null hypothesis, following Mirny and Gelfand (2002), we assume that all Z-scores arise from the standard Gaussian distribution. Then we find k* highest scores that are the least probable to constitute the tail of the Gaussian distribution, and thus indicate nonrandomly generated positions.

The described procedure relies on the distribution of Z-scores. It can be shown that the distribution of the mutual information asymptotically lies between the Gaussian and exponential distributions. On real data, the procedure is robust relative to the distribution, and the set of SDP is almost the same assuming Gaussian and exponentially distributed Z-scores.

The obtained k* is called the Bernoulli estimator, or the B-cutoff. It gives the number k* of high-scoring positions that are predicted to determine the specificity.

Assignment of specificity to new members of protein families

Using an obtained set of SDP, one can build a profile (SDP profile) for every specificity group in a standard way. The weight of amino acid α at position p in the profile for group i is

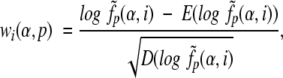where 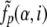is the smoothed frequency of α in group i at position p calculated as described earlier using the matrix selected for group i, E(•) and D(•) are the mean and the variance over all positions of the considered MSA, respectively, given a prior distribution of amino acid frequencies (as the prior distribution, we take the frequencies of amino acids in the whole MSA). For a new protein we calculate N profile scores:

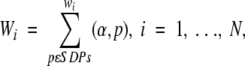where α is the amino acid in position p in the new protein and N is the total number of the specificity groups. With this choice of the positional weights, the score of a target sequence by the profile for a given group is a linear function of the logarithm of the probability that the target sequence was generated by the positional probabilities of amino acids for this group (e.g., Berg and von Hippel 1987). The maximum of W_i indicates that the new protein most probably belongs to the i-th specificity group.

To estimate the significance of such predictions, we calculate 1000•N scores 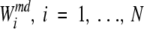, using random profiles, that is, profiles built by random sampling of m positions from the given MSA (m is the number of positions in the SDP profile). To identify how well the SDP profile distinguishes between the specificity groups, we calculated the following Z-scores:

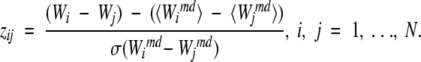High positive Z-scores for all j indicate that the new protein is more similar to the i-th specificity group in the SDP than to any other j-th group, and that the level of similarity of the new protein to the i-th group in SDP significantly exceeds that expected given the average similarity.