Analysis of forces that determine helix formation in α-proteins

Abstract

A model for prediction of α-helical regions in amino acid sequences has been tested on the mainly-α protein structure class. The modeling represents the construction of a continuous hypothetical α-helical conformation for the whole protein chain, and was performed using molecular mechanics tools. The positive prediction of α-helical and non-α-helical pentapeptide fragments of the proteins is 79%. The model considers only local interactions in the polypeptide chain without the influence of the tertiary structure. It was shown that the local interaction defines the α-helical conformation for 85% of the native α-helical regions. The relative energy contributions to the energy of the model were analyzed with the finding that the van der Waals component determines the formation of α-helices. Hydrogen bonds remain at constant energy independently whether α-helix or non-α-helix occurs in the native protein, and do not determine the location of helical regions. In contrast to existing methods, this approach additionally permits the prediction of conformations of side chains. The model suggests the correct values for ~60% of all χ-angles of α-helical residues.

Although the α-helical conformation of the polypeptide chain was successfully predicted by Pauling and coworkers as early as 1951 (Pauling et al. 1951), the role of different forces that determine the helix formation is still being studied. The α-helix was shown as the most stable and energetically favorable configuration of the protein polypeptide chain. Pauling made this remarkable prediction on the basis of calculations of the optimal van der Waals interactions of the main-chain atoms with each other and with the side-chain atoms. At the same time, the principle of the maximal saturation of interpeptide hydrogen bonds was proposed. In the α-helix in its canonical Pauling form, all hydrogen bonds were formed by intramolecular interactions. The interactions between side chains were not discussed at that time.

In native proteins, the order of amino acids in the sequence influences the presence of the α-helical conformation, as exemplified by the statistics of residue distribution along the α-helices (Kumar and Bansal 1998). Nevertheless, those secondary structure prediction methods, which are based only on residue propensities derived from occurrence statistics, have failed to predict above 65% accuracy for a single polypeptide chain (Barton 1995). As a consequence, prediction algorithms were developed that used evolutionary information and were based on homology alignments (Rost 2001). The significant role of side-chain interactions for α-helix formation was described recently and analyzed extensively, both theoretically and experimentally (Fisinger et al. 2001). Current thinking on the matter implies that for the more accurate prediction, one should take into account the physical reasons for α-helix stabilization and address the question of the ratio between interactions in the local sequence and in the tertiary structure, that is, between the local and long-range interactions.

The role of different forces that favor the formation of an α-helix is also not fully resolved. Hydrogen bonds were initially suggested as the main contributor to protein stability; later, the hydrophobic effect became the first candidate (for an excellent historical review, see Pace et al. 1996). Recently, the focus has been on the balance between hydrogen bonds and hydrophobic effect as important factors for the stability of α-helices, both in native proteins (Krantz et al. 2002) and in models (Huang et al. 2002). Most of the work in this field is based on studying either model polypeptides or complete proteins. The models use only artificial sequences, mainly polyAla-based peptides (Chakrabartty and Baldwin 1995). Studies on native proteins reveal either single amino-acid propensities (Chakrabartty and Baldwin 1995) or integrative characteristics of the protein structure, from which it is difficult to separate the contributions of different types of secondary structure (Robertson and Murphy 1997; Krantz et al. 2002). In this work, we do not address the importance of the particular forces acting in folding/unfolding of modeled helical compounds. By using a sequence-specific model for the native proteins, we instead aimed to reveal the forces that favor α-helices in comparison to non-α-helical regions of a polypeptide chain.

Recently, we proposed a wholly α-helical model of a protein molecule for studying the contribution of local amino-acid sequence to the formation of α-helical conformations (Kilosanidze et al. 2002a,b). The segments of the polypeptide chain that are predisposed to α-helix formation and are helical in the native protein retain this property in our continuous model of an α-helix for the whole chain. In the current work, we demonstrate how this strategy allows us to identify α-helical patterns of the sequence showing sufficient stability in terms of the model. The role of local interactions along the primary structure of the protein for the formation of α-helical structure is discussed in terms of the contribution of different forces.

Results and Discussion

The main energy term

In the previous study (Kilosanidze et al. 2002a,b), it was shown that the artificial α-model can predict amino-acid sequences that are biased to form α-helices, as well as those that will not adopt α-helical conformation. The prediction for a given sequence can be deduced from the van der Waals energy profile of a hypothetical continuous α-helical conformation of the sequence. In the present work, we have analyzed the influence of hydrogen bonding and electrostatic forces in the stabilization of the model structure, in which interactions in tertiary structure (long-range interactions) are lacking.

Figure 1A ▶ illustrates the contributions of those force-field components into the total energy profile of cytochrome C-553 (PDB code 1c75) amino-acid sequence as an example. The contribution of the combined hydrogen bonding and electrostatic components to the energy is ~20% in the α-helical regions. This local contribution of nonsteric interactions to the stabilization of an α-helix is thus significantly less then the van der Waals interactions.

Figure 1.

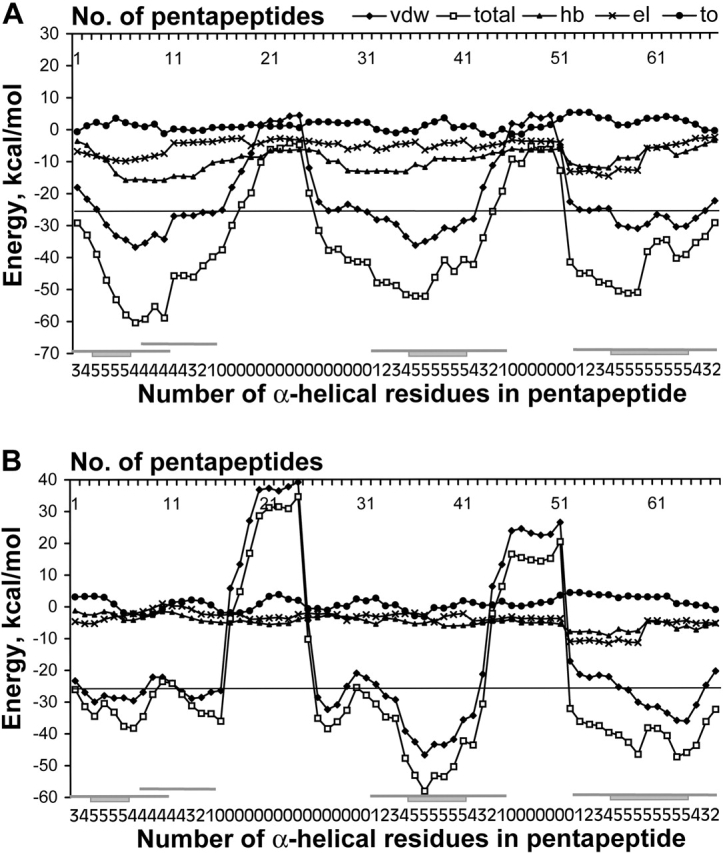
Total and all components energy profiles for α-helical model of cytochrome (PDB code 1c75). (A) Profiles are calculated for the standard stereochemistry of residues. (B) Profiles are calculated for the native stereochemistry of residues. Designations of energy terms are as follows: (total) total energy; (vdw) van der Waals energy; (hb) energy of hydrogen bonding; (el) energy of electrostatic interactions; (to) torsion energy. Along the axis of pentapeptide each point, i corresponds to the energy calculated for a pentapeptide fragment comprising residues i to i+4. The line for prediction of α-helices is drawn at −26 kcal/mole (see section “Choice of energy threshold” in Results and Discussion). Designations of regions of α-helices in the native protein are beneath the graph and are as follows. For each pentapeptide fragment, a number of residues that are α-helical in the native structure of the protein is indicated. Rectangle and adjunct lines denote, respectively, the wholly α-helical pentapeptides and the pentapeptides, including at least one α-helical residue in accordance with the native structure of the protein.

Additionally, electrostatic and hydrogen-bonding terms vary slightly along the polypeptide chain of the model; the average absolute variances of both terms along the model are only 0.95 kcal/mole for each of the profiles, and 0.86 kcal/mole for the torsion profile, whereas the variance of total energy amounts to 4.75 kcal/mole. The major point shown by this analysis is that the variation of these components’ profiles does not correlate with the regions that are α-helical in the native structure of the cytochrome molecule.

It can be argued that specific packing of side chains may disturb the main-chain hydrogen bonds in some cases. We do not find this hypothetical effect either in the segments that are α-helical in the native structures or in the segments that are non-α-helical in all proteins analyzed.

On the other hand, profile minima of the model structure of cytochrome occupy the same positions, both for the total energy and the van der Waals component energy, and correspond to three α-helices in the native structure of the protein (see Fig. 1A ▶). Moreover, the trace of the total energy profile for the model mainly follows the van der Waals component trace. The van der Waals term varies significantly along the model, with average absolute variance 3.41 kcal/mole, that is, fourfold more than hydrogen bonding or electrostatic energies. Thus, it is the van der Waals term that determines the barriers on the graph and the regions of amino-acid sequence that cannot adopt α-helical conformation.

Comparison of structures modeled with standard and native geometry

Because this method is applicable for secondary structure prediction as shown previously (Kilosanidze et al. 2002a) and discussed in more detail below, we used the steric parameters with standard values according to Scheraga and coworkers (Nemethy et al. 1992) for the modeled structure. Only χ-, ϕ- and ψ-angles were changed as described in Material and Methods. We wondered whether the real stereochemistry observed in experimental structures have significant influence on energy of stabilization of α-helices, and which of the energy terms are affected in the main.

We constructed the continuous α-helical model for the same cytochrome amino-acid sequence, but the steric parameters were obtained from high-resolution X-ray data (0.97 Å resolution, PDB code 1c75). The χ-, ϕ-, and ψ-angles were changeable again under structure optimization.

The profiles of either the total or the van der Waals energies reproduce in general the trace of respective profiles for standard geometry (Fig. 1B ▶). Residue-by-residue accuracy Q₃ of prediction for α- and non-α-helical regions for the cytochrome amounts to 84% by standard geometry and 78% by experimental geometry.

The van der Waals energy component is mostly affected by the discrepancy of experimental geometry from standard geometry in contrast to hydrogen bonding and electrostatic interactions. Nevertheless, as one can see for the profile of the model with experimental geometry (Fig. 1B ▶), the van der Waals component also determines the total energy profile, whereas hydrogen bonding and electrostatic interactions again give only minor contributions to the total energy profile. The comparison of the profiles of both models thus confirms the correct choice of the van der Waals energy for determination of α-helical conformation in the presence of local and absence of long-range interactions.

Some important differences in energy between ideal—that is, constructed with standard stereochemistry—and experimental models should be mentioned as well. In the ideal model, the hydrogen bonds form a classic α-helical regular net, interrupted only by prolines. The hydrogen bonds have hydrogen-acceptor length close to the ideal – the average length is 1.88 Å. On the other hand, the hydrogen bonds in the experimental model are less energetically stable, which is observed on the profile as a decrease of hydrogen-bonding energy (Fig. 1 ▶, cf. B and A). The average length of the hydrogen bonds in the experimental model is 2.1 Å. Some bonds are lost in regions corresponding to non-α-helical patterns in the native structure of the protein (data not shown). Thus, the real stereochemistry does not favor, in principle, the formation of a regular net of the hydrogen bonds in non-α-helical regions of native proteins.

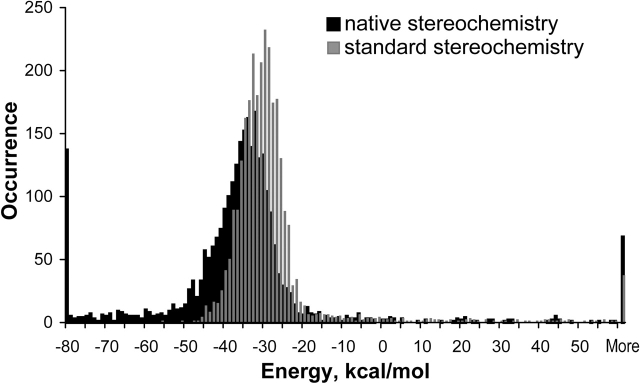
Energy distributions of standard and native models

We performed an extensive comparative analysis of energies of pentapeptide fragments that are entirely α-helical in the native proteins for the models both with standard and experimental values of angles and bond lengths. The analyzed set of 58 different protein domains consists of 2796 pentapeptide fragments (Fig. 2 ▶). As observed in the figure, the main parts for energy distributions of α-helical pentapeptide fragments occupy similar energy regions for both types of geometries. This means that the real stereochemistry of the protein as a result of its tertiary structure does not have a significant influence on the energy of local stabilization of α-helices. Therefore, this confirms the applicability of our method, which is based on the standard geometry for the purposes of prediction and energy description of helices.

Figure 2.

van der Waals energy distributions of entirely α-helical pentapeptide fragments for the model with standard stereochemistry of residues and the model with experimental stereochemistry of residues in the native structure of the tested proteins.

A total of 90% percent of α-helical pentapeptide fragments that had been modeled with standard parameterization fell into the region between −22 and −41 kcal/mole, whereas the same amount of pentapeptides modeled with experimental geometry occupied a rather broad energy region from 2 to −71 kcal/mole. The low-energy tail for the latter resulted from the necessity of compensation of high-energy regions during optimization of the experimental model. Such regions of the polypeptide chain correspond to loops in the protein structure. Errors in experimental X-ray data in determination of atom coordinates in loop regions occur more frequently than in regions of standard conformations, resulting in an overestimation of the van der Waals energy of loop regions. Generally speaking, both distributions follow the Gaussian distribution, providing evidence of the rationality of this approach.

Energy profiles of α-helical model of de novo and nonglobular proteins

De novo proteins

We took into consideration not only natural proteins, but also some de novo-designed proteins. Such proteins are usually solved to high resolution, reducing the influence of errors in α-helix boundaries. Of special interest, was the examination of a short polypeptide chain without long-range interactions in the native structure of the protein. For example, Figure 3A ▶ shows the energy profile of the α-helical model for designed alpha-1 peptide (PDB code 3al1) of 13 amino acids in length, which consists of only one α-helix. Both ends of the helix are predicted correctly and all residues are predicted to be α-helical.

Figure 3.

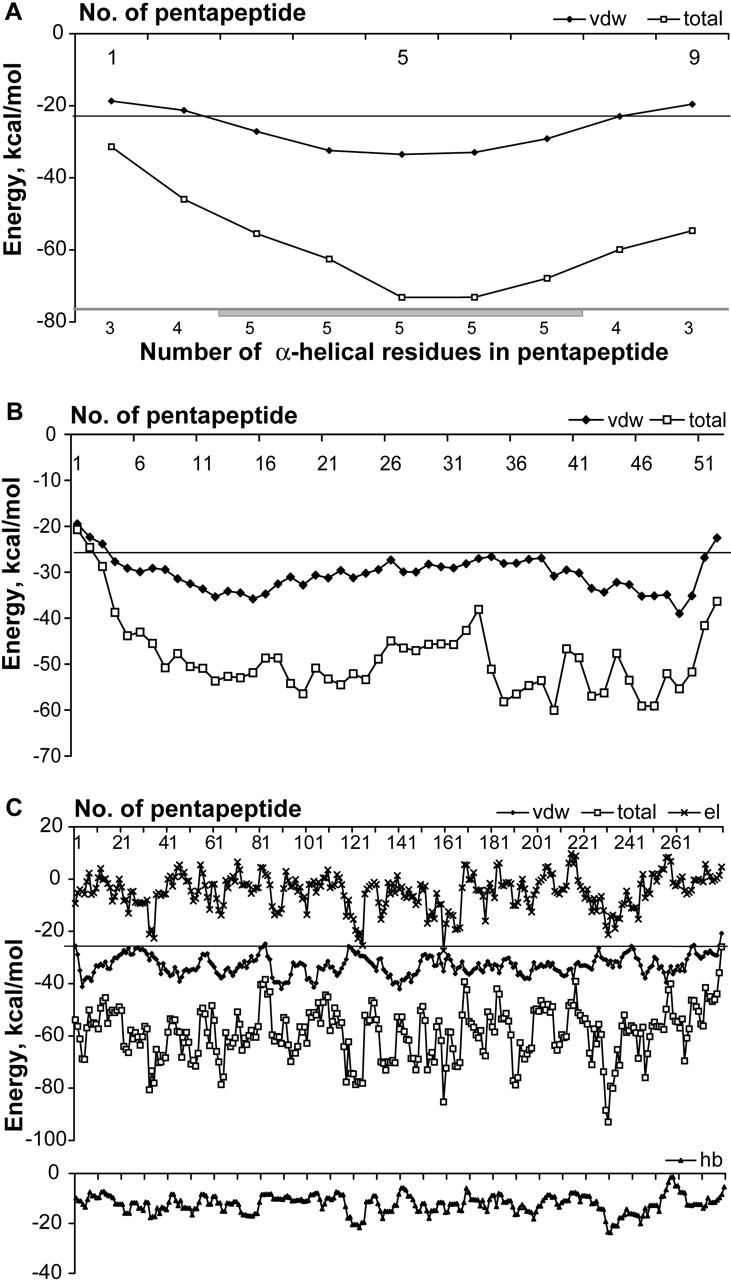
Energy profiles of α-helical models of de novo and nonglobular proteins. Energies are calculated for the standard stereochemistry of residues. All notations are as in Figure 1 ▶. (A) Total and van der Waals energy profiles for the designed alpha-1 peptide (PDB code 3al1). (B) Total and van der Waals energy profiles for the membrane protein (PDB code 1eq7). (C) Total, van der Waals, electrostatic interaction, and hydrogen-bonding energy profiles of α-helical model for tropomyosin (PDB code 1c1g).

Nonglobular proteins

The usability of the method was also analyzed for a number of nonglobular proteins, namely, some membrane and viral protein domains (e.g., see Fig. 3B ▶) and tropomyosin (Fig. 3C ▶). It was confirmed that our approach is applicable for such types of proteins.

Tropomyosin represents a typical fibrous protein and consists of a parallel coiled coil with periodic patterns of amino acids along the sequence (Brändén and Tooze 1999; Hitchcock-DeGregori et al. 2001). Such sequences are repetitive with a period of seven residues. The analysis of the energy profiles for the protein 1c1g (Fig. 3C ▶) has revealed the same periodicity (6–7 residues) inherent in our model constructed for this tropomyosin. A distinguishing feature of this result is that the determinative component for the trace of the total energy profile of this protein is the electrostatic and not the van der Waals component; nevertheless, the van der Waals energy is still typical for α-helical patterns.

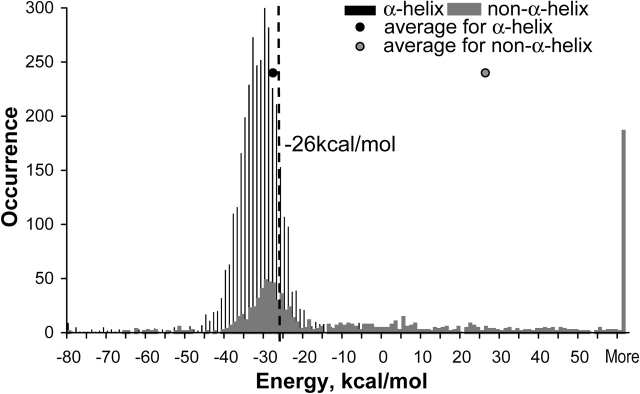
Choice of energy threshold

In a previous study (Kilosanidze et al. 2002a), we proposed as a threshold between α-helical and nonhelical states of amino-acid sequence the value of −28 kcal/mole for the van der Waals energy of a pentapeptide fragment on the basis of a sample of eight proteins. Here, we describe the choice of the best threshold value using all proteins in the current study. We analyzed 3640 entirely α-helical pentapeptide fragments and 957 entirely non-α-helical pentapeptide fragments. The results are presented in a histogram (Fig. 4 ▶) of energy values distribution within only α-helical pentapeptides and only non-α-helical ones. The average value of the van der Waals component is −28 kcal/mole for the former and 25 kcal/mole for the latter. Because the amount of pentapeptide fragments in the α-helical state is fourfold more than in the other state, one could not use standard Q₃ criteria—maximum of positive predictions of both α-helical and non-α-helical states, to estimate the best threshold, as it would lead to more false-negative predictions of minor, non-α-helical state. Therefore, we chose the threshold at a value in which the maximum of the sum of positive predictions for each state (Q_α + Q_non-α) is reached and, at the same time, the prediction of non-α-helical state (Q_non-α) is still biased. As one can see from Table 1, the value of −26 kcal/mole provides the threshold.

Figure 4.

The histogram of van der Waals energy distributions of entirely α-helical pentapeptide fragments and entirely non-α pentapeptide fragments for the tested sample of proteins. Energies are calculated for standard geometry of residues in the modeled structures.

Table 1.

Choice of threshold

	Positive predictions, %
van der Waals energy of pentapeptide, kcal/mole	α-Helical state, Qα	Non α-helical state, Qnon-α	Both states	Qα +Qnon-α
−28	74	64	72	138
−27	80	61	76	141
−26	85	58	79	143
−25	88	55	81	143
−24	90	53	82	143
−10	97	33	84	130

Prediction of side-chain conformation

To check whether the proposed model truly reflects physical conditions in a protein, namely, if the model would constrain a variety of residue side-chain conformations correctly, an analysis of dihedral χ-angles was performed. We calculated the difference between values of all residue χ-angles from the native structures and the same angles taken from the model structures. In both types of structures, the standard rotamers were also compared. We analyzed only the models with bond angles and bond lengths given from the X-ray, that is, with experimental stereochemistry.

The rotamer distribution of residues in the model conformation mainly follows the distribution typical for α-helices (Dunbrack Jr. 2002); thus, in the regions of native α-helices, 70% of χ₁-rotamers are the same in the models and in the native structures. In the non-α-helical regions, the model rotamers differ from the native ones and coincidence between χ₁-rotamers in model and native structures is 52%. It should be mentioned here that the accordance between model and native structures would be significantly less in non-α-helical regions, unless the α-helical rotamers were usually also highly populated for loop regions, as was shown for the native proteins (Dunbrack Jr. 2002) and for modeled structures (Creamer and Rose 1992).

We also found a high coincidence of values of all dihedral angles of side chains. We assumed that the angles from the native structure and the model were the same if the absolute difference between native structure and optimized model angles values was less than or equal to 20° (the accuracy of X-ray analysis). In the α-helices of all 74 investigated domains, 59% of all χ-angles were similar in the model and experimental tertiary structures, and this value varies only a little from one protein to another; standard deviation on the set of proteins is 7%. Among α-helical residues that showed a difference in side-chain torsion angles, 70% are polar or charged, which implies a definite influence of tertiary structure on the side-chain conformation of such residues. In non-α-helical regions, 43% of χ-angles were similar, with the same standard deviation.

Thus, in addition to the prediction of α-helical and non-α-helical regions of main chain, our model suggests the right side-chain conformation of α-helical residues in more than half of the residues.

Conclusions

In our previous work (Kilosanidze et al. 2002a,b), we demonstrated the use of the helical model in the prediction of a limited sample of proteins. In the current study, we have confirmed the previous results using a larger data set. In this work, the prediction of α-helical and non-α-helical states is 79% correct. We only analyzed proteins of mainly-α class to escape a detection of β-structures in the absence of an appropriate model for it. It is important to note that our approach belongs under the one-sequence group of secondary structure prediction methods. Our method does not use homology alignment with related proteins, in contrast to the most frequently used current techniques.

In the model of extended hypothetical structure—all protein, one α-helix—long-range interactions are absent, and thus, cannot be investigated. For the local interaction, the strong influence of the van der Waals interactions on α-helix formation is clearly demonstrated.

Another conclusion that can be drawn from the energy analysis of the model conformation regards the real role of hydrogen bonding in the stability of helical configurations in the polypeptide chain. Hydrogen bonds are usually profitable both in helical and nonhelical regions of the model of the polypeptide chain. However, hydrogen bonds neither provide a significant contribution to the energy of α-helices, nor determine the location of α-helical regions along the main chain. In the model within the regions of native loops, the influence of hydrogen bonding cannot overcome the dominant-negative van der Waals contribution, which does not allow the loop sequence to adopt an α-helical conformation.

We also estimated the influence of the native structure of the protein on an α-helix energy by comparing the experimentally observed stereochemistry of residues with standard stereochemistry. The relative energy contributions are similar in both models and the van der Waals component has the prevalent role in the model with the experimental stereochemistry as well.

In addition, we would like to note that the statements presented here are to be considered as an outcome of the approximations, used for modeling, force-field, and rigid-geometry approximation for the stereochemical parameters. Nevertheless, the coincidence of predicted and real α-helical patterns is essential, and the results are unaffected by the choice of either standard or native stereochemistry. Both facts offer a support of the validity of used approximations. This also emphasizes the specific composition of energy terms that were used and the ratio between them for an α-helix stability.

Finally, the side-chain conformation can be predicted in α-helical regions by use of this method. Thus, the real conditions that define the packing of side chains in the native protein are reproduced with good accuracy in the proposed simplified model.

Materials and methods

Tested sample

We have used the CATH database, release v2.4 and data of DHS (Dictionary of Homologous Superfamilies) as a summary of structural and functional features for CATH Homologous Superfamilies to select a subset of nonhomologous protein domains.

CATH is a novel hierarchical classification of protein domain structures, which clusters proteins at four major levels, Class, Architecture, Topology, and Homologous superfamily (Orengo et al. 1997). In our subset, one class of mainly-α structure and all domain architectures of this class are represented. The selected proteins’ crystal structures have been solved to resolution of 2.5 Å or better with 77% of those resolved by 1.95 Å and less.

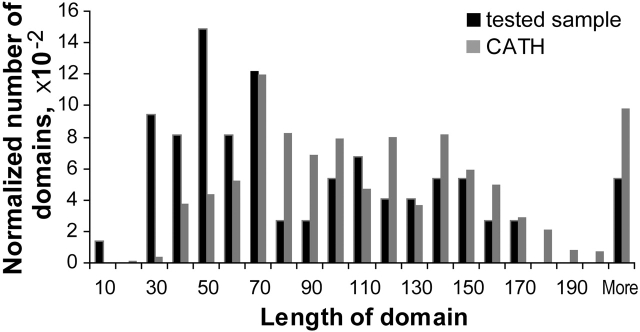
The subset contains 74 domains, of which 56 are from 220 types of domains classified in CATH as α-helical Homologous Superfamilies (these 56 domain types are represented by 61 different domains from CATH level of Nonidentical sequences) and 13 mainly-α structures that are nonclassified in CATH in more details. One additional domain representing fibrous proteins, tropomyosin, was also analyzed. The subset under study comprises a wide variety of domain lengths (Fig. 5 ▶) similar to the domain lengths distribution of the Nonidentical relatives level in the CATH databank comprising 852 members of α-helical domains. Total number of α-helices in the domains used in this study was 316.

Figure 5.

Distributions of domain lengths for the tested sample of proteins (74 domains) and for the mainly-α structures in nonidentical relatives level of CATH databank (852 domains). Occurrence of domains is normalized.

The modeling procedure

The modeling was carried out by the molecular mechanics program ICM using the optimal bias Monte Carlo minimization algorithm (Abagyan et al. 1994; Abagyan and Totrov 1999). The calculations were performed with use of ECEPP force field (Nemethy et al. 1992) and with approximation of fixed bond angles and bond lengths, the so-called rigid-geometry approximation. The rigid-geometry model is valid for the studies of the conformational energy of proteins (Gibson and Scheraga 1998).

Modeling of α-helical conformation and energy profile construction

From the amino-acid sequences of selected domains, models of continuous α-helices were constructed, one for each domain. The model was built as follows: The protein chain with standard steric parameters for residues according to Scheraga and coworkers (Nemethy et al. 1992) was folded into a continuous α-helix, starting values of dihedral angles were φ = −57°, ψ = −47°. Then, the model structure was optimized to find a local energy minimum of the system; at the last step of optimization, the φ,ψ angles of the backbone were restrained. An explicit description of the modeling procedure is given previously (Kilosanidze et al. 2002a). The torsion angles of proline were ϕ = −27.43° and ψ = −62.56° according to Scheraga’s parameterization.

Taking into account constant and nearly constant contributions in energy that vary from residue to residue, the baseline conformation of the polypeptide chain of the protein was also obtained. The φ,ψ angles of model α-helix conformation were altered to −160°, +160°, respectively, and additional optimization was performed.

The energies of pentapeptide fragments were estimated separately for the helical and for the extended conformation. The total energy was calculated as the sum of van der Waals, hydrogen bonding, electrostatic interactions, and torsion energies. The resultant profile is a subtraction of energies of the helical and the extended conformations.

The average absolute variance of profile was calculated as the average of absolute difference of neighborhood points of the profile along the model.

Parameters of Monte Carlo minimizations

Monte Carlo minimizations were performed with different parameters: 1000 and 10,000 random moves of all dihedral angles per one residue side chain; 300, 600, and 900 K as starting temperature of the optimization process. Similar energy profiles with insignificant variations were obtained with this analysis. Thus, the minimization reaches the optimal conformation of the model. As a result, we chose more optimal values; 1000 as the number of Monte Carlo variations and 600 K – in order to reduce computer time and for usable output.

Model with native stereochemistry of residues

The model with native stereochemistry of residues was constructed in the same way as the model with standard steric parameters for residues. Starting values of dihedral angles were φ = −57°, ψ = −47° for the continuous α-helical conformation as well. But all bond lengths and bond angles were given from the X-ray data in accordance with atom coordinates presented in PDB data for each protein. The optimization procedure was carried out as described above for the model with standard stereochemistry.

Residue-by-residue performance estimation

We followed the standard Q_3α formula for two-state prediction (positive correct and negative correct predictions) as in Schulz and Schirmer (1979). The boundaries of secondary structure were assigned by DSSP data (Kabsch and Sander 1983).