Skip to main content
NCBI home page
Protein Science : A Publication of the Protein Society logoLink to Protein Science : A Publication of the Protein Society
. 2004 Mar;13(3):608–616. doi: 10.1110/ps.03299804

Rapid evolution in conformational space: A study of loop regions in a ubiquitous GTP binding domain

Christian Blouin 1,2, Davin Butt 2, Andrew James Roger 1,3
PMCID: PMC2286719  PMID: 14978301

Abstract

The rapidly evolving subsets of a protein are often evident in multiple sequence alignments as poorly defined, gap-containing regions. We investigated the 3D context of these regions observed in 28 protein structures containing a GTP-binding domain assumed to be homologous to the transforming factor p21-RAS. The phylogenetic depth of this data set is such that it is possible to observe lineages sharing a common protein core that diverged early in the eukaryotic cell history. The sequence variability among these homolog proteins is directly linked to the structural variability of surface loops. We demonstrate that these regions are self-contained and thus mostly free of the evolutionary constraints imposed by the conserved core of the domain. These intraloop interactions have the property to create stem-like structures. Interestingly, these stem-like structures can be observed in loops of varying size, up to the size of small protein domains. We propose a model under which the diversity of protein topologies observed in these loops can be the product of a stochastic sampling of sequence and conformational space in a near-neutral fashion, while the proximity of the functional features of the domain core allows novel beneficial traits to be fixed. Our comparative observations, limited here to the proteins containing the RAS-like GTP-binding domain, suggest that a stochastic process of insertion/deletion analogous to “budding” of loops is a likely mechanism of structural innovation. Such a framework could be experimentally exploited to investigate the folding of increasingly complex model inserts.

Keywords: G-protein, evolution, structural alignment, loop, insertion

The presence of variable length gaps in multiple sequence alignments indicates that the 3D spatial constraints on the “backbone” (Cα) trajectory are more relaxed in some regions of proteins than in others. Evolutionarily constrained elements define the set of shared structural characteristics of a data set that are homologous (Grishin 2001). However, homology on the basis of structure in gap-containing regions of alignments cannot be assumed a priori. Variable length regions in alignments that are bounded on either side by conserved polypeptide stretches typically correspond to surface loops in proteins (Lesk 2001). More generally, for the purpose of this discussion, the term “loop” will refer to any polypeptide segment (1) whose extremities are proximal and (2) whose content display a lineage specific structural variability. These surface residues are, on average, involved in fewer intramolecular side-chain interactions than their buried counterparts. The resulting lowered constraint on side-chain identity makes surface loop sites candidates for rapid evolution. Here, we present a comparative study of insertion and deletion events in a specific GTP binding domain family. These observations are then considered with respect to the problem of the emergence of novel protein architectures.

The generation of radically novel protein folds during evolution is often seen to be problematic. In this text, the term “fold” will refer to the backbone trajectory of a domain. It is unclear how a protein with one fold could evolve into a different fold without going through unstable and nonfunctional intermediates that would be subject to purifying selection (Blanco et al. 1999). The fitness of a protein is a quantitative concept that describes the relevance of a protein to its host organism. Fitness thus depends on a collection of criteria such as biological activity, stability, and rapid folding (Govindarajan and Goldstein 1997). Biologically fit proteins must efficiently fold to their native conformation and thus minimize the time spent traversing conformational space (Ortiz and Skolnick 2000). Simulation studies point to the critical role of early forming near-native topologies to direct the main chain folding along the proper folding path (Dinner et al. 1996, 1999a). Selection, therefore, not only applies to the equilibrium structure but also to the sites involved in the kinetics of folding.

Considering the number of constraints involved in the folding of a protein domain, a drift in sequence space of a gene is unlikely to produce a useful gene product: This process would have to rely on the neutral evolution of pseudogenes for extended periods while remaining free of nonsense mutations. This is an improbable scenario at best (Blanco et al. 1999). Likewise, other processes can lead to novel protein architecture, such as: (1) circular permutation, (2) invasion/withdrawal of β-strands have been reported (Grishin 2001) or (3) in ambiguously folding regions that can be used as a pivot for the spontaneous generation of new folds. However, the sequential and successful repetition of these events to generate novel protein architectures seems to be unlikely. Although such events clearly have occurred as isolated cases, it is unclear whether such sequences of improbable events have occurred with sufficient frequency to account for the diversity of known folds in proteins.

It is unwise to reject an explanation solely on the basis of its apparent unlikeliness. Such arguments have been made to discount the possibility of the evolutionary origin of complex biological structures such as the vertebrate eye; yet, most rational biologists accept that it must have happened. Specifically, in this case, there is no way to determine the frequency of unsuccessful trial protein fold because selection rapidly culls these from view. Thus, in principle, the limited diversity (~4000 in the PDB database on May 20, 2003) of distinct protein folds possibly could be explained by a combination of spontaneous sequence changes and larger recombination/permutation events yielding into a structural drift from an initial to a final fold. Although a probabilistic argument on its own is insufficient to invalidate this model, further improvements to our understanding of the mechanism of emergence of new protein folds can be made if an alternative and intuitively more probable hypothesis could be validated by observations.

We propose that rapid evolutionary change in loops has the potential to generate novel architectures by exploring the conformational space independently from the core protein to which they are attached. If few contacts exist between a loop and the protein’s core, these loop sites can evolve independently while “hitchhiking” on the expression of their “host” protein. The mechanism of protein fold evolution proposed herein does not assume improbable structural rearrangements within the constrained sites of a protein. Rather, it holds that sites in sequences can be inserted/deleted/substituted in a stepwise fashion while merely playing a peripheral role to biological function. This appears to be the case in the highly variable regions of the conserved GTP binding domain.

Results and Discussion

Definition of the GTP binding domain core

Figure 1 ▶ shows a structural consensus for a variety of GTP binding domains depicted on the structure of Ypt51 (1EKO). The backbone is color-coded on a continuous scale using the frequency (28 aligned structures) of each site to have a structural homolog in the other structures; from blue (always present) to red (present only in the reference structure) through green (intermediate values). The structurally conserved core of this domain excludes several surface loops and is made of a β-sheet with winding helices. The ancestral gene containing this domain possibly preceded the origin of most of the cell signaling and contemporary translational machinery in which these GTPases are typically found. This GTPase ancestral domain then: (1) duplicated and diverged to form paralogs, (2) was directly inherited in multiple lineages from a multipurpose ancestral GTPase, or (3) was incorporated by recombination into other genes.

Figure 1.

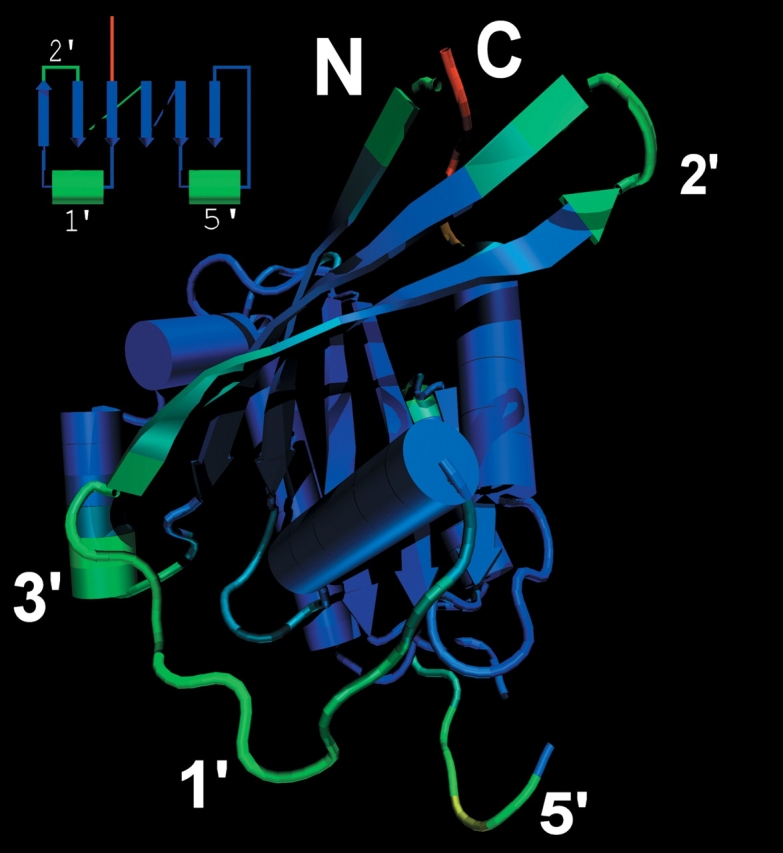
Figure 1.

Open in a new tab

Variable loops in the GTP/GDP binding domain. The frequency of occurrence of a homologous structure to the protein Ypt51 (1EKO) is color-mapped from red (no homologous substructure found) to blue (conserved structural features) through green for the intermediate values. The N and C termini are labeled for reference.

The composition of the sites that are part of the core domain is similar to those of whole proteins. There is no significant amino acid bias for buried sites in the conversed core versus the whole structure. The structurally conserved core region includes a mixture of amphipathic, polar, and hydrophobic elements similar to the full-size proteins (data not shown). Maximum likelihood phylogenetic analysis of a structure-based multiple alignment (146 positions including gaps) yielded an unresolved maximum likelihood tree (Tree-Puzzle 5.0, JTT+8Γ rate categories, α = 0.99). The ancient phylogenetic signal relating these proteins has apparently been eroded by saturating multiple substitutions.

Insertion/deletion hot spots

The structure of Ypt51 (1EKO) was used as the template protein because it has a minimal number of nonconsensus regions, which results in a streamlined GTP binding domain. A minimal GTP-binding domain is not necessarily a better representative of the hypothetical ancestor domain, but is nonetheless a representative template model for structural comparisons.

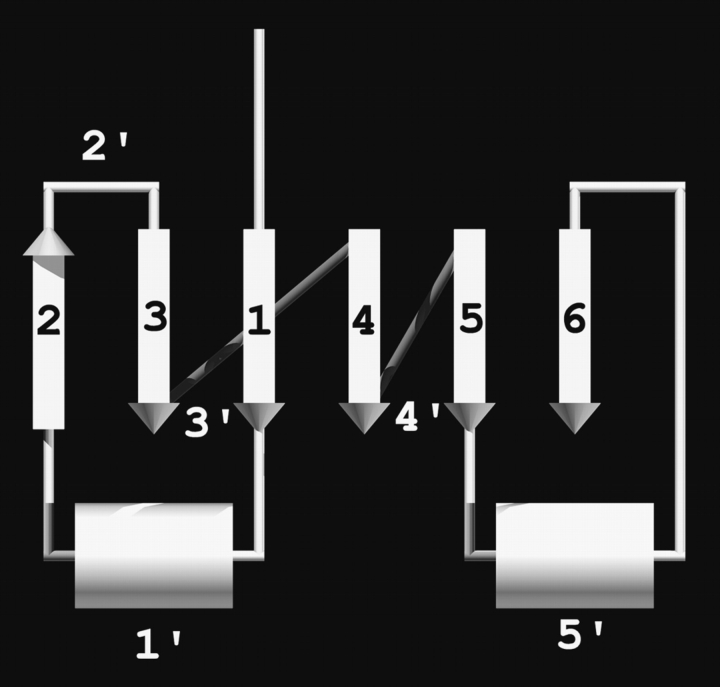
In this data set, the regions between secondary structure elements are common sites of insertion, deletion, or main chain perturbation leading to their lack of structural similarity among lineages. However, indels occur preferentially at positions 1′, 2′, and 5′ (refer to Fig. 2 ▶ for the nomenclature of loops). The preference for indels in these regions may be due in part to the proximity of these regions to functionally important features of the core domain. For instance, the 1′ loop region acts as a molecular switch for a conformation change and contains the p-loop responsible for the binding of the γ-phosphate of GTP (Sprang 1997). There is evidence that the 5′ loop plays a role in dimer interactions (such as bovine Gs-α; Sunahara et al. 1997). Another common source of length variability comes from the extension of β-hairpins at position 2′ or formation of new β-hairpins that have joined the main β-sheet. Examples of this latter case can be found in EF1α (6′ loop), and EF–Tu(1′ loop; see Supplemental Material).

Figure 2.

Figure 2.

Open in a new tab

Nomenclature of β-strands and loops in the GTP-binding domain. The β-strands are labeled by their sequential order, and each loop is named after its preceding β-strand. Some α-Helices are not displayed for clarity.

As previously shown using the mapping of amino acid substitution rates at sites estimated by maximum likelihood (Blouin et al. 2003), the evolutionary constraints imposed on a site are mostly dictated by the flexibility of the site’s interacting partners to adapt to change. Sites that are embedded in the protein matrix (Dean et al. 2002), involved in catalysis or allosteric binding (Pupko et al. 2002), must coevolve with a subset of interacting partners. The constraints due to intramolecular interactions exist to a lesser extent to the side chains extending outside the protein matrix. Furthermore, there are no intrinsic constraints on length and backbone trajectory of peptides in loops between the fixed extremities. These relaxed constraints make loops “hot spots” for rapid evolution.

Dynamics of insertion/deletion

Comparison of closely related orthologous structures often reveal small insertions or deletions of one or two sites. More distantly related sequences will tend to have more variability in insert length. This observation indicates that there is a relationship between the length of loop regions and the evolutionary distance between two proteins (Benner et al. 1993). Here, evolutionary distance refers to the total numbers of changes (substitutions per site) between two sequences in alignable regions, a quantity that is thus a function of both evolutionary time and the mean rate of evolution. The relationship between variation in insert size and evolutionary distance leads to two possibilities. First, insertion and deletion of large segments of sequence may be rare events, and will only be observed if there is a long elapsed time since the last common ancestor of two sequences. A second possibility (yet not mutually exclusive to the first) is that variable loop regions grow or shrink incrementally by stepwise insertion/deletion.

However, quantitative correlation between average variable loop length and evolutionary distance is not clear. In multiple sequence and structural alignments, the length of some insertions is often constant, and could in some cases parsimoniously be traced to a single, en bloc insertion or deletion. This would be consistent with the first possibility described above. However, other regions of alignments are highly variable in length (Fig. 3 ▶), arguing against a unique mechanism of insertions/deletions in proteins.

Figure 3.

Figure 3.

Open in a new tab

Aligned sites bounding the 5′ loop region in the Pfam alignment ras. The tree to the left of the sequence alignment was generated from a gap-free edited alignment using maximum likelihood. Although the overall tree is not well resolved, several clusters of sequences (denoted by letters A–E) display variable patterns in the length of this loop.

The variability in length of loop regions was studied in more detail using a subset of sequences. This subset is the seed alignment of the Pfam family ras (Bateman et al. 2002). The phylogeny inference using only the sites for which homology could be unambiguously assigned was used to build a tree. The maximum likelihood tree recovered by quartet puzzling (Strimmer and von Haeseler 1996) has an unresolved backbone that nonetheless clearly identifies major clusters of sequences (Fig. 3 ▶). The length of the 5′ loop can either be completely fixed or variable, depending on which cluster of sequences is under consideration. Clusters A, B, and D are variable in length, while cluster C shows a limited variability where the polypeptides can have only one of two discrete lengths. The other sequences whose positions in the phylogeny could not be clearly resolved display a range of insert lengths at this position that is consistent with the hypothesis that loop regions are allowed to extend/streamline following a stochastic process.

The presence of a long insert in otherwise close homologs (cluster C, Fig. 5 ▶) suggests that an alternative mechanism of insertion led to the observed data in this particular group of sequences. The length of this loop in the sequences of Rhoα, RAB2α (Canis familiaris) RAB5 (Nicotiana tabacum), Rho3, and 2, YpT52, YpT53 from Saccharomyces cerevisiae, Ypt5 (Schizosaccharomyces pombe) and Ras2 (Drosophilia megalonaster) seems to be constrained (except for taxon Rho4 (S. cerevisiae), which has a 33 residues-long insert). Little is known about the precise function of the yeast RHOx proteins except that these appear to be involved in the cellular budding process by interacting with the cytoskeleton (Roumanie et al. 2000). However, the lack of variation in sequence length in the 5′ loop of the genes of the C-cluster implies increased purifying selection on its length and hints at an important novel function for this region in this cluster of sequences. It is unclear what this function may be, although it could be related to dimerization as has been shown in the case of bovine Gs-α (Sunahara et al. 1997).

Figure 5.

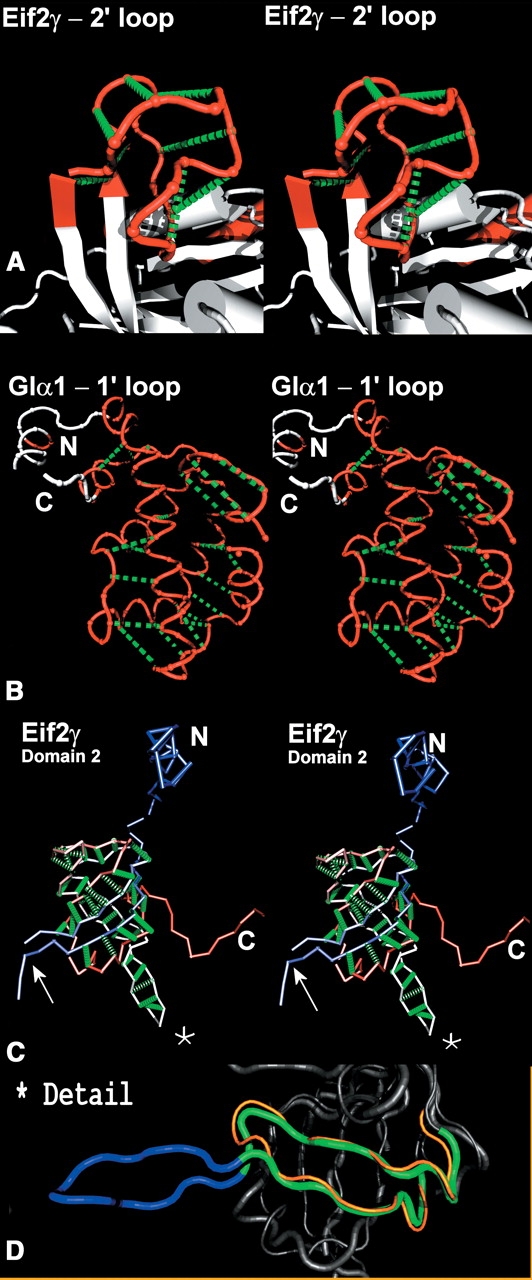
Figure 5.

Open in a new tab

Stem-like structures of independently folding units in (A) EF-2γ loop 2′ (residues 59–80), (B) GIα1 1′ loop (residues 50–180), and (C) EF-2γ domain 2 (residues 205–320). Only the backbone of these loops is displayed—red for A and B. The green dotted lines highlight the antiparallel fold of these polypeptide substructures but do not explicitly represent atomic interactions. N and C termini are labeled in ambiguous cases. The example in the bottom panel is not strictly a loop but domain 2 of eIF2γ. In this case, the backbone is color-coded from blue to red based in the index of the residues in the sequence. The peculiar folding of this domain is almost entirely antiparallel, or stem-like, except for a bulge where the polypeptide information is missing (arrow) and a bifurcation at the extremity of the stem. (D) Details the β-hairpin in eF1α (270–290, orange) and eIF2γ (244–275 green and blue). The part of eIF2γ β-hairpin with structural homology is shown in green, while the “extra” loop region (residues 254–266) is shown in blue.

Inserts are self-contained

β-Hairpins are frequently observed in the GTP binding domain data set. This is a probable loop structure for a short stretch of peptide to adopt because it is locally stable, does not depend on other folding elements, and benefits from the proximity of its extremities to seed its folding (Dinner et al. 1999b). Self-containment is likely to be important even for loops that do not fold into β-hairpins. These loops are not strictly independently folding as their extremities are constrained by the core protein. However, the contacts between the sites in the loop and the protein are kept to a minimum as to avoid competing interaction with the core (Ortiz and Skolnick 2000), thus enhancing the folding rate of the native conformation (Dinner et al. 1998). As a result, some methods for prediction of loop conformation assume that loops can be considered as “mini ab initio” folding problems (Xiang et al. 2002).

Therefore, one possible assumption of a stochastic evolutionary model of insertion/deletion would be that loops of variable length should be able to self-contain at any point in evolutionary time. If this is the case in nature, a consistent pattern of independent folding with tethered extremities should be detectable. Close inspection (Figs. 4 ▶, 5 ▶) of loop structures reveals a “stem-like” folding pattern in most loops found in this data set. Here we define a stem-like folding pattern in protein as analog to base-paired stems or hairpin loops in RNA structures. In the simplest case a series of contacts can be traced between site 1 and n of a loop, the contact distance between backbone atoms is minimized by pairing the sites from 1 and subsequently in an ascending order to site n and subsequently in a descending order. Characteristically, this folding pattern leaves an antidiagonal signature in a Cα–Cα distance matrix (see arrows in Fig. 4 ▶). Figure 5 ▶ illustrates this relationship, as traced by the series of dashed green lines highlighting this antiparallel polypeptide trajectory pairing for a selection of loops found in the GTP binding domain and domain 2 of EF1α/EF–Tu/eIF2γ. One property of these substructures is that, assuming the extension of the polypeptide occurred preferentially at the end of the stem, even if a given peptide was a fraction of its full length at any point in time, the loop would still be able to fold to a locally stable conformation. Figure 5 ▶ shows three cases of antiparallel folding of protein substructures that are not simple extensions of an antiparallel pair of β-strands. The 2′ loop of the GTP binding domain of eIF2γ (Fig. 5A ▶) is a 22mer loop hosting a tetracoordinated zinc (Schmidt et al. 2002) that has no structural homolog among any of the host GTP binding domains investigated in this study. It folds independently by using exclusively local intraloop interactions including the coordination of the zinc ion. The 1′ loop in the protein Gs-α also forms an independently folding unit with an all α-helix topology (Fig. 5B ▶). This contrasts with the host GTP binding domain that does not have an antiparallel stem-like pattern beyond the close proximity of first and last few sites. Finally, the second domain in Eif2γ, which is homologous and nearly identical to that of EF1α and EF–Tu, can be partially unfolded to a stem-like structure as shown in Figure 5C ▶. This domain, however, has a bulge in the N-terminal region of the polypeptide chain and another bulge where the stem bifurcates into two stems. The N-terminal bulge in eIF2γ apparently postdates the paralogous divergence of EF1α + EF–Tu/eIF2γ, as there is no structural analogy at this position between the two systems. This insert is likewise self-contained as a loop within a loop (Fig. 5D ▶).

Figure 4.

Figure 4.

Open in a new tab

Signature of stem-like structures in proteins. This plot was generated using the intramolecular Cα–Cα distance for each site in the proteins Gsα (1AZT: Sunohara et al. 1997) and eIF2γ (1KK0: Schmitt et al. 2002). Any Cα–Cα distance 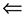Inline graphic 15 Å are shown in white. Black marks indicate the boundaries of the three substructures shown in Figure 5 ▶. The arrows indicate the signature of the stem going across the boxed substructures.

Emergence and maturation of protein folds

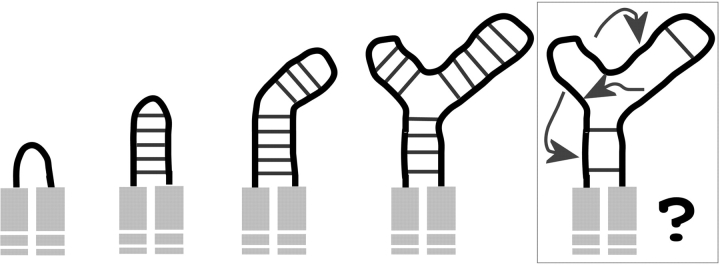
In Figure 6 ▶, we propose a cartoon model of stochastic polypeptide growth that is consistent with the foregoing observations. This model accounts for the importance for variable loops to independently fold without disrupting the folding pathway of the polypeptide chain of the core “host” protein. The model also accounts for the observation that self-contained, protein domains, for example, units have proximal extremities.

Figure 6.

Figure 6.

Open in a new tab

Proposed model of emergence of novel protein fold through a stochastic insertion process. The progression is shown from left to right. The loop (black) between conserved elements (light gray) grows in a stem-like fashion through intraloop interactions (dark gray). Cycles of stochastic substitutions and selection for efficient folding are not expected to preserve the stem structure over time, as it is not expected to be an efficient folding template for longer inserts (last panel).

The stochastic process of DNA insertion/deletion leaves traces almost exclusively in regions of low constraints such as surface loops. As proteins evolve through time, insertions can accumulate without adversely affecting the protein, providing that these sites do not interfere with the structure of the core protein. The involvement of the extra sites in the folding pathway of the core protein would affect its folding efficiency, potentially its equilibrium stability, and thus subject the gene to purifying selection. Using locally stable structures, loops form stems folded onto themselves. The accumulation of insertion events would tend to be at the extremity of the stem, resulting in an apparent “growth” of the loops. Some examples are simple β-hairpins, turns, or more complex examples as presented in Figure 5 ▶. The identity of sites within growing loops would be subjected to additional constraints as the number of local interactions increases. These constraints will not be homogenously distributed along the polypeptide chain. Some least constrained positions within the loop thus may tolerate the formation of bulges via the same insertion mechanism as can be observed in the second domain of EF1α/eIF2γ (Fig. 5C,D ▶). As bulges and perturbations accumulate, especially in large inserts where the stem structures will not efficiently fold, maturing protein structures would optimize an increasing number of local interactions with topologically distant side chains.

It has been observed that the extremities of a domain are generally proximal to each other, and can be preserved by circular permutation events (Grishin 2001) and be required for the modular assembly of multidomain proteins.

Therefore, evolution of loop regions offers the possibility to explore conformational space in a quasi-neutral fashion for as long as the fitness of the host protein is not negatively affected. Occasionally, novel structural features in loops may acquire substructures relevant to existing functions and be positively selected; hence, the preference for loops 1′, 2′, and 5′ in the GTP binding domain system. These can eventually be recombined as independently folding units either in tandem with other domains or as an insert within a host domain.

A possible example of this phenomenon can be found in a domain of the specialized enzyme chitosanase. The 1′ insert domain of GIα1/Gsα is unique to the trimeric G proteins (Sprang 1997), but has a structural analog detectable in a domain of chitosanase between the residues 71 and 179 (using the algorithms of VAST and CE). Assuming that these two domains did not evolve independently, and that the enzyme chitosanase (PDB: 1CHK; Marcotte et al. 1996), is a more recently evolved protein than the GIα1/Gsα’s gene involved in cell signaling, it seems possible at least that the chitosanase domain is homologous to (and arose from) the 1′ loop in Gsα/GIα. If so, this domain of chitosanase would represent an example of a protein domain that was born as a loop in a parent GTPase protein that was eventually recruited as an autonomous domain through the processes of recombination. It is likely that many other examples of “loops” that escaped their host proteins exist, although it may be difficult to prove such cases definitively. Of course, one should keep in mind that this general α-helices construct may have arisen twice via the same process.

Conclusion

The details and relative importance of various mechanisms of protein structural evolution are still a matter of conjecture. With over 21,007 structures in the PDB database (20.05.2003), many of which are redundant or are engineered protein variants, there is still too little structural information to definitively address how the diversity of the “universe” of protein folds has evolved. We have argued that there is evidence that new conformational space can be explored “independently” from cooperatively stabilized protein folds. This process is, in essence, an atomic-level analog of already well-characterized evolutionary processes in biology. This model assumes that the regions of fastest rate of evolution are the most probable sites for the occurrence of rare events. This makes loops a suitable source of protein folds that may be precursors to novel protein domains. There is a concern that the observation made on these 28 homologous structures may not be relevant to protein evolution in general. It is now necessary to test this hypothesis against a larger sample of structural contexts. There should be a continuum of stem topologies from short loops to mature protein domains. The definition of stem and loop has to be formalized as to avoid manual inspection of all systems and enable genome scale survey. This work is under development in our group.

This process can also be tested by simulation and experimentally by creating a system of incremental growth of loops whose initial short length and constrained extremities makes the conformational space tractable. The properties of the architectures generated under this hypothesis could then be compared to the observation made in this discussion.

Materials and methods

Structural alignment

A data set of homologous protein structures was generated by gathering VAST structural similarity search hits (Madej et al. 1995; Gibrat et al. 1996) in the PDB protein structure database (Berman et al. 2000) to the GTP binding domain of EF1α (1IJF; Andersen et al. 2001). Mutant structures and solved complexes with redundant protein structures were discarded to yield a collection of representative proteins containing the GTP binding domain. These structures are listed in Table 1. Further similarity searches were performed using the CE algorithm (Shindyalov and Bourne 1998) where a data set of protein structures was compared to a reference structure in a pairwise fashion. Each input structure was then output with sites mapped as: (1) a residue with a structural equivalent in the reference structure, (2) a residue part of an insertion with respect to the reference structure, or (3) a residue with no structural equivalence in the reference structure. Finally, the reference structure was output with each site mapped with the proportion of homologous sites found in the entire data set.

Table 1.

PDB entries used in this study

PDB entry key Chain Protein Reference
1H65 A Toc34 GTPase - P. Sativum (Sun et al. 2002)
1G7T A 1F2/EiF5β - M. thermoauto-trophicum (Roll-Mecak et al. 2000)
1BOF — Giα1 - R. norvegicus (Coleman and Sprang 1998)
1AZT A Gs-α - B. taurus (Sunahara et al. 1997)
1EGA A ERA - E. coli (Chen et al. 1999)
1CTQ A P21 Ras - H. sapiens (Scheidig et al. 1999)
1KY2 A Ypt7P - S. cerevisiae (Constantinescu et al. 2002)
1KK0 A eIF2γ - P. Abyssi (Schmitt et al. 2002)
1G17 A Sec4 - S. cerevisiae (Stroupe and Brunger 2000)
1EKO A Ypt51 - S. cerevisiae (Esters et al. 2000)
1TX4 B Transforming protein ρα (Rittinger et al. 1997b)
1BWP A Platelet-Activating Factor Acetylhydrolase (Ho et al. 1999)
1FNM A EF-TU - T. Thermophilus (Laurberg et al. 2000)
1RRP A Ran - H. sapiens (Vetter et al. 1999b)
1F6B B Sarl - C. griseus (Huang et al. 2001)
1F5N A GIα1 - H. sapiens (Prakash et al. 2000)
1D2E A EF-TU - B. Taurus (mito.) (Andersen et al. 2000)
1D8T A EF-TU - E. coli (Heffron and Jurnak 2000)
1IJF A EF1a - S. cerevisiae (Andersen et al. 2001)
1KAO — Rap2A - H. sapiens (Cherfils et al. 1997)
1MH1 — Rac1 - H. sapiens (Hirshberg et al. 1997)
1AM4 A P50 RhoGap - H. Sapiens (Rittinger et al. 1997a)
1D5C A Rab6 - P. falciparum (Chattopadhyay et al. 2000)
1DS6 A P21 Rac2 - H. sapiens (Scheffzek et al. 2000)
1IBR A Ran - H. sapiens (Vetter et al. 1999a)
1K8R A P21 H-RAS-1 - H. sapiens (Scheffzek et al. 2001)
3RAB A Rab3α - R. Norvegicus (Dumas et al. 1999)
Open in a new tab

Molecular graphics

Protein models were viewed and manipulated using VMD (Humphrey et al. 1996) and raytraced using POV-ray v.3.1g.

Phylogeny

The protein sequences of the GTP-binding domain were gathered from the Pfam (Bateman et al. 2002) data set “ras.” An estimate of the maximum likelihood phylogeny was inferred using the quartet-puzzling algorithm implemented in PUZZLE 5.0 (Strimmer and von Haeseler 1996) using the JTT substitution matrix (Jones et al. 1992) with a rates across sites process modeled by 8 Γ-distributed, equiprobable rate categories.

Acknowledgments

We thank Dr. Y. Inagaki and Dr. M. O’Malley for helpful discussions. C.B. thanks NSERC for postdoctoral fellowship support. A.J.R. thanks the Canadian Institute for Advanced Research for fellowship support. This work was supported by an NSERC Operating Grant 227085-00 awarded to A.J.R. and by Genome Atlantic/Genome Canada.

The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.

Supplemental material: See www.proteinscience.org

Article and publication are at http://www.proteinscience.org/cgi/doi/10.1110/ps.03299804.

References

  1. Andersen, G.R., Thirup, S., Spremulli, L.L., and Nyborg, J. 2000. High resolution crystal structure of bovine mitochondrial EF-Tu in complex with GDP. J. Mol. Biol. 297 421–436. [DOI] [PubMed] [Google Scholar]
  2. Andersen, G.R., Valente, L., Pedersen, L., Kinzy, T.G., and Nyborg, J. 2001. Crystal structures of nucleotide exchange intermediates in the eEF1A–eEF1Bαcomplex. Nat. Struct. Biol. 8 531–534. [DOI] [PubMed] [Google Scholar]
  3. Bateman, A., Birney, E., Cerruti, L., Durbin, R., Etwiller, L., Eddy, S.R., Griffiths-Jones, S., Howe, K.L., Marshall, M., and Sonnhammer, E.L. 2002. The Pfam protein families database. Nucleic Acids Res. 30 276–280. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Benner, S.A., Cohen, M.A., and Gonnet, G.H. 1993. Empirical and structural models for insertions and deletions in the divergent evolution of proteins. J. Mol. Biol. 229 1065–1082. [DOI] [PubMed] [Google Scholar]
  5. Berman, H.M., Westbrook, J., Feng, Z., Gilliland, G., Bhat, T.N., Weissig, H., Shindyalov, I.N., and Bourne, P.E. 2000. The Protein Data Bank. Nucleic Acids Res. 28 235–242. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Blanco, F.J., Angrand, I., and Serrano, L. 1999. Exploring the conformational properties of the sequence space between two proteins with different folds: An experimental study. J. Mol. Biol. 285 741–753. [DOI] [PubMed] [Google Scholar]
  7. Blouin, C., Boucher, Y., and Roger, A.J. 2003. Inferring functional constraints and divergence in protein families using 3D mapping of phylogenetic information. Nucleic Acids Res. 31 790–797. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Chattopadhyay, D., Langsley, G., Carson, M., Recacha, R., DeLucas, L., and Smith, C. 2000. Structure of the nucleotide-binding domain of Plasmodium falciparum rab6 in the GDP-bound form. Acta Crystallogr. D Biol. Crystallogr. 56 937–944. [DOI] [PubMed] [Google Scholar]
  9. Chen, X., Court, D.L., and Ji, X. 1999. Crystal structure of ERA: A GTPase-dependent cell cycle regulator containing an RNA binding motif. Proc. Natl. Acad. Sci. 96 8396–8401. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Cherfils, J., Menetrey, J., Le Bras, G., Janoueix-Lerosey, I., de Gunzburg, J., Garel, J.R., and Auzat, I. 1997. Crystal structures of the small G protein Rap2A in complex with its substrate GTP, with GDP and with GTPγS. EMBO J. 16 5582–5591. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Coleman, D.E. and Sprang, S.R. 1998. Crystal structures of the G protein Gi α 1 complexed with GDP and Mg2+: A crystallographic titration experiment. Biochemistry 37 14376–14385. [DOI] [PubMed] [Google Scholar]
  12. Constantinescu, A.T., Rak, A., Alexandrov, K., Esters, H., Goody, R.S., and Scheidig, A.J. 2002. Rab-subfamily-specific regions of Ypt7p are structurally different from other RabGTPases. Structure (Camb) 10 569–579. [DOI] [PubMed] [Google Scholar]
  13. Dean, A.M., Neuhauser, C., Grenier, E., and Golding, G.B. 2002. The pattern of amino acid replacements in α/β-barrels. Mol. Biol. Evol. 19 1846–1864. [DOI] [PubMed] [Google Scholar]
  14. Dinner, A.R., Sali, A., and Karplus, M. 1996. The folding mechanism of larger model proteins: Role of native structure. Proc. Natl. Acad. Sci. 93 8356–8361. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Dinner, A.R., So, S.S., and Karplus, M. 1998. Use of quantitative structure–property relationships to predict the folding ability of model proteins. Proteins 33 177–203. [DOI] [PubMed] [Google Scholar]
  16. Dinner, A.R., Abkevich, V., Shakhnovich, E., and Karplus, M. 1999a. Factors that affect the folding ability of proteins. Proteins 35 34–40. [DOI] [PubMed] [Google Scholar]
  17. Dinner, A.R., Lazaridis, T., and Karplus, M. 1999b. Understanding β-hairpin formation. Proc. Natl. Acad. Sci. 96 9068–9073. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Dumas, J.J., Zhu, Z., Connolly, J.L., and Lambright, D.G. 1999. Structural basis of activation and GTP hydrolysis in Rab proteins. Structure Fold. Des. 7 413–423. [DOI] [PubMed] [Google Scholar]
  19. Esters, H., Alexandrov, K., Constantinescu, A.T., Goody, R.S., and Scheidig, A.J. 2000. High-resolution crystal structure of S. cerevisiae Ypt51(DeltaC15)GppNHp, a small GTP-binding protein involved in regulation of endocytosis. J. Mol. Biol. 298 111–121. [DOI] [PubMed] [Google Scholar]
  20. Gibrat, J.F., Madej, T., and Bryant, S.H. 1996. Surprising similarities in structure comparison. Curr. Opin. Struct. Biol. 6 377–385. [DOI] [PubMed] [Google Scholar]
  21. Govindarajan, S. and Goldstein, R.A. 1997. Evolution of model proteins on a foldability landscape. Proteins 29 461–466. [DOI] [PubMed] [Google Scholar]
  22. Grishin, N.V. 2001. Fold change in evolution of protein structures. J. Struct. Biol. 134 167–185. [DOI] [PubMed] [Google Scholar]
  23. Heffron, S.E. and Jurnak, F. 2000. Structure of an EF–Tu complex with a thiazolyl peptide antibiotic determined at 2.35 Å resolution: Atomic basis for GE2270A inhibition of EF–Tu. Biochemistry 39 37–45. [DOI] [PubMed] [Google Scholar]
  24. Hirshberg, M., Stockley, R.W., Dodson, G., and Webb, M.R. 1997. The crystal structure of human rac1, a member of the rho-family complexed with a GTP analogue. Nat. Struct. Biol. 4 147–152. [DOI] [PubMed] [Google Scholar]
  25. Ho, Y.S., Sheffield, P.J., Masuyama, J., Arai, H., Li, J., Aoki, J., Inoue, K., Derewenda, U., and Derewenda, Z.S. 1999. Probing the substrate specificity of the intracellular brain platelet-activating factor acetylhydrolase. Protein Eng. 12 693–700. [DOI] [PubMed] [Google Scholar]
  26. Huang, M., Weissman, J.T., Beraud-Dufour, S., Luan, P., Wang, C., Chen, W., Aridor, M., Wilson, I.A., and Balch, W.E. 2001. Crystal structure of Sar1-GDP at 1.7 Å resolution and the role of the NH2 terminus in ER export. J. Cell Biol. 155 937–948. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Humphrey, W., Dalke, A., and Schulten, K. 1996. VMD: Visual molecular dynamics. J. Mol. Graph. 14 27–28, 33–38. [DOI] [PubMed] [Google Scholar]
  28. Jones, D.T., Taylor, W.R., and Thornton, J.M. 1992. The rapid generation of mutation data matrices from protein sequences. Comput. Appl. Biosci. 8 275–282. [DOI] [PubMed] [Google Scholar]
  29. Laurberg, M., Kristensen, O., Martemyanov, K., Gudkov, A.T., Nagaev, I., Hughes, D., and Liljas, A. 2000. Structure of a mutant EF-G reveals domain III and possibly the fusidic acid binding site. J. Mol. Biol. 303 593–603. [DOI] [PubMed] [Google Scholar]
  30. Lesk, A. 2001. Introduction to protein architecture, 1st ed., p. 347. Oxford University Press, Oxford, UK.
  31. Madej, T., Gibrat, J.F., and Bryant, S.H. 1995. Threading a database of protein cores. Proteins 23 356–369. [DOI] [PubMed] [Google Scholar]
  32. Marcotte, E.M., Monzingo, A.F., Ernst, S.R., Brzezinski, R., and Robertus, J.D. 1996. X-ray structure of an anti-fungal chitosanase from streptomyces N174. Nat. Struct. Biol. 3 155–162. [DOI] [PubMed] [Google Scholar]
  33. Ortiz, A.R. and Skolnick, J. 2000. Sequence evolution and the mechanism of protein folding. Biophys. J. 79 1787–1799. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Prakash, B., Renault, L., Praefcke, G.J., Herrmann, C., and Wittinghofer, A. 2000. Triphosphate structure of guanylate-binding protein 1 and implications for nucleotide binding and GTPase mechanism. EMBO J. 19 4555–4564. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Pupko, T., Bell, R.E., Mayrose, I., Glaser, F., and Ben-Tal, N. 2002. Rate4Site: An algorithmic tool for the identification of functional regions in proteins by surface mapping of evolutionary determinants within their homologues. Bioinformatics 18(Suppl. 1) S71–S77. [DOI] [PubMed] [Google Scholar]
  36. Rittinger, K., Walker, P.A., Eccleston, J.F., Nurmahomed, K., Owen, D., Laue, E., Gamblin, S.J., and Smerdon, S.J. 1997a. Crystal structure of a small G protein in complex with the GTPase-activating protein rhoGAP. Nature 388 693–697. [DOI] [PubMed] [Google Scholar]
  37. Rittinger, K., Walker, P.A., Eccleston, J.F., Smerdon, S.J., and Gamblin, S.J. 1997b. Structure at 1.65 Å of RhoA and its GTPase-activating protein in complex with a transition-state analogue. Nature 389 758–762. [DOI] [PubMed] [Google Scholar]
  38. Roll-Mecak, A., Cao, C., Dever, T.E., and Burley, S.K. 2000. X-ray structures of the universal translation initiation factor IF2/eIF5B: Conformational changes on GDP and GTP binding. Cell 103 781–792. [DOI] [PubMed] [Google Scholar]
  39. Roumanie, O., Peypouquet, M.F., Bonneu, M., Thoraval, D., Doignon, F., and Crouzet, M. 2000. Evidence for the genetic interaction between the actin-binding protein Vrp1 and the RhoGAP Rgd1 mediated through Rho3p and Rho4p in Saccharomyces cerevisiae. Mol. Microbiol. 36 1403–1414. [DOI] [PubMed] [Google Scholar]
  40. Scheffzek, K., Stephan, I., Jensen, O.N., Illenberger, D., and Gierschik, P. 2000. The Rac-RhoGDI complex and the structural basis for the regulation of Rho proteins by RhoGDI. Nat. Struct. Biol. 7 122–126. [DOI] [PubMed] [Google Scholar]
  41. Scheffzek, K., Grunewald, P., Wohlgemuth, S., Kabsch, W., Tu, H., Wigler, M., Wittinghofer, A., and Herrmann, C. 2001. The Ras-Byr2RBD complex: Structural basis for Ras effector recognition in yeast. Structure (Camb) 9 1043–1050. [DOI] [PubMed] [Google Scholar]
  42. Scheidig, A.J., Burmester, C., and Goody, R.S. 1999. The pre-hydrolysis state of p21(ras) in complex with GTP: New insights into the role of water molecules in the GTP hydrolysis reaction of ras-like proteins. Structure Fold. Des. 7 1311–1324. [DOI] [PubMed] [Google Scholar]
  43. Schmidt, E., Blanquet, S., and Mechulam, Y. 2002. The large subunit of initiation factor aIF2 is a close structural homologue of elongation factors. EMBO J. 21 1821–1832. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Shindyalov, I.N. and Bourne, P.E. 1998. Protein structure alignment by incremental combinatorial extension (CE) of the optimal path. Protein Eng. 11 739–747. [DOI] [PubMed] [Google Scholar]
  45. Sprang, S.R. 1997. G protein mechanisms: Insights from structural analysis. Annu. Rev. Biochem. 66 639–678. [DOI] [PubMed] [Google Scholar]
  46. Strimmer, K. and von Haeseler, A. 1996. Quartet puzzling: A quartet maximum likelihood method for reconstructing tree topologies. J. Mol. Biol. 13 964–969. [Google Scholar]
  47. Stroupe, C. and Brunger, A.T. 2000. Crystal structures of a Rab protein in its inactive and active conformations. J. Mol. Biol. 304 585–598. [DOI] [PubMed] [Google Scholar]
  48. Sun, Y.J., Forouhar, F., Li Hm, H.M., Tu, S.L., Yeh, Y.H., Kao, S., Shr, H.L., Chou, C.C., Chen, C., and Hsiao, C.D. 2002. Crystal structure of pea Toc34, a novel GTPase of the chloroplast protein translocon. Nat. Struct. Biol. 9 95–100. [DOI] [PubMed] [Google Scholar]
  49. Sunahara, R.K., Tesmer, J.J., Gilman, A.G., and Sprang, S.R. 1997. Crystal structure of the adenylyl cyclase activator Gsα. Science 278 1943–1947. [DOI] [PubMed] [Google Scholar]
  50. Vetter, I.R., Arndt, A., Kutay, U., Gorlich, D., and Wittinghofer, A. 1999a. Structural view of the Ran-Importin β interaction at 2.3 Å resolution. Cell 97 635–646. [DOI] [PubMed] [Google Scholar]
  51. Vetter, I.R., Nowak, C., Nishimoto, T., Kuhlmann, J., and Wittinghofer, A. 1999b. Structure of a Ran-binding domain complexed with Ran bound to a GTP analogue: Implications for nuclear transport. Nature 398 39–46. [DOI] [PubMed] [Google Scholar]
  52. Xiang, Z., Soto, C.S., and Honig, B. 2002. Evaluating conformational free energies: The colony energy and its application to the problem of loop prediction. Proc. Natl. Acad. Sci. 99 7432–7437. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Protein Science : A Publication of the Protein Society are provided here courtesy of The Protein Society

RESOURCES