Skip to main content
NCBI home page
Protein Science : A Publication of the Protein Society logoLink to Protein Science : A Publication of the Protein Society
. 2004 Mar;13(3):596–607. doi: 10.1110/ps.03373104

Analysis and prediction of affinity of TAP binding peptides using cascade SVM

Manoj Bhasin 1, GPS Raghava 1
PMCID: PMC2286721  PMID: 14978300

Abstract

The generation of cytotoxic T lymphocyte (CTL) epitopes from an antigenic sequence involves number of intracellular processes, including production of peptide fragments by proteasome and transport of peptides to endoplasmic reticulum through transporter associated with antigen processing (TAP). In this study, 409 peptides that bind to human TAP transporter with varying affinity were analyzed to explore the selectivity and specificity of TAP transporter. The abundance of each amino acid from P1 to P9 positions in high-, intermediate-, and low-affinity TAP binders were examined. The rules for predicting TAP binding regions in an antigenic sequence were derived from the above analysis. The quantitative matrix was generated on the basis of contribution of each position and residue in binding affinity. The correlation of r = 0.65 was obtained between experimentally determined and predicted binding affinity by using a quantitative matrix. Further a support vector machine (SVM)-based method has been developed to model the TAP binding affinity of peptides. The correlation (r = 0.80) was obtained between the predicted and experimental measured values by using sequence-based SVM. The reliability of prediction was further improved by cascade SVM that uses features of amino acids along with sequence. An extremely good correlation (r = 0.88) was obtained between measured and predicted values, when the cascade SVM-based method was evaluated through jackknife testing. A Web service, TAPPred (http://www.imtech.res.in/raghava/tappred/ or http://bioinformatics.uams.edu/mirror/tappred/), has been developed based on this approach.

Keywords: TAP binder, cascade SVM, TAP transporter, CTL epitopes

In this era of proteomics, subunit vaccine designing is an integral part of vaccine design strategy. Development of subunit vaccines critically requires identification of regions in the protein sequences, which are recognized by cytotoxic T lymphocyte (CTL) cells (Schirle et al. 2001; De Groot et al. 2002). The recognition of such immunologically relevant regions by CTLs involve breakdown of a protein into peptides by proteasome complex in cytosol, translocation of subsequent peptides to endoplasmic reticulum (ER), and binding of a subset of these translocated peptides to MHC class I molecules (Nussbaum et al. 2003). These adducts of MHC-peptide were translocated on to the surface of antigen presenting cells (APCs), where they are recognized by T-cell receptors (TCR) of CTLs to elicit an immune response (Hammerling et al. 1999). These immunologically active regions that can spark immune response are known as T-cell epitopes. In the past decade, understanding of various processes involved in generating T-cell epitopes has increased tremendously. Understanding of the rules governing each of these processes made it possible to formulate prediction algorithms. These computational algorithms will complement laboratory experiments and speed up knowledge-based discoveries (Brusic et al. 1999).

In the past, a number of algorithms have been developed for predicting CTL epitopes from antigenic sequence. These algorithms predict CTL epitopes either directly (DeLisi and Berzofsky 1985; Margalit et al. 1987) or indirectly by identifying proteasomal cleavage sites (Holzhutterer et al. 1999) or MHC class I binders (Parker et al. 1994; Rammensee et al. 1995; Gulukota et al. 1997; Doytchinova and Flower 2001; Donnes and Elofsson 2002) or a combination of both (Singh and Raghava 2003). In contrast, only limited algorithms were developed to explore TAP binding and translocation efficiency of peptides due to the lesser amount of data. The JenPep is the first publicly available compilation having ~400 TAP binding peptides (Blythe et al. 2002). The TAP binding peptides are also included in version 3.1 of MHCBN (Bhasin et al. 2003). TAP is a main channel for the transport of the antigenic fragments/peptides from cytosol to ER, where they bind to MHC molecules (Lankat-Buttgereit and Tampe 2002). This is a heterodimeric transporter belonging to the family of ABC transporters that uses the energy provided by ATP to translocate the peptides across the membrane (Abele and Tampe 1999; van Endert et al. 2002). Because of extensive polymorphism in TAP2 subunit of rat transporter, distinct set of peptides bind and are translocated by TAP transporter with varying efficiency (Uebel and Tampe et al. 1999). The understanding of selectivity and specificity of TAP may contribute significantly in prediction of the MHC class I restricted T-cell epitopes.

A TAP transporter can translocate peptides of 8 to 40 amino acids, with preference for peptides of length 8 to 11 amino acids (Heemels and Ploegh 1994; Schumacher et al. 1994). Beside length preference, the nature of peptides also influences the peptide selectivity. TAP from human as well as rat strain RT1a translocates peptides with broad specificity (hydrophobic or basic amino acids at C terminus), whereas TAP from mouse and rat strain RT1u prefers peptides with hydrophobic C termini (Heemels et al. 1993; Androlewicz and Cresswell 1994; Neefies et al. 1995). Further, it was shown that TAP strongly favors hydrophobic residues at position 3 (P3) and charged and hydrophobic residues at P2, although aromatic and acidic residues in P1 have very deleterious effects (van Endert et al. 1995; Lankat-Buttgereit and Tampe 1999). van Endert and coworkers also observed that proline in P1 and P2 has very deleterious effects on the TAP binding affinity of peptides (van Endert et al. 1994; Uebel et al. 1997).

On the basis of above analysis, few methods for the prediction of TAP binding affinity of peptides have been developed. The previously published methods are based on TAP motifs, consensus matrix, or machine-learning techniques (ANN; Daniel et al. 1998; Brusic et al. 1999; Peters et al. 2003). The selectivity of TAP transporter has been modeled with fair accuracy by these methods, but so far, none of TAP binder prediction methods are available online. This motivated us to analyze TAP binding peptides and develop an online tool for predicting TAP binding affinity of peptides.

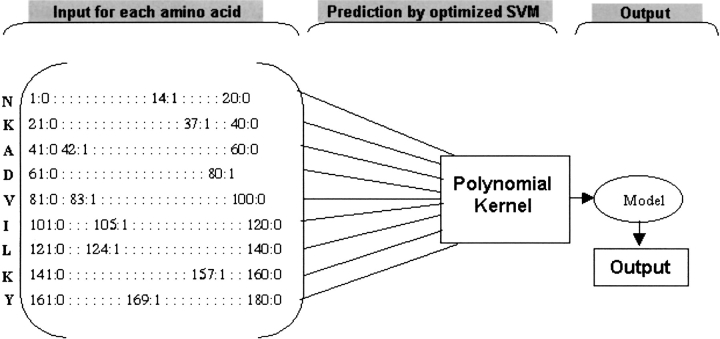
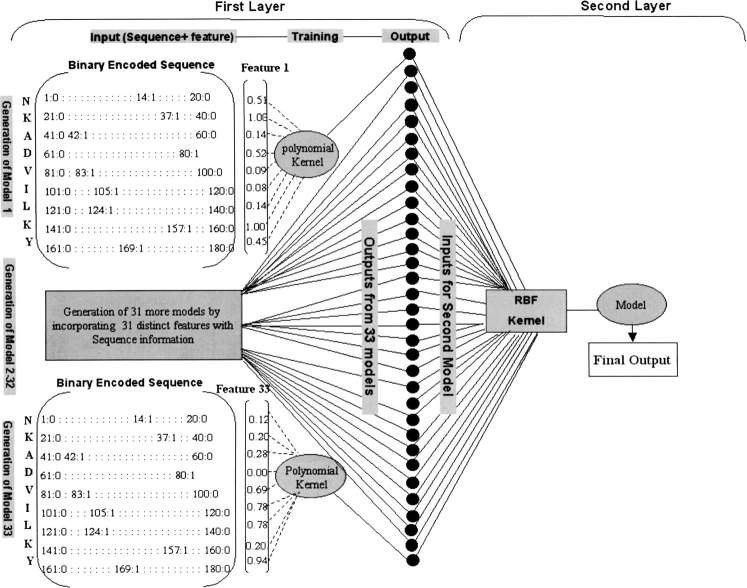
In this study, the features of a large number of peptides are analyzed with quantitative TAP binding affinity that is known. The features were analyzed by studying the abundance of amino acids and variations in features (physicochemical properties) from P1 to P9 positions of TAP binders. On the basis of this analysis, rules were derived for developing more accurate TAP prediction methods. First, a quantitative matrix–based method has been developed to model the TAP binding affinity of peptides. A fairly good correlation (r = 0.65) was obtained between experimentally determined and predicted IC50 values. To further improve the reliability of prediction, a support vector machine was applied. Support vector machines can handle noise and nonlinearity in data very well. We have developed an SVM-based method for predicting TAP binding affinity of peptides. Prediction is based either on complex patterns extracted from sequence (Fig. 1 ▶) or on sequence along with 33 features of amino acids. A new strategy, cascade SVM, was developed that consists of two layers of SVM to incorporate features with sequence (Fig. 2 ▶). By using cascade SVM, an extremely good correlation (r = 0.88) was achieved between experimentally determined and predicted binding affinity of TAP peptides. Based on this approach, an online method, TAPPred, has been developed (http://www.imtech.res.in/raghava/tappred/).

Figure 1.

Figure 1.

Open in a new tab

Diagrammatic representation of sequence-based SVM method.

Figure 2.

Figure 2.

Open in a new tab

The schematic representation of cascade SVM–based prediction method. The prediction is performed by using two layers of SVM. In the first layer, prediction is based on the features and sequence information. At the second layer, prediction is based on the output of the first layer.

Results

The prediction of TAP binding affinity of peptides can assist in subunit vaccine design. The prediction of TAP binding affinity and translocation efficiency of peptides is still in its infancy, due to limited amount of well-characterized data. In past, based on analysis of TAP binding peptides, few methods for the prediction of TAP binding affinity of peptides have been designed. Each of the currently available methods has its own merits and demerits. In this article, we analyze the TAP binding peptides thoroughly to devise rules for formulating a more reliable prediction method.

Relative abundance of amino acids in TAP binders

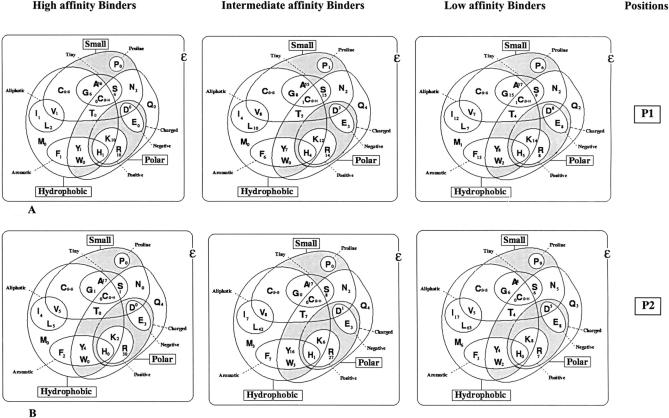
The relative abundance of amino acids from positions P1 to P9 of high, intermediate, and low TAP binders was studied and illustrated by generating Venn diagrams. Venn diagrams have been generated for each position in peptide. Venn diagrams illustrate features (physicochemical) and abundance of each natural amino acids at specific position in TAP binders, as shown in Figure 3 ▶, thus providing an idea about which type of residues (physicochemical properties) are preferred for particular position. The analysis demonstrated that three positions at the N terminus and one position at the C terminus have preferences for distinct types of amino acids. At position P1 in TAP binder (high, intermediate, and low), tiny and aliphatic residues (alanine) are most preferred, as shown in Figure 3A ▶. Arginine and leucine are the most abundant residues at the second position, indicating that bulky and aliphatic residues are most preferred at the second position, as shown in Figure 3B ▶. Large, hydrophobic, and aromatics residues are highly favored at the third position, as illustrated in Figure 3C ▶. The ninth position of TAP binders has an inclination toward large, hydrophobic, and aromatic residues, as depicted in Figure 3d ▶.

Figure 3.

Figure 3.

Figure 3.

Open in a new tab

The abundance and features of amino acids occurring in high-, intermediate-, and low-affinity binders at the first, second, third, and ninth positions. High, Intermediate, and Low specifies the high-, intermediate-, and low-affinity TAP binders. Positions 1, 2, 3, and 9 of TAP binders are specified by P1, P2, P3, and P9, respectively.

Correlation between amino acid features and TAP binding affinities

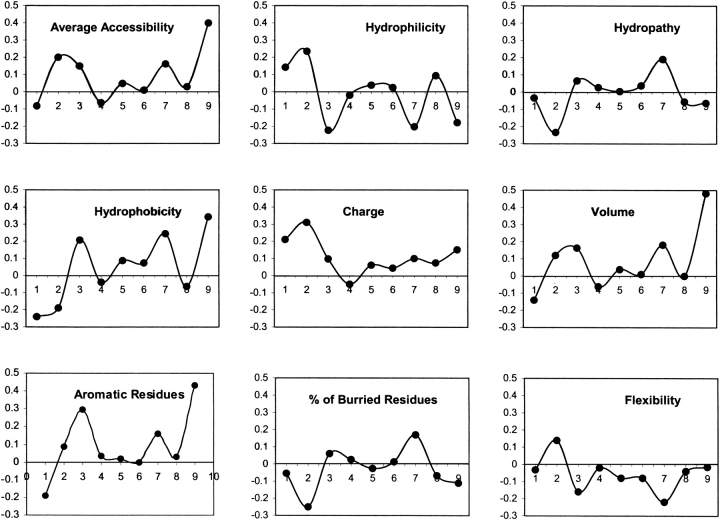
To understand the correlation between binding affinity and features (physicochemical properties), the analysis was further extended. The analysis was done for nine features of amino acids mentioned in Materials and Methods and Table 2. The results of the analysis of each feature are illustrated in graphical form in Figure 4 ▶.

Table 2.

The list of the features (physicochemical properties) of amino acids along with bibliographic details used in the development of cascade SVM–based methods

S.NO Major feature Details of features
1 Hydrophobicity Hydrophobicity in folded forma; hydrophobicity in unfolded forma; hydrophobicity gaina; surrounding hydrophobicity in α-helixa; surrounding hydrophobicity in β-sheeta; surrounding hydrophobicity in β-turna; hydrophobicityb; average surrounding hydrophobicityc; hydrophobicityd
2 Hydrophilicity Hydrophilicitye; hydrophilicity from HPLCf
3 Accessibility Average accessibility surface areag; accessibility reduction ratioa; accessible surface area in the standard stateh; average accessible surface area in folded proteinsh
4 Flexibility Flexibilityi; local flexibilityj; flexibility for no rigid neighborsk; flexibility for one rigid neighbork; flexibility for two rigid neighborsk
5 Distribution ratio Normalized frequency of α-helix with weightsl; normalized frequency of β-sheet with weightsl; normalized frequency for reverse turn with weightsl; percentage of buried residuesa; Percentage of exposed residuesa
6 Other features Free energy of transfer to surfacea; polaritya; volumem; refractivityd; aromatic amino acidsd; charge of amino acidsl; average number of surrounding residuesa; hydropathyn
Open in a new tab

aBull and Breese (1974)

bEisenberg (1984)

cManavalan and Ponnuswamy (1978)

d J. Jones (1975)

eHopp and Woods (1981)

fParker et al. (1986)

gJanin and Wodak (1978)

hRose et al. (1985)

iRagone et al. (1989)

jBhaskaran and Ponnuswamy (1988)

kKarplus and Schulz (1985)

lLevitt (1978)

mChothia (1975)

nKyte and Doolittle (1982)

Figure 4.

Figure 4.

Open in a new tab

Positional correlation between features of amino acids and TAP binding affinity of peptides. The correlation was obtained for nine features of amino acids, as discussed in Materials and Methods and shown by different graphs. The x-axes and y-axes in all graphs represent the peptide positions (P1 to P9) and correlation coefficient, respectively.

These graphs clearly demonstrate that the first three N-terminal amino acids and C-terminal residues have significant differences in physicochemical features. P1 of peptides favors the charged hydrophilic residues, not the aromatic higher-volume and hydrophobic residues. Higher-volume, charged, hydrophilic, accessible, and flexible residues are favored at the second position of the peptides. The third position mostly possesses hydrophobic aromatic accessible residues.

The C terminus of peptides prefer higher-volume, charged, aromatic, hydrophobic, and accessible residues. These results complement the previous observation that the C terminus of TAP binding peptides is hydrophobic (van Endert et al. 1995). Along with the above-discussed positions, the seventh position of peptides has preference for higher-volume, charged, aromatic, and hydrophobic amino acids. Distribution of buried residues in TAP binders was also studied. The seventh position of the peptides favors buried residues, whereas the buried residues are disliked at the second and ninth positions. The rest of the positions of peptide did not show any preference for residues with specific features; thus, these positions might not be responsible in determining the specificity of TAP transporter (Lankat-Buttgereit and Tampe 2002). This analysis has proven that the first three residues at the N terminus and one residue at the C terminus are responsible for the specificity of TAP binding peptides. Our finding complements the previous finding of van Endert et al. (1995), which demonstrates the effects of N- and C-terminal residues of peptide in TAP binding. Further details of preference for specific residues can be obtained by thoroughly analyzing the Figures 3 ▶ and 4 ▶.

Quantitative matrix–based prediction of affinity of TAP binding peptides

We have developed quantitative matrix–based method to predict TAP binding regions of sequence, as shown in Table 1. The performance of this quantitative matrix was evaluated by using jackknife testing. An impressive correlation (r = 0.65) was achieved between the experimentally determined and predicted binding affinity. The performance of the quantitative matrix–based method is slightly lesser than the performance (r = 0.732) of the previously developed ANN-based method (Daniel et al. 1998). To find out the contribution of position (P1 to P9) in binding the ratio of top1/bottom1, top2/bottom2, and top3/bottom3 residues were obtained. The analysis demonstrate that ratio of one, two, or three highest and least contributing residues is maximum for P9. Thus, the ninth position of TAP contributes significantly in binding compared with all other positions. Similarly, the ratio of first two positions at the N terminus demonstrate that these positions also contribute significantly in determining the TAP binding affinity of peptides.

Table 1.

A quantitative matrix for predicting TAP binding affinity of peptides generated from 431 peptides interacting with TAP transporter

P1 P2 P3 P4 P5 P6 P7 P8 P9
A 0.53 0.58 0.45 0.50 0.47 0.47 0.46 0.49 0.43
C 0.28 0.00 0.28 0.33 0.11 0.28 0.00 0.78 0.00
D 0.25 0.22 0.35 0.47 0.43 0.44 0.38 0.32 0.15
E 0.27 0.41 0.26 0.45 0.47 0.46 0.24 0.50 0.06
F 0.29 0.52 0.54 0.50 0.46 0.45 0.53 0.44 0.60
G 0.41 0.30 0.43 0.46 0.31 0.31 0.30 0.36 0.24
H 0.34 0.22 0.53 0.18 0.37 0.41 0.44 0.31 0.30
I 0.30 0.37 0.44 0.47 0.49 0.49 0.60 0.36 0.36
K 0.53 0.45 0.40 0.43 0.55 0.49 0.46 0.53 0.46
L 0.42 0.34 0.37 0.43 0.38 0.37 0.48 0.36 0.48
M 0.22 0.26 0.42 0.31 0.61 0.17 0.67 0.20 0.37
N 0.62 0.28 0.26 0.59 0.37 0.33 0.30 0.34 0.14
P 0.13 0.14 0.33 0.40 0.46 0.47 0.29 0.29 0.44
Q 0.35 0.55 0.36 0.42 0.30 0.29 0.26 0.41 0.27
R 0.58 0.67 0.47 0.42 0.44 0.55 0.51 0.55 0.52
S 0.50 0.36 0.40 0.44 0.42 0.44 0.35 0.41 0.19
T 0.40 0.46 0.37 0.44 0.38 0.35 0.40 0.43 0.24
V 0.40 0.52 0.43 0.35 0.44 0.49 0.44 0.39 0.34
W 0.11 0.40 0.66 0.48 0.64 0.58 0.76 0.63 0.42
Y 0.31 0.54 0.69 0.44 0.41 0.38 0.54 0.47 0.72
Top1/bottom1 5.6 3.0 2.6 3.2 2.1 3.41 3.16 3.15 12
Top2/bottom2 5.0 3.5 2.6 2.2 2.0 2.4 2.86 2.46 6.6
Top3/bottom3 3.76 3.0 2.2 1.9 1.8 2.0 2.5 2.13 5.29
Open in a new tab

Each number represents the independent contribution of a specific residue in binding at specific position. The 20 amino acids are indicated by single-letter code; peptide positions, by P1 to P9. The residues having the highest score for each position, P1 to P9, are shown in bold. At bottom of the table the ratio of score of top1/bottom1, top2/bottom2, and top3/bottom3 residues has been shown. Top1/bottom1 represents the ratio of maximum and minimum values at a given position. Top2/bottom2 represents the ratio of average of the top two (two residues with the highest values at specific positions) and bottom two (two residues with the least values at specific positions) values. Similarly, top3/bottom3 represents the ratio of the average of the three highest-value and three least-value residues. The contribution of C has not been considered due to drastic variation in its values from P1 to P9.

Prediction with simple SVM

To predict TAP binding affinity of peptides more accurately, we have developed a statistical learning or SVM-based method. The supervised learning was conducted with each type of kernel (polynomial, RBF, and linear) by spending hours of computational power to develop the best method. The best model of particular kernel was chosen on the basis of correlation between predicted and experimentally determined binding affinity. The performance of models generated by using each type of kernel was tested by using jackknife testing.

Regression mode of SVM was applied on the binary encoded sequence to predict TAP binding affinity of peptides. Table 3 illustrates the best results of kernels along with parameters. From the Table 3, it is clear that the overall performance of RBF and polynomial kernel is promising. The correlation (r = 0.81) between the predicted and experimentally measured binding affinity is best with the polynomial kernel. The correlation (r = 0.81) of the SVM-based methods is better compared with the previously published ANN-based method (r = 0.732).

Table 3.

Performance comparison of various SVM models for predicting TAP binding affinity of peptides after jackknife testing

Polynomial kernel RBF kernel
SVM models Parameters Correlation coefficient (r) Parameters Correlation coefficient (r)
Only sequence based C = 5.00 0.812 C = 15.00 0.795
D = 1 G = 0.005
Only features based (33 physicochemical) C = 5.05 0.80 C = 14.1 0.793
D = 1 G = 0.005
Sequence + 33 features based (33) C = 0.5 0.819 C = 16.1 0.825
D = 1 G = 0.005
Cascade SVM
First modela (average results of 33 models) C = 5.00 0.80
D = 1
Second model C = 1 0.86 C = 30 0.88
D = 3 G = 2.0
Open in a new tab

The best value achieved using various approaches has been shown in bold.

a Average results of 33 models generated in first layer of SVM. Thirty-three models were generated by combining one feature of amino acids with sequence information each time.

Prediction with cascade SVM

In cascade SVM, prediction of TAP binding affinity of peptides was done by using two layers of SVM. In first layer, 33 models were generated by considering 33 features (e.g., charge, volume, polarity) of amino acids. The analysis of the results demonstrated that none of the features of amino acids in combination with sequence information resulted in significant improvement in correlation between the predicted and experimentally measured binding affinity.

By using another model of SVM, we have correlated the results of models generated in first layer. Models were generated by using both polynomial and RBF kernels. The best result is the one in which the highest correlation was obtained between predicted and measured binding affinity after jackknife testing. By using second model, the value of correlation coefficient between predicted and measured binding affinity reached 0.88, which is significantly higher in comparison to only sequence-based prediction. Thus, SVM model generated in the second layer led to tremendous improvement in the prediction performance by filtering results of first layer. The summary of the results obtained by using different kernels is illustrated in Table 3.

We have also generated models by combining sequence with 33 features simultaneously. The input units for each amino acid consisted of 53 units: 20 binary units for sequence, and 33 scalar values of 33 features. The SVM models were generated by using nonlinear and linear type of kernels. The RBF kernel was able to classify the data more accurately compared with other type of kernels. The correlation obtained was 0.82, which is marginally higher in comparison to prediction based on sequence only. The model was discarded due to insignificant improvement in prediction accuracy.

Another SVM model was generated on the basis of the 33 features of amino acids. The input vector was a 34-dimensional first unit representing target value or binding affinity and rest 33 real values represent features of amino acids. The best results were obtained by using the polynomial kernel. This model was discarded due to poorer performance in comparison to the results obtained by sequence-based models.

In conclusion, cascade SVM method (based on two layers) is a more reliable method for predicting TAP binding affinity of peptides. The performance of other SVM models (sequence based, sequence + 33 features, 33 features only) is also quite impressive and better in comparison to previously published TAP binder prediction methods.

Discussion

TAP is an important transporter involved in the translocation of peptides from cytosol to ER. TAP binds and translocates selective peptides for binding to specific MHC molecules. The efficiency of TAP-mediated translocation of peptides has been shown to be proportional to its TAP binding affinity (Brusic et al. 1999). Thus, understanding the nature of peptides, which bind to TAP with high affinity, is one of the crucial steps in endogenous antigen processing.

The analysis of TAP binding peptides demonstrated that peptides binding to human TAP transporter have binding motifs at P1, P2, P3, P7, and P9 positions. The analysis also demonstrated the favored amino acids as well as privileged features (physical and chemical properties) of each position in TAP binders. Table 4 and Figures 3 ▶ and 4 ▶ outline the nature of various positions in TAP binding peptides. To bind with a TAP molecule, a peptide should possess preferably charged, high-volume, and hydrophobic residues at C terminus. In the first two positions of TAP binding peptides, charged accessible residues are favored. A TAP binder has strong preference for hydrophobic and accessible residues at third position. Proline is the most disliked amino acid at the first three positions of TAP binders, as depicted in Figure 3 ▶. The positions P1, P2, P3, P7, and P9 may be crucial in determining the binding specificity of peptides toward human TAP transporter. This observation supports the already proven fact that TAP binding peptides have motifs at positions 1, 2, 3, and 9 (van Endert et al. 1995). The analysis also complements the previous observation that the C terminus of TAP binding peptides is mostly hydrophobic (Lankat-Buttgereit and Tampe 2002). In TAP binders, anchor residues are not specific, as in case of MHC class I binders. In TAP binders, an array of anchor or preferred residues occur at N and C termini. The analysis proved the fact that peptides bind to TAP transporter at N and C termini only. This observation is tempting to speculate that longer peptides may bind to TAP from their termini where their central part bulges out from the binding sites.

Table 4.

The summary favorable or unfavorable effect of features from position P1 to P9 in TAP binders

Peptide positions
Features P1 P2 P3 P4 P5 P6 P7 P8 P9
Volume − ++ ++ ++ ++
Charge ++ ++ ++ ++
Aromatic − ++ ++ ++++
Hydrophobic − − ++ ++ ++
Hydrophilic ++ ++ − − −
Hydropathy − ++
Accessibility ++ ++ ++
Flexibility ++ − −
% buried residues − ++ −
Open in a new tab

++ and − illustrates positive and negatives effect of features at specific position in TAP binding affinity of peptides.

The experimental evaluation of TAP binding affinity of a large number of peptides from the antigenic sequence is very cumbersome and time-consuming. Thus, to speed up the process of efficient T-cell epitope identification, we have developed a method for TAP binders prediction based on the above-mentioned observations.

The method is based on quantitative matrix, SVM, and cascade SVM. In this study, SVM has been introduced for the first time to predict TAP binding affinity of peptides. In this report, a novel machine learning-approach cascade SVM consisting of two layers of SVM has been designed to enhance the reliability of method. The total data set has 431 peptides with quantitative binding affinity toward the TAP transporter. Out of 431 peptides of varying binding affinity, 179 are HLA binding peptides. Most of the high-affinity MHC binders are also high-affinity TAP binders. This lays stress on the observation that TAP selects mostly those peptides, which have favorable residues for binding to MHC molecules.

First, to model the TAP binding affinity of peptides, a quantitative matrix has been designed. The predictability (r = 0.65) of the methods is relatively poor compared with previously published methods (Daniel et al. 1998). To handle the nonlinearity of data and to enrich the reliability, a simple SVM-based method has been developed. By using jackknife testing, correlation of 0.81 was achieved between the predicted and experimentally measured values. The correlation obtained is better than that of all available methods to date. This observation has proven that SVM is better in comparison to other machine-learning approaches in classifying biological data.

To improve the reliability of prediction, features of amino acids were also included along with the sequence for training the SVM. The SVM model was generated by incorporating 33 features of amino acids along with sequence information. This results in an insignificant improvement in performance of the prediction method. Significant lack of improvement in the performance of prediction methods may be the result of complexity of input patterns. Another SVM model generated only on the basis of features of amino acids performed poorer in comparison to only the sequence-based SVM model. The poor performance of the features-based method may be due to overlapping features of amino acids.

In the end, for more reliable prediction, cascade SVM was developed, in which the prediction is performed through two layers of SVM. In the first layer, 33 models were generated by incorporating features to avoid the complexity. In the second layer, another model was generated to filter and combine the output of these models. The second model was able to improve the prediction performance in terms of correlation between the predicted and measured binding affinity. The performance of the method is better compared with that of all the algorithms available to date. However, for more reliable prediction of TAP affinities of individual peptides, it can be envisioned to increase the predictive performance by retaining the SVM with additional data. The method has been implemented online for public use at http://www.imtech.res.in/raghava/tappred. So far, this is the only available online method for predicting human TAP binding peptides from sequence.

As human TAP may skew the HLA class I–associated system of antigen processing and presentation to its main task, the display of abundent nonself proteins derived from viral or bacterial sources, as well as the accurate prediction of peptides transportable into class I pathway, greatly enhances the ability to select immunologically active peptides suitable for use in peptide vaccines.

Materials and methods

Data set

The data set of nine mer peptides with affinity with TAP that has been determined experimentally was kindly provided by Peter van Endert (INSERM U580, Institut Necker, Paris France). TAP binding assay was carried out to determine the affinity of these peptides to TAP and is expressed in terms of IC50 value. The peptides have diverse binding affinity from very high (<0.03 nM) to negligible or no binding (2600 nM). Duplicate peptides and peptides with unnatural amino acids were removed from the data set. The final data set contains 431 peptides with high, intermediate, low, or negligible binding affinity toward TAP transporter. Out of 431 peptides, 409 bind to TAP with varying affinity, and 22 peptides have negligible or no binding affinity.

Normalization of binding affinity

The binding affinity (IC50 value) of peptides used in the analysis was expressed on the scale of 0 to 10, representing a 5-log range of normalized IC50 value from >1000 (score: zero) to <0.003 (score: 10), with a score increment of 1 corresponding to threefold smaller IC50 value (Daniel et al. 1998). Hereafter, normalized binding affinity is referred as target value varying from 0 to 10.

Generation of quantitative matrix

As quantitative matrices have been recently used successfully to predict MHC binders, in this report we attempted to develop a quantitative matrix-based method to predict the TAP binding affinity of peptides. The quantitative matrix was not generated on the basis of probability or frequency of an amino acid at particular position. It was generated on the basis of average score of an amino acid at particular position in peptide data set as shown in equation 1. For generating the quantitative matrix, a data set of 431 peptides (binding affinity expressed on scale of 1 to 10) was used:

graphic file with name M1.gif (1)

Where Ai,r is the matrix entry of residue r in position i, r can be any natural amino acid, and the value of i can vary from one to nine.

A matrix of 9 × 20 dimensions was generated after determining the average score of all 20 natural amino acids from position P1 to P9 of peptides, as shown in Table 1. The predictability of newly generated quantitative matrix was evaluated by using jackknife testing. To understand the contribution of each position in determining the binding affinity of peptides, the ratio of top1/bottom1, top2/bottom2, and top3/bottom3 has been calculated as shown at the base of Table 1. The top2/bottom2 and top3/bottom3 values were obtained by using equations 2 and 3, respectively.

graphic file with name M2.gif (2)
graphic file with name M3.gif (3)

The previous investigations have proven that machine-learning techniques are more accurate in classifying nonlinear data. Thus, to increase the reliability of TAP binders prediction, we have developed a SVM-based method.

SVM training and prediction

Support vector machines are a relatively new type of supervised machine-learning techniques proven to be particularly attractive to biological analysis due to their ability to handle noise and large input spaces (Brown et al. 2000; Ding and Dubchak 2001). SVM simulation was achieved by using the SVM_light package (Joachims 1999). This package enables the user to define a number of parameters and to select a choice of inbuilt kernel functions, including Polynomial, RBF, Linear, and Sigmoid. In this study the regression mode of SVM was used to model the TAP binding affinity of peptides.

Let us assume that we have a series of TAP interacting peptides xi¯ɛRd (i = 1, 2,...,N) with corresponding targeted value yi ɛ {〈target value〉}(i = 1,2,...,N). The xi¯ corresponds to the representation of amino acid sequence of the peptides to SVM. Here, target value is a real value varying from 0 to 10.

The SVM maps the input vectors xi¯ into high-dimensional feature space and constructs a hyper plane where the error is minimal on the training set. The decision function implemented by SVM can be written as follows:

graphic file with name M4.gif

The value of the αi is given by the task of quadratic programming task, maximize subject to 0 ≤ αi ≤ C, where C is the regulatory parameter controlling the trade off between the margin and training error. Choosing a kernel type for SVM is analogous to the problem of choosing an architecture for neural network.

In the present work, SVM parameters were all set to default, except kernel function and regularization parameter C. Readers interested in more details of SVM_light specifications and terminologies can consult Vapnik’s articles on SVM (Cristianini and Shawe-Taylor 2000).

In this study, two types of SVM-based methods have been developed: simple SVM, based on binary encoding of sequence, and cascade SVM, based on the binary encoded sequence plus features of amino acids. The schematic views of simple and cascade SVM are shown in Figures 1 ▶ and 2 ▶.

Simple SVM

The model was generated on the basis of sparse binary encoding of sequence, as depicted in Figure 1 ▶. Each amino acid was encoded as a 20-bit string with a unique position set at one and all other positions set at zero. Each peptide of nine amino acids was represented by 180 inputs and a target value during model generation. The models were generated by using the different types of kernels such as polynomial, RBF, and linear. The performance of standard kernel function was evaluated by using jackknife testing. The performance of a kernel was determined by measuring the correlation coefficient between predicted and experimentally measured values. The output was obtained on scale of zero to 10, where zero corresponds to a IC50 of >1000 and 10 corresponds to an IC50 of <0.03.

Cascade SVM

In cascade SVM, prediction was based on the sequence and features of amino acids. The prediction was performed by using two layers of SVM, as shown in Figure 2 ▶. In the first layer, 33 models were generated by combining 33 features of amino acids with sequence information (one each time). In the second layer, a final model was generated by giving the output of 33 models generated at the first layer as input.

First layer of SVM

Models were generated on the basis of sequence and features of amino acids. The features (physical and chemical properties) of amino acids used in study are shown in Table 2. The input vector for each amino acid was 21-dimensional. Among these, first 20 units of the vector stood for one type of amino acid. To specify particular features of an amino acid, such as charge and volume, the 21st unit was added for each residue. The first 20 inputs were binary encoding of residue, and 21st is a real value. Each peptide of nine amino acids was represented by 189 inputs. The type of kernel and its various parameters were optimized to obtain the best results. In this manner, combining single features of amino acids to sequence information resulted in 33 feature-specific models, as shown in Figure 2 ▶.

Second layer of SVM

The second layer model takes the output of the 33 models generated at the first level and yields the final output on the basis of these outputs. Each peptide of nine amino acids was encoded by 34 real value units, where one unit codes for the targeted value and the remaining 33 inputs are outputs of each peptide from 33 models generated at first layer (Fig. 2 ▶). The best model was chosen after varying both kernels types and their parameters. The model was fine-tuned by changing the value of regulatory parameter C. The best model was considered on the basis of the correlation between predicted and measured values after jackknife testing.

The SVM models were also generated on basis (sequence + 33 features of amino acids) and only on the basis of 33 features (physical or chemical properties) of amino acids. In first and second cases, the input vector for each amino acid consists of 53 and 33 units, respectively.

Analysis of TAP peptides using Venn diagrams

All high-, intermediate-, and low-affinity TAP binders were analyzed for distribution of amino acids from position P1 to P9 of peptides. The abundance of all natural amino acids was calculated for each position in peptide separately for high-, intermediate-, and low-affinity binders. Abundance of a particular amino acid from P1 to P9 was depicted by generating Venn diagrams. The Venn diagrams provide information whether an amino acid with specific features is preferred at particular position or not.

Further, to obtain better correlation between features (physicochemical properties) and binding affinity, TAP binders were analyzed by considering the following features: volume, charge, aromatic, hydrophobicity, hydrophilicity, average accessibility, flexibility, hydropathy, and percentage buried. The values of each feature were normalized between zero and one. The effect of each feature on binding affinity was examined by obtaining the form between the specific feature and experimentally determined binding affinity for every position (P1 to P9) of TAP binder. The variation in position specific features of TAP binders was analyzed by plotting correlation (r) for each position (P1 to P9).

Evaluation of methods using jackknife validation

The performance of a computational algorithm is often tested by the cross-validation or jackknife method (Zhang and Chou 1995). In this study, the performance of SVM-based models was tested by jackknife testing (testing of each peptide of the data set) due to small size of the data set. The jackknife method is the most extreme and accurate type of cross-validation test. In jackknife testing the data set having n peptides is broken in n subsets, each having one example. The classifier was trained on n − 1 subset and evaluated on nth subset. The process was repeated n times using each subset as the testing set and rest of peptides for training once. The results of test subsets were combined to get an overall estimate of training procedure. The performance of quantitative matrice-, simple SVM-, or cascade SVM-based methods was tested by jackknife validation test.

Acknowledgments

We thank Dr. Peter van Endert, INSERM U580, Institut Necker, Paris, France, for providing data for designing of this method. We thank the Council of Scientific and Industrial Research (CSIR) and Department of Biotechnology (DBT), India, for financial assistance.

The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.

Article and publication are at http://www.proteinscience.org/cgi/doi/10.1110/ps.03373104.

References

  1. Abele, R. and Tampe, R. 1999. Function of the transport complex TAP in cellular immune recognition. Biochim. Biophys. Acta. 1461 405–419. [DOI] [PubMed] [Google Scholar]
  2. Androlewicz, M.J. and Cresswell, P. 1994. Human transporters associated with antigen processing possess a promiscuous peptide-binding site. Immunity 1 7–14. [DOI] [PubMed] [Google Scholar]
  3. Bhasin, M., Singh, H., and Raghava, G.P.S. 2003. MHCBN: A comprehensive database of MHC binding and non-binding peptides. Bioinformatics 19 666–667. [DOI] [PubMed] [Google Scholar]
  4. Bhaskaran, R. and Ponnuswamy, P.K. 1988. Positional flexibilities of amino acid residues in globular proteins. Int. J. Pept. Protein Res. 32 241–255. [DOI] [PubMed] [Google Scholar]
  5. Blythe, M.J., Doytchinova, I.A., and Flower, D.R. 2002. JenPep: A database of quantitative functional peptide data for immunology. Bioinformatics 18 434–439. [DOI] [PubMed] [Google Scholar]
  6. Brown, M.P.S., Grundy, W.N., Lion, D., Cristianini, N., Sugnet, C.W., Furey, T.S., Ares Jr., M., and Haussler, D. 2000. Knowledge-based analysis of microarray gene expression data by using support vector machines. Proc. Natl. Acad. Sci. 97 262–297. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Brusic, V., van Endert, P., Zeleznikow, J., Daniel, S., Hammer, J., and Petrovsky, N. 1999. A neural network model approach to the study of human TAP transporter. In Silico Biol. 1 9–21. [PubMed] [Google Scholar]
  8. Bull, H.B. and Breese, K. 1974. Surface tension of amino acid solutions: A hydrophobicity scale of the amino acid residues. Arch. Biochem. Biophys. 161 665–670. [DOI] [PubMed] [Google Scholar]
  9. Chothia, C. 1975. Structural invariants in protein folding. Nature 254 304–308. [DOI] [PubMed] [Google Scholar]
  10. Cristianini, N. and Shawe-Taylor, J. 2000. Support vector machines and other kernel-based learning methods. Cambridge University Press, Cambridge, UK.
  11. Daniel, S., Brusic, V., Caillat-Zucman, S., Petrovsky, N., Harrison, L., Riganelli, D., Sinigaglia, F., Gallazzi, F., Hammer, J., and van Endert, P.M. 1998. Relationship between peptide selectivities of human transporters associated with antigen processing and HLA class I molecules. J. Immunol. 161 617–624. [PubMed] [Google Scholar]
  12. De Groot, A.S., Sbai, H., Aubin, C.S., McMurry, J., and Martin, W. 2002. Immuno-informatics: Mining genomes for vaccine components. Immunol. Cell Biol. 80 255–269. [DOI] [PubMed] [Google Scholar]
  13. DeLisi, C. and Berzofsky, J.A. 1985. T-cell antigenic sites tend to be amphipathic structures. Proc. Natl. Acad. Sci. 82 7048–7052. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Ding, C.H.Q. and Dubchak, I. 2001. Multi-class protein fold recognition using support vector machines and neural networks. Bioinformatics 17 349–358. [DOI] [PubMed] [Google Scholar]
  15. Donnes, P. and Elofsson, A. 2002. Prediction of MHC class I binding peptides, using SVMHC. BMC Bioinformatics 3 25. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Doytchinova, I.A. and Flower, D.R. 2001. Toward the quantitative prediction of T-cell epitopes: coMFA and coMSIA studies of peptides with affinity for the class I MHC molecule HLA-A*0201. J. Med. Chem. 44 3572–3581. [DOI] [PubMed] [Google Scholar]
  17. Eisenberg, D. 1984. Three-dimensional structure of membrane and surface proteins. Annu. Rev. Biochem. 53 595–623. [DOI] [PubMed] [Google Scholar]
  18. Gulukota, K., Sidney, J., Sette, A., and DeLisi, C. 1997. Two complementary methods for predicting peptides binding major histocompatibility complex molecules. J. Mol. Biol. 267 1258–1267. [DOI] [PubMed] [Google Scholar]
  19. Hammerling, G.J., Vogt, A.B., and Kropshofer, H. 1999. Antigen processing and presentation: Towards the millennium. Immunol. Rev. 172 5–11. [DOI] [PubMed] [Google Scholar]
  20. Heemels, M.T. and Ploegh, H.L. 1994. Substrate specificity of allelic variants of the TAP peptide transporter. Immunity 1 775. [DOI] [PubMed] [Google Scholar]
  21. Heemels, M.T., Schuhmacher, T.N.M., Wonigeit, K., and Ploegh, H.L. 1993. Peptide translocation by variants of the transporter associated with antigen processing. Science 262 2059–2063. [DOI] [PubMed] [Google Scholar]
  22. Holzhutterer, H.G., Frommel, C., and Kloetzel, P.M. 1999. A theoretical approach towards the identification of cleavage-determining amino acid motifs of the 20 S proteasome. J. Mol. Biol. 286 1251–1265. [DOI] [PubMed] [Google Scholar]
  23. Hopp, T.P. and Woods, K.R. 1981. Prediction of protein antigenic determinants from amino acid sequences. Proc. Natl. Acad. Sci. 78 3824–3828. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Janin, J. and Wodak, S. 1978. Conformation of amino acid side-chains in proteins. J. Mol. Biol. 125 357–386. [DOI] [PubMed] [Google Scholar]
  25. Joachims, T. 1999. Making large-scale SVM learning practical. In Advances in kernel methods: Support vector learning (eds. B. Scholkopf et al.), pp. 42–56, MIT Press, Cambridge, MA.
  26. Jones, D.D. 1975. ProtScale Tool: Amino acid scale: Refractivity. J. Theor. Biol. 50 167–184.1127956 [Google Scholar]
  27. Karplus, P.A. and Schultz, G.E. 1985. Prediction of chain flexibility in proteins. Naturwissenschaften 72 212–213. [Google Scholar]
  28. Kyte, J. and Doolittle, R.F. 1982. A simple method for displaying the hydropathic character of a protein. J. Mol. Biol. 157 105–132. [DOI] [PubMed] [Google Scholar]
  29. Lankat-Buttgereit, B. and Tampe, R. 1999. The transporter associated with antigen processing TAP: Structure and function.FEBS Lett. 464 108–112. [DOI] [PubMed] [Google Scholar]
  30. ———. 2002. The transporter associated with antigen processing: Function and implications in human diseases. Physiol. Rev. 82 187–204. [DOI] [PubMed] [Google Scholar]
  31. Levitt, M. 1978. Conformational preferences of amino acids in globular proteins. Biochemistry 17 4277–4285. [DOI] [PubMed] [Google Scholar]
  32. Manavalan, P. and Ponnuswamy, P.K. 1978. Hydrophobic character of amino acid residues in globular proteins. Nature 275 673–674. [DOI] [PubMed] [Google Scholar]
  33. Margalit, H., Spouge, J.L., Cornette, J.L., Cease, K.B., Delisi, C., and Berzofsky, J.A. 1987. Prediction of immunodominant helper T cell antigenic sites from the primary sequence. J. Immunol. 138 2213–2229. [PubMed] [Google Scholar]
  34. Neefjes, J., Gottfried, E., Roelse, J., Gromme, M., Obst, R., Hammerling, G.J., and Momburg, F. 1995. Analysis of the fine specificity of rat, mouse and human TAP peptide transporters. Eur. J. Immunol. 25 1133–1136. [DOI] [PubMed] [Google Scholar]
  35. Nussbaum, A.K., Kuttler, C., Tenzer, S., and Schild, H. 2003. Using the World Wide Web for predicting CTL epitopes. Curr. Opin. Immunol. 15 69–74. [DOI] [PubMed] [Google Scholar]
  36. Parker, J.M., Gao, D., and Hodges, R.S. 1986. New hydrophilicity scale derived from high-performance liquid chromatography peptide retention data: Correlation of predicted surface residues with antigenicity and X-ray–derived accessible sites. Biochemistry 25 5425–5432. [DOI] [PubMed] [Google Scholar]
  37. Parker, K.C., Bednarek, M.A., and Coligan, J.E. 1994. Scheme for ranking potential HLA-A2 binding peptides based on independent binding of individual peptide side-chains. J. Immunol. 152 163–175. [PubMed] [Google Scholar]
  38. Peters, B., Bulik, S., Tampe, R., Van Endert, P.M., and Holzhutter, H.G. 2003. Identifying MHC class I epitopes by predicting the TAP transport efficiency of epitope precursors. J. Immunol. 171 1741–1749. [DOI] [PubMed] [Google Scholar]
  39. Ragone, R., Facchiano, F., Facchiano, A., Facchiano, A.M., and Colonna, G. 1989. Flexibility plot of proteins. Protein Eng. 2 497–504. [DOI] [PubMed] [Google Scholar]
  40. Rammensee, G., Friede, T., and Stevanoviic, S. 1995. MHC ligands and peptide motifs: First listing. Immunogenetics 41 178–228. [DOI] [PubMed] [Google Scholar]
  41. Rose, G.D., Geselowitz, A.R., Lesser, G.J., Lee, R.H., and Zehfus, M.H. 1985. Hydrophobicity of amino acid residues in globular proteins. Science 229 834–838. [DOI] [PubMed] [Google Scholar]
  42. Schirle, M., Weinschenk, T., and Stevanovic, S. 2001. Combining computer algorithms with experimental approaches permits the rapid and accurate identification of T cell epitopes from defined antigens. J. Immunol. Methods 257 1–16. [DOI] [PubMed] [Google Scholar]
  43. Schumacher, T.N., Kantesaria, D.V., Heemels, M.T., Ashton-Rickardt, P.G., Shepherd, J.C., Fruh, K., Yang, Y., Peterson, P.A., Tonegawa, S., and Ploegh, H.L. 1994. Peptide length and sequence specificity of the mouse TAP1/TAP2 translocator. J. Exp. Med. 179 533–540. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Singh, H. and Raghava, G.P.S. 2003. ProPred1: Prediction of promiscuous MHC class I binding sites. Bioinformatics 19 1009–1014. [DOI] [PubMed] [Google Scholar]
  45. Uebel, S. and Tampe, R. 1999. Specificity of the proteasome and the TAP transporter. Curr. Opin. Immunol. 11 203–208. [DOI] [PubMed] [Google Scholar]
  46. Uebel, S., Kraas, W., Kienle, S., Wiesmuller, K.H., Jung, G., and Tampe, R. 1997. Recognition principle of the TAP transporter disclosed by combinatorial peptide libraries. Proc. Natl. Acad. Sci. 94 8976–8981. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. van Endert, P.M., Tampé, R., Meyer, T.H., Tisch, J., Bach, F., and McDevitt, H.O. 1994. A sequential model for peptide binding and transport by the transporters associated with antigen processing. Immunity 1 491–500. [DOI] [PubMed] [Google Scholar]
  48. van Endert, P.M., Riganelli, D., Greco, G., Fleischhauer, K., Sidney, J., Sette, A., and Bach, J.F. 1995. The peptide-binding motif for the human transporter associated with antigen processing. J. Exp. Med. 182 1883–1895. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. van Endert, P.M., Saveanu, L., Hewitt, E.W., and Lehner, P. 2002. Powering the peptide pump: TAP crosstalk with energetic nucleotides. Trends Biochem. Sci. 27 454–461. [DOI] [PubMed] [Google Scholar]
  50. Zhang, C.T. and Chou, K.C. 1995. An analysis of protein folding type prediction by seed-propagated sampling and jackknife test. J. Protein Chem. 14 583–593. [DOI] [PubMed] [Google Scholar]

Articles from Protein Science : A Publication of the Protein Society are provided here courtesy of The Protein Society

RESOURCES