Improved side-chain prediction accuracy using an ab initio potential energy function and a very large rotamer library

Abstract

Accurate prediction of the placement and comformations of protein side chains given only the backbone trace has a wide range of uses in protein design, structure prediction, and functional analysis. Prediction has most often relied on discrete rotamer libraries so that rapid fitness of side-chain rotamers can be assessed against some scoring function. Scoring functions are generally based on experimental parameters from small-molecule studies or empirical parameters based on determined protein structures. Here, we describe the NCN algorithm for predicting the placement of side chains. A predominantly first-principles approach was taken to develop the potential energy function incorporating van der Waals and electrostatics based on the OPLS parameters, and a hydrogen bonding term. The only empirical knowledge used is the frequency of rotameric states from the PDB. The rotamer library includes nearly 50,000 rotamers, and is the most extensive discrete library used to date. Although the computational time tends to be longer than most other algorithms, the overall accuracy exceeds all algorithms in the literature when placing rotamers on an accurate backbone trace. Considering only the most buried residues, 80% of the total residues tested, the placement accuracy reaches 92% for χ₁, and 83% for χ_{1 + 2}, and an overall RMS deviation of 1 Å. Additionally, we show that if information is available to restrict χ₁ to one rotamer well, then this algorithm can generate structures with an average RMS deviation of 1.0 Å for all heavy side-chains atoms and a corresponding overall χ_{1 + 2} accuracy of 85.0%.

The ability to accurately position side chains, given only the backbone fold as input, has a wide range of applications in protein folding and design. Several groups have developed algorithms to examine the side-chain conformations as well as the backbone fold with the goal of designing new ligand specificities. Wilson et al. were successful at using a computer design method to alter the substrate specificity of alpha-lytic protease to a nonnative substrate with a high level of activity (Wilson et al. 1991). The FLEXS (Lemmen et al. 1998), FLEXX (Kramer et al. 1999), and FLEXE (Claussen et al. 2001) algorithms vary side-chain and backbone conformations to characterize and design ligand sites for small molecules. Others have approached the modulation of protein–protein interactions by demonstrating that the interface between dimeric coiled coils can be altered through redesign efforts (Keating et al. 2001). Energetic predictions about specific residue substitutions at the dimer interface were possible largely because of the accuracies of the side-chain modeling.

The efficiency and accuracy of side-chain placement algorithms, brought about in part by the use of discrete rotamer libraries (Ponder and Richards 1987), has inspired many to write algorithms capable of designing mutations to modulate protein stability. Desjarlais and Handel have been able to redesign the core of proteins to the extent of making predictions about the relative stability of substitutions (Desjarlais and Handel 1995, 1999). Wernisch et al. have conducted similar studies where a large number of core residues of several proteins were reoptimized (Wernisch et al. 2000). Others have used high-speed algorithms to generate multiple native-like structures to emulate the ensemble of structures that makes up the native state of the protein. The variability of rotamer positions in the context of the ensemble has been used in an attempt to construct a partition function directly related to the conformational entropy of the folded protein (Leach and Lemon 1998).

The improved computational power of the standard desktop computer has made it possible to generate entire sequences that fit with a given backbone topology. In fact, Looger and Hellinga have demonstrated that with the proper selection of optimization procedures it is possible to repack proteins larger than 2400 residues with a fair degree of accuracy (Looger and Hellinga 2001). Using side-chain repacking methods as a tool for rational design, the DeGrado group engineered many proteins such as α-helical bundles (Regan and DeGrado 1988), introducing prosthetic groups into some (Robertson et al. 1994), and used these de novo designed proteins as models for studying protein folding and function (Hill et al. 2000). The Mayo group has undertaken perhaps the most significant protein design project where an entire protein was designed, involving optimizing the backbone and side-chain placement as well as the specific side-chain identities. The significance of their results was that the predicted structure was uniquely folded, characterizable by NMR, and showed remarkable agreement between the actual and predicted structures (Dahiyat and Mayo 1997). This was the first definitive example that given a fixed backbone position it was possible to create a sequence that would maintain the desired fold.

Side-chain repacking is a critical step in ab initio folding applications. Simulations typically alternate between backbone and side-chain optimization to reach a final structure. The goal of such simulations is to predict the three dimensional structure of the protein knowing only the sequence. Homology modeling is another approach to determining the three-dimensional fold, but rather than employing a brute-force style search of conformational space, the search is restricted by comparing the new sequence to existing structures. In these cases, repacking algorithms must be robust enough to place side chains on backbones that vary slightly between homologs. Several methods have been developed to use the local environment of the test residue compared to known structures to place rotamers on deviated backbones of a homologous structure (Eisenmenger et al. 1993; Wilson et al. 1993; Ogata and Umeyama 1997). Alternate approaches generate ensembles of protein backbones that deviate from the native structure by up to 4 Å and then assess how well an algorithm can repack side chains to resemble the native positions (Tuffery et al. 1997; Huang et al. 1998; Mendes et al. 2001).

Most repacking algorithms make use of the fact that side chains occupy discrete positions that can be modeled by a discrete rotamer library. The first example was a 67-rotamer library by Ponder and Richards (Ponder and Richards 1987). Subsequent development has led to increase in the detail, the conformational space explored, and the size of the library with the largest discrete library numbering over 7500 rotamers (Xiang and Honig 2001). Methods for sorting through the large number of combinations and the specific advantages and disadvantages for each method are described in detail by Voigt et al. (2000). Briefly, current methods can be classified into those using dead-end eliminations (Lasters et al. 1995; Dahiyat and Mayo 1997). Monte Carlo simulated annealing searches (Liang and Grishin 2002), in combination with neural networks (Hwang and Liao 1995), “branch-and-terminate” (Gordon and Mayo 1999), self-consistent mean field optimization with flexible rotamers (Mendes et al. 1999), and sequential site optimization with multiple starting points (Xiang and Honig 2001). Many algorithms use CHARMM22 (Brooks et al. 1983) as the primary potential energy parameters, but recently, Liang and Grishin provided evidence that this long-standing force-field may not be the most optimal choice for scoring functions (Liang and Grishin 2002). Their scoring function was shown to be significantly more effective.

The algorithm presented here also differs from others in that it develops a potential energy function using the OPLS parameters set (Jorgensen and Tirado-Rives 1988). It uses a simple search strategy of simulated-annealing to optimize the placement of side chains. Most importantly, it pushes the rotamer library size to nearly 50,000 discrete positions. This large library size bears associated difficulties, unrelated to computational time, that have not been addressed in previous studies. In addition, constrained simulations highlight the necessity of using local backbone interactions to drive χ₁ accuracy and, correspondingly, the overall accuracy to even higher levels. The performance of this algorithm is compared to other side-chain modeling algorithms, and yields better overall results than existing methods.

Results and Discussion

The rotamer library

The rotamer libraries used in this study were developed with the idea of sampling a reasonable amount of conformational space using fine steps between rotamers. The full details of the creation of the rotamer libraries is given in the Materials and Methods, but briefly, the range of about most dihedral angles was ±15° in 5° steps for a total of seven discrete positions for any dihedral position or a total of 21 positions for each rotatable bond. This small step size generates a corresponding increase in the total number of rotamers included. No effort was made to limit the total number of rotamers based on frequency of occurrence in the Protein Data Bank (PDB; Berman et al. 2000) or potential intraresidue steric clashes that could occur in longer side chains. Table 1 lists the number of discrete rotamers in the library for each residue type. The total number of rotamers is 49,042, making it the largest discrete rotamer library used for this type of study. The effective library size for arginine is slightly smaller (9477 rotamers) when scaled intraresidue steric clashes, consistent with the level used to perform the full repacking operations (see section on simultaneous optimization of side chains below), are used to eliminate unfavorable conformations. When rotamers were checked against an ideal backbone using the scaled steric clash parameters the effective number of rotamers in the full library was reduced to slightly more than half. The prediction accuracy was decreased slightly when using the reduced rotamer set (data not shown) suggesting that using an ideal backbone to pretest rotamers can lead to improper filtering of conformations because the backbone in actual structures does vary from ideality. The small step size, which was the primary reason for such a large library, offers potential relief positions for rotamers within the same energy well that might otherwise have been eliminated by steric clashes. A library with a coarser step size was tested in an attempt to decrease the computational time; however, the accuracy for this library was also decreased (data not shown).

Table 1.

Number of rotamers and the results of matching the library to native side chains

		Fraction of native rotamers
Residue	Number of rotamers in library	Matched within 40°	Matched within 20°	Average residue RMSD (Å)	Number of side-chain comparisons
Arg	10,935	0.984	0.850	0.58	561
Asn	630	0.998	0.976	0.15	591
Asp	315	0.999	0.986	0.16	717
Cys	21	1.000	0.996	0.11	229
Gln	6750	0.996	0.959	0.28	468
Glu	3375	0.998	0.966	0.33	584
His	2142	1.000	0.989	0.20	272
Ile	441	1.000	0.995	0.11	655
Leu	441	0.996	0.955	0.18	918
Lys	10,935	0.992	0.924	0.43	648
Met	6615	0.985	0.980	0.30	196
Phe	378	1.000	0.989	0.20	473
Pro	16	1.000	1.000	0.09	542
Ser	504	0.999	0.984	0.07	790
Thr	504	0.997	0.992	0.16	774
Trp	483	1.000	0.990	0.29	210
Tyr	4536	1.000	0.993	0.26	442
Val	21	0.999	0.984	0.08	827
	49,042		Cumulative:	0.21	9897

Table 1 also shows the fraction of native rotamer positions that can be approximated by rotamers in the library using dihedral angle deviations from native as the criteria for declaring a match. In all cases, a match was considered successful only if all side-chain dihedral angles within the same rotamer were within 20° or 40° of the native position. As can be seen for the less strict criterion, greater than 98% of all residues in the test set could be approximated by the rotamer library. The average root-mean-squared (RMS) deviation for the dihedral angles for matching rotamers was less than 7.5° for all residues, with the largest variance attributed to arginine and lysine. The reported RMS deviation is the average deviation between the best-fit rotamer and the native side chain regardless of whether it satisfies the dihedral angle criteria. Naturally, side chains with more degrees of freedom or longer length have higher average RMS deviations. This is because cumulative effects of small deviations in each angle translate into large deviations for the terminal side-chain atom positions. The cumulative predicted rotamer RMS deviation to the side chains of the test proteins is 0.21 Å per residue. This is the best the library could achieve provided the best-fit rotamers were found in all cases.

The more restrictive angle cutoff of 20° identifies which residues, namely arginine and lysine, would most likely benefit from an even larger library. Typically, for these two residues a match was usually not found for the terminal dihedrals. Relaxation of the acceptance criterion for arginine and lysine χ₄ to ±45° brings the fraction matched to 0.945 for arginine and 0.966 for lysine. Allowing the terminal arginine χ₅ position to vary ±30° increases the fraction matched even more, but only at the expense of dramatically increasing the library size. Making this extra conformational space available for arginine and lysine had little effect on the average RMS deviation for these residues (data not shown). Therefore, this sampling of extra conformational space was not used in the algorithm.

The potential energy function

The full energy function used in this study was a combination of experimental and empirically determined parameters. Briefly, the energy for a rotamer was calculated using the following equation:

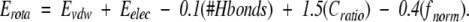The van der Waals energy (E_vdw), electrostatics (E_elec), and the number of hydrogen bonds (#Hbonds) were evaluated against the protein background in a fashion that is typical of previous applications (see below). The contact ratio (C_ratio) is the average steric violation a rotamer makes with other side chains. This term was intended to be an approximation for volume overlap and to account for some accessible surface area effects without the additional computational overhead required for such calculations. The (f_norm) is the frequency of a specific rotamer conformation based on a large set of proteins (Dunbrack Jr. and Karplus 1993) from the PDB.

The van der Waals term is derived from a Lennard-Jones 12–6 potential using parameters from the OPLS united-atom force field for proteins (Jorgensen and Tirado-Rives 1988). This set combines the van der Waals parameters for all hydrogens with the antecedent atom; however, all polar hydrogens have unique partial charge terms. The van der Waals energies were calculated between all atoms more than three bonds away including backbone atoms of the test residue. The only exception was that the C_β atom of the test residue was not used in calculations with the backbone because the energy contribution from this atom does not contribute to its side-chain placement. There was no distance cutoff for the van der Waals potential. The van der Waals term was exceedingly large relative to other terms in the energy function. To prevent this value from dominating, it was normalized to the number of heavy atoms in the side chain giving an effective van der Waals contribution per atom.

The OPLS parameters also include a partial charge list (Jorgensen and Tirado-Rives 1988), and was used here to calculate the electrostatic contributions. Electrostatic interactions were calculated between all atoms more than three bonds away, excluding intraresidue interactions. The minimum distance between charges was not allowed to be less than 0.8 times the van der Waals radii of the atoms to prevent unrealistic charge contributions, arising from random placement of rotamers forcing charges too close together, from dominating the energy of the rotamer. Again, there was no distance cutoff for the electrostatic interactions. In this analysis, the dielectric was set to a uniform value of 80 regardless of the solvent exposure of the residue.

Potential hydrogen bonds between the test rotamer and all nearby hydrogen-bonding groups were tallied. Each hydrogen bond was considered to contribute a favorable 0.1 kcal/mole to the rotamer energy independent of distance and hydrogen bonding geometry. Explicit hydrogens were used in the rotamer library such that the precise geometry could be used to predict most potential hydrogen bonding interactions. The hydrogen-acceptor (H:A) distance, the donor-hydrogen-accepter (DHA) angle, and the hydrogen-accepter-antecedent carbon (HAC) angle were used to define a hydrogen bond. The limits for these parameters (Hebert 1997) were set as follows:

• H:A distance ≤ 2.58 Å

• 110° ≤ DHA angle ≤ 180°

• 90° ≤ HAC angle ≤ 180° for sp² hybridized atoms

• 60° ≤ HAC angle ≤ 180° for sp³ hybridized atoms.

The lysine amino group was not rotated in the library making these hydrogens fixed in position so this explicit analysis method could not be used. In addition, previously placed cysteine, serine, threonine, and tyrosine hydrogens could potentially be rearranged to accommodate new potential hydrogen bonds to the test rotamer. For these residues and lysine, rather than increasing computational costs to explicitly move the hydrogens into place, a parameter set was devised to approximate hydrogen bonds in the absence of discrete hydrogen positions. For these cases the donor-acceptor distance maximum was 3.61 Å. The antecedent atom-donor-accepter angle had to be within the range of 102°–161°, and the donor-acceptor-antecedent carbon angle had to be 71°–180° when calculating hydrogen bonds with lysine, and 41°–180° for hydrogen bonds to sp³ hybridized atoms. These parameters were determined by modeling hydrogen bonds with explicit hydrogens then calculating the distance and angles between participating heavy atoms. This method was slightly less accurate at predicting hydrogen bonds than using explicit hydrogen positions, but because of the relatively low contribution from hydrogen bonds towards placement of these residues, it concluded that it was not necessary to improve upon this.

The contact ratio is the average violation of van der Waals distances between atoms in the rotamer and the other side chains. It is calculated by summing all pairwise atom comparisons where the ratio of the calculated distance divided by the sum of the actual van der Waals radii is less than 1. This sum is then divided by the total number of violations to yield an average violation per atom. Polar side-chain hydrogens were included in this calculation, but contacts with the backbone were not.

The frequency term is based on the statistical occurrence of specific dihedral combinations for a residue in the PDB. The parameters used are the backbone-dependent frequencies determined by Dunbrack Jr. and Karplus (1993). This term is the only term in the potential energy function that is not drawn from the physical properties of the predicted structure. For each residue library, the highest frequency rotamer conformation for a given backbone conformation was used as a normalization parameter such that the highest frequency was set to 1. The frequency definitions are coarse in the sense that all rotamers occupying the same dihedral region had identical frequency terms.

To combine the contact ratio and frequency terms with the other energy terms suitable coefficients were necessary. These coefficients were obtained by using a coarse grid search to find where the average RMS deviation per residue was at a minimum. The protein test set consisted of seven of the test proteins. The coefficient for the frequency term was further adjusted independently for each residue type by changing the value for a given residue, holding all others constant, and the value yielding the best accuracy for that type was kept in the final energy equation. The range of resulting frequency coefficients was from 0.2 to 1.0, which means the maximum contribution in this energy function by the frequency could only be 1 kcal/mole. Proline rotamers were not assigned frequency values in this algorithm.

Simultaneous optimization of side chains

The repacking algorithm was only given the backbone structure and sequence as input. Prior to repacking, the protein was stripped of all side chains leaving only the C_α–C_β vectors from the native structure. This vector was used later to properly orient the rotamer library relative to the backbone. Upon placement of the first trial rotamer the native C_β atom was removed. Next, a search was done for potential disulfide bonds by analyzing pairwise combinations between all cysteine rotamers at all positions where the C_α atoms were less than 9.5 Å apart. The criteria for the formation of a disulfide bond was the S–S distance must be within 2.2 ± 0.3 Å and both Cβ–S–S′ angles within 104.2 ± 30°. These parameters are a modified form of the CHARMM22 parameters for a disulfide bond. If a disulfide bond was identified the corresponding rotamers were placed on the backbone and held fixed for the remainder of the simulation.

The repacking then proceeded by testing the specific library at each position. All rotamers that clashed with the backbone or itself were removed from further consideration. Whether a clash occurred was determined using van der Waals radii scaled by 0.7 for side-chain to side-chain contacts and 0.8 for side-chain to main-chain contacts. If a particular site did not yield any passing rotamers the scaling parameters were incrementally reduced until passing rotamers were obtained. The scaling parameters can be altered at execution time by the user. The use of scaled van der Waals radii is justified because even in high-resolution crystal structures there are still van der Waals violations present, and use of the full radii would often eliminate native-like (i.e., correct) rotamers. The steric-clash tests also included comparisons to the local backbone atoms and intraresidue contacts for arginine and lysine. The filtering method eliminated a significant portion of the possible rotamers early in the simulation. This filtering could have been done during the generation of the libraries. However, the generation of the libraries used idealized placement of the backbone atoms, whereas in the crystal structures these positions were expected to vary from ideality. Although the variations could be slight, rotamers that would otherwise be removed during the generation process might pass when tested against the crystal structure backbone.

The number of rotamers that passed through the steric-clash filter averaged about 500–1000 per test site. The interaction energies with the backbone were calculated for each rotamer for later use in calculating the full energy. The initial placement of residues for the start of the repacking portion was determined randomly. Optimizing side-chain placement was carried out using a simulated annealing method (Press et al. 1992) where each new site and rotamer were selected randomly. The simulated annealing schedule and parameters can be found in Materials and Methods. The frequency of sampling any given site was dependent on the number of rotamers that passed the steric-clash test. This means that residues with three or more side-chain dihedrals generally had significantly more rotamers passing than shorter side chains, and thus were selected more often. Correspondingly, residues such as arginine might be sampled 100 times more often than a proline. This disparity will have an effect on the accuracy of the lower rotamer-count residues. To counteract this, each rotamer in the library for Asn, Asp, Leu, Ile, Phe, and Trp was duplicated, thereby doubling the number of rotamers given in Table 1, and an eightfold duplication of rotamers for the very small libraries of Val and Pro. This increased the probability that the proper rotamer was sampled sufficiently often, but had the disadvantage of increasing the sampling of improper rotamers as well as increasing computation time. Despite the apparent disadvantages, this method improved the accuracy for the core residues.

For even the largest protein in the test set, allowing the algorithm to proceed to convergence or to the point when residues were no longer changing positions was not a significant computational problem. However, because the algorithm was being tested on a large set of proteins it was desirable to find a shortcut to near convergence during development. As it turned out, this shortcut algorithm performs at nearly an identical level of prediction accuracy, and therefore became the method of choice. It differs from a standard simulated annealing in that instead of randomly setting the probability of accepting an uphill move this probability was fixed at 0.92. This parameter was determined empirically on a small subset of the proteins tested, and remained fixed during the remainder of the development process.

One consequence of fixing the unfavorable step-acceptance probability was that very unfavorable moves, such as forcing a change in dihedral positions in a confined space, become highly improbable and introduces concern that side chains might become trapped. To reduce the impact on accuracy from this condition, a method was developed to combine multiple optimizations into a final predicted structure. This method examines the predicted positions, starting with χ₁ for each residue in multiple predicted structures, determines in which one of three possible dihedral regions the majority of the conformations lies, and averages this set of dihedrals to give the final consensus position at that side-chain dihedral. Only those conformations that were part of the consensus group from the previous dihedral angle were used to determine the next dihedral-angle consensus position. If no consensus position was found for a dihedral position, the conformations were averaged to give the final predicted position. Residues that fall into this latter category tend to be positioned less accurately, so fortunately it was rare that a clear consensus position was not found.

For the results reported for this work five optimizations were performed with the number required to form the consensus in χ₁ set to 3. These values were chosen because it yielded the best results with the shortest computational time. Using only three optimization cycles was less accurate, and using seven and nine cycles did not significantly improve the accuracy to warrant the increase in computational time (data not shown).

Importance of individual potential energy terms

Of the terms in the energy function, it turns out that the E_vdw contributes most significantly to the placement of residues. This term is the primary driving force for determination of the χ₁ because only van der Waals interactions are calculated to the local backbone atoms. This result is not new in that its importance has been noted in the form of indications that steric constraints are the driving force for organizing protein conformations (Richards 1977; Srinivasan and Rose 1995). By itself, the van der Waals term predicts the χ₁ and χ_{1 + 2} positions with an accuracy of 86.4% and 70.4%, respectively (see Table 2). This term, however, tends to be much larger in magnitude, and could easily mask the contributions from the other terms. The masking problem becomes worse with increases in the number of atoms in the side chain. Larger residues will usually have larger interaction energies than small residues such that the interaction energy of a valine with the backbone cannot be compared directly to that of a tryptophan due to the differences in overall magnitude. In protein design applications, specifically where there is a high degree of conformational freedom, such as for surface residues, this most decidedly skews the results towards larger residues because more interactions are being tallied per residue. We also noticed some cases where very favorable van der Waals interactions with the backbone overwhelmed very poor electrostatics, hydrogen bonding, or other factors and led to improperly placed side chains. To avoid this, we chose to normalize the van der Waals term to the number of heavy atoms in the side chain. This approach yielded a slight increase in the prediction accuracy over using the full van der Waals energy. The effect on prediction accuracy of each of the four remaining terms in various combinations is indicated in Table 2. To maintain consistency among the simulations, the random seed and sequential order where the proteins were repacked was kept constant. This was to assure that the only changes in accuracy would be due to changes in the contributions from each energy term.

Table 2.

Influence of energy terms on prediction accuracy for 65 high-resolution crystal structures

Energy terms					Angle accuracya			Average RMSD (Å)b		Overall RMSD (Å)b
van der Waals	Electrostatics	Hydrogen bonding	Rotamer frequency	Contact ratio	All χ1/χ1+2	Core χ1/χ1+2	Surface χ1/χ1+2	All	Core	All	Core
X					86.4/70.4	93.1/84.7	78.4/55.7	0.88	0.51	1.51	0.90
X	X				87.0/72.5	93.3/85.4	79.6/59.1	0.82	0.48	1.43	0.85
X	X	X			87.7/73.4	94.0/86.1	80.1/60.2	0.80	0.44	1.40	0.77
X	X	X	X		88.9/76.8	93.9/87.1	82.9/66.0	0.73	0.44	1.29	0.78
X	X	X	X	X	89.3/77.5	94.1/87.4	83.6/67.2	0.72	0.43	1.27	0.75
X	X		X		88.8/76.5	94.0/86.7	82.6/65.9	0.73	0.44	1.29	0.76
X			X		88.4/74.8	93.7/85.6	82.0/63.5	0.76	0.47	1.34	0.82
X		X	X	X	88.5/75.5	93.7/86.1	82.3/64.5	0.75	0.46	1.33	0.82
X	X		X	X	88.8/76.7	93.9/87.1	82.8/65.9	0.73	0.44	1.27	0.76
X	X	X		X	87.4/73.2	93.9/85.9	79.7/60.0	0.80	0.45	1.42	0.80

^a Accuracy is cumulative over all proteins and not the average.

^b Average of individual protein results.

The frequency term is the single largest contributor to placement accuracy after the van der Waals term. By itself it improves the χ₁ accuracy by 2.0%, and the χ_{1 + 2} accuracy by 4.4%, as shown in Table 2, line 7, when compared to van der Waals alone (line 1). The frequency parameters in this algorithm are derived from the backbone-dependent frequencies determined by Dunbrack (Dunbrack Jr. and Karplus 1993). This term replaces calculation of torsion angle energies with a lookup table. As described above, the weight of this term is residue dependent, as determined by an iterative fitting of the energy function to a subset of the proteins. The normalizing of the frequencies to a maximum of one and the magnitude of the coefficients assures that the frequency term would never contribute more than a favorable 1 kcal/mole to the total energy of the residue. The average value for the frequency coefficient was around 0.6. Thus, the magnitude of this term is generally much smaller than the van der Waals term and the electrostatic term for polar residues. Therefore, it was surprising that the individual contribution to accuracy was so high. Replacing the backbone-dependent frequencies with backbone-independent frequencies, also from the Dunbrack group (Dunbrack Jr. and Cohen 1997) reduces the overall χ₁ and χ_{1 + 2} accuracies to 88.1% and 74.5%, respectively (data not shown).

The next largest contributor to the prediction accuracy is electrostatics and hydrogen bonding combined. The energy from an actual hydrogen bond has contributions from both van der Waals and electrostatics, so it seemed logical to include it as well. The improvement in accuracy for χ₁ and χ_{1 + 2} over van der Waals alone was 1.3% and 3.0%, respectively (Table 2, line 3). The hydrogen bond term by itself has only a marginal effect on the prediction accuracy as shown in Table 2, line 9, compared to line 5. The favorable contribution of 0.1 kcal/mole per potential hydrogen bond, determined iteratively during development, was unexpectedly low, because hydrogen bonds have been proposed to favorably contribute about 1 kcal/mole per hydrogen bond in mutational analysis studies (Myers and Pace 1996). The energy function already includes some of this energy in the form of electrostatics and van der Waals contributions, so it was not expected to be as large as −1 kcal/mole. However, adding an additional −0.5 kcal/mole per hydrogen bond adversely affected surface residue accuracy. It appeared that using high values for hydrogen bonds favored the potential formation of hydrogen bonds over more favorable van der Waals interactions. This is probably not what occurs in reality for surface residues. An accounting of the entropic cost of fixing a side chain to form a hydrogen bond to the protein leads to the observation that for surface residues, a minimum of two static hydrogen bonds must form to overcome the penalty. This gross simplification of hydrogen-bonding energetics led to the reduction of the hydrogen bond term such that it would not be the driving force for placement, but rather a term that would distinguish between two relatively favorable positions.

The role the contact ratio plays appeared to be counter to what it had been intended to do. The idea behind the contact ratio was to emulate, in a coarse sense, the volume overlap penalty for residues. Here, contact ratio values near 1 indicate low steric violations, while values closer to zero indicate high van der Waals violations. Detailed assessment of the specific effects of removing this term revealed that it played a significant role in the placement of the core residues. This leads to the conclusion that the contact ratio serves to counteract the repulsive term of the van der Waals energy by forcing residues closer together than what the repulsive term would normally allow. The contact ratio values for the final rotamer positions range between roughly 1.35 and 1.5, including the scaling coefficient. The dynamic range was therefore quite small, so any correction to the radii or energy parameters would be expected to be minor. When the coefficient for the contact ratio was allowed to vary for individual residue types during the energy function-fitting procedure we observed a wider range of values. Residues such as arginine had a coefficient of −2.0, and most hydrophobics except leucine were around −1.0, while the other polar residues and leucine had positive values. For residues such as arginine, turning off this term appears to lead to more accurate placement. The effect of removing this term from the full potential energy function is shown in Table 2, line 4.

The addition of the contact ratio and hydrogen bond terms increased the overall χ₁ and χ_{1 + 2} accuracy by 0.5% and 1.0%, respectively (Table 2, cf. line 5 and line 6). Comparing Table 2, line 6 to lines 4 and 9, shows that the effect on prediction accuracy for removing each independently to be nearly equivalent to removing both. This suggests that both terms are necessary and are somehow interdependent, and when combined, improve the surface residue χ₁ accuracy by 1.0% and the χ_{1 + 2} accuracy by 1.3%. Therefore, despite the modest improvements in overall accuracy associated with these two terms they were left as part of the energy function because the computational cost for doing so was minimal, and the combined contributions maximized prediction accuracy.

Basic performance

This algorithm was developed to make significant use of interactions with the local backbone atoms with the premise that these interactions force the side chains into the proper χ₁ position (Richards 1977; Dunbrack Jr. and Karplus 1993; Srinivasan and Rose 1995). To examine how much impact the backbone had on the placement of side chains, all proteins were subjected to the following analysis. Using only the van der Waals interactions of the side chain with the backbone, including the local backbone, the lowest energy rotamer was placed on the structure. No further optimization was performed, and all side-chain to side-chain steric clashes were ignored. This initial placement of rotamers was subjected to the same dihedral analysis as previously described. The algorithm does remarkably well, considering no optimization was performed, modeling χ₁ angles with 73% correct for all residues, and 79% correct for core residues. The composite χ_{1 + 2} was, not surprisingly, quite poor with 49% and 59% correct for all and core residues, respectively. By far, the residues placed best by this method are the hydrophobic residues, Leu, Ile, Phe, Thr, Trp, Tyr, and Val (data not shown). If the electrostatic interactions with the local backbone atoms were also included, which is not normally done by the algorithm, those levels decreased to 70% and 78% for χ₁, and 45% and 56% for χ_{1 + 2}. Using the former method to generate the starting point for optimization, rather than a random assignment of rotamers, actually decreased the accuracy of repacking. This suggested the possibility that the criteria for accepting unfavorable moves in the simulated annealing optimization was probably too restrictive when using starting points closer to the correct structure such that rotamers that were not initially placed in the proper χ₁ space could not readily escape from the wrong conformation.

Table 3 shows the results for the repacking simulations used to generate the consensus structures considering each of the five cycles independently. The simulated annealing parameters for the execution of the NCN algorithm are listed in the Materials and Methods section. Although the dihedral prediction accuracy for individual proteins, in some cases, varied substantially (data not shown), the cumulative efforts are very consistent between runs. The consensus position for each side chain was determined as described previously using all five simulations, and reported in the last row of Table 3. There is an improvement in all performance categories listed, demonstrating that the preferred method is to use multiple simulations to generate a consensus structure. The overall accuracy for χ₁ and χ_{1 + 2} is 89.3% and 77.5%, respectively, and the overall RMS deviation for all proteins is 1.27 Å, which represents an improvement over the averaged scores of the five runs. Of course, multiple-cycle simulations require correspondingly longer computational times, but the resultant consensus structures are significantly more accurate. The prediction accuracies are listed for individual proteins in Table 4, corresponding to the consensus results in the last row of Table 3.

Table 3.

Accuracy of individual optimization cycles

	Angle accuracy			Overall RMSD (Å)
Run	All χ1/χ1+2	Core χ1/χ1+2	Surface χ1/χ1+2	All	Core
1	88.3/75.7	93.2/85.7	82.5/65.3	1.32	0.83
2	88.7/76.0	93.8/86.4	82.5/65.2	1.30	0.80
3	88.6/76.0	93.9/86.6	82.3/65.0	1.31	0.80
4	88.4/75.9	93.6/86.0	82.4/65.3	1.32	0.79
5	88.5/76.1	93.5/86.1	82.5/65.7	1.32	0.79
Consensus	89.3/77.5	94.1/87.4	83.6/67.2	1.27	0.75

Table 4.

Side-chain RMS deviation and dihedral angle prediction accuracy of repacked proteins

	Side-chain dihedrals				Overall RMSD (Å)		Average RMSD (Å)
PDB	χ1	χ1+2	core χ1	core χ1+2	All	Core	All	Core	Number of core residues
153L	93.3	81.1	98.8	93.4	1.05	0.49	0.62	0.34	83
1A7S	89.9	81.0	94.0	91.7	1.49	0.80	0.76	0.40	100
1A8Q	92.4	79.4	97.1	91.7	1.29	0.74	0.67	0.40	139
1AGY	93.2	87.7	95.1	93.4	1.00	0.76	0.53	0.41	81
1AKO	87.6	75.4	92.4	84.5	1.56	1.09	0.88	0.60	132
1AMM	92.4	78.0	98.7	92.7	1.13	0.52	0.72	0.37	76
1ARB	93.1	84.3	92.8	88.6	1.08	0.79	0.52	0.46	125
1B9O	86.6	69.0	92.7	88.9	1.37	0.74	0.82	0.44	55
1BD8	86.0	75.8	93.3	89.5	1.46	0.70	0.80	0.41	60
1BJ7	83.0	67.6	91.4	79.6	1.43	1.06	0.85	0.64	70
1BYI	93.8	78.7	97.9	90.0	1.11	0.68	0.60	0.36	94
1C5E	95.8	84.1	100.0	95.0	1.02	0.38	0.51	0.29	25
1C9O	88.7	78.0	100.0	100.0	1.50	0.17	0.84	0.16	14
1CBN	97.3	90.5	100.0	100.0	0.98	0.17	0.37	0.15	11
1CC7	84.8	71.7	93.1	100.0	1.42	0.49	0.89	0.36	29
1CEM	89.0	80.8	95.2	87.5	1.18	0.84	0.66	0.42	189
1CEX	93.2	85.8	96.3	94.9	1.25	0.67	0.55	0.36	80
1CHD	87.7	73.0	91.4	85.5	1.60	0.71	0.83	0.46	81
1CKU	91.7	78.3	95.7	73.3	0.94	0.57	0.61	0.45	23
1CTJ	93.4	83.0	95.7	94.1	1.02	0.67	0.61	0.34	23
1CZ9	88.3	78.5	91.4	84.6	1.40	0.77	0.80	0.48	58
1CZB	91.0	83.8	94.4	92.1	1.18	0.58	0.68	0.35	54
1CZP	94.0	78.9	97.4	91.7	1.00	0.60	0.62	0.41	38
1D4T	93.3	75.0	95.0	75.0	1.16	0.72	0.68	0.45	40
1DHN	83.8	61.4	97.5	85.2	1.76	0.77	1.08	0.41	40
1ECA	90.7	81.5	96.2	92.7	0.92	0.62	0.61	0.44	53
1EDG	88.8	77.6	93.7	85.1	1.17	0.66	0.68	0.44	205
1GCI	94.3	84.7	97.3	88.2	1.16	1.12	0.51	0.40	113
1HCL	82.6	62.1	85.9	68.5	1.68	1.45	1.05	0.86	142
1IC6	87.3	80.9	91.2	85.0	1.29	1.24	0.65	0.52	136
1IFC	82.3	68.2	96.2	90.0	1.35	0.79	0.93	0.49	52
1IGD	90.0	83.9	100.0	100.0	0.88	0.32	0.59	0.23	14
1IXH	89.7	81.6	91.1	84.6	1.31	1.20	0.70	0.55	146
1KOE	86.8	81.2	92.7	89.3	1.45	0.68	0.74	0.43	82
1MLA	90.7	79.0	95.6	87.2	1.20	0.84	0.67	0.42	137
1MML	86.4	71.0	92.2	82.5	1.37	0.76	0.84	0.51	103
1NAR	90.1	74.1	96.1	86.4	1.17	0.68	0.72	0.46	152
1NLS	88.7	72.8	91.8	82.9	1.36	0.75	0.73	0.47	110
1NOA	95.0	87.5	100.0	100.0	0.97	0.21	0.46	0.17	33
1NPK	89.3	76.7	96.8	93.2	1.41	0.48	0.79	0.32	63
1PLC	86.6	81.0	97.2	91.7	0.88	0.51	0.58	0.36	36
1QJ4	93.6	80.7	97.7	89.8	1.14	0.77	0.65	0.41	131
1QL0	91.5	79.5	95.9	88.5	1.03	0.68	0.57	0.38	122
1QLW	89.6	76.8	93.6	86.0	1.46	0.92	0.74	0.45	157
1QNJ	89.5	80.7	94.5	94.8	1.17	0.61	0.63	0.35	110
1QQ4	90.2	84.8	89.3	89.4	0.96	0.87	0.57	0.52	84
1QTN	81.3	66.4	93.1	81.4	1.85	1.13	1.00	0.59	58
1QTW	88.5	76.8	94.8	85.3	1.42	0.83	0.74	0.46	134
1QU9	90.9	81.2	93.2	92.3	1.00	0.50	0.60	0.33	44
1RCF	93.0	82.7	93.2	85.2	1.32	1.28	0.71	0.59	74
1THV	85.0	81.3	91.3	96.1	1.41	0.55	0.75	0.40	92
1THX	92.7	78.3	97.8	93.5	1.08	0.54	0.63	0.35	46
1VFY	85.7	72.1	100.0	75.0	1.39	0.79	0.75	0.41	19
1VJS	85.2	74.4	88.5	82.6	1.40	1.16	0.80	0.63	244
1WHI	79.2	73.2	88.9	86.4	1.83	1.21	1.02	0.58	45
2BAA	89.9	81.5	93.1	89.3	1.12	0.74	0.67	0.54	102
2CPL	91.7	79.0	98.7	92.3	1.23	0.54	0.68	0.33	79
2END	92.4	80.6	96.6	84.8	1.20	0.73	0.74	0.48	59
2HVM	94.6	82.4	97.0	89.1	1.01	0.62	0.56	0.39	135
2PTH	92.1	82.9	96.2	88.1	1.16	0.93	0.65	0.46	78
2RN2	84.3	60.4	95.0	75.6	2.01	1.72	1.22	0.70	60
3LZT	91.4	82.4	96.6	100.0	1.30	0.44	0.69	0.32	59
5P21	85.4	73.8	92.3	88.7	1.56	1.03	0.88	0.49	78
5PTI	89.1	65.7	100.0	81.8	1.48	0.81	0.88	0.50	16
7RSA	87.2	80.6	92.3	96.6	1.15	0.54	0.67	0.38	52
AVG	89.5	77.9	94.9	88.7	1.27	0.75	0.72	0.43	5375

The majority of the proteins are predicted with excellent accuracy. The number of core residues identified in this study makes up almost 55% of all the test sites. This percentage is significantly higher than other studies, which typically identify 40%–45% of the residues as core residues (Holm and Sander 1991; Xiang and Honig 2001; Liang and Grishin 2002). The reason our analysis routines identified a larger number was because the standard accessible areas for residues are based on our rotamer library, and not established values from the literature, which are about 10%–20% smaller. This difference in the number of core residues is not critical except when comparing core results to other studies using different analysis programs. For this algorithm, the consensus results in Table 3 show that for the core 54.3% of the residues, the χ₁ accuracy is 94.1%, the χ_{1 + 2} accuracy is 87.4%, with an overall RMS deviation of 0.72 Å.

The assessment criteria for declaring the correct placement of a side-chain dihedral was fairly loose at 40° but is consistent with several other studies. Using stricter matching criteria has the expected effect of decreasing the reported dihedral-angle accuracy. Noting only the overall χ₁ and χ_{1 + 2} scores a 30° matching criteria decreases the number of properly predicted conformations by 1.5% for χ₁, and 3.7% for χ_{1 + 2}. Using an even stricter criterion of 20° decreases the reported accuracy by another 4.6% and 8.9% for χ₁ and χ_{1 + 2}, respectively. It should be noted that the RMS deviation score does not depend on the angle accuracy and remains constant throughout.

The effect on accuracy of restricting the conformational space available to residues

It was observed that by restricting the number of rotamers available at each site by reducing the conformational space available had a dramatic impact on accuracy. One common method for restricting conformational space is to perform minimizations one residue at a time, keeping all other residues in the native position. In such an approach all rotamers are tested at a given site and the lowest energy rotamer becomes the predicted conformation. This approach has been used by several groups (Wilson et al. 1993; Petrella et al. 1998; Xiang and Honig 2001; Liang and Grishin 2002) to validate the energy function because it eliminates the dependency of prediction accuracy on the search strategy used to sort through the combinations of residues leading to an optimal solution. Here, this method was used as a means of restricting conformational space. Each site was subjected to the same steric clash test as described previously, while all other side chains were present in their native conformation. Interestingly, the number of passing rotamers was only reduced 10%–20% from when no side chains were present. After the steric clash test, the native side chains were again stripped off, and the algorithm proceeded in an identical fashion as previously described.

The second method for reducing the number of rotamers was to restrict the χ₁ space to the native region, or one of three possible energy wells, so that two-thirds of the rotamers were eliminated without further testing. All side chains had been previously removed from the structure, so the only additional information was the χ₁ region. As shown in Table 1, most native side chains can be approximated by the rotamer library, so restricting the algorithm to the proper region should drive the χ₁ accuracy to nearly 100%. Thus, this approach tested the ability of the algorithm to effectively predict the proper χ₂ position. The number of conformations available to the simulated annealing algorithm was reduced to ~60% of the unrestricted approach. As before, the algorithm proceeded in the usual fashion to place the side chains.

The results for these tests are shown in Table 5. Both methods show improvements in all accuracy benchmarks over the consensus structures from the unrestricted method (Table 3). The restricting of rotamer space using the native side chains shows an increase in prediction accuracy of 0.6% for χ₁ and 1.0% for χ_{1 + 2} overall compared to the consensus structures. There is also an improvement in the overall RMS deviation 0.07 Å overall, and 0.08 Å for the core residues. The average residue RMS deviation improves as well. This suggests that the algorithm can still be improved somewhat, although it appears that much of the improvement is in the placement of core residues.

Table 5.

Repacking results using methods to restrict the number of rotamers

	Angle accuracy			Overall RMSD (Å)		Average RMSD (Å)
Restriction method	All χ1/χ1+2	Core χ1/χ1+2	Surface χ1/χ1+2	All	Core	All	Core
Filtering of rotamers with native side chains present:	89.9/78.5	95.0/88.8	83.9/67.7	1.20	0.67	0.69	0.44
Restricting search space to proper χ1 region:	98.8/85.0	99.3/91.1	98.2/78.7	1.00	0.61	0.55	0.35

The most dramatic results are achieved when conformational space is limited to the native χ₁ region. Considering only the χ_{1 + 2} results, the increase in accuracy is 7.5% overall, and results in a significant reduction in the average and overall RMS deviation by 0.17 Å and 0.27 Å, respectively. The significant increase in dihedral prediction accuracy is in large part due to the long side chains Arg, Lys, Glu, Gln, and Asp each increasing by 10% or more in the χ_{1 + 2} accuracy. The remaining residues all increased by at least several percent, with the exception of histidine, which showed a decrease in χ_{1 + 2} accuracy in this simulation. The χ₁ accuracy did not reach 100% because a small percentage (1.2%) of the native side chains could not be approximated by the rotamer library. This latter simulation provides a key piece of information regarding the approach that should be taken to further improve accuracy of side-chain placement algorithms. If information can be generated such that the correct χ₁ region (rotamer) can be identified, very accurate structures can be determined from just the backbone conformation.

Comparison to other repacking algorithms

Two methods were selected from the literature for comparison to gauge the relative performance of the algorithm. The selected algorithms were considered to be among the best, as judged by the reported accuracies and how the algorithm compared to others as documented in their articles. The first is the SCAP algorithm from Xiang and Honig (2001), and the second is from Liang and Grishin (2002). SCAP uses an energy function consisting of a van der Waals term and torsion-angle energies. The parameters for these terms are derived from the CHARMM force-field (Brooks et al. 1983). The rotamer library consisted of 7562 discrete rotamers with step sizes between rotamers of at least 10° extracted from 297 protein structures. The repacking method used a search strategy where all rotamers for each site were tested against the protein background, and the lowest energy rotamer kept for the next cycle. The site selection starts at the most N-terminal test site, and progresses sequentially down the backbone. This process is repeated until a static structure is reached. To overcome potential rotamer bias arising from the initial placement of residues and the order of site progression, each protein is subjected to multiple simulations. The first simulation used the rotamer with the most favorable energy to the backbone as the initial position. The next 59 used random placement to generate the starting point. The remaining 60 placed rotamers by statistical analysis of the previous simulations to bias the initial placement. The overall lowest energy rotamer from all simulations was taken as the predicted position. The reported dihedral accuracy as taken from averaging the results from Tables 4 and 5 of that paper (Xiang and Honig 2001) was 84% for χ₁ and 67% for χ₁₊₂. These results are especially impressive because the angle deviation cutoff used was 20° compared to 40° used in this and the other comparison studies. The SCAP algorithm was run with the largest rotamer libraries available, as suggested in the documents that were provided with the program. The execution parameters were set such that 60 optimization cycles were performed, all atoms were considered by the energy function, and a minimization procedure was performed on the final structure.

The Liang and Grishin algorithm (LGA) uses energy terms derived from physical and empirical properties of the side chains to yield a scoring function consisting of surface contact, volume overlap, electrostatics, rotamer frequency, and solvent accessibility of polar hydrogens. Because these terms were not necessarily of the same magnitude, the developers of the algorithm fit the scoring function to a subset of half the test proteins to yield coefficients for each term to generate the final form of the function. A Monte Carlo approach was used to optimize the side-chain placement. The rotamer library used was based on the backbone-dependent library from Dunbrack Jr. and Cohen (1997). Several modifications to the library were described, but no information regarding potential steps about the dihedral positions, so direct determination of the number of rotamers in the library was not possible. The executable for this algorithm was obtained and tested on the protein set without modification.

The combined results for all studies are reported in Table 6, quantified by methods discussed above. The total execution time is also included for reference. For the SCAP algorithm, the number of optimization cycles was increased so that the execution time would be nearly equal to the time needed for the NCN algorithm. The LGA was not given an equal opportunity because execution parameters could not be modified by the user.

Table 6.

Prediction accuracy for all 65 proteins by each algorithm

	Angle accuracy
	All χ1/χ1+2	Core χ1/χ1+2	Surface χ1/χ1+2	All average overall RMSD (Å)	Core (20%) average overall RMSD (Å)	Core (10%) average overall RMSD (Å)	All average residue RMSD (Å)	Core average residue RMSD (Å)	Execution time (h)
NCN	89.3/77.5	94.1/87.4	83.6/67.2	1.27	0.75	0.63	0.72	0.43	24
LGA	88.5/74.1	93.7/84.6	82.3/63.1	1.31	0.88	0.75	0.75	0.48	14
SCAP	83.1/70.1	91.4/84.0	73.2/55.7	1.33	0.88	0.70	0.81	0.48	24

Although the NCN algorithm described here is the slowest of the three, it does show improvement in all prediction accuracy benchmarks. The improvement in the overall χ₁ dihedral accuracy is +0.8% and +6.2% compared to the LGA and SCAP algorithm, respectively. The improvement in overall χ_{1 + 2} accuracy is more significant with an increase in accuracy of +3.4% and +7.4%, respectively. The improvement in the core by this algorithm is less, but still significant for χ_{1 + 2} prediction accuracy with +2.8% and +3.4% improvement over the LGA and SCAP algorithm, respectively. The surface residues are also included because these are the most poorly predicted due to the increased conformational space available to these residues. A recent paper by Jacobson et al. suggests a target level for χ₁ prediction accuracy of surface residues >80% (Jacobson et al. 2002). The prediction accuracy for χ₁ and χ_{1 + 2} for surface residues by the NCN algorithm are 83.6% and 67.2%, respectively. These represent an improvement of +1.3% and +4.1% over the LGA, and +10.4% and +11.5% over the SCAP algorithm. In this analysis, 54.3% of the tested residues are in the core, which is more than typical of other studies. If the analysis is repeated such that the number of residues in the core is 43.4%, which is closer to the number reported in the comparison studies (Xiang and Honig 2001; Liang and Grishin 2002), the surface residue accuracy improves to 85.0% and 69.8% for χ₁ and χ_{1 + 2}.

The improvement in the overall RMS deviation reflects what is seen for the angle accuracy, although the changes are less dramatic with only a 0.04 Å and 0.06 Å improvement over the LGA and SCAP algorithm, respectively. The improvements in the core are more significant with an overall improvement for the core 54.3% of the test residues of 0.13 Å compared to both algorithms. For residues with only 10% accessible surface area SCAP performs better than the LGA, but this algorithm still gives an improved placement of these residues as well. The averaged RMS deviation shows the same trend as the overall RMS deviation, so will not be discussed further.

From the overall results it was noted that the SCAP algorithm placed residues with 10% or less accessible surface area better than the LGA. To further quantify the performance of each algorithm on residues with varying degrees of accessible surface area the predicted proteins were analyzed starting from the most buried to the most accessible. The result of this analysis is reported in Figure 1 ▶. Residues that are below a certain accessible surface area threshold are considered yielding a fraction of the total residues analyzed for each data point. For residues that are nearly completely buried, approximately 20% of the total residues, all the algorithms perform nearly equally for χ₁ dihedral accuracy. For χ_{1 + 2}, the LGA had the lowest accuracy level, confirming the RMS deviation results from Table 6. SCAP performs consistently better than the LGA on the core residues until about 50% of the total residues are considered reflected by the improved RMS deviation for these residues. However, the NCN algorithm performs better than both algorithms over the entire range of accessible surface area. This highlights that improvements in the core were still possible.

Figure 1.

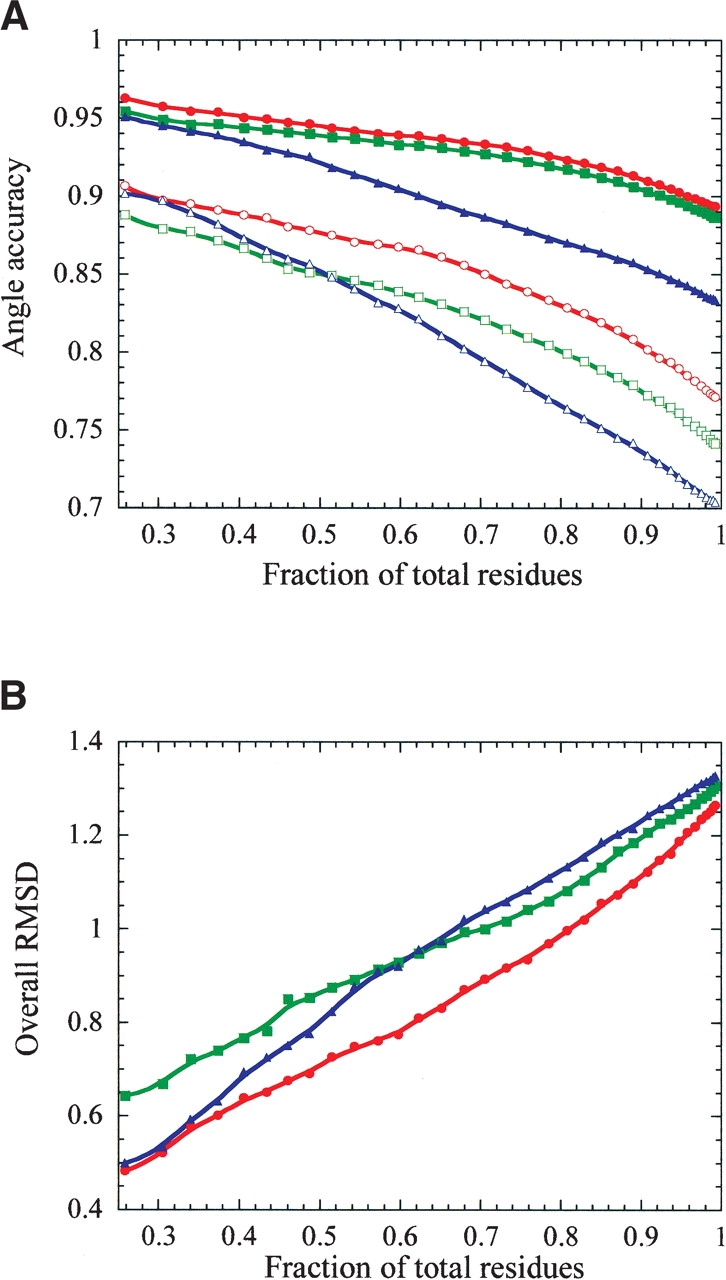
The dependency of side-chain placement accuracy as a function of residue burial. The fraction of tested positions was those residues with accessibilities lower than a set threshold. Only these residues were considered in the generation of the data points. (A) The χ₁ dihedral accuracy is represented by the closed symbols, and the χ_{1 + 2} dihedral accuracy is represented by the open symbols. The red traces are the results for the NCN algorithm, the green traces are for the LGA, and the blue traces are for the SCAP algorithm. (B) The overall RMS deviation as a function of the fraction of total residues tested.

Another way to compare the algorithms is to examine at what fraction of residues the overall RMS deviation cross some arbitrary value such as 1 Å. The SCAP algorithm predicts 66% of the residues with a χ₁ and χ_{1 + 2} accuracy of 89% and 81% at the overall RMS deviation of 1 Å. The LGA predicts 71% of the residues with a χ₁ and χ_{1 + 2} accuracy of 93% and 82% at the same overall RMS deviation. The NCN algorithm predicts 81% of the residues with a χ₁ and χ_{1 + 2} accuracy of 92% and 83%, and still maintains an overall RMS deviation of only 1 Å. We consider this to be a significant improvement in prediction accuracy, with the NCN algorithm able to predict 10% more residues and still maintain the same overall RMS deviation in the structure.

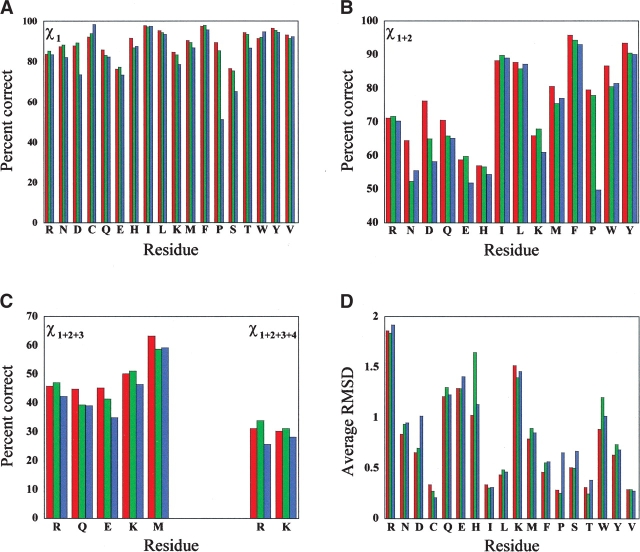
The results in Table 7 show the overall dihedral prediction accuracy for χ₁ and χ_{1 + 2} and the average RMS deviation for each type of residue. This is shown graphically in Figure 2 ▶, and includes accuracy reports for χ_{1 + 2 + 3} and χ_{1 + 2 + 3 + 4}. This method of performance analysis highlights where the strengths and weaknesses are for each approach. For most residues the NCN algorithm is comparable or outperforms SCAP in dihedral accuracy for every residue except cysteine, which was predicted less accurately by nearly 4.8%. For χ_{1 + 2}, the NCN algorithm shows significant improvement in the polar residues Asn, Asp, Gln, and Glu, but equally decreased performance in the placement of Trp. The improved placement of Gln and Glu is also apparent in the accuracy of χ_{1 + 2 + 3}. The most dramatic improvement over SCAP is in the prediction of proline, which was correctly predicted only 51.1% of the time by SCAP compared to 89.1% for χ₁ for the NCN algorithm. This deficiency has a significant impact on the overall dihedral accuracy for the SCAP program because there are 542 prolines in the test set.

Table 7.

Average residue RMS deviation and side-chain angle prediction accuracy by residue type

	NCN algorithm			LG algorithm			SCAP algorithm
	χ1	χ1+2	Average RMSD Å	χ1	χ1+2	Average RMSD Å	χ1	χ1+2	Average RMSD Å
ARG	84.3	71.1	1.91	85.2	71.7	1.84	83.4	70.2	1.92
ASN	89.2	65.8	0.80	88.2	52.3	0.93	81.9	55.5	0.95
ASP	87.9	76.6	0.65	89.3	65.0	0.70	73.5	58.2	1.01
CYS	92.1	—	0.33	93.9	—	0.27	98.3	—	0.21
GLN	86.1	70.9	1.18	82.9	65.8	1.30	82.3	65.2	1.23
GLU	75.7	58.7	1.29	77.2	59.8	1.29	73.3	51.9	1.41
HIS	91.9	58.1	1.00	86.8	56.6	1.64	87.5	54.4	1.13
ILE	97.1	87.8	0.34	97.1	89.8	0.30	97.4	89.0	0.31
LEU	95.6	88.5	0.42	94.2	85.8	0.48	93.5	87.1	0.46
LYS	84.9	67.7	1.51	83.3	67.9	1.40	78.5	61.0	1.46
MET	90.8	80.6	0.78	89.3	75.5	0.89	86.7	77.0	0.85
PHE	97.7	95.8	0.45	97.9	94.3	0.55	95.8	93.0	0.56
PRO	89.9	79.9	0.28	85.2	77.9	0.25	51.1	49.8	0.65
SER	75.6	—	0.52	75.3	—	0.50	65.1	—	0.67
THR	94.2	—	0.31	93.4	—	0.25	86.6	—	0.38
TRP	91.4	86.2	0.91	91.9	80.5	1.20	94.8	81.4	1.02
TYR	96.4	94.3	0.61	95.5	90.5	0.73	94.3	90.0	0.68
VAL	92.9	—	0.29	91.4	—	0.29	92.3	—	0.27

Figure 2.

The placement accuracy for each residue type is noted for each algorithm by dihedral angle: (A) χ₁ only, (B) χ_{1 + 2} only, (C) χ_{1 + 2 + 3} and χ_{1 + 2 + 3 + 4} dihedral angles. The last plot (D) shows the RMS deviation for each residue type averaged over all residues tested. Red is used for the results from the NCN algorithm, blue is for the LGA, and green is for the SCAP algorithm.

The NCN algorithm performed comparably to the LGA with respect to χ₁ dihedral accuracy. There is slight improvement in the placement of the χ₁ of His, Gln, and Pro by the NCN algorithm. In general, the NCN algorithm performed better in the placement of the χ₁ of hydrophobics, and less so for polar residues. The NCN algorithm did show significant increase in the accuracy of χ_{1 + 2} for Asn, Asp, Gln, Met, and Trp. This trend is continued for χ_{1 + 2 + 3} for Gln and Met. However, for Arg and Lys, the NCN algorithm did not perform quite as well as the LGA.

The average RMS deviation plot in Figure 2D ▶ offers another way to compare the effectiveness of each algorithm. The NCN algorithm performs consistently better than SCAP for all residues except Cys, Ile, Lys, and Val, although in several cases the average RMS deviation is nearly the same. The results for lysine are especially interesting because the angle prediction accuracy is better by the NCN algorithm over SCAP, but the average RMS deviation does not show the same trend. This suggests that the SCAP rotamer libraries for lysine provide a better representation of allowed conformational space for this residue. This means the library used by the NCN algorithm contains many more rotamers that deviate substantially from the average positions such that when the algorithm improperly predicts the side-chain position it is more likely to have a higher RMS deviation than the rotamers in the more restricted library used by the SCAP program. Additionally, because the size of the library for lysine and the others is very large, the potential energy well that is defined becomes much more broad and flat, making it very difficult to identify the appropriate rotamer. As mentioned previously, the libraries for lysine and arginine, used by the NCN algorithm, could be improved based on the results in Table 1 by expanding of the allowed conformational space for the terminal dihedral angles. However, this was not done to prevent further leveling of the energy well as well as for computational reasons.

Comparison of the average RMS deviation values between the LGA and the NCN algorithm show that for most residues it is fairly equal. Again, by this criterion the NCN algorithm did worse regarding the placement of lysine, but the angle accuracies are fairly equal. A reverse situation occurs for histidine in that both algorithms place the χ_{1 + 2} about the same, but the average RMS deviation is substantially lower using the NCN algorithm. This unusually poor placement of histidine was noted in the original article (Liang and Grishin 2002). The NCN algorithm also performs significantly better in the placement of Trp, which can have a substantial effect on the overall protein RMS deviation when it is placed improperly (data not shown). A prediction from the Liang and Grishin article suggested that improvements in the χ_{1 + 2} could be achieved with a more complex rotamer library than what was used in their study (Liang and Grishin 2002), and there does indeed appear to be consistent improvement in overall χ_{1 + 2} by the NCN algorithm, with a corresponding improvement in the average RMS deviation for many residues.

Conclusions

We have developed a side-chain repacking algorithm that outperforms existing algorithms in the literature. Considering the least accessible residues, 80% of the total residues tested, the χ₁ and χ_{1 + 2} dihedral accuracies were 92% and 83%, respectively. The overall RMS deviation from the native positions for these residues was only 1 Å. The remaining 20% of the residues constitute the surface residues of the protein, but even for these the NCN algorithm scored better on the dihedral angle prediction accuracy. It is not surprising that the accuracy falls off for mostly exposed residues, as these are likely to be variable in solution. There was indication that these results could have been further improved had the potential energy function been tailored specifically for each residue type. This is especially true for the longer side chains such as glutamate, glutamine, lysine, and arginine.

The success of this algorithm was due to the highly detailed rotamer library with nearly 50,000 discrete members. The fine step size about the favored dihedral positions offers potential relief positions for conformations that might otherwise have been eliminated from the proper energy well by steric clashes. Several libraries of similar design but with coarser step sizes yielded overall results that were less accurate than what was presented here, although the overall execution time was decreased due to smaller library sizes. The library used by this algorithm can be easily modified prior to execution to create libraries of any size.

A simple simulated annealing search method was used to sort through this library based on a potential energy function derived mostly from first principles. The energy function was a combination van der Waals, electrostatics, and hydrogen-bonding potentials, plus two additional terms with one being the frequency of rotameric states from the PDB. The OPLS parameter set used here for van der Waals and electrostatic terms compares favorably with the CHARMM22 set in defining the energy landscape for rotameric positions. Simulations performed here indicate that further improvements in performance can be expected by devising methods for narrowing the conformational search to the proper χ₁ region.

Materials and methods

The rotamer libraries

The libraries were built around the favored dihedral angles as listed by Dunbrack Jr. and Cohen for backbone-independent rotamer positions (Dunbrack Jr. and Cohen 1997). Except where noted, side-chain dihedral angles were moved ±15° of the favored dihedral angles in 5° steps for a total of 21 discrete positions about each dihedral. The residues Arg, Lys, Glu, and Gln, because of the high degrees of freedom, had a coarser step size. For Arg and Lys, this was 15° and for Glu, Gln, and the terminal Met dihedral it was 7.5°, for 9 and 15 discrete positions per dihedral, respectively. The conformational space for Arg and Lys was expanded to ±30° for the χ₄-dihedral position. The terminal dihedral for Asp, Asn, Glu, and Gln was allowed to rotate ±20° of the mean positions in 10° steps. Asn and Gln were rotated 180° about the final dihedral, and the movements repeated, thereby doubling the number of rotamers for these residues over Asp and Glu. The χ₂ angles for residues His, Phe, Tyr, and Trp were rotated approximately ±40° in 10° steps of 0 and 90°. Histidine was also flipped by 180° about χ₂ for dihedral positions of 180 and −90°. Histidine also required definitions for the two singly protonated states and one doubly protonated state, thus tripling the total number of rotamers for this residue. Discrete hydroxyl hydrogen positions at 15° intervals for Ser and Thr, and at 30° intervals for Tyr were included. Lysine had three discrete amino hydrogens, but these were fixed in position to keep the size of this library as small as possible.

The size of this library is substantial with 49,042 distinct rotamers (Table 1). Construction of the library used coordinates derived from the standard geometry of the ECEPP/2 force field (Momany et al. 1975; Nemethy et al. 1983) as listed in the program DYANA (Guntert et al. 1997). The atomic radii for heavy atoms were taken from Chothia (Chothia 1976), and all hydrogens in the library were assigned a radii of 1 Å. The libraries were all oriented such that the C_α–C_β vector was aligned exactly along the +z-axis with the C_α atom at the origin. The relative backbone position was such that the nitrogen atom was in the xz-plane along the −x-axis. Setting the libraries in this fashion eliminated much of the rotation and translation calculations that would otherwise be needed during algorithm execution.

The rotamer library was tested against the wild-type crystal structures to assess the degree to which natural rotamers could be approximated by a rotamer from the library (Table 1). This was done by orienting the N, C_α, and C_β atoms exactly between the native structure and library, and then searching for the rotamer in the library that best approximated the native side chain by minimizing the dihedral RMS deviation at all rotatable positions. A successful match between the library and structure was achieved only if all dihedral positions within the same rotamer were within 20° or 40° of the wild-type position. The fifth dihedral was included for arginine because it does vary in real proteins, although it is kept fixed at zero in the rotamer library. The RMS deviation for all heavy atoms in the test and native rotamer was calculated for the rotamer with the lowest dihedral RMS deviation. The atomic RMS deviation was averaged over all residues and proteins to obtain the values in Table 1. The dihedral-angle RMS deviation at each dihedral position is not reported.

Simulated annealing parameters

For the results presented for the NCN algorithm the following execution parameters were used to generate five independent structures for each protein that was used to generate a final consensus structure. The maximum number of trial rotamer conformations at each annealing temperature was set to 25% of the total number of conformations that passed the initial steric-clash test with the backbone. The number of successful moves at each temperature is 10% of the number of trial steps. The algorithm progressed to a new annealing temperature if the maximum number of successful moves or the number of trial moves was reached. The temperature was initially set to 50° and scaled by 0.7 after completion of each annealing cycle. This was repeated for a total of 15 annealing steps. The annealing schedule was very similar to that followed in the strategy of Liang and Grishin (2002).

The simulated-annealing scoring method always accepted a more energetically favorable or downhill move, and sometimes accepted an uphill move. The acceptance of an uphill move was based on the following relationship:

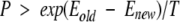where P was some probability, E_old and E_new were the energies of the old and new rotamers in their corresponding protein backgrounds, respectively, and T was the annealing temperature. Due to the large number of rotamers available as trial moves, and in the interest of reducing computational time, the criterion for accepting an uphill move was modified to use a fixed probability rather than random. The probability of accepting an uphill move, determined empirically, was set to 0.92.

Assessment of algorithm performance

There are three primary methods in the literature used to analyze the performance of algorithms such as this (De Maeyer et al. 1997). One method is to use the deviations of side-chain χ₁ and χ₂ dihedrals from experimental, another is to calculate the RMS deviation of the side-chain heavy atoms, and the last is volume overlap between native and predicted rotamers. Although the volume overlap was shown to be the most rigorous method for assessing algorithm performance, there were two reasons it was not used here. The primary reason was that most other work that this algorithm was being compared to did not use this method. The second, volume overlap, scores a successful prediction if the predicted rotamer occupies the same space as the native rotamer, but does not discriminate when Asn, His, or Gln differ from the native structure. This was a main point for classifying volume overlap as a better method for assessing performance, but in this work, we were interested in the specific orientation of the residues.

Therefore, the deviation of dihedrals and RMS deviation were used here to quantify performance of the algorithm. Residues that had multiple conformations in the structure file were included in the evaluation by checking the predicted rotamer against each discrete conformation. The symmetrical nature of Arg, Asp, Glu, Phe, and Tyr was taken into account when evaluating χ₂ and RMS deviation. The core residues were defined as residues with <20% accessible surface area in the native crystal structure calculated using the method devised by Lee and Richards (1971). The standard accessible surface area values were determined by calculating the average accessibility of the rotamers from the library placed on an extended (ϕ = 180°, ψ = −180°) Ala-X-Ala peptide. Programs were written by this lab to ensure these tests were conducted in a predictable and known fashion. These programs were thoroughly tested using secondary methods to confirm the accuracy of the analysis.

Side-chain dihedrals were calculated such that values ranged from −180 to +180. The deviation was calculated using the following simple method:

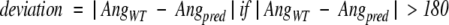else, the

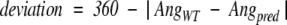where Ang_WT and Ang_pred represent the angles for the wild-type and predicted rotamers, respectively. If the deviation was less than 40°, the rotamer was considered correct for that dihedral angle. For all residues except Ser, Thr, Val, and Cys the χ₂ was also evaluated to obtain the reported composite values for χ_{1 + 2}. The χ₂ deviation was only calculated if the χ₁ position was correct. In cases where multiple conformations were present in the crystal structure the predicted rotamer was considered correct if it passed testing against any discrete native conformation. Again, for the χ_{1 + 2} composite score, the predicted χ₁ and χ₂ had to be correct within the same rotamer conformation.

The RMS deviation, in all cases, was calculated with backbones of the predicted and crystal structure overlaid exactly. This is an important distinction to methods that minimize the deviation between two structures before calculation of RMS deviation. The overall deviation from the latter method will always be less, or at worst, equal to the former method. Only the former method will give a true measure of the performance of the algorithm. The overall RMS deviation was calculated for all heavy side-chain atoms in the protein, not including alanine. The average RMS deviation differs in that it is the deviation between individual side-chains couples averaged over the entire protein. In all cases the RMS deviation included the C_β atom, which did lower the RMS deviation value because typically the deviation for this atom type was near zero. However, it was included in this study because the side-chain rotamers were not placed directly on the C_β atom of the crystal structure.

Selection of proteins in the test set

The majority of the 65 test proteins were taken from the primary test sets used in the comparison studies. Thirty of the proteins were from the work of Liang and Grishin (2002). Only 28 of 33 proteins were taken from the Xiang and Honig (2001) protein test set. The remaining five contained a significant number of missing atoms or side chains. The remaining seven proteins were selected from the PDB using the criteria of having crystallographic resolutions better than 1.2 Å, and sequence length between 150–300 residues. To maintain consistency between the Liang and Grishin study predicted structures were compared to the test proteins that had been optimized using the program REDUCE (Word et al. 1999). This utility optimizes the χ₂ dihedral for asparagine and histidine, and χ₃ dihedral for glutamine by testing the θ + 180° rotamer for improved hydrogen bonding interactions. The rotamer with the maximum number of hydrogen bonds formed was kept as the optimized conformation. If there was no difference, the original orientation was maintained. The predicted structures were not optimized prior to analysis. There was an overall improvement in the χ₂ accuracy of about 1% as a result of comparing the test set to the optimized protein structures.

Execution of the SCAP algorithm

The SCAP algorithm was run with the largest rotamer libraries available. The execution parameters were set such that 60 optimization cycles were performed, all atoms were considered, and a postminimization step was performed to arrive at the final predicted structure.