Dimethyl sulfoxide at 2.5% (v/v) alters the structural cooperativity and unfolding mechanism of dimeric bacterial NAD⁺ synthetase

Abstract

Dimethyl sulfoxide (DMSO) is commonly used as a cosolvent to improve the aqueous solubility of small organic compounds. Its use in a screen to identify novel inhibitors of the enzyme NAD⁺ synthetase led to this investigation of its potential effects on the structure and stability of this 60-kD homodimeric enzyme. Although no effects are observed on the enzyme’s catalytic activity, as low as 2.5% (v/v) DMSO led to demonstrable changes in the stability of the dimer and its unfolding mechanism. In the absence of DMSO, the dimer behaves hydrodynamically as a single ideal species, as determined by equilibrium analytical ultracentrifugation, and thermally unfolds according to a two-state dissociative mechanism, based on analysis by differential scanning calorimetry (DSC). In the presence of 2.5% (v/v) DMSO, an equilibrium between the dimer and monomer is now detectable with a measured dimer association constant, K_a, equal to 5.6 × 10⁶/M. DSC curve analysis is consistent with this finding. The data are best fit to a three-state sequential unfolding mechanism, most likely representing folded dimer ⇆ folded monomer ⇆ unfolded monomer. The unusually large change in the relative stabilities of dimer and monomer, e.g., the association equilibrium shifts from an infinitely large K_a down to ~10⁶/M, in the presence of relatively low cosolvent concentration is surprising in view of the significant buried surface area at the dimer interface, roughly 20% of the surface area of each monomer is buried. A hypothetical structural mechanism to explain this effect is presented.

Bacterial NAD⁺ synthetase (E.C. 6.3.5.1) is a member of the amidotransferase enzyme family and catalyzes the last step in both the de novo biosynthetic and salvage pathways for NAD⁺. The enzyme is critically important in the life cycle of the bacteria, because NAD⁺ and NADP⁺ are essential cellular cofactors required for many redox-dependent metabolic processes (Nessi et al. 1995). The enzyme is also important in the germination and outgrowth of spore-forming bacteria, as determined from temperature-sensitive mutations in Bacillus sp. (Albertini and Galizzi 1975; Nessi et al. 1995). NAD⁺ synthetase gene transcription is detectable as early as 12 minutes after the onset of germination, with increasing amounts synthesized during outgrowth (Albertini et al. 1987). In contrast to the eukaryotic enzyme, many bacterial NAD⁺ synthetases are simple, homodimeric enzymes that can only use ammonia in the conversion of nicotinic acid adenine dinucleotide (NaAD) to NAD⁺.

The B. subtilis enzyme has the most extensive crystallographic structural information available and is the subject of study here (Rizzi et al. 1996, 1998; Devedjiev et al. 2001; Symersky et al. 2002). Each monomer exhibits an α/β topology and contains 271 amino acids; the dimeric molecular weight is 60,480. The B. subtilis enzyme is a symmetrical homodimer that buries approximately 5200 Ų at the dimer interface, 70% of which is nonpolar. This extensive interface corresponds to about 20% of each monomer surface.

The essential role of NAD⁺ synthetase makes it an attractive target for antibacterial drug development and in this context, an enzymatic assay was developed for the purpose of screening compounds for enzyme inhibition. One component of the assay buffer is the water-miscible organic solvent, dimethyl sulfoxide (DMSO), included to improve the solubility of the compounds screened. This study was conducted to determine whether DMSO had an effect on the enzyme under the assay conditions used, because organic cosolvents have been shown to influence protein structure and stability. For example, DMSO has been shown to reduce the thermal stability, but with no change in the unfolding mechanism, of the monomeric globular proteins RNase (Jacobson and Turner 1980) and lysozyme (Fujita et al. 1982; Kotik et al. 1995; Kovrigin and Potekhin 1997). The effect may be due to either or both the preferential solvation by DMSO of the denatured state (Kovrigin and Potekhin 1997) and changes in water structure (Fujita et al. 1982). In those studies, however, considerably higher concentrations were required to detect changes in stability, for example, about 10%–25% (v/v) compared with the 2.5% (v/v) used in this study.

A powerful tool to dissect the domain and subunit architecture of a protein is a thermodynamic analysis of the unfolding/folding process (Schellman 1987). In particular, differential scanning calorimetry (DSC) has been shown to provide important insights into the structure and stability of proteins and the corresponding influence of ligands and solution conditions (Privalov 1982; Sturtevant 1987; Brandts and Lin 1990; Freire 1995). It has been especially helpful for understanding the folding and stabilization of oligomeric proteins (Edge et al. 1988; Merabet et al. 1998; Jaenicke and Lilie 2000).

Presented here is a DSC analysis of NAD⁺ synthetase thermal unfolding under enzymatic assay conditions with and without 2.5% (v/v, 0.35 M) DMSO. Three different models for unfolding were compared by fitting the data to each and deriving thermodynamic parameters. Equilibrium analytical ultracentrifugation was also performed as a function of temperature to provide the dimer dissociation equilibrium constant and corresponding heat capacity change that were used in the DSC fitting procedure. The results clearly show a change in unfolding pathway in the presence of 2.5% (v/v) DMSO. A structural model is presented to explain this effect.

Results and Discussion

Differential scanning calorimetry in the absence of DMSO

Reversibility of the transition

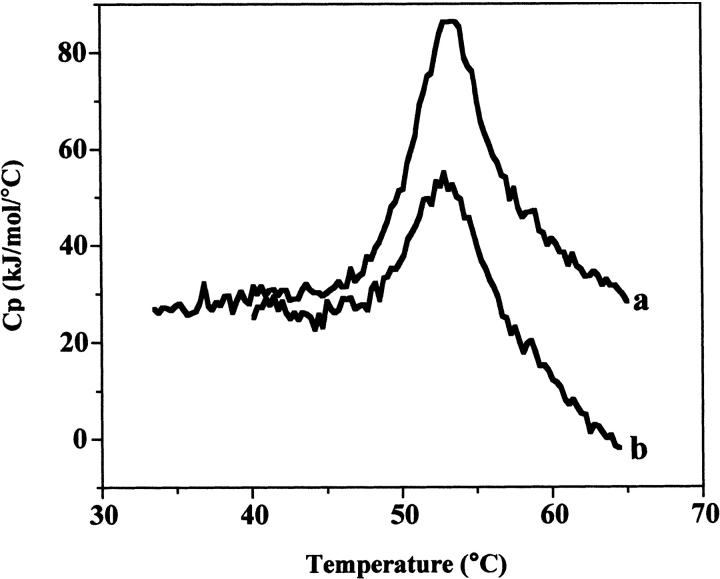
A prerequisite for using equilibrium thermodynamics for data analysis is that chemical equilibrium exists over the temperature range of the unfolding transition (Sanchez-Ruiz et al. 1988; Freire et al. 1990). A reversible, that is, repeatable, DSC transition may be the best indication (but not an absolute requirement) that the unfolding is at equilibrium. In initial experiments, the reversibility of the DSC transition was determined by cooling and rescanning the NAD⁺ synthetase (NADS) in the calorimeter and also determined by examining the effect of changes in scan rate on the transition shape and T_1/2; alterations in the transition with scan rate would suggest a kinetic influence on the thermal unfolding pathway (Sanchez-Ruiz et al. 1988). Structural changes may occur to the protein after unfolding, leading to an irreversible DSC transition, and these include high temperature covalent changes and/or aggregation of the denatured protein. If these changes occur on a time scale that is longer than that for protein unfolding to occur, the DSC transition can be analyzed by equilibrium methods even though it is irreversible (Lumry and Eyring 1954; Freire et al. 1990).⁶

Thermal unfolding is partially reversible for NADS in the absence and presence of DMSO (Fig. 1 ▶). The extent of reversibility at various points through the DSC unfolding transition was examined. The results indicate the transition is largely reversible at 1.5°/min (100% reversiblity at 25%–30% unfolding and ~75% reversibility at 50%–60% unfolding) until the protein is nearly completely unfolded (95%), at which point the transition is still about 50% reversible (Table 1). A very small effect on scan rate is also observed. Over the scan rates of 0.45°–1.5°/min, the T_1/2 varies from 52.2°C to 54.1°C (data not shown). Overall, these results support an equilibrium unfolding process over the majority of the transition temperature range and were used to justify performing a thermodynamic analysis of the DSC data. The subsequent correspondence found between the calorimetric enthalpy and the calculated van’t Hoff enthalpies derived from either the protein concentration dependence of the transition or curve fitting, provide further evidence for the validity of this approach (Edge et al. 1985; Manly et al. 1985; Hu and Sturtevant 1987). The details of these analyses are described next.

Figure 1.

Two consecutive DSC scans of the same NAD⁺ synthetase sample. (a) First scan; (b) second scan. Total protein concentration: 1 mg/mL; Buffer: 60 mM EPPS at pH 8.5, 20 mM KCl, 19 mM NH₄Cl, 10 mM MgCl₂, without DMSO. Scan rate: 1.1°C/min.

Table 1.

Percent reversible NADS unfolding as a function of percent unfolding

	% Reversible unfolding
% Unfolding	Without DMSO	With 2.5% (v/v) DMSO
25–30	100	100
50–60	77	75
75–80	69	57
95	49	50

NADS unfolding without DMSO is two-state

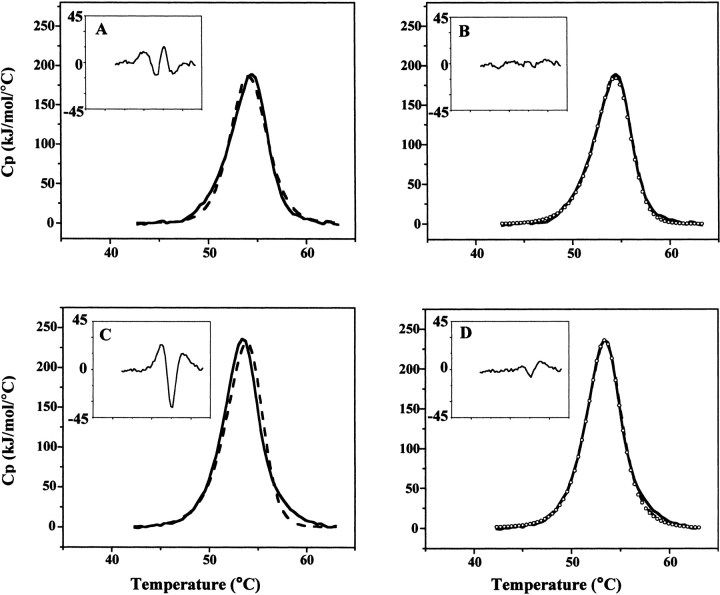
The simplest model that describes unfolding is the two-state, that is, where only the initial, folded, and final, unfolded states are significantly populated during the course of unfolding. For the NADS homodimer, if the unfolded state is monomeric, the two-state process would be described by the equilibrium of folded dimer with unfolded monomer, D_f ⇆ 2U, which is a two-state dissociative model. Without dissociation, the two-state model is simply F ⇆ U. Fits of the NADS DSC transition to these two models are shown in Figure 2 ▶, A and B. It is apparent that a better fit is obtained with the two-state dissociative model. A fit obtained using only data collected through 50% unfolding (at which point the transition is 77% reversible) is also shown to fit the entire DSC transition well. A third possible model that may describe the unfolding of dimeric NADS is one in which dissociation precedes monomer unfolding, that is, D_f ⇆ 2M_f ⇆ 2U (Bowie and Sauer 1989; Mann et al. 1993). The fit to this model was not improved over the simpler, two-state dissociative model (data not shown).

Figure 2.

DSC curve fitting of NAD⁺ synthetase thermal unfolding. (A,B) DSC scan of NAD synthetase (0.8 mg/mL) in 60 mM EPPS (pH 8.5), 20 mM KCl, 19 mM NH₄Cl, 10 mM MgCl₂. Scan rate: 1.5°C/min. (A) The DSC data (solid line) is shown in comparison to the fit to a two-state model (dashed line). (Inset) Residual errors in excess heat capacity for the two-state fit of the DSC data. (B) The DSC data (solid line) is shown in comparison to the fit to a two-state dissociative model, using the entire DSC data (dashed line). Circles represent the fit of the first half of the DSC data (up to T_1/2). (Inset) Residual errors in excess heat capacity for the two-state with dissociation fit of the DSC data. (C,D) DSC scan of NAD⁺ synthetase (0.9 mg/mL) in 60 mM EPPS (pH 8.5), 20 mM KCl, 19 mM NH₄Cl, 10 mM MgCl₂, 2.5% (v/v) DMSO. Scan rate: 1.5°C/min. (C) The DSC data (solid line) is shown in comparison to the fit to a two-state dissociative model (dashed line). (Inset) Residual errors in excess heat capacity for the two-state dissociative fit of the DSC data. (D) The DSC data (solid line) is shown in comparison to the fit to a sequential three-state model using the entire DSC data (dashed line). Circles represent the fit of the first half of the DSC data. (Inset) Residual errors in excess heat capacity for the sequential three-state fit of the DSC data.

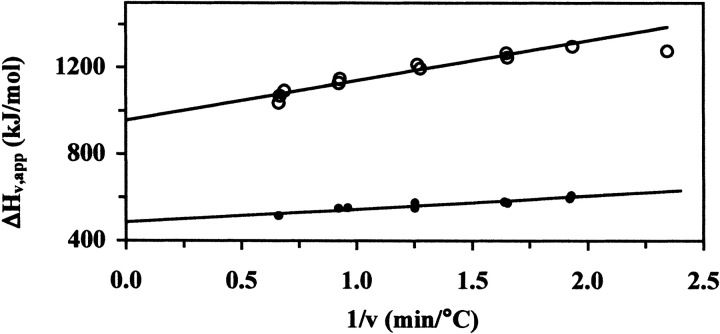
The calculated, model-dependent van’t Hoff enthalpy, ΔH_v, is one of the parameters obtained from the fit shown in Figure 2B ▶. As was mentioned above, the NADS DSC transition shows a small scan-rate dependence of the T_1/2 and the ΔH_v,app (apparent van’t Hoff enthalpy). Because the transition is largely reversible, it seemed reasonable to analyze the transition in terms of a reversible unfolding process followed by an irreversible step, that is, D_f ⇆ 2U → I (Sanchez-Ruiz et al. 1988; Freire et al. 1990; Tello-Solis and Hernandez-Arana 1995). In this case, extrapolation of the linear plot of ΔH_v,app versus the inverse scan rate (1/) will yield a y-intercept at infinite scan rate (1/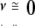) equal to the scan-rate independent ΔH_v (Fig. 3 ▶). This extrapolated ΔH_v compares well to the calorimetric enthalpy, ΔH_c (Table 2).

Figure 3.

Scan-rate dependence of the apparent van’t Hoff enthalpy (ΔH_v,app). Plots of ΔH_v,app vs. the reciprocal of the scan rate (1/v) for NAD⁺ synthetase unfolding without (open circles) and with (solid circles) DMSO. (Open circles) NAD⁺ synthetase (~1 mg/mL) in 60 mM EPPS (pH 8.5) with 20 mM KCl, 19 mM NH₄Cl, 10 mM MgCl₂. Data fitting used the two-state dissociative model. The extrapolated ΔH_v value at infinite scan rate is 953 (±17) kJ/mole. The rightmost point was excluded from the linear regression. (Solid circles) NAD⁺ synthetase in 60 mM EPPS (pH 8.5) with 20 mM KCl, 19 mM NH₄Cl, 10 mM MgCl₂, 2.5% DMSO. Data fitting used the sequential three-state fit model. The extrapolated ΔH_v for unfolding (Equilibrium 2; see Materials and Methods for details) at infinite scan rate was 487(±10) kJ/mole. The calculated total ΔH_v for both equilibria is 1151 (±17) kJ/mole (see Table 2).

Table 2.

Comparison of NADS unfolding enthalpy, ΔH, obtained from DSC curve analysis1

ΔH Parameter	Without DMSO	With 2.5% (v/v) DMSO2
ΔHc (integrated)3	946 ± 17	1145 ± 24
ΔHc (calc)4	941 ± 17	1198 ± 20
ΔHv (fit)5	953 ± 17	1151 ± 17
ΔHv ([Pt] dependent)6	858 ± 84	—

¹ Units are kjoules/mole.

² Reported ΔH values are the sum of equilibria 1 and 2.

³ Average and S.D. for 10 separate experiments.

⁴ Obtained from fitted curve; average and S.D. for 10 separate experiments.

⁵ Scan-rate independent curve fitted ΔH_v obtained from y-intercept of plot in Fig. 3 ▶.

⁶ Derived from slope of line in Fig. 4 ▶.

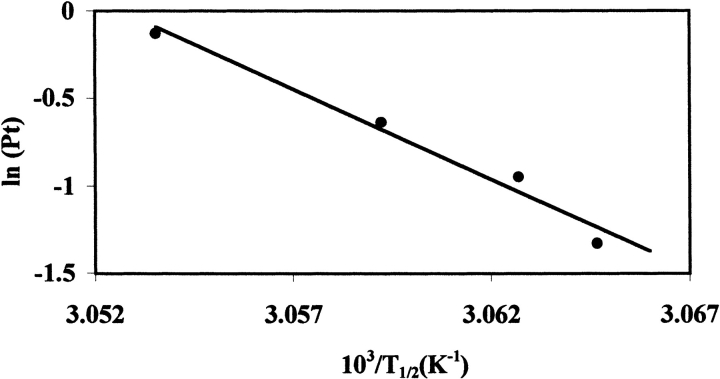
Further support for the dissociative model is the concentration dependence of the unfolding. A derivation of the van’t Hoff equation for the unfolding model, D_f ⇆ 2U, yields

where R is the gas constant, T is temperature in Kelvin, n is the number of subunits (equal to 2 for dimeric NADS), and Pt is the total protein concentration of NADS (Takahashi and Sturtevant 1981). A plot of ln(Pt) versus 1/T will yield a straight line, from which ΔH_v may be obtained from the slope, as shown in Figure 4 ▶. The ΔH_v derived in this way compares well to ΔH_c and to the ΔH_v obtained from curve fitting (Table 2).

Figure 4.

Dependence of T_1/2 (in Kelvin) on the total protein concentration, for NAD⁺ synthetase unfolding without DMSO. T_1/2 values for 0.265, 0.388, 0.53, and 0.88 mg/mL Pt were included. Buffering condition: 60 mM EPPS at pH8.5, 20 mM KCl, 19 mM NH₄Cl, 10 mM MgCl₂. The straight line has a slope of −1.03 (±0.1) × 10⁵ K, which corresponds to a ΔH_v of 858 (±84) kcal/mole; see text for details.

Equilibrium analytical ultracentrifugation

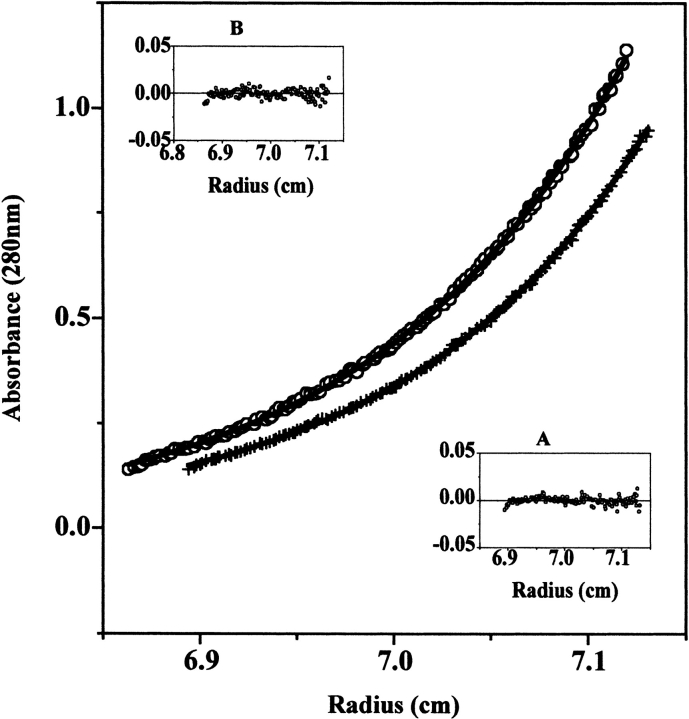
The NADS DSC transition is altered in the presence of DMSO (described in the next section). This result presented the need for a series of sedimentation equilibrium experiments to determine how DMSO affected the stability of the dimer at temperatures below the unfolding temperature. Figure 5 ▶ shows an example of a single run for NADS with and without 2.5% (v/v) DMSO at 20°C. The results indicate that NADS in the absence of DMSO behaves as a single species; there is no monomer present. The molecular weight determined by fitting the sedimentation equilibrium data to a single ideal species is 61.1 (±1.4) × 10³ (see Fig. 5 ▶), which compares very well with the theoretical value of 60.5 × 10³. However, with 2.5% (v/v) DMSO, an equilibrium is established between dimer and monomer with an association constant, K_a, of 5.6 × 10⁶/M.

Figure 5.

DMSO effect on the dimerization equilibrium of NAD⁺ synthetase measured by sedimentation equilibrium at 20°C and 12500 rpm. (Bottom curve) 0.75 mg/mL protein in 60 mM EPPS (pH 8.5) with 20 mM KCl, 19 mM NH₄Cl, 10 mM MgCl₂, without DMSO. The curve defined by “+” symbols is a mathematical fit using a single ideal species model. (Inset A) Residual plot of the fit. The calculated molecular weight of the species is 61.1 ± 1.4 kD (average of 6 runs), which corresponds to the molecular weight of the NAD⁺ Synthetase homodimer. (Top curve) 0.75 mg/mL protein in 60 mM EPPS (pH 8.5) with 20 mM KCl, 19 mM NH₄Cl, 10 mM MgCl₂, 2.5% (v/v) DMSO. The curve defined by open circle symbols is a mathematical global fit to all 6 runs performed at 20°C, using the self-association model. (Inset B) Residual plot of the fit. The calculated association constant (K_a) for dimerization is (5.6 ± 0.02) × 10⁶/M.

As a reminder, these experiments were performed after determining the need to include 2.5% DMSO in the enzyme assay. It was found, in fact, that apparent activity, as monitored by the rate of product production in a kinetic assay, did not change with DMSO concentrations of up to 10%. The Km also did not change with up to 2.5% DMSO, but nothing is known about kcat or Km above this value (data not shown). This result is interesting in light of the fact that the NaAD substrate binding site is created at the dimer interface, that is, residues from both monomers interact with NaAD. However, under the conditions of the reaction, NaAD is in excess and its binding to the dimer probably shifts the monomer–dimer equilibrium towards dimer. This may "mask" the effect of the DMSO, although other possibilities may exist as the substrates NaAD, ATP, and ammonia are not included in the DSC or sedimentation equilibrium experiments.

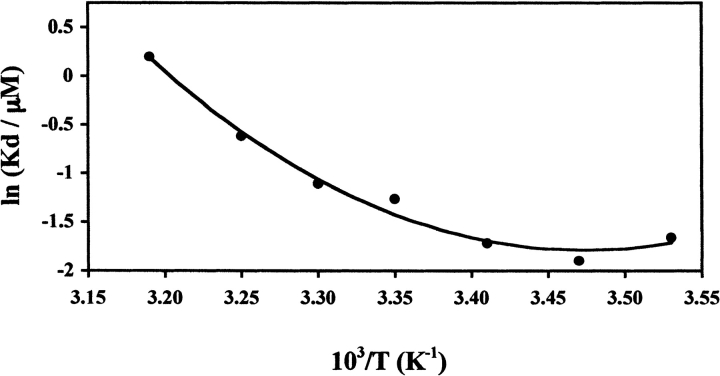
The temperature dependence of the dimer–monomer equilibrium was established from 10°–40°C. The ΔC_p1 and ΔH_v1 (defined as the heat capacity change and van’t Hoff enthalpy change for "Equilibrium 1"; see Materials and Methods for details) were calculated by a van’t Hoff analysis of the temperature dependence of the K_d (Fig. 6 ▶). The calculated K_d, ΔH_v1, and ΔC_p1 were used in the fitting algorithm for the DSC transition, as described in the next section.

Figure 6.

Dissociation constant of the NAD⁺ synthetase dimer (K_d) in the presence of 2.5% (v/v) DMSO as a function of the reciprocal of temperature. The smooth curve is a fit for the data, using a simple van’t Hoff analysis (equation 14; see Materials and Methods for details). The van’t Hoff enthalpy (ΔH_v1) from the fit is 113.3 (±10) kJ/mole at T = 39.0°C and the change in heat capacity (ΔCp₁) is 4.67(±0.8) kJ/(mole-K). Each data point represents the K_d calculated from a global fit of six different experimental runs at temperatures 15°, 20°, 25°, 35°, and 40°C, and three different runs at 10° and 30°C. The S.D. of each data point is smaller than the diameter of the symbol.

Differential scanning calorimetry in the presence of DMSO

NADS unfolding with 2.5% (v/v) DMSO is three-state

Figure 2 ▶, C and D, respectively, shows fits for NADS unfolding with 2.5%(v/v) DMSO, to a two-state dissociative, D_f ⇆ 2U, and a sequential three-state, D_f ⇆ 2M_f ⇆ 2U, model. The three-state unfolding model, in which folded (or partially folded) monomer is formed prior to monomer unfolding, is the better fit. A fit obtained using only data collected through 50% unfolding (at which point the transition is better than 75% reversible) is also shown to fit the entire DSC transition well. A simple two-state model did not fit as well as either of these models (data not shown). The K_d, ΔH_v1, and ΔC_p1 provided by the sedimentation equilibrium experiments were used to fit the data to a three-state model. With these defined, it was possible to obtain fits for the monomer unfolding ΔH_c2, ΔH_v2, and T_1/2. It was impossible to obtain a solution to the fit if the parameters for dimer dissociation were included among those parameters to be fit (see Materials and Methods for details). As far as we know, this is the first example where sedimentation equilibrium data has been used in the fit of a DSC unfolding transition. The resulting goodness of fit supports the proposed model that the folded monomer is in equilibrium with dimer below the unfolding transition, and that it is the monomer that unfolds at high temperature. Table 2 shows a comparison of the fitted and experimental DSC parameters for the three-state model. Similar to the data without DMSO, there is a small scan-rate dependence observed for the T_1/2 and ΔH_v,app (over the scan rates of 0.5–1.5°/min, the T_1/2 varied from 52.0°C to 53.4°C, respectively) and so an extrapolated ΔH_v is given in Table 2 (see Fig. 3 ▶). A simulation of the unfolding process using the three-state model, for a NADS dimer concentration equal to 7.6 μM, shows that monomer exists over the temperature range of 20°–60°C. The fraction of monomer increases from about 0.1 to a maximum of 0.3 at ~51°C, and then decreases to 0 at above 60°C.

Structural model for NADS unfolding in the presence of 2.5% (v/v) DMSO

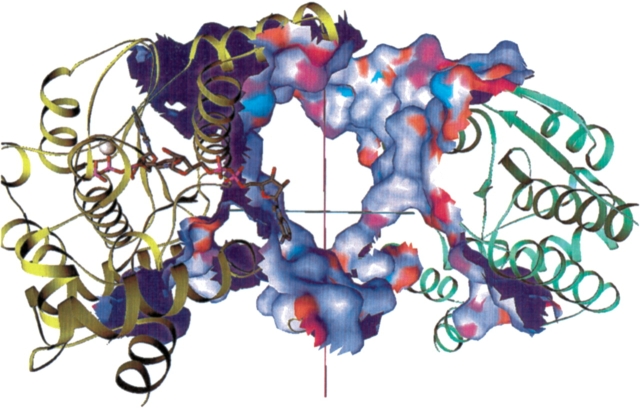
The two independent subunits (A and B) in the dimer crystal structure are related by a non-crystallographic twofold rotational axis of symmetry (Devedjiev et al. 2001). Figure 7 ▶, top, presents the crystallographic dimer as a ribbon diagram (Carson 1997) aligned with the symmetry axis. The extensive dimer interface rendered in Figure 7 ▶, middle, covers about 2600 Ų per monomer (totaling 5200 Ų buried overall) and is predominantly hydrophobic (70% of the residues are nonpolar). The interface is dominated by the interactions of helices E and F (residues 103 to 150) with the symmetry related helices E′ and F′. In addition to this large, continuous surface, two arms of the surface are formed by the respective C-terminal residues 257 to 271. The Ct′ region of the B-subunit interacts with residues near the N terminus of the A subunit, His 11 and helix B (24–35), as well as residues 170–182 on loop L. Interestingly, the interface appears to be unchanged by substrate binding.

Figure 7.

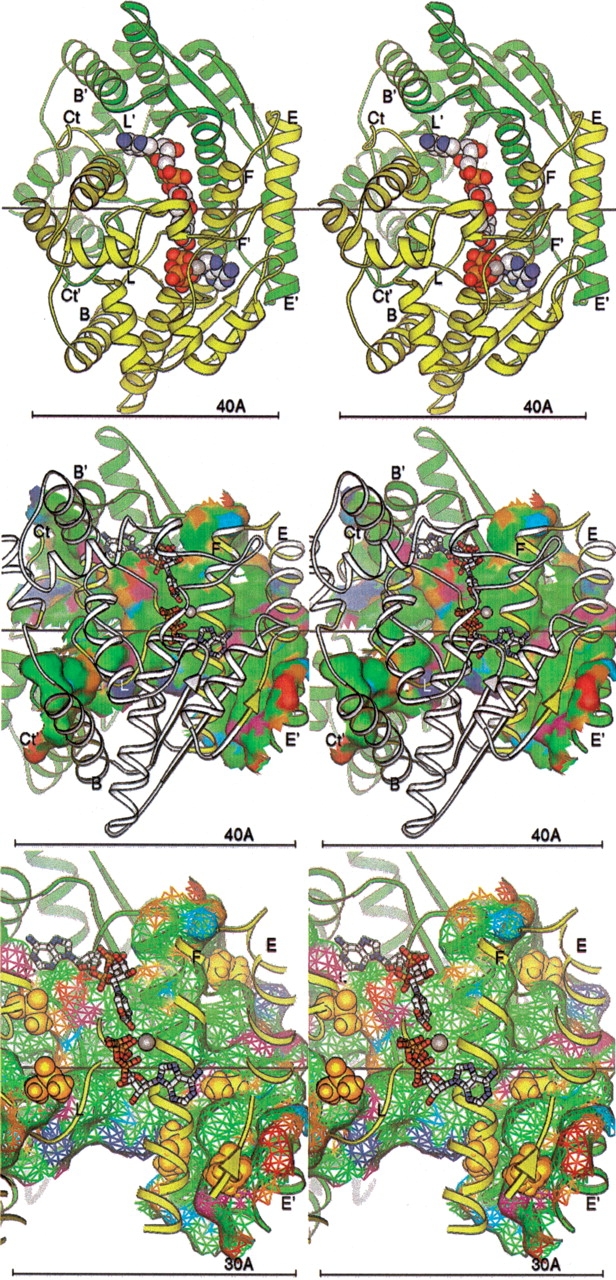
(Top) NAD⁺ synthetase dimer. The A (yellow) and B (green) subunits are represented by ribbons. Key secondary structural elements are labeled; those of the B subunit are primed. The cofactors NaAD, ATP, and Mg⁺² ion are shown as spheres. The twofold symmetry axis is shown as a black line, aligned with the X-axis of the page. All molecular figures created with Ribbons (Carson 1997; see also http://sgce.cbse.uab.edu/ribbons). (Middle) NAD⁺ synthetase dimer interface. The orientation is rotated about 45° about the Y-axis of the image above, to show the maximal amount of surface, and enlarged slightly. The cofactors are shown as ball-and-stick forms, and the A ribbons are drawn smaller to reduce clutter. Only the residues of the A subunit involved in the dimer interface are colored yellow; the rest are now white. Subunit B is green as before. The molecular surface of subunit B within 5 Å of any atom of subunit A is shown colored by atom type assigned for the docking experiments: positive charge, blue; negative charge, red; H-bond donor, cyan; H-bond acceptor, orange; polar, magenta; hydrophobic, green. (Bottom) DMSO docking at the NAD⁺ synthetase dimer interface. The orientation and style is that of the middle panel, but enlarged. Only the residues of the A subunit involved in the dimer interface (yellow) are shown in the ribbon. The surface is shown as a mesh. The DMSO molecules docked to the dimer in the computer simulation are shown as gold spheres.

The DSC and sedimentation equilibrium experiments indicate that a different unfolding mechanism exists in the presence of low concentrations of DMSO, resulting in different relative stabilities of dimer and monomer. The T_1/2 is essentially the same with and without DMSO (52.0°C vs. 52.2°C, respectively). This could suggest that the relative stability of folded to unfolded state remains the same and that the folded dimer, is therefore, less stable than the folded monomer in the presence of DMSO. The experimentally derived heat capacity change for dimer dissociation, ΔC_p1, is relatively large and positive (4.67 ± 0.8 kJ/mole-deg), as expected for the exposure of mostly hydrophobic groups (Fig. 6 ▶). The ΔC_p1 was also calculated based on the expected solvent exposure of hydrophobic groups at the interface when the dimer dissociates into monomers (Murphy et al. 1993; Baker and Murphy 1998). The dimer crystal structure (shown in Fig. 7 ▶) provided the model for the monomer structure. This calculation yields a smaller ΔC_p1 (1.25 kJ/mole-deg) than is derived from the experimental data, raising the possibility that a conformational change or some monomer unfolding (with concomitant additional exposure of hydrophobic groups) occurs upon dimer dissociation in the presence of DMSO.⁷ Therefore, the DMSO may have multiple effects that cannot be distinguished with the present experiments, which include either or both destabilization of the dimer and stabilization of an altered monomer conformation.

Other studies report that DMSO can reduce the stability of proteins at concentrations considerably higher than 2.5% (v/v) and one model proposed for this effect was the preferential solvation of the denatured state (Kovrigin and Potekhin 1997). The mechanism through which DMSO causes an alteration in the relative stabilities of the NADS dimer and monomer may involve specific interactions with the dimer. This question was addressed by computationally docking DMSO molecules into the dimer structure to determine whether the DMSO had an affinity to specific sites on the molecule. Computational docking of DMSO was executed with an implementation of the method of Jiang and Kim (1991). The docking results are given in Figure 7 ▶, bottom. The highest scoring binding positions for DMSO were observed either in a hydrophobic pocket near the active site ATP phosphates (left foreground) or symmetrically near the dimer interface where the end of the sheet leading to helix E packs against helix E′. All other high-scoring solutions were also at the dimer interface, packed at various locations. Interestingly, no ordered waters are found in the sites where DMSO was found to dock (Symersky et al. 2002), although presumably water must fill these sites ordinarily. No binding sites for DMSO were observed on the surface of the dimer nor were previous interface solutions observed for the simulation on the isolated A subunit; only the high-scoring site in the interior of the molecule near the ATP was found. This latter observation may suggest that if DMSO stabilizes the monomer through specific interactions, dimer dissociation may be accompanied by a conformational change that exposes binding site(s) for DMSO. Although this is only a computational model, the presence of high-scoring DMSO binding sites almost exclusively at the interface suggests this may be a likely mechanism through which DMSO destabilizes the dimer. The DMSO may "weaken" the hydrophobic effect, the primary driving force for dimerization. Crystallography experiments wherein DMSO is soaked into crystals are planned to determine whether DMSO binding sites can be observed.

It was of interest to determine whether dissociation would involve forces other than those associated with exposure of the hydrophobic interface, such as unfolding of secondary structural elements to relieve steric interference in the course of dissociation. For this purpose, visual experiments with custom molecular graphics software showed the dimers could be pulled apart by a simple translation perpendicular to the symmetry axis with little or no steric clash between the moving atoms. Figure 8 ▶ shows this translation movement. The figure depicting the interface between the monomers is aligned with this translation mostly in the plane of the page along the y-axis.

Figure 8.

Screenshot from a custom SGI Inventor program to “pull apart” the dimer. The subunits are shown as green and yellow ribbons. The substrate associated with the yellow subunit is shown in ball-and-stick form with the Mg⁺² as a silver sphere. The contact surfaces on each subunit (within 5 Å of the other subunit) are shown colored by atomic chemical property and are color coded as shown in Fig. 7 ▶ except for hydrophobic residues, which are shown in white. The interior (backfacing) surface is deep blue. The purple line marks the twofold axis of the dimer (not in the plane of the image.) The cyan line marks the "pull apart" path, perpendicular to the twofold (magenta line).

Conclusions

The study reported here explored the effect of the organic cosolvent DMSO, at low concentration, on the structure of dimeric NAD⁺ synthetase, with the unexpected result that the dimer–monomer equilibrium was selectively and markedly affected without a noticeable effect on the thermal stability of the enzyme. A practical outcome of this work is the knowledge that significant changes in the structure of an enzyme may occur upon addition of small concentrations of additives that, nevertheless, have no apparent effect on the enzymatic reaction under the employed conditions. It is shown that the NAD⁺ synthetase dimer is transformed from what is effectively a unimolecular species to an equilibrating system, which, under the right conditions, can create a significant concentration of inactive monomer. This suggests the intriguing possibility of a biologically relevant mechanism for modulating the activity of the enzyme.

Materials and methods

Materials

An E. coli expression system for B. subtilis NAD⁺ synthetase production has been described previously (Devedjiev et al. 2001). Cells from a 5-L overnight growth were harvested by centrifugation and resuspended in 80 mL of Tris buffer (50 mM Tris at pH 7.5, 1 mM EDTA, 1 mM DTT, 0.1 mM PMSF, 1% glycerol). Following cell disruption, the supernatant was loaded onto a Biologics Supradex-75 column equilibrated with the SDX-buffer (50 mM Tris at pH 7.5, 0.1 M NaCl, 0.1 mM PMSF, 1 mM DTT, 1% glycerol). The column was eluted with the same buffer. Fractions containing the protein were pooled and then loaded onto a BioRad-Q column equilibrated with 50 mM Tris at pH 7.5. The column was eluted in this buffer using a linear gradient of 0–500 mM NaCl. The NAD⁺ synthetase fraction from this column was passed through the Supradex-75 column again and the NAD⁺ synthetase fractions were concentrated and stored at −20°C in 50 mM Tris, 1 mM EDTA, 1 mM DTT, 0.1 mM PMSF, 180 mM NaCl, and 5% glycerol. Prior to each experiment, protein solutions were dialyzed into the desired buffer. Protein concentration was calculated based on OD_280nm using an extinction coefficient of 0.886 cm⁻¹(mg/mL)⁻¹. This extinction coefficient was calculated based on the amino acid sequence using Gill and von Hipples’s method (Gill and von Hipple 1989).

Analytical ultracentrifugation

Sedimentation equilibrium measurements of the NAD⁺ synthetase dimer ⇆ monomer equilibrium were performed on a Beckman XL-A analytical ultracentrifuge. The protein samples in these experiments were dialyzed into the assay buffer at pH 8.5, 60 mM EPPS buffer, with 20 mM KCl, 19 mM NH₄Cl, 10 mM MgCl₂. For those experiments containing DMSO, the solvent was added after dialysis. NADS without DMSO was studied at 20°C and the experimental temperature was varied from 5°C to 40°C for NADS with DMSO, in order to obtain the temperature dependence of the equilibrium constant (K_d). Rotor speeds at different temperatures were calculated based on the following equation:

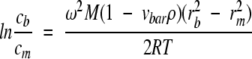where M is the molecular weight of the protein, v_bar is the partial specific volume, ρ is the solvent density, R is the universal gas constant, T is absolute temperature, r_b and r_m are the reference radial positions at the cell bottom and meniscus, c_b and c_m are the protein concentration at the cell bottom and meniscus, ω is the angular velocity, which is related to rotor speed f (in rpm unit) by the equation ω = f(2π)/60. c_b/c_m was set at 20 in order to calculate the appropriate rotor speed. In these experiments, the rotor speeds ranged from 12500 rpm to 18200 rpm. Typically, for each temperature, a set of six centrifuge runs were performed, as shown in Table 3, with the exception of the 10°C and 30°C runs for which only 3 runs were performed. These runs usually consisted of three different protein concentrations from 0.5 to 1.5 mg/mL and two different rotor speeds (the second speed was usually 40% higher than the first speed).

Table 3.

AUC experimental conditions for NADS with 2.5% (v/v) DMSO

Temperature (°C)	Concentration (mg/mL)	Equilibrium speed (RPM)
10	1.34, 1.0, 0.52	13500
15	1.3, 0.9, 0.5	12600, 17600
20a	1.0, 0.75, 0.5	12500, 16500
25	1.3, 0.9, 0.5	12800, 17900
30	1.34, 1.0, 0.52	13500
35	1.2, 0.9, 0.6	13000, 18000
40	1.0, 0.75, 0.5	14000, 20000

^a The conditions shown for 20°C were also those used for NADS without DMSO.

Data analysis was performed using the self-association model in the Origin analysis software provided by Beckman, and using the software, Multifit, developed by L. Holladay. K_d at each temperature was calculated by a global analysis of the set of six runs. The partial specific volume and density of solvent were either computed using the "sednterp" program (Hayes et al. 1999), or measured with a 50-mL specific gravity bottle, thermostated to 25.0°C.

The heat capacity change, ΔCp, for dimer dissociation was experimentally determined from the temperature dependence of the dimer dissociation, K_d (using equation 14; see next section). ΔCp was also calculated from empirical parameters developed by Murphy and others (Murphy et al. 1993; Baker and Murphy 1998). For this calculation, knowledge of the change in polar and nonpolar solvent accessible surface area is required. The change in surface area upon dimer dissociation was obtained from the crystal structure of the dimer (PDB code 1EE1; Devedjiev et al. 2001) using the program NACCESS (Hubbard and Thornton 1996).

Differential scanning calorimetry

All calorimetric scans were performed with a MicroCal MC-II differential scanning calorimeter. The calorimetric unit was interfaced to an IBM PC microcomputer using a DT2801 I/O board for automatic data collection. Protein concentrations in the range of 0.1 to 1.0 mg/mL were used. All protein solutions were dialyzed against the assay buffer (60 mM EPPS at pH 8.5, 20 mM KCl, 19 mM NH₄Cl, 10 mM MgCl₂). For those experiments containing DMSO, the solvent was added after dialysis. All solutions were degassed under vacuum with stirring for 5 min before loading into the cells. Approximately 1.3 mL of protein solution was introduced into the sample cell and the same amount of buffer into the reference cell. Calorimetric scans were carried out at scan rates ranging from 30°C/h to 90°C/h, under a constant pressure of 30 psi. The Origin software package (MicroCal) was used for data collection and analysis.

DSC data analysis

All data analysis was performed on a TOSHIBA Equium microcomputer with Pentium processor. Nonlinear curve fitting was performed using the Origin 5.0 software package. The built-in models for DSC data analysis, provided by MicroCal, were used for the simple two-state analysis. Other mathematical equations needed were written in a format recognizable by Origin, based on the equations that follow next.

A two-state unfolding process with dissociation is represented by:

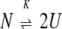The temperature dependence of the equilibrium constant for this reaction, K, can be described by the van’t Hoff equation:

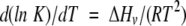(1)

where ΔH_v is the model-dependent van’t Hoff enthalpy change for unfolding, R is the gas constant, and T is temperature in Kelvin.

Integration of equation 1 from a reference temperature, T_o, to T, yields

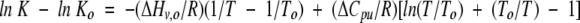(2)

where ΔC_pu is the heat capacity change attributable to unfolding.

The equilibrium constant, K, for the two-state dissociative process is defined as:

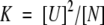(3a)

Because P_t = 0.5[U] + [N], where P_t is the total molar concentration of the protein dimer,

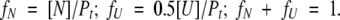So, substituting into equation 3a yields

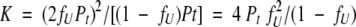(3b)

Rearranging equation 3b yields

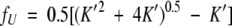(4)

where K′ = K/(4P_t).

Differentiating with respect to temperature yields

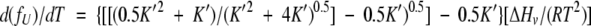(5)

For simplicity, the reference temperature is chosen to be the temperature where f_U is 0.5, and is defined as “T_1/2”. (In simple two-state unfolding, it is common to choose as the reference temperature the point of maximum heat capacity, T_m, which is also the temperature where K = 1 and f_U = 0.5. In the dissociative mechanism, K_1/2 ≠ 1 and T_1/2 is not the temperature of maximum heat capacity.)

At T_1/2, equation 3b simplifies to,

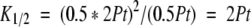(6)

Equations 6 and 2 are combined, yielding

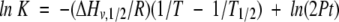(7)

where the unfolding heat capacity change, ΔC_pu = 0.⁸

The molar heat capacity, C_p, of the system is

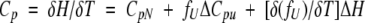(8)

The excess heat capacity function, with ΔC_pu = 0, is

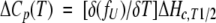(9)

Substitution of equation 5 yields

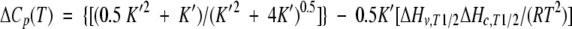(10)

A similar derivation may be found in Freire 1989.

Two sequential equilibria are represented by the reactions:

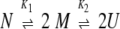where N is the native dimer, M is the native monomer, U is the unfolded monomer, and K₁ and K₂ are the equilibrium constants for the dissociation of the dimer (Equilibrium 1) and the unfolding of the monomer (Equilibrium 2), respectively.

The fractions of the three species are defined as:

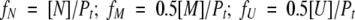(11)

where P_t is the total protein (dimer) concentration.

The equilibrium constants can be expressed as:

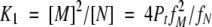(12)

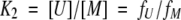(13)

Equilibrium 1

An equation similar to equation 2 can be written for Equilibrium 1:

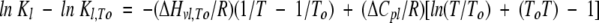(14)

where T_o is a reference temperature, which is different from the unfolding T_1/2 of the protein. Because Equilibrium 1 represents the dimer dissociation, it was convenient to define T_o as 313 K, which is close to the beginning of DSC data collection, for the purpose of curve fitting. ΔH_v1,To, ΔC_p1, and K_1,To are the van’t Hoff enthalpy change, heat capacity change, and equilibrium constant for Equilibrium 1 at T_o. K_1,To can be measured directly in the sedimentation equilibrium experiments. ΔH_v1,To and ΔC_p1 can be obtained through fitting the curve obtained from a plot of lnK₁ versus (1/T) using equation 14, as shown in Figure 6 ▶. ΔC_p1 obtained in this way was used to derive ΔH_v1 and K₁ at any temperature as required for equations 20 and 21 (see below).

Equilibrium 2

Similar to Equilibrium 1, equation 15 represents the integrated form of the temperature dependence of the equilibrium constant:

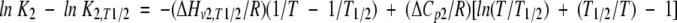(15)

where ΔH_v2,T1/2, ΔC_p2, and K_2,T1/2 are the corresponding thermodynamic parameters at T_1/2.

T_1/2 is the temperature where f_U is 0.5. At T_1/2, there exists the following relation:

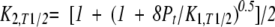(16)

where K_1,T1/2 is the equilibrium constant for Equilibrium 1 (dimer dissociation) at T_1/2.

Substitution of equation 16 into equation 15 allows computation of the equilibrium constant K₂ over the entire temperature range.

The fractions of the three species have the following relationships:

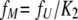(17)

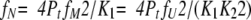(18)

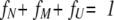(19)

Combining these three equations, f_U can be represented by

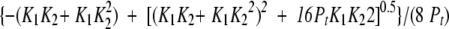(20)

The excess heat capacity function is represented as

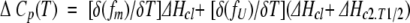(21)

where ΔC_p2 = 0.

The two partial derivatives of fu and fm with respect to T in equation 21 are solvable but are not included in this section because of the complexity of the equations. A similar derivation may be found in Azuaga et al. (1995). For curve fitting, ΔC_p2 was set equal to 0. Because an experimental value was on hand, ΔH_c1 was set equal to ΔH_v1 (derived from the sedimentation equilibrium data).

Computational docking of DMSO

Computational docking of DMSO to NAD⁺ synthetase, PDB file 1EE1 (Devedjiev et al. 2001) was executed with the program SoftDock (W.M. Carson, unpubl.), an implementation of the method of Jiang and Kim (1991). The docking procedure holds the protein molecule stationary, while a full six degrees of freedom search is performed with the rigid DMSO probe molecule. For each discrete rotational orientation (typically about 10,000), a molecular dot surface (Connolly 1993) is calculated and classified per atom type. Each molecule is partitioned into cubes and classified as solvent, surface, or internal, and then compared cube by cube for each possible translation. The scoring function results in a qualitative rank ordering of binding sites. It rewards geometric and chemical complementarity between two surfaces, while penalizing internal volume overlap. The geometric complementarity requires the surface normals to be oriented toward each other, within an angular tolerance. The chemical complementarity is based on six atomic classes, as shown in the surface of Figure 7 ▶: positive charge (blue), negative charge (red), H-bond donor (cyan), H-bond acceptor (orange), polar (magenta), and hydrophobic (green). A simple ±1 sum is accumulated pairwise over the surface dots inside each cube; for example, a positive charge interacting with hydrophobic is −1; a positive charge interacting with a hydrogen-bond acceptor is +1. All solutions are clustered within input rotational/translation tolerances.

Computational docking was carried out using the protein atoms only for the two crystal forms of NAD⁺ synthetase, as well as the two forms transformed to align the cartesian axis as in the figures. Although this is a simple rigid-body transformation and the relative orientation of the coordinates does not change, the cubes sampled by the docking algorithm will change. Another docking run was performed on the A subunit only.