Defining the minimum size of a hydrophobic cluster in two-stranded α-helical coiled-coils: Effects on protein stability

Abstract

The α-helical coiled-coil motif is characterized by a heptad repeat pattern (abcdefg)_n in which residues a and d form the hydrophobic core. Long coiled-coils (e.g., tropomyosin, 284 residues per polypeptide chain) typically do not have a continuous hydrophobic core of stabilizing residues, but rather one that consists of alternating clusters of stabilizing and destabilizing residues. We have arbitrarily defined a cluster as a minimum of three consecutive stabilizing or destabilizing residues in the hydrophobic core. We report here on a series of two-stranded, disulfide-bridged parallel α-helical coiled-coils that contain a central cassette of three consecutive hydrophobic core positions (d, a, and d) with a destabilizing cluster of three consecutive Ala residues in the hydrophobic core on each side of the cassette. The effect of adding one to three stabilizing hydrophobes in these positions (Leu or Ile; denoted as •) was investigated. Alanine residues (denoted as ○) are used to represent destabilizing residues. The peptide with three Ala residues in the d a d cassette positions (○○○) was among the least stable coiled-coil (T_m = 39.3°C and Urea_1/2 = 1.9 M). Surprisingly, the addition of one stabilizing hydrophobe (Leu) to the cassette or two stabilizing hydrophobes (Leu), still interspersed by an Ala in the cassette (•○•), also did not lead to any gain in stability. However, peptides with two adjacent hydrophobes in the cassette (••○)(○••) did show a gain in stability of 0.9 kcal/mole over the peptide with two interspersed hydrophobes (•○•). Because the latter three peptides have the same inherent hydrophobicity, the juxtaposition of stabilizing hydrophobes leads to a synergistic effect, and thus a clustering effect. The addition of a third stabilizing hydrophobe to the cassette (•••) resulted in a further synergistic gain in stability of 1.7 kcal/mole (T_m = 54.1°C and Urea_1/2 = 3.3M). Therefore, the role of hydrophobicity in the hydrophobic core of coiled-coils is extremely context dependent and clustering is an important aspect of protein folding and stability.

Protein folding is still a dauntingly complex problem, despite the abundance of research devoted to its resolution. Protein folding is not a random sampling of conformational space, but rather the concerted action of multiple driving forces (Levinthal 1968; Dill 1990; Daggett and Fersht 2003). Collapse of hydrophobic side chains away from bulk solvent and the formation of secondary structures are two events that must occur for proper folding of native structures. Secondary structural elements must then associate together to obtain the native structure. However, the interplay between these forces is less clear; for example, does hydrophobic collapse drive secondary structure formation or are these concomitant events? It has been well established that hydrophobic collapse is the main driving force in protein folding (Kauzman 1959; ^{Dill 1990}), consistent with the observation that the protein interior is generally well packed with hydrophobic side chains.

Clearly, in the case of coiled-coil proteins, it is not just the packing of hydrophobes in the hydrophobic core that is critical to stability and function, because we observed alternating densely packed regions of larger hydrophobes followed by less dense regions of small hydrophobes (e.g., Ala). This observation suggests that clustering of hydrophobic residues must play an important role in protein folding pathways and stability. We chose to investigate the role of hydrophobic clusters in the hydrophobic core of the two-stranded α-helical coiled-coil because its rod-like nature makes the hydrophobic core a one-dimensional problem compared with more complex globular proteins.

The coiled-coil motif consists of two interacting amphipathic α-helices that form a left-handed super-helix. The rod-like nature of this motif removes the complexity of the hydrophobic core observed in globular proteins, which involves hydrophobic packing from distant parts of the primary sequence. This protein fold is widely observed in known protein structures and it has been previously estimated that ~3% of all helical sequences exist as coiled-coils (Wolf et al. 1997). Coiled-coils are characterized by a heptad repeat motif (abcdefg)_n in which residues a and d form the hydrophobic core analogous to the protein interior in globular proteins; residues e and g are adjacent to the hydrophobic core and are often involved in i to i′ + 5 interchain salt bridges that further bury the hydrophobic core; and residues b, c, and f form the solvent-exposed surface typically containing polar and charged residues (Zhou et al. 1992a; Hodges 1996; Lupas 1996; Burkhard et al. 2001). Many natural coiled-coils such as tropomyosin, myosin, hemagglutinin, and others are long helical proteins. Their sequences show the characteristic 3–4 hydrophobic repeat, but, interestingly, in very long coiled-coils, heptad breaks (stutters or stammers) are often observed (Brown et al. 1996; Strelkov and Burkhard 2002). Alternatively, many nonoptimal residues are found in hydrophobic core positions but are tolerated if the overall coiled-coil stability is sufficient. These polar and charged residues found in hydrophobic core positions have been shown to control oligomerization state and chain orientation in model peptides and numerous native dimerization domains (Harbury et al. 1993; Wagschal et al. 1999b; Tripet et al. 2000; Akey et al. 2001). Recently, Hodges and coworkers substituted 20 amino acid residues at positions a and d in model coiled-coils and showed that single amino acid substitution can make a wide range of contributions to stability depending on the residue (~7 kcal/mole range at each a and d position; Wagschal et al. 1999a^,b; Tripet et al. 2000).

One of the earliest and best-studied coiled-coils is tropomyosin, an unusually long coiled-coil of 40 heptads (or 284 residues) per polypeptide chain. This was the first coiled-coil sequenced that identified the 3–4 hydrophobic repeat responsible for the formation and stabilization of the structure (Hodges et al. 1972; Sodek et al. 1972). The 3–4 or 4–3 hydrophobic repeat is continuous throughout the sequence of tropomyosin. Interestingly, tropomyosin binds actin filaments and regulates the actin–myosin interaction responsible for Ca⁺²-dependent muscle regulation (for recent review, see Perry 2001). Its movement on the actin filament during the contraction process implicates a possible transmission of a conformation change from the troponin complex on binding Ca⁺² through the tropomyosin coiled-coil to the actin filament. Thus, understanding the variations in stability along the length of the coiled-coil could be critical in understanding the complex mechanism of muscle regulation in addition to the basics of protein folding and stability in general (the subject of this paper). The hydrophobic core a and d residues can be represented as a linear array corresponding to every third or fourth residue in the primary sequence (Kwok and Hodges 2003). The distribution of these core residues shows that a continuous hydrophobic surface of large hydrophobes is broken up or interspersed with small hydrophobic residues such as alanine or hydrophilic polar or charged residues that create alternating clusters of what we define as stabilizing and destabilizing residues in the hydrophobic core. Based on the results of Hodges and coworkers (Wagschal et al. 1999b; Tripet et al. 2000), the following residues were classified as stabilizing residues (Leu, Ile, Val, Met, Phe, and Tyr). All others are classified as destabilizing residues. In this case, we consider three or more consecutive core residues of the same classification (stabilizing or destabilizing) as a cluster. Interestingly, stabilizing and destabilizing clusters are conserved in known tropomyosin sequences (Fig. 1 ▶). Many have postulated that tropomyosin shows regions of local instability that are important for function (Brown et al. 2001; Hitchcock-DeGregori et al. 2002). Numerous truncation studies have attempted to identify the critical regions of stability in tropomyosin that regulate folding and stability (Landis et al. 1999; Holtzer et al. 2001; Hitchcock-DeGregori et al. 2002; Paulucci et al. 2002). Recently, Suarez et al. (2001) showed that tropomyosin is pressure sensitive, and that sensitive and less sensitive regions exist along the length of the molecule. Although no clear picture has yet emerged concerning the relationship between primary sequence and folding, and overall stability, the unusual distribution of clusters (stabilizing and destabilizing) are key to understanding this problem.

Figure 1.

The a and d positions of the heptad repeats (abcdefg)_n throughout the 284-residue sequence of tropomyosin are indicated by filled circles, open circles, or half-filled circles, where a and d are the positions in the hydrophobic core of the two-stranded coiled-coil. The filled circle denotes a stabilizing residue (L,M,I,V,F,Y), represented by J, and the open circle denotes a destabilizing residue (remaining 14 amino acid residues) represented by X, when that type of residue is conserved >67% of the time. The half-filled circle denotes that both a stabilizing and destabilizing residue appears in at least 13 of 34 sequences. The consensus residue is indicated for each position in the sequence if it appears >50% of the time. No consensus residue is indicated by a dash. Residues that appear >20% of the time are listed below the consensus sequence. The superscript denotes the number of times a stabilizing or destabilizing or a particular residue appears (e.g., J³⁴, a stabilizing residue, appears 34/34 times and L³⁰ denotes that leucine appears 30/34 times). S1 to S8 denotes stabilizing clusters and D1 to D5 denotes destabilizing clusters. Clusters (boxed) are defined as a minimum of three consecutive a and d residues of the same type. The 34 sequences analyzed (from the SWISSPROT database) are full-length (284-residue) tropomyosin sequences: TPM1_BIOGL, TPM2_BIOGL, TPM_MYTED, TPM_MYTGA, TPM1_SCHMA, TPM_ECHMU, TPM2_SCHMA, TPM1_DROME, TPMM_LOCMI, TPM_PERAM, TPM1_HOMAM, TPM_DERPT, TPM_LEPDS, TPMM_ANISI, TPMM_TRICO, TPM2_DROME, TPM1_BRARE, TPM1_CHICK, TPM1_COTJA, TPM1_RANTE, TPM1_XENLA, TPM1_HUMAN, TPM1_MOUSE, TPM1_RABIT, TPM1_RAT, TPM1_PIG, TPM3_HUMAN, TPM3_MOUSE, TPM2_CHICK, TPM2_HUMAN, TPM2_MOUSE, TPM2_RABIT, TPM2_RAT, and TPM1_CIOIN.

Hydrophobic packing in the core a and d positions is the most significant factor that contributes to coiled-coil stability (Wagschal et al. 1999b; Tripet et al. 2000). Intrachain (i, i + 3, or i + 4) and interchain i to i′ + 5 (g, e′) electrostatics (Kohn et al. 1998) and helical propensity (O’Neil and DeGrado 1990; Chakrabartty et al. 1994; Zhou et al. 1994) can also modulate stability. Recent work (Kwok and Hodges 2003) showed that shuffling of two hydrophobic core residues, which disrupted a stabilizing cluster, led to a dramatic decrease in stability despite equivalent composition and hydrophobicity in the hydrophobic core. In order to study this effect in more detail, we designed another series of peptides with a central cassette in which the number of hydrophobes (Ile, Leu) increases in the hydrophobic core, and determined the minimum number of hydrophobes required to form a stable hydrophobic cluster.

Results and Discussion

Analysis of tropomyosin sequences

The protein sequences of 34 full-length (284-residue) tropomyosins (obtained from the SwissProt database) were aligned using the program MultiAlign, and the distribution of residues at each position was examined. Although we examined the conservation of residues at every heptad position, the importance of the hydrophobic core residues to coiled-coil stability led us to focus on the a and d residues (Fig. 1 ▶). Kwok and Hodges (2003) showed that in rabbit tropomyosin the distribution of stabilizing and destabilizing residues in the hydrophobic core positions was clustered into groups in which a “cluster” was defined as three or more consecutive hydrophobic core residues of the same type, stabilizing or destabilizing. Analysis on the 34 tropomyosin sequences (Fig. 1 ▶) resulted in the classification of each hydrophobic core residue as either stabilizing (Ile, Leu, Met, Val, Phe, Tyr, denoted J) or destabilizing (all other residues, denoted X) using a criteria of 67% conservation. This is indicated by the filled and the open circles that represent conserved stabilizing and destabilizing residues, respectively. The half-filled circle indicates that both stabilizing and destabilizing residues are found at this hydrophobic core position in significant numbers (at least 13 of 34 sequences). Interestingly, both stabilizing and destabilizing clusters were found as indicated by the boxes. Tropomyosin shows eight stabilizing clusters (indicated as S1 to S8 in Fig. 1 ▶) and five destabilizing clusters (D1 to D5, Fig. 1 ▶). The stabilizing hydrophobic clusters varied from a minimum of three consecutive core residues to a maximum of five stabilizing hydrophobes per cluster. Interestingly, there are four destabilizing clusters of three consecutive core residues consisting of mainly Ala and Ser residues and one long destabilizing cluster of seven consecutive core residues consisting of Ala, Lys, and Ser (D1, Fig. 1 ▶). We then further investigated the sequence conservation at each position, either within a cluster or outside a cluster. Residues were found to be 85.2% identical in the stabilizing clusters and 83.6% identical in the destabilizing clusters, but only 64.3% identical in regions outside of the clusters. Therefore, the cluster regions represent regions of higher sequence conservation and presumably important roles in tropomyosin’s folding, stability, and function.

Peptide design

We designed a series of two-stranded parallel α-helical coiled-coils, 60 residues per strand, which are disulfide bridged at the C terminus, similar to those described in Kwok and Hodges (2003). All peptides in this series contain two hydrophobic clusters (the C-terminal cluster has three consecutive core positions, whereas the N-terminal cluster contains four consecutive core positions occupied by stabilizing large aliphatic hydrophobes, Ile and Leu at positions a and d, respectively) along with favorable interchain Glu (i) to Lys (i′ + 5) salt bridges. The center of each chain contains a cassette designed to test the effect of individual hydrophobes and hydrophobic clustering on stability.

In order to minimize context-dependence effects, the central cassette is isolated from the stabilizing hydrophobic clusters by three consecutive alanine residues in the hydrophobic core (a destabilizing cluster) on each side of the cassette (Fig. 2 ▶). The central cassette contains three hydrophobic core positions (positions d, a, and d), which are occupied with either Ile (at position a) or Leu (at position d), both of which are stabilizing hydrophobic residues (denoted as a filled circle) or Ala for a destabilizing residue (denoted as an open circle). The peptide sequences are shown in Figure 2 ▶ (upper panel) and schematically in the lower panel. Leucine and isoleucine were shown to be major stabilizing residues at the hydrophobic core a and d positions, relative to Ala (Zhou et al. 1992b; Zhu et al. 1993; Wagschal et al. 1999b; Tripet et al. 2000). Ile at position a and Leu at position d were also shown to favor the two-stranded coiled-coil over higher-order oligomers (Harbury et al. 1993). These studies showed alanine to be a destabilizing residue in hydrophobic core positions despite its high helical propensity (Zhou et al. 1994). Thus, we have eight peptides ranging from zero to three stabilizing residues in the cassette, positions d, a, d. It should be noted that the most stable peptide (with three large aliphatic hydrophobes in the cassette, peptide 1) contains three hydrophobic clusters per chain, each of which is interspersed with a destabilizing cluster of alanines. The least stable peptide of the series (with no large aliphatic hydrophobes in the cassette, only three Ala residues, peptide 8) contains nine consecutive alanine residues along the length of the hydrophobic core. The stability of peptide 8 also serves as our baseline, as it contains the least number of stabilizing residues in the hydrophobic core.

Figure 2.

Peptide sequences are shown in the upper panel. All peptides used were oxidized to disulfide-bridged homo-two-stranded α-helical coiled-coils. Residues at heptad positions a and d are bold. A schematic representation of the hydrophobic core residues is shown in the lower panel. Each residue at positions a and d is indicated by a dot, where the filled circle denotes Ile at position a or Leu at position d and the open circle denotes Ala. The cassette region is indicated by the boxed region. Ac denotes an N^α-acetyl group. The brackets denote three peptides with one or two large hydrophobes in the cassette.

Characterization of α-helical structure

The circular dichroism (CD) spectra of peptides 1 and 8 in benign buffer and 50% trifluoroethanol (TFE) are shown in Figure 3 ▶. These CD spectra are representative of all the peptides in this series. The observed molar ellipticity values for all peptides in this series (measured at ~20 μM) are tabulated in Table 1. All peptides show good helical structure with canonical helical double minima at 208 and 222 nm. Addition of the helix-inducing solvent TFE leads only to slight induction of additional helical structure, indicating that these peptides are essentially fully folded (>86% helical content; Table 1). These peptides also show that the characteristic Θ_222/208 ratio shifts from slightly greater than unity in benign buffer to slightly less than unity in TFE (Lau et al. 1984). All peptides in this series are also disulfide-bridged homo-two-stranded coiled-coils, thus eliminating the concentration dependence of the monomer-to-dimer equilibrium. Reduced peptides showed reasonable helical structure but were of insufficient stability for meaningful stability comparisons (data not shown). The observed molar ellipticity values for these peptides are slightly less than that calculated for a theoretical helix of 56 helical residues ([Θ]_{222(theoretical)} = −35740; Chen et al. 1974). This is not surprising, as we have purposefully designed these peptides with a minimum of six alanine residues in the hydrophobic core to isolate the cassette. These six alanine residues in the hydrophobic core destabilize the overall coiled-coil structure. Of particular interest is peptide 8, which is expected to be the least stable peptide of the series. As this peptide shows good helical structure, we are confident that the addition of stabilizing hydrophobes into the cassette will represent changes in coiled-coil stability and not any significant changes in helical structure.

Figure 3.

Circular dichroism spectra of peptide 1 (18.8 μM) (A) and peptide 8 (19.7 μM) (B). Filled circles represent the spectra in benign buffer (50 mM potassium phosphate at pH 7, 100 mM potassium chloride) whereas open circles represent the spectra in benign buffer + 50% trifluoroethanol.

Table 1.

Circular dichroism data

Peptide	Cassette designationa	[Θ]222nm (benign)b	[Θ]222nm (50% TFE)b	[Θ]222/208 nm (benign)c	[Θ]222/208 nm (50% TFE)c	% Helixd
1	•••	−28,700	−31,100	1.05	0.96	92.3
2	••○	−28,400	−30,000	1.01	0.92	94.7
3	○••	−33,100	−32,100	1.03	0.93	103.1
4	•○•	−26,900	−29,600	1.01	0.94	90.9
5	•○○	−29,000	−32,300	1.02	0.94	89.8
6	○•○	−35,400	−34,600	1.05	0.92	102.3
7	○○•	−28,300	−32,500	1.00	0.93	87.0
8	○○○	−28,200	−32,600	1.00	0.92	86.5

^a Sequences are shown in Figure 2 ▶. Filled circles denote Ile or Leu and open circles denote Ala in the a and d positions of the cassette shown in Figure 2 ▶.

^b Calculated from the following formula: [Θ] = Θ_obs × MRW / [10 × path length (cm) × concentration (mg/mL)] where MRW is the mean residue weight (molecular mass of the peptide divided by the number of helical residues). Benign refers to 50 mM potassium phosphate buffer, 0.1 M KCl (pH 7.0), and TFE is trifluoroethanol.

^c [Θ]_{222/208 nm} is the ratio of the [Θ]₂₂₂ divided by the [Θ]_208nm.

^d % Helix is calculated from the molar ellipticity at 222 nm divided by the molar ellipticity in 50% TFE times 100. The value in 50% TFE represents the maximum α-helical content and is taken as 100%.

Thermal stability

Short coiled-coil peptides show highly cooperative transitions indicative of two-state denaturations (folded coiled-coil to random-coil), which are easily monitored by CD spectroscopy (Thompson Kenar et al. 1995; Wendt et al. 1995; Yu et al. 1996; Dürr and Jelesarov 2000). The two-state denaturation assumption of coiled-coil peptides was recently addressed by Dragan and Privalov (2002). Coiled-coils show a linear increase in ellipticity prior to the sigmoidal transition by CD. The linear portion of the profile is a concentration-independent transition and attributed to end fraying and molecular motion that does not lead to helix dissociation/unfolding. This transition is accounted for in our data fitting by the pretransition baseline, which describes the temperature dependence of the native folded coiled-coil prior to the dominant concentration-dependent cooperative unfolding transition.

The effect of increasing the number of stabilizing residues in the cassette was studied by measuring the stability of these coiled-coils, both by thermal and chemical denaturation. Ellipticity at 222 nm was monitored as a function of temperature, and the results for thermal stability measurements are shown in Figure 4 ▶ and Table 2. All peptides were diluted to 20 μM. Peptide 1 was expected to be the most stable peptide of this series, as it has a full cassette of three stabilizing residues (Leu, Ile, and Leu in positions d, a, and d; Fig. 2 ▶), and thus a stabilizing cluster. This was indeed the case with a measured transition midpoint of 54.1°C. Of particular interest are peptides 2–4, which each have two stabilizing residues in the cassette, but at differing positions (Fig. 4 ▶, middle panel). Peptides 2 and 3 are more stable (T_m = 44.4°C and 42.6°C) than peptide 4 (T_m = 38.1°C) despite all three peptides having identical inherent hydrophobicity. Although peptides 2 and 3 (with an Ile at a and a Leu at d in the cassette) differ slightly in composition than peptide 4 (with two Leu residues at both d positions in the cassette), these changes were shown to be equivalent changes relative to Ala in model peptides (Wagschal et al. 1999b; Tripet et al. 2000). This suggests that two adjacent stabilizing residues in the hydrophobic core (peptides 2 and 3) show some clustering effect as compared with peptide 4 (with two leucines interspersed by an alanine). This will be discussed in more detail below.

Figure 4.

Temperature denaturation profile of peptides 1 and 8 are shown in the top panel. Molar ellipticity data were directly fit to obtain T_m values, accounting for the pre- and posttransition baselines. These data were converted to fraction folded (as described in Materials and Methods) to allow for visual comparison among analogs. Temperature denaturation profiles of peptides 1–4 (middle panel), denoted P1 to P4, and of peptides 4–8 (bottom panel), denoted P4 to P8, are shown.

Table 2.

Thermal and chemical stability data

Peptide	Cassette designationa	Tmb (°C)	Urea1/2c (M)	md (kcal mole−1M−1)	ΔΔGe (kcal/mole)	Average ΔΔGf (kcal/mole)
1	•••	54.1	3.3	−1.68	−2.16	−2.2
2	••○	44.4	2.3	−1.42	−0.57	−0.5
3	○••	42.6	2.2	−1.68	−0.46
4	•○•	38.1	1.6	−1.07	0.37
5	•○○	37.4	1.7	−1.50	0.29	0.4
6	○•○	38.1	1.7	−1.28	0.27
7	○○•	37.2	1.5	−1.09	0.50
8	○○○	39.3	1.9	−1.41	0.00	0.0

^a Sequences are shown in Figure 2 ▶. Filled circles denote Ile or Leu and open circles denote Ala in the a and d positions of the cassette shown in Figure 2 ▶.

^b T_m is the thermal denaturation midpoint (°C) calculated as described in Materials and Methods.

^c Urea_1/2 is the chemical denaturation midpoint (M) calculated as described in Materials and Methods.

^d m is the slope term near the transition midpoint from the equation ΔG_u = ΔG_u^H2O − m[denaturant], which is derived from the direct fitting of data (see Materials and Methods).

^e ΔΔG is the free energy difference between two analogs and is calculated using ΔΔG = ([Urea]_1/2(pept.x) − [Urea]_1/2(pept.8)) × (m_{(pept x)} + m_(pept8))/2

^f Average ΔΔG value for analogs with the same number of large hydrophobes in the cassette (Fig. 2 ▶) relative to peptide 8.

The remaining peptides (peptides 5–8) all show similar stability to peptide 4 (Table 2; Fig. 4 ▶, lower panel). This is somewhat surprising in that adding a stabilizing residue shows no gain in stability relative to three alanines in the cassette (peptide 8). Even more surprising is that the addition of two stabilizing hydrophobes to the cassette (peptide 4) show slight destabilization relative to three alanine residues. This may stem from the fact that peptide 8 contains a long string of nine contiguous destabilizing core residues (alanine), which may have slightly different interchain packing of the smaller methyl side chains. Recent crystal structures of the Escherichia coli outer membrane lipoprotein trimerization domain peptide (Lpp56) showed that increasing the number of alanine substitutions in the hydrophobic core positions led to a decrease in the superhelical radius (Liu et al. 2002). Also, a similar decrease in the coiled-coil radius was observed in the high-resolution structure of the N domain of tropomyosin residues 1–81 in regions where a large number of consecutive alanine residues are found in the hydrophobic core (Brown et al. 2001). We infer that the same will occur in the two-stranded coiled-coils described here; that is, the addition of a large hydrophobic residue will disrupt the close packing of the methyl side chains of alanine, an energetic penalty that must be overcome before any additional gain in stability due to increased hydrophobicity is realized.

Chemical stability using urea as the denaturant

Urea was used instead of guanidine hydrochloride because urea measures the contribution of both the hydrophobic core and electrostatics to stability (Monera et al. 1994). The advantage of using chemical denaturation is that the free energy of unfolding is readily calculated using the method of Pace (1986) and Santoro and Bolen (1988). The relative stabilities (Fig. 5 ▶) were the same as that seen for thermal denaturation with peptide 1 as the most stable (Urea_1/2 = 3.3 M), followed by peptides 2 and 3 (Urea_1/2~2.2 M), with the remaining peptides showing similar but decreased stability (Urea_1/2~1.7 M). The free energy change in stability was calculated relative to peptide 8 and tabulated in Table 2.

Figure 5.

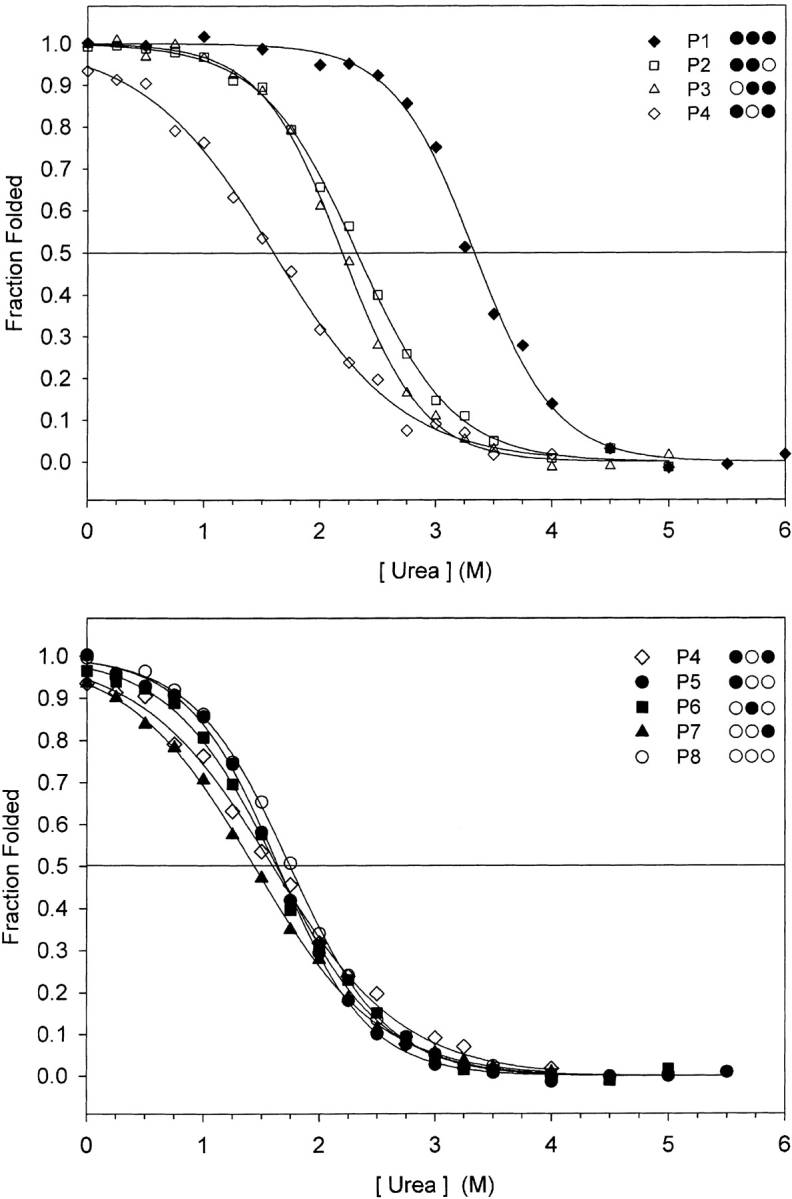
Chemical denaturation profiles of peptides 1–4 (top panel), denoted P1 to P4, and peptides 4–8 (bottom panel), denoted P5 to P8, are shown. Aliquots of peptide and urea were mixed in a series of increasing denaturation concentration and the helical signal at 222 nm of each was measured. Ellipticity data were converted to fraction folded, accounting for the pre- and posttransition baselines, as described in Materials and Methods.

The eight peptides described in this study fall into four groups. Peptide 1 is the most stable with three stabilizing residues in the cassette and three stabilizing clusters overall. Peptides 2 and 3 form the next group with two adjacent stabilizing residues in the cassette. Peptide 8 is the reference or baseline peptide in this series, as it does not contain any stabilizing residues in the cassette. The last group contains peptides 5–7 with one stabilizing residue in the cassette and peptide 4 with two stabilizing residues but interspersed with a destabilizing alanine. The average change in free energy of adding a stabilizing hydrophobe to the cassette is also shown in Table 2. Addition of one stabilizing hydrophobe to the cassette did not result in any gain in stability, but rather a slight loss of stability (0.4 kcal/mole). There was no observed gain in stability until two stabilizing hydrophobes were inserted into the cassette at adjacent positions (0.5 kcal/mole) relative to peptide 8. That is, increase in stability of 0.9 kcal/mole relative for peptides 2 and 3 to peptide 4 (Table 2) was observed. Two large aliphatic hydrophobes that are interspersed by an alanine yielded no gain in stability despite the substantial increase in hydrophobicity of leucine residues compared with Ala. There is a further nonadditive gain in stability when increasing the cluster to three adjacent large aliphatic hydrophobes (1.7 kcal/mole; Table 2, cf. peptide 1 with peptides 2 and 3).

Sedimentation equilibrium

Previous studies with coiled-coil model peptides have shown that higher-order oligomers can exist, even in the oxidized peptides (Harbury et al. 1993; Tripet et al. 2000). As such, we sought to determine that the peptides studied here remain as homo-two-stranded coiled-coils at the concentrations used. Sedimentation equilibrium measurements were performed at three different concentrations and three different rotor speeds each (representative data shown in Fig. 6 ▶). Data were first fit to a single-species model at each concentration (with three rotor speeds) and showed no indication of higher-order species. Therefore, we fit the data for each peptide to a single-species model using a global fit with all nine data sets. The results showed good agreement with the expected mass of the disulfide-bridged homo-two-stranded coiled-coil (Fig. 6 ▶).

Figure 6.

Sedimentation equilibrium data for peptide 1 (left column) and peptide 8 (right column) are shown at a peptide concentration of 20 μM and rotor speed of 30,000 rpm. The global fit (solid line) to experimental data (open circles) is shown in the middle panels, and the residuals between the calculated concentration distribution and experimental data in the top panels. The lower panels show ln Y versus r² of the experimental data (open circles) compared with the theoretical monomer (m), dimer (d), and trimer (t) single-species plots (solid lines), where y is absorbance, which is proportional to concentration.

Role of hydrophobic clustering on protein folding

The clustering effect we observe in this set of peptides can be considered a context-dependent hydrophobicity effect. One striking observation about the stability studies here is that the observed changes in the stability are much lower than that expected from previous model peptides (Wagschal et al. 1999a). This is likely due to the context in which we have designed our cassette. The helical heptad repeat places hydrophobic residues i − 4, i, and i + 3 in close spatial proximity, that is, positions d, a, d on each helix, to create a continuous hydrophobic surface (Fig. 7 ▶). Therefore, this is the local environment that must be considered. Consider peptides 5–7, which have only one isolated large aliphatic hydrophobe. There is a lack of another stabilizing hydrophobic residue to create a continuous large hydrophobic surface area; thus, the effect of increased hydrophobicity is minimal. This Ala→Leu (or Ala→Ile) substitution leads to no gain in stability. Other model coiled-coils with well-packed hydrophobic cores show that the same Ala→Leu substitution leads to a 3.8 kcal/mole gain in stability (Wagschal et al. 1999b; Tripet et al. 2000). Thus, the context dependence must be considered when considering substitutions and their effect on stability. In addition, there is a synergistic effect of rearranging the stabilizing hydrophobes from nonadjacent (peptide 4) to adjacent core positions (peptides 2 and 3). This synergy resulted in a 0.9 kcal/mole (Table 2) increase in stability even though there was no increase in hydrophobicity. All three peptides have two stabilizing hydrophobes in the cassette region. Increasing the size of the continuous hydrophobic patch (cf. peptides 2 and 3 with peptide 1), there is an additional gain of 1.7 kcal/mole. As noted earlier, peptide 4 has two leucine residues in the cassette that are interspersed by an alanine residue in the cassette; thus the two leucine residues are still isolated and not able to form a continuous hydrophobic patch on the surface of the helix. Thus, there is no increase in stability over the cassette with three alanines (peptide 8).

Figure 7.

A schematic space-filling model of the cassette region, denoted X_d, X_a, and X_d, and the surrounding Ala hydrophobic core (Figure 2 ▶) in this model peptide. The three residues that comprise the cassette are shown in dark gray (helical positions d) and black (helical position a). The hydrophobic core residues occupied by alanine residues are shown in light gray. Interchain electrostatic interactions between Lys at positions g and Glu at positions e (i to i′ + 5) are indicated by the black double-headed arrow. Only a portion of the peptide chains are shown (K¹⁵ to E⁴⁵, Figure 2 ▶).

The addition of an isoleucine to peptide 4 would be more similar to other model coiled-coils because there are two neighboring leucine residues already present in peptide 4. This Ala→Ile change (peptide 4→peptide 1) leads to a 2.6 kcal/mole gain in stability. However, this is still less than the 3.8 kcal/mole change in stability previously observed in Wagschal et al. (1999b) and Tripet et al. (2000). This can be explained by the alanine residues on each side of the hydrophobic patch of Leu, Ile, and Leu in positions d, a, and d. The coiled-coil models of Hodges and coworkers (Wagschal et al. 1999a) had at least four large aliphatic hydrophobes in the hydrophobic core on each side of the substitution site. This implies that a much larger hydrophobic patch on each helix must be present to maximize stability. In addition, the peptides described in this work were designed with favorable interchain electrostatic interactions that lie across the hydrophobic core. We speculate that the large number of alanine residues in hydrophobic core positions will lead to a decrease in superhelical radius, which will strengthen the hydrophobic core interactions as well as the i to i′ + 5 salt bridges that lie across the hydrophobic core. Thus, an Ala-to-Leu substitution in this environment would not be as great as it would be in the absence of these salt bridges. The 3.8-kcal/mole decrease in stability on substituting Leu with Ala was in an environment lacking the salt bridges across the hydrophobic interface. When Ala is in the hydrophobic core, the salt bridges could provide a much greater stabilizing effect than the 0.4 kcal/mole per salt bridge measured by Kohn et al. (1998) when the hydrophobic core consisted of a continuous repeat of large aliphatic hydrophobes. Packing interactions in coiled-coils involve not only residues in the a and d positions, but also residues at positions e and g, which can also interact with the hydrophobic core (Lee et al. 2003). For example, their results show that hydrophobic residues (i.e., Leu) in positions e and g can provide an increase in stability of 0.7 kcal/mole and that the i to i′ + 5 (g to e′) salt bridge contribution to stability is dependent on the nature of the hydrophobic core residues that it overlays (Lee et al. 2003).

Coiled-coil prediction programs such as COILS (Lupas et al. 1991), Paircoils (Berger et al. 1995), or Multicoil (Wolf et al. 1997) are useful for identifying coiled-coil domains in protein sequences and are based on the statistical occurrence of amino acid residues in known coiled-coils. This is quite different from the program STABLECOIL (Tripet and Hodges 2001), which identifies coiled-coil domains based on experimentally derived data on the contribution of all residues to stability. As we have shown here, for any given site in a hydrophobic core position of a coiled-coil, one must consider the residues at preceding and following the hydrophobic core position. We have implemented a weighting scheme in the latest version of STABLECOIL (D. Brinkmann, B. Tripet, and R.S. Hodges, in prep.) that will account for the effect of clustering.

In our initial analysis of hydrophobic clusters, we arbitrarily defined a cluster as three consecutive residues in the hydrophobic core positions. In this series of peptides, we found that three consecutive stabilizing large aliphatic residues was indeed the minimum size for a stabilizing hydrophobic cluster as shown by the synergistic increase in stability. Interestingly, our sequence analysis of tropomyosin sequences identifies not only stabilizing clusters, but also destabilizing clusters, and that three residues appears to be a consensus minimum size for a stabilizing or destabilizing cluster.

Materials and methods

Peptide synthesis and purification

Peptides were synthesized manually using standard solid-phase N-α-t-butyloxylcarbonyl (t-Boc) chemistry and 4-methyl-benzhydrylamine resin. The α-amino t-Boc protecting group was removed with 50% (v/v) trifluoroacetic acid (TFA) in dichloromethane (DCM), then neutralized with 20% (v/v) diisopropylethylamine (DIEA) in DCM. Amino acids (fivefold excess over resin substitution) were activated with 2–(1H-benzotriazole-1-yl)-1,1,3,3-tetramethyl-uronium hexafluorophosphate (1 equivalent), N-hydroxybenzotriazole (1 equivalent), and N-methylmorphine (1.1 equivalents) in dimethylformamide. This cycle was repeated for each residue coupled. Coupling completion was monitored by ninhydrin tests. The N terminus was acetylated with acetic anhydride and DIEA (1:1 v/v) in DCM. Peptides were cleaved from the resin with hydrogen fluoride (HF; 10 mL per gram of resin) containing 10% anisole (v/v) and 2% 1,2-ethanedithiol at −4°C for 1 h. Following cleavage and removal of HF, the crude peptide was washed with ethyl ether, then extracted with 50% acetonitrile/water (v/v) and lyophilized.

Crude peptides were purified using reversed-phase chromatography on an Agilent Zorbax 300SB-C8 9.4-mm ID × 250-mm column (5 μm particle size, 300 Å pore size). Separations were performed on a Beckman System Gold HPLC at a flow rate of 3 mL/min with a linear AB gradient rate of 0.1% B per minute, where eluent A was aqueous 0.05% TFA and eluent B was 0.05% TFA in acetonitrile. Fractions were collected at 2-min intervals and analyzed on a 4.6-mm ID × 150-mm Zorbax C8 column at 1 mL/min flow rate and 2.0% B per minute gradient rate. Peptide identity was verified by mass spectrometry (Mariner instrument, Perceptive Applied Biosystems) and amino acid analysis on a Beckman 6300 amino acid analyzer (Beckman-Coulter). Purified peptides were allowed to oxidize in ammonium bicarbonate buffer (pH 8.5), stirring in open vials overnight to form the interchain disulfide bridge.

CD spectroscopy and denaturation measurements

CD spectroscopy was carried out at 20°C on a Jasco J-820 spectropolarimeter with constant N₂ flushing (Jasco). Cylindrical cells (0.2-mm path length) were used for spectra and urea denaturations with an average of eight scans reported. A 1-mm path length rectangular cell was used for thermal denaturation with the Pelltier temperature control accessory. Spectra were subsequently expressed as mean residue molar ellipticity [Θ] (deg*cm²*dmole⁻¹), which was as calculated in the following manner:

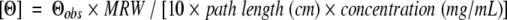where MRW is the mean residue weight (molecular mass of the peptide divided by the number of residues). Peptides were prepared as stock solution in benign buffer (50 mM phosphate at pH 7, 100 mM KCl) at ~3 mg/mL. Exact peptide concentrations were determined by amino acid analysis in triplicate. For spectra scans, peptides were diluted to ~0.5 mg/mL in either benign buffer or TFE (50% v/v) and ellipticity was measured from 190–260 nm. For thermal denaturations, Θ_{222 nm} was monitored as a function of temperature with a scan rate of 30°C/h. The transition midpoint was determined by fitting molar ellipticity as a function of temperature in the following manner as described by Lavigne et al. (1995):

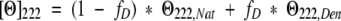where f_D is the fraction of peptide that is unfolded and Θ_222,Nat and Θ_222,Den represent the pre- and posttransition baselines that were treated as linear functions of temperature. The fraction folded was described by the following:

because ΔG = −RT ln K and ΔG is the Gibb-Helmholtz free energy of unfolding:

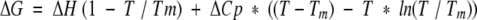The thermal denaturation curves were all fitted in this manner and the Tm are reported in Table 2. As molar ellipticity values are not normalized in this treatment, it is difficult to visually compare different peptides. Therefore, we chose to plot the data in terms of fraction folded versus temperature using the derived parameters for the pre- and posttransition baselines. This allows the reader to visually compare analogs more easily.

For chemical denaturation measurements, peptide stock solutions were mixed with 10 M urea and benign buffer in a dilution series such that the peptide concentration was constant but the denaturant concentration varied from 0 to 6 M. These samples were allowed to equilibrate overnight and Θ_{222 nm} was determined for each. In an analogous manner, chemical denaturation data were fitted the same equations except that, for chemical denaturation, ΔG represents the free energy of unfolding defined as ΔG_obs = ΔG°_(N→D) + m[denaturant], as described by Santoro and Bolen (1988) and Pace (1986). As with the thermal denaturation curves, the data were converted to fraction folded using the derived baseline parameters. Transitions were then fitted to the simple sigmoidal three-parameter fit:

where x is the urea concentration, X_m is the transition midpoint, a is the upper limit (a~1), and b is a scaling constant. The free energy of unfolding was calculated by linear extrapolation to the absence of denaturation (Pace 1986), which is derived from the previous fitting procedure. However, the changes in free energy between peptides were calculated using data near the transition midpoints using the method of Kellis et al. (1989) where

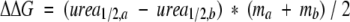in order to reduce errors in extrapolation to the absence of denaturant.

Sedimentation equilibrium

Average molecular weights were determined by sedimentation equilibrium on a Beckman XLA analytical ultracentrifuge (equipped with absorbance optics) according to the manufacturer’s protocols. Peptide solutions were dialyzed against 50 mM sodium phosphate (pH 7), 150 mM NaCl overnight. Each peptide was spun at three different speeds (15,000, 30,000, and 45,000 rpm) at three concentrations (5, 10, and 20 μM) and absorbance was monitored at 230 nm. Each run was allowed to equilibrate for at least 16 h and convergence was verified by identical successive radial scans before increasing rotor speed. Data were fit using SEDNTERP v. 1.06 (Hayes et al. 2003) and WINNONLIN v. 1.06 (Yphantis et al. 1997). Data were fit first using a fixed peptide concentration and three different rotor speeds with a single-species model. As the single-species average molecular weights did not vary by >8% between concentrations, a global fit was then used with nine data sets (three concentrations and three speeds) to obtain the single-species average molecular weight. Data were deemed a good fit when the sum of the residuals was <1.5 × 10⁻². As an additional criterion, a plot of ln(Absorbance) versus r² was used to compare experimental data with theoretical monomer, dimer, and trimer single-species models, where the theoretical concentration distribution is described by:

where c_r is the concentration at a given radius r, c_o is the concentration at the meniscus, M is the molecular weight, v_bar is the partial specific volume, ρ is the solvent density, and ω is the angular velocity. The experimental data clearly fit the single-species monomer distribution of c_r versus r² corresponding to the disulfide-bridge two-stranded coiled-coil.