Correspondence between anomalous m- and Δ C_p-values in protein folding

Abstract

Proteins folding according to a classical two-state system characteristically show V-shaped chevron plots. We have previously interpreted the symmetrically curved chevron plot of the protein U1A as denaturant-dependent movements in the position of the transition state ensemble (TSE). S6, a structural analog of U1A, shows a classical V-shaped chevron plot indicative of straightforward two-state kinetics, but the mutant LA30 has a curved unfolding limb, which is most consistent with TSE mobility. The kinetic m-values (derivatives of the rate constants with respect to denaturant concentration) in themselves depend on denaturant concentration. To obtain complementary information about putative mobile TSEs, we have carried out a thermodynamic analysis of the three proteins, based on data for refolding and unfolding over the range 10°C to 70°C. The data at all temperatures can be fitted to two-state model systems. Importantly, for all three proteins the activation heat capacities are, within error, identical to the heat capacities measured in independent experiments under equilibrium conditions. Although the equilibrium heat capacities are essentially invariant with regard to denaturant concentration, the activation heat capacities, similar to the structurally equivalent kinetic m-values, show marked denaturant dependence. Furthermore, the values of β‡ at different denaturant concentrations measured by m-values and by heat capacity values are very similar. These observations are consistent with significant transition state movements within the framework of two-state folding. The basis for TSE movement appears to be enthalpic rather than entropic, suggesting that the binding energy of denaturant–protein interactions is a major determinant of the response of energy landscape contours to changing environments.

Protein stability and folding kinetics are most frequently measured with the help of chemical denaturants, such as guanidinium chloride (GdmCl), based on a simple linear relationship between the log of equilibrium constants K or rate constants k and the GdmCl concentration (Tanford 1970). In addition to K and k, this approach yields parameters (m-values) for the sensitivity of log K and log k to GdmCl concentration. m-values for a given transition are generally interpreted as a measure of the change in solvent exposure for that transition (Tanford 1970), and this makes them useful estimates of the gross compactness of different states on the folding pathway relative to the two end-stations, the denatured state D and the native state N. For example, for a protein folding without any intermediates, the ratio of the m-value for refolding (m_f) to the m-value for equilibrium denaturation (m_D–N) defines how compact the rate-limiting transition state ensemble (TSE) ‡ is compared to D and N. This ratio, here termed β‡, is a simple measure of the position of the TSE on the reaction coordinate between D (β_D = 0) and N (β_N = 1).

Most two-state proteins have a constant β‡ value (Jackson and Fersht 1991a; Alexander et al. 1992; Milla and Sauer 1994; Kragelund et al. 1995; Schindler and Schmid 1996; Jackson 1998; Perl et al. 1998; Reid et al. 1998), indicating that the structure of the TSE is not sensitive to denaturant concentration. However, we have previously shown that β‡ varies with GdmCl concentration for the protein U1A, which otherwise appears to fold by two-state kinetics (Silow and Oliveberg 1997; Otzen et al. 1999). This proposal was based on pronounced curvature in the refolding and unfolding limbs of U1A’s chevron plot (the log of the observed rate constant k_obs vs. [GdmCl]). Curvature may also be induced by suitable mutations. The protein S6 from the small ribosomal subunit of Thermus thermophilus manifests a straight V-shaped chevron plot, giving a constant β‡. However, the mutant LA30 shows very pronounced unfolding curvature, leading to a gradual increase in the value of β‡ with GdmCl concentration (Otzen et al. 1999). We have interpreted these phenomena in terms of structural changes, or movement, in the TSE. In other words, the TSE is an ensemble of states with structure (in this context, compactness) that varies with solvent conditions; it may also be explained by saying that as the solvent conditions change, so different ensembles of states become the ensemble with the highest free energy on the reaction coordinate. Thus, rising values of β‡, which accompany the increase in [GdmCl], translate to an increasing compactness of the TSE, and structural characteristics of the energy landscape are reflected in the details of the unfolding limb. For example, smooth curvature in the unfolding limb can arise when activation barriers to folding form a shallow top in a rather flat landscape; the landscape surface tilts in response to changes in solvent conditions and thus alters the position of the hilltop (Otzen et al. 1999). Kinks may arise if the landscape is more rugged, so that one peak replaces another as the point of highest energy over a relatively narrow denaturant concentration range.

To analyze the thermodynamic basis for these postulated TSE movements, we have examined the folding kinetics of U1A, wild-type S6, and the S6 mutant Leu → Ala30 (LA30) in the temperature interval 10°C to 70°C. By introducing temperature as a physical variable in addition to denaturant concentration, we can extract values for the activation enthalpy, entropy, and heat capacity of folding and unfolding, which may provide important complementary information. Generally, thermodynamic parameters for the folding and unfolding of polymers in aqueous environments should be approached with caution, because they result from a combination of very large favorable and unfavorable energetic contributions which almost cancel out (Creighton 1993). The reduction in conformational entropy upon folding is balanced by an increase in the entropy of dehydration as bound water molecules are released (the hydrophobic effect). Conversely, the change in enthalpy upon unfolding is composed of contributions from (1) the gain in enthalpy from loss of van der Waals interactions and hydrogen bonds, (2) the loss in enthalpy from interactions between water molecules and surfaces exposed upon unfolding and the removal of steric repulsion in the native state, and (3) the gain in enthalpy due to the disruption of water interactions upon solvating freshly exposed protein surfaces (Johnson and Fersht 1995). However, the link between thermodynamic changes and conformational transitions becomes less unequivocal in the case of the heat capacity change ΔC_p. This parameter predominantly reflects a negative contribution from desolvation of nonpolar groups (Makhatadze and Privalov 1990; Livingstone et al. 1991; Spolar et al. 1992), with the nuances that heat capacity changes for aliphatic and aromatic groups differ to a certain extent (Spolar et al. 1992) and that the desolvation of polar groups makes a small but positive contribution to ΔC_p (Spolar et al. 1992). However, the effect of these groups on the m-value is less clear. The configurational freedom gained upon protein unfolding accounts for <20% of the total heat capacity increase (Privalov and Makhatadze 1990).

Because heat capacity changes and m-values both reflect the burial of nonpolar groups, they should go hand in hand; indeed, for the cold-shock protein CspB, 90% of the total heat capacity change and 96% of the m-value change occur between the unfolded state and the TSE (Schindler and Schmid 1996). CspB has a fixed β‡; consistent with this, its activation heat capacities for folding and unfolding (ΔC_p^f and ΔC_p^u, respectively) are essentially insensitive to denaturant concentration. However, we expect that the activation heat capacity for folding and unfolding of U1A should be sensitive to denaturant concentration and, furthermore, that the ΔC_p^u of LA30 should be more sensitive than that of S6 wild type. Both predictions are borne out by the experimental data.

It should be pointed out that kinetic data by their very nature generally lend themselves to more than one mechanistic interpretation. Protein folding is a complex multivariable reaction and is no exception to this rule, particularly when it comes to the interpretation of thermodynamic parameters. In addition to moving TSEs, we certainly do not exclude the possibility that other scenarios may be at work that also lead to curvature. These scenarios include the existence of discrete unfolding intermediates or several TSEs. However, for reasons detailed in Materials and Methods, we regard them as less probable. Instead, we will take the opportunity to examine in what way the temperature data may shed more light on the thermodynamic properties of the moving TSE.

Results

The thermodynamic data are consistent with two-state folding

Kinetic data are shown in Figure 1 ▶ for the three proteins over the temperature interval 10°C to 70°C, and the data are summarized in Table 1. At all temperatures, the chevron plots for each protein retain the characteristic features previously reported at 25°C (Otzen et al. 1999), namely, symmetrical curvature for U1A, a V-shape for S6, and curvature in the unfolding region for LA30.

Figure 1.

Kinetic data for U1A (A), S6 wild type (B), and LA30 (C) over the temperature range 10°C (•) to 70°C (×) at 10°C intervals (the rate constants increase monotonically from 10°C to 70°C). The lines represent fits based on equations 4 through 6 and parameters in Table 1.

Table 1.

Kinetic and equilibrium parameters for the folding and unfolding of U1A, S6 wild type, and LA30

		U1A		S6 wild type		LA30
Parametera	Units	Refolding (U →TSE)	Unfolding (TSE →N)	Refolding (U → TSE)	Unfolding (TSE → N)	Refolding (U → TSE)	Unfolding (TSE → N)
ΔHTo	kcal mol−1	12.4 ± 0.3	−35.9 ± 0.8	11.7 ± 0.6	−24.1 ± 1.1	13.2 ± 0.8	−14.6 ± 0.9
mh	kcal mol−1 M−1	−0.13 ± 0.12	3.59 ± 0.16	2.83 ± 0.36	1.61 ± 0.20	2.65 ± 0.81	1.58 ± 0.18
m*h	kcal mol−1 M−2	0.137 ± 0.005	−0.10 ± 0.006	b	b	−0.22 ± 0.05	−0.071 ± 0.005
−ToΔSTo	kcal mol−1	−7.34 ± 0.27	21.2 ± 0.8	−7.05 ± 0.64	11.5 ± 1.1	−8.05 ± 0.85	1.88 ± 0.86
Toms	kcal mol−1 M−1	−0.39 ± 0.12	−1.65 ± 0.13	1.13 ± 0.36	0.94 ± 0.20	b	b
ΔCp	cal mol−1 K−1	350 ± 20	760 ± 50	392 ± 40	423 ± 60	441 ± 60	712 ± 60
mc	cal mol−1 K−1 M−1	55 ± 10	−64 ± 10	54 ± 25	−10 ± 10	115 ± 68	−116 ± 13
ΔCpD–N c	cal mol−1 K−1	(1110 ± 54) − (9 ± 14) * [GdmCl]		(815 ± 72) + (44 ± 27) * [GdmCl]		(1153 ± 84) − (1±69) * [GdmCl]
Δ Cpd	cal mol1− K−1	1200 ± 100e		1008 ± 76f, 958 ± 42g		976 ± 56f
tΔGD–Nmin h	°C	14		19		29

^a The parameters are described in Equations 4, 5, and 8. All values at 0 M GdmCl. Except for ΔC_p^D–N and ΔC_p, all values refer to activation parameters rather than equilibrium parameters.

^b Parameter set to zero because its inclusion did not improve the quality of the fit. Typically the associated errors of this parameter were larger than the actual values.

^c The sum ΔC_p^f + ΔC_p^u

^d Heat capacity change for the D → N transition from equilibrium denaturation measurements.

^e Data from Lu and Hall (1997) based on differential scanning calorimetry.

^f From CD thermal scans.

^g From equilibrium denaturation in GdmCl at different temperatures.

^h The temperature where ΔG_D–N (calculated as RT*ln10*log(k_f/k_u)) attains its maximal value.

We have argued that these different plots may all be viewed as different instances of two-state folding in which the TSE of each protein shows different levels of sensitivity to solvent conditions (Otzen et al. 1999). The combined data for each fit were therefore analyzed according to a two-state model (equation 6), combined with the temperature dependence of the activation energy of unfolding (equation 7) and denaturant-dependencies of the three thermodynamic parameters (equation 8). The parameters from our fits are listed in Table 1. The rate constants calculated from these parameters fit well to the actual rate constants at all concentrations (Fig. 1 ▶). Table 1 only lists those parameters necessary to improve the quality of the fit.

Equivalence of equilibrium and kinetic ΔC_p-values

Having obtained values of ΔC_p from kinetic experiments, we now compare them with values obtained from equilibrium denaturation data. In a two-state system, the sum of ΔC_p^f and ΔC_p^u equals the heat capacity difference between the native and denatured state ΔC_p^D–N.

U1A

The ΔC_p^D–N of U1A has been determined by Lu and Hall (1997) to be 1200 ± 100 cal/mol/K using differential scanning calorimetry. Our kinetic data extrapolated to 0 molar denaturant should be directly comparable to this value. ΔC_p^f and ΔC_p^u are 350 ± 20 and 760 ± 50 cal/mol/K, respectively. The sum is 1110 ± 54 cal/mol/K, which agrees well with the DSC-value. Both ΔC_p^f and ΔC_p^u show a significant dependence on the denaturant concentration, but in opposite directions, namely, 55 and −64 cal/mol/K/M, respectively. As a consequence, the sum ΔC_p^f + ΔC_p^u remains essentially invariant over the entire GdmCl-range (Table 1). An analogous behavior is seen for the kinetic m-values m_f and m_u of U1A. At 25°C, they depend on [GdmCl] as follows (Silow and Oliveberg 1997):

(1a)

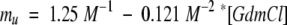(1b)

Thus, the equilibrium m-value m_D–N = m_f − m_u is essentially constant at −1.67 M⁻¹−0.019 M⁻²*[GdmCl].

S6

DSC studies at low pH in the absence of denaturant did not yield useful data for S6 due to poor data quality (data not shown). Instead, we have determined ΔC_p^D–N by two independent approaches. First, we have performed thermal scanning experiments for S6 wild type and LA30 by using circular dichroism (CD) (Fig. 2A ▶). ΔC_p^D–N can be obtained as the slope of the plot of the enthapy of unfolding ΔH_Tm versus the denaturation temperature T_m. Different values of ΔH_Tm and T_m were obtained by carrying out the thermal scans at different GdmCl concentrations. If ΔC_p^D–N depends on the GdmCl concentration, there will be a systematic deviation between the value obtained by this approach as opposed to measuring it in the absence of denaturant, for example, at low pH values. This is elaborated in the Discussion. For both proteins, there is a reasonable linear correlation between the two parameters (Fig. 2B ▶), which leads to a ΔC_p^D–N value of 1008 ± 79 and 976 ± 56 cal/mol/K for wild type and LA30, respectively.

Figure 2.

(A) Thermal scans for unfolding of S6 at different GdmCl concentrations as indicated. Data are fitted to equation 9 to obtain the values of T_m and ΔH_Tm at each GdmCl concentration. (B) ΔH_Tm plotted versus T_m from CD thermal scans for S6 wild type (•) and LA30 (○). The lines represent the best linear fits. The slopes, which represent the equilibrium heat capacity values, are 1050 ± 50 cal/mol/K for S6 wild type and 976 ± 56 cal/mol/K for LA30. (C) The dependence of T_m for S6 wild type (•) and LA30 (○) on GdmCl concentration. The lines represent the best linear fits. The slopes are 20.6 ± 0.5 and 23.5 ± 2.1°C/M and the intercepts 110.1 ± 1.1 and 87.7 ± 2.5°C for S6 wild type and LA30, respectively. (D) The dependence of ΔH_Tm for S6 wild type (•) and LA30 (○) on GdmCl concentration. The lines represent the best linear fits. The slopes are 20.8 ± 1.8 kcal/mol/M and 23.3 ± 2.4 kcal/mol/M and the intercepts 89.8 ± 3.4 and 69.6 ± 2.9 kcal/mol for S6 wild type and LA30, respectively.

Second, we carried out equilibrium isothermal denaturation in GdmCl for S6 wild type between 10°C and 60°C (Fig. 3A ▶). At each temperature, the free energy of unfolding ΔG_D–N is extrapolated back to 0 molar denaturant by using equation 10. When ΔG_D–N is plotted versus temperature and the data fitted to equation 11 (Fig. 3B ▶), a ΔC_p^D–N value of 930 ± 45 cal/mol/K is obtained. The T_m value in 0M GdmCl required for this fit (383.13 ± 1.07 K) is estimated as an extrapolation from the observed linear relationship between T_m and the GdmCl concentration (Fig. 2C ▶). Note that although the error on ΔC_p^D–N is small, the ΔC_p^D–N value is very sensitive to the value of T_m, and altering T_m by a few degrees leads to significant changes in ΔC_p^D–N. This makes the heat capacity determined by this approach less reliable. However, the agreement with the ΔC_p^D–N value obtained from CD scans is reassuring.

Figure 3.

(A) Equilibrium denaturation of S6 wild type in GdmCl at 10°C (•), 20°C (○), 30°C (▪), 40°C (□), 50°C (+), and 60°C (×). Fluorescence emission intensities are normalized to a maximum value of 100. (B) Stability of S6 wild type between 10°C and 60°C measured by isothermal chemical denaturation. The stability at each temperature is calculated from equation 10. The data are then fitted to equation 11 to yield a ΔC_p value of 930 ± 45 cal/mol/K and a ΔH_Tm value of 76.7 ± 1 kcal/mol.

How do these data compare with the kinetic values? For both S6 wild type and LA30, the individual kinetic heat capacities are sensitive to denaturant concentration, but when ΔC_p^f and ΔC_p^u are summed to give ΔC_p^D–N in 0 molar denaturant (815 ± 72 and 1153 ± 84 ca/mol/K for wild type and LA30, respectively), the dependence completely cancels out for LA30 and is reduced for wild type (Table 1). The correspondence with the values obtained from thermal scans is reasonable. If we extrapolate ΔC_p^f + ΔC_p^u to the midpoint of the denaturation of S6 wild types (3.3M GdmCl), the agreement becomes even better, namely, 960 ± 70 cal/mol/K. Overall, the accuracy of our data is comparable to that of calorimetric measurements (Pace and Laurents 1989; Lu and Hall 1997), although the errors are certainly not <10%.

Temperature optima of the three proteins and cold denaturation

Based on the free energy of unfolding in a two-state system (ΔG_D–N = RT*ln10*log(k_f/k_u)) and the temperature dependence of the rate constants (equation 7), we can calculate the free energy of unfolding as a function of temperature (Fig. 4 ▶) and estimate the temperature at which each protein is most stable (Table 1). It is not surprising that U1A has a somewhat lower TΔG_D–N ^max than does S6 (Table 1) because U1A is from a mesophilic organism and S6 from a thermophile. By contrast, it may seem odd that LA30 has a higher TΔG_D–N ^max than does S6 wild type. However, the changes in the thermodynamic parameters compared with S6 wild type simply shift the position of the minimum. Although LA30 unfolds at significantly lower denaturant concentrations than does S6 wild type, the difference in stability between S6 wild type and LA30 is close to 0 at room temperature. This is because of the curvature in the unfolding limb of LA30, which is absent in S6 wild type. The curvature means that the unfolding rates of the two proteins are very similar when extrapolated to 0 molar denaturant (Otzen et al. 1999).

Figure 4.

Variation in the free energy of unfolding in water ΔG_D–N with temperature for U1A (•), S6 wild type (○), and LA30 (▪). This is calculated by using the relationship ΔG_D–N = RT*ln10*log(k_f/k_u), where the temperature dependence of the rate constants may be calculated from equation 7.

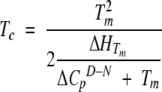
Because of the temperature dependence of the enthalpy of unfolding, lowering the temperature will eventually reduce the enthalpy sufficiently to lead to cold denaturation. Although the phenomenon is well documented (Privalov 1990), the midpoint of cold denaturation T_c is generally so low as not to be experimentally accessible. T_c can be calculated as (Privalov 1990):

(2)

Because we already know the GdmCl-dependence of T_m (Fig. 2C ▶), ΔH_Tm (Fig. 2D ▶) and ΔC_p^D–N (Table 1), we can calculate T_c as a function of denaturant concentration. For S6 wild type, T_c only rises to 2.5°C around the midpoint of denaturation, whereas the corresponding value for LA30 is 7.7°C. In practice, this means that cold denaturation is not experimentally accessible for these two proteins.

The nature and temperature-dependence of the activation barrier

Although the enthalpic and entropic parameters obtained in this study do not lend themselves so easily to a structural interpretation as the heat capacity, they merit some comments. At 25°C, all three proteins manifest a massive enthalpic barrier to both folding and unfolding. The barrier is largest for unfolding, because this process primarily represents the breaking of non-covalent bonds stabilizing the native state. This lopsidedness is also seen for other two-state proteins such as CI2 (Jackson and Fersht 1991b; Oliveberg et al. 1995) and CspB (Schindler and Schmid 1996). At all temperatures, there is very clear “entropy-enthalpy compensation” with regard to the effect of the mutation LA30, resulting in a very small net change in free energy (Table 2). However, at 25°C, LA30 shows a significant reduction in the equilibrium enthalpy of unfolding (calculated as the difference between the activation entalpy of unfolding and of refolding; 1.4 ± 1.2 kcal/mol) compared to S6 wild type (12.4 ± 1.3 kcal/mol). This loss of 11 kcal/mol most probably reflects the loss of stabilizing interactions due to the mutation. At 25°C, the average change in activation enthalpy caused by the removal of a core methylene group in the protein CD2.d1 is 3.7 ± 1.8 kcal/mol (Lorch et al. 2000). For a Leu → Ala mutation, this translates into 11.1 kcal/mol, very close to the above data. Most of the enthalpy reduction translates into a decrease in the activation enthalpy of unfolding, showing that the enthalpically favorable side-chain interactions involving Leu30 in the native state are largely broken in the TSE. An extensive φ-value analysis (Otzen and Oliveberg 2002) of S6 shows that the TSE has a very diffuse folding nucleus, centered around four residues, including Leu 30 (Otzen and Oliveberg 2002). Because of the diffuse nature of the nucleus, the φ-values of these four residues are rather low. φ-Values are a reflection of the environment of the side chain in the TSE, with high φ-values indicating a native-like structure (Fersht et al. 1992). This is consistent with our thermodynamic data, which suggest that most stabilizing side-chain interactions are only formed very late in the folding process after the rate-limiting step.

Table 2.

Enthalpy–entropy compensations at different temperatures in 0 M GdmCl

	ΔH (kcal mol−1)a			−TΔS (kcal mol−1)b			Changes S6wt → LA30
Temperature	U1A	S6wt	LA30	U1A	S6wt	LA30	Δ ΔH	−ΔTΔS	Δ ΔG
Refolding parameters (U → TSE)
283	17.65	17.58	19.82	−12.09	−12.42	−14.09	−2.24	1.67	−0.57
313	7.15	5.82	6.59	−2.33	−1.38	−1.68	−0.77	0.30	−0.47
343	−3.35	−5.94	−6.65	8.44	10.79	12.01	0.70	−1.21	−0.51
Unfolding parameters (TSE → N)
283	−24.50	−17.76	−3.92	9.02	4.74	−8.62	−13.84	13.36	−0.48
313	−47.30	−30.45	−25.28	33.95	18.58	12.92	−5.17	5.66	0.50
343	−70.10	−43.14	−46.64	61.06	33.64	36.51	3.51	−2.87	0.64

^a Calculated according to the equation ΔH_T = ΔH_Tm + ΔC_p (T_o − T). Values for ΔH_Tm, ΔS_Tm, and ΔC_p in Table 1.

^b Calculated according to the equation −TΔS_Tm = −TΔS_Tm – ΔC_pTln10*log(T/T_o).

In refolding, the height of the enthalpic barrier is probably composed of the breaking of solvent–protein bonds combined with unsatisfied solvent–solvent bonding potentials. In contrast, entropy favors both unfolding and refolding. The favorable entropy for refolding is probably due to the hydrophobic effect, in which the desolvation of nonpolar groups (leading to increased freedom of freed water molecules) overrides the loss of conformational entropy accompanying folding, whereas the favorable entropy for unfolding probably reflects the increase in conformational entropy.

Increasing the temperature does not alter the roles allocated to enthalpy and entropy in the unfolding activation barrier. The barrier to unfolding becomes increasingly enthalpic, whereas the entropic component favors the unfolding process. The temperature-associated increase in the magnitude of the enthalpic and entropic values is largest for LA30, because of its large ΔC_p^u. However, for refolding, the entropy–enthalpy compensation changes between 10°C and 70°C (Table 2), as seen for CspB (Schindler and Schmid 1996). At high temperatures, the activation barrier for refolding becomes entropic, probably because the entropy of desolvation becomes less favorable: the enthalpy and entropy of desolvation of hydrophobic residues are very large at low temperatures but decrease strongly with increasing temperature (Murphy et al. 1990).

Discussion

Denaturant-dependence of ΔC_p

In this study, we attempt to shed further light on the apparent mobility of the TSE with denaturant concentration seen for U1A and the S6 mutant LA30. The concept of the moving TSE was prompted by the observation of curved chevron plots. When interpreted within a two-state system, such curvature directly suggested that the m-values, and hence the reaction coordinate of the TSE, changed with denaturant concentration (Silow and Oliveberg 1997; Otzen et al. 1999). The virtue of a thermodynamic analysis is that it provides us with a parameter with essentially the same structural information as the m-values, namely, the heat capacity. Are our thermodynamic data compatible with this proposal?

Variations in ΔC_p^f and ΔC_p^u of U1A show a remarkable correlation with the variation in the m-values (Fig. 5A ▶). For S6 wild type, ΔC_p^u is essentially invariant with denaturant concentration, whereas ΔC_p^f changes to a small extent. Encouragingly, ΔC_p^u of LA30 has become sensitive to unfolding, and the sensitivity of ΔC_p^f has increased (Table 1). This generally correlates well with the mobilization of the TSE deduced from the chevron plot at 25°C (Otzen et al. 1999).

Figure 5.

(A) Variation with [GdmCl] of U1A’s activation heat capacities of refolding (ΔC_p^f) (□) and unfolding (ΔC_p^u) (▪), as well as the variations in m_f (○) and m_u (•). m-values measured at 25°C. (B) Variation in m-values for refolding and unfolding (equations 3–5) with temperature. U1A at 4 M GdmCl (•,○) and S6 wild type (▪,□) and LA30 at 2 M GdmCl (♦,⋄). (C) Change in the position of the TSE (β‡) with temperature for U1A at 4 M GdmCl (•) and S6 wild type (○) and LA30 at 2 M GdmCl (▪). β‡ is calculated as -m_f/(m_u − m_f). Essentially the same movement was seen at the midpoint of denaturation. (D) Variation with [GdmCl] of the three proteins’ β‡ measured by m-values respective ΔC_p‡. U1A (•,○), S6 wild type (▪,□) and LA30 (♦,⋄).

It is interesting that the ΔC_p^D–N values for all three proteins are essentially denaturant independent. Generally, ΔH_D–N decreases with urea, whereas ΔC_p increases (Johnson and Fersht 1995). This is because denaturant–protein interactions are exothermic, in contrast to the intrinsically endothermic enthalpy of unfolding. Thus, unfolding in urea is a composite of two opposite enthalpic effects, and at high urea concentrations, the enthalpy of unfolding at a given T_m is significantly lower in urea than in the absence of urea (Johnson and Fersht 1995). This leads to a larger variation of ΔH_D–N with T_m when urea rather than pH is used as a perturbant, and as a result, the apparent ΔC_p can be significantly overestimated. For barnase, the intrinsic ΔC_p is 1.7 kcal/mol/K, whereas it is 2.7 kcal/mol/K when measured by using urea (Johnson and Fersht 1995). Because the effects of denaturant and temperature on ΔH_D–N are linear and thus additive, ΔC_p increases linearly with denaturant concentration, as demonstrated directly for several proteins (Pfeil and Privalov 1976; Griko and Privalov 1992; Makhatadze and Privalov 1992; Johnson and Fersht 1995). Some proteins, however, appear to show low denaturant sensitivity with regards to the heat capacity. For example, the ΔC_p^D–N of the two-state protein CspB actually decreases slightly with [urea] (Schindler and Schmid 1996), and the ΔC_p^D–N value obtained by thermal scanning of thioredoxin in different urea concentrations was in good agreement with isothermal titration data (Santoro and Bolen 1992). The good correspondence between the ΔC_p values for S6 wild type and LA30 obtained by different methods, including thermal scans at different denaturant concentrations, suggests that the denaturant insensitivity is a genuine phenomenon for some proteins. Although this invariance may be difficult to explain, it conveniently simplifies the situation for a structural interpretation of the kinetic ΔC_p values.

Movement of the TSE: An enthalpic rather than entropic phenomenon

The variation in m_f and m_u with temperature for all three proteins is shown in Figure 5B ▶. With these values, we can calculate the position of the TSE on the reaction coordinate by using the relationship β‡ = −m_f/(m_u − m_f) (Fig. 5C ▶). The increase in β‡ with temperature means that as the TSE becomes less stable at higher temperatures, it moves closer to the native state. This is entirely in accord with the Hammond postulate (Hammond 1955). A similar shift in β‡ with temperature has been seen for CI2, barnase, and lysozyme (Matouschek and Fersht 1993; Matouschek et al. 1995). β‡ can also be calculated from the heat capacities, viz. β‡ = ΔC_p^f/(ΔC_p^f + ΔC_p^u). Importantly, the variation in β‡ deduced from heat capacities and m-values is strikingly similar for U1A and also good for S6 wild type and LA30 (Fig. 5D ▶). This provides additional support for the moving TSE model.

The curvature underpinning TSE movement appears to be linked entirely to the activation enthalpy (Table 1), which for U1A and LA30 shows significant nonzero values of m^*h (equation 8) for both refolding and unfolding. There is no contribution from the activation entropy, because inclusion of an m^*_s parameter does not lead to an increase in the quality of the fits and is associated with large errors. We have previously discussed the nature of the moving TSE barrier and the way it shifts in response to changes in the denaturant concentration, but we have not been able to pin it down to any specific thermodynamic phenomenon. In the light of the data presented in this article, its enthalpic origin leads to a straightforward and reasonable conclusion: The plasticity of the energy landscape (that is, its response to denaturant concentration) is primarily governed by the strength of the enthalpic, namely, direct binding, interactions between denaturant molecules and the protein, rather than by any entropic parameters. Thus, the entropic effect of the changes in compaction of the TSE at different denaturant concentrations, and the liberation or immobilization of denaturant molecules with regard to the protein, is overruled by the enthalpic effect.

In summary, we have presented thermodynamic evidence to support our model for moving TSEs. This approach illustrates how complex thermodynamics can be derived relatively simply from kinetics by using linear relationships between energies and denaturant concentrations.

Materials and methods

Stopped-flow kinetics

U1A, S6 wild type, and LA30 were expressed and purified as described (Otzen et al. 1999). All kinetic data were performed in 50 mM MES (pH 6.3) on an Applied Photophysics SX-18.MV stopped-flow reaction analyzer over the temperature range 10°C to 70°C at 5°C (U1A, S6 wild type) or 10°C (LA30) intervals at protein concentrations of ~1 μM. Refolding and unfolding rate constants were measured between 0 and 7 M GdmCl and analyzed according to the following equations as described (Otzen et al. 1999):

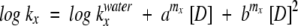(3)

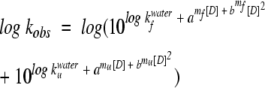(4)

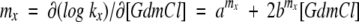(5)

where x is refolding or unfolding, D is denaturant, a^mx and b^mx are constants (for which b^mf_{S6 wild type} = b^{m u}_{S6 wild type} = b^mf _LA30 = 0). Equation 3 describes the relationship between log k and denaturant concentration (which is curved for b^mx = 0), whereas equation 4 derives from the two-state relationship (equation 6).

Equilibrium denaturation experiments

CD thermal scans were monitored for wild-type S6 and LA30 at 225 nm in a 1-mm cell on a Jasco 720 CD spectrometer equipped with a Peltier element over the temperature range 20°C to 100°C at varying [GdmCl] (1 to 3 M) in 50 mM MES (pH 6.3). Protein concentrations were 30 μM. Equilibrium denaturation data between 0 and 6 M GdmCl at a given temperature were performed as described (Otzen et al. 1999). We were unable to obtain reliable data from CD thermal scans of U1A due to extensive aggregation at elevated temperatures (data not shown).

Thermodynamic analysis in a two-state system

For each protein, a global analysis fit was performed with GraFit (Erithacus Software), in which the following two equations were combined:

(6)

where k_u and k_f are the rates of unfolding and refolding, respectively.

(2) Temperature dependence of the rate constants:

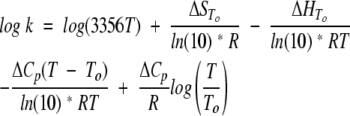(7)

where T_o = 298K. The term for vibrational frequency (κkBT/hÅ, ~1013 s⁻¹), which is conventionally used in the analysis of simple chemical reactions, has been replaced with the factor 3356T (which is 106 s⁻¹ at 298K). This figure constant represents the fastest step in protein folding, namely, closing of a loop (Hagen et al. 1996, 1997). The absolute value of this factor only affects the entropy of activation. The thermodynamic parameters had the following denaturant dependencies:

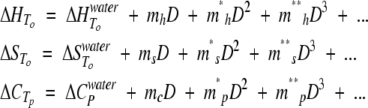(8)

ΔH_To and ΔS_To refer to the activation enthalpy and entropy of either folding or unfolding and ΔC_p to the activation heat capacity of folding or unfolding.

The m-values are constants. In practice, we find that all m-values linked to D² and higher concentrations can be omitted because they do not improve the quality of the fit, except for m_h^* (as judged by the value of the χ² factor and statistical errors of deviation). Although there is some evidence that activation heat capacity is temperature dependent (Oliveberg et al. 1995), we will for simplicity assume that ΔC_p is temperature independent in the range 10°C to 70°C. CD thermal scans were fitted to the following equation (Oliveberg et al. 1994):

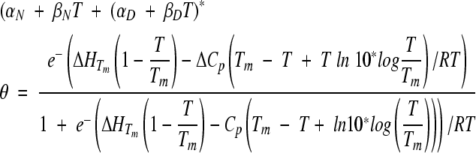(9)

where θ is the raw CD signal in millidegrees, α_N and α_D are the θ-values for the folded and denatured states at 298K, β_N and β_D are the linear slopes of α_N and α_D versus T, ΔH_Tm is the enthalpy of unfolding at the midpoint of denaturation T_m, and ΔC_p is the heat capacity difference between the native and denatured state. However, the ΔC_p value derived from a single thermal scan is highly inaccurate. A much more reliable value is obtained as the slope of the plot of ΔH_Tm versus T_m, in which T_m is varied by altering the denaturant concentration (see Results).

ΔC_p was also calculated from equilibrium denaturation experiments in GdmCl at 10°C to 60°C as follows. At each temperature, the free energy of unfolding in water (ΔG_D–Nwater) was calculated according to the following equation (Pace 1986):

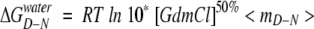(10)

where [GdmCl]50% is the midpoint of denaturation and 〈m_D–N〉, the average dependence of the logarithm of the equilibrium constant for unfolding (K_D–N) on [GdmCl] based on a large number of mutants, has a value of 1.75 ± 0.044 M⁻¹ (Otzen et al. 1999). We used an average m-value, because individual m-values are typically measured with errors of at least 0.20 kcal/mol/M, and there was no systematic variation of m_D–N with temperature (data not shown). The data were then fitted to the equation:

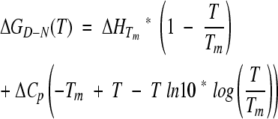(11)

where T_m is the midpoint denaturation temperature of S6 in 0 molar denaturant (383.13 ± 1.07 K). This value is extrapolated from a plot of T_m versus [GdmCl], based on CD-monitored thermal scans (see Results).

Analysis using other kinetic models

Different kinetic models can often account for the same data. The curvature in the unfolding limb of LA30 could in principle also be explained by the transient accumulation of an unfolding intermediate at high denaturant concentrations, according to the following scheme:

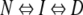(scheme 1)

We have previously argued against this scheme. First, there is no spectroscopic evidence (e.g., burst-phase effects) for such an intermediate. Second, the high m_u-value of LA30 (significantly larger than that of wild-type S6) is difficult to explain from scheme 1 (Otzen et al. 1999), which is highly unlikely, because side-chain interactions are most structured, and thus stabilizing, in N, unless they were all engaged in nonnative interactions in I. Third, kinetic data from a series of S6 mutants fitted to scheme 1 led to the paradoxical conclusion that the mutated side chains generally stabilized I more than N (Otzen et al. 1999). The thermodynamic data do not support Scheme 1 either. Although the individual chevron plots fitted well to scheme 1, there was no consistent pattern in the temperature dependence of the parameters derived from the scheme (data not shown).

Unfolding limb curvature could, however, arise from a discrete jump between two peaks in the TSE (Otzen et al. 1999).

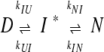(scheme 2)

Although I^* never accumulates, it will give rise to two TSEs during unfolding, one between N and I* (TSE₁), the other between I* and D (TSE₂). This model has recently been extended to explicitly include parameters defining the stability of the intermediate that by definition resides between the two peaks (Bachmann and Kiefhaber 2001). At low denaturant concentrations, TSE₁ will be ratelimiting, whereas TSE₂ becomes ratelimiting at high denaturant concentrations (Bachmann and Kiefhaber 2001). This has been proposed to account for the folding behavior of tendamistat (Bachmann and Kiefhaber 2001) and S6 (Sánchez and Kiefhaber 2003). When we analyzed our LA30 data according to this scheme, however, we were unable to determine the parameters relating to the conversion of I^*, unlike the case for tendamistat. We were able to vary m_IU between around −0.5 and 2.0 M⁻¹ without any effect on the fit’s appearance at different temperatures, provided the difference m_IU − m_IN remained constant. At all temperatures, the only restriction on k_IU and k_IN was that k_IU/k_IN had to be ~5.0 and k_IU at least 10⁵ s⁻¹. The model in scheme 2 implies that different degrees of curvature in different mutants can be rationalized by the effects of the mutation on the relative stability of the two TSEs, whereas the m-values remain constant. However, a global fit of scheme 2 to a large number of S6 mutants failed to converge to a common set of m-values (M. Lindberg, D.E. Otzen, and M. Oliveberg, unpubl.). Therefore, we decided not to pursue scheme 2 any further.

Abbreviations

• ΔC_p^D–N, heat capacity difference between the native and denatured state

• ΔC_p^f, activation heat capacity of folding

• ΔC_p^u, activation heat capacity of unfolding

• TSE, transition state ensemble

Article and publication are at http://www.proteinscience.org/cgi/doi/10.1110/ps.04991004.