Probabilistic cross-link analysis and experiment planning for high-throughput elucidation of protein structure

Abstract

Emerging high-throughput techniques for the characterization of protein and protein-complex structures yield noisy data with sparse information content, placing a significant burden on computation to properly interpret the experimental data. One such technique uses cross-linking (chemical or by cysteine oxidation) to confirm or select among proposed structural models (e.g., from fold recognition, ab initio prediction, or docking) by testing the consistency between cross-linking data and model geometry. This paper develops a probabilistic framework for analyzing the information content in cross-linking experiments, accounting for anticipated experimental error. This framework supports a mechanism for planning experiments to optimize the information gained. We evaluate potential experiment plans using explicit trade-offs among key properties of practical importance: discriminability, coverage, balance, ambiguity, and cost. We devise a greedy algorithm that considers those properties and, from a large number of combinatorial possibilities, rapidly selects sets of experiments expected to discriminate pairs of models efficiently. In an application to residue-specific chemical cross-linking, we demonstrate the ability of our approach to plan experiments effectively involving combinations of cross-linkers and introduced mutations. We also describe an experiment plan for the bacteriophage λ Tfa chaperone protein in which we plan dicysteine mutants for discriminating threading models by disulfide formation. Preliminary results from a subset of the planned experiments are consistent and demonstrate the practicality of planning. Our methods provide the experimenter with a valuable tool (available from the authors) for understanding and optimizing cross-linking experiments.

A growing number of groups have demonstrated the utility of cross-linking for identifying geometric features of protein and complex structure. In contrast to other biophysical techniques, such as FRET (Dong et al. 2000) and EPR spin labeling (Voss et al. 1995; Gaponenko et al. 2000), which yield a number of approximate distances, cross-linking generally provides only the information that some pairs of residues are closer than a maximal cross-linking distance at some point during the reaction. That this information can be sufficient for discriminating among predicted structural models has been demonstrated (Cohen and Sternberg 1980; Swaney 1986; Haniu et al. 1993; Scaloni et al. 1998; Kwaw et al. 2000; Young et al. 2000; Chen et al. 2001; Schilling et al. 2003; Trester-Zedlitz et al. 2003). As illustrated in Figure 1 ▶, initial computational analyses provide possible models of a protein’s structure, for example, by fold recognition (Godzik 2003; Kurowski and Bujnicki 2003) or ab initio (Simons et al. 1997; Kihara et al. 2001), or a complex’s interaction, for example, by docking (Smith and Sternberg 2002). Specific sites in the protein(s) are cross-linked, either by using residue-specific cross-linker molecules, such as the lysine-specific bis-sulfo-succinimidyl suberate (BS³) (Swaney 1986; Haniu at al. 1993; Kwaw et al. 2000; Young et al. 2000; Chen et al. 2001; Schilling et al. 2003; Trester-Zedlitz et al. 2003), or by disulfide bonding of cysteines (Careaga and Falke 1992; Hughes et al. 1993; Kwaw et al. 2000). Cross-links are then detected by protein chemical means (Haniu et al. 1993; Tellinghuisen and Kuhn 2000) and/or mass spectrometry (Young et al. 2000; Kruppa et al. 2003; Schilling et al. 2003; Trester-Zedlitz et al. 2003), or by alteration in electrophoretic mobility (Careaga and Falke 1992; Kwaw et al. 2000).

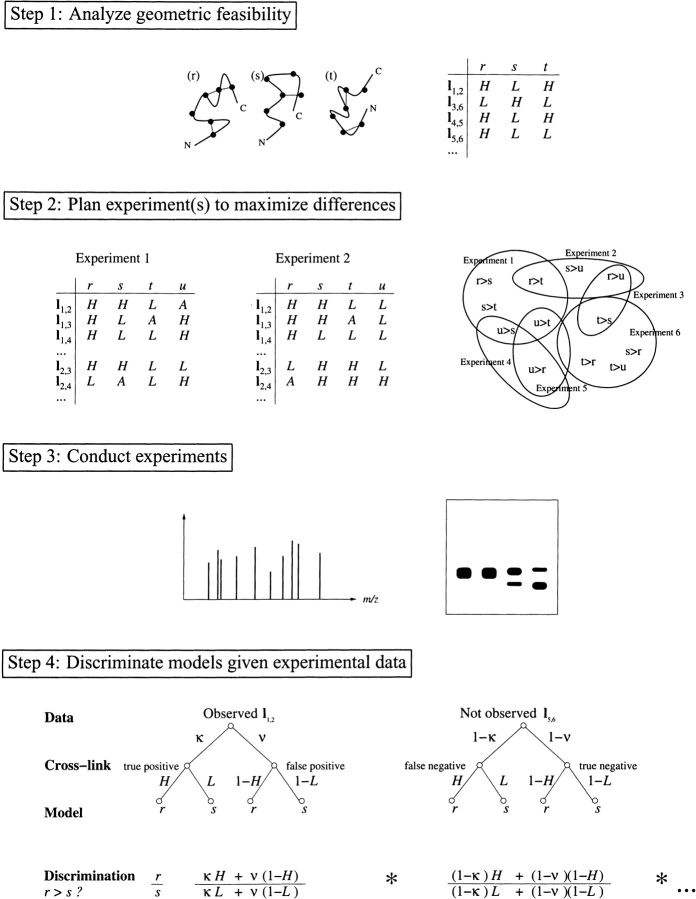
Figure 1.

Model discrimination by cross-linking. (1) Different predicted models of a protein have different patterns of feasible cross-links (dotted lines). Cross-link maps capture the feasibilities (H, L, or A) in terms of conditional relationships for cross-links (rows) given models (columns). (2) Different experimental choices (cross-linkers, mutations) yield different cross-link maps. An experiment could enable selection of one model, if correct, over another (e.g., r > s) if the first model has enough potential positive support (H entries in the cross-link map) where the other doesn’t (L entries). Some experiments provide only ambiguous information for a particular model (A entries). An experiment plan evaluates the relative potential for positive support to select a set of experiments (ovals) to cover the various possible pairwise discriminations. (3) Experimental data, for example, from mass spectrometry or gel electrophoresis, provide support for particular cross-links. (4) Experimental identification of cross-link l_1,2 provides evidence for and against models r and s, based on consistency with cross-link maps and modulated by the capture and noise rates of the experimental method (here constant values κ and ν, for capture and noise, respectively). The discrimination ratio combines terms for both observed and unobserved cross-links.

In these experiments, the cross-linking reaction is determined by the geometric feasibility between pairs of sites and the reactivity and accessibility of individual sites. In interpreting cross-linking experiments, models have so far been evaluated solely on the geometric feasibility of observed cross-links (Haniu et al. 1993; Bass and Falke 1998; Young et al. 2000). In the simplest case, straight-line distance between cross-link sites (Young et al. 2000) has been used. We have proposed alternative methods computing lower and upper bounds on the lengths of paths exterior to a protein and thus accessible to a cross-linker without steric clashes (Potluri et al. 2004). Either geometric method could be combined with molecular dynamics to account for flexibility, although this has not yet been fully implemented (A. Khan, S. Potluri, A.M. Friedman, and C. Bailey-Kellogg, unpubl.). See “Residue-specific cross-linking” below for comments about the effects of accessibility and reactivity.

Several independent experiments have demonstrated successful application of the method, providing models that correlate with prior or subsequent crystal or NMR structures. Using Edman sequencing and mass spectroscopy of the cross-links, Haniu et al. (1993) developed a model of human erythropoietin via lysine-specific cross-linking, while Young et al. (2000^; Kruppa et al. 2003) pioneered the use of high-resolution mass spectroscopy alone to correctly discriminate threading models correctly. Cross-linking has also been used to determine quaternary arrangements of proteins (Hughes et al. 1993; Scaloni et al. 1998; Tellinghuisen and Kuhn 2000; Back et al. 2002; Trester-Zedlitz et al. 2003). These methods are particularly valuable for proteins, such as membrane proteins (Bass and Falke 1998; Kwaw et al. 2000), that are inherently resistant to traditional structure determination methods. Large sets of cross-links have also been treated as distance restraints in an alternative distance geometry structure determination protocol to determine the arrangement of transmembrane helices in lac permease (Sorgen et al. 2002), a case in which no models were available beforehand.

Experimentation with several proteins has thus demonstrated the effectiveness of cross-linking, whereas associated computational work has proposed techniques for both data interpretation (Cohen and Sternberg 1980; Bailey-Kellogg et al. 2001; Chen et al. 2001; Albrecht et al. 2002; Schilling et al. 2003) and analysis of model geometry (Young et al. 2000; Potluri et al. 2004). However, these efforts have not addressed the essential question of the information content available from a cross-linking experiment, a question required to determine and optimize the utility of conducting any particular experiment. Any realistic analysis must also include consideration of multiple sources of experimental error. Our contribution here addresses these requirements with a probabilistic analysis mechanism that explicitly accounts for the expected experimental limitations. We also develop associated algorithms for planning optimal experiments, subject to trade-offs in experimental design. Our mechanism enables the selection of the most suitable set of probes (e.g., different cross-linkers, possible mutations) to maximize experimental discrimination.

Results and Discussion

Our probabilistic cross-link analysis and experiment planning method are summarized in Figure 1 ▶ and detailed in Materials and Methods. First, predicted models of a protein are developed by fold recognition or ab initio techniques. Because a cross-linker can span only some maximum distance between a pair of residues, the feasibility of the possible cross-links varies across models. We perform this geometric feasibility analysis and collect the information into “cross-link maps.” Each cross-link map indicates the conditional probabilities for cross-links for each model, under the particular experimental conditions. The example simply indicates high (H) or low (L) probability for some potential cross-links. The potential for cross-linking for some pairs will be hard to evaluate, especially when significant dynamics are possible. These cross-links can be put into a third, ambiguous (A) class.

Once experimental data are collected, characterization of the set of observed (and potentially the unobserved) cross-links provides evidence regarding the consistency of the models with the data. An observed high-feasibility cross-link supports a model. A low-feasibility cross-link that is not observed can also support a model, once the likelihood of cross-link detection is explicitly considered. Conversely, unobserved high-feasibility and observed low-feasibility cross-links provide evidence against a model. To account for limitations in the experimental detection of cross-links and potential experimental errors, we include two parameters, capture rate κ, indicating the rate of detection of feasible cross-links (i.e., 1 - κ equals the rate of false negatives), and noise rate ν, the detection rate of spurious infeasible ones (i.e., false positives). Support for models provides probabilities (equation 1), which are used in a ratio to compare two models (equation 3). When one model is sufficiently better than every other, model selection results.

It is advantageous to consider the possible outcomes of probabilistic cross-link analysis before an experiment is conducted, to optimize experimental parameters and obtain the most information from an experiment. Similarly, if interpretation of the results of an experiment proves to be ambiguous, a subsequent experiment can be optimized to reduce the ambiguity. Variable experimental parameters include the cross-linker (particularly specificity and length) and the sequence itself, altered by planned mutations that are unlikely to affect the parent structure. For example, we could make a conservative change to Lys to introduce additional possible cross-links for BS³, or make nondrastic substitutions in two residues to the widely accepted Cys to test disulfide bond formation. Selecting cross-linker and mutation can be repeated, generating a family of experiments, each potentially providing additional information for model selection.

The central idea of planning is for experiments to probe features for which the models most disagree. We evaluate an experiment plan in terms of key properties of practical importance: cost, capturing the number and types of experiments and their relative difficulty; discriminability, a minimum difference Δ by which we would like the score of the selected model to exceed that of any other model after data are collected; coverage, the number of model-pairs that are expected to achieve the desired discriminability; balance, the desire to equalize the positive evidence for one model over another, so that models are not discriminated solely on negative data. The cross-link map provides a natural metric for testing discriminability, a directed cross-link map difference, counting the number of cross-links significantly favoring one model over another. Although many methods of making comparisons are possible, we have chosen a conservative pairwise one that has as its goal ensuring that no matter which model wins, it will have been selected over every other by sufficient positive evidence. Our implementation then maximizes coverage and balance, for an experimenter-selected level of desired discriminability, while minimizing the number of experiments. Although full coverage of all directed pairs is a planning goal, it is not always possible (e.g., when two models are too similar) and often requires a large number of experiments. In practice, full coverage is not required for selecting a model, because, given experimental data, we must only find that one model is sufficiently better than the rest. Ranking all possible pairs is not required. The simulations below address the relationship between pairwise coverage and the likelihood of successful discrimination.

Our algorithm, XlinkPlan (see Materials and Methods), optimizes experiments by considering for each experiment which directed pairs of models the experiment could potentially discriminate by at least Δ. It selects a subset of experiments that will adequately cover the various pairs. This problem is NP-hard, implying that it is expected that no algorithm can be guaranteed to solve all problem instances both optimally and efficiently. To solve this problem in practice, our algorithm adopts a heuristic, greedy approach, selecting the experiment that looks best in the current context. In particular, it keeps track of a weight on each model-pair, indicating how much coverage is still required. To select an additional experiment, it then identifies the one that adds the most coverage, according to the weights. This weighted approach optimizes for coverage and balance, and minimizes the number of experiments. We demonstrate here that this approach is extremely efficient and produces high-quality designs.

Residue-specific cross-linking

We first studied probabilistic discriminability analysis and experiment planning using lysine-specific cross-linking and three different proteins. The primary test case is basic fibroblast growth factor (FGF-2, PDB IDs 4FGF, crystal, and 1BLA, NMR) because of its earlier use in model discrimination by cross-linking (Young et al. 2000). Alternative threading models for FGF-2, using 12 of the published template structures, were obtained via the protein-fold-recognition meta-server (Kurowski and Bujnicki 2003); several of the published templates could not be suitably matched to the FGF-2 sequence given current threading programs queried by the server. Two of the models are of the same fold (β-trefoil) as the current structure, and the correct NMR structure (PDB ID 1BLA) is also included in the model set. The other test cases were chosen from CASP4 (Moult et al. 2001) targets with many high-quality models: deoxyribonucleoside kinase (PDB ID 1J90) and α-catenin (PDB ID 1L7C). Predicted models that are less complete than the correct one are ignored. In total we used 13 models for FGF-2, 85 models for deoxyribonucleoside kinase, and 50 models for α-catenin.

We consider five commercially available, water-soluble, and primary amine-reactive N-hydroxysuccinimide, sulfoN-hydroxysuccinimide, or imido ester cross-linkers with different lengths between the reactive groups: sulfo-DST cross-links Lys N_ζ to Lys N_ζ at a distance of 6.4 Å, DSG at 7.7 Å, DMP at 9.2 Å, BS³ at 11.4 Å, and sulfo-EGS at 16.1 Å. Previously, only information of geometric feasibility has been used for making structural inference from cross-linking. We follow that procedure here, while recognizing that accessibility and reactivity can be measured separately by reaction with monofunctional reagents (Novak et al. 2004). Because our probabilistic Bayesian approach allows ready incorporation of other information, future versions of our method will use such measurements to improve model discrimination.

Following earlier work (Young et al. 2000), for each model, we computed the Lys C_α to Lys C_α straight-line distance (the position of the reactive N_ζ atom is generally both uncertain and mobile); this requires adding 12.4 (2 × 6.2) Å to the maximal cross-linker length to allow for the maximal C_α–N_ζ side-chain length. Because distributions of cross-linker distances less than maximal are most highly populated in solution (Green et al. 2001), it is reasonable that potential cross-links with distances that are some value less than the maximum should be considered most feasible. At the same time, cross-links with distances exceeding the maximum are considered infeasible, whereas those in between are considered ambiguous. Our strategy of ignoring the ambiguous cross-links for model discrimination leads to a smaller number of utilized cross-links and thus a smaller probability of making a decision. However, it simultaneously reduces the possibility of using a spurious cross-link and thus increases the probability that, when a decision is made, it is a correct one.

Chemically, there are two components to the reduction in effective cross-linker length. One arises from the relative rarity of the maximally extended conformation of the cross-linker, and the other from lack of maximum extent and deviation from in-line orientation of the lysine side chains. For cross-linker BS³, the cross-linker conformation component is 2.5 Å (Green et al. 2001), and we estimate the same value for the side-chain component. This creates an ambiguous region 5 Å wide where cross-links are feasible but less probable. For BS³, this region extends from 19 Å to the maximum C_α–C_α distance of 24 Å. We have checked this ambiguity region against FGF-2 cross-linking data (Young et al. 2000), and have found that, as expected, the capture rate for geometrically feasible cross-links (<19 Å) is greater than that for the ambiguous ones (19 Å–24 Å), 31% versus 24%. For the rest of the paper, then, we use a capture rate κ of ⅓. In addition to the expected effect on κ, the application of an ambiguity region is expected also to improve our ability to accurately classify potential cross-links as feasible or infeasible (increase the difference between the probabilities H and L). In all subsequent analyses, we define each cross-linker’s ambiguity region ranging from its maximum extent to 5 Å less.

The discriminability Δ reflects the extent of confidence that we plan for in the selection of one model over another in a pair. It is the anticipated discriminability value for positive data if all possible cross-links in a planned set of experiments were detected without errors. Owing to the inevitability of errors, the expected level achievable on average is κΔ- νΔ (see Materials and Methods). Thus, the experimenter must plan for discriminability greater than the level that is satisfactory for discrimination after collecting experimental data. An extreme example arises if we expect a low capture rate, as from residue-specific cross-linking; then we must require a high Δ so that the expected contribution to discrimination is sufficient. Thus, when we plan for Δ = 6 but have a capture rate of κ = ⅓ and noise rate of ν = 0.05, we can expect actually to observe 1.7 discriminatory cross-links on average in favor of the winning model.

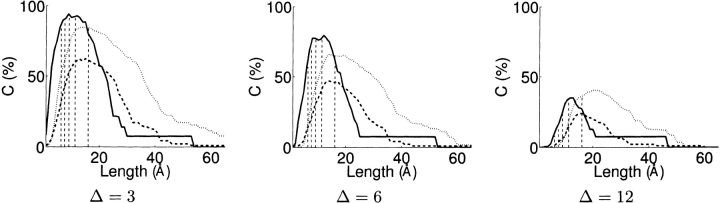
In Figure 2 ▶, we plot the discriminable model-pair percent coverage at Δ of 3, 6, and 12, while varying the potential cross-linker length for the three test proteins. The optimal cross-linker length, summarized in Table 1 for our examples, depends on the models and the relative positions of the reactive sites. Theoretically, with the same number of reactive sites and a random distribution of them on the protein surface, the optimal cross-linker length would be a function of protein size—the larger the protein, the longer the optimal cross-linker length. The three proteins have a similar number of lysines; hence, the larger proteins deoxyribonucleoside kinase and α-catenin are better discriminated with longer cross-linkers than the smaller FGF-2. Our planning method can be used for choosing suitable cross-linkers for a particular protein or as a guide for designing novel cross-linkers (Trester-Zedlitz et al. 2003). The strange right tail of the FGF-2 curve is due to the elongated model based on the D-UTPase (β-Clip) template, which requires longer cross-linkers for discrimination.

Figure 2.

Optimal cross-linker lengths for three different sets of protein models—FGF-2 (solid line), deoxyribonucleoside kinase (dashed line), α-catenin (dotted line)—over potential lengths from 1 Å to 65 Å in 1 Å steps. For each length, discriminable model-pair (directed) coverage was determined at Δ of 3, 6, and 12, respectively. Lengths are indicated (thin dashed vertical lines) for five commercially available cross-linkers: sulfo-DST (6.4 Å), DSG (7.7 Å), DMP (9.2 Å), BS³ (11.4Å), and sulfo-EGS (16.1 Å). The results are tabulated in Table 1.

Table 1.

Optimal cross-linker length for three proteins of varying size, with Δ at 3, 6, and 12

				Optimal cross-linker length Δ
Protein	No. of residues	No. of lysines	No. of models	3	6	12
FGF-2	146	14	13	9 Å	12 Å	12 Å
Deoxyribonucleoside kinase	230	13	85	15 Å	14 Å	15 Å
α-Catenin	269	14	50	15 Å	14 Å	20 Å

Among the five commercially available cross-linkers, we predict that three of them, DMP (9.2 Å), BS³ (11.4 Å), and sulfo-EGS (16.1 Å), would be variously optimal for these models.

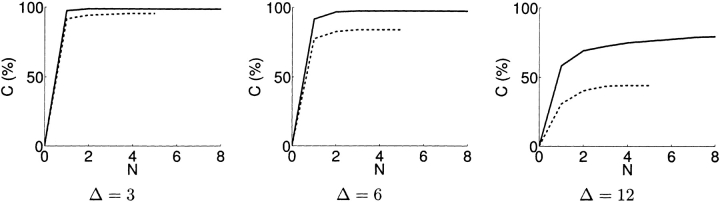
Figure 3 ▶ shows the coverage achieved as additional experiments are added to the plan by XlinkPlan. For residue-specific cross-linking, data from each experiment are handled independently; that is, each pair is distinguished based on data gathered from a single experiment. This allows closer approximation to the probabilistic assumption of independence. For each experiment, selecting the optimal cross-linker improves coverage, although a plateau of diminishing returns is reached. Simulations (Fig. 5 ▶, below) demonstrate the relationship between planned coverage and experimental success.

Figure 3.

Improvement in coverage by multiple-experiment plans for FGF-2. Sets of experiments were planned by XlinkPlan, choosing for each experiment a cross-linker from among five commercially available reagents (dashed line) or choosing both a cross-linker and a possible conservative mutation to Lys (solid line). Sets of up to five experiments were planned for the former case, saturating the possibilities of cross-linker choice, whereas sets of up to eight were planned for the latter case, which includes mutations. The coverage was determined for each plan, at different choices for discriminability Δ. The set of eight experiments selected with choice of mutation at Δ = 12 is listed in Table 2.

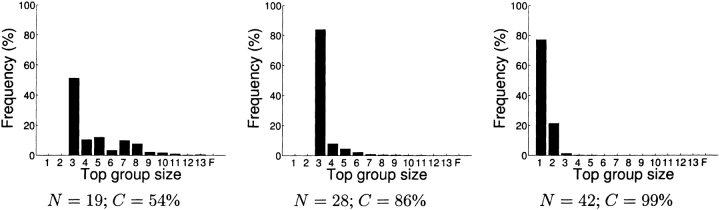
Figure 5.

Simulation of disulfide trapping for FGF-2, using a set of planned experiments for each coverage level, at Δ = 3. Simulations use high feasibility, H = 0.9; low feasibility, L = 0.1; capture rate, κ = 0.95; and noise rate, ν = 0.05; hence λ = γ = 5.31. As explained in the text, we plan conservatively for Δ = 3 and discriminate with Δ = 2 to allow for the anticipated errors. In this case, the appropriate threshold for the posterior ratio is still >400-fold (λ^1.8γ^1.8). Shown is the frequency of the size of the top group in each simulation, over 1000 runs. The failure group (F) indicates cases in which the correct structure has been eliminated from the top group.

With the ease of making site-directed mutations by high-throughput means, a natural extension to cross-linking strategies is the creation of new sites for cross-linking reaction. In particular, conservative mutations (from Arg, Asn, Gln, or His) to Lys can be planned to add reactive sites. As can be seen, the addition of making just one conservative mutation as an experimental option allows higher coverage and/or discriminability, demonstrating that this is a valuable strategy if the number of natural sites is insufficient. Table 2 shows a sample planning result for a set of eight experiments with one cross-linker choice and one mutation possible per experiment, increasing the coverage from 58.3% to 79.5% after combining eight. In this strategy, if there are k possibilities for conservative changes in a protein and l choices of cross-linkers, then there are 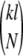possible experiment plans for N experiments. For FGF-2 and five potential cross-linkers, there were 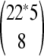≈ 4.1 * 10¹¹ possibilities for this eight-experiment plan; our algorithm provides a valuable tool for selecting the best ones.

Table 2.

Cross-linking experiment plan for FGF-2

Experiment	Cross-linker (length, Å)	Mutated residue	Single-experiment coverage	Cumulative coverage
1	DMP (9.2)	Arg 69	58.33%	58.33%
2	BS3 (11.4)	Arg 116	53.85%	69.23%
3	BS3 (11.4)	Arg 53	58.33%	72.44%
4	Sulfo-EGS (16.1)	Arg 90	41.03%	75.00%
5	DMP (9.2)	Arg 106	50.64%	76.28%
6	Sulfo-EGS (16.1)	Arg 118	44.23%	77.56%
7	DMP (9.2)	Asn 110	52.56%	78.85%
8	DMP (9.2)	Arg 129	55.77%	79.49%
Total				79.49%

The greedy set of eight experiments, each involving one possible Arg, Asn, Gln, or His to Lys mutation, and a choice of commercially available cross-linker, was determined. Each experiment is shown on a line, along with the coverage (percentage of directed model-pairs discriminated) at Δ = 12. The total coverage provided by all eight experiments is 79.49% of the 156 directed model pairs, which is very close to the plateau value of 80.13%.

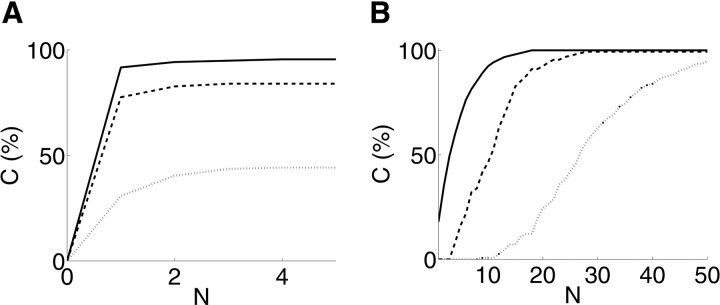
The threshold discriminability value Δ has a significant influence on the planning result. Different levels of Δ affect the choice of experiments, as well as the coverage attainable. Figure 4A ▶ shows the coverage resulting from multiple experiments at different Δ values. Although good coverage can be achieved at low Δ values with a smaller number of experiments, the chance for error is higher.

Figure 4.

Coverage of FGF-2 models by (A) lysine-specific and (B) di-sulfide cross-linking experiments planned by XlinkPlan, as a function of desired discriminability Δ. (A) The set of N (from 1 to 5) experiments planned by XlinkPlan involving five commercially available cross-linkers was planned using Δ of 3 (solid line), 6 (dashed line), or 12 (dotted line). The coverage at the chosen discriminability is indicated for each set of experiments. (B) The XlinkPlan set of N (from 1 to 50) disulfide trapping experiments was planned using Δ of 1 (solid line), 2 (dashed line), or 4 (dotted line), and an ambiguity region of 9–21 Å.

Disulfide trapping for model discrimination

Cross-linking by oxidation of introduced dicysteine residues has several favorable properties for elucidating protein (Bass and Falke 1998) and complex (Hughes et al. 1993) structure and properties. Because each pair of cysteine substitutions is made and tested directly for cross-linking, independence is assured and the cross-link capture rate κ becomes very close to 1 (some false-positive errors may still occur). Finally, the error rate ν can be reduced because the approach eliminates the possibility of assignment error in MS, and both κ and ν can potentially be improved by the detailed examination of cross-linking kinetics that this method allows (see below).

In planning for disulfide trapping, XlinkPlan considers pairs of residues for cysteine mutation (excluding drastic mutations from Phe, Trp, Tyr, Pro, and Gly). As before, planning parameters include the desired discriminability level Δ and the ambiguity region A. In this case, we construct A around a model C_β–C_β distance of 13 Å, the midpoint of a sigmoidal transition of a 3 log difference in rates of disulfide formation (Careaga and Falke 1992), and expand A in increments of −1 and +2 to account for the asymmetry in the distribution of C_β–C_β distances relative to the transition midpoint value. Beyond estimating C_β–C_β distances, we do not construct a full geometric analysis of disulfide geometry (Sowdhamini et al. 1989), because protein dynamics override these considerations for many proteins (Careaga and Falke 1992) and our method does not require picking those disulfides that impart the greatest stability.

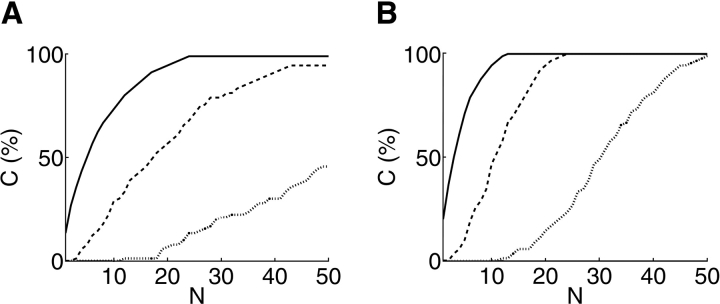
Figure 4B ▶ shows disulfide trapping experiment plans for FGF-2, produced by XlinkPlan. Although, as with residue-specific cross-linking, there are diminishing returns from doing more experiments, the enormous variety of possible disulfide experiments allows nearly full coverage to be achieved even at high Δ levels if enough experiments are conducted. Assuming, as above, that κ in lysine-specific cross-linking is ~1/3, the Δ = 3, 6, 12 curves in Figure 4A ▶ are analogous to the Δ = 1, 2, 4 curves in Figure 4B ▶.

Because Phe, Trp, Tyr, Pro, and Gly comprise ~21% of the residues in an average protein, the number of possible disulfide trapping experiments is about 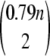≈ 0.31n²; for N planned experiments, the number of possible combinations is about . In the FGF-2 case, there are in total 5565 possible dicysteine mutations. The number of all possible combinations of choosing five experiments from these is >10¹⁶, whereas choosing 50 is >10¹²⁰. These numbers are clearly intractable to an exhaustive search for the optimal plan.

In disulfide trapping, different numbers of experiments generate a wide range of coverage. Depending on the planned Δ, 100% coverage is achieved only with a large number of experiments. However, coverage can be viewed as a conservative estimate of ability to discriminate, and practical experiment plans need not attain 100% coverage. To illuminate the relationship between coverage and experimental success, a simulation of a disulfide experiment plan at Δ = 3 was conducted, using different numbers of experiments and corresponding coverage levels (Fig. 5 ▶). The result of each disulfide cross-linking experiment was simulated according to the geometric feasibility in the correct structure. Simulated errors were introduced according to the specified capture and noise rates. By planning for Δ = 3, confident discrimination by a ratio corresponding to Δ = 2 can be expected even in the presence of this noise. In each simulation, we determined, with respect to the Δ = 2 threshold, which models were eliminated by losing a pairwise comparison. The remaining “top group” of unelimi-nated models typically contains the correct structure and as few as one or two others, typically the other β-trefoil models. With 86% coverage, the top group contains only these models in >80% of the cases. With sufficiently many experiments (N = 42), even the two most similar models can be distinguished >75% of the time. Because of false positives and negatives (because κ ≠ 1 and ν ≠ 0), the correct structure might be eliminated. However, in this simulation, elimination of the correct model happens infrequently (<0.01%) because we require a sufficiently high ratio to make a decision.

Practical example: Disulfide trapping for Tfa model discrimination

We put our planning mechanism into practice on the Tfa protein of bacteriophage λ. The Tfa protein and its homologs are chaperones required for the assembly of trimeric tail fibers in those phage λ strains (“Ur-lambda”) resembling the original wild-type isolate (Hendrix and Duda 1992), and in related phages such as T4 (Montag and Henning 1987; Hashemolhosseini et al. 1996). Genetic data suggest that the activity of Tfa and its homologs is an extreme example of chaperone activity, in which the structure of the final tail fibers (their ability to bind host membrane components) is partially determined by the structure of the chaperone (Hashemolhosseini et al. 1994).

λ Tfa is a small 194-amino-acid protein, but no structural information is available for it or any homolog. Crystallization trials of Tfa readily yield crystals, but they fail to diffract (Hashemolhosseini et al. 1996; M.J. van der Woerd and A.M. Friedman, unpubl.). We submitted the Tfa sequence to our fold-recognition meta-server (Kurowski and Bujnicki 2003). Three potential templates were identified by different fold-recognition programs (Table 3). The functional relationship between Tfa and the hsp70 chaperone DnaK was suggestive, and we used the domain structure of DnaK to suggest sites where the intact molecule might be divided for easier experimentation. A Tfa fragment of residues 1–108 was constructed and found to express a soluble protein that folds cooperatively. To investigate the relationship to DnaK and consider alternatives, complete models were built of the 1–108 Tfa fragment using the three templates. Many decoy models were also developed with the ab initio folding program Rosetta (Simons et al. 1997); one representative model was selected from each of the 100 largest clusters obtained from 15,456 decoys.

Table 3.

Three potential templates for Tfa protein, their source, fold, and function

Index	Program	Template	Fold-type	Function
1	Fugue	1 dkz	DnaK-like	Chaperone DnaK substrate-binding domain
2	3D-PSSM	1 liz	OB-fold	Heme chaperone Ccme
3	Fugue	1 ckm	OB-fold	mRNA-capping enzyme

If our primary concern is to distinguish the three high-quality threading models, their small number allows explicitly attaining balance by seeking dicysteine mutations for all feasibility patterns of desired coverage, here two (Table 4). Because of the small number of models, there are many dicysteine mutations with the same model-pair coverage, so we used as a tie-breaking metric the standard deviation of the difference in cross-linking distance across the model-pairs. The final plan with ambiguity region 10 Å–19 Å is summarized in Table 4. Some automatically selected residue pairs were manually excluded from further consideration when the residues were poorly modeled, when there was substantial protein between two close residues (which would require internal motions to allow cross-linking), or when there was thought to be insufficient mobility to allow cross-linking.

Table 4.

A full coverage plan for three Tfa models with potential templates in Table 3 with discriminability Δ = 2, ambiguity region 10–19 Å, and number of experiments N = 6

		Distances			Feasibilities			Coverage pattern
Residue Pair		1	2	3	1	2	3	1 vs 2	1 vs 3	2 vs 1	2 vs 3	3 vs 1	3 vs 2
ASN 59	VAL 68	26.95	28.33	5.63	L	L	H	0	0	0	0	1	1
ALA 40	ALA 63	21.19	6.86	40.99	L	H	L	0	0	1	1	0	0
GLN 8	ASP 83	8.61	24.04	23.62	H	L	L	1	1	0	0	0	0
THR 75	SER 88	6.79	6.92	24.52	H	H	L	0	1	0	1	0	0
LEU 18	ASP 83	29.98	8.40	8.95	L	H	H	0	0	1	0	1	0
LYS 13	ASN 22	4.94	19.88	3.15	H	L	H	1	0	0	0	0	1
Total					3 H, 3 L	3 H, 3 L	3 H, 3 L	2	2	2	2	2	2

Each model pair is covered twice (a coverage pattern value of 1 indicates support for the first model over the second), and each model is expecting the same number (3) of high feasibility and low feasibility cross-links, a perfect balanced design [ib(S, Δ) = 0].

Although the complete experiment is still in progress, Figure 6 ▶ shows the results of oxidizing mutants with patterns [H H L] and [L H H]. Oxidation by atmospheric oxygen, using a Cu²⁺ catalyst, reveals that [H H L] oxidizes at least 20-fold faster than [L H H]. Concentrations of catalyst from 5 μM to 25 μM give consistent results, whereas millimolar concentrations of catalyst rapidly oxidize both proteins. A complete kinetic analysis for the entire experiment plan is beyond the computational focus of the present paper; however, these preliminary results point out the importance of a kinetic analysis to avoid false positives and thus improve ν. Such an analysis will be reported elsewhere.

Figure 6.

Disulfide cross-linking of mutants (A) [H H L] and (B) [L H H]. Oxidation of dicysteine mutants by atmospheric oxygen was catalyzed by 15 μM Cu²⁺ ions for the indicated time before quenching. The dicysteine mutant [H H L] has only 11 residues between the two cysteines, resulting in an unobservable difference in mobility on SDS gels (data not shown). This mutant was thus analyzed by isoelectric focusing (A). The disulfide form runs further from the anode, which is at the bottom of the gel as shown. The mutant [L H H] was analyzed on 20% homogeneous Phast gels (B), where the disulfide form has slightly greater electrophoretic mobility.

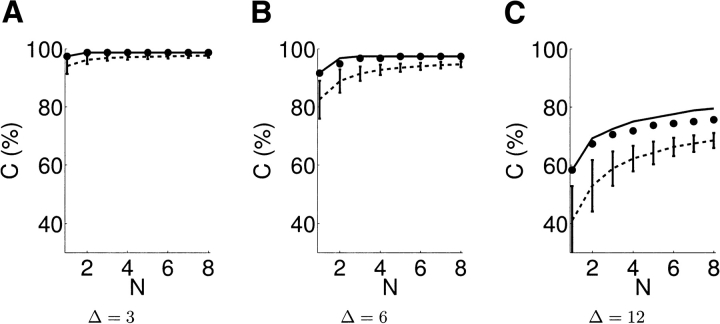
We have also analyzed the potential to discriminate the entire set of 103 models (three threading models plus 100 Rosetta decoys) under disulfide cross-linking. We applied our planning algorithm with an ambiguity region of 9 Å–21 Å. Figure 7 ▶ summarizes the results in terms of the three planning parameters—number of experiments N, discriminability threshold Δ, and coverage C (%). The 3D plot of these three variables in shown in Figure 7A ▶; 2D slices in several directions are shown in Figure 7, B, C, and D ▶.

Figure 7.

The relationship between coverage percentage C (%), discriminability Δ, and number of experiments N in disulfide experiments planned by XlinkPlan for 103 Tfa models with ambiguity region 9 Å–21 Å. (A) Varying all parameters. (B–D) Varying pairs of parameters, while fixing the third at the indicated values.

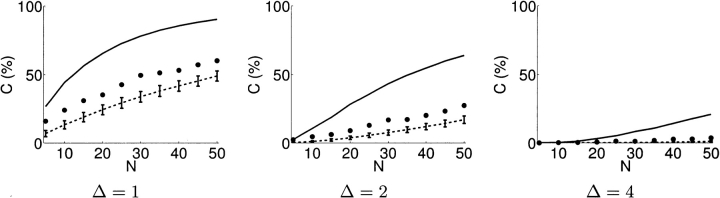
We further focused on the differential ability to discriminate sets of relatively different models as compared with relatively similar ones. We identified a set of 21 decoys all contained within a single one of the 100 Rosetta clusters. They have pairwise RMSDs ranging from 4.1 Å to 9.9 Å (mean 7.9 Å) according to a MaxSub (Siew et al. 2000) superposition. We then identified a same-size (21-member) random subset of the 100 decoys. These have significantly larger pairwise RMSDs, ranging from 8.5 Å to 17.0 Å (mean 13.5 Å) in a MaxSub superposition. Figure 8 ▶ shows the coverage as a function of number of experiments, at different discriminability thresholds. As would be expected, planning for discrimination of more similar models reduces the coverage achievable for any given number of experiments, but significant coverage is still attainable, even within a cluster of similar models.

Figure 8.

The impact of structural similarity on disulfide experiments planned by XlinkPlan. The plots show the relationship between coverage percentage C (%), and number of experiments N, at various discriminability levels (solid, Δ = 1; dashed, Δ = 2; dotted, Δ = 4). (A) A set of 21 similar Tfa decoys, all contained within one of the 100 Rosetta clusters, was used for planning. They have a mean pairwise RMSD of 7.9 Å. (B) A random subset of 21 of the 100 final Rosetta decoys was used for planning. They have a mean pairwise RMSD of 13.5 Å.

The trends in Figure 7 ▶ make the diminishing returns in experiment coverage very apparent; for example, for most discriminability levels, moving from 90% to 99% requires a much bigger investment than moving from 50% to 90% (Fig. 7D ▶). At the same time, as shown by the simulations above (Fig. 5 ▶), full coverage is generally not required. These two results suggest an efficient semisequential experiment planning approach: Instead of conducting >100 experiments (90% coverage with Δ = 2) as the first step, conduct ~20 experiments (25% coverage with Δ = 2) and then plan additional experiments only if the result proves to be ambiguous. Because we seek one model that overrides others, the result of these experiments could be sufficient to select such a model unambiguously. If additional experiments are required, losing models need not be planned for, thereby pruning the planning problem. As an example, if the results anticipated for threading model 1 were found in the six experiments of the three-model plan (Table 4), then 34 of the 103 models would be eliminated according to Δ = 2. This process could be repeated, ending in a final experiment that is explicitly balanced as in the three-model plan, to discriminate the last few, most similar models.

Algorithmic considerations

Before this experiment planning method was proposed, investigators might have conducted cross-linking experiments less systematically. We have compared the effects of non-systematic experimentation with our planning method (Figs. 9 ▶, 10 ▶). One method would be simply to select experiments without any planning. The expected results and variation of this “planning-free” approach are illustrated by the mean and standard deviation of 1000 random plans. A better alternative, once the problem has been formulated as here, would be randomly to generate sets of plans and select the best. This approach is illustrated by the best of 1000 random plans. Our planning algorithm bests both of these methods, especially with the enormous degrees of freedom and complex restraints of disulfide trapping planned at high Δ. At the same time, our algorithm also achieves balance.

Figure 9.

Relative performance of different approaches to planning lysine-specific experiments for FGF-2 model discrimination. Shown are a “planning-free” expectation over 1000 random plans (mean is shown as dashed line with standard deviation error bars), a randomized planning approach (separate circles) considering the best from the set of random plans, and finally XlinkPlan (solid line).

Figure 10.

Relative performance of different approaches to planning disulfide trapping experiments for Tfa model discrimination. Shown are a “planning-free” expectation over 1000 random plans (mean is shown as dashed line with standard deviation error bars), a randomized planning approach (separate circles) considering the best from the set of random plans, and finally XlinkPlan (solid line). Experiments that don’t discriminate any model-pairs are excluded beforehand.

Our planning algorithm (Fig. 11 ▶) effectively navigates the design space defined by discriminability, coverage, balance, and cost. Its direct encoding of these terms offers advantages over other approaches such as decision trees. For example, multiple coverage of a particular model-pair (to attain desired discriminability) is achieved straightforwardly by using initial weights >1, and decrementing them with each covering experiment. Similarly, balance is achieved automatically by basing our analysis on directed model-pairs, 〈r, s〉 and 〈s, r〉, and using only positive evidence for planning. Although we use uniform initial weights and weight decrements for all pairs in our algorithm, differential weights and reductions are possible and would provide greater flexibility in trading off among desired criteria for experimental design, either to focus on models of interest or to avoid spending resources on barely distinguishable pairs. Although there is additional cost in explicitly considering each pair of models (rather than using a linear-cost metric such as entropy), we have found that the coverage is sparse, with each experiment covering many fewer than the possible quadratic number of model-pairs. Thus, in practice, thousands of models can be handled quite efficiently.

Figure 11.

Greedy algorithm, XlinkPlan, given a set S of models, a set of possible experiments, desired discriminability ɛ , ambiguity region A, and maximum number of experiments N_max and coverage C_max′. The output is a subset ɛ′of experiments covering a subset P′ of model-pairs. For residue-specific cross-linking plans, a model-pair must be covered by a single experiment at the given Δ level. For disulfide trapping plans, the weight w on a model-pair keeps track of the remaining coverage to complete Δ, to be provided by subsequent experiments.

A comparison with the best possible scenario shows that, in practice, our planner often proposes experiments near the minimum. The best possible scenario has no experimental redundancy (i.e., each structure pair is covered by exactly Δ experiments). Therefore, the total number of structure pair discriminations must be at least CΔP to reach C percentage coverage at discriminability Δ for P pairs. Also under the best possible scenario, each experiment will discriminate a disjoint set of model-pairs. This disjointness can be approximated by not considering which model-pairs an experiment covers, but only taking the number of expected discriminable pairs. The smallest number of experiments whose expected discriminable pairs sum to the CΔP threshold (again, without considering which pairs are covered) defines a lower bound on the optimal experiment number. The plans in Figure 7 ▶ are within roughly twice this very simplistic lower bound. Because the true minimum will be greater than this simplistic bound, the selected experiments are well within twofold of the optimal number.

Our algorithm balances speed and quality. It takes only seconds on a Pentium 4 computer to generate any of the plans in this paper, even with reasonably large sets of models and sizes of experiment plans. As previously discussed, the problem is NP-hard, and as we further illustrate, the combinatorics do not permit an exhaustive exploration even for the problem sizes studied here. Yet XlinkPlan results are well within a factor of 2 of optimal, and significantly better than a randomized algorithm as the number of degrees of freedom increase.

Our algorithm has been implemented in platform-independent Python scripts. The software can be freely obtained for academic use by request from the authors.

Summary

We have developed a probabilistic mechanism for analyzing cross-linking information with respect to a set of protein structure models, estimating the ability of experiments to discriminate among those models, and optimizing experiments accordingly. A probabilistic framework allows explicit characterization of errors that are present in all experimental data, enabling careful quantification of the extent of support for a particular model. The probabilistic approach allows explicit consideration of the experiment in classical statistical terms of sensitivity and power (type I and type II errors). Under our mechanism, an experimenter can establish and plan for a sufficient level of evidence required to support model selection, and thereby avoid false confidence in committing to an ambiguous decision. Similarly, the ability to select a posterior ratio as well as plan further discriminatory experiments provides control over type II errors.

We use a small set of readily interpretable parameters to characterize key factors underlying errors in data (κ, ν) and interpretation (H, L). Such parameters remain unstated in other approaches; for example, a violation-counting approach (Young et al. 2000) implicitly assumes ν = 0 (no false positives), and H = 1 and L = 0 (no errors in interpretation of models). Although we adopt the simplest possible forms for these parameters (fixed constant values), we show that they can constitute a rational basis for interpretation and planning. Furthermore, as we found with Figure 5 ▶, the results are fairly insensitive to the exact parameter values. Future work will focus on a more complete accounting of these error parameters either with a classical sensitivity analysis, or within a Bayesian formulation that incorporates distributions over the values of the parameters.

Our formulation of experiment planning makes explicit the key factors of discriminability, coverage, balance, ambiguity, and cost. Although the experiments we plan here contain from 10¹¹ to 10¹²⁰ combinatorial possibilities, our greedy algorithm is efficient and effective in identifying plans expected to achieve these specified criteria. When confident selection requires planning larger experiments, a proposed semisequential approach, conducting batches of experiments that focus on remaining ambiguities, allows researchers to balance the desire for conservative plans with the need for experimental efficiency. This approach can also potentially integrate residue-specific and disulfide cross-linking, once put on common probabilistic ground, using an initial residue-specific experiment to eliminate many models and subsequent disulfide experiments to discriminate remaining ones. Disulfide cross-linking could also readily be supplemented by the use of cysteine-specific cross-linkers operating on the same dicysteine mutants to obtain more distance information (Kwaw et al. 2000). These semisequential and hybrid mechanisms are very general, and we also plan to study incorporating different types of experimental data, for example, the combination of cross-linking and mutagenesis. Finally, our planner can be applied to additional discrimination problems, for example, selecting among models of protein–protein complexes provided by docking procedures.

Our analysis raises some questions about the value of residue-specific cross-linking, especially when compared with disulfide trapping. If many residue-specific cross-links can be identified in a single experiment, then residue-specific cross-linking can be very powerful. However, whenever residue-specific cross-links are difficult to identify, then our analysis indicates that disulfide cross-linking is a more powerful alternative. We believe a major practical problem, then, is the low and variable capture rate of residue-specific experiments. Even extensive experimentation (Young et al. 2000) yielded a capture rate κ of only ~⅓, whereas less extensive experiments (Haniu et al. 1993) gave far less (<10%). New cross-linkers and new detection methods would improve these results, but at present κ is far less than can be achieved with disulfide cross-linking. As a result of the low capture rate, residue-specific experiments effectively provide less information. We estimate that under the current κ and ν, one disulfide cross-link is approximately equivalent to several expected residue-specific ones. In addition, the coverage of residue-specific experiments “saturates” early and dramatically, whereas disulfide trapping experiments provide enormous degrees of freedom for further, fine-grained model discrimination.

The optimal experiment plan (Table 4) for discrimination of the threading models of the λ Tfa protein is currently being conducted. Thus far the data consistently support one model. As a final note, the mutagenesis and disulfide oxidation approach is simple and amenable to robotic automation. The combination of robotics with experiment planning should prove very powerful in the rapid elucidation of protein structure.

Materials and methods

Probabilistic cross-link analysis

In this section, we develop a basic framework for probabilistic reasoning about cross-links. Most functions depend on the choice of experimental parameters; we leave those terms implicit except where necessary for clarity. We are given a set S of predicted structure models, for a protein or complex. Each model s ɛ S has a prior probability, p(s), which can be uniform or can incorporate scoring information from the modeling process. The task is to identify the model in S that is best, in terms of the prior and agreement with experimental data regarding a set ℒ of possible cross-links. We bridge the gap between model and data in two steps: (1) consistency of cross-links with models, and (2) evidence for cross-links from data.

Consistency of a cross-link l_i with a model s is modeled with a conditional probability p(l_i|s). By analogy to contact maps, which show pairs of residues that are “close,” we call each set of conditional probabilities for a particular model and experiment a cross-link map. Figure 1 ▶, Step 1, has examples for three models. In general, cross-link map values would be determined by the reactivity of the protein groups being linked, their accessibility to the cross-linking reagent and the geometric feasibility of the cross-linking reaction given the finite length of the cross-linking molecule. The reactivity of the protein groups cannot be easily extracted from the model, but can be corrected for by measurements of reactivity with monofunctional reagents (Novak et al. 2004). For the studies here, we assume constant reactivity. Similar considerations hold for accessibility (although some portion of the relative accessibility of sites may be extracted from the predicted model). Finally, geometric feasibility depends on whether or not the cross-linker can bridge the distance between cross-linked atoms in the model, potentially with consideration for protein dynamics. For example, the cross-linker bis-sulfo-succinimidyl suberate (BS³) reacts with amino groups, including the N terminus and the N_ζ of Lys residues, and forms a bridge of up to 11 Å between such pairs. Similarly, in disulfide trapping (Careaga and Falke 1992), disulfide bonds are formed upon oxidation of cysteines whose C_β approach within 4.6 Å, with proper geometry, during the experiment.

Support for a cross-link l_i from experimental data d is modeled with likelihood p(d | l_i). Because this paper concentrates on the information content available via cross-linking, we take as given an interpretation of the data. For example, in the case of cross-link identification by mass spectrometry, likelihoods could be computed by predicting expected mass peaks for a given cross-link and comparing with observed spectra, using a distribution to model measurement error, and a mixture model to handle experimental complexities (e.g., missed proteolytic cleavage). A key part of these likelihoods that we explicitly model is the sparsity (false negatives) and noise (false positives) of the data. Feasible cross-links are detected at some capture rate κ, whereas infeasible cross-links show up, spuriously, at some noise rate ν. These rates depend on the cross-linker and peptides involved, the detection methods, and the experimental effort, but we consider the simplest case of fixed rates.

Combining these terms then yields the support for each model from the data, by marginalizing over cross-link existence. In this paper, we treat cross-links as independent, although it is certainly possible to model dependence due to such effects as common reactivity arising from cross-links sharing an amino acid side chain. Similarly, a model is conditionally independent of the data given the cross-links (models are not, e.g., optimized with respect to the data). Thus we have

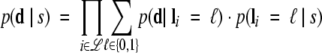(1)

In this approach, a model is supported by high-feasibility cross-links that are observed and low feasibility ones that aren’t. It is penalized by low-feasibility cross-links that are observed and high-feasibility ones that aren’t. Figure 1 ▶, Step 4, has two simple examples for one observed and one unobserved cross-link. The p(d | l_i) terms are the noise and capture rates, and the p(l_i | s) terms arise from the cross-link map.

An interesting consequence of this realistic model is that, depending on the number of potential cross-links, and their cross-link feasibility (H, L), capture (κ), and noise (ν) values, we should expect to observe some cross-links that are considered low feasibility in the correct structure. The expected number of identified cross-links among B low feasibility ones is [κL + ν (1 − L)] • B. If κ = ⅓ ν = 0.05, L = 0.1, and B = 25, we expect to see about two infeasible cross-links wrongly identified. The potential identification of incorrect cross-links points out the need for multiple possible cross-links supporting a model selection (see discussion of selection threshold below). Further analysis of this effect and its implications for model discrimination will be reported elsewhere.

Using equation 1, we can reweight the prior distribution p(s) by the information provided by the data:

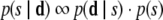(2)

and identify the maximum a posteriori model, or maximum likelihood model in the absence of informative priors.

A posterior ratio allows comparison of the consistency of two models (r, s ɛ S) with the data.

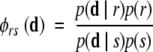(3)

In the present context, we allow for the possibility of priors, although we treat them as uniform. When priors are ignored, this ratio becomes a so-called Bayes factor. A model can be confidently selected when the ratio with respect to every other model is sufficiently large.

Experiment planning

Planning metrics

The problem of characterizing the utility of an experiment has been well-studied in the statistical literature; for example, model entropy or relative entropy (Kullback-Leibler distance) between posterior and prior distributions is one natural approach that would capture the expected effects of reweighting the models given data. We use a complementary approach that uses pairwise differences in cross-link maps so that we can make explicit trade-offs among key properties of practical importance for our application—discriminability, coverage, balance, ambiguity, and cost. In the present paper, we treat experimental cost as uniform within an experiment type, so that cost becomes simply the number of experiments.

Intuitively, a pair of models with very different cross-link maps (i.e., disagreeing about feasibility of many cross-links) has a higher probability of being discriminated than a pair with very similar cross-link maps. We separately consider the two directed discriminations in favor of one or the other model, which we characterize as cross-link map differences, d(r, s) and d(s, r). Using H and L feasibilities as in Figure 1, d ▶(r, s) would simply be the size of the set ℒ_r of cross-links that have H in r and L in s, and similarly for d(s, r) = | ℒ_s | (note that cross-links for which they agree cancel out in the discriminability ratio, equation 3). Now we consider whether the discriminability ratio φ is sufficient to select r if r is indeed correct. Because this analysis is done before data are collected, we must take the expectation over all possible data sets:

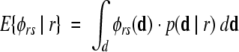(4)

In general, this integral cannot be evaluated analytically. However, it can be simplified under the assumptions we have been discussing: independent feasibility of cross-links using fixed H and L, detected under fixed rates for capture κ and noise ν. The probability of capturing a high-feasibility cross-link is then α = Hκ + (1 − H) ν, the sum of capturing it correctly and of it showing up incorrectly. The probability of capturing a low-feasibility cross-link is β = Lκ + (1 − L)ν. If r is the correct model, then each cross-link from ℒ_r contributes α/β to the ratio if observed or (1 − α)/(1 − β) if not (both contribution ratios are reciprocated for the ℒ_s cross-links). Assuming independence of cross-links, the expected value is multiplicative, and we can separately analyze the expected contribution of each cross-link to the ratio. Each cross-link in ℒ_r contributes:

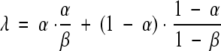(5)

Cross-links in ℒ_s have a similar formula with α and β switched, giving γ. Examination of γ and λ demonstrates that ν must be greater than ν for effective discrimination, and the greater the difference, the greater the effectiveness of the experimental system.

The expected ratio in equation 4 then becomes

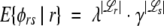(6)

We can rewrite λ as

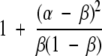(7)

to see that it is >1 (assuming κ> ν). Similarly, γ> 1, thus the expectation of the ratio E{φ_rs |r} increases monotonically with |ℒ_r|and |ℒ_s|. Thus, we can use the cross-link map differences as an easily interpretable measurement of the potential for correctly making a selection.

Averaging (or simply summing) the expectation of ratios over all model-pairs yields a measure of the overall expected information provided by an experiment. In our cross-link map difference approach, we simply sum up the number of model-pairs with a cross-link map difference of at least some threshold Δ:

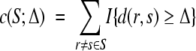(8)

where the indicator I takes value 1 if the predicate is true and 0 if it is false. We call this the discriminable model-pair coverage of the experiment. We note that this metric does not require the same data to be used to achieve acceptable discriminability for one model against different models (e.g., r can be better than s and t under two different subsets of its cross-links). Although model selection only requires finding one model to be better than the rest, the coverage metric seeks to support discrimination of all pairs of models. In the absence of an informative prior, any model could be the selected one, thus we must consider all pairwise discriminations.

Whether an observed cross-link in ℒ_r or an unobserved cross-link in ℒ_s provides a larger contribution for r (i.e., whether λ or γ is bigger) depends on the values of H, L, κ, and ν. The uncertainty in the relative values of λ and γ provides additional motivation for a balanced design, that is, an (approximately) equal number of cross-links in ℒ_r and ℒ_s. Formally, we evaluate imbalance ib in terms of the potential positive evidence for each pair of models, as measured by cross-link map differences, with Δ difference considered always sufficient. Additional discriminability greater than Δ is neither penalized nor selected for in our planning algorithm.

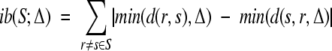(9)

Because variability in H and L arises from modeling uncertainty and protein flexibility, it is intuitively desirable to use for discrimination only cross-links that are most feasible in one model and least feasible in the other. We make this property explicit in terms of a parameter we call the distance ambiguity region A—a range of cross-linking distances that cannot be associated with strong feasibility or infeasibility with respect to a model. In the current case of discrete cross-link map differences, we simply don’t include such positions in the formulas for discriminability and coverage. In the more general case, this region would be reflected in the choice of distribution for p(l_i |s).

Planning algorithms

Our experiment planning mechanism takes as input a set of possible experiments ℰ to be considered, each with an associated set of cross-link maps p(l_i |s; e). It then determines experiments to be conducted ℰ ⊂ ℰ, so as to maximize discriminable model-pair coverage C and minimize imbalance ib and number of experiments N = |ℰ′|.

The optimization problem can be shown to be a member of the class of NP-hard problems. NP-hardness follows by reduction from SetCover: The objects to be covered correspond to model-pairs, the covering sets correspond to experiments, and a binary cross-link map indicates which objects (model-pairs) a particular set (experiment) covers (discriminates). In fact, our problem generalizes many variations on SetCover that maximize coverage and minimize the number of sets. Greedy algorithms have proved effective in such contexts, both practically and theoretically (e.g., the greedy algorithm for SetCover would provide an approximation to 1 + log|S| in covering a set S [Johnson 1974]). Thus we pursue a greedy approach.

Figure 11 ▶ outlines our algorithm, XlinkPlan. We use directed pairs of models (i.e., both 〈r, s〉and 〈s, r〉), rather than undirected pairs, to reach balanced design. A potential cross-link l_i is informative in discriminating a directed model-pair if its cross-linking distance (denoted ||l_i||) is short enough in the first model and long enough in the second, relative to the ambiguity region. In this manner, the algorithm considers only positive evidence toward a particular discrimination goal, minimizing imbalance. Negative evidence will also arise in the experiment and contribute additional discrimination as in equation 1 (but this is not considered in planning). For lysine-specific experiments, a particular experiment is noted as covering a model-pair if at least Δ cross-links are informative. For disulfide experiments, coverage is accumulated over multiple experiments, and thus each experiment is considered as (partially) covering if it has an informative cross-link. The total number of covering experiments must then reach Δ, and a pair’s weight w keeps track of the remaining coverage required. The algorithm greedily selects experiments, stopping when the number of experiments reaches the maximum number N_max or the desired coverage C_max is satisfied. At each point, the marginal utility of an additional experiment is evaluated by the weighted coverage sum, in which the weight w represents the current importance of covering a particular model-pair. Each pair’s weight is initially simply 1 (residue-specific) or the desired discriminability Δ (disulfide), and coverage by an experiment then decrements the weight.

Simulations

Cross-linking experiments are simulated by randomly selecting observed cross-links from among the geometrically feasible ones according to the capture rate κ (and from the infeasible set according to ν). This yields a simulated data set of observed cross-links, which are then used to evaluate the posterior probabilities (equation 2) of the models. In the posterior ratio for a pair of models, positive and negative evidence are weighted by λ and γ, respectively. In our simulations, these weights are evaluated with H = 0.9 and L = 0.1 and κ and ν as appropriate for the experimental type, lysine-specific (κ = ⅓, ν = 0.05) or disulfide (κ = 0.95, ν = 0.05). The simulation results are robust to a range of these parameters (data not shown). Models are discriminated based on the posterior ratio exceeding a selected threshold. If we plan for a particular Δ, positive evidence (cross-links expected by the winning model that correctly show up, minus those expected by the losing model that spuriously show up) is expected to contribute a factor of γ^{κΔ − νΔ} to the posterior ratio, and negative evidence (cross-links expected by the losing model that correctly don’t show up, minus those expected by the winning model that fail to show up) contributes λ ^{(1 − ν)Δ − (1 − κ)Δ} (equation 6, adjusted for expected error). When the posterior ratio exceeds the product of these factors for the Δ chosen for discrimination, a model is selected. Simulation results are presented by computing the number of models that are still possible after pairwise discrimination. The viable models typically include the correct structure; the number of times the correct model is eliminated is indicated as a failure in discrimination.

Structure prediction of Tfa protein

Alignments returned from the fold-recognition meta-server (Kurowski and Bujnicki 2003; see also the references to the individual methods cited therein) were evaluated based on the agreement between the patterns of secondary structure predicted for Tfa and observed in the potential templates, as well as via structural assessment of the resulting crude models (Kosinski et al. 2003). The DnaK template (1DKZ) reported by FUGUE (Shi et al. 2001) was selected as a potential template and used to build a model of the full-length Tfa protein using the “Frankenstein’s monster approach” (Kosinski et al. 2003). Additional fold-recognition analyses were performed using the multiple sequence alignment of the pfam02413 family, of which Tfa is a member. Templates 1LIZ and 1CKM of the OB-fold were found using the pfam alignment and used to generate two additional models.

Ab initio models were generated for the 1–108 residue fragment of Tfa using Rosetta (Simons et al. 1997) and the default options. 15,456 decoy models were clustered, and 100 top clusters were selected for further analysis. Rosetta was only rarely able to generate decoy models with high contact order, presumably because of the high β-strand content. Poorly modeled regions provide further incentive for requiring positive data in discrimination.

Protein mutagenesis, expression, and purification

The phage λ Tfa1–108 fragment was produced from the intact Tfa protein by PCR subcloning into the pET30 vector (Novagen) using the restriction sites NdeI and HindIII, leaving a product without Nor C-terminal tags. Dicysteine mutants of the Tfa1–108 fragment were made by the Quik-Change method (Stratagene), and confirmed by sequencing both strands of the entire gene. Proteins were overexpressed in Escherichia coli strain BL21(DE3)/pRIL, and purified by ammonium sulfate precipitation, hydrophobic interaction chromatography on Bakerbond HI-Propyl (Baker), followed by ion exchange chromatography on HiTrap Q (Pharmacia). Purified proteins were more than 95% homogeneous as detected by SDS-PAGE.

Disulfide cross-linking

For disulfide cross-linking (disulfide trapping), we used oxidation by atmospheric oxygen with a Cu²⁺ catalyst and generally followed previously published methods (Careaga and Falke 1992). For cross-linking, a stock solution of 150 mM CuSO₄ (Sigma) and 500 mM 1,10-phenanthroline (Sigma) was made in 4:1 water:ethanol (v/v). Purified dicysteine mutants for cross-linking were eluted from the HiTrap Q column into a buffer of 10 mM Tris-HCl (pH 8), 160 mM NaCl, 1 mM EDTA, 0.02% sodium azide, 0.01 mM PMSF, and 0.5 mM DTE (Sigma), but no other reductant. Protein was diluted to 15 μM in 10 mM Tris-HCl (pH 7.5) but lacking DTE and containing 1 mM NaAsO₂ (Sigma). A preoxidation sample was removed and quenched by addition of an equal volume of 2× SDS gel buffer with 10 mM N-ethylmaleimide (Sigma), 200 mM EDTA, 2 mM NaAsO₂, followed by heating to 95°C for 2 min. Cu–phenanthroline complexes were added to the indicated concentration of Cu²⁺ ions to start the reaction. The reaction was incubated at 27°C, and time points were removed and quenched as above. All buffers were in equilibrium with atmospheric oxygen.

Oxidation products were analyzed by SDS-PAGE on 20% homogeneous PAA Phast Gels (Pharmacia). Gels were stained with Coomassie blue or by silver staining. Gels were imaged on a BioImaging Systems EPI ChemiII Darkroom and gel bands quantified with Labworks version 4.0.0.8. In the case of mutant [H H L], the introduced cysteines were too closely spaced to yield measurable differences in SDS gel mobility upon cross-linking. In this case, reaction time points were quenched in the same quench buffer but without SDS and bromphenol blue, and oxidation products were analyzed by IEF on pI 3–9 Phast Gels (Pharmacia). Control reactions without Cu²⁺ catalyst revealed no detectable oxidation in >16 h. Additional control reactions include dilution into buffer containing urea and additional catalyst before the reaction and at the reaction time points to reveal the fraction of material still capable of reaction. Disulfides formed rapidly in the denatured protein. There was only a small reduction over time in the fraction of protein capable of reacting, thus indicating only slow oxidation to unreactive forms. The rate of disulfide cross-linking was determined as described (Careaga and Falke 1992).

Article and publication are at http://www.proteinscience.org/cgi/doi/10.1110/ps.04846604.