Simulation of the activation of α-chymotrypsin: Analysis of the pathway and role of the propeptide

Abstract

α-Chymotrypsin undergoes a reversible conformational change from an inactive chymotrypsinogen-like structure at high pH to an active conformation at neutral pH. In order to gain insight into this process on a structural level, we applied molecular dynamics and targeted molecular dynamics simulations in aqueous environment on the activation and inactivation processes of three different types of chymotrypsin. These are the wild-type bovine chymotrypsin containing the propeptide and the bovine and rat chymotrypsin lacking the propeptide. From these simulations, the importance of the propeptide and of the sequence differences between the rat and bovine variants from the viewpoint of activation could be evaluated and compared with previous fluorescence stopped flow results. The obtained results show the unambiguous influence of the propeptide on the explored conformational space, whereas the sequence differences between bovine and rat chymotrypsin play a minor role. The main features of activation are present in both the wild type and the variant lacking the propeptide, despite the fact that different parts of the conformational space were explored. The comparison of all trajectories shows that particular amino acid residues, such as 17, 18, 19, 187, 217, 218, and 223, undergo large dihedral transitions during the activation process, suggesting a role as hinge residues during the conformational change.

Conformational changes play an essential role in the modulation of biological activity in proteins. Proteases are synthesized as inactive proenzymes, zymogens, and perform a series of conformational changes toward their active conformation in order to provide a site- and time-specific regulation of their proteolytic activity. The inactive protein precursors often consist of the intact protease with an N-terminal extension or prosegment, stabilizing the inactive enzyme conformation. Activation of the enzyme is then accomplished by limited cleavage of the propeptide in the zymogen. A typical example is the activation of chymotrypsinogen to chymotrypsin occurring after tryptic cleavage of the peptide bond between amino acid residues 15 and 16. This cleavage triggers a series of conformational changes that activates the enzyme (Bode et al. 1978; Bode 1979; Wang et al. 1985; Wroblowski et al. 1997). It allows the formation of a salt bridge between the newly released Ile 16 N terminus and the Asp 194 carboxyl group. This activation of the zymogen can also be mimicked by a pH jump from an inactive chymotrypsinogen-like structure at high pH to an active conformation around pH 7 and so can be followed spectroscopically (Fersht and Renard 1974; Stoesz and Lumry 1978; Heremans and Heremans 1989a,b; Verheyden et al. 2004).

Despite the many studies that describe in large detail the structure of bovine chymotrypsinogen and its derivatives both in their active and inactive form (Cohen et al. 1981; Blevins and Tulinsky 1985; Tsukada and Blow 1985; Wang et al. 1985), the propagation path of the activation process and details about the accompanying conformational changes and the corresponding energy profile of the activation remained unknown.

To overcome this problem, computational methods can be used in order to obtain more specific information about the way that the transition occurs. This can be done by modeling plausible intermediate conformations of the activation path. Former experiments have shown that the conformational changes accompanying the activation take place on the millisecond timescale (Fersht and Renard 1974; Stoesz and Lumry 1979). A conformational change of that size is unlikely to happen in an ordinary MD simulation without having the computing capacity for a large number of simulations (Zagrovic et al. 2002). Therefore the method TMD (Schlitter et al. 1993, 1994; Swegat et al. 1997) has been used. The technique is based on an MD simulation that uses a constraint in order to enable the conformational change.

Only one TMD study of the activation process of chymotrypsin has been published until now. It used the chymotrypsinogen-like high-pH conformer as an inactive conformer and the neutral pH bovine α-chymotrypsin as an active conformer (Wroblowski et al. 1997). This study has already provided information concerning the pathway. However, the simulations were performed under vacuum conditions; that is, potentially important protein–solvent interactions might have been neglected. We have extended the previous approach and performed a series of TMD simulations on different species (bWT, rWT, and rΔA), taking into account the explicit solvent molecules as explained in the Materials and Methods. By doing so, we had the opportunity to create a more realistic environment for the studied protein and to double-check the activation path generated in a vacuum.

In a previous study by our group, fluorescence stopped flow (FSF) kinetic experiments were also performed on two variants, namely, on the bWT and rΔA enzymes (Verheyden et al. 2004). Because the c-DNA of bovine chymotrypsin(ogen) is not available, it was not possible to perform FSF measurements on the ΔA mutant of the bovine species (bΔA). That is why the already cloned and very homologous in sequence (>80%) rat chymotrypsin(ogen) was used instead (Fig. 1 ▶; Verheyden et al. 2000). In addition, the pro-peptide (A-chain) of chymotrypsin was substituted by the one of trypsinogen in order to provide a higher expression level and a more stable zymogen. Cys 122 was also mutated to serine in order to avoid unpaired cysteines that might cause folding problems in the molecule (Fig. 1 ▶; Venekei et al. 1996). Because the cysteine bridge between residue 1 and 122 is absent in this chimera, the propeptide, which in the WT stays with the active enzyme, dissociates from the mature active chymotrypsin after conversion of the inactive precursor rΔΑin to rΔΑac by the specific limited proteolysis with enterokinase.

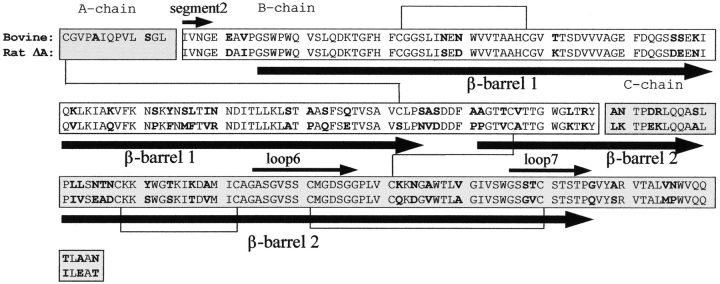
Figure 1.

Sequence alignment of WT bovine chymotrypsin and rat-Δ A-chymotrypsin (lacking the propeptide). Boldface letters outline the differences in amino acid sequence. The three polypeptide chains (1–13, 16–146, 149–245) are indicated in different bars. The five inter- and intrachain disulfide bridges are shown by the black connections. Arrows below and above the sequence bar indicate the β-barrel structures and the structural elements such as segment2, loop6, and loop7, respectively.

Until recently, no other role was attributed to the propeptides of the serine proteases other than the function as a chaperone for proper folding and as a prerequisite for stability and compartmentalization of the zymogen (Venekei et al. 1996). For the chymotrypsin chimera, it was even shown that the lack of the propeptide had no effect on the catalytic efficiency, substrate specificity, or folding of the protein (Venekei et al. 1996). Recent studies, however, proved that the disulfide-linked prosegment of chymotrypsin(ogen) stabilizes the active enzyme as well (Kardos et al. 1999). These findings document for the first time an effect of the covalently linked cleaved propeptide on the active pancreatic protease and suggest a further role of the disulfide-linked segment.

As shown in Table 1, the FSF kinetic experiments (Verheyden et al. 2004) resulted in different activation enthalpy (ΔH^#) and entropy (ΔS^#) changes for the activation processes of the bWTin and of the rΔΑin enzymes. However, these experiments did not clarify whether the differences in activation are due to the difference in sequence and/or the presence (absence) of the propeptide (Fig. 1 ▶). In order to get a deeper insight into the activation process of the enzyme and to have further hints about whether it is the sequence or the propeptide that is the determining factor, we performed TMD simulations of the activation and inactivation pathways of three different types of chymotrypsin, bWT, bΔA, and rΔΑ, and compared the generated conformational changes. To check the reproducibility, we carried out additional MD simulations and activation TMD calculations with different random number generator seeds, as explained in the Materials and Methods. The results of these simulations are shown in the Supplemental Material. For each variant, the additional activation pathways are in good agreement with the trajectories generated by the first set of random numbers. Therefore, in the following section, only the first set of data, in which the inactivation pathway is also present, is going to be discussed.

Table 1.

Activation rate constant k, activation enthalpy ΔH# and activation entropy ΔS# values as the function of temperature, for the bWT and rΔA variants, measured by the FSF experiments

Chymotrypsin variant	t (°C)	k (s−1)	ΔH# (kJ • mol−1)	ΔS# (J • mol−1K−1)
bWT	16.4	0.434 ± 0.008	145 = 1	249 ± 4
	20.9	1.070 ± 0.070
	25.0	2.5 ± 0.2
	29.4	6.1 ± 0.10
	34.3	15.0 ± 1.0
rΔA	11.3	0.58 ± 0.13	89 ± 6	64 ± 19
	15.7	0.98 ± 0.20
	20.1	2.04 ± 0.22
	25.0	3.84 ± 0.69
	28.5	4.7 ± 1.0

Reproduced for convenience from Verheyden et al. 2004.

Results and Discussion

Analysis of the free MD simulations

MD simulations of the bWTin/ac, bΔAin/ac, and rΔAin/ac variants were carried out over 200 psec (Table 2 and see Materials and Methods). Analysis of the potential energy and rms positional differences during the equilibration process showed for all MD simulations an equilibrium situation after ~100 psec of simulation time (data not shown). Although, because of the presence of water, the relaxation time is approximately double the value observed in vacuum (Wroblowski et al. 1997), no other striking differences could be observed between the vacuum and solvent MD trajectories.

Table 2.

Parameters of the MD-simulations

Start structure	4CHA	2CGA	bWTac	bWTin	b/rΔAac	b/rΔAin
Modifications	G12, L13 added	Residues 14, 15, 147, 148 deleted	Residues 1–15 deleted	Residues 1–15 deleted	Residues mutated to rat	Residues mutated to rat
No. of atoms	15,005	13,499	15,110	13,571	14,670	13,587
No. of solvent molecules	4235	3733	4305	3792	4163	3802
No. of charged groups
Glu	5	5	5	5	8	8
Asp	9	9	9	9	11	11
C terminus	3	3	2	2	2	2
Arg	3	3	3	3	2	2
LysH	14	14	14	14	9	9
HisH	2	2	2	2	2	2
N terminus	3	3	2	2	2	2
No. of counter ions	Na+: 17 Cl−: 22	Na+: 17 Cl−: 22	Na+: 16 Cl−: 21	Na+: 16 Cl−: 21	Na+: 21 Cl−: 15	Na+: 21 Cl−: 15
Box geometry	Truncated octahedron	Truncated octahedron	Truncated octahedron	Truncated octahedron	Truncated octahedron	Truncated octahedron
Box size (Å)	68.4	66.4	68.4	66.4	68.0	66.5
Temperature	300K	300K	300K	300K	300K	300K
Simulation time	200 psec	200 psec	200 psec	200 psec	200 psec	200 psec
Nonbonded cut-off (Å)	14	14	14	14	14	14

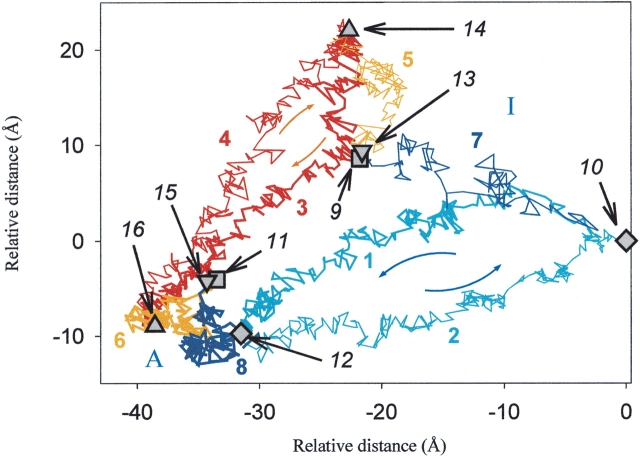
The conformational space covered by the MD simulations and by the subsequent TMD simulations of the activation/inactivation pathways of the different types of chymotrypsin was monitored by the “best plane projection” (Diamond 1974; Levitt 1983). The averaged rms positional differences of the C_α-atoms between each of the selected intermediate structures on the pathway (generated by the MD and TMD) were calculated, and afterward the best plane projection was applied (Fig. 2 ▶). This representation allows the comparison of relative differences between the trajectories in a two-dimensional plot. Figure 2 ▶ shows the differences that are already visible during the 200-psec MD simulations between the behavior of the bWT and bΔA chymotrypsins. During the time course of the MD simulations, the structures starting from nearly the same initial point in the conformational space become more dissimilar. They do not show a tendency to overlap but a tendency to diverge, as indicated by lines 5, 6, 7, and 8 on Figure 2 ▶. The inactive structures move farther away from their initial structures (lines 5 and 7) than the active ones (lines 6 and 8), suggesting, in agreement with previous findings (Wroblowski et al. 1997) and with the crystallographic B-values of the 4CHA and 2CGA files, that the inactive conformers are less stable than the active ones.

Figure 2.

Best plane projection (Diamond 1974; Levitt 1983; Kruger and Szameit 1992) of the rms distances between every second picosecond structure of the MD and TMD simulations of bWT and bΔA. Every structure is represented by a vector of 3N =3 × 241 (respectively 3 × 228) coordinates for the C_α atoms of the corresponding type of chymotrypsin: (1) bWT-chymotrypsin TMD simulation, inactive to active (activation); (2) bWT-chymotrypsin TMD simulation, active to inactive (inactivation); (3) bΔA-chymotrypsin TMD simulation, inactive to active (activation); (4) bΔA-chymotrypsin TMD simulation, active to inactive (inactivation); (5) bΔAin-chymotrypsin equilibrium MD simulation; (6) bΔAac-chymotrypsin equilibrium MD simulation; (7) bWTin-chymotrypsin equilibrium MD simulation; (8) bWTac-chymotrypsin equilibrium MD simulation; (9,13) bWTin- and bΔAin-chymotrypsins before the MD simulation; (10) bWTin-chymotrypsin after 200-psec MD; (11,15) bWTac- and bΔAac-chymotryp-sin before MD simulation; (12) bWTac-chymotrypsin after 200-psec MD; (14) bΔAin-chymotrypsin after 200-psec MD; (16) bΔAac-chymotrypsin after 200-psec MD. A and I indicate the active and inactive regions.

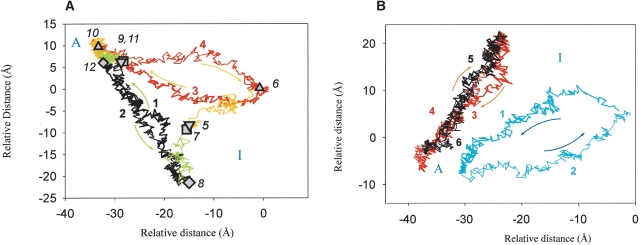
A comparison of the behavior of two ΔA variants (rΔA and bΔA) during the 200-psec MD simulations (Fig. 3A ▶) shows that the active structures differ less extensively from each other than do the inactive ones, just as in the bWT-bΔA case (Figs. 2 ▶, 3A ▶). The difference between the corresponding active and inactive trajectories is less pronounced than in the case of the bΔA and bWT variants (Fig. 2 ▶). This indicates that the influence of the sequence differences is less important than the presence of the propeptide. The TMD simulations, as will be discussed in the following section, point out this phenomenon even more remarkably.

Figure 3.

(A) Best plane projection (Diamond 1974; Levitt 1983; Kruger and Szameit 1992) of the rms distances between every second picosecond structure of the MD and TMD simulations of the bovine and rat-ΔA-chymotrypsin (b/rΔA): (1) Activation of rΔAin-chymotrypsin; (2) inactivation of rΔAac-chymotrypsin; (3) activation of bΔAin-chymotrypsin; (4) inactivation of bΔAac-chymotrypsin; (5) starting structure of the bΔAin-chymotrypsin equilibrium MD simulation; (6) final structure of the bΔAin-chymotrypsin equilibrium MD simulation; (7) starting structure of the rΔAin-chymotrypsin equilibrium MD simulation; (8) final structure of the rΔAin-chymotrypsin equilibrium MD simulation; (9) starting structure of the bΔAac-chymotrypsin equilibrium MD simulation; (10) final structure of the bΔAac-chymotrypsin equilibrium MD simulation; (11) starting structure of the rΔAac-chymotrypsin equilibrium MD simulation; (12) final structure of the rΔAac-chymotrypsin equilibrium MD simulation. “A” and “I” indicate the active and inactive regions. (B) Best plane projection (Diamond 1974; Levitt 1983; Kruger and Szameit 1992) of the rms distances between every second picosecond structure of the TMD simulations of WT bovine chymotrypsin (bWT) and bovine and rat-ΔA-chymotrypsin (b/rΔA) structures. (1) Activation of bWTin-chymotrypsin; (2) inactivation of bWTac-chymotrypsin; (3) activation of bΔAin-chymotrypsin; (4) inactivation of bΔAac-chymotrypsin; (5) activation of rΔAin-chymotrypsin; (6) inactivation of rΔAac-chymotrypsin. “A” and “I” indicate the active and inactive regions.

During the 200-psec MD runs, in the case of all three variants (bWT, bΔA, and rΔA), both the inactive and active conformations are maintained without significant change in their structure, as monitored by the rmsd values toward the corresponding X-ray structures and by three main structural indicators such as the I16–D194 salt bridge and the position of residues M192 and G193. The rmsd values, as measured to the 2CGA and 4CHA structures, respectively, are in none of the cases larger than 2 Å. In each active structure and in none of the inactive structures, the I16–D194 salt bridge is formed, residue M192 is exposed to the surface, and residue G193 is located in the area of the Ramachandran plot that is determined by X-ray in 4CHA. Because during the 200-psec MD simulations no tendency toward a conformational change resulting in the activation (or inactivation) process could be found, subsequent TMD calculations were performed on each enzyme type. For each TMD simulation, the final structures of the preceding 200-psec MD simulations were used as initial and target structures, that is, active as final and inactive as initial structures in activation TMD runs and vice versa in the inactivation TMD simulations.

Analysis and overall comparison of the pathways obtained by the TMD simulations

During the TMD simulation, no pronounced enthalpic energy barrier that could be attributed to a transition state is visible. In contrast, it shows noisy energy trajectories with many small maxima and minima, indicating that the protein undergoes a lot of local transitions on the pathway (data not shown). Each simulation runs for 500 psec, which is 300 psec longer than the previous vacuum simulation (Wroblowski et al. 1997). Even so, the main features of the activation and inactivation processes, such as the pattern of the I16–D194 distance change (data not shown) and the order of the activation events, are unaltered and the same characteristic dihedral angle changes are involved, as will be shown later. This is probably because the observed events are crucial for the activation, so that the protein has to go through these transitions in order to reach the active state whether the simulations were performed in vacuum or in water. Analyzing the H-bonds formed by the residues involved in the activation process, that is, the rather hydrophobic segment2 (residues I16–G19) (Fig. 1 ▶), residues M192 and D194 and the surrounding water molecules, we could not find significant differences in the H-bond pattern of the active or inactive states.

The activation trajectories of the bWT and the bΔA variants are shown on Figure 2 ▶ by lines 1, 2 and 3, 4, respectively. It can be seen that both the activation and inactivation pathways occupy different parts of the conformational space in the two different enzyme species.

The conformational space of activation of the rΔAin and bΔΑin variants is compared with the one of bWΔin enzyme by a best plane projection in Figure 3B ▶. As was mentioned earlier, the structures of the starting and target points of the TMD calculations were generated by the preceding 200-psec MD runs. These structures are very similar, as they occupy nearby regions of the conformational space, and the rms difference is <1.9 Å, using as reference the rΔAin/ac structures, respectively. The TMD pathways cover nearby regions of the conformational space as well (Fig. 3B ▶), indicating, together with the MD simulations, that the two species lacking the propeptide, rΔAin and bΔΑin, respectively, behave very similarly despite their difference in amino acid sequence. This means that the difference in sequence between the two chymotrypsins is less determinant than the presence of the propeptide. From the comparison of the different simulated pathways, it can be concluded that the propeptide (A-chain) plays an important role in defining the conformational space that will be explored during the activation. In contrast, the sequence differences between bovine and rat chymotrypsin play a less pronounced role in the whole transition process.

Previous studies that showed the existence of different noncovalent interactions among the propeptide residues and between 11 amino acid residues in the propeptide and the rest of the protein in the zymogen and the active enzyme support the importance of the propeptide (Wang et al. 1985; Kardos et al. 1999). These residues are, in contrast to the other serine proteases, conserved in bovine, dog, and rat chymotrypsin and in elastase 2. Therefore, it was assumed that these noncovalent interactions themselves were responsible for the higher stability of chymotrypsin harboring the propeptide (Kardos et al. 1999). We can support this assumption by analyzing the H-bonds formed by the propeptide during the simulation. We found that residues E20, A120, Q157, and W207 form H-bonds with the propeptide in both the active and inactive structures and during 90%–100% of the simulation time, whereas residues such as I16, V17, N18, G19, S26, S159, and G205 form H-bonds occasionally. As the residues that are interacting with the propeptide can be found in both β-barrels, the propeptide links these two parts of the protein, ensuring a tighter packing of the WT enzyme as compared with the ΔA variant.

Rms fluctuations

In order to find out in which protein segments the main deviations of the activation pathways of the different chymotrypsin types occur, we monitored the rms fluctuations for each residue during the time course of the MD and TMD simulations for the inactive structures and for the activation processes, as explained in Materials and Methods.

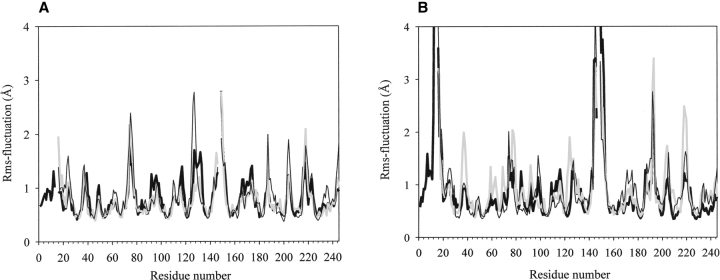
During the MD simulations, the inchoation of the differences in the behavior of the WT and ΔA variants can be observed (Fig. 4A ▶). Although some fluctuations that were found by the TMD (Fig. 4B ▶) simulations can be seen on the MD fluctuation graph as well, they are on a smaller scale, especially for regions that are rearranging the most on activation, such as segment2 (residues I16–G19), loop6 (residues G184–G197), and loop7 (residues G216–G/Q226) (Fig. 1 ▶). During the MD simulations, the fluctuations are more disturbed by random motions than during the TMD runs; they are more local fluctuations rather than being directed by any tendency. This phenomenon can be seen by looking at Figure 4A ▶ at the peaks at residues 46 and at 76, where the fluctuations become smaller in the TMD (Fig. 4B ▶) than they were at the final state of the MD. In the TMD simulations, the local fluctuations are dominated by the movements resulting from the conformational transition. The patterns of the rms fluctuations show that during the activation process, the same segments are subjected to conformational changes in all variants. However, rat-ΔA-chymotrypsin and bΔA-chymotrypsin to undergo even more pronounced rms fluctuations in the loops 34–42, 68–80, 122–136, 184–197, 201–210, and 216–226 and for the individual residue Met 192 than the bWT variant; that is, these segments reorganize on a larger scale in the b/rΔA than in bWT species on activation. From these segments, loops 34–42, 68–80, and 122–136 are to a large extent surface exposed, but residues 184–197 and 201–210 are located in that part of the protein that is directly involved in the activation process, that is, in loop6 and loop7 in β-barrel2 (residues A/P132–G/Q226), as shown by Figure 1 ▶. We calculated, using the TMD pathways after applying main chain fitting for both β-barrel structures, the rmsd values between their positions in the corresponding active and inactive conformations in the bWT and b/rΔA variants. We could find for β-barrel1 (residues G25–S/N125) (Fig. 1 ▶) a 1.53 Å and for β-barrel2 a 1.60 Å difference in the bWT enzyme. In the case of the bΔA variant, these values are 2.10 Å and 2.62 Å, and for rΔA 1.82 Å and 2.48 Å, respectively. Similar to the rms fluctuation patterns, these rmsd values are indicative of larger-scale rearrangements, especially for β-barrel2 in the b/rΔA mutant as compared with the bWT.

Figure 4.

Rms fluctuations (Kruger and Szameit 1992) plotted vs. the amino acid sequence number (WT chymotrypsin numbering; see Materials and Methods and Fig. 1 ▶), calculated for the MD simulations on the inactive structures (A) and for the TMD activation paths (B) of bWT (black bold line), bΔA-chymotrypsin (gray bold line), and rΔA-chymotrypsin (black line).

Comparison of the TMD results with the previous FSF experiments

The larger-scale movements shown by the rms fluctuations graphs and the larger rmsd values measured for each β-barrel between their active and inactive state for the b/rΔA structures as compared with the WT can be attributed to the lack of the propeptide, because in the WT the presence of the β-chain that spans both β-barrel structures ensures a tighter packing of the protein as compared with the ΔA variants, by anchoring the A-chain residues to the adjacent surface loops via the Cys 1–Cys 122 disulfide bridge and the noncovalent interactions, such as the H-bonds that were described earlier. Consequently, this leads to a looser protein structure that is more susceptible to structural fluctuations and thus perturbing forces, that is, denaturation or proteolysis.

These observations correlate with the results of the previous FSF experiments (Verheyden et al. 2004) that show different activation kinetics of the bWT and rΔA enzymes, resulting in different values for the rate constant, k (Table 1; Fig. 5 ▶), and for the activation enthalpy and entropy changes, for the ΔH^# and ΔS^#, respectively (Table 1). The smaller ΔH^# and ΔS^# values belonging to the ΔA variant can indicate a less stable and less tight packed inactive structure as compared with the WT. For the WT, the rate constant k has smaller values in the 5°–27°C interval than for the ΔΑ mutant but increases faster with the increasing temperature (Fig. 5 ▶). This phenomenon indicates a kinetic retardation on the activation reaction due to the presence of the propeptide. However, with increasing temperature, the guiding effect of the propeptide predominates over its restriction on the motion of segment2, which results, at the physiological temperature, in a faster activation of the WT than of the Δ Αmutant.

Figure 5.

Rate constants measured at the activation of the bWT and the rΔA as a function of the temperature. (Reproduced from Verheyden et al. 2004.)

From the extended H-bond network between the propeptide and the rest of the protein and the differences in the ΔS^# and ΔH^# values measured for the bWT and b/rΔA variants, it can be postulated, in accordance with previous studies (Kardos et al. 1999), that the noncovalent interactions between the propeptide and the rest of the protein and the cysteine bridge Cys 1–Cys 122 are both important to ensure a stable structure. The noncovalent interactions, apart from their direct stabilizing effect, have also an indirect but important role to strengthen the binding of Cys 1 to Cys 122 in a cooperative manner (Kardos et al. 1999). The Cys 1–Cys 122 disulfide bridge is essential as preincubation of ΔA-chymotrypsin with exogenous chymotrypsinogen propeptide, in which the Cys in position 1 was exchanged by Ser, failed to increase the stability of the enzyme against thermal or guanidine hydrochloride denaturation (Kardos et al. 1999).

Graphical analysis of the generated pathways and description of the conformational change

The different activation pathways show common features in the main activation steps that were described earlier (Wroblowski et al. 1997), despite the differences in the activation conformational space of the bWT and the ΔA species (Figs. 2 ▶, 3B ▶). All of the activation pathways consist of several sequential transitions in different parts of the molecule, leading to the active conformation. The biggest changes occur in segment2 (I16–G19), loop6 (G184–G197), loop7 (G216–G226) and the cleavage region between the β and α chains, L143–Y146 and A149–P152, respectively. The sequence of these events is similar in all activation pathways under consideration (Fig. 6 ▶). The activation process is accompanied by the movement of loop7, which is part of the substrate-binding pocket. This is mainly a rigid body movement around the hinges Gly 216–Ser 217 and Thr 222–Ser 223. Because the cysteine bridge Cys 191–Cys 220 is important for the high activity of chymotrypsin (Varallyay et al. 1997), it can be assumed that this movement is necessary to trigger the conformational change in loop6. Because of the movement of Cys 191, Met 192 will reorient. This residue has already been proven to be important in the activation process (Stoesz and Lumry 1979; Wroblowski et al. 1997), as the side chain of Met 192 moves from a buried place in the core of the molecule to the surface, triggering the motion of the neighbors Gly 193 and Asp 194, and leaves a cavity behind that is necessary for the penetration of residue Ile 16 into the protein. As the final step, the side chain of Asp 194 reorients and forms the stabilizing salt bridge with the N terminus of residue I16. Through this salt bridge, the catalytic Ser 195 residue obtains and can maintain its correct conformation, and the active site, the oxyanion hole, and the substrate-binding cleft are secured.

Figure 6.

Snapshots of the calculated TMD pathways showing, by ribbon representation of the backbone atoms of ΔA-chymotrypsin, the most important subsequent transitions during the activation process (Kraulis 1991). The amino acid residues that show important dihedral angle transitions during the activation process are indicated. In the inactive conformation (A), Ile 16 is still lying at the outside of the protein structure. During the reorientation of the N terminus of the B-chain, Ile 16 moves closer (B) to the place where a cavity is created by a reorientation of Met 192. After penetration of Ile 16 in this cavity (C), Asp 194 undergoes a big reorientation to form, in the next step (D), the stabilizing salt bridge with the Ile 16 N terminus.

Segments 143–146 and 149–152, because of their solvent-exposed free termini, present large-scale fluctuations. Despite the big structural reorganizations of these segments, they probably do not play an essential role in the activation process because π-chymotrypsin, lacking these two extra termini, is also active. However, the autodigestion leads to a new C terminus, which participates in the formation of a β-barrel in the active conformation and thus contributes to the stability of the active form.

Time course of selected backbone dihedral angles

A more detailed description of the influence of the conformational change on the backbone of the polypeptide chain can be obtained by analyzing the evolution of the backbone dihedral ϕ and ψ angles along the activation pathway. This gives a notion about the hinges that are involved in the conformational transition. Figure 7 ▶ summarizes the most important dihedral angle transitions (>50°) in the activation domains segment2 and loop6 during the 500-psec simulation of the activation process of bWTin. The patterns of the other chymotrypsin molecules are very similar to it (data not shown).

Figure 7.

Dihedral angle transitions (>50°) observed during the activation pathway of the bWTin enzyme in segments 16–20 and 184–197 plotted vs. time. (Solid line) Dihedral angle is unchanged compared with its previous value; (dot) transition occurs; (no line) dihedral angle has reached its final value.

During the activation process, many conformational transitions occur in almost all of the residues of segment2. They show the necessity for the overall flexibility of this part of the chain in order to obtain a correct orientation of Ile 16 for penetration and salt-bridge formation. Residue 19 shows the largest number of dihedral angle transitions, indicating the role of Gly 19 as a hinge residue in the activation process (Wang et al. 1985). In loop6, residues 185, 186, and 189 undergo only dihedral transitions in the beginning of the activation process. At the final part of the activation process, when the most important conformational changes occur in the active site, Gly 187 and Val 188 will serve as hinges. These transitions seem to be triggered by the motion of Cys 191. The transitions occurring in this residue also induce other reorientations in the backbone of the adjacent residues Ser 190 and Met 192. The conformational changes in the backbone of the latter residue then cause a reorientation of Gly 193(N) in the direction of the substrate binding site and a rotation around the C_α-C bond of Asp 194 of ~180°. This allows the formation of the salt bridge between Ile 16 and Asp 194.

In contrast to these two segments, there are nonpronounced sudden transitions in the substrate-binding loop, that is, loop7. Instead of distinct transitions, residues 217, 218 and 222, 223 showed a very high (>60°) flexibility in their dihedral angles (data not shown). The high fluctuation of the φ, ψ dihedral angles of these residues during the transition can also indicate their role as hinges.

Conclusions and outlook

We have performed MD and TMD calculations of the activation and inactivation processes of three different types of α-chymotrypsin: bWT, bΔA, and rΔA. In contrast to a previous study on bWT chymotrypsin (Wroblowski et al. 1997), the solvent has been taken into account explicitly. Our aim was to compare different pathways and to learn more about the importance of the propeptide and the differences in amino acid sequences in the stability and the activation process of chymotrypsin. The pathways generated by the simulations belong at least to a set of possible trajectories. For bWT and rΔA chymotrypsins, the simulations were compared with previously published FSF kinetic experiments that were carried out on these variants (Verheyden et al. 2004).

In the present study, we found that the propeptide, in contrast to the sequence differences between bovine and rat variants, has an important influence on the activation’s course; that is, different conformational space is explored in the WT and in the ΔΑ species during activation. We could detect H-bonds formed between the residues of the propeptide and the main part of the protein. As the H-bonding residues can be found in both β-barrels, the propeptide spans the two β-barrels, ensuring a tight packing of the enzyme. By the rms fluctuation analysis, the same, but more fluctuating, regions in the ΔA variants as compared with the WT species were observed (Fig. 4B ▶), showing that the missing propeptide does not change the main characteristics of activation but does affect the loop mobility and tightness of the structure. The lower ΔS^# and ΔH^# values obtained from the previous FSF experiments (Verheyden et al. 2004) for the ΔA mutant as compared with the WT and the different temperature dependence of the rate constant (k) suggest that the switches to the transition state in the ΔA mutant is accompanied by less bond breaking and a smaller increase in disorder as compared with the WT. Most probably this is due to a more disordered inactive structure, as indicated by the MD and TMD results and elucidated by the best plane projection, H-bond analysis, and rmsd analysis.

Our results support the concept (Wang et al. 1985; Kardos et al. 1999) that, next to the Cys 1–Cys 122 disulfide bridge, the noncovalent interactions between the propeptide and the rest of the enzyme are also important in order to ensure a stable protein structure, certainly in the inactive form, and to limit the conformational space that is likely to be explored during the activation, that is, to provide guidance for the rotation of residue I16 toward residue D194 at physiological temperature.

The sequence of the activation process can be deduced from the simulations, and its main features are the same in all variants: The movement of loop7 triggers via a disulfide bridge the movement of loop6 and, subsequently, the reorientation of Met 192. The flip of Met 192 from a buried to a more surface-exposed state results in the relocation of residues Gly 193, Asp 194, and Ile 16, where residues Asp 194 and Ile 16 form the stabilizing salt bridge.

A description of the sequence of events during the conformational change was also possible on the basis of the analysis of the dihedral angle transitions. From this analysis, it can be concluded that all of the calculated activation processes proceed via dihedral switches in the backbone of amino acid residues 17, 18, 19, 187, 217, 218, and 223, which thus serve as hinges.

The model proposed on the basis of the simulations is a starting point for the design of mutants. Predictions can be made, for example, on hinge residues or on residues that hamper the movement of the segment 192–194. The predicted role of these amino acid residues can be controlled by kinetic experiments and further simulations carried out on the mutants.

Materials and methods

Programs used

All energy minimizations and MD and TMD simulations were performed with the GROMOS96 program package (Van Gunsteren 1996) having the extension for the TMD calculation (Swegat et al. 1997). All of the simulations were performed in a water-and counterion-containing environment. The analysis of the trajectory was performed with the program SIMLYS (Kruger et al. 1991; Kruger and Szameit 1992). The program WHATIF (Vriend 1990) was used to model the structure of rat chymotrypsin. For visual inspection of the trajectories, the programs RasMol V2.7.1 (Sayle and Milner-White 1995) and Swiss-PdbViewer (Guex and Peitsch 1997) were used.

Modeling of the initial structures

The coordinates of bovine α-chymotrypsin (4CHA; Tsukada and Blow 1985) (1.68 Å resolution, R value 0.234) and of bovine chymotrypsinogen (2CGA; Wang et al. 1985) (1.80 Å resolution, R value 0.170) were obtained from the Brookhaven Protein Data Bank (Bernstein et al. 1977). For further details, see Table 2. Because the PDB entry of chymotrypsin (4CHA) lacks the flexible C-terminal residues Gly 12 and Leu 13 of the propeptide (A-chain), they were modeled using the BUILD option of WHATIF. In order to generate the chymotrypsinogen-like inactive structure of α-chymotrypsin that is present at high pH (~11) (Verheyden et al. 2004), we deleted the residues Ser 14, Arg 15, and Thr 147 and Asn 148 from the original chymotrypsinogen coordinates (2CGA). The missing atoms of the newly generated C termini were added using the Gromos96 program. Polar hydrogens were added using standard geometries. All other nonpolar hydrogen atoms (CH, CH₂, CH₃) were included in the corresponding carbon atom. The two different structures of the WT bovine enzyme are the neutral pH active bovine α-chymotrypsin conformer with A-chain (bWTac) and the high pH inactive bovine α-chymotrypsin conformer with A-chain (bWTin).

The bovine structures lacking the propeptide (bΔA) were obtained by deleting the first 15 residues from the structures bWTac and bWTin. This resulted in two different structures of the bovine α-chymotrypsin, without the prosegment: the active form (bΔAac) and the inactive form (bΔAin).

Because the coordinates of rat chymotrypsin and rat chymotrypsinogen are not available yet, the rat active and inactive conformations without the propeptide were modeled. A reasonable modeling of the structures was possible because of the high sequence homology between rat and bovine chymotrypsin. For this purpose, the active and inactive forms of bovine ΔA-chymotrypsin were taken as reference structure (bΔAac and bΔAin, respectively). The MUTATE option of WHATIF was used and the placement of the amino acid chain was optimized using the option DEBUMP. The obtained structures were called “rΔAac” (the active rat-α-chymotrypsin conformer, lacking the propeptide) and “rΔAin” (the inactive rat-α-chymotrypsin conformer, lacking the propeptide). Every further step of the set-up procedure and the MD/TMD simulations were done on these modeled structures, as explained later.

MD simulations

In order to reduce conformational stress, we first subjected the structures to a 500-step steepest descent energy minimization without solvent. The structures were placed in a truncated octahedral box of SPC water (Berendsen et al. 1981) with a minimum distance of 0.7 nm between the protein and the wall of the box. The specifications can be seen in Table 2. The protein–water system contained also the counterions Cl⁻ and Na⁺. The protein and the water molecules were again subjected to a 500-step steepest-descent energy minimization. In order to start the MD simulation, we assigned the velocities of the atoms to follow a Maxwellian distribution of the velocity at 100K with different sets of random number generator seed. The systems were heated in five consecutive steps of 1 psec to 300K, and a free MD simulation in water was performed over 200 psec. The temperature of the protein and the solvent was kept fixed at 300K using a separate weak coupling to an external water bath (Berendsen et al. 1984) with a coupling constant of 0.1 psec. The pressure was also kept constant at 1 atm by coupling to an external pressure bath (Berendsen et al. 1984) with a coupling constant of 0.5 psec. All MD simulations were performed under the same conditions: The integration step was 2 fsec, nonbonded (Van der Waals and electrostatic) interactions closer to 1.4 nm were included, and the nonbonded pairs were updated every 10 steps. The calculations were performed using an Indigo2 (R10000 processor) workstation.

After 200 psec simulation, the final structures of the MD simulations could be regarded as equilibrated in terms of the potential energy and rms positional differences. The best plane projection (Diamond 1974) also indicates a stable state for those structures (Figs. 2 ▶, 3A ▶). The final structures of the equilibrium simulation were used as the initial and the target structures to start the subsequent pathway calculations.

TMD pathway calculations

The TMD pathway calculations are performed by introducing a constraint force (Schlitter et al. 1993, 1994; Wroblowski et al. 1997). The constraint is defined by the sum of the distances between all atoms of the initial and final structure. The initial and final molecules are superimposed on each other. The constraint is made time dependent during the simulation; that is, the distance between the two structures is reduced constantly in each step of the simulation and varies linearly with the simulation time. This ensures the conformational change from an initial conformation to a target conformation in the limited time interval of the TMD simulation. Because only one degree of freedom is constrained, the system has still a considerable flexibility during the transformation. Previous simulations have shown that segments of the molecule can move relatively independently. The simulation parameters for the TMD calculations correspond to those for the MD simulation. The time-dependent distance parameter ρ(t) decreased within 500 psec. The exact overlap with the target structure after 500 psec would mean ρ = 0 and the absence of thermal fluctuations. Therefore the simulation is stopped when a distance ρ_final = 0.05 nm is reached, which corresponds to the average (thermal) conformational fluctuation of the final structure.

The following pathway calculations, simulations with different random number generator seeds, that is, with different initial velocity vectors, were performed in water using the TMD method: the activation and deactivation pathways for WT bovine chymotrypsin (bWT) and bovine and rat-ΔA-chymotrypsin (bΔA and rΔA) using as initial and target structures the final structures of the 200-psec MD runs obtained with the first set of random number generator seeds under the conditions given in Tables 2 and 3. Keeping the initial coordinates and parameters the same as in Table 2, we performed MD simulations with two other sets of random number generator seeds on the active and inactive structures for bWT and bΔA. Using the final structures of these MD simulations and the parameters shown in Table 3 for the bWT and bΔA species, we generated two other activation pathways by TMD. For the rΔA variant, five MD and TMD activation simulations were carried out following the same procedure. There is a good agreement between the tendency of the first set of trajectories and the corresponding trajectories generated by the other sets of simulations, as analyzed by the best plane projection (Diamond 1974). Therefore, in this paper we show and analyze in detail the first set of results in which the inactivation paths are also simulated. The diamond plots of the multiple trajectories generated using different random number seeds are given as supplementary data by Supplementary Figures 1 ▶–3 ▶.

Table 3.

Parameters of the TMD-simulations

Initial conformation	Final conformation	Simulation time (psec)	Atoms to which constraint is applied	Box size (Å)	Number of solvent molecules
bWTin	bWTac	500	1–2261	66.4	3733
bΔAin	bΔAac	500	1–2158	66.4	3792
rΔAin	rΔAac	500	1–2145	66.5	3802
bWTac	bWTin	500	1–2261	68.4	4235
bΔAac	bΔAin	500	1–2158	68.4	4305
rΔAac	rΔAin	500	1–2145	68.0	4163

Rms fluctuation

The definition of the rms fluctuation is given by the formula

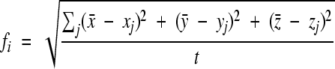where f_i is the rms fluctuation of atom i and x̄, ȳ, and z̄ coordinates give the average position of atom i over the total time frame of the simulation, that is, 200 psec in the case of MD and 500 psec in the case of TMD simulations. Variables x_j, y_j, and z_j are the coordinates of time step j. Variable t is the number of time steps. For Figure 4, A and B ▶, the C-α atoms and j = 200 for the MD plots and j = 500 for the TMD plots were used. The rms fluctuation reflects the local mobility of atoms. It gives an additional insight into their movements during the transition as compared with the rms deviation values. In the case of the TMD simulation, the local fluctuations are dominated by the shift caused by the movement toward the target structure. Using the rms fluctuation values, we can efficiently detect the regions that show significant differences in their motion in the three different variants (bWT, b/rΔA).

Rms difference calculations

If it is not denoted otherwise, each rmsd value in the text was calculated after an all-atom fit to the defined template using backbone atoms for the calculation. For fitting, the Magic Fit option of the program called Swiss-PdbViewer was used (Guex and Peitsch 1997).

FSF experiments

All of the FSF experiments presented in this paper were described in our previously published paper (Verheyden et al. 2004). In order to facilitate the comparison of the simulation results presented in this paper with the previously published FSF results (Verheyden et al. 2004), we reproduced some data here again.

Electronic supplemental material

Three figures are given as Supplemental Material: The first shows three activation TMD trajectories of the bWT species together with the corresponding MD runs. The second shows three activation TMD trajectories and the corresponding MD trajectories for the bΔA variant. The third figure presents five activation TMD trajectories of the rΔA species and the MD trajectories belonging to the activation TMD trajectory that is discussed in detail in the text. We omitted the rest of the MD trajectories because we wanted to keep the clarity of the figure and show more than three activation TMD trajectories at the same time.

In all cases of additional MD simulations (active and inactive) a 1-psec MD run was performed to generate different initial velocity vectors according to the different random number seeds starting from the same initial coordinates. That 1-psec-MD generated the initial coordinates for each individual MD simulation; these coordinates are indicated, together with the final structures, by individual symbols. Each additional activation TMD run was performed starting from the final structure of the inactive MD simulations and targeting toward the final structure of the active MD simulation.

Abbreviations

• rms, root mean square

• MD, molecular dynamics

• rmsd, root mean square deviation

• TMD, targeted molecular dynamics

• ΔA-chymotrypsin, variants without propeptide (A-chain)

• WT, wild-type variants with pro-peptide (A-chain)

• letter “b,” bovine variants

• letter “r,” rat variants

• ac, active form

• in, inactive form

• bWTac, active conformation of bovine wild-type chymotrypsin

• bWTin, inactive conformation of bovine wild-type chymotrypsin

• bΔAac, active conformation of bovine chymotrypsin without propeptide

• bΔAin, inactive conformation of bovine chymotrypsin without propeptide

• rΔAac, active conformation of rat chymotrypsin without propeptide

• rΔAin, inactive conformation of rat chymotrypsin without propeptide

Article and publication are at http://www.proteinscience.org/cgi/doi/10.1110/ps.04825004.