Democracy in animals: the evolution of shared group decisions

Abstract

A ‘consensus decision’ is when the members of a group choose, collectively, between mutually exclusive actions. In humans, consensus decisions are often made democratically or in an ‘equally shared’ manner, i.e. all group members contribute to the decision. Biologists are only now realizing that shared consensus decisions also occur in social animals (other than eusocial insects). Sharing of decisions is, in principle, more profitable for groups than accepting the ‘unshared’ decision of a single dominant member. However, this is not true for all individual group members, posing a question as to how shared decision making could evolve. Here, we use a game theory model to show that sharing of decisions can evolve under a wide range of circumstances but especially in the following ones: when groups are heterogeneous in composition; when alternative decision outcomes differ in potential costs and these costs are large; when grouping benefits are marginal; or when groups are close to, or above, optimal size. Since these conditions are common in nature, it is easy to see how mechanisms for shared decision making could have arisen in a wide range of species, including early human ancestors.

1. Introduction

Consider a group of primates deciding where to travel after a rest period, a flock of birds deciding when to leave a foraging patch or a swarm of bees choosing a new nest site; unless all members decide on the same action, some will be left behind and will forfeit, at least temporarily, the advantages of group living (e.g. Black 1988; Seeley & Buhrman 1999; Byrne 2000; Krause & Ruxton 2002; Conradt & Roper 2003). Thus, in order to maintain group cohesion, social animals—like humans—have to make consensus decisions, chiefly about the timing and nature of activities and about future travel destinations (Lusseau 2003; Simons 2004; Conradt & Roper 2005). Moreover, as in humans, consensus decisions in animals often lead to conflict of interest between group members (Conradt & Roper 2003, 2005), owing to the fact that individual members often differ with respect to their optimal activity budgets (e.g. Clutton-Brock et al. 1982; Gompper 1996; Ruckstuhl 1998, 1999; Ruckstuhl & Neuhaus 2002; Rands et al. 2003). Therefore, in order to reach a consensus, group members often have to compromise, thereby incurring a fitness cost (the ‘consensus cost’; Conradt 1998; Conradt & Roper 2003). Consensus costs can be substantial; for example, in some circumstances they are sufficient to prevent a consensus from being reached, thereby causing groups to fragment (Conradt 1998; Ruckstuhl 1998, 1999; Conradt & Roper 2000; Ruckstuhl & Neuhaus 2002).

At one extreme, a group can reach a consensus by accepting the decision of a single dominant member (‘unshared’ decision; Conradt & Roper 2003). At the other extreme, all group members could contribute equally to the decision (‘equally shared’ decision). In the latter case, the group could ‘agree’ on the decision outcome that is preferred by a majority of members (as humans often do when voting; Conradt & Roper 2003), but other ‘thresholds’ (e.g. the preferences of a sub- or super-majority of members; List 2004; Conradt & Roper 2005; Couzin et al. 2005) could also be used as the ‘consensus decision rule’. For example, a group could agree to leave a patch when at least one-third of group members are in favour of leaving. This decision would, thus, be equally shared with a sub-majority threshold of one-third of members (List 2004). Both shared and unshared decisions appear to be widespread in animals, with examples reported in species ranging from insects to primates (see Conradt & Roper 2005 for a review).

Consensus costs depend on which group members contribute to the decision. For many group members, equally shared decisions result in lower consensus costs than unshared decisions (Conradt & Roper 2003). However, this is not true for all group members because at least for the dominant, and usually for several other individuals, consensus costs are lower in unshared than in equally shared decisions (Conradt & Roper 2003). Those members should therefore prefer unshared decision making. Consequently, since equal sharing of decisions requires cooperation by all group members (e.g. Prins 1996; Couzin et al. 2005), it is unclear how it could evolve other than for making decisions that are conflict free (Conradt & Roper 2005).

Here, we develop an evolutionary game theory model to investigate how and when equally shared and unshared decision making can evolve. We then investigate which conditions favour the evolution of equally shared versus unshared decision making. Our model looks at consensus decisions about the timing of activities in groups in which global communication between group members is possible (Conradt & Roper 2005), because both shared and unshared decision making have been observed in such groups (e.g. Kummer 1968; Norton 1986; Black 1988; Lamprecht 1992; Stewart & Harcourt 1994; Beauchamp 2000; Byrne 2000; Conradt & Roper 2003, 2005).

2. Model of the evolution of consensus decisions

(a) Model type

We use a game theory model to investigate the evolution of equally shared and unshared consensus decisions. Game theory is often used as a model for phenotypic evolution in asexual populations, but its results can be extended to sexual populations if there are no more than two pure strategies (Maynard Smith 1989), as is the case here. We assume that net gains (see §2c) represent increases in the fitness of an individual (Maynard Smith 1989). An evolutionarily stable strategy (‘ESS’) is a pure or complex strategy that, if used by most members of a population, cannot be invaded by individuals using other strategies (Maynard Smith 1989). Depending on the starting position of a population, an ESS can evolve through, and then subsequently be maintained by, individual selection (Maynard Smith 1989).

(b) Basic model assumptions

1. There are benefits (‘grouping benefits’) to group members of remaining in a cohesive group, which depend on group size (Krause & Ruxton 2002).

2. There are costs to individual group members (‘consensus costs’) when the consensus decision outcome differs from their own optimal decision outcome, and these costs increase with the discrepancy between an individual's own optimal outcome and the group's consensus decision outcome (e.g. Gompper 1996; Prins 1996; Conradt 1998; Ruckstuhl 1998, 1999; Conradt & Roper 2000, 2003). In general, consensus costs are lower than grouping benefits, since otherwise the animals in question would not be social (Krause & Ruxton 2002).

3. Group members cannot be coerced by force into complying with decisions by the dominant, because either the dominant is not physically capable of coercion (e.g. Clutton-Brock et al. 1982, 1998) or the costs of coercion would exceed the benefits (Conradt & Roper 2003). Therefore, group members can decide individually whether, and to what extent, they insist on their own preferred decision outcome or submit to the wishes of other group members, including those of the dominant.

4. Group members cannot predict each other's eventual behaviour with certainty (for a detailed justification of this assumption, see electronic supplementary material).

5. The behaviour of individual group members can depend on whether they are dominant or not (Clutton-Brock 1998; Rutte et al. 2006).

6. Group members can communicate their individual preference, so that individuals know how many other group members want to change or not change activity at a given time (e.g. Black 1988; Boinski & Campbell 1995; Conradt & Roper 2003, 2005).

(c) Model structure

Imagine, for example, a group of animals at a resting site, where each group member has a different optimal time at which to leave the resting site and start foraging elsewhere. In order to avoid splitting up, the group has to arrive at a consensus decision about the time at which to change activity from resting to foraging. According to logic, during the decision-making process, each group member can ultimately either (i) insist on its own optimal preference of activity change/no change (i.e. play ‘INSIST’) or (ii) give in to other members' preferences (i.e. play ‘GIVE IN’). If more than one member plays INSIST and their preferences differ, the group necessarily splits, since in consensus decisions different preferences are mutually exclusive (Conradt & Roper 2005).

Group members can play INSIST or GIVE IN depending on whether they are dominant or not, and on how much their own optimal decision outcome differs from that of other group members; that is, on whether they are the 1st, 2nd, …, ith, … or nth member (in time), which prefers to change activity (assumptions (v) and (vi)). Let r_is/d (for all 1≤i≤n, where n is the group size) be the probability that a focal group member will play INSIST (and therefore (1−r_is/d) the probability that it will play GIVE IN) if it is the ith member (in terms of time) that prefers to change activity and is either a subordinate (r_is) or the dominant (r_id) (table 1). The focal has, thus, phenotype (r_1s, r_2s, …, r_ns)/(r_1d, r_2d, …, r_nd). We assume further that other group members are drawn randomly from the population and have the respective probabilities R_1s, R_2s, …, R_ns and R_1d, R_2d, …, R_nd to play INSIST. Because it pays each group member to ‘bluff’ and pretend that it will play INSIST, we assume that group members cannot know whether other members are ultimately going to play INSIST or GIVE IN (assumption (iv)) and, thus, cannot exploit such knowledge (in mathematical terms, the values of r_is/d and R_is/d of members during a decision are independent of each other).

Table 1.

Definition of variables.

variable	definition
ris/rid	probability that a focal group member will play INSIST if it is the ith member (in terms of time) that prefers to change activity and is either a subordinate (ris) or dominant (rid)
(1−ris)/(1−rid)	probability that a focal group member will play GIVE IN if it is the ith member (in terms of time) that prefers to change activity and is either a subordinate (1−ris) or dominant (1−rid)
Ris/Rid	probability that an individual drawn at random from a population will play INSIST if it is the ith member (in terms of time) that prefers to change activity and is either a subordinate (Ris) or dominant (Rid)
(1−Ris)/(1−Rid)	probability that an individual drawn at random from a population will play GIVE IN if it is the ith member (in terms of time) that prefers to change activity and is either a subordinate (1−Ris) or dominant (1−Rid)
B3/B2	expected grouping benefits gained by being in a group with three (B3) or two (B2) members
C1	expected consensus costs if changing activity a bit too early or too late (in the case of symmetric costs in homogeneous groups)
C2	expected consensus costs if changing activity much too early or too late (in the case of symmetric costs in homogeneous groups)
Csmall	expected consensus cost arising through timing differences between the small- and medium-sized or between the large- and medium-sized group members in a heterogeneous group (assuming symmetric costs)
Clarge	expected consensus cost arising through timing differences between the smallest and largest group members in a heterogeneous group (assuming symmetric costs)
C1late	expected consensus costs if changing activity a bit too late (in the case of asymmetric costs in homogeneous groups)
C2late	expected consensus costs if changing activity much too late (in the case of asymmetric costs in homogeneous groups)
C1early	expected consensus costs if changing activity a bit too early (in the case of asymmetric costs in homogeneous groups)
C2early	expected consensus costs if changing activity much too early (in the case of asymmetric costs in homogeneous groups)

The gains to the focal individual depend on its own behaviour and that of all other group members. Using the probabilities for different behaviours, and assuming that a member which plays GIVE IN and has a choice between two members which play INSIST gives preferably in to that member which results in the lowest consensus costs to itself, we calculate the expected gains to a given phenotype (r_1s, r_2s, …, r_ns)/(r_1d, r_2d, …, r_nd) in a given population (R_1s, R_2s, …, R_ns)/(R_1d, R_2d, …, R_nd), as follows.

3. Decisions in groups with three members

(a) Gains to a focal group member

We start with a homogeneous group with three members of similar body size (and therefore with similar resource-holding potential and similar time budgets; Ruckstuhl 1999), so that each group member has a probability of 1/3 to be the 1st, 2nd or 3rd member to prefer an activity change and a probability of 1/3 to be dominant. We also assume symmetric consensus costs (i.e. changing activity too late costs the same as changing too early; Conradt & Roper 2003). By summing the gains to the focal individuals for all possible permutations of focal preferences, focal behaviour, dominance relationships and preferences and behaviour of the other two group members, weighted by the respective probabilities, we calculate the overall expected gains to the focal depending on its own behavioural strategy (r_1s, r_2s, r_3s)/(r_1d, r_2d, r_3d) and the strategies encountered in the population (R_1s, R_2s, R_3s)/(R_1d, R_2d, R_3d), as follows:

$$\text{gains}[(r_{1\text{s}},r_{2\text{s}},r_{3\text{s}})/(r_{1\text{d}},r_{2\text{d}},r_{3\text{d}}),(R_{1\text{s}},R_{2\text{s}},R_{3\text{s}})/(R_{1\text{d}},R_{2\text{d}},R_{3\text{d}})]=\frac{1}{3}·\left(\frac{1}{3}·[r_{1\text{d}}·f(R_{2\text{s}},R_{3\text{s}})+(1-r_{1\text{d}})·g(R_{2\text{s}},R_{3\text{s}})+r_{2\text{d}}·h(R_{1\text{s}},R_{3\text{s}})+(1-r_{2\text{d}})·k(R_{1\text{s}},R_{3\text{s}})+r_{3\text{d}}·f(R_{2\text{s}},R_{1\text{s}})+(1-r_{3\text{d}})·g(R_{2\text{s}},R_{1\text{s}})]+\frac{1}{3}·\left[r_{1\text{s}}·(f(R_{2\text{d}},R_{3\text{s}})+f(R_{2\text{s}},R_{3\text{d}}))+(1-r_{1\text{s}})·(g(R_{2\text{d}},R_{3\text{s}})+g(R_{2\text{s}},R_{3\text{d}}))+r_{2\text{s}}·(h(R_{1\text{d}},R_{3\text{s}})+h(R_{1\text{s}},R_{3\text{d}}))+(1-r_{2\text{s}})·(k(R_{1\text{d}},R_{3\text{s}})+k(R_{1\text{s}},R_{3\text{d}}))+r_{3\text{s}}·(f(R_{2\text{d}},R_{1\text{s}})+f(R_{2\text{s}},R_{1\text{d}}))+(1-r_{3\text{s}})·(g(R_{2\text{d}},R_{1\text{s}})+g(R_{2\text{s}},R_{1\text{d}}))\right]\right),$$ (3.1)

where f(R_a,R_b)=(1−R_a)[(1−R_b)B3+R_b·B2/2]; g(R_a,R_b)=(1−R_a)[B3−(1−R_b)(C1+C2)/3−R_b·C2]+R_a·[R_b·B2+(1−R_b)B3−C1]; h(R_a,R_b)=(1−R_a)[(1−R_b)B3+R_b·B2]+R_a·(1−R_b)B2; k(R_a,R_b)=(1−R_a)[B3−(1−R_b)·2C1/3−R_b·C1]+R_a·[(1−R_b)·B3+R_b·B2−C1]; B2 is the grouping benefits gained by being in a group with two members; B3 is the grouping benefits gained by being in a group with three members; C1 is the expected consensus costs if changing activity a bit too early or too late; and C2 is the expected consensus costs if changing activity much too early or too late (table 1).

(b) Evolutionarily stable strategies

Since we are interested in social groups that make collective consensus decisions, we consider only strategies that lead to group stability. Thus, we have to assume that grouping benefits (B2, B3) are large relative to consensus costs (C1, C2), since otherwise animals should not be social. Further, we ignore the trivial case that consensus decisions involve no costs (i.e. we assume C1>0 and C2>0). It can be shown that these assumptions leave only four candidate strategies for ESSs (see electronic supplementary material), which we term: (i) ‘equally shared decision making requiring a majority threshold for the consensus’, (ii) ‘equally shared decision making requiring a sub-majority threshold for the consensus’, (iii) ‘equally shared decision making requiring a super-majority threshold for the consensus’, and (iv) ‘unshared decision making’. In the following, we investigate each of these four candidate strategies in turn.

We first investigate whether the strategy ‘equally shared decision making requiring a majority threshold for the consensus’ is an ESS. In a group of three, a simple majority is reached when two members prefer an activity change. Thus, a phenotype ŕ_1s, ŕ_2s, ŕ_3s)/(ŕ_1d, ŕ_2d, ŕ_3d) with the strategy of equally shared decision making with a majority threshold plays INSIST if it is the 2nd member (in time) that prefers an activity change, regardless of dominance status (i.e. ŕ_2s=ŕ_2d=1), otherwise it plays GIVE IN (i.e. ŕ_1s=ŕ_1d=ŕ_3s=ŕ_3d=0). It is thus phenotype (0,1,0)/(0,1,0). Therefore, for a population of equally sharing decision makers with a majority threshold, R_1s=R_1d=0, R_2s=R_2d=1, R_3s=R_3d=0. Using equation (3.1), it follows that the expected gains to any potentially invading phenotype (r_1s, r_2s, r_3s)/(r_1d, r_2d, r_3d) into a population (0,1,0)/(0,1,0) are

$$\text{gains}[(r_{1\text{s}},r_{2\text{s}},r_{3\text{s}})/(r_{1\text{d}},r_{2\text{d}},r_{3\text{d}}),(0,1,0)/(0,1,0)]=B3-8/9·C1-[r_{1\text{d}}+2r_{1\text{s}}]/9·(B3-C1)+[r_{2\text{d}}+2r_{2\text{s}}]·2C1/27-[r_{3\text{d}}+2r_{3\text{s}}]/9·(B3-C1).$$ (3.2)

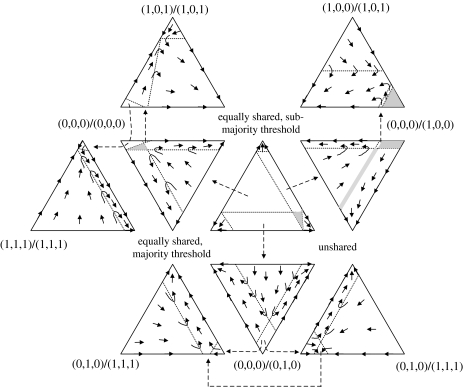
Thus, if consensus costs are low relative to grouping benefits (i.e. if B3>C1; see assumption (ii)), expected gains are maximal for r_1s=r_1d=r_3s=r3d=0 and r_2s=r_2d=1. Thus, a population of phenotypes (0,1,0)/(0,1,0) cannot be invaded, and equally shared decision making with a majority threshold is an ESS (figure 1).

Figure 1.

Phenotypic evolution in groups with three members. Each trilinear coordinate system (‘TCS’; equilateral triangle of unit height: the three perpendiculars from each point within the triangle to the sides represent proportions of the respective phenotypes marked at the corners; Edwards 2000) represents populations consisting of three different phenotypes. Different TCSs are shown closely together to indicate the overall dynamics. Arrows show the directions in which the system evolves (parameter assumptions as in §3b). Broken arrows indicate where the system evolves from one TCS to another. For clarity, in shaded areas, the direction of evolution is not shown, and the shown dynamics are not exhaustive (e.g. substituting ‘sub-majority’ for ‘super-majority’ phenotypes leads to similar dynamics).

We next investigate whether the strategy ‘equally shared decision making requiring a sub-majority threshold for the consensus’ is an ESS. In a group of three, a sub-majority is reached when the 1st member prefers an activity change. Thus, a phenotype (ŕ_1s, ŕ_2s, ŕ_3s)/(ŕ_1d, ŕ_2d, ŕ_3d) with the strategy of equally shared decision making with a sub-majority threshold plays INSIST if it is the 1st member to prefer an activity change, regardless of dominance status (i.e. ŕ_1s=ŕ_1d=1), otherwise it plays GIVE IN (i.e. ŕ_2s=ŕ_2d=ŕ_3s=ŕ_3d=0). It is thus phenotype (1,0,0)/(1,0,0). Using equation (3.1), it follows that the expected gains to any potentially invading phenotype (r_1s, r_2s, r_3s)/(r_1d, r_2d, r_3d) into a population of phenotypes (1,0,0)/(1,0,0) are

$$\text{gains}[(r_{1\text{s}},r_{2\text{s}},r_{3\text{s}})/(r_{1\text{d}},r_{2\text{d}},r_{3\text{d}}),(1,0,0)/(1,0,0)]=B3-4/9·(C1+C2)+[r_{1\text{d}}+2r_{1\text{s}}](C1+C2)/27-[r_{2\text{d}}+2r_{2\text{s}}]/9·(B3-B2-C1)-[r_{3\text{d}}+2r_{3\text{s}}]/9·(B3-B2/2-C2).$$ (3.3)

If grouping benefits of being in a large group are higher than net benefits of saving consensus costs but being in a smaller group (i.e. if B3>C1+B2 and B3>C2+B2/2), expected gains are maximal for r_2s=r_2d=r_3s=r_3d=0 and r_1s=r_1d=1. Thus, a population of phenotypes (1,0,0)/(1,0,0) could not be invaded, and equally shared decision making with a sub-majority threshold is an ESS (figure 1). For symmetry reasons, the same is true for equally shared decision making with a super-majority threshold (phenotype (0,0,1)/(0,0,1)).

Finally, we investigate whether the strategy ‘unshared decision making’ is also an ESS. A phenotype (ŕ_1s, ŕ_2s, ŕ_3s)/(ŕ_1d, ŕ_2d, ŕ_3d) with the strategy of unshared (i.e. dominant) decision making plays INSIST if it is dominant (i.e. ŕ_1d=ŕ_2d=ŕ_3d=1), otherwise it plays GIVE IN (i.e. ŕ_1s=ŕ_2s=ŕ_3s=0). It is thus phenotype (0,0,0)/(1,1,1). Using equation (3.1), it follows that the expected gains to any potentially invading phenotype (r_1s, r_2s, r_3s)/(r_1d, r_2d, r_3d) into a population of phenotypes (0,0,0)/(1,1,1) are

$$\text{gains}[(r_{1\text{s}},r_{2\text{s}},r_{3\text{s}})/(r_{1\text{d}},r_{2\text{d}},r_{3\text{d}}),(0,0,0)/(1,1,1)]=B3-C1·16/27-C2·8/27+[r_{1\text{d}}+r_{3\text{d}}]·(C1+C2)/27+r_{2\text{d}}·2C1/27-r_{1\text{s}}·[2B3-B2/2-C2-C1]/9-2r_{2\text{s}}·[B3-B2-C1]/9-r_{3\text{s}}·[2B3-B2/2-C2-C1]/9.$$ (3.4)

If grouping benefits of being in a large group are higher than net benefits of saving consensus costs but being in a smaller group (i.e. if B3>C1+B2 and B3>C2/2+C1/2+B2/4), expected gains are maximal for r_1s=r_2s=r_3s=0 and r_1d=r_2d=r_3d=1. Thus, a population of phenotypes (0,0,0)/(1,1,1) could not be invaded and unshared decision making is also an ESS (figure 1). Note that equation (3.1) does not have any further potential ESSs than these four (see electronic supplementary material).

(c) If group size is above the optimal group size

If groups are above optimal size (i.e. B3<B2), as is the case in many natural populations (Krause & Ruxton 2002), equally shared decision making with a majority is the only ESS that leads to stable groups (see conditions for different ESSs in §3b; equations (3.2)–(3.4); see also electronic supplementary material). This is because groups other than those that make their decisions in an equally shared manner and with a majority as a threshold are unstable if they are above optimal group size.

(d) Relaxing the assumption of similar body size and equal time budgets

If members are very different in body size, they are no longer equally likely to be dominant (e.g. Clutton-Brock et al. 1982) and are often also heterogeneous with respect to time budgets (Conradt 1998; Ruckstuhl 1998, 1999). For example, assume that the largest group member is dominant and the larger a member is, the later it wants to change activity. The expected gains to individuals are as follows.

• Largest member:

  $$\text{gains}[(‐,‐,‐)/(‐,‐,r_{3\text{d}});(R_{1\text{s}},‐,‐)/(‐,‐,‐);(‐,R_{2\text{s}},‐)/(‐,‐,‐)]=r_{3\text{d}}·(1-R_{2\text{s}})·\left[R_{1\text{s}}·\frac{B2}{2}+(1-R_{1\text{s}})·B3\right]+(1-r_{3\text{d}})\times \left\{R_{2\text{s}}·[R_{1\text{s}}·B2+(1-R_{1\text{s}})·B3-C_{\text{small}}]+(1-R_{2\text{s}})\times \left[B3-R_{1\text{s}}·C_{\text{large}}-(1-R_{1\text{s}})·\frac{1}{3}·(C_{\text{small}}+C_{\text{large}})\right]\right\}.$$ (3.5)

• Medium member:

  $$\text{gains}[(‐,r_{2\text{s}},‐)/(‐,‐,‐);(R_{1\text{s}},‐,‐)/(‐,‐,‐);(‐,‐,‐)/(‐,‐,R_{3\text{d}})]=r_{2\text{s}}·[R_{1\text{s}}·(1-R_{3\text{d}})·B2+(1-R_{1\text{s}})·R_{3\text{d}}·B2+(1-R_{1\text{s}})·(1-R_{3\text{d}})·B3]+(1-r_{2\text{s}})\times \left\{R_{1\text{s}}·[R_{3\text{d}}·B2+(1-R_{3\text{d}})·B3-C_{\text{small}}]+(1-R_{1\text{s}})·\left[B3-R_{3\text{d}}·C_{\text{small}}-(1-R_{3\text{d}})·\frac{2}{3}·C_{\text{small}}\right]\right\}.$$ (3.6)

• Smallest member:

  $$\text{gains}[(r_{1\text{s}},‐,‐)/(‐,‐,‐);(‐,R_{2\text{s}},‐)/(‐,‐,‐);(‐,‐,‐)/(‐,‐,R_{3\text{d}})]=r_{1\text{s}}·(1-R_{2\text{s}})·\left[R_{3\text{d}}·\frac{B2}{2}+(1-R_{3\text{d}})·B3\right]+(1-r_{1\text{s}})·\{R_{2\text{s}}·\left[R_{3\text{d}}·B2+(1-R_{3\text{d}})·B3-C_{\text{small}}\right]+(1-R_{2\text{s}})·\left[B3-R_{3\text{d}}·C_{\text{large}}-(1-R_{3\text{d}})\times \frac{1}{3}·(C_{\text{small}}+C_{\text{large}})\right]\},$$ (3.7)

  where C_small is the expected consensus cost arising through timing differences between two group members that are relatively similar to each other in body size and optimal timing (i.e. large–medium or medium–small members; table 1), and C_large is the expected consensus cost arising through timing differences between the largest and smallest group members (i.e. C_large>C_small).

Equally shared decision making with a majority threshold (i.e. R_1s=R_3d=0 and R_2s=1) is an ESS, if B3>C_small. Equally shared decision making with a sub-majority (i.e. R_2s=R_3d=0 and R_1s=1) or super-majority threshold (i.e. R_1s=R_2s=0 and R_3d=1) and unshared decision making (i.e. R_1s=R_2s=0 and R_3d=1) are ESSs, if B3>B2+C_small and B3>B2/2+C_large. It follows that if group size is above optimal group size (i.e. if B3<B2; Krause & Ruxton 2002), only equal sharing of decisions with a majority threshold is an ESS. Furthermore, as heterogeneity of group members with respect to their time budgets increases, and thus consensus costs C_small and C_large increase, the ESS conditions are no longer met for equally shared decision making with a sub- or super-majority threshold, and for unshared decision making. Thus, equal sharing of decisions with a simple majority threshold becomes the only ESS. If heterogeneity increases even further, so that the consensus costs between the most similar group members outweigh grouping benefits, the group becomes unstable and animals segregate according to body size and time budgets, as do many sexually dimorphic ungulates (Conradt 1998; Ruckstuhl 1998, 1999; Ruckstuhl & Neuhaus 2002).

(e) Relaxing the assumption of symmetrical costs

Assume that consensus costs are asymmetric so that, for example, changing activity too late is more costly than changing activity too early (i.e. C1_late, C2_late>C1_early, C2_early; table 1). The expected gains to the focal individual are slightly different from those given in equation (3.1), because if a member plays GIVE IN and has to choose between two other members that both play INSIST, it should choose so that it pays the lowest consensus cost, as follows:

$$\text{gains}[(r_{1\text{s}},r_{2\text{s}},r_{3\text{s}})/(r_{1\text{d}},r_{2\text{d}},r_{3\text{d}}),(R_{1\text{s}},R_{2\text{s}},R_{3\text{s}})/(R_{1\text{d}},R_{2\text{d}},R_{3\text{d}})]=\frac{1}{9}·[m(r_{1\text{d}},R_{2\text{s}},R_{3\text{s}})+n(r_{2\text{d}},R_{1\text{s}},R_{3\text{s}})+o(r_{3\text{d}},R_{2\text{s}},R_{1\text{s}})+m(r_{1\text{s}},R_{2\text{d}},R_{3\text{s}})+m(r_{1\text{s}},R_{2\text{s}},R_{3\text{d}})+n(r_{2\text{s}},R_{1\text{d}},R_{3\text{s}})+n(r_{2\text{s}},R_{1\text{s}},R_{3\text{d}})+o(r_{3\text{s}},R_{2\text{d}},R_{1\text{s}})+o(r_{3\text{s}},R_{2\text{s}},R_{1\text{d}})],$$ (3.8)

where

$$m(r_a,R_b,R_c)=r_a·[(1-R_b)·[(1-R_c)·B3+R_c·B2]]+(1-r_a)·[(1-R_b)·[B3-(1-R_c)\times C{1}_{\text{late}}/2-R_c·C{2}_{late}]+R_b·[(1-R_c)·B3+R_c·B2-C{1}_{\text{late}}]],$$

$$n(r_a,R_b,R_c)=r_a·[(1-R_b)·[(1-R_c)·B3+R_c·B2]+R_b·(1-R_c)·B2]+(1-r_a)·[(1-R_b)\times [B3-(1-R_c)·C{1}_{\text{early}}/2-R_c·C{1}_{\text{late}}]+R_b·[(1-R_c)·B3+R_c·B2-C{1}_{\text{early}}]],$$

and

$$o(r_a,R_b,R_c)=r_a·(1-R_b)·(1-R_c)·B3+(1-r_a)·[(1-R_b)\times [B3-(1-R_c)·C{1}_{\text{early}}/2-R_c·C{2}_{\text{early}}]+R_b·[(1-R_c)·B3+R_c·B2-C{1}_{\text{early}}]].$$

It can be shown that equally shared decision making with a majority threshold (R_1s/d=R_3s/d=0 and R_2s/d=1) is an ESS if B3>C1_late. Equally shared decision making with a sub-majority threshold (R_2s/d=R_3s/d=0 and R_1s/d=1) is an ESS if B3>C2_early and B3>B2+C1_early. Equally shared decision making with a super-majority threshold (R_1s/d=R_2s/d=0 and R_3s/d=1) is an ESS if B3>B2+C2_late. Unshared decision making (R_1/2/3s=0 and R_1/2/3d=1) is an ESS if B3>B2/2+(C2_late+C1_late)/2 and B3>B2+(C1_late+C1_early)/2. It follows that if consensus costs are low relative to grouping benefits, the situation is similar to the case for symmetric consensus costs (see above). However, if the potential consensus costs of changing activity too late are larger than the grouping benefits (C1_late>B3, e.g. in decisions concerning escape from predators; List 2004), only equal sharing of decision making with a sub-majority as a threshold is an ESS, and groups should change activity when the first group member prefers to do so (Conradt & Roper 2003; List 2004). For example, if one group member is threatened by a predator then the whole group should flee, even if other group members are not in danger.

Similarly, if the potential consensus costs of changing activity too early are larger than the costs of changing too late (C1_late, C2_late<C1_early, C2_early), and also larger than grouping benefits (C1_early>B3, e.g. in situations where extended foraging periods only incur small additional predation risks while starvation risks are high; Rands et al. 2003; List 2004), only equal sharing of decision making with a super-majority as a threshold is an ESS, and groups should not change activity until all group members prefer to do so (the respective conditions for ESSs are as follows: equal sharing with a majority threshold, B3>C1_early; with a sub-majority threshold, B3>B2+C2_early; with a super-majority threshold, B3>B2+C1_late; unshared decisions, B3>B2/2+(C2_early+C1_early)/2 and B3>B2+(C1_late+C_1early)/2). For example, if predation risks are not high, the whole group should remain on a foraging site until the last group member is no longer so hungry that it is threatened by starvation, even if all the other members have already had enough to eat (Rands et al. 2003).

(f) Dynamics and net gains to group members

To which ESS the system evolves, and whether the ESS that is optimal to most members evolves, depends largely on the starting position of the system (figure 1). The relative net gains in populations of equally sharing decision makers with a majority, sub-majority or super-majority as a threshold, or in populations of unshared decision makers, depend on the symmetry in consensus costs (table 2). If costs are symmetric, equal sharing with a simple majority as a threshold is the optimal ESS. If changing activity too early is sufficiently more costly than changing too late, then equal sharing with a super-majority as a threshold does best. If changing activity too late is sufficiently more costly than changing too early, then equal sharing with a sub-majority as a threshold does best.

Table 2.

Average gains for ESSs. (For definition of variables, see figure 2 and table 1.)

equally shared decision makers with
majority threshold	B3−(C1late+C1early)/3
sub-majority threshold	B3−(C1early+C2early)/3
super-majority threshold	B3−(C1late+C2late)/3
unshared decision makers	B3−(2C1early+C2early+2C1late+C2late)/9

4. Decisions in groups of larger size

Consider a group with n members. We first examine whether equally shared decision making is an ESS. Therefore, assume a monomorphic population of phenotypes with equally shared decision making and a consensus decision rule with a threshold of x members (i.e. a majority threshold if x=integer[(n+1)/2], a sub-majority threshold if x<integer[(n+1)/2] or a super-majority threshold if x>integer[(n+1)/2]). These phenotypes always play INSIST if they are the xth member (in time) that prefer an activity change, otherwise they play GIVE IN. That is, R_xs=R_xd=1 (with 1<x<n, where n is the group size) and R_is=R_id=0 (for all i<n and i≠x). The expected gains to a potentially invading phenotype (r_1s,r_2s, …, r_ns)/(r_1d,r_2d, …, r_nd) of body size k are thus

$$\text{gains}\left[(r_{1\text{s}},r_{2\text{s}},\dots ,r_{n\text{s}})/(r_{1\text{d}},r_{2\text{d}},\dots ,r_{n\text{d}}),(0,0,\dots ,1,\dots ,0,0)/(0,0,\dots ,1,\dots ,0,0),k\right]=\sum _{i=1}^{x-1}{p}_i(k)·[[(1-\text{d}(k))·r_{i\text{s}}+\text{d}(k)·r_{i\text{d}}]·B{X}_i+[(1-\text{d}(k))·(1-r_{i\text{s}})+\text{d}(k)·(1-r_{i\text{d}})]\times (Bn-C_{\text{late}}|x-i|)+p_x(k)\times \left[[(1-\text{d}(k))·r_{x\text{s}}+\text{d}(k)·r_{x\text{d}}]·Bn+[(1-\text{d}(k))\times (1-r_{x\text{s}})+\text{d}(k)·(1-r_{x\text{d}})]\times (Bn-\frac{1}{n}·\sum _{j=1}^{x-1}{C}_{\text{early}}(|x-j|-\frac{1}{n}·\sum _{j=x+1}^n{C}_{\text{late}}(|x-j|)\right]+\sum _{i=x+1}^n{p}_i(k)·[[(1-\text{d}(k))·r_{i\text{s}}+\text{d}(k)·r_{i\text{d}}]·B{X}_i+[(1-\text{d}(k))·(1-r_{i\text{s}})+\text{d}(k)·(1-r_{i\text{d}})]\times (Bn-C_{\text{early}}|x-i|)],$$ (4.1)

where p_i(k) and d(k) are the probabilities that a member of body size k is the ith member (in time) to prefer changing activity and/or is dominant, respectively; X_i is the number of members that would follow the focal member in the event of a group split; Bn and BX_i are the grouping benefits of remaining in a group with n and X_i members, respectively; and C_late|x−i| (for i<x) and C_early|x−i| (for i>x) are the consensus costs if the focal is the ith member and changes activity when the xth member prefers to change activity.

Equal sharing with threshold x is an ESS, if d gains/dr_is/d<0, for i≠x, and d gains/dr_xs/d>0. Using equation (4.1), this is the case if $Bn>B{X}_i+C_{\text{late}}|x-i|$, for i<x, and $Bn>B{X}_i+C_{\text{early}}|x-i|$, for i>x. It follows that: (i) if group size is not above optimal group size (i.e. Bn>BX_i for all X_i<n) and consensus costs are small relative to grouping benefits (i.e. C_late|x−i|<Bn−BX_i and C_early|x−i|<Bn−BX_i), equal sharing of decisions with any threshold x is an ESS, (ii) if the consensus costs of changing activity too late are higher than those of changing too early (i.e. C_late|x−i|≫C_early|x−i|) and exceed grouping benefits (i.e. C_late|x−i|>Bn−BX_i for some i if x>x^*), only equally shared decision making with respective sub-majoritarian thresholds (i.e. x<x^*<1/2) remain ESSs, (iii) if the consensus costs of changing activity too early are higher than those of changing activity too late (i.e. C_late|x−i|≪C_early|x−i|) and exceed grouping benefits (i.e. C_early|x−i|>Bn−BX_i for some i if x<x^*), only equally shared decision making with respective super-majoritarian thresholds (i.e. x>x^*>1/2) remain ESSs, (iv) if the group size exceeds optimal group size but consensus costs are low, only equal sharing of decisions with a threshold close to the group size median (i.e. close to a majority threshold) is still ESSs and can lead to group stability (assuming optimal group size >Bn/2; Krause & Ruxton 2002).

Next, we consider unshared decision making. Phenotypes in a population with the strategy of unshared decision making play GIVE IN if they are subordinate and INSIST if they are dominant. That is, R_1s=R_2s=⋯=R_ns=0 and R_1d=R_2d=⋯=R_nd=1. In a monomorphic population of unshared decision makers (0, 0, …, 0)/(1, 1, …, 1), the expected gains to a potentially invading phenotype (r_1s, r_2s, …, r_ns)/(r_1d, r_2d, …, r_nd) of body size k are

$$\text{gains}[(r_{1\text{s}},r_{2\text{s}},\dots ,r_{n\text{s}})/(r_{1\text{d}},r_{2\text{d}},\dots ,r_{n\text{d}}),(0,0,\dots ,0)/(1,1,\dots ,1),k]=\sum _{i=1}^n{p}_i(k)·\left[\text{d}(k)·\left[Bn-(1-r_{i\text{d}})·\frac{1}{n}\times \left(\sum _{j=1}^{i-1}{C}_{\text{early}}|i-j|+\sum _{j=i+1}^n{C}_{\text{late}}|i-j|\right)\right]+(1-\text{d}(k))·\left(\sum _{j=1}^{i-1}p(j,k)·[r_{i\text{s}}·B{X}_{ij}+(1-r_{i\text{s}})\times (Bn-C_{\text{early}}(|j-i|))]+\sum _{j=i+1}^{n}p(j,k)·[r_{i\text{s}}·B{X}_{ij}+(1-r_{i\text{s}})\times (Bn-C_{\text{late}}(|j-i|))]\right)\right],$$ (4.2)

where p(j,k) is the probability that the jth member is dominant if the focal of size k is not dominant; X_ij is the number of members that would move with the focal if the jth member, which prefers to change activity is the dominant and the group splits.

Unshared decision making is an ESS, if d gains/dr_is<0 and d gains/dr_id>0 for all i. Using equation (4.2), this is the case, if ${\sum }_{j=i+1}^{n}p(j,k)·[Bn-B{X}_{ij}]>{\sum }_{j=i+1}^{n}p(j,k)·C_{\text{late}}|j-i|$ and ${\sum }_{j=1}^{i-1}p(j,k)·[Bn-B{X}_{ij}]>{\sum }_{j=1}^{i-1}p(j,k)·C_{\text{early}}|j-i|$ for all i. It follows that unshared decision making is an ESS if consensus costs are low relative to grouping benefits (i.e. if generally $Bn-B{X}_{ij}>C_{\text{late}}|j-i|$ and $Bn-B{X}_{ij}>C_{\text{early}}|j-i|$) and group size is not above optimal group size (i.e. Bn-BXij>0). However, if consensus costs are asymmetric and partially exceed grouping benefits (e.g. if generally $C_{\text{late}}|j-i|>C_{\text{early}}|j-i|$ and $Bn-B{X}_{ij}<C_{\text{late}}|j-i|$), or if consensus costs are very high because the group is very heterogeneous with respect to body size and time budgets (i.e. if generally $Bn-B{X}_{ij}<C_{\text{late}}|j-i|$ and $Bn-B{X}_{ij}<C_{\text{early}}|j-i|$), unshared decision making is not an ESS.

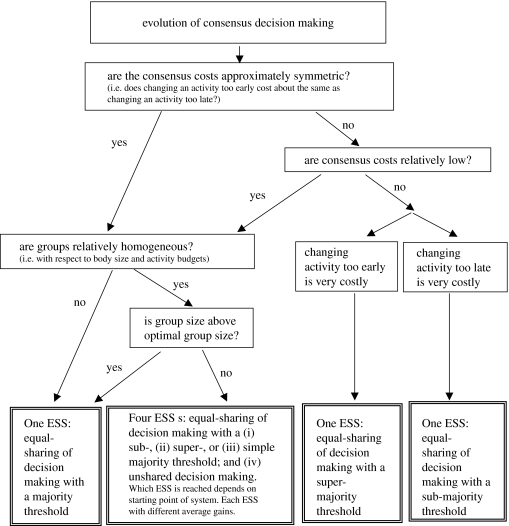
To summarize, the situation in larger groups is very similar to that in groups of three members (figures 2 and 3). If consensus costs are small relative to grouping benefits, equal sharing of decisions with any threshold and unshared decisions are ESSs. If actual group size exceeds optimal group size (Krause & Ruxton 2002), only equal sharing of decisions with a threshold close to the majority is an ESS and can maintain group stability. If consensus costs of changing activities either too early or too late exceed grouping benefits, only equal sharing of decisions with an adequate super- or sub-majority threshold (List 2004), respectively, is an ESS.

Figure 2.

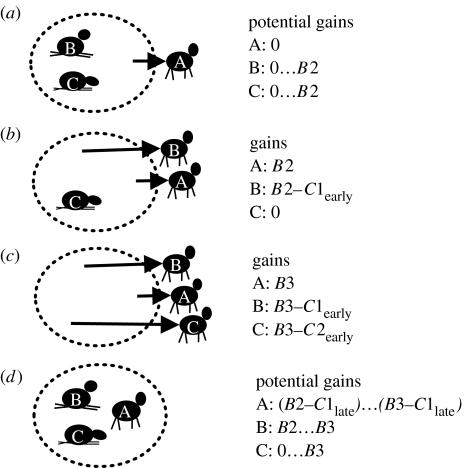
‘Poker game’ of timing a group activity (see main text for details): possible behaviours for animals A, B and C and the associated net gains (B2 and B3: grouping benefits in a group with two or three members, respectively; C1_early and C1_late: consensus costs of changing activity a bit too early or late, respectively; C2_early and C2_late: consensus costs of changing activity much too early or late, respectively). (a) A leaves immediately but B and C do not follow; (b) A and B leave immediately but C does not follow; (c) all three leave immediately; and (d) none leaves immediately.

Figure 3.

Schematic overview of main results.

5. Discussion

To date, most studies on consensus decision making in animals have addressed mechanistic rather than evolutionary questions (e.g. Seeley & Buhrman 1999; Franks et al. 2002; Couzin et al. 2005; Ame et al. 2006). For example, a key model by Couzin et al. (2005) convincingly shows how simple local behavioural rules for individual group members can lead to consensus decisions that are shared between informed group members without the need for communication. However, this model does not ask how these rules evolve and, by making the a priori assumption that all informed group members balance social alignment versus personal preference in the same manner, makes an equally shared decision a forgone conclusion. Consequently, this model avoids the question as to why no member ‘cheats’ by exerting a disproportionate influence on the decision outcome.

The only previous studies to address evolutionary questions are those by Rands et al. (2003) and Conradt & Roper (2003). Rands et al.'s (2003) model shows that the hungriest of two foraging animals, rather than the dominant, should determine group foraging decisions, implying shared decision making, but this model remains restricted to groups of size 2. Conradt & Roper (2003) show that groups of animals benefit more by equally shared than by unshared decisions, but since this is not true for each individual group member, their model stops short of explaining the evolution of equally shared decisions unless group selection arguments are invoked.

The present model shows that both equally shared and unshared decision making can evolve through, and be maintained by, individual selection. An important part of the argument that renders the evolution of equally shared decisions possible is that individual members cannot predict with certainty what other group members are going to do. This uncertainty about other members' intentions arises because it pays all individual members of a group to bluff, rather than communicating honestly about their readiness to compromise their own interests. Consequently, would-be selfish individuals cannot exploit the readiness to compromise of other group members. Rather, all members have to balance the advantages of insisting on their own personal preferences against the risks of the group splitting up.

The most important conclusions of our model are as follows. While, in principle, both equally shared and unshared decision making can evolve through individual selection, equally shared decisions can evolve under a much wider variety of conditions, specifically if: (i) group composition is relatively heterogeneous with respect to group members' requirements, (ii) alternative decision outcomes differ significantly in potential consensus costs, (iii) groups are close to, or above, optimal group size, or (iv) consensus costs are high relative to (but are not higher than) grouping benefits. The first three of these conditions are common in nature (e.g. Conradt & Roper 2000; Krause & Ruxton 2002; Ruckstuhl & Neuhaus 2002; List 2004). They result in a decreased net benefit of group living by either increasing the potential consensus costs to individual group members (conditions (i) and (ii); Conradt 1998; Ruckstuhl 1998, 1999) or decreasing the grouping benefits (condition (iii)). Thus, they potentially destabilize group cohesion (Ruckstuhl & Neuhaus 2002). It follows that shared decision making is likely to be of great importance for the evolution of stable social organizations, explaining why it appears to be common in social animals (see Conradt & Roper 2005 for a review). Conversely, higher degrees of sociality should be found in species that have more effective mechanisms for making equally shared decisions.

Appendix A.

A.1 Justification of assumption (iv)

We start by considering an example. Imagine a group of three animals, A, B and C, at a resting site (figure 2). How do they decide when to leave and move to a foraging site? Assume that for A it is optimal to leave immediately, for B it is optimal to leave soon and for C it is optimal to leave later. If A, B or C leave at a time other than their own optimal time, they incur consensus costs. On the other hand, if some animals leave while others stay and the group splits, all three animals forgo at least some grouping benefits. When should each animal leave? First, consider animal A. A could either ‘insist’ on its own optimal preference and leave immediately, or stay and wait. If A decides to leave immediately, what are the options for B? If B insists on its own optimal preference and stays, it gains at most the benefits of remaining in a group with two members, because A is leaving (figure 2a). Therefore, let us assume that B ‘gives in’ to A and also leaves immediately. In this case, what should animal C do? If C insists on its own optimal preference and stays, it gains no grouping benefits because it would now be alone (figure 2b). If C leaves and follows A and B, it gains the benefit of remaining in a group with three members, but also pays a consensus cost for changing its activity much earlier than optimal (figure 2c). If grouping benefits are larger than consensus costs, it follows that C should ‘give in’ and leave together with A and B. If C leaves with A and B, B gains the benefits of remaining in a group of three but pays the consensus cost of changing its activity somewhat earlier than optimal (figure 2c). Thus, if the difference in benefits of remaining in a group with three, rather than two, members outweighs the consensus cost, B did the right thing when it decided to follow A, rather than stay behind with C (figure 2b). A gains the benefit of remaining in a group of three and pays no consensus costs because it leaves at its own optimal time, and has thus the maximum possible net gain (figure 2c).

This example on first sight suggests that the animal that prefers to leave first should always insist on its own optimal preference and leave, and that all others should always follow. However, imagine A leaves immediately and B decides not to give in and thus not to leave immediately (figure 2a), then A would lose any grouping benefits. If A returned to the group and waited at least until B decided to leave, it would at least gain the benefits of remaining in a group of two (but pay the consensus costs of leaving later than optimal; figure 2d). Therefore, if grouping benefits exceed consensus costs, it would pay A to give in and return if B does not leave immediately. B has then the chance of gaining the maximum net benefits of remaining in a group of three and not paying any consensus costs (figure 2d). The whole situation is like a poker game (compare with McNamara & Houston 2002): if A can ‘bluff’ and convince B and C that it will insist on its own optimal preference and definitely leave immediately, it pays B and C to give in and follow (figure 2c). On the other hand, it pays B and C to bluff that they are not going to follow immediately, because that makes it more profitable for A to stay and wait, which, in turn, is advantageous to B and C (figure 2d). In a similar manner, it can be shown for larger groups, or for other types of consensus decisions involving conflict of interest in animals (see Conradt & Roper 2005 for a review), that it usually pays a group member to try to convince other members that it will insist on its own optimal preference with regard to the decision outcome, and regardless of whether it is ultimately prepared to compromise and give in or not. As a consequence, communication about ‘insisting’ versus ‘giving in’ should be dishonest, and group members cannot predict each other's ultimate behaviour with certainty.

A.2 Evolutionarily stable strategies in equation (3.1)

One can differentiate the gains function in equation (3.1). Therefore, for a strategy (ρ_1s, ρ_2sρ_3s)/(ρ_1d, ρ_2d,ρ_3d) to be an ESS, a necessary (but not sufficient) condition is that the strategy is a local optimum within a population of same strategists. Since all probabilities in all our behavioural strategies (r_1s, r_2s, r_3s)/(r_1d, r_2d, r_3d) are bounded between 0 and 1, such a local optimum can either be a local peak in the gains function or a maximum at the boundary. In mathematical terms, a strategy (ρ_1s, ρ_2s, ρ_3s)/(ρ_1d, ρ_2d,ρ_3d) can only be an ESS, if either

$$\text{d}\text{gains}[(r_{1\text{s}},r_{2\text{s}},r_{3\text{s}})/(r_{i\text{d}},r_{2\text{d}},r_{3\text{d}}),({\rho }_{1\text{s}},{\rho }_{2\text{s}},{\rho }_{3\text{s}})/({\rho }_{1\text{d}},{\rho }_{2\text{d}},{\rho }_{3\text{d}})]/\text{d}{r}_y[{\rho }_y]=0,$$ (A1a)

and

$$\text{d}{\text{gains}}^2[(r_{1\text{s}},r_{2\text{s}},r_{3\text{s}})/(r_{1\text{d}},r_{2\text{d}},r_{3\text{d}}),({\rho }_{1\text{s}},{\rho }_{2\text{s}},{\rho }_{3\text{s}})/{\rho }_{1\text{d}},{\rho }_{2\text{d}},{\rho }_{3\text{d}})]/\text{d}{(r_y)}^2[{\rho }_y]<0,$$ (A1b)

or

$$\text{d}\text{gains}[(r_{1\text{s}},r_{2\text{s}},r_{3\text{s}})/(r_{1\text{d}},r_{2\text{d}},r_{3\text{d}}),({\rho }_{1\text{s}},{\rho }_{2\text{s}},{\rho }_{3\text{s}})/({\rho }_{1\text{d}},{\rho }_{2\text{d}},{\rho }_{3\text{d}})]/\text{d}{r}_y[0]<0,$$ (A2)

or

$$\text{d}\text{gains}[(r_{1\text{s}},r_{2\text{s}},r_{3\text{s}})/(r_{1\text{d}},r_{2\text{d}},r_{3\text{d}}),({\rho }_{1\text{s}},{\rho }_{2\text{s}},{\rho }_{3\text{s}})/({\rho }_{1\text{d}},{\rho }_{2\text{d}},{\rho }_{3\text{d}})]\text{d}{r}_y[1]>0,$$ (A3)

for all y∈{1s,2s,3s,1d,2d,3d}.

Since gains[(r_1s,r_2s,r_3s)/(r_1d,r_2d,r_3d),(ρ_1s,ρ_2s,ρ_3s)/(ρ_1d, ρ_2d,ρ_3d)] is linear in each r_y (see equation (3.1)), condition (A 1b) never holds. Thus, there are no ESSs that lead to peaks in the gains function. This means that only ESSs are possible, in which each ρy takes the value of either 0 or 1. In biological terms, there are no mixed ESSs. (Note that this reasoning does not preclude the possibility of stable oscillations between strategies, but they would not be ESSs in the classical sense.) It follows that there are only 2⁶=64 candidate strategies for potential ESSs (since there are six ρ_y's, which can take each one of two values). Since we are interested in decision making in social animals, we consider only strategies as candidates for ESSs that result in stable groups (i.e. strategies which do not automatically lead to the splitting of the group). Those are groups in which no two animals with different optimal times for activity change play INSIST at the same time. One can show that only 14 of the 64 candidate strategies lead to group stability. Furthermore, assuming B3>C1, B3>C2, B2>C1, B2>C2, C1>0 and C2>0 (see main text), one can show that only the following 4 of these 14 strategies fulfil either condition (2) or (3): (0,1,0)/(0,1,0), (1,0,0)/(1,0,0), (0,0,1)/(0,0,1) and (0,0,0)/(1,1,1). Those candidates for ESSs are investigated in detail in the main text.

Supplementary Material

Mathematical notes

Explanation of the mathematics used within the paper