Abstract
Transport networks are vital components of multicellular organisms, distributing nutrients and removing waste products. Animal and plant transport systems are branching trees whose architecture is linked to universal scaling laws in these organisms. In contrast, many fungi form reticulated mycelia via the branching and fusion of thread-like hyphae that continuously adapt to the environment. Fungal networks have evolved to explore and exploit a patchy environment, rather than ramify through a three-dimensional organism. However, there has been no explicit analysis of the network structures formed, their dynamic behaviour nor how either impact on their ecological function. Using the woodland saprotroph Phanerochaete velutina, we show that fungal networks can display both high transport capacity and robustness to damage. These properties are enhanced as the network grows, while the relative cost of building the network decreases. Thus, mycelia achieve the seemingly competing goals of efficient transport and robustness, with decreasing relative investment, by selective reinforcement and recycling of transport pathways. Fungal networks demonstrate that indeterminate, decentralized systems can yield highly adaptive networks. Understanding how these relatively simple organisms have found effective transport networks through a process of natural selection may inform the design of man-made networks.
Keywords: adaptive biological networks, weighted planar networks, complex systems, nutrient transport
1. Introduction
Transport networks are vital components of multicellular organisms, distributing nutrients and removing waste products. Animal cardiovascular and respiratory systems, and plant vasculature are branching trees whose architecture is linked to universal scaling laws in these organisms (West et al. 1997, 1999a,b; Banavar et al. 1999, 2002). By contrast, it is not clear whether the transport systems of multicellular fungi (Cairney 2005) will fit into this conceptual framework, as they have evolved to explore and exploit a patchy environment rather than ramify through a three-dimensional organism (West et al. 1999a). Unlike all the other biological transport systems studied, the fungal network is not part of the organism, it is the organism.
Basidiomycete fungi are the major decomposers of plant litter in forest ecosystems and are therefore important drivers of the biogeochemical carbon cycle (Gadd 2006). The major wood decay fungi form mycelial networks at the soil–litter interface during the search for fresh organic resources or while scavenging for mineral nutrients (Boddy 1993). The network is formed by the extension, branching and fusion of thread-like hyphae (Glass et al. 2004) that may become aggregated into bundles known as cords (Thompson & Rayner 1982). These saprotrophic networks interconnect dead woody material and explore widely through the litter layers (Watkinson et al. 2006; Boddy & Jones 2007). To function efficiently, the mycelial network must both transport nutrients between spatially separated source and sink regions and also maintain its integrity in the face of continuous attack by mycophagous insects or random damage (Bebber et al. 2007; Boddy & Jones 2007). However, there has been no explicit analysis of the structure of the networks formed, their dynamic behaviour or how either impact on their ecological function.
Like any organism, a fungus must partition limited resources among competing requirements (Boddy 1993). For example, constructing a very dense, highly connected network might confer high transport capacity and robustness to damage owing to multiple transport pathways. However, such a network would incur a large material cost of construction and would cover new ground slowly. Conversely, a sparse system could extend further for the same material cost, but would have fewer alternate routes and therefore lower robustness to disconnection. The challenges that these competing demands place on the network organization have strong parallels with those faced by other foraging biological systems (Nakagaki et al. 2000; Sumpter & Pratt 2003; Buhl et al. 2004; Nakagaki et al. 2004b), and in the design of man-made infrastructure networks (Gorman & Kulkarni 2004; Gastner & Newman 2006a–c; Tero et al. 2006).
The longevity, size (Smith et al. 1992; Ferguson et al. 2003) and ecological importance (Lindahl et al. 2002) of fungi suggest that they have evolved effective solutions to network design through a process of natural selection (Weitz et al. 2007). Thus, it is possible that the solutions found by these biological systems may inform the design of adaptive, robust spatial infrastructure networks with decentralized control (Gorman & Kulkarni 2004; Boccaletti et al. 2006; Gastner & Newman 2006a–c). With this in mind, we characterized developing networks formed by Phanerochaete velutina, a representative foraging woodland fungus, to determine how these networks resolve the competing demands of exploration, exploitation, transport efficiency and robustness.
2. Material and methods
Preparation of the experimental microcosms followed Wells et al. (1997). Briefly, autoclaved beech (Fagus sylvatica) blocks (2×2×1 cm) were inoculated with P. velutina and placed onto compressed, non-sterile woodland soil in 24×24 cm trays. In three replicates, a second woodblock (additional resource) was placed 8 cm from the initial inoculum, with the three control replicates, containing a plastic cap at an equivalent location. The microcosms were kept in the dark at approximately 16°C and 100% relative humidity. The growing mycelia were photographed after 9, 18, 25, 31 and 39 days, until they had reached the margins of the trays.
Branch or fusions points, and cords, were manually ascribed to nodes and links, respectively, using a custom MatLab (The MathWorks, Nantick, MA) interface (available on request from the authors). Link diameters were automatically determined from the imaged cord intensities using an empirically determined calibration. The cords were not sufficiently well resolved to make direct measurement of their diameter from the digitized images. However, the reflected intensity, averaged over a small user-defined kernel at either end of the cord, correlated well with microscope-based measurements of cord thickness in 10 replicate microcosms (linear regression, r2=0.77, d.f.=195, p<0.0001). This calibration was therefore used to estimate cord thickness from sampled cord intensities. The inoculum and resource units were represented as single nodes, as the internal mycelial organization was not visible. Shortest paths were calculated using Johnson's shortest path algorithm implemented with the RBGL package (Carey et al. 2005) for R v. 2.4.1 (R Development Core Team 2006). Spline fits were calculated using Friedman's smoother (Friedman 1984) implemented in R. All statistical analyses were implemented in R.
3. Results
(a) Network development
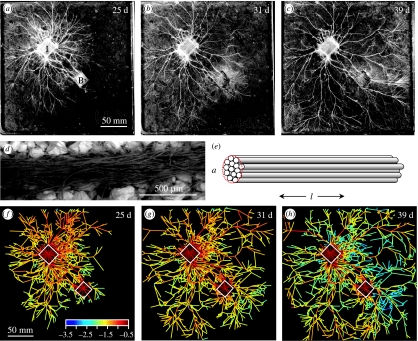
Colonies of P. velutina were grown on compressed soil from a colonized woodblock inoculum (I) in the presence and absence of additional wood resources, or ‘baits’ (B), designed to simulate the sporadic capture of wood fragments during mycelial foraging or stochastic input from the forest canopy (figure 1a–c). The mycelium spread radially across the soil surface, eventually reaching the edge of the microcosm within five to six weeks (figure 1a–c). The growing margin comprised fine branched hyphae, although their small diameter (approx. 10 μm) made it difficult to resolve the detailed organization of the mycelial fans at the very periphery. Over time, the mycelium behind the growing margin became consolidated into thicker bundles of hyphae termed cords (figure 1d), with regression of the material in between (figure 1a–c). The presence of additional resources stimulated formation of a particularly strong corded network between the inoculum and the new woodblock (figure 1). The overall architecture resembled a branching tree, particularly at the margin. A limited number of additional cross links developed, particularly in response to increased resources, to form a sparse network.
Figure 1.
Mycelial network structure. (a–c) Corded mycelium of P. velutina growing from colonized woodblock inoculum (I) over a compressed soil microcosm (22.5×22.5 cm) for 39 days. The mycelium has contacted and colonized a second woodblock (B). (d) Scanning electron micrograph of the fine structure of a cord of P. velutina, showing that cords are composed of a bundle of many parallel fine hyphae. (e) Model of a cord as a bundle of identical hyphae, with cross-sectional area a and length l. The volume of a model cord is la and the predicted transport resistance is la−1. (f–h) Models of a developing mycelial network at 25, 31 and 39 days. Links are pseudo-colour coded by log10(a) on a rainbow scale with red representing thick cords and blue representing thin cords. The positions of woodblocks are highlighted by white squares.
To analyse the network architecture of the fungal mycelia, the morphological structures observed were translated into an appropriate network representation. Thus, the structure of the network was extracted by classifying junctions (branch points and anastomoses) as nodes, and the cords between nodes as links. As the thickness of the cords varied markedly with development of the network, the cord diameter, and hence cord area a, was estimated by image analysis. The internal structure was modelled as a cylinder packed with identical hyphae (figure 1e), although it is recognized that cord anatomy can be more complex (Thompson & Rayner 1982). Therefore, network development was captured as a time series of weighted planar networks culminating in about 700 nodes and 900 links after five to six weeks growth (table 1). The weighted networks were visualized as pseudo-colour representations to emphasize the change in diameter of particular cords over time; reinforcement increasing the cord diameter shifted the hue to the red end of the spectrum and thinning out by regression shifted the hue towards the blue (figure 1f–h). Qualitatively the overall developmental pattern was consistent between replicate experiments, although the precise network architecture varied, particularly in the overall density of the network formed. The variation reflected both the highly plastic developmental programme operating in these foraging fungi (Boddy 1999) and also the precise nutrient status of the woodblocks used in the original inoculum (Boddy & Jones 2007).
Table 1.
Characteristics of fungal mycelial networks. (The spatial extent of the network was defined as the area of the convex hull of node spatial positions, minus the area of woodblocks. Area increased linearly with time t prior to the fungus reaching the edge of the dish. The number of nodes and links increased with area, the rate of increase declining with time. The total material cost of the network (Σla), increased with area. The material cost density declined with network size, with no difference between treatment (T) and control (C). Results are presented as mean±s.e.m. for three replicates.)
| 18 days | 25 days | 31 days | 39 days | ||
|---|---|---|---|---|---|
| area (cm2) | C | 229±18 | 372±17 | 484±11 | 505±3 |
| T | 215±30 | 345±40 | 436±36 | 505±1 | |
| nodes | C | 515±70 | 738±87 | 805±131 | 697±145 |
| T | 427±45 | 679±72 | 680±26 | 685±33 | |
| links | C | 644±127 | 946±159 | 1040±218 | 883±234 |
| T | 584±98 | 943±102 | 913±39 | 900±5 | |
| material cost (mm3) | C | 234±6 | 294±10 | 287±23 | 292±31 |
| T | 248±38 | 362±33 | 394±38 | 378±17 | |
| material cost density (mm3 cm−2) | C | 1.0±0.1 | 0.8±0.0 | 0.6±0.0 | 0.6±0.1 |
| T | 1.2±0.1 | 1.1±0.1 | 0.9±0.1 | 0.7±0.0 |
To determine the combined effect of reinforcement and regression on the overall cost of the network, we first estimated the total amount of material present as the sum of the link lengths multiplied by their cross-sectional areas (C=Σla). Thus, long, thick cords required more material to construct than short, thin ones. The cost density was then defined as the cost per unit area (i.e. CA−1), with the area, A, given by the smallest convex polygon that would contain the entire network. Although the network increased in physical size to fill the microcosm, the total amount of material present increased much more slowly (table 1), resulting in a decrease in the material cost density over time (linear mixed model, F1,17=19.7, p<0.001). This quantitative measure corresponds to the qualitative observation that intervening regions of redundant mycelium were recycled as the corded network formed (figure 1).
The observed change in network topology from a branching tree to a sparse network (figure 1a–c) was quantified using the meshedness or alpha coefficient (Haggett & Chorley 1969; Buhl et al. 2004). This gives the number of closed loops or cycles present as a fraction of the maximum possible for a planar network with the same number of nodes. The alpha coefficient measured over the whole colony increased over time from near zero, as expected for a branching tree, to 0.11±0.04 in control systems and to 0.20±0.05 in systems with an additional woodblock resource. Much of this change occurred in the core region behind the margin (figure 1). The alpha coefficient was significantly greater for the inner half of colony area than for the outer half (0.08±0.02 for baited colonies, 0.05±0.03 for control colonies, F1,18=22.6, p<0.001), consistent with the predominance of branching tree-like growth at the margin during initial exploration. Thus, these fungal networks progress from a branching tree to a weakly connected lattice-like network behind the growing margin through a process of fusion and reinforcement to form loops, and selective removal and recycling of excess redundant material.
(b) Predicted transport characteristics of the network
To investigate the predicted transport capacity of the network, we first estimated the resistance of each link, assuming that nutrient fluxes would be determined not only by the physical length of links in the path but also by their cross-sectional area (a), with thick connections having lower net resistance than thin ones. Within this general framework, the precise relationship between flow and cross-sectional area of the cords is less clear. For the extreme case of laminar flow through individual hyphal tubes, flow should scale with the fourth power of the tube radius in accordance with the Hagen–Poiseuille equation. However, in cords, the structure is more akin to a cylinder packed with individual hyphae in parallel (figure 1d,e). In this case, flow through the cord will scale by the number of conduits present rather than an increase in the cross-sectional area of each conduit. This would give a scaling proportional to the cross-sectional area of the cord, i.e. r2. It is recognized that the internal structure of cords can be more complex than this simple model, with both larger vessel hyphae increasing potential flow and fibre hyphae that do not contribute to transport. Nevertheless, the use of an r2 scaling here is likely to be a minimum estimate of the increase in flow expected for increasing cord diameters. Thus, we defined the functional resistance of a link as its length divided by its cross-sectional area (la−1). We then calculated the path of least resistance between each node in the functional network, using a shortest path algorithm (Gross & Yellen 2005; Carey et al. 2005), with the assumption that low node-to-node resistance indicated better connection and more efficient nutrient distribution.
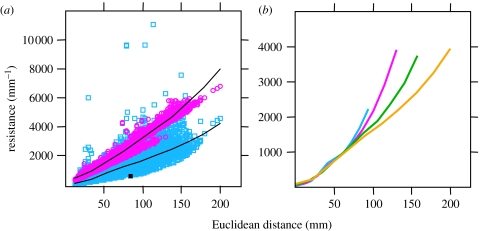
Changes in transport capacity during network growth were, therefore, followed by comparing the path of least resistance with the spatial (Euclidean) distance from the inoculum to each other node. This revealed that the resistance increased nonlinearly with colony radius (figure 2a). However, over time, reinforcement (increases in a) of transport routes reduced the resistance of links previously in the peripheral growth zone, leading to lower resistance throughout the expanding consolidation zone (figure 2b). Furthermore, the transport characteristics of the mycelium responded to the additional woodblock by specifically strengthening connections to the new resource, such that the shortest path from the inoculum to the resource was less than all other nodes at the same Euclidean distance (figure 2a).
Figure 2.
Path lengths in fungal and uniform networks. (a) Functional resistance (mm−1) versus Euclidean distance (mm) from each node to the inoculum for a fungal network (cyan squares), and a network constructed with the same topology and total cost, but uniform cross-sectional area (magenta circles), at 39 days. Lines show smoothed fits. Resistance to added resource (black square) is lower than other nodes at the same Euclidean distance. (b) Smoothed fits of functional resistance (mm−1) versus Euclidean distance (mm) from each node to the inoculum, at 18 days (cyan), 25 days (magenta), 31 days (green) and 39 days (orange). Resistance is greater at the mycelial margins but decreases at a given Euclidean distance over time as the network reinforces links.
While the changes in predicted transport resistance indicated an overall improvement in transport performance during development, they did not provide an indication of whether the network performed well in absolute terms. We therefore tested whether the real, functionally weighted, network structure led to lower transport resistances than would be expected for networks that lacked the ability to vary the cross-sectional area, a. These ‘uniform’ model networks had identical network topology, but all links were given a constant thickness, such that the total construction cost was the same as the actual weighted network. Furthermore, the uniform model networks retained all of the links formed, as their loss would amount to varying a to zero. We found that the fungal networks had significantly lower resistances than the uniform models by the end of the experiment (figure 2a).
(c) Comparative transport efficiency of the network
While consideration of shortest path distances to every node provides a useful graphical representation of the network performance, we also sought appropriate measures to summarize the overall performance of the network. The average efficiency (E), defined as the mean of the reciprocal of shortest path lengths was introduced by Latora & Marchiori (2001, 2003), as a convenient metric to describe the performance of undirected, weighted graphs. In this framework, the efficiency of transport or communication globally throughout the whole network is simply presumed to be inversely related to the shortest path distance between all pairs of nodes. Alternatively, the mean reciprocal of the shortest paths from one particular node to all others gives a measure of the local importance of that node (Latora & Marchiori 2001, 2003; Boccaletti et al. 2006). To account for varying numbers of nodes in different networks, these measures are normalized with reference to an ‘ideal’ fully connected network. This approach is useful as a first approximation for overall transport behaviour since we do not have the additional information on the flow pathways, such as the location of sources and sinks, which are needed to use models incorporating conservation laws (West et al. 1997; Banavar et al. 1999, 2002; Durand 2006, 2007).
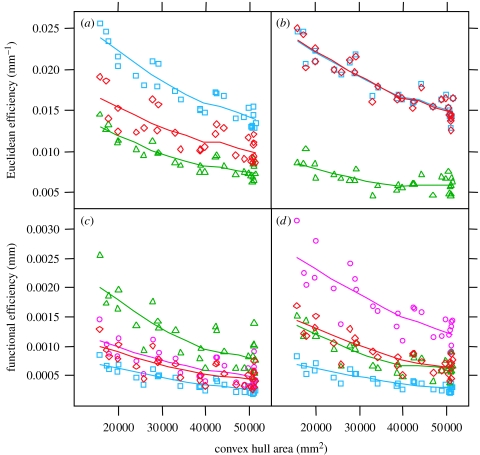
Rather than using the efficiency measures in isolation, we also compared the performance of the fungal networks with model networks constructed using well-defined neighbourhood graphs. Typically these include the minimum spanning tree (MST) as a lower bound giving a low cost, but extremely vulnerable network, and a Delaunay triangulation (DT) or Greedy triangulation (GT), giving an upper bound for a well-connected, robust, but rather expensive network (Buhl et al. 2004; Nakagaki et al. 2004b; Cardillo et al. 2006; Gastner & Newman 2006b). To date, such comparisons of spatial networks have not included the possibility of varying the link diameter, thus all links are treated as having unit diameter, but with varying Euclidean length (Buhl et al. 2004; Nakagaki et al. 2004b; Cardillo et al. 2006; Gastner & Newman 2006b). The different network topologies thus vary in both their transport efficiency and also their total cost. When analysed on the basis of Euclidean geometry alone, the global efficiency considering transport between all nodes of the fungal network declined as the colony grew and as the path lengths of necessity became longer. The Euclidean network efficiency was positioned between the MST and DT (figure 3a).
Figure 3.
Comparison of transport efficiency between weighted fungal and uniform model networks. (a) Global Euclidean efficiency (mm−1) versus network area (mm2) for DT (cyan squares), fungal network (red diamonds) and MST (green triangles). The fungal networks have intermediate global Euclidean efficiency. (b) Root Euclidean efficiency, axes and symbols as in (a). The fungal networks have similar efficiency to the well-connected DTs. (c) Global functional efficiency (mm) versus network area (mm2). Symbols as in (a), except that the fungal weighted (magenta circles) and uniform (red squares) networks are differentiated. The MSTs have the greatest functional efficiency. Fungal networks are intermediate. (d) Root functional efficiency, scales and symbols as in (c). The fungal weighted networks have the greatest root functional efficiency.
When the local efficiency from just the inoculum (or root, Gastner & Newman 2006b) to all other nodes was calculated, then the fungal network performed as well as the DT and markedly better than the MST (figure 3b). Perhaps local efficiency is most useful in the early stages of development as the central inoculum is the biologically relevant source of nutrients supplying the rest of the mycelium. The predominant flow direction would therefore be expected to be from the inoculum outwards to all other nodes. Thus, at this point we conclude that the organization of the fungal network achieves the same predicted transport efficiency from the inoculum as a fully connected network would, but with fewer connections.
We then extended the analysis further to take into account differential allocation of resources to selectively strengthen particular links in the functional network. As there was no appropriate method to assign varying cross-sectional areas to each link in the model MST or DT networks, we compared the performance of the functional network with uniform models based on the fungal topology, or the MST and DT networks, that were constructed with constant cross-sectional areas such that the total cost of the network remained the same. Effectively, we asked what the consequences for transport would be if the fungus had chosen to allocate the same amount of resource evenly over the existing network, or the MST and DT networks.
A very different picture emerged with these starting assumptions in comparison to just the Euclidean weighted networks. Across the whole colony, the DT now performed poorly, as distributing material across the large number of links present gave low a and consequent high resistance to each one of them (figure 3c). Conversely, the MST performed well as it was populated with few, but extremely thick, links. The uniform and real fungal networks were almost equivalent in performance and were again positioned between the two extremes. We calculated the relative global efficiency (Eglob) of the real network, uniform network and MST by normalizing the efficiency to that of the fully connected DT (Latora & Marchiori 2001, 2003), and found values of 1.71±0.11, 1.59±0.06 and 2.97±0.13, respectively. Perhaps the most surprising result was obtained when the local efficiency of the weighted networks from the inoculum to every other node was considered (figure 3d). The DT again performed badly, the uniform fungal network and MST were both about twofold better, but the real network outperformed all of them by a considerable margin (figure 3d). Again, by normalizing to the DT, the local efficiency (Eloc) of the real network, uniform network and MST were calculated as 4.4±0.11, 2.22±0.07 and 2.08±0.12, respectively. Thus, differential weighting of links in the real network gave a more than fourfold improvement in local efficiency in comparison with a fully connected uniform network constructed with the same total cost. We note that, although we have used a global measure to characterize the performance of the fungal network, the biological system achieves this level of performance without centralized control by implementation of local rules.
(d) Formation of alternative paths through the network through cross links
Although prediction of the transport efficiency from the root to the rest of the colony (Eloc) reflects the biological importance of source–sink nutrient flux early in development, over time connectivity between other parts of the network become increasingly important as bidirectional fluxes are known to redistribute nutrients rapidly throughout the entire system (Fricker et al. 2007; Tlalka et al. 2007). One measure that reflects the status of the inoculum as a transport hub is the proportion of shortest paths that pass through it, termed the betweenness centrality (Freeman 1977; Crucitti et al. 2006). Initially, approximately 90% of shortest paths passed through the inoculum in two- to three-week-old colonies. By five to six weeks, the betweenness centrality decreased to approximately 70% in control networks and to approximately 55% in networks with an additional added wood resource. Thus, the networks became more decentralized as they grew, forming cross links that bypassed the original inoculum. The betweenness centrality reflects the predicted functional impact of the increase in the number of cycles present (alpha coefficient) as the colony developed from a branching tree to a sparse network.
(e) The developing network architecture confers high robustness
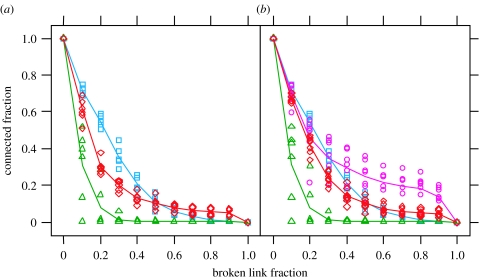
High transport capacity and low construction cost could have come at the expense of other network properties, such as robustness to damage, as there is no a priori reason why link weight allocation for one feature necessarily enhances another. This is clearly seen in the improved global transport efficiency of the uniform MST, even though the MST would be expected to be very vulnerable to disconnection during attack. In nature, mycelial cords can be broken by physical disturbance or attack by mycophagous animals (Kampichler et al. 2004). To test whether the structure of the fungal networks was robust to directed attack, we compared the effects of link breakage on models of the functional fungal networks to the corresponding uniform network, MST and DT, built with the same overall cost. We chose to look at link breakage rather than node removal, which is commonly used in other networks, as the cord is the biologically relevant target for attack. We tested two models of link breakage. In the first, we assumed that the probability of breakage increased with link length, but was independent of cord thickness. This would correspond to damage or attack based solely on the probability of encounter. In the second, we assumed the probability of breakage decreased with the cord thickness as well as length, i.e. long, thin links were more likely to break than short, thick ones. As with the transport efficiency measures, we compared the robustness of the differentially weighted network to the uniform models in which all links were assigned the same thickness to give a constant overall cost. The robustness was defined as the fraction of the total material cost of the network that remained connected to the inoculum, when a certain fraction of the total link cross-sectional area was broken.
As expected, the MST fell apart very quickly, with 50% of the mass of the network becoming disconnected after approximately 10% of the links had been removed (figure 4a). Conversely, the fully connected DT was more robust than the MST and fungal networks when attack was proportional only to link length (figure 4a). However, we found that the fungal networks had greater robustness to link removal than any of the uniform models, when link area was also taken into consideration (figure 4b). Therefore, the real network matched the DT until approximately 40% of link area had been removed, but then maintained a stronger connected core that was robust to damage following removal of a considerable proportion of link area (figure 4b). Thus, the differential strengthening of a subset of links that imparted high local transport capacity also conferred robustness, particularly to targeted attack in the developing mycelial network.
Figure 4.
Comparison of core size loss between weighted fungal and uniform model networks. (a) Euclidean core size fraction versus fraction of broken links for DTs (cyan squares), fungal networks (red diamonds) and MSTs (green triangles). Fungal networks have intermediate robustness to damage. (b) Functional core size fraction versus fraction of total link a broken. Symbols as in (a), except that the fungal weighted (magenta circles) and uniform (red squares) networks are differentiated. When more than approximately 30% of total link a has been broken, the weighted fungal networks maintain a greater connected core than other types of network.
4. Discussion
Our results show that saprotrophic fungi achieve several desirable network properties through differential allocation of resources to connecting cords and introduction of a limited number of cross links. The process of selective loss and differential reinforcement combine to give a transport system that is particularly well tuned to the expected biological function of distributing resources from the inoculum to the rest of the colony. Nevertheless, the introduction of a limited number of cross links (approx. 20% of a fully connected network) was also sufficient to give good global transport efficiency, with the resulting network architecture performing better than simulated networks built with the same amount of material distributed evenly. Differential reinforcement and cross-linking also conferred a high degree of robustness to the network, particularly for the central core and connections to the added resource. We note that both the improvement in transport efficiency and the increased interconnectivity and robustness were achieved despite a relative decrease in the amount of material used to build the network. Thus, the shift from exploration to consolidation was accompanied by more efficient use of material in the restructured network. The amount of cross-linking is comparable to the maximum figure for diverse real-world networks ranging from ant galleries (Buhl et al. 2004), acellular slime moulds (Nakagaki et al. 2004a,b; Tero et al. 2006) to city road networks (Buhl et al. 2006), and corresponds to a class of planar networks characterized by a combination of low cost, high efficiency and robustness (Buhl et al. 2004).
The results presented here for fungal networks confirm the growing awareness that inclusion of appropriate functional weighting is critical to the understanding of network performance (Barrat et al. 2004a,b, 2005; Barthelemy et al. 2005). In spatial networks, this is likely to have a profound effect on conclusions drawn from simple Euclidean interpretation of real network structures (Buhl et al. 2006; Cardillo et al. 2006; Crucitti et al. 2006; Scellato et al. 2006), when functional network measures, such as travel time (Lammer et al. 2006), are likely to be more appropriate.
The fungal network was also highly responsive to local environmental cues, modifying the relative weighting of different links and also the amount of cross-linking, to enhance the transport efficiency and robustness, particularly between the inoculum and new resource. Adaptive changes in network architecture and transport performance occur in response to local stimuli in the absence of an obvious information system that might provide integrated decision making. These emergent properties arise in an anatomically simple organism (Money 2002) that is constructed by local iterative developmental processes rather than through centralized control (Davidson et al. 1996). There is increasing evidence that consideration of network function, rather than just network topology, may achieve global optimization through local adaptive responses (Durand 2006; Tero et al. 2006). Thus, solving local conservation laws, inherent in consideration of flows through resistor or hydraulic networks (Durand 2006, 2007; Tero et al. 2006), inextricably couples behaviour across the whole network and may give rise to optimal global behaviour. Equally it is interesting to note that the predicted form of an optimal transport network with directed flows should be loopless (Durand 2006, 2007). We can suggest a number of reasons why these biological networks deviate from this ideal. First it may simply reflect the failure of a self-organized, growing network to achieve an optimum transport system. Second, it may arise as a consequence of the multiple different source–sink relationships for different nutrients that occur in a fungal network growing in a spatially heterogeneous and non-overlapping resource environment leading to a more complex optimization problem than directed flow through vascular networks, for example. Third, it may indicate the requirement to optimize overall performance for additional factors such as resilience as well as transport.
The mechanism of network development differs from most theoretical models, which have focused on rules governing the addition of new links or the rewiring of existing links (see reviews by Albert & Barabasi 2002; Newman 2003; Boccaletti et al. 2006), although recently the effects of dynamic link weighting (Bianconi 2005) and link removal on network structure have also been examined (Salathe et al. 2005). In the case of fungal systems, network development involves over-production of links and nodes in the exploratory phase, followed by selection and positive reinforcement of some links and recycling of the remainder during the consolidation phase (Falconer et al. 2005). This sequence has parallels to the process of Darwinian evolution based on overproduction, competition and selection against links that are somehow less fit, or less competitive, than those that remain. A similar sequence of events is apparent in the development of other biological transport networks including those formed by acellular slime moulds (Nakagaki et al. 2000, 2004a,b; Tero et al. 2006), foraging ant trails (Deneubourg et al. 1989; Franks et al. 1991; Beckers et al. 1993; Kost et al. 2005; Boddy & Jones 2007) and the pruning, maturation and remodelling stages of vascular development (Risau 1997), and may well represent a universal feature of self-organized biological networks. However, in each of these systems, the final network structure is likely to represent a context-specific balance between the need for efficient transport, cost and robustness. Thus, ant colony optimization (ACO) algorithms (Dorigo et al. 1999) may perform well in search operations, but are less likely to generate good templates for persistent networks that require a high degree of robustness.
We conclude that the ability of fungal networks to dynamically modify link strengths is crucial to achieve both high transport capacity and robustness while reducing overall costs. The results presented here are for just one species of fungus, P. velutina. There are many species of network-forming fungi in nature that are likely to have evolved a range of solutions to the problems of exploration, transport efficiency and robustness. The detailed characterization and modelling of such systems could be a first step in understanding how to construct efficient, robust transport networks based on local rules rather than global information, in the newly emerging field of biologistics (Helbing et al. 2006).
Acknowledgments
Research in the authors' laboratories has been supported by BBSRC (43/P19284), NERC (GR3/12946 & NER/A/S/2002/882), EPSRC (GR/S63090/01), EU Framework 6 (STREP No. 12999), Oxford University Research Infrastructure Fund and the University Dunston Bequest. Some images used in the analysis were produced by Rory Bolton. We thank J. Efstathiou, N. Johnson, F. Reed-Tsochas and members of CABDyN for their stimulating discussions and J. Langdale for comments on the manuscript. The photographs in figure 1a–c were taken by Rory Bolton.
References
- Albert R, Barabasi A.L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002;74:47–97. doi:10.1103/RevModPhys.74.47 [Google Scholar]
- Banavar J.R, Maritan A, Rinaldo A. Size and form in efficient transportation networks. Nature. 1999;399:130–132. doi: 10.1038/20144. doi:10.1038/20144 [DOI] [PubMed] [Google Scholar]
- Banavar J.R, Damuth J, Maritan A, Rinaldo A. Supply–demand balance and metabolic scaling. Proc. Natl Acad. Sci. USA. 2002;99:10 506–10 509. doi: 10.1073/pnas.162216899. doi:10.1073/pnas.162216899 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barrat A, Barthelemy M, Pastor-Satorras R, Vespignani A. The architecture of complex weighted networks. Proc. Natl Acad. Sci. USA. 2004a;101:3747–3752. doi: 10.1073/pnas.0400087101. doi:10.1073/pnas.0400087101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barrat A, Barthelemy M, Vespignani A. Modeling the evolution of weighted networks. Phys. Rev. E. 2004b;70:066149. doi: 10.1103/PhysRevE.70.066149. [DOI] [PubMed] [Google Scholar]
- Barrat A, Barthelemy M, Vespignani A. The effects of spatial constraints on the evolution of weighted complex networks. J. Stat. Mech. 2005:P05003. doi:10.1088/1742-5468/2005/05/P05003 [Google Scholar]
- Barthelemy M, Barrat A, Pastor-Satorras R, Vespignani A. Characterization and modeling of weighted networks. Physica A. 2005;346:34–43. doi:10.1016/j.physa.2004.08.047 [Google Scholar]
- Bebber, D. P., Tlalka, M., Hynes, J., Darrah, P. R., Ashford, A., Watkinson, S. C., Boddy, L. & Fricker, M. D. 2007 Imaging complex nutrient dynamics in mycelial networks. In Fungi in the environment (eds G. Dadd, S. C. Watkinson & P. S. Dyer), pp. 3–21. Cambridge, UK: Cambridge University Press. [DOI] [PubMed]
- Beckers R, Deneubourg J.L, Goss S. Modulation of trail laying in the ant Lasius niger (Hymenoptera, Formicidae) and its role in the collective selection of a food source. J. Insect Behav. 1993;6:751–759. doi:10.1007/BF01201674 [Google Scholar]
- Bianconi G. Emergence of weight–topology correlations in complex scale-free networks. Europhys. Lett. 2005;71:1029–1035. doi:10.1209/epl/i2005-10167-2 [Google Scholar]
- Boccaletti S, Latora V, Moreno Y, Chavez M, Hwang D.U. Complex networks: structure and dynamics. Phys. Lett. 2006;424:175–308. [Google Scholar]
- Boddy L. Saprotrophic cord-forming fungi—warfare strategies and other ecological aspects. Mycol. Res. 1993;97:641–655. [Google Scholar]
- Boddy L. Saprotrophic cord-forming fungi: meeting the challenge of heterogeneous environments. Mycologia. 1999;91:13–32. doi:10.2307/3761190 [Google Scholar]
- Boddy, L. & Jones, T. H. 2007 Mycelial responses in heterogeneous environments: parallels with macroorganisms. In Fungi in the environment (eds G. Dadd, S. C. Watkinson & P. S. Dyer), pp. 112–158. Cambridge, UK: Cambridge University Press.
- Buhl J, Gautrais J, Sole R.V, Kuntz P, Valverde S, Deneubourg J.L, Theraulaz G. Efficiency and robustness in ant networks of galleries. Eur. Phys. J. B. 2004;42:123–129. doi:10.1140/epjb/e2004-00364-9 [Google Scholar]
- Buhl J, Gautrais J, Reeves N, Sole R.V, Valverde S, Kuntz P, Theraulaz G. Topological patterns in street networks of self-organized urban settlements. Eur. Phys. J. B. 2006;49:513–522. doi:10.1140/epjb/e2006-00085-1 [Google Scholar]
- Cairney J.W.G. Basidiomycete mycelia in forest soils: dimensions, dynamics and roles in nutrient distribution. Mycol. Res. 2005;109:7–20. doi: 10.1017/s0953756204001753. doi:10.1017/S0953756204001753 [DOI] [PubMed] [Google Scholar]
- Cardillo A, Scellato S, Latora V, Porta S. Structural properties of planar graphs of urban street patterns. Phys. Rev. D. 2006;73:066107. doi: 10.1103/PhysRevE.73.066107. [DOI] [PubMed] [Google Scholar]
- Carey V.J, Gentry J, Whalen E, Gentleman R. Network structures and algorithms in Bioconductor. Bioinformatics. 2005;21:135–136. doi: 10.1093/bioinformatics/bth458. doi:10.1093/bioinformatics/bth458 [DOI] [PubMed] [Google Scholar]
- Crucitti P, Latora V, Porta S. Centrality measures in spatial networks of urban streets. Phys. Rev. D. 2006;73:036125. doi: 10.1103/PhysRevE.73.036125. [DOI] [PubMed] [Google Scholar]
- Davidson F.A, Sleeman B.D, Rayner A.D.M, Crawford J.W, Ritz K. Context-dependent macroscopic patterns in growing and interacting mycelial networks. Proc. R. Soc. B. 1996;263:873–880. doi:10.1098/rspb.1996.0129 [Google Scholar]
- Deneubourg J.L, Goss S, Franks N, Pasteels J.M. The blind leading the blind—modeling chemically mediated army ant raid patterns. J. Insect Behav. 1989;2:719–725. doi:10.1007/BF01065789 [Google Scholar]
- Dorigo M, Di Caro G, Gambardella L.M. Ant algorithms for discrete optimization. Artif. Life. 1999;5:137–172. doi: 10.1162/106454699568728. doi:10.1162/106454699568728 [DOI] [PubMed] [Google Scholar]
- Durand M. Architecture of optimal transport networks. Phys. Rev. E. 2006;73:016116. doi: 10.1103/PhysRevE.73.016116. doi:10.1103/PhysRevE.73.016116 [DOI] [PubMed] [Google Scholar]
- Durand M. Structure of optimal transport networks subject to a global constraint. Phys. Rev. Lett. 2007;98:088701. doi: 10.1103/PhysRevLett.98.088701. doi:10.1103/PhysRevLett.98.088701 [DOI] [PubMed] [Google Scholar]
- Falconer R.E, Bown J.L, White N.A, Crawford J.W. Biomass recycling and the origin of phenotype in fungal mycelia. Proc. R. Soc. B. 2005;272:1727–1734. doi: 10.1098/rspb.2005.3150. doi:10.1098/rspb.2005.3150 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferguson B.A, Dreisbach T.A, Parks C.G, Filip G.M, Schmitt C.L. Coarse-scale population structure of pathogenic Armillaria species in a mixed-conifer forest in the blue mountains of northeast Oregon. Can. J. Forest Res. 2003;33:612–623. doi:10.1139/x03-065 [Google Scholar]
- Franks N.R, Gomez N, Goss S, Deneubourg J.L. The blind leading the blind in army ant raid patterns—testing a model of self-organization. J. Insect Behav. 1991;4:583–607. doi:10.1007/BF01048072 [Google Scholar]
- Freeman L.C. Set of measures of centrality based on betweenness. Sociometry. 1977;40:35–41. doi:10.2307/3033543 [Google Scholar]
- Fricker, M. D., Tlalka, M., Bebber, D., Tagaki, S., Watkinson, S. C. & Darrah, P. R. 2007 Fourier-based spatial mapping of oscillatory phenomena in fungi. Fungal Genet. Biol (doi:10.1016/j.fgb.2007.02.012) [DOI] [PubMed]
- Friedman, J. H. 1984 A variable span smoother. Technical report no. LCS5, Stanford University.
- Gadd G.M, editor. Fungi in biogeochemical cycles. Cambridge University Press; Cambridge, UK: 2006. [Google Scholar]
- Gastner M.T, Newman M.E.J. Optimal design of spatial distribution networks. Phys. Rev. D. 2006a;74:016117. doi: 10.1103/PhysRevE.74.016117. [DOI] [PubMed] [Google Scholar]
- Gastner M.T, Newman M.E.J. Shape and efficiency in spatial distribution networks. J. Stat. Mech. 2006b:P01015. doi: 10.1103/PhysRevE.74.016117. doi:10.1088/1742-5468/2006/01/P01015 [DOI] [PubMed] [Google Scholar]
- Gastner M.T, Newman M.E.J. The spatial structure of networks. Eur. Phys. J. B. 2006c;49:247–252. doi:10.1140/epjb/e2006-00046-8 [Google Scholar]
- Glass N.L, Rasmussen C, Roca M.G, Read N.D. Hyphal homing, fusion and mycelial interconnectedness. Trends Microbiol. 2004;12:135–141. doi: 10.1016/j.tim.2004.01.007. doi:10.1016/j.tim.2004.01.007 [DOI] [PubMed] [Google Scholar]
- Gorman S.P, Kulkarni R. Spatial small worlds: new geographic patterns for an information economy. Environ. Plann. B. 2004;31:273–296. doi:10.1068/b29118 [Google Scholar]
- Gross J.L, Yellen J. Chapman and Hall; London, UK: 2005. Graph theory and its applications. [Google Scholar]
- Haggett P, Chorley R.J. Arnold; London, UK: 1969. Network analysis in geography. [Google Scholar]
- Helbing D, Armbruster D, Mikhallov A.S, Lefeber E. Information and material flows in complex networks. Physica A. 2006;363:xi–xviii. doi:10.1016/j.physa.2006.01.042 [Google Scholar]
- Kampichler C, Rolschewski J, Donnelly D.P, Boddy L. Collembolan grazing affects the growth strategy of the cord-forming fungus hypholoma fasciculare. Soil Biol. Biochem. 2004;36:591–599. doi:10.1016/j.soilbio.2003.12.004 [Google Scholar]
- Kost C, De Oliveira E.G, Knoch T.A, Wirth R. Spatio-temporal permanence and plasticity of foraging trails in young and mature leaf-cutting ant colonies (Atta spp.) J. Trop. Ecol. 2005;21:677–688. doi:10.1017/S0266467405002592 [Google Scholar]
- Lammer S, Gehlsen B, Helbing D. Scaling laws in the spatial structure of urban road networks. Physica A. 2006;363:89–95. doi:10.1016/j.physa.2006.01.051 [Google Scholar]
- Latora V, Marchiori M. Efficient behavior of small-world networks. Phys. Rev. Lett. 2001;87:1–4. doi: 10.1103/PhysRevLett.87.198701. doi:10.1103/PhysRevLett.87.198701 [DOI] [PubMed] [Google Scholar]
- Latora V, Marchiori M. Economic small-world behavior in weighted networks. Eur. Phys. J. B. 2003;32:249–263. doi:10.1140/epjb/e2003-00095-5 [Google Scholar]
- Lindahl B.O, Taylor A.F.S, Finlay R.D. Defining nutritional constraints on carbon cycling in boreal forests—towards a less ‘phytocentric’ perspective. Plant Soil. 2002;242:123–135. doi:10.1023/A:1019650226585 [Google Scholar]
- Money N.P. Mushroom stem cells. Bioessays. 2002;24:949–952. doi: 10.1002/bies.10160. doi:10.1002/bies.10160 [DOI] [PubMed] [Google Scholar]
- Nakagaki T, Yamada H, Toth A. Maze-solving by an amoeboid organism. Nature. 2000;407:470. doi: 10.1038/35035159. doi:10.1038/35035159 [DOI] [PubMed] [Google Scholar]
- Nakagaki T, Kobayashi R, Nishiura Y, Ueda T. Obtaining multiple separate food sources: behavioural intelligence in the Physarum plasmodium. Proc. R. Soc. B. 2004a;271:2305–2310. doi: 10.1098/rspb.2004.2856. doi:10.1098/rspb.2004.2856 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nakagaki T, Yamada H, Hara M. Smart network solutions in an amoeboid organism. Biophys. Chem. 2004b;107:1–5. doi: 10.1016/S0301-4622(03)00189-3. doi:10.1016/S0301-4622(03)00189-3 [DOI] [PubMed] [Google Scholar]
- Newman M.E.J. The structure and function of complex networks. SIAM Rev. 2003;45:167–256. doi:10.1137/S003614450342480 [Google Scholar]
- R Development Core Team. R foundation for statistical computing; Vienna, Germany: 2006. A language and environment for statistical computing. [Google Scholar]
- Risau W. Mechanisms of angiogenesis. Nature. 1997;386:671–674. doi: 10.1038/386671a0. doi:10.1038/386671a0 [DOI] [PubMed] [Google Scholar]
- Salathe M, May R.M, Bonhoeffer S. The evolution of network topology by selective removal. J. R. Soc. Interface. 2005;2:533–536. doi: 10.1098/rsif.2005.0072. doi:10.1098/rsif.2005.0072 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scellato S, Cardillo A, Latora V, Porta S. The backbone of a city. Eur. Phys. J. B. 2006;50:221–225. doi:10.1140/epjb/e2006-00066-4 [Google Scholar]
- Smith M.L, Bruhn J.N, Anderson J.B. The fungus Armillaria bulbosa is among the largest and oldest living organisms. Nature. 1992;356:428–431. doi:10.1038/356428a0 [Google Scholar]
- Sumpter D.J.T, Pratt S.C. A modelling framework for understanding social insect foraging. Behav. Ecol. Sociobiol. 2003;53:131–144. [Google Scholar]
- Tero A, Kobayashi R, Nakagaki T. Physarum solver: a biologically inspired method of road-network navigation. Physica A. 2006;363:115–119. doi:10.1016/j.physa.2006.01.053 [Google Scholar]
- Thompson W, Rayner A.D.M. Structure and development of mycelial cord systems of Phanerochaete laevis in soil. Trans. Br. Mycol. Soc. 1982;78:193–200. [Google Scholar]
- Tlalka, M., Bebber, D., Darrah, P. R., Watkinson, S. C. & Fricker, M. D. 2007 Emergence of self-organised oscillatory domains in fungal mycelia. Fungal Genet. Biol (doi:10.1016/j.fgb.2007.02.013) [DOI] [PubMed]
- Watkinson S.C, Bebber D, Darrah P.R, Fricker M.D, Tlalka M, Boddy L. The role of wood decay fungi in the carbon and nitrogen dynamics of the forest floor. In: Gadd G.M, editor. Fungi in biogeochemical cycles. Cambridge University Press; Cambridge, UK: 2006. pp. 151–181. [Google Scholar]
- Weitz J.S, Benfey P.N, Wingreen N.S. Evolution, interactions, and biological networks. PLoS Biol. 2007;5:e11. doi: 10.1371/journal.pbio.0050011. doi:10.1371/journal.pbio.0050011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wells J.M, Donnelly D.P, Boddy L. Patch formation and developmental polarity in mycelial cord systems of Phanerochaete velutina on a nutrient-depleted soil. New Phytol. 1997;136:653–665. doi: 10.1046/j.1469-8137.1997.00776.x. doi:10.1046/j.1469-8137.1997.00776.x [DOI] [PubMed] [Google Scholar]
- West G.B, Brown J.H, Enquist B.J. A general model for the origin of allometric scaling laws in biology. Science. 1997;276:122–126. doi: 10.1126/science.276.5309.122. doi:10.1126/science.276.5309.122 [DOI] [PubMed] [Google Scholar]
- West G.B, Brown J.H, Enquist B.J. The fourth dimension of life: fractal geometry and allometric scaling of organisms. Science. 1999a;284:1677–1679. doi: 10.1126/science.284.5420.1677. doi:10.1126/science.284.5420.1677 [DOI] [PubMed] [Google Scholar]
- West G.B, Brown J.H, Enquist B.J. A general model for the structure and allometry of plant vascular systems. Nature. 1999b;400:664–667. doi:10.1038/23251 [Google Scholar]