Hybrid two-dimensional navigator correction: a new technique to suppress respiratory-induced physiological noise in multi-shot echo-planar functional MRI

Abstract

A troublesome source of physiological noise in functional magnetic resonance imaging (fMRI) is due to the spatio-temporal modulation of the magnetic field in the brain caused by normal subject respiration. fMRI data acquired using echo-planar imaging is very sensitive to these respiratory-induced frequency offsets, which cause significant geometric distortions in images. Because these effects increase with main magnetic field, they can nullify the gains in statistical power expected by the use of higher magnetic fields. As a study of existing navigator correction techniques for echo-planar fMRI has shown that further improvements can be made in the suppression of respiratory-induced physiological noise, a new hybrid two-dimensional (2D) navigator is proposed. Using a priori knowledge of the slow spatial variations of these induced frequency offsets, 2D field maps are constructed for each shot using spatial frequencies between ±0.5 cm⁻¹ in k-space. For multi-shot fMRI experiments, we estimate that the improvement of hybrid 2D navigator correction over the best performance of one-dimensional navigator echo correction translates into a 15% increase in the volume of activation, 6% and 10% increases in the maximum and average t-statistics, respectively, for regions with high t-statistics, and 71% and 56% increases in the maximum and average t-statistics, respectively, in regions with low t-statistics due to contamination by residual physiological noise.

INTRODUCTION

Blood oxygenation level-dependent (BOLD) functional magnetic resonance imaging (fMRI) (Ogawa et al., 1990; Kwong et al., 1992; Ogawa et al., 1992; Bandettini et al., 1992) is the dominant technique for non-invasive investigation of brain functions. The potential benefits from high field strengths of 3 T and beyond include increases in the signal-to-noise ratio (SNR) (Edelstein et al., 1986) and BOLD contrast-to-noise ratio (CNR) (Fisel et al., 1991; Ogawa et al., 1993; Gati et al., 1997). However, sources of physiological noise also increase with field strength, creating an asymptotic limit in SNR and nullifying potential gains in CNR (Kruger and Glover, 2001; Triantafyllou et al., 2005). Sources of physiological noise related to underlying neural or vascular fluctuations in the resting brain (Biswal et al., 1995) include changes in cerebral metabolism (CMRO₂), cerebral blood flow (CBF), and cerebral blood volume (CBV), and thus their removal should be treated with care (Kruger and Glover, 2001). However, physiological noise originating from respiration and cardiac pulsatility also exist, and may be considered extraneous and removable in that it does not contribute useful information to the measured fMRI time series.

The component of physiological noise related to respiration is caused by the movement of the chest during the respiratory cycle (Hu and Kim, 1994). As the shape and volume of the lungs change during normal breathing, the air-water susceptibility difference causes fluctuations in the magnetic field throughout the brain. Raj et al. (2000) modeled the field inhomogeneities at the head induced by the oxygen in the lungs as a paramagnetic sphere within a long uniform diamagnetic cylinder aligned to the main magnetic field. As the resonant frequency is proportional to field strength, these field fluctuations manifest themselves as frequency off-resonance effects. These frequency offsets decrease as a function of distance from the chest cavity (Raj et al., 2000; Pfeuffer et al., 2002), and have been reported to be uniform (Hu and Kim, 1994) or approximately uniform (Van de Moortele et al., 2002) within an axial slice perpendicular to the main magnetic field. If these frequency offsets were approximately uniform within an axial slice, then global navigator correction (Hu and Kim, 1994) should be sufficient to estimate and compensate for this uniform shift in resonant frequency. However, more recent and accurate field maps of the brain acquired using RASTAMAP (Klassen and Menon, 2004) show clear spatial variations in the field inhomogeneities between full inhalation and exhalation, invalidating this assumption of axial uniformity and suggesting that current correction strategies may not be adequate (Barry and Menon, 2005).

Echo-planar imaging (EPI) is very sensitive to these non-uniform frequency offsets, which distort the reconstructed image by stretching or compressing it primarily in the phase-encode direction (Jezzard and Balaban, 1995). Previous work by Barry and Menon (2005) investigated the effects of respiration on the time series of a simulated whole-brain fMRI experiment in the presence of spatially varying respiratory-induced frequency offsets. Respiratory-induced signal intensity fluctuations between 1% and 5% were observed in regions of gray matter before navigator correction, and the application of global (Hu and Kim, 1994) and one-dimensional (1D) correction using the navigator echo line (Bruder et al., 1992) demonstrated location-specific reduction or amplification of this noise throughout an axial image. These results suggested that two-dimensional (2D) correction approaches should be considered.

A current 2D approach to reduce physiological noise due to respiration is RETROICOR (Glover et al., 2000). Since RETROICOR operates on pixels in the image domain, an assumption in its application is that each image is acquired at a single point in the respiratory cycle. Although this assumption is appropriate for single-shot acquisitions, it may not be valid for typical multi-shot acquisitions where TR is long to permit whole-brain coverage with high SNR. Finally, recently developed proactive approaches to reduce physiological noise include modification of the acquisition strategy in conjunction with spatial smoothing (Triantafyllou et al., 2006), and continuous updating of currents in the shim coils (van Gelderen et al., 2007). Such approaches are complementary to post-processing correction techniques.

In this study, a novel 2D navigator correction technique is presented to improve the suppression of respiratory-induced physiological noise (RIPN) in multi-shot echo-planar fMRI. As this correction would, in practice, be applied to fMRI data sets consisting of thousands of 2D images, an additional design constraint is that the algorithm must be computationally efficient while maintaining the highest possible level of correction accuracy. The algorithm is developed and tested using an fMRI simulator and then validated using in vivo data from multi-shot EPI experiments.

METHODS

Experiments were performed on a Varian Unity INOVA whole-body 4 Tesla MRI scanner (Palo Alto, CA) with a Siemens Sonata gradient coil (Erlangen, Germany). Simulations and analyses of noise measurement data were implemented using custom software written in MATLAB 7.0 (MathWorks, Natick, MA). BrainVoyager QX 1.8 (Brain Innovation, Maastricht, The Netherlands) was employed to analyze functional data acquired during the visual paradigms. Participating subjects provided written informed consent with a protocol approved by the University of Western Ontario's Human Subjects Research Ethics Board.

fMRI Simulator

To investigate the effects of RIPN in multi-shot EPI at 4 T, an fMRI simulator was previously developed by the authors to “acquire” k-space for an axial 2D image using an even number of center-out shots for arbitrary TE and TR. For each k-space datum, the 2D field inhomogeneities due to respiration were extrapolated with sinusoidal interpolation between full inhalation and exhalation in a five-second respiratory cycle. The effectiveness of navigator correction techniques to reduce the geometric distortions in a series of images may then be evaluated. The reader is referred to Barry and Menon (2005) for complete details of the fMRI simulator.

Navigator Correction – Full 2D Navigator

Whereas global correction only uses the information contained within the center point of k-space and 1D correction considers information from the entire navigator echo line, full 2D correction exploits information from every acquired point in k-space to map spatial frequency offsets in both dimensions. 2D navigator correction is a three-step process. Firstly, a complex reference image I_ref must be selected from one of the functional images, typically one collected at the beginning of each functional run.

Secondly, I_cur must be generated in complex image space for the current image. In the case of a single-shot EPI sequence, all k-space points are acquired while experiencing the same 2D frequency offset, with the assumption that temporal changes that take place during the short image acquisition time, typically a few tens of milliseconds, are small relative to the acquisition bandwidth. In this case, estimated frequency offsets between a current image and the reference image (in rad/s) is

$$\Delta {\stackrel{\rightharpoonup }{\omega }}_{est}\left(\stackrel{\rightharpoonup }{r}\right)=\frac{\varphi \left(I_{cur}\right)-\varphi (I_{ref})}{TE}$$ [1]

However, when using a 2-shot EPI sequence, the acquisition of the top and bottom halves of k-space under the influence of different frequency offsets must be considered if the shots are separated in time, as is typically done in a multi-slice interleaved acquisition (shot 1 slice 1, shot 1 slice 2, shot 1 slice 3, ...; shot 2 slice1, shot 2 slice 2, ...). If we denote the frequency offsets present during the top-half acquisition of k-space as $\Delta {\stackrel{\rightharpoonup }{\omega }}_{est}^{top}\left(\stackrel{\rightharpoonup }{r}\right)$ and the frequency offsets present during the bottom-half acquisition of k-space as $\Delta {\stackrel{\rightharpoonup }{\omega }}_{est}^{bot}\left(\stackrel{\rightharpoonup }{r}\right)$, then these frequency offsets may be calculated by

$$\Delta {\stackrel{\rightharpoonup }{\omega }}_{est}^{top}\left(\stackrel{\rightharpoonup }{r}\right)=\frac{\varphi \left(I_{cur}^{top}\right)-\varphi \left(I_{ref}^{top}\right)}{TE}$$ [2a]

$$\Delta {\stackrel{\rightharpoonup }{\omega }}_{est}^{bot}\left(\stackrel{\rightharpoonup }{r}\right)=\frac{\varphi \left(I_{cur}^{bot}\right)-\varphi \left(I_{ref}^{bot}\right)}{TE}$$ [2b]

where $I_{cur}^{top}$ and $I_{ref}^{top}$ are the zero filled inverse Fourier transforms of just the top halves of k-space, and $I_{cur}^{bot}$ and $I_{ref}^{bot}$ are the zero filled inverse Fourier transforms of just the bottom halves of k-space. A binary mask is also applied to each $\Delta {\stackrel{\rightharpoonup }{\omega }}_{est}\left(\stackrel{\rightharpoonup }{r}\right)$ to isolate the brain and remove noise from signal voids.

Partial Fourier reconstruction using only half of the phase-encode lines in k-space is a convolution by a sinc function along the phase-encode direction in image space (MacFall et al., 1988; Liang et al., 1992). The asymmetric truncation of k-space may be seen as a translation of the sampling window, and introduces a phase shift in image space; however, this phase shift is the same in both the current and reference images because the truncation window is the same, so it cancels in the phase subtraction. Thus, while 2D estimation of $\Delta \stackrel{\rightharpoonup }{\omega }\left(\stackrel{\rightharpoonup }{r}\right)$ in single-shot EPI is not sensitive to chosen orientation of the read and phase-encode gradients, the blurring of the frequencies along the phase-encode direction introduces a direction dependency in the 2D estimation of $\Delta \stackrel{\rightharpoonup }{\omega }\left(\stackrel{\rightharpoonup }{r}\right)$ for multi-shot EPI data. To avoid the blurring caused by partial Fourier reconstruction, the entirety of k-space acquired using multiple shots may be used when estimating $\Delta \stackrel{\rightharpoonup }{\omega }\left(\stackrel{\rightharpoonup }{r}\right)$. This alternate implementation would, however, decrease the accuracy of the estimation of $\Delta \stackrel{\rightharpoonup }{\omega }\left(\stackrel{\rightharpoonup }{r}\right)$ because the frequency offsets are continually modulated between shots. The concatenation of separate k-space shots to estimate $\Delta \stackrel{\rightharpoonup }{\omega }\left(\stackrel{\rightharpoonup }{r}\right)$ should be avoided unless it is necessary to avoid aliasing of $\Delta {\stackrel{\rightharpoonup }{\omega }}_{est}\left(\stackrel{\rightharpoonup }{r}\right)$.

The third and final step is to use either $\Delta {\stackrel{\rightharpoonup }{\omega }}_{est}\left(\stackrel{\rightharpoonup }{r}\right)$, or $\Delta {\stackrel{\rightharpoonup }{\omega }}_{est}^{top}\left(\stackrel{\rightharpoonup }{r}\right)$ and $\Delta {\stackrel{\rightharpoonup }{\omega }}_{est}^{bot}\left(\stackrel{\rightharpoonup }{r}\right)$,to reconstruct what each k-space point should have been had the changes in frequency offset not been present. The problem of data acquisition in the presence of field inhomogeneities can be stated in terms of a linear algebra problem where an encoding matrix is used to transform the data from one domain to another. The coefficients of this encoding matrix are Fourier coefficients in the special case when field inhomogeneities are not considered (Sutton et al., 2001). For an N × N image, the acquired k-space data k_acq (an N² × 1 vector) as a function of the signal distribution m (another N² × 1 vector) may be expressed as

$$k_{acq}=Dm$$ [3]

where D is the N² × N² encoding matrix where each row contains encoding coefficients considering the presence of both gradients and field inhomogeneities, $\exp \left(i{\int }_0^t[\gamma \stackrel{\rightharpoonup }{G}(\stackrel{\rightharpoonup }{r},t)•\stackrel{\rightharpoonup }{r}+\Delta {\stackrel{\rightharpoonup }{\omega }}_{est}\left(\stackrel{\rightharpoonup }{r}\right)]dt\right)$, for the corresponding point in k-space. The corrected image is

$$m=D^{-1}{k}_{acq}$$ [4]

where D⁻¹ is calculated by matrix inversion. If another encoding matrix G is similarly populated but only considering the applied gradients, $\exp \left(i\gamma {\int }_0^t\stackrel{\rightharpoonup }{G}(\stackrel{\rightharpoonup }{r},t)•\stackrel{\rightharpoonup }{r}dt\right)$, then the final corrected k-space is

$$k_{2Dcor}=Gm=G{D}^{-1}{k}_{acq}$$ [5]

Navigator Correction – Hybrid 2D Navigator

The implementation of full 2D correction requires the inverse encoding matrix D⁻¹ to be computed, as well as the matrix product GD⁻¹, both of which require significant memory and computational resources for large values of N. Computationally efficient numerical techniques exist to iteratively approximate the matrix inverse, and their uses in correcting MR images have been investigated (Kadah and Hu, 1998; Schomberg, 1999; Munger et al., 2000; Barmet et al., 2004). If no assumptions were made regarding the range of spatial frequencies to be corrected, then the use of the conjugate gradient algorithm (Hestenes and Stiefel, 1952) to facilitate the implementation of full 2D correction would have been investigated. However, since physiological noise dominates the distortion of k-space data where SNR is high, rigorous corrections should be most beneficial when applied to the low-frequency region of k-space.

If the dimensions of k-space are N × N, then a central δ × δ square region (1 ≤ δ ≤ N) to be corrected with the 2D algorithm may be represented as k̃_acq with dimensions δ² × 1. Since we are only interested in correcting low spatial frequencies, another ξ × ξ central square region (1 ≤ ξ ≤ N) is introduced as an ideal low pass filter to restrict the range of frequencies that contribute to the estimation of $\Delta \stackrel{\rightharpoonup }{\omega }\left(\stackrel{\rightharpoonup }{r}\right)$. If ξ < N, then spatial frequencies greater than ξ provide no additional information to influence the estimate of $\Delta \stackrel{\rightharpoonup }{\omega }\left(\stackrel{\rightharpoonup }{r}\right)$. Thus, a significant reduction in computation time with negligible impact on correction performance may be realized by downsampling $\Delta {\stackrel{\rightharpoonup }{\omega }}_{est}\left(\stackrel{\rightharpoonup }{r}\right)$ to N_r × N_r (ξ ≤ N_r ≤ N). To investigate this possibility, N_r is set to ξ for the correction shown in Fig. 4d.

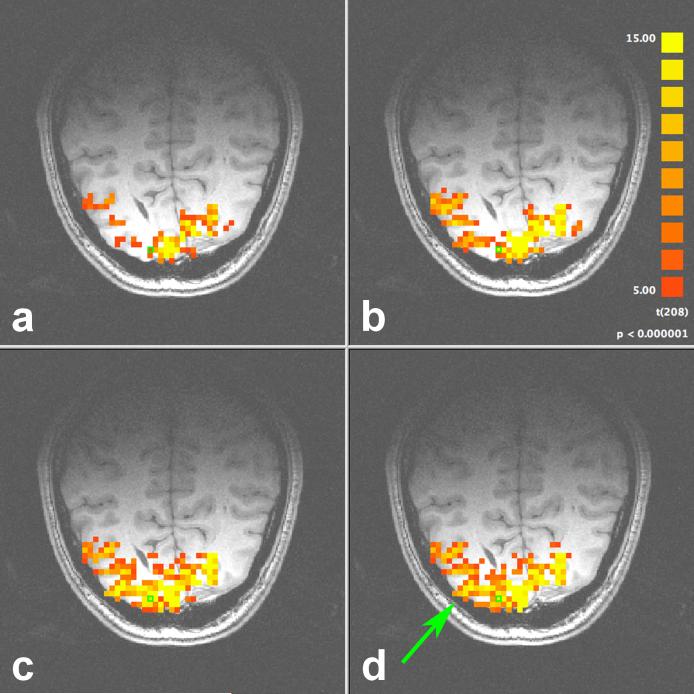
FIG. 4.

Activation map resulting from the flashing checkerboard experiment with (a) no correction, (b) 1D correction, and hybrid 2D correction with (c) δ = 21 and (d) δ = 17. The arrow highlights one region significantly improved using 2D navigator correction.

The full encoding matrices G and D are now replaced with reduced encoding matrices G̃ and D̃ that only consider k-space within the central δ × δ region. Since $\Delta {\stackrel{\rightharpoonup }{\omega }}_{est}\left(\stackrel{\rightharpoonup }{r}\right)$ may be downsampled, the dimensions of G̃ and D̃ are δ² × N_r², and the pseudo-inverse matrix D̃⁻¹ has dimensions N_r² × δ². This implementation is shown in Eq. 6.

$${\tilde{k}}_{center}=\tilde{G}{\tilde{D}}^{-1}{\tilde{k}}_{acq}$$ [6]

After the center δ² k-space points are corrected using Eq. 6, the remaining (N² – δ²) points on the periphery of k-space are corrected using either global or 1D navigator correction. When δ = ξ = N, the central region to be corrected includes all points, so full 2D navigator correction is in fact a special case of hybrid 2D navigator correction.

In the simulations, uncorrected k-space is used to construct $\Delta {\stackrel{\rightharpoonup }{\omega }}_{est}\left(\stackrel{\rightharpoonup }{r}\right)$ for hybrid 2D correction, and 1D navigator correction is applied to the periphery of k-space. This is done as a proof of concept of the proposed algorithm. In our lab, preprocessing of raw EPI data begins with an initial reference phase correction (Bruder et al., 1992) followed by 1D navigator correction. For each slice, the image with the smallest absolute phase at the center of k-space after 1D correction is chosen as the reference image, and 1D corrected k-space is used to construct estimates of $\Delta \stackrel{\rightharpoonup }{\omega }\left(\stackrel{\rightharpoonup }{r}\right)$.

The hybrid 2D algorithm just described is designed for 2-shot center-out EPI sequences. As $T_2^{\ast }$ decreases with increasing field strength, some multi-shot EPI experiments may perform full k-space coverage using four or more shots. As an example, consider a 4-shot EPI sequence where the navigator echo line k_y = 0 is acquired immediately after each RF pulse such that the center of k-space is acquired at t = TE. The order of data acquisition in 128 × 128 k-space would be k_y = 0, 2, 4, 6, ..., 64 in the first shot, k_y = 0, 1, 3, 5, ..., 63 in the second shot, k_y = 0, −1, −3, −5, ..., −63 in the third shot, and k_y = 0, −2, −4, −6, ..., −62 in the final shot (Menon et al., 1997). An estimate of $\Delta \stackrel{\rightharpoonup }{\omega }\left(\stackrel{\rightharpoonup }{r}\right)$ using just the k-space data acquired after any one of these shots would result in aliasing. To avoid aliasing artifacts, data from one shot must be combined with data from previous or subsequent shots. Four separate measurements of $\Delta {\stackrel{\rightharpoonup }{\omega }}_{est}\left(\stackrel{\rightharpoonup }{r}\right)$ must be made to correct the central δ × δ region containing data acquired after four RF pulses.

The most straightforward approach is to combine k-space data from adjacent shots. In our 4-shot EPI example, $\Delta \stackrel{\rightharpoonup }{\omega }\left(\stackrel{\rightharpoonup }{r}\right)$ for the first shot $\left(\Delta {\stackrel{\rightharpoonup }{\omega }}_{est}^{RF=1}\left(\stackrel{\rightharpoonup }{r}\right)\right)$ is estimated using k_y = 0 from the first shot and k_y = 1, 2, 3, ..., 64 from the first and second shots, and $\Delta {\stackrel{\rightharpoonup }{\omega }}_{est}^{RF=2}\left(\stackrel{\rightharpoonup }{r}\right)$ uses the same k-space data except for using k_y = 0 from the second shot. Similarly, $\Delta {\stackrel{\rightharpoonup }{\omega }}_{est}^{RF=3}\left(\stackrel{\rightharpoonup }{r}\right)$ is calculated using k_y = 0 from the third shot and k_y = −1, −2, −3, ..., −63 from the third and fourth shots, and $\Delta {\stackrel{\rightharpoonup }{\omega }}_{est}^{RF=4}\left(\stackrel{\rightharpoonup }{r}\right)$ uses the same k-space data except for using k_y = 0 from the fourth shot. Once the estimates of $\Delta \stackrel{\rightharpoonup }{\omega }\left(\stackrel{\rightharpoonup }{r}\right)$ are made, Eq. 6 is employed as before to correct the central region of k-space, and the periphery k-space data is corrected using the navigator echo line measured at the beginning of each interleave. The 4-shot and 8-shot EPI simulations presented in this paper employ this approach to estimate $\Delta \stackrel{\rightharpoonup }{\omega }\left(\stackrel{\rightharpoonup }{r}\right)$ for each shot.

Another approach to reduce the temporal blurring in the estimation of $\Delta \stackrel{\rightharpoonup }{\omega }\left(\stackrel{\rightharpoonup }{r}\right)$ for multi-shot acquisitions is a retrospective binning of k-space segments by monitoring the phase of the center of each navigator echo line to combine data from different shots that are at similar points in the respiration cycle. This approach is also the first step in extending the application of hybrid 2D navigator correction to data acquired with multi-shot linear EPI trajectories – retrospective k-space binning may be used in conjunction with Eq. 1 to estimate $\Delta \stackrel{\rightharpoonup }{\omega }\left(\stackrel{\rightharpoonup }{r}\right)$ for each shot without the need for partial Fourier reconstruction.

A third approach to estimating 2D field inhomogeneities is the introduction of a separate navigator to sample low-frequency k-space immediately before the start of every echo train (Miller and Pauly, 2003; Butts et al., 1997). Although a separate navigator may be useful in a future implementation, the advantages of the first two approaches are that they enable the correction to be retrospectively applied to any previously acquired multi-shot EPI data and no modification of the acquisition sequence is required.

Simulation Designs

Two simulations were performed using the proposed 2D navigator correction technique in the theoretical case of infinite image SNR. Any fluctuation in the time series of a ROI may be attributed solely to RIPN, and a “perfect” navigator correction algorithm would completely remove these fluctuations. Therefore, these simulations are useful in identifying the conditions under which these fluctuations are minimized using 2D navigator correction. The use of a model with infinite SNR is an important step to improve our understanding of the manifestation of RIPN in multi-shot EPI data – the effects of which may have otherwise been obscured by real data inconveniences such as thermal noise, subject motion, and other sources of physiological noise.

The goals of the first simulation were to validate the use of full 2D correction as an improvement over 1D correction, and to investigate the performance of hybrid 2D correction in comparison to full 2D correction for increasing δ. Analyses were performed on a sequence of 20 simulated images (2-shot EPI, 64 × 64, TE = 22 ms, TR = 525 ms) acquired under the influence of respiratory-induced frequency offsets. The second simulation explores (1) the dependence of RIPN on TR and the number of shots in high-resolution multi-shot EPI by conducting 2-shot, 4-shot, and 8-shot EPI fMRI acquisitions (128 × 128, TE = 15 ms) under the influence of the same respiratory-induced frequency offsets with TR = 525 ms, 265 ms, 135 ms, and 65 ms (3 × 4 = 12 configurations); and (2) the performance of hybrid 2D correction (δ = 16) for each acquisition configuration. Finally, ξ = N to keep the method of estimating $\Delta \stackrel{\rightharpoonup }{\omega }\left(\stackrel{\rightharpoonup }{r}\right)$ consistent for all simulations.

Measurements of the respiratory-induced frequency offsets at 4 T showed that within an axial slice they vary considerably in the anterior-posterior direction and comparatively less in the left-right direction. As the partial Fourier reconstruction described for 2D correction of multi-shot EPI data convolves the frequency estimate in the phase-encode direction, the best 2D estimate of $\Delta \stackrel{\rightharpoonup }{\omega }\left(\stackrel{\rightharpoonup }{r}\right)$ will be obtained with the phase-encode gradient set in the direction of least spatial variation (left-right) and the read gradient in the anterior-posterior direction. This is also the preferred configuration for 1D navigator echo correction to be most effective (Barry and Menon, 2005). However, to demonstrate the benefits of 2D correction in the situation where the navigator echo line maps frequency offsets in the direction of most spatial variation, the “less preferred” (alternative) configuration is chosen for the first simulation (read gradient in the left-right direction and phase-encode gradient in the anterior-posterior direction) with the philosophy that if 2D navigator corrections perform well using the alternative configuration, then they should perform better with the preferred configuration. The second simulation employs both gradient configurations to confirm this statement.

To achieve an accurate measurement of the noise fluctuations throughout an image and an unbiased comparison between correction methods, a gray matter (GM) region of interest (ROI) was defined by segmenting gray matter throughout the axial brain image, and includes 400 pixels in the 64 × 64 image and 1500 pixels in the 128 × 128 image. The low-resolution GM ROI was used for the first simulation and the high-resolution GM ROI was used for the second simulation. The simulation results presented are therefore the mean peak-to-peak single pixel noise intensity fluctuations across all gray matter.

In Vivo Experiments

A noise measurement experiment was performed on a subject to estimate the suppression of RIPN using navigator corrections in a typical human fMRI study. A single mid-axial slice was selected, and a T₂*-weighted 2-shot centre-outwards 64 × 64 EPI sequence (TE = 15 ms, TR = 500 ms, θ_E = 42°, field of view (FOV) = 19.2 cm, slice thickness = 6 mm) was used to acquire 480 resting-state images during an 8-minute scan. The read gradient was chosen to be in the anterior-posterior direction to maximize the effectiveness of 1D navigator correction.

External physiological monitoring equipment was not required because it has been shown that the respiration cycle may be extracted simply from the phase of the center of k-space (i.e., the global navigator) (Hu and Kim, 1994). The normalized power spectrum density (PSD) of the global navigator revealed the respiration peak to be at 0.26 Hz with 28% of the noise power within a 0.1 Hz bandwidth. To avoid regions of signal void, a minimum pixel SNR of 10:1 was set, resulting in an image mask consisting of 1508 pixels. Before the images underwent navigator correction, the area under the normalized PSD between 0.21 Hz and 0.31 Hz was computed for each pixel to measure RIPN with no correction. This area under the PSD was then calculated for each pixel after 1D correction and 2D correction (for a given δ and ξ). The ratio of the area after 2D correction to the area after 1D correction (denoted as β) measures the improvement of the proposed algorithm with respect to the current method used in our lab. If β < 1, then 2D navigator correction further decreased RIPN for that pixel. The mean (μ) and standard deviation (σ) of β across the image mask are used to gauge the performance of hybrid 2D navigator correction. As this performance is dependent on both δ and ξ, 17 values of δ (= 1, 3, 5, ..., 31, 33) were considered for 19 values of ξ (= 3, 5, 7, ..., 31, 33, 43, 53, 64), resulting in 323 correction configurations.

To validate the use of 2D navigator correction, the same subject underwent a visual activation experiment using an 8 Hz radial flashing checkerboard. The paradigm was a block design with seven segments (four baseline and three activation), and started with a baseline resting state followed by alternating segments of activation (flashing checkerboard) and baseline (central fixation). With a quadrature surface coil centered on the occipital pole, five oblique slices were planned parallel to the calcarine sulcus, and a 2-shot EPI sequence (matrix = 64 × 64, TE = 15 ms, TR = 500 ms, θ = 22°, FOV = 19.2 cm, slice thickness = 3 mm) was used to acquire 210 images. As before, the read gradient was set along the anterior-posterior direction. A general linear model (GLM) with a predictor formed by convolving a boxcar waveform coincident with the paradigm with a double-Gamma hemodynamic response function was used to generate the functional activation maps. Other routine pre-processing steps (spatial smoothing, linear trend removal, etc.) were not performed in order to isolate the effects of navigator correction on the activation maps.

Finally, to measure the improvement expected from 2D navigator correction in typical fMRI studies, eight additional subjects were recruited to each perform three functional runs using the same flashing checkerboard paradigm. A transmit-receive volume head coil was used with a 2-shot EPI sequence (matrix = 64 × 64, TE = 15 ms, TR = 1000 ms, θ = 40°, FOV = 19.2 cm, slice thickness = 3 mm, read gradient in anterior-posterior direction). Data from two subjects were discarded due to excessive movement. Each of the remaining 18 runs were processed in two ways – using 1D correction and hybrid 2D correction (δ = 17, ξ = 21) – before undergoing within-plane spatial smoothing using a 2.5-pixel (7.5 mm) full-width at half-maximum Gaussian kernel. For each run, two volumes of interest (VOIs) were selected in the visual cortex that included pixels with a t-statistic of 5.0 or higher: one using 1D navigator corrected data and the other using 2D navigator corrected data. From these VOIs, the increase in activation volume is calculated, as well as two new VOIs from the logical AND and XOR operations of the 1D and 2D corrected VOIs. This approach simplifies the analysis by separating the original overlapping VOIs into regions active in both (AND), and active in either 2D or 1D navigator corrected data but not both (XOR). The previously described GLM analysis was then used to calculate the maximum (t_max) and average (t_avg) t-statistics for both the AND and XOR regions of the 2D and 1D navigator corrected data. The average and maximum t-statistics for the AND and XOR regions in the 2D navigator corrected data are expressed as percentage increases from the average and maximum t-statistics for the same regions in the 1D navigator corrected data.

RESULTS

SIMULATIONS

The mean noise fluctuation for the simulated 2-shot EPI sequence was 2.47% without correction, and decreased to 1.83% with 1D navigator correction. As the first step in 2D navigator corrections (the choice of reference image I_ref ) is inherently subject to some variability, we investigated the degree of influence that the choice of reference image has on full 2D correction. The first reference image was acquired with uniform frequency offsets, and represents the “ideal” reference image that could be selected from the initial functional images. The second reference image was constructed when the top half of k-space was acquired at a peak value of the global navigator, and the bottom half acquired at an opposite peak; this represents the “worst case” reference image. Full 2D correction using these “ideal” and “worst case” reference images decreased this noise by about an additional factor of two to 0.807% and 0.915%, respectively. The maximum difference in the performance of 2D correction based on the choice of reference image is 0.1%, which is an order of magnitude less than the noise being suppressed (2% vs. 0.1%). Thus, it is reasonable to state that the process of choosing a reference image does not have a critical influence on the performance of full 2D correction, although a reference image with minimal geometric distortions is clearly preferable. The “ideal” reference image is used for all subsequent 2D corrections.

Figure 1 shows the mean noise fluctuation with no correction, 1D correction, hybrid 2D navigator correction, and full 2D navigator correction. This plot shows a trend that the performance of hybrid 2D correction improves as δ increases. When δ = 16, this noise decreases to a minimum of 0.799%, which is virtually identical to full 2D correction (0.807%). This result supports the hypothesis that rigorous non-linear corrections are most beneficial when applied to the center of k-space.

FIG. 1.

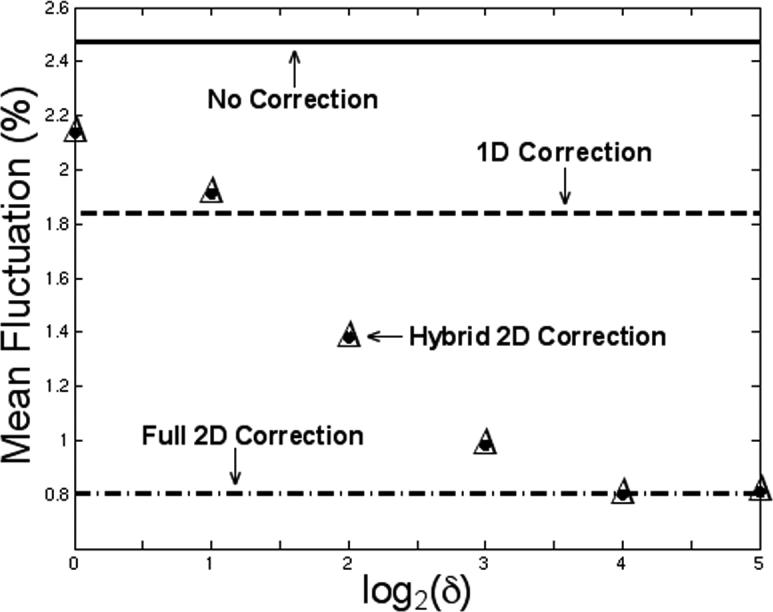
Mean percentage noise fluctuation in the GM ROI with hybrid 2D navigator correction for δ = 1, 2, 4, 8, 16, and 32. The mean noise fluctuation with no correction, 1D correction, and full 2D correction are shown for comparison. When δ = 16, the performance of hybrid 2D correction is virtually identical to full 2D correction.

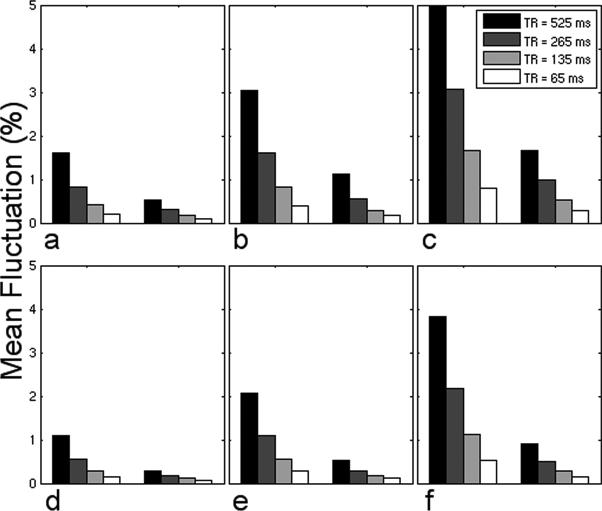
Figure 2 presents the mean noise fluctuation in high-resolution images as a function of increasing the number of shots and decreasing TR using the alternative (a–c) and preferred (d–f) gradient configurations. Based on our findings from the first simulation, only the results for δ = 16 are displayed for hybrid 2D correction.

FIG. 2.

Mean percentage noise fluctuation in the GM ROI using 2-shot (a,d), 4-shot (b,e), and 8-shot (c,f) EPI sequences employing the alternative (a,b,c) and preferred (d,e,f) gradient configurations with no correction (left groupings) and hybrid 2D navigator correction using δ = 16 (right groupings) for the four values of TR considered.

IN VIVO EXPERIMENTS

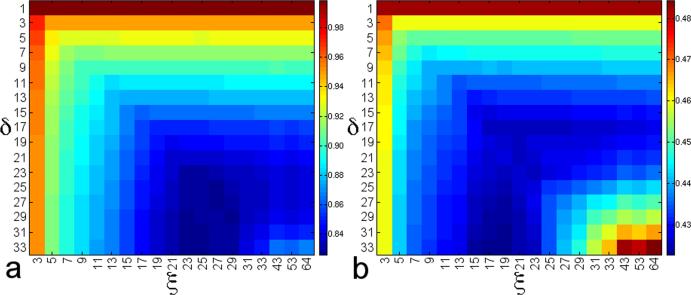
As the optimal range of spatial frequencies to correct is not known a priori, appropriate values for δ and ξ must be inferred from the data. Figure 3 displays the value of μ and σ, respectively, for each δ (rows) and ξ (columns). In Fig. 3a, there is a trend towards decreasing μ as both δ and ξ increase, with δ = 17 and ξ ≥ 17 marking the point of diminishing returns in the reduction of RIPN. For δ ≥ 23, there is no benefit in increasing ξ past 23. In Fig. 3b, σ is a minimum when ξ = 19 for δ ≥ 23, and increases sharply for ξ > 23. Therefore, 19 ≤ ξ ≤ 23 is an appropriate range for ξ. Based on this reasoning, ξ is set to 21, which corresponds to spatial frequencies up to ±0.52 cm⁻¹. In this low-frequency regime, k-space is dominated by physiological noise; the inclusion of spatial frequencies higher than this only adds extraneous thermal noise to the estimation of ΔB, and explains the increase in μ for ξ > 23.

FIG. 3.

As metrics to quantify the reduction of RIPN, the (a) mean and (b) standard deviation of all β are calculated for a physiological noise measurement experiment. Each combination of δ and ξ is a slightly different configuration for hybrid 2D correction.

Setting δ = 21 to match ξ corresponds to μ = 0.836 (σ = 0.426). However, as δ = 21 is computationally expensive and not appropriate for large data sets, a value of δ = 17 provides comparable results (μ = 0.851, σ = 0.426) in a fraction of the time. Using 1D correction, the percentage of pixels with β < 1 (denoted as P) is 90.5%. When δ = 17 and ξ = 21, P= 96.3%, indicating that 6% more pixels benefit from suppressed RIPN with this configuration.

The activation map for one representative slice through the visual cortex is shown in Fig. 4 with (a) no correction, (b) 1D correction, and hybrid 2D correction with (c) δ = ξ = 21 and (d) δ = 17, ξ = 21. In Fig. 4d, cubic spline interpolation was used to resample $\Delta {\stackrel{\rightharpoonup }{\omega }}_{est}\left(\stackrel{\rightharpoonup }{r}\right)$ from its original 64 × 64 resolution to a minimum 21 × 21 resolution to reduce the computation time. The time series for a pixel severely contaminated with RIPN (highlighted by the green box) is shown in Fig. 5. This pixel has a t-value of 6.80 with (a) no correction, and is increased in (b) to 16.8 with 1D navigator correction. In (c), hybrid 2D correction (δ = 17, ξ = 21, and $\Delta {\stackrel{\rightharpoonup }{\omega }}_{est}\left(\stackrel{\rightharpoonup }{r}\right)$ downsampled) further improves the t-value to 24.5.

FIG. 5.

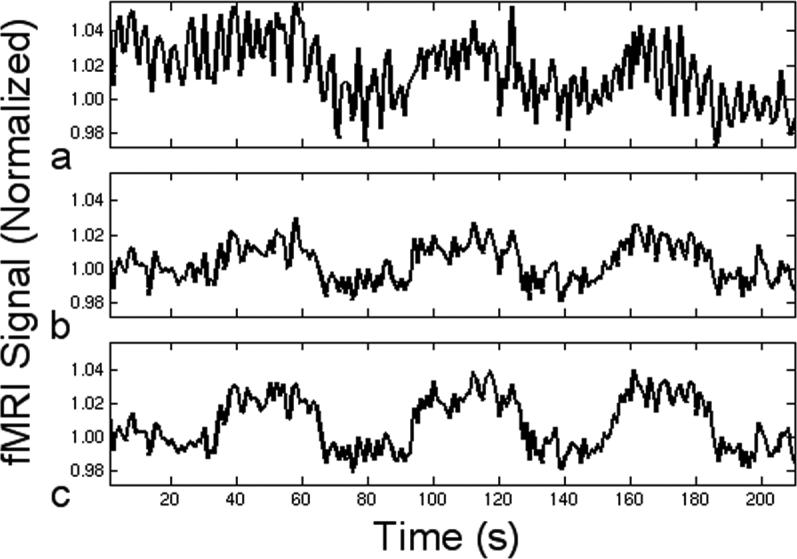
Time course for a gray matter pixel (a) without navigator correction, and the application of (b) 1D correction and (c) hybrid 2D correction to reduce troublesome fluctuations due to respiration.

In the group analysis of 18 functional runs, the 95% confidence interval (CI) (Cumming and Finch, 2005; Masson and Loftus, 2003) is used to confirm that all increases are statistically significant at the 95% confidence level (because the interval does not contain zero). A 15.25% increase in the volume of activation was observed with a CI of (11.38% to 19.12%) when going from 1D to 2D navigator correction. Within the AND regions (common to both 2D and 1D navigator corrected data), there was a 6.18% increase (CI = 2.37% to 9.99%) in t_max and a 10.08% increase (CI = 7.85% to 12.31%) in t_avg. Within the XOR regions, there was 71.38% increase (CI = 57.15% to 85.61%) in t_max and a 55.63% increase (CI = 49.28% to 61.99%) in t_avg. The vast majority of XOR volume consisted of activation present in 2D navigator corrected data but not 1D navigator corrected data.

DISCUSSION

SIMULATIONS

As shown in Fig. 2, RIPN increases approximately linearly as the number of shots increases for a fixed TR. For example, in Fig. 2(a–c), when TR = 265 ms, the mean noise without navigator correction increases from 0.822% (2-shot) to 1.61% (4-shot) to 3.07% (8-shot). Similarly, for a given number of shots, RIPN increases linearly with increasing TR (for the values of TR considered). In Fig. 2a, the mean noise increases from 0.204% (TR = 65 ms) to 1.60% (TR = 525 ms) without correction. In both cases, the change in RIPN may be attributed to the same mechanism that the geometric distortions are heavily influenced by respiratory-induced phase inconsistencies in k-space between consecutive RF pulses within a given slice (Noll et al., 1998). The observation that the mean noise fluctuation after correction for 4-shot and 8-shot sequences is higher than that for 2-shot sequences is due to the previously described temporal blurring, which may be improved with retrospective binning of k-space segments. From the point of view of suppressing RIPN, it may be advantageous to acquire fMRI data using single-shot EPI sequences, SENSE type acquisitions (Pruessmann et al., 1999), or multi-shot EPI sequences with a short TR. Finally, although hybrid 2D correction can be applied to data acquired using either gradient configuration, this simulation suggests that improvement by an additional factor of approximately two may be achieved by using the preferred gradient configuration. It should also be noted that none of the navigator correction techniques examined were able to completely remove RIPN, and residual geometric distortions existed in all (infinite SNR) simulations.

IN VIVO EXPERIMENTS

The most striking observation in Fig. 4 is the sheer importance of using navigator correction to increase BOLD CNR throughout the brain. Significant improvement is realized using 1D navigator correction, and as expected, even more improvement is possible with hybrid 2D correction. Minor differences are observed between Figs. 4c and 4d, confirming earlier hypotheses that (1) correcting spatial frequencies up to ±0.42 cm⁻¹ (δ = 17) and (2) downsampling $\Delta {\stackrel{\rightharpoonup }{\omega }}_{est}\left(\stackrel{\rightharpoonup }{r}\right)$ to ξ × ξ are both appropriate compromises between correction accuracy and computation time. In regions where the navigator echo line is not sufficient to accurately measure local field fluctuations, the benefit of 2D navigator correction is clear. For example, the green arrow in Fig. 4d draws attention to the improved statistics along the middle occipital gyrus. In this region, the maximum t-value increases from 5.7 with no correction to 12.4 with 1D correction, and finally to 16.3 with hybrid 2D correction.

As the preferred gradient configuration is used in all in vivo experiments, the percentage increases reported are with respect to the best performance of 1D navigator correction. In AND regions with the highest t-statistics (typically t_max = 20+ and t_avg = 8−10), hybrid 2D navigator correction provided a 6% increase in t_max and a 10% increase in t_avg. In XOR regions with lower t-statistics (typically t_max = 8−10 and t_avg = 3−4), 2D correction provided a 71% increase in t_max and a 56% increase in t_avg. Although all active regions clearly benefit from 2D navigator correction, this navigator is especially useful for detecting subtle BOLD activation in regions that experience decreased BOLD CNR due to contamination by residual physiological noise.

When N_r = N, the approximate correction time per image is about one minute for δ = 21 and less than half a minute for δ = 17 (executed on a 1.6 GHz single-processor desktop). Downsampling $\Delta {\stackrel{\rightharpoonup }{\omega }}_{est}\left(\stackrel{\rightharpoonup }{r}\right)$ to 21 × 21 (in Fig. 4d) reduces the time to about two seconds per image, making this algorithm practical without significantly compromising its effectiveness. Furthermore, as the correction of one image is independent of any other image, parallel processing may also be used to further reduce the overall computation time.

Since respiratory-induced field inhomogeneities are dependent on the shape and volume of the lungs and the movement of the chest, the practical implementation of this algorithm requires a one-time optimization for ξ for each class of subject (human adult, human child, cat, rat, etc.). For each class, a matrix like Fig. 3 would be constructed for multiple subjects using typical sets of fMRI acquisition parameters (with a sufficient sampling rate to avoid aliasing of respiration frequencies). For human adults, we observed the optimal spatial cut-off frequency to be approximately ±0.5 cm⁻¹. Having selected a cut-off frequency, ξ is automatically known for each experiment as it only depends on the field of view. Finally, δ should be set as high as possible (≤ ξ) given an acceptable processing time.

CONCLUSIONS

Developed through simulations and validated using in vivo experiments, hybrid 2D navigator correction has been presented as a new computationally-efficient correction technique that offers improvement in the reduction of RIPN compared to the best performance of 1D navigator correction. For typical fMRI experiments, we estimate this improvement to be a 15% increase in the volume of activation, 6% and 10% increases in the maximum and average t-statistics, respectively, for regions with high t-statistics, and 71% and 56% increases in the maximum and average t-statistics, respectively, in regions with low t-statistics due to contamination by residual physiological noise. The implementation of this algorithm does not require any modification to our set-up or pulse sequence, and may be retroactively applied to any EPI data set where raw k-space is retained and the acquisition parameters are known. Other avenues of research that may also benefit from 2D navigator correction include single-shot acquisitions, spiral trajectories, and parallel imaging. Although this research was motivated by respiratory-induced physiological noise, hybrid 2D navigator correction may also be useful in correcting geometric distortions produced by other sources of non-trivial field perturbations, such as paradigm-related subject motion.