Spatial considerations for the allocation of pre-pandemic influenza vaccination in the United States

Abstract

The impact of the next influenza pandemic may be mitigated by inducing immunity in individuals prior to the start of national epidemics using a pre-pandemic vaccine targeted against current avian influenza strains. The US Department of Health and Human Services (HHS) intends that pre-pandemic vaccines will be allocated to states in proportion to the size of their population in predefined priority groups, i.e. approximately pro-rata. We show that such an equitable policy is likely to be the least efficient in terms of the number of infections averted. We demonstrate that the potential benefits could be substantial if a fully discretionary policy is allowed, i.e. if some regions are allocated sufficient vaccines to achieve herd immunity while other regions are allocated no vaccine. Since such an inequitable policy may be impractical, we consider the sensitivity of an intermediate policy (in which 50% of the stockpile is allocated on a pro-rata basis) to key transmission uncertainties. The benefits of the 50% discretionary policy are sensitive to parameter values which cannot be known in advance. Therefore, despite substantial potential benefits of non-pro-rata policies, our results suggest that the current HHS policy of pro-rata allocation by state is a good compromise in terms of simplicity, robustness, equity and efficiency.

1. Introduction

The use of a pre-pandemic vaccine against the dominant avian influenza strain circulating is now being considered as an option to mitigate the next influenza pandemic (Bresson et al. 2006; Lin et al. 2006; Treanor et al. 2006). However, it is unlikely that supply will be sufficient to provide high coverage for most populations, including the United States (Monto 2006; Nichol & Treanor 2006). According to the current US Health and Human Services (HHS) Pandemic Influenza Plan (www.hhs.gov/pandemicflu/plan/sup6.html), each state will receive pandemic vaccines in proportion to the size of its population in predefined priority groups. These groups include frontline healthcare workers, emergency service personnel and the elderly. Because the size of priority groups scales approximately linearly with the total population size, this policy approximates to pro-rata allocation under which vaccines are allocated according to the population size of each state.

A pro-rata policy is intuitively appealing because it is equitable and simple, i.e. states are allocated vaccines according to population size. Thus, every individual in principle has an equal chance of vaccination (equitable) and the policy requires no additional epidemiological information for implementation (simple). However, its public health consequences have not been examined in terms of efficiency and robustness which are also desirable properties of any vaccine distribution policy, i.e. would such an allocation policy avert as many infections as possible (efficiency) and would it perform well under a range of as yet uncertain epidemiological scenarios (robustness). Here we show that pro-rata or equitable allocation may be the least efficient policy in terms of minimizing the population infection attack rate (IAR). Motivated by this observation, we then quantify the tradeoff among the other three goals of equity, simplicity and robustness for more efficient spatial allocation policies in the distribution of pre-pandemic vaccines. Because tradeoff among these objectives is common in control of epidemics, the insights from this study are not only restricted to pre-pandemic vaccinations but also applicable to general problems of epidemic control.

We analyse a range of policies under which some portion of the vaccine stockpile is distributed pro-rata while the remaining is allocated to minimize IAR. Following the terminology introduced in Kaplan & Merson (2002), we call the latter portion of the stockpile the discretionary stockpile and the associated policies discretionary policies. Specifically, a d% discretionary policy reserves d% of the vaccines for the discretionary stockpile with the remaining (100−d)% distributed pro-rata. The associated IAR is denoted by IAR(d). In this study, an allocation policy is defined as a map, in the mathematical sense, that takes the basic reproductive number R₀ and coverage c as inputs and generates a geographical vaccine allocation α=(α₁, …, α_K), where α_i is the proportion of stockpile allocated to geographical area i. We use a deterministic meta-population model parameterized with detailed travel data (see §2) to predict the epidemiological consequences of alternative allocation policies. A similar modelling approach has been used in recent studies to analyse allocation policies of HIV resources (Wilson et al. 2006). The quantity IAR(d) is used as the primary outcome for efficiency when evaluating policies. The gain in efficiency provided by discretionary policies over pro-rata can therefore be measured by ΔIAR(d)=IAR(d)−IAR(0). Values for ΔIAR(d) are given in absolute terms.

2. Material and methods

We partition the continental US into the 10 Standard Federal Regions established by the US Office of Management and Budget (figure 1a). Our results are not significantly different when a 4-region (defined by the Census Bureau) or 49-‘state’ (the 48 continental states plus the District of Columbia) model is used (see figure 1 in the electronic supplementary material). Transmissibility of the virus is characterized by its basic reproductive number R₀, defined as the average number of secondary infections generated by a typically infectious individual in an otherwise susceptible population (Anderson & May 1991). We assume in the base case that transmissibility is the same in every region with R₀ ranging from 1 to 3 (Mills et al. 2004; Ferguson et al. 2006; Germann et al. 2006). We assume that vaccine-induced immunity has fully developed before the pandemic reaches the vaccinated populations and remains constant throughout the course of the first wave of the pandemic. Parameter values and assumptions are summarized in table 1.

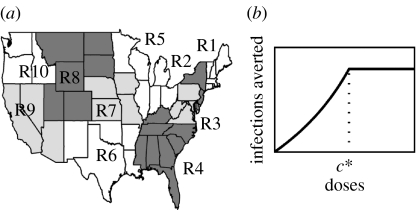
Figure 1.

(a) The 10 standard Federal Regions established by Office of Management and Budget Circular A-105, ‘Standard Federal Regions’. (b) The relationship between reduction in IAR and coverage. Epidemic is impossible if coverage is higher than the critical coverage c^*.

Table 1.

Parameter values and assumptions. Local transmissibility of region i is given by ${\beta }_i={\hat{R}}_0\left(1+ϵ\right)h/D_{\text{I}}$, where ${\hat{R}}_0$is the basic reproductive number assumed when constructing the discretionary policies.

parameter	base case assumptions	sensitivity	sources
$\left\{z_i^{\text{S}}\right\}$, reduction in susceptibility after vaccination, and {pi}, the probability distribution of $\left\{z_i^{\text{S}}\right\}$	vaccine efficacy for susceptibility VES=0.69 when antigenic match is perfect	driven by μ: $z_i^{\text{S}}\leftarrow \mu ·z_i^{\text{S}}$	Riley et al. (2007)
VEI, vaccine efficacy for infectiousness	VEI=0.8 when antigenic match is perfect	driven by μ: $V{E}_{\text{I}}\leftarrow \mu ·V{E}_{\text{I}}$	Longini et al. (2004); Patel et al. (2005)
ϵ, error in estimate of transmissibility	no error, i.e. ϵ=0	[−0.5, 0.5]	Mills et al. (2004); Viboud et al. (2006)
hi, relative hazard for transmissibility in region i	transmissibility is the same for all regions, i.e. hi=1 for all i	[0.5, 1.5]	Mills et al. (2004); Viboud et al. (2006)
δ, relative level of inter-regional mixing	inter-regional mixing is at normal level; δ=1 by definition	[0, 2] $m_{ij}\leftarrow \delta m_{ij},i\ne j$
μ, antigenic match between vaccine strain and pandemic strain	imperfect match with μ=0.7	[0, 1]

(a) A meta-population SIR model

We denote the population size of region i by N_i and let the total population size be $N={\sum }_{i=1}^K{N}_i$ where K=10. Let S_i, I_i and R_i be the number of susceptible, infectious and removed (dead or recovered) individuals in region i with N_i=S_i+I_i+R_i. Epidemic dynamics in different regions are coupled by a mixing matrix M={m_ij}, where m_ij is the average proportion of time that a resident of region i spends in region j (see electronic supplementary material, for the construction of M). The model without vaccination is defined by

$$\frac{\text{d}{S}_i}{\text{d}t}=-S_i\sum _{j=1}^K{m}_{ij}{\beta }_j\frac{\sum _{l=1}^K{m}_{lj}{I}_l}{\sum _{l=1}^K{m}_{lj}{N}_l}\text{and}\frac{\text{d}{I}_i}{\text{d}t}=-\frac{\text{d}{S}_i}{\text{d}t}-\frac{I_i}{D_I},$$

for i=1, …, K, where D_I is the mean infectious duration. The model can be interpreted as follows. We assume homogeneous mixing within each region. Given that a resident of region i is present in region j at time t, which occurs with probability m_ij, infectious contacts are made with other individuals present in region j at rate β_j and the proportion of infectious individuals in population j at time t is ${\sum }_{l=1}^K{m}_{lj}{I}_l/{\sum }_{l=1}^K{m}_{lj}{N}_l$. Since we are interested only in final attack rates, we can omit the latent stage. In the presence of vaccination, the model further classifies individuals by their immune states but otherwise follows the same dynamics (see electronic supplementary material). We develop an algorithm to compute the final number of infections in each region, denoted by U_1, …,U_K, by solving a system of K nonlinear equations regardless of the number of immune states (see electronic supplementary material).

(b) Vaccine efficacy

We assume that the pre-pandemic vaccine has efficacy for both susceptibility and infectiousness (Longini et al. 2004; Patel et al. 2005). We use a multi-state leaky vaccine response model that we developed in a previous study (Riley et al. 2007) to describe the distribution of reduction in susceptibility given by the most potent pre-pandemic vaccine that has been tested in clinical trials (Lin et al. 2006). We do not assume a distribution of reduction in infectiousness because it is not important as long as the mean reduction in infectiousness is the same (see electronic supplementary material for details on the vaccine response model). We assume that vaccine efficacy for both susceptibility and infectiousness are multiplied by μ∈[0, 1], which reflects the degree of antigenic match between vaccine and pandemic strains (μ=1 for perfect match).

(c) Optimization of vaccine allocation

Let (α₁, …, α_K) denote an arbitrary vaccine allocation. Given a set of transmission parameters and the size of vaccine stockpile V, the allocation for the d% discretionary policy is obtained by solving the following nonlinear programme in which the total number of infections is minimized:

$$\begin{array}{cc}\text{minimize}& \sum _{i=1}^K{U}_i\\ \text{subject}\text{to}& \left(1-\frac{d}{100}\right)\frac{N_i}{N}\le {\alpha }_i\le \text{min}\left\{\frac{N_i}{V},1\right\},1\le i\le K,\sum _{i=1}^K{\alpha }_i=1.\end{array}$$

The lower-bound on (α₁, …, α_K) is the discretionary stockpile size constraint. The upper bound says that vaccines allocated to a region cannot exceed its population size or the stockpile size.

3. Results

(a) Pro-rata may be the least efficient policy

We first give a simple example to illustrate why pro-rata may be inefficient by failing to minimize the population IAR. When we present results from the US 10-region model later in this section, we will use this example again to explain the structure of the discretionary policies. We define the function r(c) to be the reduction in IAR achieved by vaccine coverage level c, which is defined as the proportion of population vaccinated. Owing to herd immunity, the marginal number of infections averted per additional individual vaccinated increases as coverage rises until control is achieved (see electronic supplementary material for justification of this claim). That is, as c increases, the gradient of r(c) increases (i.e. r(c) is convex) and r(c) becomes flat only after the critical coverage level c^* has been achieved (figure 1b). (A function is convex if its gradient is increasing.) Suppose K populations of sizes N₁, …, N_K are isolated from each other but have the same disease dynamics (i.e. r(c) is the same for all populations). Given V doses of vaccines and an allocation α=(α₁, …, α_K), where α_i is the proportion of the overall stockpile allocated to population i, the total number of infections averted is $T(\mathit{\alpha })=N_{1}r({\alpha }_{1}V/N_1)+\cdots +N_{K}r({\alpha }_{K}V/N_K)$. Throughout this paper, we consider only ‘sensible’ allocations that do not prescribe coverage higher than the critical level c^* in any population; coverage beyond c^* has no benefit. We denote the pro-rata allocation by $\mathit{p}=(N_1/{\sum }_{i=1}^K{N}_i,\dots ,N_K/{\sum }_{i=1}^K{N}_i)$ and note that p minimizes T because T is convex and p is the unique stationary point of T (see electronic supplementary material). Therefore, in terms of minimizing IAR, pro-rata is the least efficient policy (among all sensible allocations) in this hypothetical example.

In the remainder of this section, we present results from the US 10-region model.

(b) The 100% discretionary policy

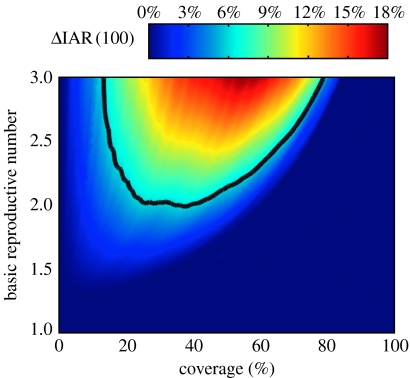
We first compare pro-rata with the 100% discretionary policy. Figure 2 shows that as R₀ varies between 1 and 3, ΔIAR(100) can be as large as 17.8% but remains below 6% when R₀≤2, which is suggested as the most probable range in recent studies of influenza pandemic mitigation (Mills et al. 2004; Ferguson et al. 2006; Germann et al. 2006). At low coverage, ΔIAR(100) is close to zero because allocation policy makes no difference when only a small amount of vaccines is available. At high enough coverage, ΔIAR(100) also approaches zero because control is achieved under both policies. ΔIAR(100) becomes non-negligible with higher R₀ values. If there is no inter-regional mixing, ΔIAR(100) shows similar patterns but can be as large as 26.6% (see figure 2 in the electronic supplementary material). In general, ΔIAR(100) is inversely related to the degree of inter-regional mixing. Since the level of inter-regional mixing will probably be lower than normal during a pandemic, our base case estimates of gain in efficiency will tend to be conservative.

Figure 2.

ΔIAR(100) as a function of basic reproductive number R₀ and coverage c for the 10-region model. The black contour marks the boundary below which ΔIAR(100)≤6%.

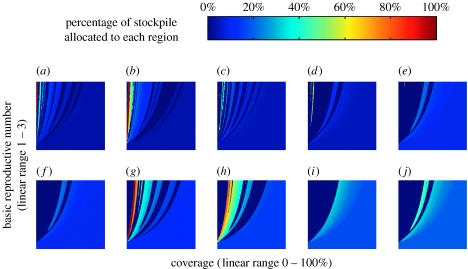
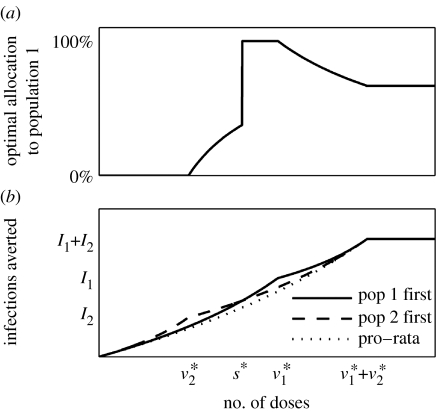
Figure 3 shows that the 100% discretionary policy typically achieves a lower IAR by sacrificing some regions to which no or relatively few vaccines are allocated, i.e. concentration of coverage and absence of equity. Furthermore, the policy is ‘choppy’ with many discontinuities as R₀ and c change, i.e. the associated allocation may exhibit sudden swings with small changes in R₀ and c. For example, with an R₀ of 2.4, the allocation to Region 8 falls from 100 to 0% as c increases from 2 to 2.1%. All discretionary policies exhibit concentration of coverage and choppiness, the degree of which scale with the discretionary stockpile size. These properties are the consequence of the convex relation between coverage and reduction in IAR (figure 1b). To see this, consider the simple example in figure 4, which is a special case of the example given in the beginning of this section where two non-interacting populations with sizes N₁>N₂ have the same transmission dynamics (see electronic supplementary material for mathematical details). Because the number of infections averted is a convex function of allocation, it is never optimal (in terms of minimizing IAR) to split the stockpile between the two populations unless control has been achieved in at least one of them. The optimal policy can therefore be identified by comparing only two policies: (i) vaccinate Population 1 then Population 2 and (ii) vaccinate Population 2 then Population 1. It is this immediate consequence of local herd-immunity effects that accounts for concentration of coverage. Figure 4 shows that there is a switching point s^* such that it is optimal to follow policy (i) if the stockpile size exceeds s^* and follow policy (ii) otherwise. As a result, at the switching point s^*, the optimal allocation to Population 2 drops discontinuously from 100 to 0%. This accounts for choppiness. In our meta-population model, inter-regional mixing is low because individuals spend more than 97% of their time in their home regions on average. This level of mixing is low enough such that concentration of coverage and choppiness are preserved in the 100% discretionary policy as shown in figure 3. Concentration of coverage has also been observed in previous studies that optimize vaccine allocations to different age groups (Longini et al. 1978; Patel et al. 2005). In those studies, however, mixing among age groups is high and concentration of coverage is a result of targeting high-prevalence groups (e.g. school children) or high-mortality groups (e.g. elderly). Here in our spatial model, inter-population mixing is low and concentration of coverage arises owing to different population sizes and the convex relation between reduction in IAR and coverage.

Figure 3.

The 100% discretionary policy. The percentage of stockpile allocated to the region is shown as a function of the basic reproductive number (R₀, which ranges from 1 to 3 on the y-axis) and coverage (c, which ranges from 0 to 100% on the x-axis). The percentage of population residing in each region is shown: (a) region 8 (3.4%), (b) region 10 (3.9%), (c) region 7 (4.5%), (d) region 1 (4.8%), (e) region 2 (9.5%), (f) region 3 (9.8%), (g) region 6 (12.1%), (h) region 9 (15.1%), (i) region 5 (17.4%), and (j) region 4 (19.5%). For simplicity, we set the optimal policy to be pro-rata when ΔIAR(100) is less than10⁻⁸. As a result, the 100% discretionary policy is flat (with colours that correspond to pro-rata) when both policies achieve control (towards the right). Choppiness in allocation corresponds to abrupt changes in colour.

Figure 4.

(a) The most efficient allocation policy exhibits concentration of coverage and choppiness. Populations 1 and 2 are non-interacting with sizes N₁>N₂. In both populations, reduction in IAR is a convex function of coverage unless critical coverage c^* is reached (figure 1b). (b) For Population i, the number of infections is I_i without vaccination and ${\nu }_i^{*}=c^{*}{N}_i$ doses of vaccines are needed to achieve control. The optimal policy is to give vaccination priority to the smaller population (i.e. Population 2 first) if stockpile size is less than s^* and to the larger population (i.e. Population 1 first) otherwise. Note that pro-rata is the least efficient policy.

(c) Gain in efficiency as a function of discretionary stockpile size

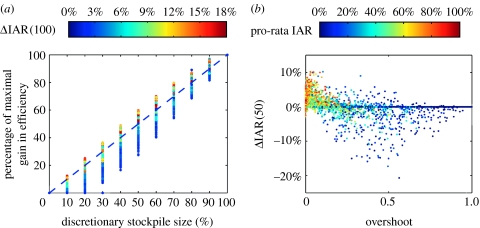
Consider the quantity ρ(d)=ΔIAR(d)/ΔIAR(100) which represents the proportion of maximal gain in efficiency (given by the 100% discretionary policy) that can be attained by the d% discretionary policy. The relation between discretionary stockpile size d and ρ(d) is a critical component of the equity–efficiency tradeoff. If the gain in efficiency is close to maximal (i.e. ΔIAR(100)) with a relatively small discretionary stockpile size (say 30%), an inequitable allocation, which is a necessary condition under discretionary policies, may be justifiable (Kaplan & Merson 2002). This corresponds to the d–ρ(d) relation being concave (i.e. the gradient of ρ(d) decreases as d increases). We consider only cases where ΔIAR(100)≥2%. Figure 5a shows that the relation is roughly linear for large values of ΔIAR(100), which means that if d% of the vaccines is reserved for the discretionary stockpile, then ΔIAR(d) is approximately d% of that shown in figure 2. As ΔIAR(100) drops below 6% (which corresponds to R₀≤2), the d–ρ(d) relation becomes mostly convex. Thus, the efficiency gain of discretionary policies described here is minimal unless equity is substantially compromised.

Figure 5.

(a) The percentage of maximal gain in efficiency (i.e. ΔIAR(100)) realized by a discretionary policy is an increasing function of its discretionary stockpile size d. This figure is generated as follows: for each stockpile size d, the quantity ρ(d)=ΔIAR(d)/ΔIAR(100) is computed for a 51 by 51 rectangular grid of the (R₀, c) plane. The colour of each point is colour-coded by the corresponding value of ΔIAR(100) using the same colour key in figure 2 (repeated here). The d–ρ(d) relation, which varies with (R₀, c), can be visualized by connecting points of the same colour. (b) To perform a multivariate sensitivity analysis on the 50% discretionary policy, we generate 5000 sets of model parameters in the ranges shown in table 1 using Latin hypercube sampling. Since inter-regional mixing is weak, the critical coverage $c_i^{*}$, i=1, …, K, are close to that when there is no inter-regional mixing, which are given by $(1-1/R_0^i)/VE$, i=1, …, K, where $R_0^i$ is the basic reproductive number in region i and $VE=1-(1-V{E}_{\text{S}})(1-V{E}_{\text{I}})$ is the overall vaccine efficacy. Therefore, given an allocation (α₁, …, α_K), the degree of overshoot can be accurately measured by $(1/cN){\sum }_{i=1}^K\text{max}(0,{\alpha }_{i}cN-c_i^{*}{N}_i)$ which is the proportion of stockpile misallocated due to overshooting when inter-regional mixing is zero. ΔIAR(50) drops sharply as the degree of overshoot increases. Each point of ΔIAR(50) is colour-coded by ΔIAR(0), which is the IAR under pro-rata. Overshoot is more likely when pro-rata IAR is low. That is, overshoot is more likely when the impact of the pandemic is relatively mild in the presence of pre-pandemic vaccination. ΔIAR(50) drops far below zero when there is overshoot and pro-rata IAR is below 50%.

(d) The risk associated with efficiency maximization

We have shown that regardless of the transmission scenario, the 100% discretionary policy prescribes highly inequitable allocations and is thus likely to be impractical. As a result, we switch our focus to the 50% discretionary policy, which represents a more equitable allocation policy, to test the robustness of reduction in IAR provided by discretionary policies (constructed using the base case parameter values in table 1). Qualitative results obtained from the sensitivity analyses below hold for all discretionary policies.

First, we conduct univariate sensitivity analyses on the 50% discretionary policy for each of the following parameters: (i) relative level of inter-regional mixing δ, (ii) antigenic match μ, and (iii) error in estimate of transmissibility ϵ. Graphical illustrations of these sensitivity analyses can be found in figure 3 in the electronic supplementary material. ΔIAR(50) increases as δ decreases because concentration of coverage is more effective when regions are isolated from each other (figure 3a in the electronic supplementary material). As antigenic match μ deviates from the base case value of 70%, ΔIAR(50) drops (figure 3b in the electronic supplementary material). ΔIAR(50) can become negative when μ is near 1 (i.e. antigenic match is underestimated) or when ϵ is below zero (i.e. transmissibility is overestimated; figure 3b,c in the electronic supplementary material). The effect of the former condition is much weaker because μ affects all discretionary policies while ϵ has no effect on pro-rata. Both conditions translate into underestimating vaccine effectiveness in reducing transmission, thus overestimating critical coverage. In these cases, the strategy of concentrating coverage into a few regions, which is the cornerstone of discretionary policies, performs poorly when the prescribed coverage is higher than the critical levels in these regions. Coverage beyond the critical level is misallocated because it generates very little or no reduction in IAR. We term this situation overshoot. Pro-rata has a smaller risk of overshoot because it has no dependence on transmissibility and it diversifies coverage among regions. Underestimating transmissibility (ϵ>0) has little effect on ΔIAR(50) in the range of ϵ considered (±50%). This suggests that when constructing the discretionary policies, assuming a lower transmissibility (within the range of equally plausible estimates) may alleviate the risk of overshoot and thereby enhance robustness. Finally, we perform a multivariate sensitivity analysis on δ, μ, ϵ, as well as the relative hazards for local transmissibility h_i, i=1, …, K (table 1). Together, these parametric variations represent model uncertainties that cannot be accurately predicted until the pandemic strikes. These include heterogeneities in local transmissibility and efficacies of mitigation interventions besides pre-pandemic vaccination. In the presence of these parametric variations, the resultant ΔIAR(50) is mostly smaller (up to 28%) than the base case ΔIAR(50) (figure 3d in the electronic supplementary material), which is the reduction in IAR expected from the 50% discretionary policy if all base case assumptions are satisfied. Figure 4b shows that the 50% discretionary policy can perform significantly worse than pro-rata (by more than 5% in IAR) when (i) there is overshoot and (ii) the pro-rata IAR is low (ΔIAR(0)≤50%). The latter condition corresponds to an intrinsically weak pandemic or a very effective mitigation programme. Such a scenario is unlikely when pre-pandemic vaccination is the only intervention but becomes more plausible in the presence of other interventions. In general, the larger the size of the discretionary stockpile, the higher the risk of overshoot and the associated magnitude of underperformance (relative to pro-rata).

4. Discussion

Other studies have considered targeted allocation of influenza vaccine based on non-spatial population heterogeneities (Longini et al. 1978; Patel et al. 2005). Generally, our results are consistent with these other studies in which we find that policies other than pro-rata are potentially more efficient. However, for the spatial sub-populations of the United States, although pro-rata may be the least efficient policy, the work presented here suggests that it does strike an attractive balance between equity, efficiency, robustness and ease of implementation. Because the basic reproductive number R₀ for pandemic influenza is likely to be less than 2, our estimated gain in efficiency from discretionary policies is not large enough (reduction in IAR≤6%) to justify the associated inequity. Moreover, this gain in efficiency can be severely attenuated when the assumptions used to construct the discretionary policies are violated (figure 3d in the electronic supplementary material). In some cases, significant overshoot occurs and renders discretionary policies less efficient than pro-rata (figure 5b). Such cases become more likely when other mitigation interventions are present (see below). Finally, while discretionary policies require detailed knowledge of the epidemiology of pandemic influenza (a transmission model and parameter estimates), pro-rata has no such requirement and is therefore much more straightforward to implement. These conclusions are robust against a range of model assumptions and structures. Therefore, despite substantial potential benefits of non-pro-rata policies, our results suggest that the current HHS policy of pro-rata allocation by state is a good compromise in terms of equity, efficiency, simplicity and robustness.

The validity of our results, as with all similar studies, is somewhat limited by the underlying assumptions of our model. We have used a deterministic model to evaluate vaccine allocation policies. Although stochastic effects may be important when control is nearly achieved in one or more regions, we expect that a stochastic model will lead to similar conclusions because the population sizes are large and parameter uncertainties have a much larger effect. We have assumed in our base case that transmissibility is the same in all regions. If transmissibility differs among regions, the relation between reduction in IAR and coverage (figure 1b) will also differ (e.g. different c^*) but the general shape (convexity) will remain unchanged for all regions. Consequently, discretionary policies will still exhibit concentration of coverage and choppiness, and their efficiency remains susceptible to overshoot. The gain in efficiency over pro-rata will require further analysis. However, it is not yet clear how a systematic difference in local–regional transmissibility, if it exists, can be estimated to support such an analysis: estimation of R₀ for the 1918 pandemic influenza strain in 45 US cities showed no correlation between R₀ and various city characteristics (including population size, latitude and longitude; Mills et al. 2004).

Here, we have considered the minimization of attack rate to be the main objective of pre-pandemic vaccination policies. There are a number of alternative approaches that could be taken. One would be to minimize the post-vaccination reproductive number (Ball & Lyne 2002). In the electronic supplementary material, we show that the reproductive number under pro-rata is near optimal (within 15%) under this objective. We also show that allocations which minimize the reproductive number do not necessarily minimize the attack rate, and vice versa, because the reproductive number describes the early dynamics of the epidemic while the attack rate is a summary outcome of the entire epidemic. Minimization of the reproductive number may be suitable if the objective is to minimize the initial epidemic growth rate (instead of the eventual total number of infections averted) which may help maintain healthcare services during the early phase of the pandemic. A second alternative policy goal might be to minimize the number of deaths. Because the case fatality ratio will probably be age-specific, this objective would require detailed knowledge of the age-specific mortality rate for the novel influenza strain, which was very different during the different pandemics of the twentieth century. The resulting formulation is similar to cases where geographical vaccine allocation is further optimized by targeting high-risk groups or high-prevalence groups (Patel et al. 2005; Bansal et al. 2006). In these cases, the relation between reduction in IAR r(c) and coverage c will take a more complicated form than that shown in figure 1b. For instance, if there are two risk groups in each population and vaccination priority is given to the group that has higher infectiousness (e.g. children), the c–r(c) relation comprises two convex regions (see figure 4 in the electronic supplementary material). Suppose all high-risk groups must be vaccinated (Phase 1) before any of the low-risk groups can be vaccinated (Phase 2) within each of these two phases, the discretionary policies will have the same structure shown here because convexity is preserved. However, if some low-risk groups can be vaccinated before all high-risk groups have been fully vaccinated, the structure of the discretionary policies will be more complex and would require further investigation.

Recent studies of pandemic influenza mitigation have come to the consensus that an effective programme will comprise multiple targeted, layered interventions including quarantine, isolation, vaccination and antiviral prophylaxis (Ferguson et al. 2006; Germann et al. 2006; Wu et al. 2006). Our conclusions will probably remain valid in the context of multi-component mitigation as long as the relation between reduction in IAR and coverage takes the form as shown in figure 1b. For instance, the presence of other interventions is roughly equivalent to lower transmissibility (lower R₀), which in turn means a smaller ΔIAR(100) (figure 2). In this case, the relationship between gain in efficiency and discretionary stockpile size that we describe remains applicable because we have characterized how this relation depends on ΔIAR(100) (figure 5a): ΔIAR(d) will probably be lower when other interventions are in place and the tradeoff between discretionary stockpile size and gain in efficiency is worsened. This further strengthens our conclusion that pro-rata is the most appropriate policy for allocating pre-pandemic vaccines to different geographical areas.

Although we have focused on evaluating pre-pandemic influenza vaccine allocation policies throughout this paper, our major results are applicable in a wider epidemiological context. Specifically, we have shown that for a meta-population with different population sizes and low inter-population mixing: (i) the convex relation between IAR reduction and vaccination coverage result in concentration of coverage and choppiness for policies that minimizes attack rate, (ii) the performance of these policies are susceptible to overshoot and therefore very sensitive to estimates of key epidemiological parameters, and (iii) minimization of attack rate is different from minimization of reproductive number both in terms of the underlying policies and the associated outcomes.

Supplementary Material

Supplementary text and figures

Spatial considerations for the allocation of pre-pandemic influenza vaccination in the United States