An Analysis of the Relationship Between Metabolism, Developmental Schedules, and Longevity Using Phylogenetic Independent Contrasts

Abstract

Comparative studies of aging are often difficult to interpret because of the different factors that tend to correlate with longevity. We used the AnAge database to study these factors, particularly metabolism and developmental schedules, previously associated with longevity in vertebrate species. Our results show that, after correcting for body mass and phylogeny, basal metabolic rate does not correlate with longevity in eutherians or birds, although it negatively correlates with marsupial longevity and time to maturity. We confirm the idea that age at maturity is typically proportional to adult life span, and show that mammals that live longer for their body size, such as bats and primates, also tend to have a longer developmental time for their body size. Lastly, postnatal growth rates were negatively correlated with adult life span in mammals but not in birds. Our work provides a detailed view of factors related to species longevity with implications for how comparative studies of aging are interpreted.

One of the major questions in gerontology is why similar species, such as mammals and primates, age at such markedly different paces. Identifying the genetic mechanisms that regulate the pace of aging across species is a top priority in gerontology with possibly many biomedical applications (1–3). Despite their great potential as a tool for gerontological research, however, comparative studies of aging are still riddled by a few methodological problems. At present, there is no accurate method to determine rate of aging for a given species, and so longevity—which, unless otherwise stated, herein refers to maximum longevity (t_max), also called maximum life span—is usually used as an approximation (3). Indeed, numerous experiments have been carried out attempting to correlate some parameter under study with the longevity of different species (4), yet the use of simple correlations between some factor and t_max, although potentially informative, may lead to further problems (5). Particularly, comparative studies of aging are often difficult to interpret and may even be biased because of the different factors, which may or may not be related to aging, that tend to correlate with longevity. In this work, we took advantage of AnAge, an online database with over 3000 animal species designed for the comparative biology of aging (6), to analyze in unprecedented detail the nonmechanistic factors that correlate with longevity in vertebrates.

Factors correlating with maximum and average longevity have been studied before, particularly in life history theory (7,8). One such factor is adult body size—here represented by body mass (M), a standard measure of body size—with larger animals living, on average, longer than smaller ones (7,9–11). Biological scaling can be described by the well-established allometric equation (9,10): Y = aM^b, where Y is some biological variable, a is a constant representing the proportionality coefficient, and b is the scaling exponent. Due to its association with longevity, M is a potentially confounding factor in comparative studies of aging that must be taken into consideration (11). In addition, animals that do not fit the allometry of life span may hold clues about the evolutionary forces shaping longevity and aging. Therefore, in this work we first evaluated allometric scaling in respect to t_max as well as in respect to the other factors under study: metabolic rates and developmental schedules.

Faster metabolic rates have for a long time been implicated with a faster biochemical activity and a faster aging process (12,13), but results so far have been mixed (5,14–16). Bats and marsupials, for instance, have been shown to be exceptions of this “rate of living theory” (17). Nonetheless, it has been argued that these exceptions do not disprove the overall trends of that theory (18). Indeed, metabolic rates are still considered by many authors as a possible factor influencing longevity and aging and one that researchers must consider when designing and interpreting comparative studies of aging (1,19–21).

In contrast, life history traits, such as developmental schedules and life span, have been shown to be associated with one another in a “fast–slow continuum” (7,8,15). In mammals, maximum adult life span has been shown to correlate with age at maturity (22), and growth rates have been negatively correlated with demographic aging rates (23). These associations could potentially bias comparative studies of aging. For example, cellular processes may be associated with growth rates (24), which (if not taken into consideration in comparative studies of aging) may lead to incorrect interpretations by assuming a false association of experimental results with aging.

Herein, we wanted to determine the relationship between metabolic rate, developmental schedules—namely, time to maturity (t_sex; see Method section) and postnatal growth rate (K)—and longevity. The methods used in creating AnAge have resulted in what is arguably the most complete and accurate data set of longevity in, at least, mammals (6). Our goal then was to obtain the most precise evaluation to date of nonmechanistic factors associated with longevity that are relevant for designing and interpreting comparative studies of aging and for understanding the evolution of longevity. We were careful in our data selection and, unlike many previous such studies, we used modern statistical methods that correct for the effects of body size and phylogeny (5). By performing phylogenetically controlled tests that also statistically control for body size (15), we wanted to test previous reports—which did not consider phylogeny in their statistical analyses—of correlations between longevity and both metabolic rates (16) and developmental time (22). Because humans are mammals, special emphasis was given to this class, although birds were also studied.

Methods

Estimation of Aging Rates

The main variable under study was maximum longevity (t_max) estimated from longevity records obtained, like all data used in this work, from AnAge build 9 (6). From a comparative viewpoint, differences in t_max are, under ideal circumstances, proportional to genetic limitations on longevity among species, and t_max has been argued by many to be related to a species’ rate of physiological aging (25–28). Albeit not perfect, t_max is probably the best available estimator of a species’ aging rate (3). There are, nonetheless, limitations in the use of t_max as a measure of aging (11,29): For example, t_max is unlikely to have been shaped by natural selection, it can be influenced by mortality rates that are independent of aging-related mortality, and most of all it is affected by sample size (n). Some studies have estimated the numeric impact of n on t_max to be ln[ln(n)], and hence small when compared to the impact of aging-related mortality on t_max (26,27). These predictions, however, are based on the Gompertz mortality model that assumes accelerating mortality rates with age, which is not true for many species in which mortality rate accelerations slow extensively at later ages, thus resulting in a bigger effect of population size on t_max than predicted from the Gompertz model (11,27). Therefore, we cannot discard an effect of population size on record longevity, although as detailed below we tried to minimize this potential source of error.

The longevity records present in AnAge were obtained from a variety of sources (30–33), which include the recent compilation by Richard Weigl of longevity records of mammals in captivity; this compilation extends the previous work of longevity expert Marvin Jones, and is arguably the most comprehensive data set on mammalian longevity in captivity (34). AnAge also includes the data set compiled by Steven Austad, which includes personal correspondence with zoo personnel, field biologists, and veterinarians (17).

One potential problem is that longevity records obtained in captivity are expected to be higher (17). Indeed, using previously published data sets (33), birds and mammals in captivity outlived animals in the wild: Mammals in captivity (n = 219) lived 9.54 ± 39.8% years (standard deviation) longer, whereas birds in captivity (n = 49) lived 27.5 ± 54.6% years longer. Consequently, in the case of mammals, the large majority of longevity records used in this work was derived from captive specimens. Only exceptional cases of longevity records obtained in the wild were considered. Most notably, many longevity records for bats (order: Chiroptera) come from banding studies. Given the long longevity of bats when compared to size-equivalent mammals (17), data from bats represent an important source of information, and eliminating it would limit our analysis. In contrast, cetaceans (order: Cetacea) were excluded from our analysis because most of their longevity records were obtained from studies in the wild often using indirect methods. For birds, however, the data set contains many longevity records from studies and observations in the wild. Obviously, when more than one longevity record was available, the highest value was used to estimate t_max.

Each longevity record was verified to come from credible sources. If evidence of inadequate husbandry exists for a given species, such as the inability to breed or indications of high mortality in captivity, longevity records were normally excluded—with the exception of bats and birds, as mentioned above. For each species, estimates of the number of captive specimens and whether these breed in captivity were obtained from the literature and from the International Species Information System (ISIS) (http://www.isis.org/). Longevity records based on single or a few animals were normally excluded from our data set (6). Nevertheless, some longevity records might reflect small sample sizes or recent additions to zoo collections. Other sources of bias (such as a bias in captivity towards inexpensive animals) that could not be systematically avoided were ignored (17).

In addition to t_max, other estimates of aging rates include demographic measurements of aging, such as the mortality rate doubling time (MRDT). Like t_max, MRDT values are not perfect measurements of the pace of aging at a physiological level but have been argued to be more accurate than t_max (4,11,28). Although the debate regarding which parameter, t_max or MRDT, is a better measurement of physiological aging rates has not been settled (3), MRDT values were used to provide an additional measurement of aging rates and to further strengthen our analyses.

Data Selection Criteria for Additional Life History Variables

The other life history traits used in this work, such as adult body mass, gestation or incubation time, and age at sexual maturity, represent averages or typical values. Particularly for adult body mass, which varies considerably between individuals of the same species, notably in sexually dimorphic species, values are expected to serve as a basis for inter-species comparisons even if they fail to capture intra-species diversity. If values differed between males and females or if a range of values was available, the arithmetic mean was calculated. In case both were available, field data took priority over zoo data (17). t_sex was defined as the time from conception to sexual maturity, and so gestation or incubation time was taken into account (4): t_sex = age at sexual maturity + (gestation or incubation). Gestational diapause was excluded in estimates of gestation. Although an overlap between age at sexual maturity and age at first reproduction is frequently witnessed, age at sexual maturity was preferred because our work mostly focused on the physiological aspects of reproduction rather than its ecological implications. Adult life span was defined as the maximum length of time animals of a given species can survive after maturity: Adult life span = t_max − age at sexual maturity. Life history traits were derived from standard sources (30,31,35,36).

Values of postnatal growth rate (K) appropriate for a comparative analysis were primarily obtained from the work of Zullinger and colleagues (37) for mammals and from Starck and Ricklefs (38) for birds. These estimates are expressed in days^{− 1} and were calculated by fitting empirical data taken from published growth curves to sigmoidal growth functions (37,38). In addition, we included values obtained from more recent references estimated using the same method.

Data Selection Criteria for Estimating Metabolic Intensity

Even though basal metabolic rate (BMR) is an artificial trait animals rarely show under natural conditions, it remains an established benchmark for comparing metabolic intensity between species (16,39). Body mass and BMR pairs of values were obtained from published data sets compiled according to strict criteria (39–42). Pairs of values for BMR and body mass were always obtained from the same source. If more than one pair of values was available, the logarithmic average was used. If discrepancies were noticed between two or more pairs of values, then only the most recent pair was used. For mammals, the compilation of Savage and colleagues (42) was considered to be the benchmark of BMR data. As argued before (39), we excluded lineages for which the conditions required for BMR measurement were suspected to be difficult or impossible to achieve and could bias the results. The lineages excluded were Artiodactyla, Macropodidae, Lagomorpha, and Soricidae. The reasons for exclusion are detailed elsewhere (39). Regarding birds, the data compilation by McKechnie and Wolf (41), which is based on earlier works (40,43), served as our benchmark. In contrast to McKechnie and Wolf, but in agreement with Reynolds and Lee (43), we included BMR estimates based on fewer than three animals, provided that the conditions for the measurement of BMR met the standards set by McKechnie and Wolf (41). Several BMR estimates [including some of the data points from Bennett and Harvey (40)] that did not meet the standards set by McKechnie and Wolf (41), such as BMR values estimated in the active phase of the daily cycle, were not used in our analyses.

One major factor determining BMR is body temperature (T). For mammals, we obtained previously published body temperature values determined, like BMR, from animals that were considered normothermic (39), and we included body temperature in our analyses. To do this, we calculated the difference between the body temperature of a given mammalian species and the average body temperature of all 333 analyzed mammals (36.3 ± 1.7°C): T_d = T − 36.3. When analyzing a lower taxon, average body temperature was calculated for the species within the lower taxon. In addition to investigating a potential relationship between body temperature and longevity, we also corrected the BMR (cBMR) for body temperature using Q10 principles, as detailed before (16,39), and determined whether cBMR in mammals was related to longevity.

The entire data set used in this work, as well as the complete list of references, is available on the AnAge Web site (http://genomics.senescence.info/species/).

Statistical Analyses

The independent contrasts method was used to eliminate phylogenetic effects (44). Phylogenetic independent contrasts were calculated using the PDAP module for Mesquite version 1.07 (45) and Mesquite version 1.06 (46). Phylogenetic relationships were taken from the Tree of Life Project (47) and various published sources (48,49). All branch lengths were assumed to be equal. Polytomies were arbitrarily resolved to give only one contrast. Although the exact phylogeny of many taxa remains under debate, we doubt that an improved phylogeny will dramatically alter our results and conclusions. To assure that contrasts were properly standardized, we verified that the absolute values of the standardized contrasts did not vary in relation to their standard deviations, as described (50). Except T_d, because its values can be negative, data were ln-transformed before being analyzed. All correlations were forced through the origin (50).

In addition to using individual species, we used the independent contrasts method using data for at least three species as terminal taxa. Estimating an average value for a higher taxonomic level reduces degrees of freedom and addresses the nonindependence problem present in non-phylogenetically informed analyses (15,39,51). It also minimizes problems that could be present in some of our data points, such as the aforementioned impact of population size on t_max, approximations when calculating body mass, or unreliable phylogenies in lower taxa.

Being y any allometric parameter such as BMR, t_max, t_sex, or k, we used least-squares regression as the basis for calculating the parameters residuals (51) The use of regression analysis is necessary to eliminate the confounding effect of M on a given parameter Y (52). When studying a given variable within a given taxon, the least-squares regression coefficients were estimated and used to calculate residuals for each species of the taxon being analyzed. In analyses across taxa, regression coefficients were estimated for a higher taxonomic level and were then used to correct M in each of the taxa at the taxonomic level being analyzed. This procedure eliminated the confounding effects of body size (52).

A double-tailed t test was used to calculate the p values. To determine whether the scaling exponent b was different between two cohorts, we compared the slopes of the linear regression curves using ln-transformed values and a “dummy variables” test (28). We used the SPSS package version 11.5 (SPSS Inc., Chicago, IL) to assist us in the statistical analyses.

Results

Allometric Scaling of Life History Traits and Metabolic Rates

Many others have studied the relationship between body mass and variables such as longevity, metabolism, and development (7–11,16). Nonetheless, an analysis of allometric scaling is necessary in this work. We require precise knowledge of the allometric parameters obtained from our more recent and larger data set so that we can adequately normalize the effect of body mass with respect to the variables under study (11).

Data from 1456 mammals, birds, amphibians, and reptiles were used to estimate the logarithmic relation between M and t_max. Fishes were not studied in this work. Even though their maximum longevity also appears to correlate with adult body size (not shown), we lacked accurate data regarding the metabolism and life history of fishes, and t_max data for fishes come primarily from estimates obtained from animals in the wild. By using all data points from mammals—including cetaceans—birds, amphibians, and reptiles, we found that body mass explained 63% of the variation in t_max (Figure 1A).

Figure 1.

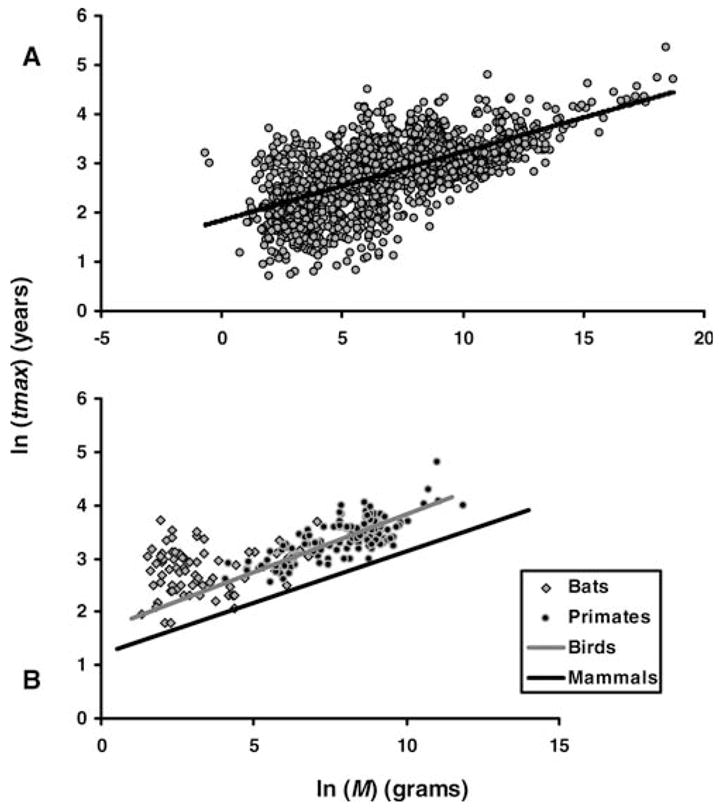
Plot of the ln-transformed relationship between body mass (M) and maximum longevity (t_max) across vertebrates. A, Gray circles: all mammal, bird, reptile, and amphibian species in AnAge (n = 1456). B, Gray line: avian regression curve; black line: mammalian regression curve minus bats and cetaceans. Closed circles: primates (n = 137); gray squares: bats (n = 73), the two longest-lived mammalian orders for their body size.

To estimate the mammalian allometric equation and the regression coefficients, we excluded cetaceans (see Method section). Body mass explained 66% of t_max variation among mammals (n =856), and the equation was t_max = 4.88M^0.153 with t_max in years and M in grams. Our results also suggest that the relationship between body mass and longevity is taxon-specific rather than widespread, which is consistent with other works suggesting that b varies across mammalian orders (8,11). Bats and primates, for instance, are above the regression curve relating t_max to body weight; that is, they live longer than expected for their body mass (Figure 1B), as shown before (8,17).

Previously, no statistically significant relationship was found between body size and longevity in bats, so these were excluded from the mammalian regression analysis (17). In our analysis of the allometry of longevity, bats (n = 73) were indeed the clearest outlier, and we observed no correlation between ln-transformed M and t_max (p = .17). If bats were excluded from the mammalian allometric equation, body mass explained 76% of the variation in t_max (Table 1). In recent years, however, it has been argued that species values do not represent statistically independent data, which can bias statistical analyses (1,51). To address this problem, we used phylogenetically independent contrasts throughout this work (see Method section). Using contrasts and ln-transformed values, we found that M significantly correlates with t_max in bats (r² = 0.14 and p = .001); this finding suggests that the evolution of body size in bats is indeed associated with the evolution of longevity, and demonstrates how different results can be obtained by statistically considering the effects of phylogeny. Therefore, we decided to include bats in our regression analysis because we wanted it to be as representative of the diversity of mammals as possible. We used a Loess plot to confirm that the data were approximately linear across the spectrum of M even when bats were included (not shown).

Table 1.

Allometric Scaling in Relation to Body Mass (Expressed in Grams) of the Major Variables Under Study in This Work Estimated by Regression Analysis

Variable (Units)	Group	N	r2	b	a
tmax (y)	Mammals, birds, reptiles, and amphibians	1456	0.40	0.139	6.32
tmax (y)	Mammals minus cetaceans	856	0.43	0.153	4.88
tmax (y)	Mammals minus cetaceans and bats	783	0.57	0.193	3.34
tmax (y)	Bats	73	0.027	0.050	13.7
tmax (y)	Primates	137	0.57	0.189	6.47
tmax (y)	Birds	518	0.49	0.218	5.22
tmax (y)	Passerines	198	0.32	0.274	4.18
tmax (y)	Nonpasserines	320	0.26	0.174	7.02
tmax (y)	Reptiles	30	0.35	0.137	10.4
tmax (y)	Amphibians	17	0.046	0.069	15.0
MRDT (y)	Mammals, birds, and reptiles	20	0.14	0.116	1.42
Adult life span (y)	Mammals minus cetaceans	606	0.49	0.162	4.11
Adult life span (y)	Birds	69	0.31	0.181	6.64
BMR (W)	Mammals minus cetaceans and dubious taxa (see Methods section)	300	0.95	0.713	0.0190
BMR (W)	Birds	167	0.97	0.652	0.0427
cBMR (W)	Mammals minus cetaceans and dubious taxa (see Methods section)	247	0.97	0.696	0.0208
Td (K)	Mammals minus cetaceans	333	0.020	0.100	0.552
tsex (y)	Mammals minus cetaceans	606	0.50	0.214	0.263
tsex (y)	Birds	69	0.41	0.303	0.214
K (d− 1)	Mammals minus cetaceans	204	0.67	− 0.297	0.126
K (d− 1)	Birds	208	0.67	− 0.321	1.10

Note: t_max = maximum longevity; MRDT = mortality rate doubling time; BMR = basal metabolic rate; cBMR = temperature-corrected BMR; T_d = difference between the body temperature of a given species and the overall average for all studied mammals; t_sex = time to maturity; K = postnatal growth rate.

In the case of birds (n = 518), body mass explained 70% of the variation in t_max, and the allometric equation was t_max = 5.22M^0.218 (t_max in years and M in grams). It has been argued that passerines (order: Passeriformes) follow different scaling laws with regard to longevity than do other birds (10), and our results support the idea that b is different in passerines: p =.008 using data from 198 passerines (Table 1). The longevity of passerines is on average 52% shorter than that of nonpasserines, but passerines also weigh 95% less. Still, after correcting for body mass, passerines appear to have a shorter longevity than nonpasserines (p = .014). Following the same criteria used for mammals, however, we included all birds in our regression analysis. In amphibians (n = 17), M and t_max did not appear to correlate (p = .24 using ln-transformed phylogenetic independent contrasts), and in reptiles (n = 30), body mass explained only 59% of the variation in t_max (Table 1). Further data are likely necessary concerning these classes, and they were not studied in relation to metabolism or developmental schedules in this work.

Interestingly, MRDT correlated weakly with M (r² = 0.14) using data from mammals, birds, and reptiles (n =20). In contrast, MRDT correlated strongly with t_max after ln-transformation: r² =0.73 and n =26, confirming the idea that maximum longevity and demographic measurements of aging are strongly associated (25,27) [as shown before in rodent cohorts (28)] and supporting the notion that t_max is an adequate measure of aging. Another measure of aging, maximum adult life span (see Method section), was found to correlate with M in mammals (n = 606) according to the equation: adult life span =4.11M^0.162, which, as expected, is similar to that of t_max.

Different factors influence BMR, but the effect of body mass is clear (39,53). In this work, we wanted to study the relationship between BMR and t_max independent of body mass. We used BMR data from 300 mammals and 167 birds to determine the allometry of BMR so that we could later eliminate the influence of M on BMR. Using ln-transformed values, we calculated the linear regression equations for mammals [ln(BMR) = 0.713ln(M) − 3.96 with r² = 0.95, and birds: ln(BMR) = 0.652ln(M) − 3.15 with r² = 0.97]; these findings are in accordance with previous results (39,53). Allometric exponents varied slightly across orders of the same class (not shown), once again in line with previous results (39). For cBMR, the equation using data from 247 mammals and ln-transformed values was: ln(cBMR) = 0.696ln(M) − 3.87, with r² = 0.97.

Previously, body temperature was shown to slightly correlate with body size in mammals (39). We calculated T_d, the difference between the body temperature for a given species and the overall average for the 333 studied mammals (see Method section). Although we had to use ln[ln(M)] to obtain properly standardized phylogenetic independent contrasts, we found no significant correlation between T_d and ln[ln(M)] (p = .42). Body temperature was not studied in birds.

Bigger animals take longer, on average, to reach adulthood (7,8), and we calculated the relationship between body mass and t_sex. The regression analysis equation using ln-transformed values for mammals (n = 606) was ln(t_sex) = 0.214ln(M) − 1.34 with t_sex in years and M in grams (r² = 0.50), in line with results using similar parameters (7). It is also expected that small animals grow quicker than larger ones do (37). For postnatal growth rate (K), the equation for mammals (n = 204) using ln-transformed values was: ln(K) =−0.297ln(M) − 2.07, with K expressed in days^{− 1} and M in grams; in birds (n = 208) the equation was: ln(K) = −0.321ln(M) + 0.094.

The results from our analysis of the logarithmic relationship between the variables under study in this work and M, as well as the regression coefficients, are recapped in Table 1. They are mostly confirmatory of previous reports but are essential to obtain residuals that normalize the effect of body mass on the different variables under study herein. If lower taxa were being analyzed or if it became necessary to exclude a lower taxon from a given class, then new equations were calculated.

Metabolic Rate, Temperature, and Longevity

The well-established influence of body mass on metabolism must be statistically eliminated so we can focus solely on the relationship between metabolism and longevity, yet normalizing the effects of body mass on metabolism has been a source of controversy. Because BMR varies allometrically with M, we corrected for M based on our analysis of covariance, as argued by others (52), and by calculating the residual to the fitted relationship between mass and metabolism, as detailed before (54). Values were ln-transformed before calculations. Our results show that residual BMR does not correlate with longevity across mammals (Figure 2A) or birds (Figure 2B). In other words, animals with a lower BMR for their body size do not tend to live longer and vice versa.

Figure 2.

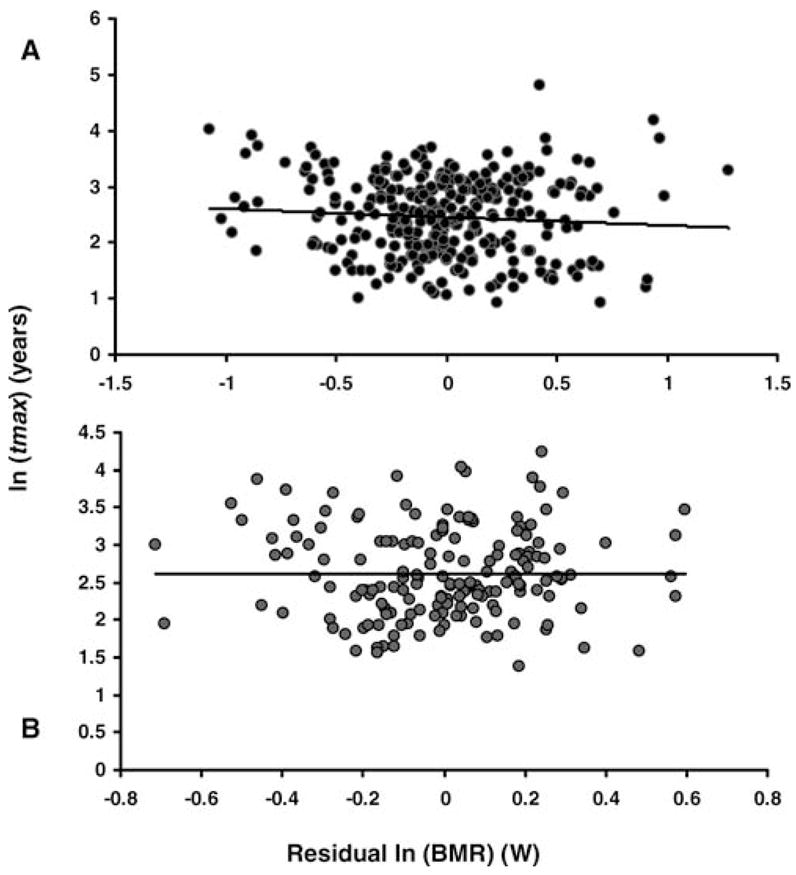
Ln-transformed relationship between basal metabolic rate (BMR) residuals and maximum longevity (t_max) in mammals (A; n =300) and birds (B; n = 167). Closed circles: individual mammalian species (A); gray circles: individual bird species (B). Both correlations are not statistically significant, even though they do not consider the effects of phylogeny.

As mentioned above, a potential bias due to phylogeny is possible. Using phylogenetic independent contrasts, there was no significant correlation between BMR residuals and t_max in mammals (p = .68 with n = 300). These results suggest that the evolution of a high mass-optimized BMR in mammals does not tend to be associated with the evolution of a shorter longevity and vice versa. Considering the potential problems of estimating t_max, however, contrasts between similar species can be a source of error, and so we used an additional set of contrasts based not on individual species but in taxa with at least three species (see Method section). Using this method and 36 terminal taxa, we found no correlation between BMR residuals and t_max (p = .38).

In bird species (n=167), there was no correlation between BMR residuals and t_max (p =.99). It must be noted, however, that these results do not take into account the effects of phylogeny, because we could not properly standardize BMR residuals and t_max contrasts in birds—that is, the absolute values of the standardized contrasts showed a statistically significant correlation with their standard deviations, even though we tried different types of data transformation.

Another factor influencing BMR is body temperature (T). As expected, for 247 mammalian species, BMR residuals correlated with T_d (r² = 0.38). We found no statistical evidence of a correlation between T_d and t_max contrasts in 271 mammals (p = .072, but see Discussion section). Even so, we repeated our analysis of BMR residuals using data corrected to a common body temperature (see Method section). With cBMR data for 247 mammalian species, we found no evidence of a relationship between cBMR residuals and t_max (not shown).

Allometry of life-span exceptions do not appear to be explained by a lower metabolism, in line with previous results (17). Birds tend to live longer than size-equivalent mammals (Figure 1B) but have a higher body temperature and BMR (16). Among birds, whether passerines have higher metabolic rates remains a subject of debate that mostly depends on the criteria used for measuring BMR. According to the most stringent, and likely more accurate, criteria of McKechnie and Wolf (41), there is no difference in BMR between passerine and nonpasserine birds after correcting for body mass, thus differences in longevity between passerines and nonpasserines are unlikely to be due to differences in metabolic rates. Similarly, in mammals, our results do not suggest that primates or bats have lower metabolic rates than predicted for their body size. They do confirm previous results that marsupials have a lower BMR—about 17%—than predicted for their body size while having a longevity, on average, about 40% shorter than predicted for their body size. Monotremes may live longer than expected for their body size and have a lower BMR for their body mass, but with n = 3 this observation remains open to debate.

Contrasts of BMR residuals and t_max residuals did not correlate in mammals (p = .35) or in the 36 mammalian terminal taxa with at least three data points (p =.72). Again we could not properly standardize the bird contrasts; without considering the effects of phylogeny, we found no evidence of a correlation between BMR residuals and t_max residuals in birds (p = .99). Previously, a relationship between mass-independent BMR and t_max was reported in some mammalian orders such as rodents, carnivores, and marsupial orders (16). Within marsupial orders we did not find any significant correlation between BMR residuals and t_max residuals (not shown). When considering all marsupials (n =47), however, the negative correlation between BMR residuals and t_max residuals (r² = 0.096) was statistically significant at the .05 level using phylogenetic independent contrasts (p = .021). This correlation could be due to the impact of body temperature on BMR, because we found no evidence of a correlation between cBMR residuals and t_max residuals in marsupials (p =.60 with n =42), despite failing to find any significant evidence of a correlation between T_d and t_max (or t_max residuals) in marsupials (not shown). In eutherians (n = 250), we found no correlation between BMR residuals and t_max residuals after considering the effects of phylogeny (p = .75). Likewise, we found no statistical evidence, after eliminating the effects of phylogeny (but see Discussion section), of a correlation between BMR residuals and t_max residuals in any eutherian order, including rodents (p = .32; n = 108) and carnivores (p = .083; n = 50). In eutherians, analyses using cBMR residuals produced similar results—that is, no evidence of a correlation with t_max residuals—to those obtained with BMR residuals (not shown). Lastly, in primates (n = 24), and using phylogenetic independent contrasts, BMR residuals did not correlate with t_max (p = .95) or with t_max residuals (p = .82).

Developmental Schedules and Longevity

We investigated the relationship between developmental schedules, body mass, and longevity in 606 mammals and 69 birds. Longevity, of course, includes developmental time, which can potentially bias our analysis. Therefore, we used maximum adult life span, defined as t_max minus age at sexual maturity (see Method section). Time to maturity (t_sex) was deemed a good predictor of the timing of development and was defined as gestation or incubation time plus age at sexual maturity (see Method section). Overall, adult life span correlated with t_sex among mammals according to the equation: Adult life span =11.8t_sex^0.622, with both adult life span and t_sex in years (Figure 3A). In birds, however, the best fit model was a linear regression: Adult life span = 5.27t_sex + 14.0, with t_sex and adult life span in years. We speculate the reason for this is that developmental time tends to be longer in birds than in other classes and life history events occur within a smaller range—e.g., t_sex and t_max varied less in birds (not shown). It could also be that our data set does not contain enough data points from birds or that the large proportion of longevity records from wild animals biases our calculations, and so we focused the rest of our analyses of t_sex on mammals. Nonetheless, it is interesting to note that, for those 69 birds, t_sex and adult life span are, respectively, 47% and 84% longer than in size-equivalent mammals—i.e., using the mammalian regression curve.

Figure 3.

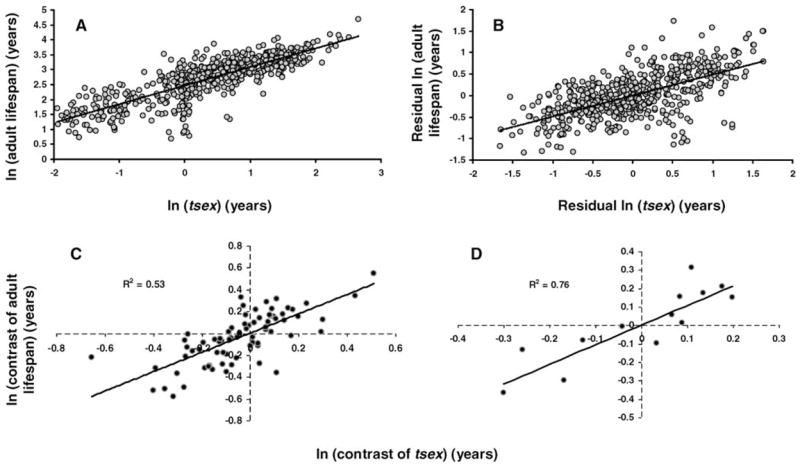
A, Relationship between ln-transformed time to maturity (t_sex) and adult life span in mammals. Gray circles: individual species (n = 606). Correlation is statistically significant, even though it does not consider the effects of phylogeny. B, Ln-transformed relationship between time to maturity residuals and adult life-span residuals in mammals. Gray circles: individual species (n =606). Although it does not consider the effects of phylogeny, the correlation is statistically significant. C and D, Relationship between the logarithm of independent contrasts of age at maturity and adult life span in mammals (C) and primates (D). Both correlations are statistically significant. Terminal taxa contain data for at least three species.

The relationship between t_sex and adult life span in mammals has been suggested by several earlier reports (7,8,15,22). It can be argued, however, that such a relationship is the result of a number of sources of bias not always previously eliminated, such as body mass and particularly phylogeny, and we investigated these concerns. Residuals for t_sex correlated with adult life span residuals (Figure 3B). Primates and bats, the two main exceptions to the allometry of life span, were also the two orders with the longest mass-optimized t_sex, whereas, in contrast, marsupials and rodents appear to have a shorter adult life span than expected for their body size and a shorter developmental period for their body size (Table 2). The only clear outliers were marsupial orders, such as the Dasyuromorphia order, of which the Antechinus genus is a member. This genus is unique among mammals in featuring cases of semelparity and an aging phenotype unlike any other mammal (4). Overall, these results indicate that, independently of body size, developmental time is strongly associated with maximum adult life span.

Table 2.

Mass-Optimized Time to Maturity and Postnatal Growth Rate for Different Mammalian Orders in Comparison With Mass-Optimized Adult Life Span

	Time to Maturity Versus Adult Life Span			Growth Rate Versus Adult Life Span
Order	No. of Species	% Predicted Time to Maturity	% Predicted Adult Life Span	No. of Species	% Predicted Growth Rate	% Predicted Adult Life Span
Eutherians
Artiodactyla	119	75%	80%	24	131%	77%
Carnivora	115	98%	107%	42	133%	107%
Chiroptera	25	238%	247%	13	108%	270%
Insectivora	19	86%	56%	13	160%	61%
Lagomorpha	7	52%	73%	4	162%	69%
Macroscelidea	4	52%	104%	1	ND	ND
Perissodactyla	11	111%	97%	2	ND	ND
Primates	98	231%	180%	20	33%	196%
Rodentia	126	64%	76%	58	94%	78%
Sirenia	3	132%	152%	1	ND	ND
Xenarthra	11	99%	135%	4	105%	181%
Marsupials
Dasyuromorphia	21	136%	56%	1	ND	ND
Didelphimorphia	4	57%	46%	1	ND	ND
Diprotodontia	31	85%	91%	13	87%	96%
Peramelemorphia	4	36%	51%	3	85%	49%

Notes: Values represent the average residuals of the time to maturity, adult life span, and growth rate calculated from regression analysis and expressed as a percentage of the expected value estimated from the allometric equation. Only orders with data for at least three species are displayed. Taxonomy was retrieved from the Integrated Taxonomic Information System (ITIS) (http://www.itis.usda.gov).

ND = not determined.

As in our previous analyses, we used phylogenetically independent contrasts to minimize a potential overestimation of degrees of freedom. A statistically significant correlation was found between t_sex and adult life span contrasts: r² = 0.12 with p < .001. Although weaker (r² = 0.034) the correlation between t_sex residuals and adult life span residuals using phylogenetic independent contrasts was highly significant (p < .001). Given the potential problems of estimating adult life span and t_sex, using as terminal taxa three or more species seems particularly appropriate in this case. Indeed, with 75 taxa, the correlation between t_sex and adult life span contrasts was statistically significant (p < .001) and more robust (r² = 0.53) than using individual species (Figure 3C). The correlation between t_sex and adult life span contrasts was also strong (r² = 0.76) and highly significant (p < .001) among 14 primate taxa (Figure 3D). These results show that a longer development in mammals and primates not only correlates with a longer adult life span but the evolution of a longer development is associated with the evolution of a longer adult life span. The relationship also appears to be independent of body size. Using residuals for adult life span and t_sex, the correlation of the contrasts was weaker in mammal (r² = 0.17) and primate (r² = 0.43) terminal taxa, but still statistically significant (respectively, p < .001 and p = .014).

It can also be argued that t_max and adult life span are approximations of aging rates (11). Therefore, we used the MRDT as an estimate of rate of aging, as described (4,28). We found a strong correlation (r² = 0.57) between ln-transformed MRDT and t_sex using phylogenetic independent contrasts. Nonetheless, because n =13, and even though the correlation was statistically significant at the .01 level (p = .003), these results cannot be considered as definitive.

We investigated the relationship between the rate of postnatal growth (K) and adult life span. (Again, we preferred maximum adult life span to t_max to avoid any potential bias from the association between K and developmental time. For instance, there was a strong negative correlation between t_sex and K in 204 mammals: r² =0.58.) In mammals (n = 204), we found a robust negative correlation between adult life span and K (Figure 4A). This correlation was statistically significant using phylogenetic independent contrasts: p < .001 with r² =0.22. Likewise, ln-transformed MRDT and K contrasts correlated negatively and strongly (r² =0.48), but with n =9 from only three orders, and even though p = .037, this result must be interpreted with care.

Figure 4.

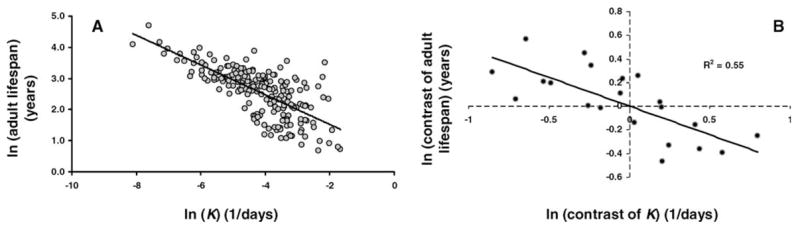
A, Ln-transformed relationship between postnatal growth rate (K) and adult life span in mammals. Gray circles: individual species (n =204). Although it does not consider the effects of phylogeny, the correlation is statistically significant. B, Relationship between the logarithm of independent contrasts of growth rate and adult life span in mammals. The correlation is statistically significant. Terminal taxa contain data for at least three species.

As mentioned before, body size is a potentially confounding factor, and we investigated this possibility. K residuals correlated with adult life-span residuals using phylogenetic independent contrasts, though the correlation was weak (r² =0.050), even if statistically significant at the .01 level (p = .001). Similarly, K residuals and adult life span residuals were also negatively correlated among mammalian orders, but the association was not as obvious as that between t_sex residuals and adult life-span residuals (Table 2). Whereas primates live considerably longer and grow much slower than expected for their body size, bats appear to grow at about the rate predicted for their body size. The strongest outlier was Peramelemorphia, a marsupial order like Dasyuromorphia.

In agreement with our previous analyses, we used as terminal taxa at least three species to minimize potential problems in estimating K and adult life span. The negative correlation between K and adult life-span contrasts was robust (r² = 0.55) and statistically significant (p < .001) among 22 taxa (Figure 4B). Although weaker (r² = 0.20), the negative correlation between contrasts of K residuals and adult life-span residuals was also statistically significant (p = .043). This result confirms the association between growth rates and adult life span, and further indicates that mammals that grow faster than predicted for their body size tend to have a shorter adult longevity for their body size. Although predicted by life history theory (7), as far as we know, these results are novel.

In birds (n = 43), the negative correlation between contrasts of adult life span and K was less obvious (r² = 0.14), even if significant at the .05 level (p = .014). Adult life-span residuals, however, did not correlate with K residuals when using phylogenetic independent contrasts (p = .90). Similarly, using t_max rather than adult life span—to obtain a larger data set (n = 208)—the negative correlation between t_max and K contrasts was weak (r² = 0.076) but significant (p < .001), yet there was no significant correlation between contrasts of K residuals and t_max residuals (p = .85). These results suggest that growth rates are not associated with longevity in birds when body size is corrected for.

Previously, it was reported that developmental schedules are not associated with metabolic rates in mammals (14). Using our data set (n = 275), we found a very weak (r² = 0.024) negative correlation between BMR residuals and t_sex in mammals. We were unable to validate the statistical significance of this correlation, however, because we could not properly standardize the contrasts. Similarly to our results with t_max, we found no evidence of an association between BMR residuals and t_sex or between BMR residuals and t_sex residuals within mammalian orders (not shown), except in marsupials (n = 37) in which we found a statistically significant (p = .018) negative correlation between BMR residuals and t_sex contrasts (r² = 0.084) and between cBMR residuals and t_sex contrasts (p = .028). Regarding the relationship between temperature and mammalian (n = 254) development, the negative correlation between T_d and t_sex was weak (r² =0.036) but significant at the .01 level using phylogenetic independent contrasts (p = .002). As for mammalian growth rates (n = 119), we found no significant correlation between K and BMR residuals (p = .20) or between K and T_d (p = .89) using phylogenetic independent contrasts.

Discussion

Body Mass Is Likely Associated With Longevity due to Ecological Constraints

Many others have discussed the well-established relationship between body mass and longevity, and evolutionary ecological factors appear to be the most plausible explanation. Bigger animals are less prone to predation and thus expected to have lower mortality rates, which in turn leads to longer life spans and, according to evolutionary theory, the evolution of a slower aging process (21,55). As reported before, our results show that even though, on average, larger animals live longer than smaller ones, that is not a widespread trend. Bats and primates, for instance, are above the mammalian regression curve relating t_max to M (Figure 1B). This happens because these taxa possess crucial ecological advantages that allow for lower mortality rates: Bats—like birds, whose regression curve is also above that of mammals—have the ability to fly, and primates have large brains for their body size. Further examples are abundant: Subterranean animals, like bathyergids (family: Bathyergidae) that are among the longest-lived rodents (t_max > 20 years) despite their relatively small size (< 200 grams) or like the Palestine mole rat (Nannospalax ehrenbergi), a small (< 200 grams) muroid (superfamily: Muroidea) that can live up to 15 years, can be explained by their underground environment which minimizes predation and mortality (56). Therefore, and in accordance with the evolutionary theory of aging, organisms above the mammalian regression curve occupy less hazardous niches (17,21,55).

Body size could be a determinant of ecological opportunities and habitat that affects mortality, which then influences the evolutionary forces shaping longevity and aging (8,21). Alternatively, body size could be determined by extrinsic mortality, in turn a result of different ecological factors (7). Whatever the explanation, it is likely that the association between body size and longevity is a result of ecological constraints during the evolution of life histories (15). Because of the coevolution of body size and longevity, however, traits associated with body size will also tend to be associated with longevity, independently of their relationship to longevity. Therefore, as pointed out by many others (5,11,51), body size can be a potentially confounding factor in comparative studies of aging. In that sense, our analysis of allometric scaling with regard to several traits (Table 1) can be useful to derive residuals for different types of comparative studies, and we included mammalian longevity residuals—obtained from the equations calculated in this work—in the AnAge database.

The Contentious Relationship Between Metabolism and Longevity

The relationship between metabolic rates and aging has been studied and debated by many researchers (1,14,15,17), including those who have argued that a causal relationship exists and that faster metabolic rates lead to a faster aging process (12,13,18–20). Recent studies testing whether BMR is associated with longevity after correcting for the effects of body size have reported mixed results, with some authors failing to find evidence of an association between BMR and t_max in mammals and birds (5,57), and others reporting statistically significant correlations in mammals, including in eutherians (16). None of these previous works, however, corrected for the effects of phylogeny. Hence, our work using an updated data set and the most modern statistical analyses offers an unprecedented opportunity to test the relationship between BMR and longevity.

Our results suggest that metabolic rates, when corrected for body size, are not associated with longevity in eutherians and probably not in birds either. Although we could not correctly analyze the relationship between BMR residuals and t_max contrasts in birds, considering the apparent lack of correlation between these two variables (Figure 2B) and between BMR residuals and t_max residuals, we have no reason to suspect that BMR, corrected for body mass, is associated with bird longevity.

It is possible that metabolic rates correlate, even if weakly, with longevity in marsupials. We found that, even after correcting for body mass, both time to maturity and longevity are associated with BMR in this superorder. Although the causality of this association is impossible to determine at this point, it is tempting to speculate that these results suggest a potential influence of metabolic rates on the timing of life history events in marsupials, although we also cannot exclude a potential bias due to body temperature. Marsupials were often outliers in our analyses of both metabolism and developmental schedules, hinting that life history traits in marsupials may not compare well to those in eutherians, as suggested before (17). Nonetheless, our results provide fresh evidence that metabolic rates could be related to the evolution of developmental schedules and longevity in marsupials and, if confirmed, would indicate a novel and intriguing physiological distinction between marsupials and eutherians.

Contrary to previous results (16), we failed to find an association between BMR or cBMR residuals and t_max residuals in eutherian orders. Nevertheless, we should point that there was a marginal negative correlation between BMR residuals and t_max residuals in rodents (r² = 0.085) and carnivores (r² = 0.012), even if neither correlation was statistically significant after eliminating the effects of phylogeny. Interestingly, though, the correlation in rodents was statistically significant if the effects of phylogeny were not considered, again demonstrating how the use of phylogenetic correctness can affect the results. On the subject of our method, it is noteworthy to point out that, even though we excluded some taxa from our analyses of metabolic rates (see Method section), including them would not change our results and conclusions: For example, BMR residuals continued not to correlate with t_max using phylogenetic independent contrasts of all mammalian data points (p = .80 with n = 338). In light of our findings, it appears that the evolution of longevity in eutherians has been by and large independent of metabolic rate, challenging the view that metabolic rates are associated with differences in longevity and aging between eutherian species. Nevertheless, because of the suggestive relationship between BMR residuals and t_max residuals in rodents and carnivores, we cannot exclude that the evolution of longevity in some eutherian taxa might have been slightly associated with metabolic rates. Primates, however, are unlikely to be one of such taxa.

Although BMR remains the benchmark measurement in comparative physiology, it is not without its limitations (57,58). In some small species the thermoneutral zone is fairly large and, for instance, some species of bats have been reported to show variable temperature rather than the “usual homeothermy” of other mammals (58). The use of BMR corrected for body temperature—that is, cBMR—may reduce these problems, though some errors probably persist. Because of uncertainties associated not only with BMR but also with t_max (see Method section) and with the use of phylogenetic correctness (51), we analyzed our data using different types of approaches each with its own strengths and weaknesses. The large majority of these approaches offer concordant results, yet we wanted to allow researchers to interpret the results using the approach they consider most appropriate. Lastly, our data set is available online in the AnAge Web site (http://genomics.senescence.info/species/) if researchers wish to conduct additional analyses.

Regarding temperature, we found a negative correlation between body temperature and time to maturity in mammals, which as far as we know is new. The correlation was weak, however. Because we also found a suggestive (r² = 0.014), nearly statistically significant (p = .072) negative correlation between temperature and longevity in mammals, it could be that temperature is associated—even if to a small degree—with the timing of life history events, including longevity, in mammals.

Experimentally, our results are relevant in the design and interpretation of comparative studies of aging. The attention given so far to metabolic rates in such studies, mainly to those conducted in eutherians, appears unjustified. Our findings suggest that correcting for BMR is unnecessary in comparative studies of aging. Interestingly, our inter-species results are in accordance with recent experimental intra-species results in rodents. Contrary to the rate of living theory, some results suggest that higher metabolic rates may in some cases be associated with a longer life span (54,59). Although the debate of whether metabolic rates and temperature influence longevity in homeotherms will probably not be settled any time soon, any relationship between these traits and species longevity, particularly in eutherians, appears very small or even negligible.

Development and Growth Are Associated With Longevity

Our results using phylogenetic independent contrasts confirm the previously reported idea that time to maturity is associated with adult life span in mammals, and further suggest that this association may be even stronger than previously thought. The maximum amount of time a mammal can expect to live after maturity, even in captivity, is typically proportional to the amount of time it took that animal to reach maturity. Our results showing that a faster growth rate is associated with a shorter life span in mammals, independently of body size, are new, even if predicted by life history theory. In addition, our results show that allometry of life-span exceptions are associated with developmental schedules (Table 2), particularly developmental time (Figure 3B). Species that tend to have a longer longevity for their body size, such as bats and primates, also tend to have a longer developmental phase for their body size. Moreover, even though MRDT data is limited and cannot be considered as definitive, it can serve as a confirmation of the trends found using other estimates of aging. The way the MRDT correlates with time to maturity to a larger extent than with body mass—and not at all with BMR residuals (not shown)—further strengthens our suggestion that aging rates correlate with developmental schedules. Finally, it is interesting to point out that our results are in agreement with recent experimental findings in rodents, such as the slower growth rate and delayed maturity found in some long-lived mouse strains (60).

In birds, we found no evidence of a correlation between growth rates and longevity after correcting for body size, as hinted before using demographic measurements of aging (23). Nevertheless, life history analyses in birds, although not as complete as those for mammals, suggest an association between rapid maturity and a short life span and vice versa (61). More extensive data are needed to investigate this hypothesis and its relevance to aging research.

It can be argued that mortality rates affect the evolution of age at maturity, growth rates, and life span. Life history theory predicts that animals with a higher adult mortality rate will evolve a higher mass-specific growth rate and an earlier age at reproduction (7), the so-called “fast-slow continuum” (15). Indeed, we found that the time to maturity—that is, t_sex—was strongly associated with K, so the causal relationship, if any, between the traits being studied is not obvious. The causality of how these factors evolved, however, is outside the scope of this work. What we can conclude from our results is that, in mammals, developmental schedules are associated with longevity and possibly with aging rates with implications for how comparative studies of aging are designed and interpreted. Although an association between t_sex and adult life span has been reported before (22), it has been largely disregarded in comparative studies of aging. We hope that our results showing a robust correlation between t_sex and adult life span encourage researchers to consider this potential source of bias. Developmental schedules such as the time to maturity and growth rates have a physiological basis (for instance, at a hormonal and cellular level) that should be taken into consideration in the comparative biology of aging. Otherwise, comparative studies of aging may infer that mechanisms involved in development—e.g., rates of cellular proliferation—are associated with aging when instead such association may be a result of the correlation between developmental schedules and longevity (62).

Conclusion

This work is new in the completeness and accuracy of the data set used, particularly for mammals, by including the recent work of Weigl (34), verifying the longevity records, and featuring carefully selected life history traits and metabolic rate data from recent manually curated sources (41,42). Our analyses are also strengthened by the control for phylogenetic independence and body size, which were not always present in previous such works. These reasons make the analyses of factors previously associated with longevity reported in this work a benchmark for designing and interpreting comparative studies of aging and for understanding the evolution of life histories.

Associations between nonmechanistic parameters and longevity are only a first step in understanding species differences in longevity. Much more detailed studies involving modern biochemistry, cell biology, or molecular physiology will be necessary to understand the genetic and molecular mechanisms by which different animal species age at different paces. Our work, however, is important for the design and interpretation of such experiments because it establishes those parameters coevolving with longevity that represent potential sources of bias. Furthermore, both this work and the AnAge database can be used to select species for comparative studies of aging having in consideration the potential confounding factors detailed herein. In conclusion, the design and interpretation of comparative studies of aging in vertebrates, and especially in eutherians, should take body mass and developmental schedules (but possibly not metabolic rates) into consideration as potential sources of bias.