Quantitative characterization of animal behavior following blast exposure

Abstract

The simplest approach to quantifying animal behavior begins by identifying a list of discrete behaviors and observing the animal’s behavior at regular intervals for a specified period of time. The behavioral distribution (the fraction of observations corresponding to each behavior) is then determined. This is an incomplete characterization of behavior, and in some instances, mild injury is not reflected by statistically significant changes in the distribution even though a human observer can confidently and correctly assert that the animal is not behaving normally. In these circumstances, an examination of the sequential structure of the animal’s behavior may, however, show significant alteration. This contribution describes procedures derived from symbolic dynamics for quantifying the sequential structure of animal behavior. Normalization procedures for complexity estimates are presented, and the limitations of complexity measures are discussed.

Statement of the problem

Animal behavior changes as the result of injury. Similarly, animal behavior changes as the result of the administration of drugs, particularly drugs of abuse. These are commonplace observations, and as observers of animal behavior we are often able to discriminate between injured and uninjured animals by direct observation with a high degree of confidence and accuracy. Quantifying the degree of behavioral distortion, especially in response to mild or intermediate degrees of injury or drug intoxication, is surprisingly difficult.

The simplest classical approach to quantifying animal behavior begins by identifying a list of defined discrete behaviors. For example, in the case of rats in a free field observation environment, that list could include sleeping, eating, drinking, moving, rearing, and grooming. The animal is observed at regular time intervals, say every 20 s. The fraction of observations corresponding to each behavior is calculated. Suppose five behaviors are defined and labeled A, B, C, D, and E. The distribution of fractions of observations in each behavior is denoted by 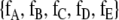. In the case of severe head injury, for example, the fraction of observations recorded as sleep will often increase. After the administration of amphetamines, the fraction of observations of moving, rearing, and grooming may increase.

While this is a beginning of the characterization of animal behavior, it is often found to be inadequate. In response to mild injury or low drug dosages, the distribution of behaviors in experimental animals may be statistically indistinguishable from the distributions observed with untreated control animals. Nonetheless, in some of these cases a human observer can confidently and correctly assert that the treated animal is not behaving normally. A possible response to this problem is to examine the sequential structure of animal behavior by calculating its complexity.

Defining and calculating complexity

Consider again the hypothetical example constructed with five behaviors. Suppose that two behavioral sequences are observed.

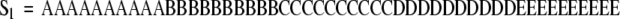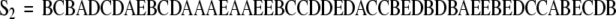An observer would state that the second sequence is more complex than the first even though the behavior distributions of both sequences are identical (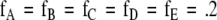). Complexity measures are used to quantify these differences. As the term is used here, complexity is a measure of structure in a symbol sequence. There are several mathematical definitions of complexity. Different definitions emphasize different aspects of sequence sensitive structure. The choice of definition is informed by its functional utility in discriminating between experimental groups. It should be noted that different measures of complexity can be highly correlated. For example, Lempel–Ziv complexity (Lempel and Ziv 1976) and the context free grammar complexity (Ebeling and Jiménez-Montaño 1980; Rapp et al. 1991) are highly correlated. In test computations, the Pearson linear correlation coefficient between these measures is r = .998 (Rapp et al. 2001). A review of complexity measures is given in Rapp and Schmah (1996). A taxonomic classification of complexity measures appears in Rapp and Schmah (2000).

In the examples presented in this contribution, the Lempel–Ziv complexity is computed. In the taxonomic structure of Rapp and Schmah, this is a nonprobabilistic, model-based, randomness-finding measure of complexity. It gives a high value of complexity for random sequences and lower values for structured sequences. A presentation of the definition and pseudo-code for its calculation is given in Appendix A of Watanabe et al. (2003). This includes an example calculation that illustrates the algorithmic implementation of the definition. In the case of sequence S₁ given above, the Lempel–Ziv complexity is 6 bits. The complexity of S₂ is 22 bits.

Compromised animals can present pathological stereotypic behaviors. A decrease in complexity is expected. The magnitude of this decrease should be correlated with the magnitude of the injury or drug dose. This correlation need not, however, be linear. The possibility of nonmonotonic relationships between behavior, as quantified by complexity, and the magnitude of the challenge is suggested by inverted-U relationships between drug dose and behavior (Braida et al. 1996; Picciotto 2003; Zernig et al. 2004).

Normalization: How often should behavior be sampled? How long should behavior be observed?

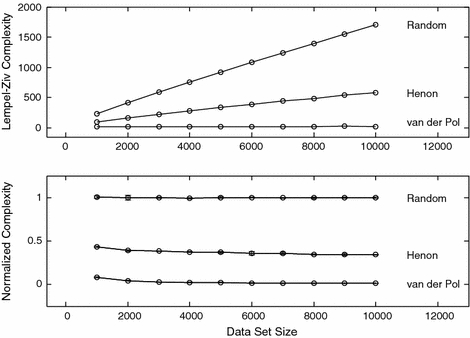
When estimating the complexity of animal behavior, several operational questions must be considered. How often should behavior be sampled and how long must behavior be observed? These questions can be probed empirically. In order to approach this empirical assessment systematically, the question of normalization must be considered. Lempel–Ziv complexity and other complexity measures in this group depend on two things, (i) the dynamics of the process generating the symbol sequence and (ii) the length of the symbol sequence. This dual dependence is shown in the upper panel of the first diagram. Three dynamical systems are considered, a random number generator, the Hénon system which is a chaotic dynamical system, and the periodic van der Pol oscillator. Time series data from these systems were partitioned uniformly onto a five symbol alphabet. In this partition, the smallest 20% of the values were mapped to Symbol A. The next 20% were mapped to symbol B, and so on. In Fig. 1 it is seen that the Lempel–Ziv complexity of the random and chaotic dynamical systems increases with data set size even though the underlying dynamical process is unchanged. (The Lempel–Ziv complexity of the periodic van der Pol oscillator also increases with the length of the symbol sequence. The increase is much smaller than that observed with the other two systems and is not discernable at this scale.) This increase can give a false impression that the intrinsic complexity is increasing during the observation period. This problem can be addressed by constructing an appropriate normalization. A detailed presentation of normalization procedures for complexity measurements is given in Rapp et al. (2005). A summary is given here. A normalized value of complexity, C_NORM, is defined by

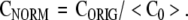Fig. 1.

Lempel–Ziv complexity and normalized complexity as a function of data set size. The upper panel shows the Lempel–Ziv complexity for three systems as a function of data set size. The three systems are random numbers uniformly distributed on [0,1], data generated by the chaotic Henon attractor, and data generated by the periodic van der Pol oscillator. In each case the Lempel–Ziv complexity increases as a function of data set size. The lower panel shows the normalized complexity calculated from the Lempel–Ziv complexity using the procedures outlined in the text. In each case, the sensitivity to data set size is largely lost while the differences due to the intrinsic complexity of the generating dynamical process are still expressed. Error bars for the normalized complexity were computed using the formula in the text. All complexity calculations were performed with a five symbol alphabet. Thirty surrogates were used in each calculation of normalized complexity

C_ORIG is the complexity of the original symbol sequence. <C₀> is the mean complexity obtained with random equiprobable surrogate symbol sequences of the same length using the same symbol alphabet. An equiprobable symbol sequence is one in which the probability of each symbol is equal. In these example calculations there are five symbols in the alphabet giving a frequency of .2 for each symbol. Under this normalization a constant signal will have a complexity approaching zero and a random signal will have a complexity approaching one. An expression for the uncertainty of C_NORM (Rapp et al. 2004) is given by

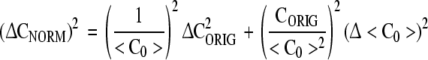Δ<C₀> is the standard deviation of the mean <C₀>. ΔC_ORIG is the uncertainty of the estimate of C_ORIG. It is approximated by

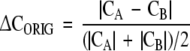where C_A is the complexity obtained using the first half of the original symbol sequence and C_B is the complexity obtained using the second half of the original symbol sequence. It is seen in Fig. 1 that the normalized complexity is relatively insensitive to data set size.

It should be stressed that the insensitivity of C_NORM to N_DATA shown in Fig. 1 requires two things. First, the data set size, N_DATA, must exceed some minimum size; the value of N_DATA required to obtain a stable value of C_NORM depends on the dynamical system under observation and the quality of the data. In some cases, several thousand observations can be required. Estimates of C_NORM can be obtained with smaller data sets, but it should be recognized that these calculations will give only an approximate estimate of the complexity of the underlying dynamical process. In many cases, however, an imperfect estimate can be valuable. The second condition required for the insensitivity of C_NORM to N_DATA is the dynamical stationarity of the signal-generating system during the observation period. If, for example, the system undergoes a transition from periodic to chaotic behavior C_NORM will not be constant, nor should it be. An example of this is shown in Fig. 2. The first 5,000 points of the time series were generated by the periodic van der Pol equation. The second 5,000 points were random numbers uniformly distributed on [0,1]. C_NORM increases as the fraction of the total data set composed by random numbers increases. The uncertainty in the estimate of C_NORM also increases after the introduction of random elements into the time series. The greatest uncertainty is observed when N_DATA = 10,000. The large value of ΔC_NORM can be understood by referring to the preceding equation. When N_DATA = 10,000, C_A is the Lempel–Ziv complexity calculated using 5,000 points from the van der Pol system, and C_B is the calculated using 5,000 random numbers. The N_DATA = 10,000 case gives the maximum difference between C_A and C_B.

Fig. 2.

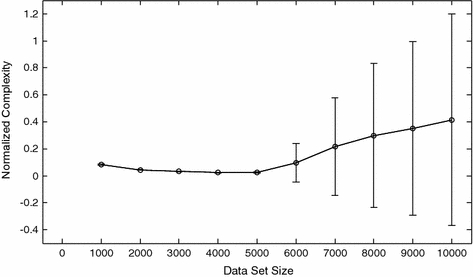
Normalized complexity as a function of data set size during a dynamical transition. The data set examined in this diagram consisted of 5,000 points calculated with the periodic van der Pol system and 5,000 random numbers uniformly distributed on [0,1]. For data set sizes less than or equal to 5,000 points the complexity corresponds to that expected from the periodic van der Pol system. For data set sizes greater than 5,000 points, the fraction of the time series generated by a random number generator increases and the complexity, even though normalized, increases. The uncertainty in the estimated normalized complexity also increases. All complexity calculations were performed with a five symbol alphabet. Thirty surrogates were used in each calculation of normalized complexity

With the definition of C_NORM in hand, we can now return to the motivating questions. How often should behavior be sampled, and how long should behavior be observed? These questions can be addressed empirically by finding sampling intervals and observation epochs that give stable values of C_NORM. By normalizing complexity, the artifactual dependence on data set size is minimized. In the ideal case it may be possible to find a broad range of conditions in which C_NORM is insensitive to both sampling interval and observation period. Nonetheless, as will be emphasized in the next section, there are fundamental limitations to complexity calculations. It is therefore essential to include a specification of epoch duration and sampling frequency in any report of normalized complexity.

You only know what you see: a fundamental limitation of complexity calculations

The calculations of Fig. 2 show that a stable value of normalized complexity is obtained only if the process generating the signal is dynamically stable. This point is also made in the calculations displayed in Fig. 3. The first value of C_NORM in that diagram was computed using 100 random numbers uniformly distributed on [0,1]. Data was partitioned on a five symbol alphabet. As expected, a value of C_NORM very close to one was obtained (C_NORM = .992). The second point in that curve was produced by a 200 point data set. The first 100 points were the random numbers used to calculate the first value of complexity. These 100 points were repeated without change in the same sequence to produce the second 100 elements of the 200 point data set. The introduction of a repeated sequence results in a significantly lower value of normalized complexity (C_NORM = .596). The use of normalized complexity, which reduces sensitivity to data set size, is essential to this observation. This process is repeated. The time series is expanded iteratively by repeating the first 100 points. The time series become increasingly periodic. The complexity of a periodic signal, when corrected for length of data set, is low. A similar analysis using a binary partition has been published in Rapp et al. (2004).

Fig. 3.

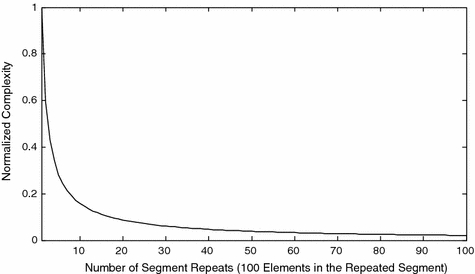
Normalized complexity of a complex periodic time series. A 10,000 point time series was formed by 100 repeats of an identical segment of 100 random numbers. As the length of the times series is increased, the periodic behavior becomes increasingly evident and the normalized complexity decreases. Data were partitioned on a five symbol alphabet. Thirty surrogates were used to calculate the normalized complexity

All complexity measurements carry this uncertainty. A complex signal may begin to repeat itself. What initially appears complex may be seen to be simple when the observation period is increased. The results of Fig. 2 make the converse point. A seemingly simple signal may be seen to be complex when observed for a longer period of time. An absolute value of complexity cannot be obtained empirically.

First order Markov surrogates: probing the fine structure of behavior

The simplest probabilistic model of a symbol sequence is a first order Markov process which can be expressed as a probability transition matrix. P_IJ is the probability that Symbol I is followed by Symbol J. Does the observed symbol sequence contain a deeper structure? Stated more precisely, for a given symbol sequence and a given measure of complexity, can that measure be used to show that there is a nonrandom structure in the symbol sequence that is not contained in the specification of [P_IJ]? This question can be addressed by comparing the complexity obtained with the original symbol sequence against values obtained with first order Markov surrogates of equal length.

The method of surrogate data is a powerful statistical procedure for examining hypotheses about the structure of dynamical systems (Theiler et al. 1992; Rapp et al. 1993). An investigation with surrogate data has three components. First, a dynamical measure M is applied to the original time series or symbol sequence. The resulting value is denoted by M_ORIG. In the examination of sequential animal behavior, the measure could be the previously described normalized complexity. In the second step, the original data set is used to generate surrogate data sets. As will be explained, the procedure for generating surrogate data depends on the null hypothesis being examined. The same dynamical measure is then applied to surrogate data resulting in the set of values 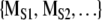. In the third step, M_ORIG is compared statistically against 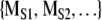. If M_ORIG is sufficiently different from 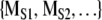, the null hypothesis can be rejected.

The procedure used to generate surrogates depends on the null hypothesis being investigated. If it is hypothesized that there is no nonrandom sequential structure in the time series, the surrogates can be generated by random shuffles of the original data. If the null hypothesis is that, under the chosen dynamical measure, the time series is indistinguishable from linearly filtered random numbers, then random phase surrogates can be used (Theiler et al. 1992).

When investigating symbol sequences with Markov surrogates, we address the following question: using the specified complexity measure is the original symbol sequence distinguishable from a randomly generated symbol sequence of the same length that has the same transition matrix [P_IJ]? To implement this procedure [P_IJ] is calculated from the original symbol sequence. A random number generator is used to generate a collection of surrogate symbol sequences that have the same length and same [P_IJ]. The same complexity measure is applied to the original symbol sequence to yield M_ORIG and to each surrogate sequence to generate 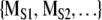. We then ask is M_ORIG significantly different from 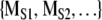? The simplest statistical procedure to test this separation is a calculation of the Monte Carlo probability of the null hypothesis (Rapp et al. 1994). In this case the null hypothesis is M_ORIG and 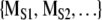are indistinguishable.

The total number of cases is the number of surrogates plus one. The null hypothesis can be rejected if P_NULL is less than a previously specified rejection criterion. Rejection of the null hypothesis indicates that there is a structure in the symbol sequence that cannot be reproduced by the constrained random process used to generate the surrogates.

A limitation of this computation should be recognized. The conclusions are specific to the complexity measure used. Suppose Lempel–Ziv complexity is used and the null hypothesis is not rejected. This does not mean that there is not a structure in the symbol sequence that is not implicit in [P_IJ]. Rather, it can only be said that Lempel–Ziv complexity failed to find evidence for this structure. It remains possible that the null hypothesis could be rejected if a different measure was applied to the data and its surrogates. Additionally, rejection of the random-[P_IJ] null hypothesis does not identify the additional structure in the symbol sequence. It does, however, indicate that this structure exists and is potentially discoverable.

In addition to statistical testing, values of complexity obtained with Markov surrogates can also be used to normalize complexity measurements obtained with the original symbol sequence and produce an alternative to the definition of C_NORM defined in the third section.

Generalizations to animal locomotion

In the first section of this paper it was suggested that symbolic dynamics can be used to explore the sequential structure of animal behavior by examining a time-ordered record of discrete behaviors. A complementary measure can be obtained by quantifying the animal’s movement in a free field behavior space. If the space is partitioned into a finite number of elements, with each element being assigned a unique symbol, and if the animal’s position is recorded at regular intervals, then the previously described methods can be used to quantify the animal’s trajectory. In the case of compromised animals where the presentation includes stereotypic motor behavior, the complexity of the position sequence would be lower than that observed in control animals. An investigation of animal movement following blast exposure is encouraged by a prior literature showing changes in dynamical measures of movement following the administration of psychoactive compounds (Paulus et al. 1990, 1993; Paulus and Geyer 1992, 1993).

Quantitative characterization of animal locomotion does not need to be limited to measures derived from symbolic dynamics. A nonlinear analysis of fish movement using the characteristic fractal dimension, the Richardson dimension, the Hurst coefficient, and relative dispersion in addition to Lempel–Ziv complexity has been published by Neumeister et al. (2004).

Conclusions and recommendations

The focus of this paper has been the analysis of animal behavior. It should be noted that these methods can be used in the analysis of behavioral patterns in humans. For example, Paulus et al. (1996) analyzed data from a binary choice task by calculating dynamical entropy and local subsequence entropies. Results obtained with schizophrenic patients were compared against results obtained with control subjects. Compared to controls, schizophrenics “exhibited significantly less consistency in their response selection and ordering, characterized by a greater contribution of both highly preservative and highly unpredictable subsequences of responses within a test session.”

Reports of dynamical analysis of animal behavior in a free field environment that are based on symbolic dynamics should include the following:

1. A description of the environment including its size, contents, and ambient lighting should be given.

2. Since behavior is sensitive to circadian time, the report should include an indication of the time of day during the measurement.

3. A specification of the scored behaviors and the scoring criteria should be given.

4. The sampling interval should be defined.

5. The duration of the observation period should be reported.

6. The definition of the complexity measure used should be provided. This report should include a description of any normalization procedure employed and a specification of the number of surrogates used to construct the normalization.