An oscillatory correlation model of auditory streaming

Abstract

We present a neurocomputational model for auditory streaming, which is a prominent phenomenon of auditory scene analysis. The proposed model represents auditory scene analysis by oscillatory correlation, where a perceptual stream corresponds to a synchronized assembly of neural oscillators and different streams correspond to desynchronized oscillator assemblies. The underlying neural architecture is a two-dimensional network of relaxation oscillators with lateral excitation and global inhibition, where one dimension represents time and another dimension frequency. By employing dynamic connections along the frequency dimension and a random element in global inhibition, the proposed model produces a temporal coherence boundary and a fissure boundary that closely match those from the psychophysical data of auditory streaming. Several issues are discussed, including how to represent physical time and how to relate shifting synchronization to auditory attention.

Introduction

A listener in a realistic environment is typically exposed to an acoustic input from different sound sources. Yet the human listener with normal hearing has no problem in organizing the elements of the input into their underlying sources to perceive the acoustic environment. This process of organization, called auditory scene analysis (ASA), is a main part of auditory perception which pertains to the perceptual grouping of auditory stimuli into coherent auditory streams (Bregman 1990). A stream is an auditory object that corresponds to a sound source in the physical world.

The ability of the auditory system to organize the acoustic input is exemplified by the fact that a listener is capable of speech communication in a cocktail party. The problem that auditory scene analysis must solve in such an environment is popularly known as the cocktail party problem, a term coined by Cherry (1953). The sound wave that impinges on the eardrum is, quoting Helmholtz (1863, p. 26), “complicated beyond conception.” Despite intense effort aiming to construct a machine that can solve the cocktail party problem, “we are still far from achieving machine performance that is comparable with that of human listeners” (Wang and Brown 2006, p. 36). ASA is a truly remarkable accomplishment by the auditory system.

According to Bregman (1990; see also Yost 1997 and Warren 1999), auditory organization is governed by mechanisms that are analogous to Gestalt grouping principles revealed in visual perception. Major ASA mechanisms include:

• Proximity in frequency. When listening to two tones of different frequencies, the tones that are close in frequency tend to be grouped into the same stream.

• Proximity in time. Similar to proximity in frequency, tones close in time (fast presentation) are likely to be grouped into the same stream.

• Common onset and offset. If two sounds have the same onset time or, to a lesser degree, the same offset time, they tend to be grouped into one stream.

• Common amplitude and frequency modulation. Simultaneous tones that undergo the same kind of amplitude or frequency modulation tend to be grouped into the same stream.

• Familiarity. Components that belong to the same familiar pattern have the tendency to be grouped.

Of the above mechanisms, proximity in frequency and time is considered of primary importance in ASA. While familiarity is viewed as a top-down, schema-based process, the other ASA mechanisms belong to primitive organization which is viewed as a bottom-up, innate process. According to Bregman (1990), ASA is mainly a primitive process which is aided by schema-based organization.

Although much of the work in computational auditory scene analysis (CASA) is driven by performance concerns, i.e., to develop algorithms for solving the cocktail party problem (Wang and Brown 2006), this paper presents a neurocomputational model for auditory scene analysis. In particular, we are interested in quantitatively simulating a set of perceptual data pertinent to auditory streaming, or stream segregation of alternating tones. The auditory streaming phenomenon occurs when a sequence of alternating high- and low-frequency tones is presented to listeners (Miller and Heise 1950; Bregman and Campbell 1971; van Noorden 1975). The perceptual organization of alternating tones critically depends on the frequency difference between the high tones and the low tones and the rate of presentation (or time difference). Roughly speaking (see section “Auditory streaming phenomenon” for details), larger frequency separation or faster presentation leads to the segregation of a tone sequence into two streams, one corresponding to high tones and the other low tones. Smaller frequency separation or slower presentation results in a single stream that consists of all high and low tones. With intermediate levels of frequency separation and presentation rate, perception is ambiguous: A listener at a time may organize a tone sequence in either way and can switch between the two with conscious effort. The psychophysical data from auditory streaming experiments provide a major source of empirical evidence for Bregman’s ASA account of auditory organization (Bregman 1990).

A number of computational models have been proposed to account for the auditory streaming phenomenon (see among others Beauvois and Meddis 1991; Wang 1996; McCabe and Denham 1997; Baird 1997; Brown and Cooke 1998; Norris 2003; Almonte et al. 2005; see Brown and Wang 2006 for a recent review). Inspired by neurophysiological evidence supporting coherent neural oscillations in the auditory system (see section “Biological plausibility”), we further develop an oscillatory correlation model that was originally proposed by Wang (1996). The two most important aspects of the model are:

• Stream segregation is represented by oscillatory correlation. That is, a stream corresponds to an assembly of synchronized neural oscillators, and multiple streams correspond to different oscillator assemblies that are desynchronized. Hence stream segregation corresponds to the formation of oscillator assemblies (von der Malsburg and Schneider 1986). See Wang (2005) for a comprehensive account of oscillatory correlation theory for general scene analysis.

• The neural architecture is a two-dimensional LEGION network, where building blocks are relaxation oscillators and the connectivity among the oscillators is of two kinds: Local (lateral) excitation and global inhibition. The two dimensions correspond to time and frequency. In particular, physical time is converted into a separate dimension via a set of systematic delays, corresponding to a kind of place coding (Helmholtz 1863; Jeffress 1948; Licklider 1951).

In this model, small separation in frequency and time is translated into strong excitatory connections between oscillators, which encourage synchronization. On the other hand, large frequency separation between high and low tones results in weak excitatory connections that cannot overcome global inhibition, causing multiple desynchronized assemblies, or segregated streams. On the basis of this model, Wang (1996) qualitatively simulated the dependency of auditory streaming on frequency and time proximity as well as the perceptual phenomena of sequential capturing and competition among different organizations.

A major extension of Wang’s model was made by Norris (2003). With a more accurate implementation of oscillatory dynamics, Norris introduces a measure of synchrony as the proportion of the time when oscillators are simultaneously active compared to the time when any is active. This measure allows him to quantitatively evaluate Wang’s model on auditory streaming data. His version of the model gives a reasonable match to human data, although the match is not close. Also, he extends the original model to simulate two additional aspects of auditory streaming: Grouping by onset synchrony and stream bias adaptation, the latter pertaining to the gradual build up and decay of stream segregation. The extension adds a new set of excitatory connections among the oscillators whose corresponding onset detectors are activated simultaneously, and a time-dependent bias to each oscillator.

In the context of modeling auditory scene analysis by oscillatory correlation, this study introduces a new mechanism of dynamic connectivity to quantitatively simulate the auditory streaming phenomenon. This mechanism allows for connection strengths along frequency to dynamically change with respect to tone repetition time, which is the interval between the onset times of two consecutive tones in a sequence of alternating high and low tones. This way of forming dynamic connections, together with some randomness in global inhibition, enables us to obtain a close match to a set of quantitative data of auditory streaming.

The next section describes the auditory streaming phenomenon. Section “Model description” describes the oscillatory correlation model and its implementation. Section “Simulation results” presents simulation results and comparisons with related models. In Section “Discussion,” we discuss several issues related to our model, including its biological foundation, the representation of time, and the shifting synchronization theory for auditory streaming.

Auditory streaming phenomenon

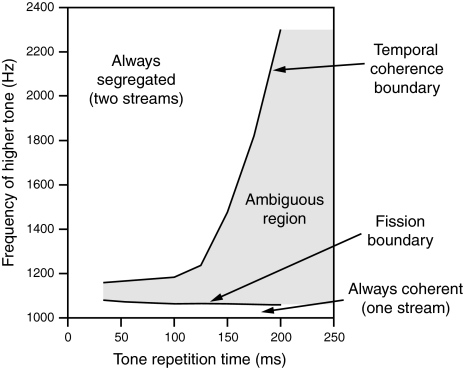
Extending the experiments by Miller and Heise (1950) and Bregman and Campbell (1971), Van Noorden (1975) conducted a thorough study on the perception of alternating tone sequences. In sequences where pure tones follow one another in quick succession, his experiments show that listeners do not process each tone individually. Instead, the listener perceives a sequence of alternating tones with small frequency separation to be coherent—the entire sequence forms a single stream—while a sequence of alternating tones with large frequency separation is perceptually segregated into two separate streams, one for high tones and one for low tones. The frequency separation at which a coherent stream segregates into two separate ones also depends on tone repetition time (TRT), or inter-onset interval, which is the time interval between the onset times of two successive tones in a sequence. Furthermore, depending on TRT, there exists a frequency range in which the listener can switch between the percept of a coherent stream and that of segregated streams, using selective attention.

Based on these observations, van Noorden introduces two boundaries called temporal coherence boundary (TCB) and fission boundary (FB), to quantitatively describe the frequency differences of alternating tones that cause the listener to perceive one percept over another, with respect to different TRTs. In his experiments, each tone in an alternating sequence is 40 ms long, and he varies TRT between 48 and 200 ms. His experimental results are summarized in Fig. 1. Given a TRT, for frequency separation above the TCB the listener inevitably loses the perception of temporal coherence and segregates the alternating tones into two streams, and for frequency separation below the FB the listener always perceives the alternating tones as one coherent stream. Between the two boundaries is the ambiguous region, where the listener can perceive either one coherent stream or two segregated ones, and may switch between the two different percepts either spontaneously or with conscious attentional control. From the experimental results in Fig. 1, we can see that TCB shows clear dependence on TRT whereas FB is basically independent of TRT.

Fig. 1.

Psychophysical measurements of auditory streaming by van Noorden (1975). The data show a temporal coherence boundary and a fission boundary. This figure is redrawn from McAdams and Bregman (1979) and Beauvois and Meddis (1996) with original data from van Noorden (1975). For the alternating-tone sequences used in van Noorden’s study, the frequency of the lower tone is fixed at 1,000 Hz, and the frequency of the higher tone is shown on the ordinate

Model description

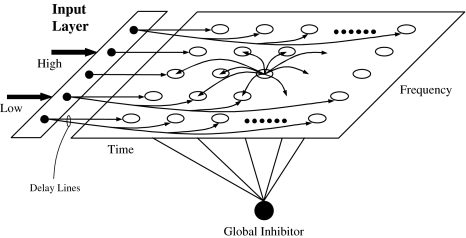
Our oscillatory correlation model for auditory streaming is a two-dimensional (2-D) network of relaxation oscillators where the two dimensions correspond to frequency and time, respectively. Figure 2 shows the network architecture. The existence of a frequency dimension is well supported by the anatomy and physiology of the cochlea and the prevalence of tonotopic organization throughout the auditory system (Kandel et al. 1991). We assume that the dimension of time is formed via a systematic set of delay lines which are arranged so that delays increase from left to right; the biological plausibility of a separate time dimension will be discussed in section “Representation of time.” The network receives time-varying input from an input layer, which corresponds to auditory peripheral analysis. To focus on the modeling of the auditory streaming phenomenon, we have opted for a simplified version of peripheral analysis, which amounts to the detection of a specific frequency component at a particular time (see also Wang 1996; Norris 2003); the reader is referred to Wang and Brown (2006) for more biologically realistic modeling of auditory periphery. Therefore, an oscillator in the 2-D network is stimulated by an external input of a specific frequency at a specific time relative to the present time. Consistent with physiology and psychophysics, the frequency dimension has a logarithmic scale. On the other hand, the time dimension is assumed to be linear (see Section “Representation of time” for more discussion).

Fig. 2.

Model diagram. The proposed model consists of a two-dimensional oscillator network where the two dimensions correspond to time and frequency. Each oscillator receives input from its corresponding frequency channel in the input layer via a delay line. “High” and “Low” indicate frequency. In the network each oscillator, shown as an open circle, is laterally connected with other oscillators through excitatory and dynamically changing links. For clarity the figure only shows lateral connections from one typical oscillator. In addition, a global inhibitor, shown as the filled circle, is connected with every oscillator

Model of a single oscillator

The building block of the proposed model is a single relaxation oscillator, i, which is defined as interacting pair of an excitatory unit x_i and an inhibitory unit y_i (Terman and Wang 1995):

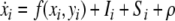1a

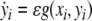1b

where f(x_i, y_i) = 3x_i−x³_i + 2−y_i and 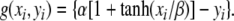I_i denotes external stimulation to the oscillator and S_i represents the overall coupling from the other oscillators in the network as well as from a global inhibitor. The symbol ρ denotes the amplitude of an intrinsic Gaussian noise term.

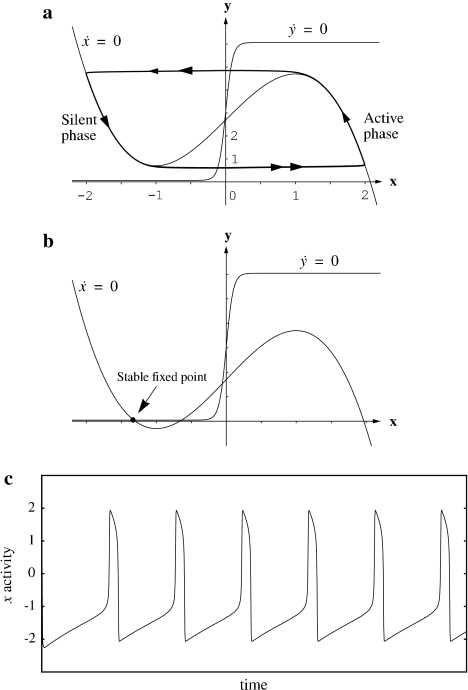
The parameter ɛ in (1b) is chosen to be a small, positive number. As a result, when the coupling and noise terms are ignored, Eq. 1 defines a typical relaxation oscillator with two time scales (van der Pol 1926; Wang 1999). The x-nullcline (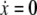) and y-nullcline of (1) are a cubic curve and a sigmoid, respectively, as shown in Fig. 3a. For I_i > 0, the two nullclines intersect only on the middle branch of the cubic, and (1) gives rise to a stable periodic orbit. In this case, the oscillator is referred to as enabled. The periodic solution alternates between an active phase of high values of x, and a silent phase of low values of x. The alternation between the two phases takes place on a fast time scale compared to the behavior within each of the two phases. For I_i < 0, the two nullclines intersect on the left branch of the cubic, and (1) produces a stable fixed point as shown in Fig. 3b. In this case, no oscillation occurs and the oscillator is referred to as excitable.

Fig. 3.

Behavior of a single relaxation oscillator. (a) Enabled oscillator. An enabled oscillator produces a stable periodic orbit shown in bold with the direction of movement indicated by the arrows. The periodic solution alternates between an active phase of relatively high values of x, and a silent phase of relatively low values of x, and the jumps between the two phases are indicated by double arrows. (b) Excitable oscillator. In this state, the oscillator produces a stable fixed point at a low value of x. (c) Temporal activity of an enabled oscillator. The curve shows the x activity of the oscillator

The above analysis shows that whether the state of an oscillator is enabled or excitable depends solely on external stimulation. Hence the oscillation is stimulus dependent. Figure 3c illustrates the typical x activity of an enabled oscillator, which resembles a spike train. Relaxation oscillators have been widely used as models of single neurons, where x is interpreted as the membrane potential of a neuron and y the activation state of ion channels (FitzHugh 1961; Nagumo et al. 1962; Morris and Lecar 1981). Relaxation oscillations may also be interpreted as oscillating bursts of neuronal impulses, and in this interpretation x corresponds to the envelope of a burst.

Network connectivity

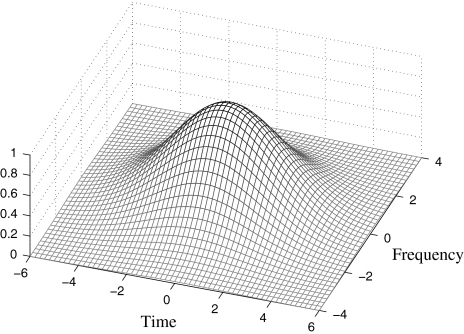
The network shown in Fig. 2 is composed of identical relaxation oscillators as defined in Eq. 1. The connectivity among the oscillators has two components: Lateral excitation and global inhibition. Similar to Wang (1996), lateral excitation takes on the form of a 2-D Gaussian function; in other words, the connection strength between two oscillators falls off exponentially as shown in Fig. 4. Furthermore, we extend the idea of dynamic connections (von der Malsburg 1981; Wang 1995) by allowing the weights of lateral connections to change dynamically, depending on the state of the network. Examining Fig. 1 reveals that the upper bound of frequency separation to maintain temporal coherence increases dramatically with increasing TRT. This suggests a change in the shape of the Gaussian connectivity with respect to a change in TRT. We propose to dynamically adapt the width of the Gaussian function along the frequency dimension so that it widens with increasing TRT. The increased strengths will serve to enlarge the frequency range of temporal coherence at large TRTs. Specifically, Gaussian dynamic connectivity is described as:

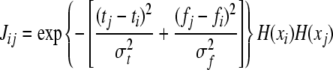2

where J_ij stands for the weight of connection from oscillator j to oscillator i, t_i and f_i denote the position of i along the time and frequency axes, respectively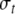, and and 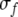represent the widths of the Gaussian function along the time and frequency axis, respectively. The function H(x) is a Heaviside function used to detect whether oscillator i is in the active phase, and it equals 1 if x is greater than or equal to 0 and equals 0 otherwise.

Fig. 4.

Two-dimensional Gaussian lateral connectivity. This pattern depicts the strengths of the excitatory connections of the center oscillator

Note that the frequency axis is on a logarithmic scale so that the frequency subtraction in (2) corresponds to a frequency ratio on a linear frequency scale. Self connectivity J_ii is set to 0. 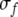represents the dynamic Gaussian width along the frequency dimension depending on TRT. This implies that the model needs a map of tone onsets, which we assume to be available to the network. The idea of having a map of tone onsets for modeling auditory streaming has been proposed by Norris (2003). We propose the following sigmoidal relationship between 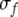and TRT:

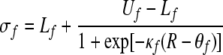3

where R is a parameter that represents the rhythmic period of an auditory stimulus, which corresponds to TRT when simulating the auditory streaming phenomenon. U_f and L_f denote the upper and lower bounds of the Gaussian width along the frequency axis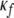, and and 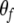are the parameters of the sigmoid. We have adopted a curve fitting algorithm for logistic functions (Cavallini 1993) on a preliminary set of data points in order to choose appropriate values of the parameters, and the resulting values are: U_f = 11, L_f = 2.3, 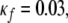and 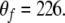In addition, we set 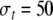which is much larger than U_f. This implies that the connection strengths taper off more slowly along the time dimension than along the frequency axis, or the connections along the time axis are relatively stronger.

With this extension, the connection strengths in frequency now dynamically change according to the stimulus presentation rate. Such short-term weight adaptation is consistent with physiological evidence relating to rapid task-dependent plasticity of spectrotemporal receptive fields (Fritz et al. 2003). Another requirement for the weight adaptation is a map of detected onsets in order to compute R, or TRT in this paper. Various onset detecting neurons have been identified in the auditory system (Pickles 1988; Popper and Fay 1992). Although we equate R with TRT in this study, R representing the rhythmic period of an external auditory input is a broad concept that is not limited to modeling auditory streaming. Jones and colleagues have argued that general auditory events exhibit rhythmic structure, and auditory streaming is influenced by rhythmic organization of auditory stimuli (Jones et al. 1981, 1995). Large and Jones (1999) model the tracking of auditory events using an oscillator network. Effort has also been made to perform onset and offset detection and employ detected onsets and offsets to segment real signals (Smith 1994; Hu and Wang 2007).

The role of global inhibition is to desynchronize multiple oscillator assemblies representing different streams. The global inhibitor, z, is defined as:

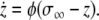4

In this formulation, 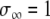if at least one oscillator is in the active phase, and 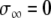otherwise. If none of the oscillators in the network are in the active phase, the global inhibitor will not receive any input and z will approach 0 rapidly; in this case, oscillators in the network will not receive any inhibition. If at least one oscillator is in the active phase, z will rapidly approach 1, exerting inhibition on the entire network.

As discussed in the Section “Auditory streaming phenomenon,” between the TCB and the FB, listeners are able to switch between the percepts of temporal coherence and segregated streams, either spontaneously or through attentional control. Depending on TRT, there can be a large range of frequency differences where ambiguous streaming occurs (see Fig. 1). Given an oscillator network with fixed parameters, the network likely approaches stable behavior. In other words, the oscillator network tends not to show ambiguous behavior. To model the spontaneity and conscious control in auditory streaming, we introduce a random element in the inhibitory connections of the global inhibitor, which is well situated to influence the outcome of oscillator assembly formation. Specifically, we introduce a new variable, r_z, whose activity is randomly generated depending on the parameter R:

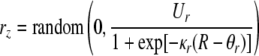5

Again, we use a sigmoidal function to define the random activity due to its natural bounds. U_r gives the upper bound of the random activity. 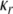and 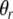denote the parameters for the sigmoid. The random function indicates a uniform distribution in a range from 0 to a value specified by the sigmoid. Following similar logistic curve fitting described earlier leads to the following parameter values: U_r = 0.27, 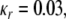and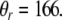

We now define the overall coupling of the oscillator network to oscillator i, the term S_i from Eq. 1, which combines lateral excitation and global inhibition:

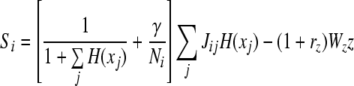6

Here N_i denotes the number of the enabled (stimulated) oscillators that have the same frequency coordinate as that of oscillator i, i.e., they are on the same row in the model diagram of Fig. 2. The first term in (6) specifies the amount of lateral excitation received by i. The weighted sum in the term allows for the strengths of excitatory connections to increase as more oscillators are activated. On the other hand, the increase of the lateral excitation is subject to two normalizing factors: The total number of active oscillators and the number of the enabled isofrequency oscillators. 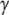is a constant that specifies the relative importance of these two factors. Physiologically speaking, such a form of normalization is an instance of shunting (divisive) inhibition (Arbib 2003). The second term in (6) specifies the connection from the global inhibitor, and W_z is the weight of the global inhibition. In this study, we set 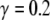and W_z = 0.96.

In Wang (1996), dynamic connection weights were normalized so that each oscillator has the equal strength of excitatory connections. Such weight normalization is introduced primarily for the purpose of facilitating synchronization within an oscillator assembly (Wang 1995; Terman and Wang 1995). The two normalizing factors in (6) serve different purposes—the aim here is to regulate the growth of lateral excitation in an activity-dependent way.

LEGION dynamics and implementation

The segregation network defined above, with lateral excitation and global inhibition, may be viewed as a LEGION network; LEGION, introduced by Terman and Wang (1995; see also Wang and Terman 1995), stands for locally excitatory globally inhibitory oscillator network. Terman and Wang (1995) have conducted an extensive analysis of LEGION dynamics. In particular, LEGION is governed by the selective gating mechanism, where an enabled oscillator jumping to the active phase rapidly recruits the oscillators stimulated by the same pattern, while preventing oscillators representing other patterns from jumping up. Synchronization within an oscillator assembly—those stimulated by the same pattern—and desynchronization among different assemblies are reached rapidly in LEGION networks. Desynchronized oscillators do not stay in the active phase simultaneously.

In terms of computer implementation, Terman and Wang (1995) originally integrate the differential equations defining LEGION numerically using the standard fourth-order Runge–Kutta method. The Runge–Kutta method has a high degree of accuracy but is slow when dealing with a sizable network. Later, Linsay and Wang (1998) developed a more specific numerical method for relaxation oscillator networks. Their method is based on analyzing the characteristic behavior of relaxation oscillations in the singular limit, thus called the singular limit method. The idea is to solve the system in the singular limit when it evolves on the slow time scale, while approximating the system when it evolves on the fast time scale. The singular limit method substantially improves the computational efficiency of LEGION implementation without losing much of numerical accuracy.

Although the singular limit method makes it possible to implement a reasonably sized LEGION network, it still requires significant computation time when dealing with large-scale networks. Here we adopt an algorithmic approximation described in Wang (1996). The algorithmic steps are given below (see Wang 1996, p. 427):

• When no oscillator is in the active phase, the one closest to the jumping point among all enabled oscillators is selected to jump to the active phase.

• An enabled oscillator jumps to the active phase immediately if the overall coupling it receives is positive (cf. Eq. 6).

• The alternation between the active phase and the silent phase of an oscillator takes one time step only.

• All of the oscillators in the active phase jump down if no more oscillators can jump up. The situation occurs when the oscillators of the same assembly have all jumped up.

This algorithm preserves the essential properties of assembly formation, i.e., synchronization and desynchronization. However, it is a high-level approximation to the underlying dynamics, and caution needs to be exercised when observations are generalized. Also, the original analysis on LEGION does not treat lateral connections that are introduced to synchronize multiple connected oscillator blocks, as used in our model. In this situation, global inhibition is needed to inhibit not only the oscillators that do not receive excitatory input from the currently active oscillators but also those that receive relatively weak lateral excitation. Nonetheless, Norris (2003) found that this approximation produces very similar results to those produced by the numerically accurate, singular limit method.

Simulation results

As stated earlier, an input stimulus—a sequence of alternating tones—is represented as a shifting binary matrix on the 2-D oscillator network shown in Fig. 2, where a binary element of the matrix indicates the presence or absence of the stimulus at a particular frequency and a particular time. The delay lines in the network provide a form of short-term memory (STM) that keeps a recent history of external stimulation. In order to relate to real time, the time difference between two neighboring isofrequency oscillators is set to 10 ms. This representation of time is consistent with standard spectrogram and cochleagram representations where the input waveform is divided into time frames of typically 10 or 20 ms. The number of oscillators in a row needs to be large enough so that a sequence of slowly presented tones can be adequately represented in the network. To simulate the data in Fig. 1, we use 600 ms as the length of STM. Figure 5 shows a typical snapshot of an alternating tone sequence presented to our model network.

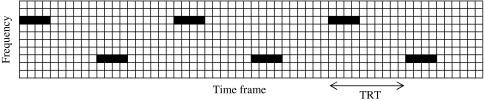
Fig. 5.

Snapshot of an alternating tone sequence presented to the proposed model. Each oscillator is indicated by a square, and the tones are indicated by black horizontal bars. The network represents 60 time frames, corresponding to 600 ms. Each tone is 40 ms long and the tones are presented with the TRT of 100 ms

To be consistent with the gamma frequency range (30–70 Hz) of synchronous oscillations in the brain (Eckhorn et al. 1988; Gray et al. 1989; Brosch et al. 2002; Fries et al. 2007), we set the frequency of intrinsic oscillations of each oscillator to 50 Hz, translating to a period of 20 ms. With a 10-ms frame shift, this means that an input will be updated twice by the network during one cycle of executing the algorithm given in Section “LEGION dynamics and implementation.” Specifically, the external input to the network is updated once at the beginning of the first step of the algorithm and once after the last step, i.e., once before jumping up and once after jumping down. In the algorithm, external stimulation enables an oscillator. Therefore, depending on the input, appropriate oscillators will be stimulated during each oscillation period.

Quantitative evaluation

We measure the behavior of the proposed model in terms of oscillator synchrony and desynchrony. To relate the network behavior to the psychophysical results shown in Fig. 1, a metric is needed to measure the degree of auditory streaming (Norris 2003). As long as external input is continuously provided, the model will keep on looping through the four steps given in Section “LEGION dynamics and implementation.” The x value of an oscillator indicates whether it is in the active phase, or is active. For each oscillation cycle, or looping through the 4-step algorithm once, we consider the model in the coherent state when all of the enabled oscillators are synchronized (i.e., simultaneously active) and it in the segregated state when all of the enabled isofrequency oscillators are synchronized while oscillators at different rows of the network are desynchronized. As described in Section “Network connectivity,” lateral connection strengths along the time axis are independent of the TRT and relatively strong. This ensures that, for the range of TRT considered in this study, enabled isofrequency oscillators will synchronize. Because of this, our measure of streaming is simpler than the one introduced by Norris (2003), which considers cases where oscillator blocks corresponding to different tones of the same frequency are not synchronous.

For a particular TRT and frequency separation of an alternating tone sequence, we run a simulation for a finite number of iterations through the algorithmic loop. We then calculate the number of cycles the system is in the coherent state and the number of cycles the system is the segregated state. Such numbers are compared with the total number of simulated cycles. If the system is in the coherent state for at least 95% of the cycles, we consider the system in the coherent state for this specific TRT and frequency separation. Likewise, if the system is in the segregated state for at least 95% of the cycles, we consider the system in the segregated state for the TRT and frequency separation. Otherwise, the system is considered in the ambiguous state. In order to let the system stabilize first, we run the algorithm for 10 cycles before collecting the simulation results.

We simulate the system defined in Section “Model description” using the parameter values given there. In terms of frequency separation between the high and the low tones in an alternating tone sequence, we vary the frequency ratio from 1.1 to 4.0 in steps of 0.02. In terms of TRT, we vary it from 50 to 200 ms in steps of 50 ms. Each combination of frequency difference and TRT results in a different simulation. Hence, a total of 584 simulations are run. In the simulations, the tone duration is fixed at 40 ms as shown in Fig. 5, which means that each tone stimulates 4 oscillators.

Each simulation is run for 110 loops, corresponding to 2.2 s in real time, and data collection commences after the first 10 loops. The analysis of the collected data results in a decision of coherence, segregation, or ambiguity. Then, simulated fission and temporal coherence boundaries are calculated by identifying, for each TRT, one boundary below which all frequency ratios lead to coherence and another boundary above which all frequency ratios lead to segregation. Linearly interpolating these boundary points yields the simulated TCB and FB. The simulation results are shown in Fig. 6.

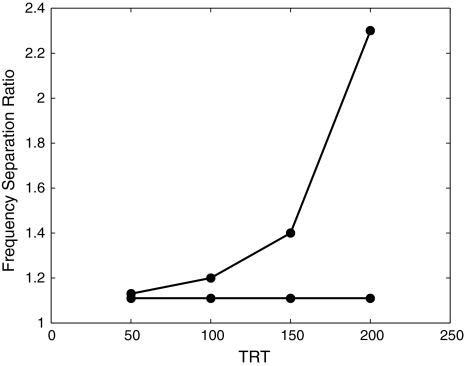
Fig. 6.

Simulation results. Simulations are conducted at the tone repetition times of 50, 100, 150, and 200 ms and frequency ratios from 1.1 to 4.0. The top curve represents the TCB of the model and the bottom one represents the FB of the model

A comparison the simulation results in Fig. 6 and the corresponding data in Fig. 1 shows a close match between the model outputs and the human data. The simulated temporal coherence boundary shows the same exponential increase with TRT, and the simulated fission boundary is similarly constant with respect to TRT. Although the FB in Fig. 1 shows a slight increase with decreasing TRT when TRT is less than 100 ms, this effect is insignificant as van Noorden observes a slight reverse trend in a different experiment (see Fig. 2.7, van Noorden 1975). Note that the data in Fig. 1 represent the average of two listeners, and individual results can vary considerably (van Noorden 1975).

Comparisons

As mentioned in Section “Introduction,” Wang’s original model only simulates the streaming phenomenon qualitatively. With a measure of synchrony, Norris (2003) has systematically quantified the output of Wang’s model with respect of frequency separation and TRT. He finds that the model with the original set of parameter values produces the TCB and the FB that qualitatively match those of human listeners. Furthermore, by choosing different parameter values that define Gaussian lateral connectivity, Norris is able to significantly improve the fit to the data, but there is still a gap between the simulated TCB and FB and those shown in Fig. 1. With a new form of dynamic connections and a random element in global inhibition, our model has essentially closed this gap.

Brown and Cooke (1998) present a different model of auditory streaming, also based on synchronous oscillations. They use a more realistic model of auditory periphery and include an onset map. There is no explicit representation of external time, and each frequency channel is represented by a single oscillator described by a sine circle map which shows a chaotic response. The oscillators representing different frequencies are fully connected. Different TRTs and frequency distances trigger different levels of onset responses, which are used in a weight update rule to produce different model outputs. They have compared the model results with the listener results in the study by Beauvois and Meddis (1991), and obtained a reasonable, but not close, match. It is unclear how well their model can reproduce the TCB and the FB in Fig. 1.

Inspired by the rhythmic effects of auditory streaming, Baird (1997) develops a model using a network of oscillators that keeps track of different rhythms. These oscillators are synchronized to the salient rhythms of external stimuli, hence naturally sensitive to TRT (see also Large and Jones 1999). Oscillations generate rhythmic expectation, which directs attention to subsequent tones. Rhythmic attention groups those tones that conform to the expectation, and deviations from the expectation cause the formation of a new stream. The evaluation of the model is qualitative, and it is questionable whether it can simulate the TCB and the FB. A recent model by Almonte et al. (2005) approaches the streaming phenomenon differently. Their model is composed of two dynamical systems. The first system transforms an input into a neural field, and its spatiotemporal activity is integrated into an input signal to the second system that performs dynamical classification. The output of the classification system is in the form of a one-stream percept (the coherent state), a two-stream percept (the segregated state), and an ambiguous percept identified with a bistable state (with two stable fixed points). Their system has been systematically evaluated and its results match well to van Noorden’s data. On the other hand, the complexity of the dynamical systems and the specificity of the model to alternating tone sequences make its scalability to general ASA doubtful.

Several other models have been proposed to account for the auditory streaming phenomenon. Beauvois and Meddis (1991, 1996) describe a model that achieves streaming primarily on the basis of peripheral analysis. After processing by a bank of auditory filters, an alternating tone sequence activates two corresponding frequency channels. Different channels compete and all except the winning channel reduce their activities. A random bias is built into each channel to cause the winning channel to switch between the two channels corresponding to low and high tones. The model considers the output in the segregated state if the two corresponding channels show different levels of activity; otherwise the output is considered to be in the coherent state. Using this model, Beauvois and Meddis (1996) are able to obtain a close match with the TCB and the FB shown in Fig.  1, with the exception that the model does not yield a TCB when TRT is greater than 190 ms. McCabe and Denham (1997) propose a competitive neural network that includes a foreground layer and a background layer. These two layers have inhibitory interactions between their frequency channels. In addition, each layer also includes self-inhibition. Inhibition is graded, depending on frequency proximity. They have shown that their model is able to produce streaming effects sensitive to frequency difference and TRT. In particular, their model closely fits a set of streaming data from Beauvois and Meddis (1991), although no direct comparison with the data in Fig.  1 is made.

In addition to interpreting streaming as oscillatory correlation, our model differs from the above models in an important way: The representation of time. We use an explicit time dimension in the form of delay lines, which keeps a recent history of an acoustic input. Time is implicitly represented in the above models, either in terms of the time course of a neuronal response or the period of rhythmic attention. From an information processing point of view, we would argue that lacking an explicit representation of time limits the generality of such models in dealing with naturalistic acoustic input such as speech (Brown and Wang 2006). We will discuss the plausibility of such a representation in the next section.

Discussion

This study extends the previous oscillation models by Wang (1996) and Norris (2003). In order to accurately simulate the temporal coherence boundary and the fission boundary, we have introduced two mechanisms into oscillator networks for auditory streaming. The first is dynamical change to lateral excitatory connections. Specifically, the strengths of lateral connections along the frequency axis are dependent on the rhythm of the external input so that faster rhythms lead to weaker connections in frequency, hence encouraging segregation. The second mechanism adds a random element to the weight of global inhibition. This element produces a stochastic switch between the state of coherence and the state of segregation within a range of frequency separation and tone repetition time. With these mechanisms, our oscillatory correlation model yields a close fit to the quantitative data of auditory streaming.

These extensions mainly influence the spread of the Gaussian connectivity depending on the rhythm of the input. As a result, our model is expected to exhibit the other phenomena of auditory streaming simulated in Wang (1996), i.e., alternating sequences of frequency modulation tones, sequential capturing and competition among different organizations, because these phenomena involve frequency relationships, not temporal relationships, between tones. Grouping by onset synchrony simulated by Norris (2003) is also expected to hold in our network with the addition of an onset map assumed in our network. In addition, our dynamic connections provide a potential mechanism to account for the well-known effect of stream bias adaptation, or the gradual build up and decay of auditory streaming over several seconds. The current model does not consider the dynamical process of the weight change in Eq. 3, which must take a certain amount of time to realize in any physical system. A bias adaptation effect might then be explained by assuming strong initial connections that are gradually reduced to the steady frequency spread of Eq. 3 triggered by the detection of some external rhythm. Using lateral dynamic connections as a mechanism to account for stream bias adaptation is an alternative to Norris’s method which uses another set of connections between oscillators (Norris 2003).

It is worth noting that the basic oscillatory correlation architecture of Fig.  2 for auditory segregation has been extended to deal with segregation of real acoustic sources. Wang and Brown (1999) introduce a two-layer network of relaxation oscillators to separate speech from interference, employing a realistic model of the auditory periphery. The first oscillator layer separates an auditory scene into a collection of auditory segments, each corresponding to a contiguous region on a time-frequency network akin to that of Fig.  2. The second layer groups the segments from the first layer into a foreground stream corresponding to target speech and a background stream corresponding to interference on the basis of a periodicity analysis. Pichevar and Rouat (2007) recently propose a related two-layer network for speech segregation. The input to their network is auditory features derived from a cochleagram and an amplitude modulation spectrum. Their first layer is similar to that in Wang and Brown, but with connections that reflect harmonic relations. The second layer is one-dimensional, with each oscillator representing a frequency channel, with a global inhibitor. The oscillators in the second layer are fully connected, but the connection weights are dynamically adjusted according to the temporal correlation between the activities of different frequency channels. The output from the second layer gives the results of separation in terms of synchrony and desynchrony.

In what follows, we discuss the biological plausibility of the oscillatory correlation theory as well as the important issues of how to represent time and auditory attention.

Biological plausibility

The biological foundation of the oscillatory correlation theory is the assumption of synchronous oscillations. In the auditory system, early experiments reveal oscillations of evoked potentials in the gamma frequency range (Galambos et al. 1981; Madler and Pöppel 1987; Mäkelä and Hari 1987). Ribary et al. (1991) and Llinas and Ribary (1993) observed gamma oscillations in localized brain regions at the cortical and thalamic levels of the auditory system. In addition, such oscillations elicited by appropriate stimuli are synchronized over a considerable range of the auditory system. Joliot et al. (1994) further reported that coherent oscillations are correlated with perceptual grouping of clicks.

Synchronous oscillations are also found from the recordings of cortical neurons (deCharms and Merzenich 1996; Maldonado and Gerstein 1996; Brosch et al. 2002). Barth and MacDonald (1996) find evidence suggesting that coherent oscillations in the auditory cortex are caused by intracortical connections. Brosch et al. (2002) find that, in the monkey auditory cortex, stimulus-dependent gamma oscillations correlate with the match between stimulus frequency and the preferred frequency of a cortical unit. In addition, synchronization occurs between different cortical sites depending on their distance and their preferred frequencies. Edwards et al. (2005) recently recorded human responses from the frontal and temporal cortices of awake neurosurgical patients. They find gamma activity in response to salient auditory stimuli.

Coherent oscillations are found to correlate with attentional control. Fries et al. (2001) find that neurons activated by an attended visual stimulus produce increased synchronization in the gamma frequency range. A similar finding is made by Taylor et al. (2005) who observe that attention enhances gamma oscillations in the visual area V4 of monkeys, indicating stronger synchronization of V4 neurons associated with the attended object. In a visual change detection task, Womenlsdorf et al. (2006) recently report that the level of gamma band synchronization of V4 neurons activated by an attended stimulus predicts monkeys’ reaction times for performing the task.

Representation of time

A major characteristic of our oscillatory correlation model lies in the representation of time as a separate dimension, on a par with the representation of frequency. A separate dimension of time is implicitly assumed in Bregman’s ASA account of auditory organization (Bregman 1990), and commonly used in speech and other acoustic processing literature. On the other hand, time also plays a fundamental role of binding in our model: Different streams are segregated in time. Furthermore, temporal properties of stimulus onset and offset are perceptual cues for ASA (see Section “Introduction”). The multiple roles of time need to be clarified as they raise potential difficulties for the oscillation correlation theory (Shadlen and Movshon 1999; Brown 2003).

Wang (2005) distinguishes between external time and internal time; the former refers to physical time and the latter the dynamical process of oscillatory correlation. He argues that these two kinds of time can coexist by adopting a place coding of external time like that depicted in Fig.  2. As shown in the present study as well as in Wang (1996) and Norris (2003), once external time is converted into a spatial dimension, oscillatory correlation can take place in auditory organization much like in visual organization where an object is naturally represented in spatial dimensions. As for grouping by common onset and offset, onset/offset detectors exist in the auditory system (Popper and Fay 1992) and have been assumed in previous auditory models. As demonstrated by Norris (2003), with such detectors auditory organization based on common onset and offset is not unlike organization using other ASA cues.

The linear axis of external time created by systematic delays shown in Fig.  2 is meant to be a model of STM. Other STM models include decay traces that encode time implicitly through the time course (via time constants) of neural responses, and exponential kernels that convert time into a logarithmic axis (Wang 2003). A logarithmic axis of time, where more recent history is coded with higher temporal resolution, allows past events to fade away gradually, hence more elegant than the linear axis. Figure 7 illustrates a logarithmic axis of time, where an oscillator represents a progressively longer interval for a deeper past. It is worth noting that a model of STM is indispensable for general temporal pattern processing, and exponential kernels including gamma kernels have been proposed to sample external time (Wang 2003). Such a time representation has rather interesting resemblance to how frequency is represented by auditory filters such as gammatone filters (Wang and Brown 2006).

Fig. 7.

Logarithmic axis of time. The time dimension is sampled logarithmically so that more units are devoted to representing a recent past

The supposed place coding for auditory streaming in our model requires time delays on the order of hundreds of milliseconds to even seconds. There is strong physiological evidence for systematic delays in the computation of interaural time difference for sound localization (Popper and Fay 1992). However, such delays are in the microseconds range. Systematic delays are also assumed in the autocorrelation model of pitch detection (de Cheveigne 2006), and these delays are on the order of milliseconds, perhaps as long as 20 ms. While the physiological notion of spectrotemporal receptive fields (Rutkowski et al. 2002; Linden et al. 2003) is consistent with the use of long delays (or latencies) to code time, direct physiological support is yet to be established for a place code of external time (see Brown and Wang 2006).

Whether or not place coding of external time, or a temporotopic map, exists in the auditory system, STM in the range of milliseconds to seconds (Crooks and Stein 1991) has to be coded in the brain somehow. Baird’s model suggests an alternative representation of time where intrinsic oscillators are entrained to rhythms of external input (Baird 1997; see also Large and Jones 1999). In this representation, external time at multiple scales is coded by oscillators of various intrinsic frequencies. Although intriguing, how to represent acoustic stimuli lacking regular periodicities (e.g., unvoiced speech) is unclear in this representation. Also, physiological support for this representation of time is no stronger than that for a temporotopic map.

Shifting synchronization theory

In addition to modeling several aspects of auditory streaming, Wang (1996) proposed a neurocomputational theory, called shifting synchronization theory, for explaining primitive stream segregation effects. The basic assertion of the theory is that the neural basis of stream segregation is oscillatory correlation. More specifically, a set of tones forms the same stream if their underlying oscillators synchronize, and the tones form different streams if the underlying oscillators organize into multiple oscillator assemblies that desynchronize from one another. The theory is used to explain the loss of order between successive tones when alternating tones are segregated into two streams.

An aspect of the shifting synchronization theory involves auditory attention. In Wang (1996), it is claimed that attention is directed to a stream when the stream’s corresponding oscillators are in the active phase. Wrigley and Brown (2004) point out that such an attentional process leads to a rapid switch of attention between the two streams and all streams are equally attended to, which seems incompatible with the observation that, when segregation occurs, listeners tend to perceive one stream as dominant at a time. Instead, they proposed a model of auditory attention that selects one stream using an interactive loop between an oscillator network for stream segregation, and an attentional unit called attentional leaky integrator. The interactive loop is subject to modulation from an intrinsic, “endogenous” attentional interest that decides which stream to select. A stream is considered to be attended to if its oscillatory activity resonates with that of the attentional unit. Their model can simulate several streaming phenomena such as two-tone streaming in the presence of a competing task.

In light of Wrigley and Brown’s study and other developments since Wang (1996), the shifting synchronization theory requires a revision when it comes to auditory attention. The revision involves a division between selective attention and divided attention (Pashler 1998). Primitive auditory segregation really involves divided attention rather than selective attention. Divided attention can hold multiple items within the attentional span, or attention is divided among attended items. Given this, we now claim that there is no rapid shifting of attention among different oscillator assemblies corresponding to multiple segregated streams, which coexist in the attentional span. Instead, different oscillation phases serve to distinguish between the items, or objects, within the attentional span. Given that the shifting synchronization theory is concerned with primitive ASA, auditory selective attention requires a separate process like the Wrigley and Brown model. In the context of visual object selection, Wang (1999) proposed a model that selects one or a small number of objects from the output of a LEGION network using slow global competition. Such selection among multiple oscillator assemblies corresponds to a process of selective attention, whereas LEGION segregation corresponds to a process of divided attention.