Abstract
We study spike–burst neural activity and investigate its transitions to synchronized states under electrical coupling. Our reported results include the following: (1) Synchronization of spike–burst activity is a multi-time scale phenomenon and burst synchrony is easier to achieve than spike synchrony. (2) Synchrony of networks with time-delayed connections can be achieved at lower coupling strengths than within the same network with instantaneous couplings. (3) The introduction of parameter dispersion into the network destroys the existence of synchrony in the strict sense, but the network dynamics in major regimes of the parameter space can still be effectively captured by a mean field approach if the couplings are excitatory. Our results on synchronization of spiking networks are general of nature and will aid in the development of minimal models of neuronal populations. The latter are the building blocks of large scale brain networks relevant for cognitive processing.
Keywords: Synchronization, Neural network, Spiking, Bursting, Dispersion, Time delay
Introduction
Neuronal spiking–bursting behaviors play an important role in information processing in the brain on a variety of scales in space and time. Relevant for cognitive function, large scale neural network dynamics is thought to be its primary neuronal correlate in the brain (Bressler and Kelso 2001; Bressler and Tognoli 2006; Bullmore et al. 1996; Jirsa 2004; McIntosh 2000; Mesulam 1998; Mountcastle 1998). To understand the neural basis of cognition, theoretical and analytical means must be developed which are specifically targeted to the properties of large scale network dynamics (see Jirsa and McIntosh 2007) for a comprehensive overview of the field). The functional expression of a cognitive operation seems to require the co-activation of certain subnetworks. Such co-activation does not necessarily require a simultaneous activation of all network components, but may be represented in a characteristic spatio-temporal network dynamics with both simultaneous and sequential activations. Examples of large scale neural dynamics include the slow (<1 Hz) oscillations, observed in the electroencephalograpic (EEG) recordings of naturally sleeping humans and other mammals, which are considered to be the result of a synchronized spike–burst activity of billions of neurons in the brain (Amzica and Steriade 1998; Steriade et al. 1993). Some clinical disorders, such as Parkinson’s disease, schizophrenia, and drug addiction, are found to be originated from some imbalance in these neurons (Koob et al. 1987; Ljungberg et al. 1992; Weinberger 1987). Interestingly, some types of epileptic seizures are also believed to depend on rhythmic burst firing in thalamic and thalamocortical circuits (Avoli et al. 1990; Hosford et al. 1992; Snead 1995).
To account for large scale brain dynamics on a computationally tractable level, large scale models have the implicit assumption to be based upon neurocomputational units (Breakspear and Jirsa 2007), which are more macroscopic than single neurons. The macroscopic units are thought of as populations of neurons, which display a sufficiently similar behavior. In the current context, "sufficiently similar" means that either the details of neuronal spike firings are irrelevant for the large scale network dynamics or that the neuronal population displays close to synchronized behavior. In the former case, so-called mean-field approximations, well-known from statistical physics, lead to firing rate models. Though its basic assumptions are mostly not rigorously justified, it often provides an astonishingly good qualitative insight into the description of many models. The dissenting view posits that the information is encoded in the interactions among spikes and hence spike correlations must not be ignored (for detailed discussions of neuronal encoding see (Koch 1999)). Considerable evidence exists that single cells may fire spikes at predictable intervals as long as 200 ms with a precision of 1 ms (Abeles et al. 1993). The latter is the key observation leading to the theory of synfire chains for cortical processing (Abeles 1991). Certain cells in the mammal brain, for example neurons in the thalamus during the periods of drowsiness, inattentiveness and sleep, are known to exhibit spiking–bursting activity (McCormick and Fesser 1990; Scherman et al. 1986; Steriade and Llinas 1988; Steriade et al. 1993). Midbrain dopaminergic neurons, which have great importance in different aspects of brain function such as reward-mediated learning, movement control, cognition and motivation (Schultz 2000), also exhibit two modes of action-potential firing: spike-firing and burst-firing (Freeman et al. 1985; Grace and Bunney 1984). As of today, it is not clear to what degree the neural system uses firing rate or spike coding mechanisms. Experimental evidence exists for both and accumulates with every day (Koch 1999). Most likely a synchronized neural dynamics will play a lesser role for extended periods of time during which a large scale synchronization is more likely to indicate pathological network activity such as epilepsy (see Milton et al. 2007). However, the understanding of the conditions leading to the emergence of synchronization will likely be important to understanding the neurocognitive processes such as feature binding (Crick and Koch 1990; Singer and Gary 1995) and multisensory integration (Treisman 1986; Von Stein et al. 1999). In fact, the onset of coherent oscillatory activity has been interpreted to be fundamental for the formation of higher-order percepts (Bressler 1990).
To shed light on the relevant properties of the building blocks of large scale networks, i.e., neuronal populations, we depart from the perspective of synchronously firing ensembles of spike–burst neurons. We wish to systematically discuss the influences of coupling strength, time delay and dispersion including the two extreme cases of a randomly firing and a fully synchronized population. Our motivation is to gain some insight into the relevance of these factors with the ultimate goal to obtain a reduced description of neuronal population dynamics. Synchronization of spike–burst is a multi-time scaled phenomenon and may involve synchrony of individual spikes, and/or synchrony of bursts, or both. There have been some theoretical studies on the classification of bursting behaviors from neuron models (Izhikevich 2000; Rinzel and Lee 1987). The bursting activity is typically viewed as being the result of interaction between the multi-time scaled (fast and slow) subsystems and the slow subsystem is considered responsible for switching the dynamics of the fast subsystem between rest and bursting states. In a coupled system, burst synchronization is more often found easier to achieve than spike synchronization. However, the question of systematic transition to synchronized state and the order of synchronization in multi-time scaled system of coupled oscillators remains partly unexplored. In an instantaneously coupled system of certain chaotic oscillators, as the coupling strength is increased from zero, the oscillations become less and less incoherent, and finally completely coherent – first, synchronization in phase and then synchronization in amplitude emerge (Pecora and Carroll 1990; Rosenblum et al. 1996). The question of general interest is then about the role of different time-scales (as in neurons) and coupling strength on coherence of oscillations in a coupled system. Besides connectivity, two major determinants for network synchronization are time delay and parameter dispersion. Despite large time delays, neural synchronization was reported to occur between the brain areas separated by distances up to several centimeters (Desmedt and Tomberg 1994; Miltner et al. 1999; Tallon-Baudry 2001). Visuomotor integration was found to be associated with zero time-lag synchronization of signals recorded from the visual and parietal areas, and motor and parietal areas of the awake cat (Roelfsema et al. 1997). Dispersion on the other hand destroys the existence of the synchronized state in its strict sense, but still allows for clustered solutions. An empirical example can be found in CA1 stratum oriens interneurones in the hippocampus. Evidence from electrophysiological recordings show that hypothermia induced seizures in developing rats causes an increase in the variance of the resting membrane potential without causing a change in the mean resting potential (Aradi and Soltesz 2002).
In this article, we will discuss the synchronization behavior of networks of oscillators with multiple time-scales from these three different perspectives. In the next two sections we follow (Dhamala et al. 2004a; Dhamala et al. 2004b) and review their findings on the effects of coupling strength on the coherence of oscillations, in general, and the order of synchronization of slow and fast dynamics in an instantaneously coupled system of neurons with spiking–bursting behaviors. We discuss the synchronization behavior of networks with time delays in the couplings among the oscillators, for instance via finite transmission speeds along the coupling pathways. In most scenarios, time delays are viewed as detrimental for the synchronization of a network (MacDonald 1989), but this may prove different for oscillators with multiple time scales as considered here. Finally in the last section, we study the effects of parameter dispersion on the synchronization behavior of globally and instantaneously coupled spike–burst neurons.
Burst and spike synchrony
Using a coupled system of Hindmarsh–Rose (Hindmarsh and Rose 1982; 1984) neurons, we present evidence that the coupling strength can increase incoherence first and then induce two different transitions to synchronized states, one associated with burst (slow time-scale dynamics) and the other with spikes (fast time-scale dynamics). A multi-time scaled dynamical system (for example, a neuron with spiking–bursting behaviors) can be written in a singularly perturbed form: 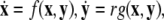 where
where  is a vector of fast variables,
is a vector of fast variables, 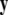 is a vector of slow variables that modulates the fast activity, and r ≪ 1 is a ratio of fast/slow time scales. In such a system, one usually observes an almost instant jump in
is a vector of slow variables that modulates the fast activity, and r ≪ 1 is a ratio of fast/slow time scales. In such a system, one usually observes an almost instant jump in 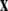 -components followed by a finite speed motion in the
-components followed by a finite speed motion in the 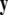 -components. Setting r = 0 yields the equations:
-components. Setting r = 0 yields the equations: 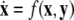 for the fast subsystem with a constraint,
for the fast subsystem with a constraint, 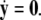 Equivalently, rescaling time with τ = rt and setting r = 0, one obtains the equation for the slow subsystem as:
Equivalently, rescaling time with τ = rt and setting r = 0, one obtains the equation for the slow subsystem as: 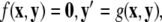 where ′ = d/dτ. Note that r does not appear in the expression for
where ′ = d/dτ. Note that r does not appear in the expression for 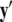 due to the rescaling of time. Here,
due to the rescaling of time. Here, 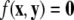 represents the slow manifold. The here outlined decomposition into two time scales is useful, because the slow and fast subsystems can be treated separately and, as a consequence, their common asymptotic state can be used to estimate the state of the full system.
represents the slow manifold. The here outlined decomposition into two time scales is useful, because the slow and fast subsystems can be treated separately and, as a consequence, their common asymptotic state can be used to estimate the state of the full system.
As an example of a multi-time scaled system, we consider the Hindmarsh–Rose neuron described by the following equations of motion (Hindmarsh and Rose 1984):
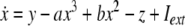 |
1 |
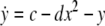 |
2 |
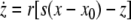 |
3 |
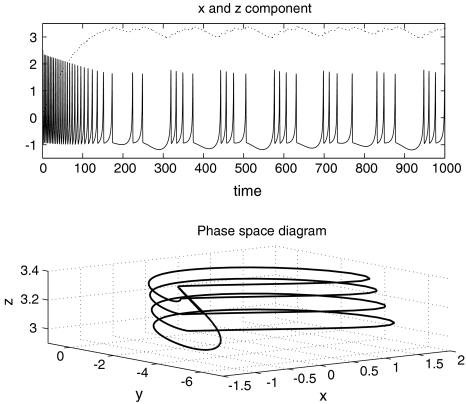
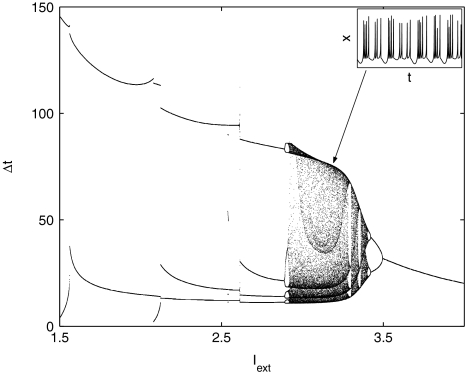
where x is the membrane potential, y is associated with the fast current, Na+ or K+, and z with the slow current, for example, Ca2+. Here, a = 1.0, b = 3.0, c = 1.0, d = 5.0, s = 4.0, r = 0.006, x0 = −1.60, and Iext is the external current input. x, y are fast variables and z is a slow variable. r is the ratio of fast/slow time scales. This system exhibits a multi-time scaled burst–spike chaotic behavior for 2.92 < Iext < 3.40, as shown in Fig. 1. Non-chaotic spikes–burst behavior is obtained for Iext > 1.32 and a stable fixed point exists for Iext < 1.32. The bifurcation diagram is plotted in Fig. 2, in which the time interval (Δt) between spikes is plotted against Iext.
Fig. 1.
Hindmarsh–Rose neuron model with Iext = 3.25. The time series of the x-component (solid line) and the z-component (dotted line) are plotted in the top graph. The axes are in arbitrary units. The bottom graph shows the phase portrait
Fig. 2.
Bifurcation diagram. The time interval (Δt) between spikes is plotted against Iext. The chaotic regime extends as 2.92 < Iext < 3.40. The inserts shows a characteristic time series of the x-component
Now we consider two Hindmarsh–Rose neurons, which are coupled through an instantaneous and linear difference term via the x-component. Such coupling is typically considered to be of electric nature and connects neurons via gap junctions. The resulting equations read
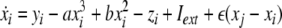 |
4 |
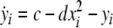 |
5 |
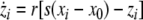 |
6 |
where 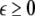 is the coupling strength and i = 1, 2, j = 2,1 are the indices. The synchronized state will then be represented by the equations of the uncoupled dynamics, (1-3) as the differences |x1 − x2|,|y1 − y2|,|z1 − z2| vanish in the limit of t → ∞. This occurs when the synchronization manifold becomes completely stable. If we now transform to x⊥ = x1 − x2, y⊥ = y1 − y2, and z⊥ = z1 − z2, in the limit when these variables are very small (x21 − x22 ≈ 2xx⊥ and x31 − x32 ≈ 3x2x⊥), the motion transverse to the synchronization manifold can be described by the following equations:
is the coupling strength and i = 1, 2, j = 2,1 are the indices. The synchronized state will then be represented by the equations of the uncoupled dynamics, (1-3) as the differences |x1 − x2|,|y1 − y2|,|z1 − z2| vanish in the limit of t → ∞. This occurs when the synchronization manifold becomes completely stable. If we now transform to x⊥ = x1 − x2, y⊥ = y1 − y2, and z⊥ = z1 − z2, in the limit when these variables are very small (x21 − x22 ≈ 2xx⊥ and x31 − x32 ≈ 3x2x⊥), the motion transverse to the synchronization manifold can be described by the following equations:
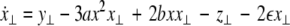 |
7 |
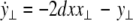 |
8 |
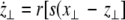 |
9 |
The solutions of the Eqs. 7–9 will tell us about the stability whether the variations (x⊥,y⊥,z⊥) will grow or damp out as t → ∞. The minimal condition for stability of the synchronized state represented by Eqs. 1–3 is to have the Lyapunov exponents associated with Eqs. (7–9) be negative for the transverse subsystem. By solving Eqs. (7–9) in combination with Eqs. (1–3), we determine the transverse Lyapunov exponents, two of those shown in Fig. 3. As the coupling strength 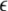 is increased from zero, the initially zero exponent starts to increase, reaches a peak, and then starts to decrease along with the other positive exponent. These exponents cross zeros at two different coupling strengths and both become negative. It implies that coupling may not always increase coherence, instead it may decrease coherence of oscillations in an instantaneously coupled system. This is also evidence that, in a multi-time scaled system of coupled oscillators, a low coupling strength makes the system more incoherent and higher coupling strengths can synchronize slow subsystem, or both the slow and fast subsystems. In fact, Fig. 3 nicely underscores this point. The first transition occurs at
is increased from zero, the initially zero exponent starts to increase, reaches a peak, and then starts to decrease along with the other positive exponent. These exponents cross zeros at two different coupling strengths and both become negative. It implies that coupling may not always increase coherence, instead it may decrease coherence of oscillations in an instantaneously coupled system. This is also evidence that, in a multi-time scaled system of coupled oscillators, a low coupling strength makes the system more incoherent and higher coupling strengths can synchronize slow subsystem, or both the slow and fast subsystems. In fact, Fig. 3 nicely underscores this point. The first transition occurs at 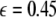 and the second transition at
and the second transition at 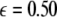 corresponding, respectively, to the synchronization of the slow and fast oscillations of the coupled system. We now consider the slow subsystem and estimate the coupling strength of its transition to the synchronized state with an approximate mathematical approach. When we rescale the time with τ = rt and set r → 0 in Eqs. 1–3 and 7–9, then the resulting equations represent the slow subsystem, whose asymptotic state (< >∞) is described by z′ = [s(x∞ − x0) − z], and z′⊥ = sx⊥∞ − z⊥ with the constraints: 0 = c − (d − b)x2∞ − ax3∞ − z∞ + Iext, and
corresponding, respectively, to the synchronization of the slow and fast oscillations of the coupled system. We now consider the slow subsystem and estimate the coupling strength of its transition to the synchronized state with an approximate mathematical approach. When we rescale the time with τ = rt and set r → 0 in Eqs. 1–3 and 7–9, then the resulting equations represent the slow subsystem, whose asymptotic state (< >∞) is described by z′ = [s(x∞ − x0) − z], and z′⊥ = sx⊥∞ − z⊥ with the constraints: 0 = c − (d − b)x2∞ − ax3∞ − z∞ + Iext, and 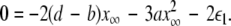 Here
Here 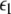 is the positive coupling strength beyond which, z⊥∞→ 0. Intuitively, z∞ ≈ < z > and from the asymptotic state of the attractor in numerics, < z > ≈ 3.15. From the equations of the constraints, this yields
is the positive coupling strength beyond which, z⊥∞→ 0. Intuitively, z∞ ≈ < z > and from the asymptotic state of the attractor in numerics, < z > ≈ 3.15. From the equations of the constraints, this yields 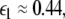 which compares very well with
which compares very well with 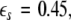 the first transition in Fig. 3. This alternative analytical approach also confirms that the first transition is associated with the slow subsystem.
the first transition in Fig. 3. This alternative analytical approach also confirms that the first transition is associated with the slow subsystem.
Fig. 3.
Transverse Lyapunov exponents. As the coupling strength 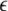 increases, the first two largest transverse Lyapunov exponents are plotted. The insert shows a magnification of the regime, where they cross the zero line
increases, the first two largest transverse Lyapunov exponents are plotted. The insert shows a magnification of the regime, where they cross the zero line
In general, for an N-neuron network, one can follow a similar scheme as used by (Dhamala et al. 2004b; Pecora and Carroll 1998) who consider the variations transverse to the synchronization manifold. For example, let us consider an N-neuron network described by the following equation:
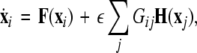 |
10 |
where 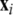 is the dynamical variable vector (xi,yi,zi) for site i in an N-oscillator array. The isolated dynamics for each neuron is described by
is the dynamical variable vector (xi,yi,zi) for site i in an N-oscillator array. The isolated dynamics for each neuron is described by 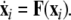
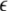 is the coupling strength,
is the coupling strength, 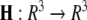 is the coupling function, and G is an arbitrary N × N-matrix which determines the connectivity. The N − 1 constraints
is the coupling function, and G is an arbitrary N × N-matrix which determines the connectivity. The N − 1 constraints 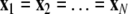 define the synchronization manifold. To maintain invariance of the synchronization manifold, the rows of Gij are chosen such that: ∑Nj = 1Gij = 0. Considering perturbations to the synchronized state
define the synchronization manifold. To maintain invariance of the synchronization manifold, the rows of Gij are chosen such that: ∑Nj = 1Gij = 0. Considering perturbations to the synchronized state 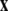 and diagonalizing
and diagonalizing 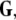 we arrive at the generic variational equation for the transverse directions, the so-called Master stability equation:
we arrive at the generic variational equation for the transverse directions, the so-called Master stability equation:  where (α + iβ) is an eigenvalue of
where (α + iβ) is an eigenvalue of 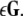
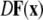 is the Jacobian matrix evaluated on the synchronization manifold and
is the Jacobian matrix evaluated on the synchronization manifold and 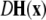 is an 3 × 3-matrix that determines which of the oscillator components are coupled. For example, for x-component coupling in a network of Hindmarsh–Rose neurons, only the first element of the 3 × 3-matrix is 1 and all the other are 0. Separating
is an 3 × 3-matrix that determines which of the oscillator components are coupled. For example, for x-component coupling in a network of Hindmarsh–Rose neurons, only the first element of the 3 × 3-matrix is 1 and all the other are 0. Separating 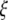 into real part
into real part 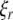 and imaginary part
and imaginary part 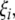 we get
we get
 |
11 |
 |
12 |
Given the coupling matrix 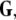 the transverse Lyapunov exponents can be estimated by solving Eqs. 11–12. The variations of the two maximum transverse Lyapunov exponents with
the transverse Lyapunov exponents can be estimated by solving Eqs. 11–12. The variations of the two maximum transverse Lyapunov exponents with 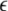 can determine the transitions to synchronized states on different time scale oscillations. However, to achieve just the minimal condition for stability of the synchronized state, only the first maximum Lyapunov exponent needs to be checked for a negative value. The calculation of Lyapunov exponents can be done for a network of N neurons in a similar way. (Dhamala et al. 2004b) carried out the numerical simulation for an electrically coupled nearest neighbor network of eight-neurons and also found the two characteristic transition points for spike and burst synchronization.
can determine the transitions to synchronized states on different time scale oscillations. However, to achieve just the minimal condition for stability of the synchronized state, only the first maximum Lyapunov exponent needs to be checked for a negative value. The calculation of Lyapunov exponents can be done for a network of N neurons in a similar way. (Dhamala et al. 2004b) carried out the numerical simulation for an electrically coupled nearest neighbor network of eight-neurons and also found the two characteristic transition points for spike and burst synchronization.
The primary finding is that coupling does not always decrease the Lyapunov exponents, but instead, it decreases the degree of synchronization in multi-scale dynamical systems like coupled neurons. Only for a further increase in the coupling, the system then synchronizes. There is an order of synchrony for increasing coupling values: first synchrony on the slow time-scale oscillations (for example, burst synchrony) and then synchrony on the fast time-scale oscillations (spike synchrony).
Enhancement of neural synchrony by time delay
To study the effect of time delays in the coupling matrix, we consider two Hindmarsh–Rose neurons coupled linearly via x-component as follows
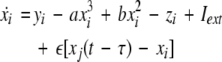 |
13 |
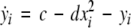 |
14 |
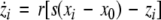 |
15 |
where 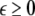 is the coupling strength, τ ≥ 0 is a measure of the time delay, and the indices i = 1, 2, j = 2,1. The first neuron receives the signal from the second neuron after a time delay τ and vice versa. This time delay will generally not be caused by the synaptic transmission, since gap junctions are fast, but will be due to signal propagation along axons and dendrites. The dynamics of the synchronized state, (x1,y1,z1) = (x2,y2,z2), will then be represented by:
is the coupling strength, τ ≥ 0 is a measure of the time delay, and the indices i = 1, 2, j = 2,1. The first neuron receives the signal from the second neuron after a time delay τ and vice versa. This time delay will generally not be caused by the synaptic transmission, since gap junctions are fast, but will be due to signal propagation along axons and dendrites. The dynamics of the synchronized state, (x1,y1,z1) = (x2,y2,z2), will then be represented by:
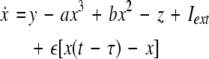 |
16 |
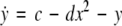 |
17 |
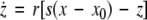 |
18 |
As in the previous section, we now transform to x⊥ = x1 − x2, y⊥ = y1 − y2, and z⊥ = z1 − z2, in the limit when these variables are very small. Then the motion transverse to the synchronization manifold can be described by the following equations:
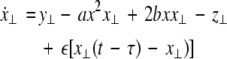 |
19 |
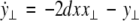 |
20 |
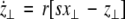 |
21 |
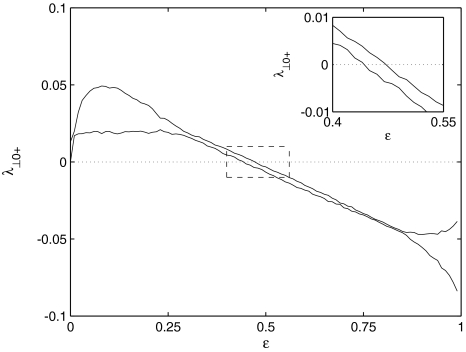
The solutions of Eqs. 19–21 determine the stability whether the variations (x⊥,y⊥,z⊥) will grow or shrink as t → ∞. By solving the latter equations together with Eqs. 16–18, we determine the maximum transverse Lyapunov exponent for τ ≥ 0. Figure 4 is a plot of the exponent in the 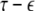 parameter space. Here, we see that even at very low coupling strengths, there is a region of stability (as shown by the arrow) for synchronized states. In contrast, there is no synchrony for
parameter space. Here, we see that even at very low coupling strengths, there is a region of stability (as shown by the arrow) for synchronized states. In contrast, there is no synchrony for 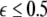 if the coupling is instantaneous, that is τ = 0. This underscores the point that time-delay can also enhance synchrony in multi-time scale oscillations such as coupled Hindmarsh–Rose neurons.
if the coupling is instantaneous, that is τ = 0. This underscores the point that time-delay can also enhance synchrony in multi-time scale oscillations such as coupled Hindmarsh–Rose neurons.
Fig. 4.
Stability diagram. On the top, the value of the largest transverse Lyapunov exponent of a two neuron network is plotted as a function of coupling strength and no time delay, τ = 0. Below, the stability diagram is shown as a function of coupling and time delay. The arrow points at a region of negative Lyapunov exponents for small coupling and non-zero time delay
To generalize our results, we formulate a general master stability function including a time-delay in the coupling, but no self-delay term:
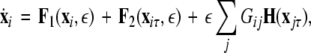 |
22 |
where, for an x-component coupling, for instance, 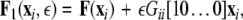 and
and 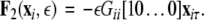 To simplify our notation, we indicate the presence of time delay τ in the index, that is
To simplify our notation, we indicate the presence of time delay τ in the index, that is 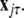 The synchronized state is:
The synchronized state is: 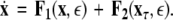 This results in the following master stability equations:
This results in the following master stability equations:
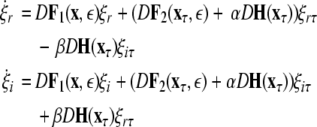 |
23 |
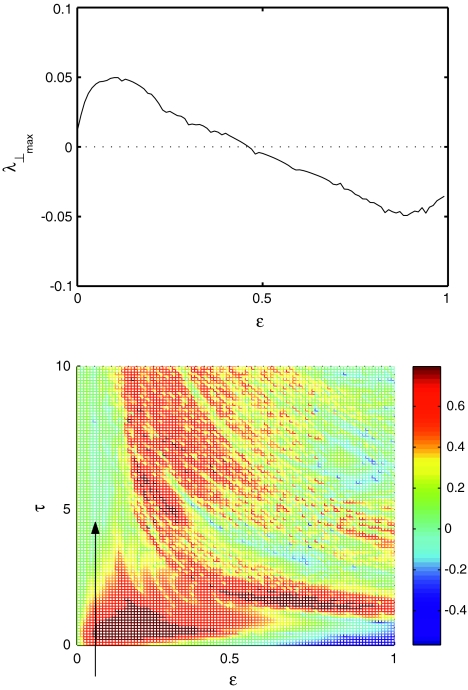
The maximum transverse Lyapunov exponent (λ⊥max) can be estimated from these equations. The synchronized state also depends on 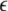 value. Figure 5 shows the master stability curves for such a system at
value. Figure 5 shows the master stability curves for such a system at 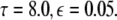 There is a stable region close to the α-axis near the origin in the negative side. This is evidence that time delay does not always destabilize synchronized states, but also it stabilizes the synchronized states for the right choice of parameters. Thus, the phenomenon of enhancement of synchrony by delay can be observed in a coupled system of N Hindmarsh–Rose neurons. The first more detailed analysis of synchrony enhancement via time delay has been given in (Dhamala et al. 2004a).
There is a stable region close to the α-axis near the origin in the negative side. This is evidence that time delay does not always destabilize synchronized states, but also it stabilizes the synchronized states for the right choice of parameters. Thus, the phenomenon of enhancement of synchrony by delay can be observed in a coupled system of N Hindmarsh–Rose neurons. The first more detailed analysis of synchrony enhancement via time delay has been given in (Dhamala et al. 2004a).
Fig. 5.
Master stability for network with time delay τ = 0. The contour lines of the largest transverse Lyapunov exponent is plotted as a function of connectivity. There is a small region of stability for −1 < α < 0
In conclusion, we have presented the phenomenon of enhancement of spike synchrony by time delay in a coupled system of neurons. Even for significant time delays, a stable synchronized state exists at a very low coupling strength, which may account for long-range neural synchrony observed in experiments.
Weak synchrony and clustering in networks with global coupling and parameter dispersion
The introduction of dispersion destroys the synchronized network state in the strict sense, i.e., the differences |x1 − x2|,|y1 − y2|,|z1 − z2| between any two neurons will not vanish in the limit of t → ∞. However, networks with dispersed parameters may still show low-dimensional dynamics including phase clustering and spatiotemporal quasiperiodic and chaotic dynamics (Matthews and Strogatz 1990). For this reason we invoke the following notion of weak synchrony: A subset Γ of dispersed neurons is considered weakly synchronized, if the differences |xi − x|, |yi − y|, |zi − z| are small for all i neurons within the subset after an initial transient. Here x, y, z are the coordinates of the mean field of the subset Γ. The variance of the mean field of a subset then quantifies the local degree of synchrony. In the previous sections, we discussed networks with identical neurons for arbitrary connection topologies. For the discussion of networks with non-identical, that is dispersed, neurons, we limit ourselves to a global coupling topology, i.e., each neuron feels the input of a mean field of activity X(t). This type of topology implies that we consider only networks extending over small spatial scales, since no spatial decay of coupling and no time delays are present. A compact representation of the network behavior under these conditions will be a good candidate to serve as the microscopic neurocomputational unit in a large scale network. Networks with parameter dispersion and global coupling have been successfully described using a mean field approach (Monte et al. 2003) which relies on a local expansion around the synchronized solution. These authors derive two sets of reduced equations, in which the first describes the dynamics on the synchronization manifold and the second describes the deviations from synchrony. However, because the approach is valid only in the neighborhood of the synchronous solution, global network behaviors such as phase clustering cannot be described low-dimensionally (Rubin and Terman 2000; Strogata and Mirollo 1993). Within a small volume of cortical tissue populations of neurons are strongly connected and have been interpreted as the functional units of cortical processing (Sporns et al. 1989). These volume elements are described by a low dimensional ‘effective’ neuron (Buhmann 1989), identical to the mean field, which will be only legitimate if the local network dynamics is synchronized. Assisi et al. (2005) developed a mode decomposition approach which does not require the existence of a single synchronization manifold, but allows for multiple clusters of synchronized activity. They studied a network of globally coupled FitzHugh–Nagumo oscillators as a function of dispersion displaying clustering into different oscillator states distinguished by their phases, clustering into quiescent and oscillatory states as well as oscillator death. In the following we investigate the parameter space of globally coupled Hindmarsh–Rose neurons for two scenarios, first close to the onset of oscillatory behavior, I = 1.25, and second close to the onset of chaotic behavior, I = 2.8. The first scenario resembles the network of FitzHugh–Nagumo oscillators initially studied by (Assisi et al. 2005), but incorporates the multiple time scales present in the Hindmarsh–Rose neuron. Here we would naively expect a separation into individual synchronized clusters separating the oscillatory from the quiescent dynamics. The second scenario will address the degree of difficulty to synchronize the network in the proximity of chaotic onset.
We extend the Eqs. 1–3 to include global coupling and parameter dispersion as follows
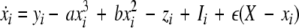 |
24 |
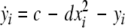 |
25 |
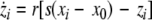 |
26 |
where 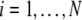 and
and 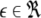 is the coupling strength. Here we preserved the linear nature of the coupling term, though it now represents the deviation of the membrane potential xi of the i-th neuron from the mean field
is the coupling strength. Here we preserved the linear nature of the coupling term, though it now represents the deviation of the membrane potential xi of the i-th neuron from the mean field 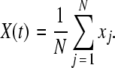 The mean field of the network, X, drives each neuron, implying that every node is connected to every other node and the coupling strength between any two nodes is
The mean field of the network, X, drives each neuron, implying that every node is connected to every other node and the coupling strength between any two nodes is 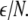 Such is obviously a simplification, even for a small and uniform neurocomputational unit. We here have to limit ourselves to view the global coupling as a first linear approximation of a mixed electric and chemical coupling within the unit. To consider inhibitory components, we also include
Such is obviously a simplification, even for a small and uniform neurocomputational unit. We here have to limit ourselves to view the global coupling as a first linear approximation of a mixed electric and chemical coupling within the unit. To consider inhibitory components, we also include 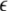 to be negative in our discussion. We introduce non-uniformity in the elements of the network by choosing the parameters Ii from a distribution with mean μ and standard deviation σ. Figure 6 shows the time series of all N neurons in the left column for various values of dispersion σ and coupling
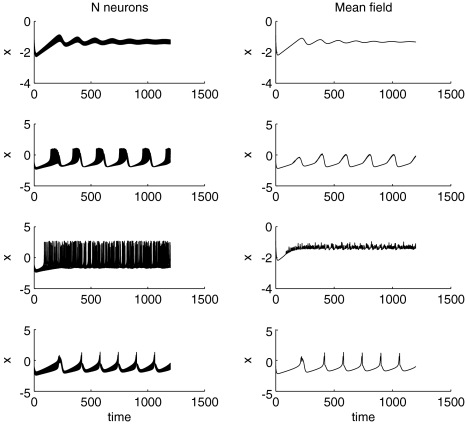
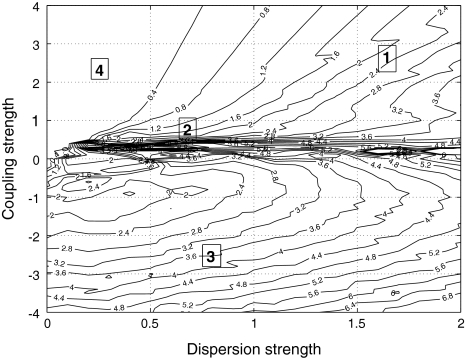
to be negative in our discussion. We introduce non-uniformity in the elements of the network by choosing the parameters Ii from a distribution with mean μ and standard deviation σ. Figure 6 shows the time series of all N neurons in the left column for various values of dispersion σ and coupling 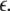 The mean value of input current, μ = 1.25, has been chosen right at the (non-chaotic) oscillation onset. The right column shows the corresponding time series of the mean field. Basically four characteristic scenarios exist (from top to bottom in Fig. 6): (i) Oscillator death, in which neurons seize firing after an initial transient. (ii) Bursts are synchronized, but the spikes are not. (iii) Neither bursts, nor spikes are synchronized. (iv) Both, spikes and bursts, are synchronized. Figure 7 shows the time-averaged variance of the mean field for the entire network at μ = 1.25 as a function of dispersion and coupling strength. Regimes of low variance indicate the degree of synchrony in the entire network and quantify how well the mean field characterizes the network dynamics. For large positive coupling strength, either oscillator death (regime 4) or synchronization of spike and bursts (regime 1) can occur. For decreasing coupling strength, the spikes lose synchrony as seen in an increase of variance. For very low or negative coupling (regime 3), neither spikes nor bursts are synchronized and the mean field displays just irregular activity.
The mean value of input current, μ = 1.25, has been chosen right at the (non-chaotic) oscillation onset. The right column shows the corresponding time series of the mean field. Basically four characteristic scenarios exist (from top to bottom in Fig. 6): (i) Oscillator death, in which neurons seize firing after an initial transient. (ii) Bursts are synchronized, but the spikes are not. (iii) Neither bursts, nor spikes are synchronized. (iv) Both, spikes and bursts, are synchronized. Figure 7 shows the time-averaged variance of the mean field for the entire network at μ = 1.25 as a function of dispersion and coupling strength. Regimes of low variance indicate the degree of synchrony in the entire network and quantify how well the mean field characterizes the network dynamics. For large positive coupling strength, either oscillator death (regime 4) or synchronization of spike and bursts (regime 1) can occur. For decreasing coupling strength, the spikes lose synchrony as seen in an increase of variance. For very low or negative coupling (regime 3), neither spikes nor bursts are synchronized and the mean field displays just irregular activity.
Fig. 6.
Time series for μ = 1.25. In the left column, N = 50 time series are plotted for uniformly distributed parameters Iext. In the right column, the corresponding mean field is plotted over time. The units are arbitrary. The parameter values read (from top to bottom): (i) 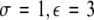 , (ii)
, (ii) 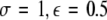 , (iii)
, (iii) 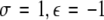 , (iv)
, (iv) 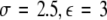
Fig. 7.
Variance of the mean field for μ = 1.25. As a measure of the degree of synchrony of the total mean field, the variance is plotted as a function of coupling strength 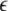 and dispersion strength σ
and dispersion strength σ
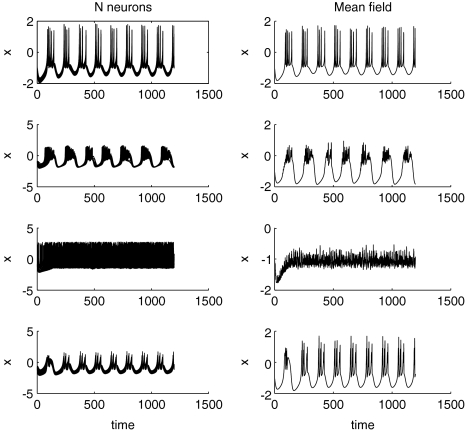
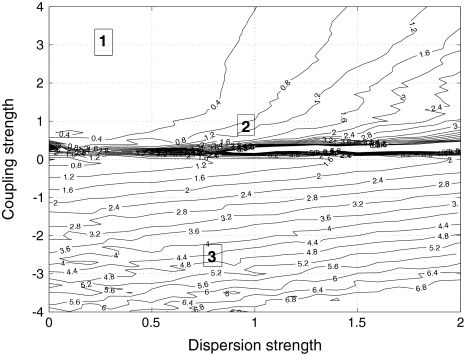
If the Hindmarsh–Rose oscillators are taken to the chaotic onset around μ = 2.8, the situation changes. Figure 8 displays the times series of the N network neurons and their mean field for the same values of coupling and dispersion as in Fig. 6. No oscillator death is possible, but rather spikes and bursts are synchronized for large coupling and small dispersion. In general, the variance of the mean field network activity is smaller across all positive coupling values implying that the network is easier to synchronize when it is closer to the chaotic onset. Figure 9 shows the variance of the mean field as a function of coupling and dispersion.
Fig. 8.
Time series for μ = 2.80. The same situation as in Fig. 6 is shown, but closer to the chaotic onset
Fig. 9.
Variance of the mean field for μ = 2.80. The same situation as in Fig. 7 is shown, but close to the chaotic onset
Conclusions
Coupled neurons, which display multi-time scaled dynamics such as spikes and bursts, synchronize at different coupling strengths. In general, bursts are easier to synchronize than spikes. This has been known for non-chaotic elliptic bursters (Izhikevich 2000) and is also true for chaotic spike–burst systems (Dhamala et al. 2004b) as we discussed here. If a constant time delay is introduced, then spike–burst synchronization can be achieved easier, that is at smaller coupling strengths than in the instantaneously coupled network. There seems to be the general trend that small amounts of coupling decrease the network coherence initially, but then increase it again for further increase in coupling strength. This increase in coherence occurs successively by first synchronizing the bursts, then the spikes. For non-identical neurons, the synchronized network state does not exist in the strict sense. However, the closer the average neuron resembles chaotic dynamics, the easier it is to cluster the spikes and bursts in a set with low variance ("weak synchrony") for excitatory coupling. Surprisingly the strength of the dispersion plays only a minor role, whereas neither spike nor burst synchronization can be achieved for inhibitory coupling at all.
Acknowledgments
I wish to thank Mukesh Dhamala and Collins Assisi for many discussions, as well as assistance with some of the numerical simulations. This research was previously presented at the ENOC 2005 and funded by the grants Brain NRG JSM22002082, ATIP (CNRS), and ONR grant N000140510104.
References
- Abeles M (1991) Corticonics. Cambridge University Press, New York
- Abeles M, Bergman H, Margalit E, Vaadia E (1993) Spatiotemporal firing patterns in the frontal cortex of behaving monkeys. J Neurophysiol 70:1629–1638 [DOI] [PubMed]
- Amzica F, Steriade M (1998) Electrophysiological correlates of sleep delta waves. Electroencephalogr Clin Neurophysiol 107(2):69–83 [DOI] [PubMed]
- Aradi I, Soltesz I (2002) Modulation of network behaviour by changes in variance in interneuronal properties. J Physiol 538(Pt 1):227–251 [DOI] [PMC free article] [PubMed]
- Assisi CG, Jirsa VK, Kelso JAS (2005) Synchrony and clustering in heterogeneous networks with global coupling and parameter dispersion. Phys Rev Lett 94(1):018106 [DOI] [PubMed]
- Avoli M, Gloor P, Kostopoulos G, Naquet R (1990) Generalized epilepsy. Neurobiological approaches. Birkhauser, Boston
- Breakspear M, Jirsa V (2007) Handbook of Brain Connectivity, chapter Neuronal Dynamics and Brain Connectivity. Springer, New York
- Bressler S (1990) The gamma wave: a cortical information carrier?. Trends Neurosci 13(5):161–162 [DOI] [PubMed]
- Bressler S, Kelso JAS (2001) Cortical coordination dynamics. Trends Cogn Sci 5:26–36 [DOI] [PubMed]
- Bressler SL, Tognoli E (2006) Operational principles of neurocognitive networks. Int J Psychophysiol 60(2):139–148 [DOI] [PubMed]
- Buhmann J (1989) Oscillations and low firing rates in associative memory neural networks. Phys Rev A 40(7):4145–4148 [DOI] [PubMed]
- Bullmore E, Rabe-Hesketh S, Morris RG, Williams SC, Gregory L, Gray JA, Brammer MJ (1996) Functional magnetic resonance image analysis of a large-scale neurocognitive network. Neuroimage 4:16–33 [DOI] [PubMed]
- Crick F, Koch C (1990) Towards a neurobiological theory of consciousness. Semin Neurosci 2:263–275
- Desmedt JE, Tomberg C (1994) Transient phase-locking of 40 hz electrical oscillations in prefrontal and parietal human cortex reflects the process of conscious somatic perception. Neurosci Lett 168(1–2):126–129 [DOI] [PubMed]
- Dhamala M, Jirsa VK, Ding M (2004a) Enhancement of neural synchrony by time delay. Phys Rev Lett 92(7):074104 [DOI] [PubMed]
- Dhamala M, Jirsa VK, Ding M (2004b). Transitions to synchrony in coupled bursting neurons. Phys Rev Lett 92(2):028101 [DOI] [PubMed]
- Freeman AS, Meltzer LT, Bunney BS (1985) Firing properties of substantia nigra dopaminergic neurons in freely moving rats. Life Sci 36(20):1983–1994 [DOI] [PubMed]
- Grace AA, Bunney BS (1984) The control of firing pattern in nigral dopamine neurons: burst firing. J Neurosci 4(11):2877–2890 [DOI] [PMC free article] [PubMed]
- Hindmarsh JL, Rose RM (1982) A model of the nerve impulse using two first-order differential equations. Nature 296(5853):162–164 [DOI] [PubMed]
- Hindmarsh JL, Rose RM (1984) A model of neuronal bursting using three coupled first order differential equations. Proc R Soc Lond B Biol Sci 221(1222):87–102 [DOI] [PubMed]
- Hosford DA, Clark S, Cao Z, Wilson WA, Lin FH, Morrisett RA, Huin A (1992) The role of GABAB receptor activation in absence seizures of lethargic (lh/lh) mice. Science 257(5068):398–401 [DOI] [PubMed]
- Izhikevich EM (2000) Neural excitability, spiking and bursting. Int J Bifurcation Chaos 10(6):1171–1266 doi:10.1142/S0218127400000840
- Jirsa VK (2004) Connectivity and dynamics of neural information processing. Neuroinformatics 2(2):183–204 [DOI] [PubMed]
- Jirsa VK, McIntosh AR (2007) Handbook of brain connectivity. Springer, Berlin Heidelberg New York
- Koch C (1999) Biophysics of computation. Information processing in single neurons, Oxford University Press
- Koob GF, Vaccarino FJ, Amalric M, Bloom FE (1987) Brain reward systems and abuse. Raven Press, New York, pp 35
- Ljungberg T, Apicella P, Schultz W (1992) Responses of monkey dopamine neurons during learning of behavioral reactions. J Neurophysiol 67(1):145–163 [DOI] [PubMed]
- MacDonald N (1989) Biological delay systems: linear stability theory. Cambridge University Press ISBN: 0521340845
- Matthews PC, Strogatz SH (1990) Phase diagram for the collective behavior of limit-cycle oscillators. Phys Rev Lett 65(14):1701–1704 [DOI] [PubMed]
- McCormick DA, Feeser HR (1990) Functional implications of burst firing and single spike activity in lateral geniculate relay neurons. Neuroscience 39(1):103–113 [DOI] [PubMed]
- McIntosh AR (2000) Towards a network theory of cognition. Neural Netw 13:861–876 [DOI] [PubMed]
- Mesulam MM (1998) From sensation to cognition. Ann Neurol 28:597–613 [DOI] [PubMed]
- Miltner WH, Braun C, Arnold M, Witte H, Taub E (1999) Coherence of gamma-band EEG activity as a basis for associative learning. Nature 397(6718):434–6 [DOI] [PubMed]
- Milton J, Chkhenkeli S, Towle V (2007) Handbook of Brain Connectivity, chapter Brain Connectivity and the Spread of Epileptic Seizures. Springer, Berlin Heidelberg New York
- Monte SD, d’Ovidio F, Mosekilde E (2003) Coherent regimes of globally coupled dynamical systems. Phys Rev Lett 90(5):054102 [DOI] [PubMed]
- Mountcastle VB (1998) Perceptual Neuroscience: the cerebral cortex. Harvard University Press, Cambridge
- Pecora LM, Carroll TL (1990). Synchronization in chaotic systems. Phys Rev Lett 64(8):821–824 [DOI] [PubMed]
- Pecora LM, Carroll TL (1998) Master stability functions for synchronized coupled systems. Phys Rev Lett 80(10):2109–2112 [DOI]
- Rinzel J, Lee YS (1987) Dissection of a model for neuronal parabolic bursting. J Math Biol 25(6):653–675 [DOI] [PubMed]
- Roelfsema PR, Engel AK, Knig P, Singer W (1997) Visuomotor integration is associated with zero time-lag synchronization among cortical areas. Nature 385(6612):157–161 [DOI] [PubMed]
- Rosenblum MG, Pikovsky AS, Kurths J (1996) Phase synchronization of chaotic oscillators. Physical Review Letters 76(11):1804–1807 [DOI] [PubMed]
- Rubin J, Terman D (2000) Analysis of clustered firing patterns in synaptically coupled networks of oscillators. J Math Biol 41(6):513–545 [DOI] [PubMed]
- Schultz W (1998) Predictive reward signal of dopamine neurons. J Neurophysiol 80(1):1–27 [DOI] [PubMed]
- Sherman SM, Kock C (1986) The control of retinogeniculate transmission in the mammalian lateral geniculate nucleus. Exp Brain Res 63:120 [DOI] [PubMed]
- Singer W, Gary CM (1995) Visual feature integration and the temporal correlation hypothesis. Annu Rev Neurosci 18:555–586 [DOI] [PubMed]
- Snead OC (1995) Basic mechanisms of generalized absence seizures. Ann Neurol 37(2):146–157 [DOI] [PubMed]
- Sporns O, Gally JA, Reeke GN, Edelman GM (1989) Reentrant signaling among simulated neuronal groups leads to coherency in their oscillatory activity. Proc Natl Acad Sci USA, 86(18):7265–7269 [DOI] [PMC free article] [PubMed]
- Steriade M, Llinas RR (1988) The functional states of the thalamus and the associated neuronal interplay. Physiol Rev 68(3):649–742 [DOI] [PubMed]
- Steriade M, McCormick DA, Sejnowski TJ (1993) Thalamocortical oscillations in the sleeping and aroused brain. Science 262(5134):679–685 [DOI] [PubMed]
- Strogatz SH, Mirollo RE (1993). Splay states in globally coupled Josephson arrays: analytical prediction of Floquet multipliers. Physical Review E 47(1):220–227 [DOI] [PubMed]
- Tallon-Baudry C, Bertrand O, Fischer C (2001) Oscillatory synchrony between human extrastriate areas during visual short-term memory maintenance. J Neurosci 21(RC177):1–5 [DOI] [PMC free article] [PubMed]
- Treisman A (1996) The binding problem. Curr Opin Neurobiol 6:171–178 [DOI] [PubMed]
- Von Stein A, Rappelsberger P, Sarnthein J, Petsche H (1999) Synchronization between temporal and parietal cortex during multimodal object processing in man. Cereb Cortex 9:137–150 [DOI] [PubMed]
- Weinberger DR (1987) Implications of normal brain development for the pathogenesis of schizophrenia. Arch Gen Psychiatry 44(7):660–669 [DOI] [PubMed]