Spatial invasion of cooperation

Abstract

The evolutionary puzzle of cooperation describes situations where cooperators provide a fitness benefit to other individuals at some cost to themselves. Under Darwinian selection, the evolution of cooperation is a conundrum, whereas non-cooperation (or defection) is not. In the absence of supporting mechanisms, cooperators perform poorly and decrease in abundance. Evolutionary game theory provides a powerful mathematical framework to address the problem of cooperation using the prisoner’s dilemma. One well-studied possibility to maintain cooperation is to consider structured populations, where each individual interacts only with a limited subset of the population. This enables cooperators to form clusters such that they are more likely to interact with other cooperators instead of being exploited by defectors. Here we present a detailed analysis of how a few cooperators invade and expand in a world of defectors. If the invasion succeeds, the expansion process takes place in two stages: first, cooperators and defectors quickly establish a local equilibrium and then they uniformly expand in space. The second stage provides good estimates for the global equilibrium frequencies of cooperators and defectors. Under hospitable conditions, cooperators typically form a single, ever growing cluster interspersed with specks of defectors, whereas under more hostile conditions, cooperators form isolated, compact clusters that minimize exploitation by defectors. We provide the first quantitative assessment of the way cooperators arrange in space during invasion and find that the macroscopic properties and the emerging spatial patterns reveal information about the characteristics of the underlying microscopic interactions.

1 Introduction

Cooperation is a fundamental principle of biological systems that organizes lower level entities into higher level units – genes form chromosomes, cells form organisms, and individuals form societies (Maynard Smith & Szathmáry, 1995). However, the emergence of cooperation poses an enduring challenge to evolutionary biologists: If cooperation is costly to the individual and benefits only the interaction partners, then Darwinian selection should favour non-cooperating defectors and eliminate cooperation. In the absence of supporting mechanisms, this outcome is inevitable, despite the fact that mutual cooperation is preferred over mutual defection. The most prominent mathematical metaphor to study such interactions is given by the prisoner’s dilemma: in pairwise interactions, cooperation (C) provides a benefit b to the partner at some cost c to the cooperator (b > c), while defection (D) neither bears any costs nor provides any benefits. The net gains for the player’s joint behaviour can be written in the form of a payoff matrix:

$$\begin{array}{lcc} & \text{If co­player cooperates}& \text{If co­player defects}\\ \text{Payoff to cooperator:}& b-c& -c\\ \text{Payoff to defector:}& b& 0\end{array}$$ (1)

Strictly speaking the prisoner’s dilemma is defined in terms of the ranking of the four payoffs. This particular parameterization in terms of b and c is biologically intuitive and mathematically convenient. The crucial point is that defection pays more irrespective of the partner’s decision and is thus the dominant strategy. Cooperators will therefore dwindle and eventually everybody ends up with a payoff of zero instead of the more favourable reward for mutual cooperation b - c. This characterizes the conflict of interest between individuals and the group, which defines social dilemmas (Dawes, 1980, Hauert et al., 2006). Over the last decades, different mechanisms have been proposed to promote and maintain cooperation (Hamilton, 1964, Hauert et al., 2002, 2007, Nowak, 2006b, Nowak & Sigmund, 1998, Trivers, 1971, Wilson & Sober, 1994) including spatially structured populations with limited local interactions (Nowak & May, 1992). If individuals are arranged on a lattice and interact only with their nearest neighbours, then cooperators may thrive by forming compact clusters, which increases interactions with other cooperators while reducing exploitation by defectors.

Spatial structure affects the evolutionary process in general 2 × 2 games, i.e. in pairwise interactions with two strategic options (Hauert, 2002, Ohtsuki & Nowak, 2006a), and notably enables cooperators to survive in populations playing the prisoner’s dilemma. Considering the equilibrium frequencies of cooperators and defectors in lattice populations demonstrates that the clustering advantages are substantial for small cost-to-benefit ratios c/b, but are unable to offset the exploitation by defectors above a threshold value, c/b > λ, such that cooperators disappear (Szabó & T oke, 1998). For increasing c/b, the system undergoes a critical phase transition, characterized by diverging fluctuations in the cooperator and defector frequencies (Szabó & Hauert, 2002a). These results have led to the common belief that spatial structure is necessarily beneficial for cooperation. While this holds for prisoner’s dilemma interactions, it is not universally applicable. In fact, in the snowdrift game – a closely related social dilemma with relaxed conditions such that cooperators and defectors can co-exist under conditions where cooperators are doomed in the prisoner’s dilemma – spatial structure often turns out to be detrimental to cooperation (Doebeli & Hauert, 2005, Hauert, 2006a, Hauert & Doebeli, 2004).

In finite populations, evolution is stochastic such that the combination of selection and random drift eventually leads to the fixation of one or the other strategic type (Nowak, 2006a, Nowak et al., 2004). In such situations, cooperation is favoured if the fixation probability of a single cooperator, ρ_C, in a defector population exceeds the fixation probability of a neutral mutant (ρ_C> 1/N where N is the population size). For weak selection, i.e. if payoff differences between cooperators and defectors are small, ρ_C is analytically accessible for various types of microscopic updating mechanisms (Ohtsuki et al., 2006, Taylor et al., 2007). In particular, for the payoff matrix (1), the condition ρ_C> 1/N implies that the fixation probability of a single defector, ρ_D, in a cooperator population is ρ_D < 1/N (Taylor et al., 2007, Wild & Traulsen, 2007). Hence, if mutations are rare, the population spends more time in the cooperator state than in the defector state. In the prisoner’s dilemma, if the death of a randomly chosen individual triggers a competition among its neighbours to repopulate the vacant site with a success rate proportional to their payoffs, then a particularly simple condition is obtained: evolution favours cooperation whenever b > c · k holds, where k denotes the number of interaction partners.

This work complements studies on prisoner’s dilemma games in structured populations by investigating the process of cooperators invading a world of defectors. We demonstrate that after an initial relaxation time, the number of cooperators always grows quadratically irrespective of the cost-to-benefit ratio c/b, and we find that two distinct modes of growth exist: (i) for small c/b, cooperators expand essentially as a single ever growing cluster whereas (ii) for larger c/b, cooperators form an increasing number of small clusters with little variation in size. Our simulations confirm that the probability of invasion is essentially independent of the initial number of cooperators provided that they form at least a 3 × 3 cluster (Hauert, 2001, Killingback et al., 1999, Page et al., 2000). In addition, our simulations show that behind the invasion front, cooperators and defectors quickly reach a local equilibrium, which supports analytical results based on pair approximation (Ellner et al., 1998, Le Gaillard et al., 2003, Ohtsuki et al., 2006, van Baalen & Rand, 1998).

2 Model

In order to investigate the invasion dynamics of cooperators in detail, consider a square lattice S × S where every site is occupied by a single individual. Initially, all individuals are defectors, except for a s × s cluster of cooperators in the centre of the lattice (s = 1, 3, 5, . . ., 15 and 30). Each individual engages in pairwise interactions within its Moore neighbourhood, i.e. with the eight nearest neighbours reachable by a chess king’s move. The payoffs accrued in these interactions determine the individual’s reproductive fitness (or its propensity to propagate its strategy). Rescaling of the payoff matrix (1) reduces the prisoner’s dilemma to a single parameter c/b:

$$\left(\begin{array}{cc}1& 0\\ 1+c/b& c/b\end{array}\right).$$ (2)

The updating of the strategy of every individual as well as of the population can be implemented in various ways as illustrated by the diversity of approaches in the literature (see e.g. Hauert, 2002, Nakamaru et al., 1997, 1998, Ohtsuki & Nowak, 2006a,b, Szabó & T oke, 1998). The characteristic features of the invasion process that we present here, however, are essentially independent of the detailed updating procedure. We verified this robustness using various update rules of the individuals (fully deterministic to highly stochastic) and of the population (synchronous updating or non-overlapping generations versus asynchronous updating or continuous time). For the simulations presented in the following section, we chose asynchronous updating of the population and an individual updating of intermediate stochasticity, which can be interpreted as a spatial analogue of the replicator dynamics: (i) a focal individual x is randomly selected to reassess and update its strategy; (ii) the payoff of x and of all its neighbours are determined and (iii) the focal player x probabilistically compares its payoff with the payoff of its neighbours. x adopts the strategy of neighbour y with a probability w_y = (P_y - P_x)/Δ provided that the payoff of y exceeds the payoff of x, and with probability zero otherwise. Δ = P_max –P_min is a normalization constant to ensure w_y ε [0, 1]. Given w_y for all neighbours, x does not change strategy with probability p_x = Π_y(1-w_y) With probability 1-p_x the focal player adopts the strategy of a neighbour with relative probability w_y/w where w = Σ_y w_y This approach recovers the replicator dynamics (Hofbauer & Sigmund, 1998, Taylor & Jonker, 1978) in the limit of infinite population sizes and large neighbourhoods where the focal individual compares its payoff to a single randomly chosen neighbour.

The above microscopic update procedure refers to a mechanism where individuals preferentially imitate the strategy of more successful neighbours. An equivalent interpretation in terms of replication can be obtained by translating the different probabilities into propensities that each neighbour succeeds in placing clonal offspring on the focal site.

3 Results

3.1 Cooperator Survival

Cooperation is inherently prone to exploitation by defectors and thus the survival probability of cooperators, σ_C, hinges on the cooperator’s ability to offset the costs of cooperation with benefits accrued from interactions with other cooperators. A single cooperator in a sea of defectors performs poorly, and its only hope is to propagate its strategy through random drift. Since players never adopt worse performing strategies in our setup, single cooperators never survive and readily disappear. For other, more stochastic update rules the odds of survival are not zero but the chances remain slim. For example, even if evolution favours cooperation in the Moran process under weak selection, the survival probability of a single cooperator is only of the order of 1/N and hence only for small population sizes reliable results can be achieved through individual based simulations. Moreover, under weak selection random drift dominates, which makes it much harder to extract characteristic features of the evolutionary process. In contrast, our approach based on strong selection facilitates clear-cut conclusions.

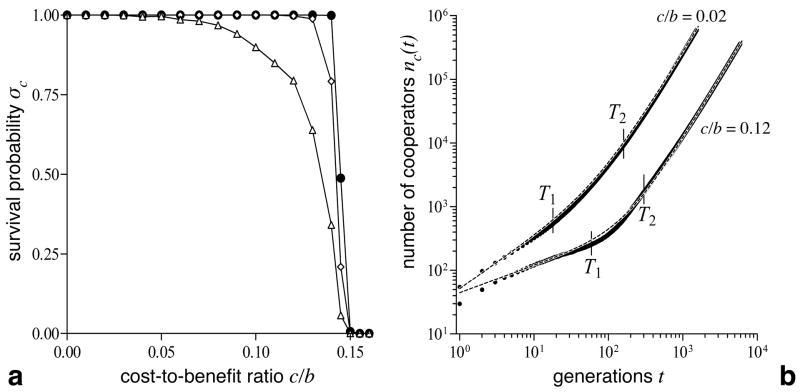
For c/b < λ ≈ 0.15 the survival probability σ_C of an initial cluster of s × s cooperators (s ≥ 3) is very high and only marginally affected by the cost-to-benefit ratio c/b (see Fig. 1a). The pivotal role of 3 × 3 clusters in determining whether cooperators thrive has been recognized earlier (Hauert, 2001, Killingback et al., 1999, Nowak & May, 1993, Page et al., 2000) and is confirmed by our results. For c/b < λ, cooperators can survive by forming compact clusters and thereby minimizing exploitation by defectors. For c/b > λ however, the clustering advantage provided by the spatial setting is insufficient, and cooperators invariably go extinct irrespective of their initial abundance.

Figure 1.

Survival probability σ_C and growth characteristics of invading cooperators. a For initial cluster sizes of s × s with s ≥ 3, the survival probability is close to 1 and essentially independent of s (Δ, s = 3; ⋄, s = 5; •, s = 15) and the cost-to-benefit ratio c/b up to the extinction threshold λ ≈ 0.15, where cooperators can no longer survive irrespective of their initial abundance. σ_C is determined over 1000 runs on a 115 × 115 lattice and cooperators are assumed to survive if they reached the boundary. b The growth of the number of cooperators n_c(t) displays two distinct regimes: A first phase of slow growth that corresponds to a local equilibration process of the initial cluster, followed by a second phase representing the expansion of cooperators. Both regimes follow a power function of the form n_c(t) = a_it^d_I but with distinct growth exponents (d₁ < 1 in the first phase and d₂ ≈ 2 in the second phase; see Table 1). The dashed line shows the superposition of the two fits n_c(t) = a₁t^d₁ + a₂t^d₂. Vertical lines mark the end of the first (T₁)and the beginning of the second growth phase (T₂) as used for fitting the power function. The expansion process is shown for a 30 × 30 cluster on a 1000² lattice averaged over 100 runs.

3.2 Cooperator Expansion

A close inspection of the invasion process of cooperators reveals two distinct dynamical regimes: an initial phase of slower growth giving way to a phase of significantly faster expansion (see Fig. 1b). The invasion dynamics in both phases follows a power function, i.e. the number of cooperators n_c increases as a function of time t according to n_c(t) = a_i t^d_I where a_i indicates the growth rate of cooperators in each phase (i = 1, 2) and the exponents d_i characterize their spreading in space. Estimates of the parameters a_i, d_i were obtained by two separate fits: the first fit up to time T₁, which marks the end of the first phase, and the second fit after T₂, which indicates the beginning of the second phase. The transient phase between T₁ and T₂ is ade- quately described by a superposition of the two power functions:n_c(t) = a₁ t^d₁ + a₂ t^d₂ (see Fig. 1b).

In the first phase, both parameters a₁ and d₁ decrease with increasing cost-to-benefit ratios c/b, which indicates slower growth under less favourable conditions for cooperators. The factor a₁ also depends on the size of the initial cluster of cooperators. The small exponents, d₁ < 1, are remarkable because an arbitrary but uniform spatial expansion process yields an exponent of 2 (or, more generally, an exponent of D in D-dimensional space). The reason for the observed small d₁ is that cooperators expand during the first phase, but defectors simultaneously invade the cooperator’s initial territory. This indicates that a local equilibration process among cooperators and defectors is taking place behind the invasion front. In line with this, the relaxation time T₁ of this initial phase increases with the size of the initial cluster and also increases for larger cost-to-benefit ratios c/b, because higher costs or smaller benefits hinder the propagation of cooperation.

In the second phase, the growth rate of cooperators a₂ again decreases with increasing c/b-ratios, but the growth exponent remains essentially constant at d₂ ≈ 2, which confirms the theoretical expectations of a uniform spatial expansion process. Note that d₂ shows small variations around 2 because the rate of growth is not locally uniform and depends on the cluster shape: cooperators along smooth edges have higher propensities to proliferate than cooperators sitting on corners. However, as the expansion progresses and the number of cooperators increases, such effects become less important and are averaged out, which suggests that lim_{t →∞} d₂ → 2 holds.

The growth exponents d₁, d₂ not only characterize the spreading of cooperators in space, but also determine the growth of the region exposed to the invasion of cooperators or, equivalently, determine the information propagation speed. Thus, in the second phase, the number of individuals that are aware of the invading cooperators grows approximately as N₂(t) = α₂ t^d₂ ≈ α₂ t² Note that N₂(t) essentially corresponds to the area enveloping the not necessarily contiguous cluster(s) of cooperators. The equilibrium frequency of cooperators is therefore given by f_c = lim_{t →∞} n_c(t)/N₂(t). Note that n_c(t)/N₂(t) = a₂/α₂, which is independent of time. Thus, if n_c(t) and N₂(t) are known at some particular times (they do not need to be measured simultaneously) good estimates of the equilibrium frequencies of cooperators and defectors can be obtained. In simulations, a convenient time T is defined by the first cooperator reaching the boundary of the lattice. At this time, N₂(T ) = S2π/4 provides a good approximation with S² representing the lattice or population size. Note that this tends to systematically overestimate N₂(T) because (i) the centre of the area covered by cooperators may have shifted over time and (ii) only a single cooperator reached the boundary at time T. A conservative estimation of the equilibrium fraction of cooperators f_c is therefore given by

$$f_c=\frac{a_2}{{\alpha }_2}\approx \frac{a_2{T}^2}{N_2(T)}=\frac{4}{S^2\pi }{a}_2{T}^2.$$ (3)

For good estimates, T should lie well in the second regime of the invasion process. The estimation of f_c is not applicable to the first growth phase because it relies on the fact that cooperators and defectors behind the invasion front have reached a local equilibrium, and this is violated in early stages of the invasion process. A summary of the fit data and equilibrium estimates is given in Table 1. Since N₂(t) relates to the area affected by the invasion of cooperators, it indicates an accessible quantity for experimental approaches, for example experiments of growing microbial populations on plates.

Table 1.

Fit and simulation data characterizing the invasion of cooperators for two different initial cluster sizes and two cost-to-benefit ratios. The number of cooperators n_c(t) increases according to n_c(t) = a_it^d_I,where i refers to the first and second growth phase (cf. Fig. 1b). T indicates the number of generations until the first cooperator reaches the boundary on a 1000² lattice (averaged over 100 runs). The estimated and simulated equilibrium fractions of cooperators are given by $f_c^{\text{theory}}$ (see Eq. (3)) and $f_c^{\text{sims}}$ respectively.

c/b	initial cluster size	a1	d1	a2	d2	T	$f_c^{\text{theory}}$	$f_c^{\text{sims}}$
0.02	3 × 3	3.34	1.17	0.14	2.07	1683	0.849	0.932
0.02	30 × 30	51.14	0.80	0.36	1.95	1625	0.848	0.932
0.12	3 × 3	1.11	1.03	0.01	2.06	6515	0.519	0.578
0.12	30 × 30	44.51	0.43	0.02	1.94	6280	0.514	0.578

3.3 Cluster Size

The fraction of cooperators f_c depicted in Fig. 1b is linked to the spatial arrangement of cooperators, which in turn is determined by the geometry, the updating and the payoff matrix. Macroscopic features such as the number of contiguous clusters of cooperators, their typical size as well as their shape during cooperator expansion reveal therefore interesting characteristics of the underlying microscopic interactions. Fig. 2 shows typical snapshots of the distinct spatial patterns for two different values of the cost-to-benefit ratio c/b at time T, i.e. when the first cooperator reaches the boundary of the necessarily finite lattice in our simulations. Under benign conditions for cooperation (small c/b), usually a single large contiguous cluster of cooperators grows with small embedded specks of defectors. Only along the invasion front, several isolated cooperators and tiny separated cooperator formations are found. A contiguous cluster consists of cooperators that have at least one other cooperator among their neighbours. In contrast, under more hostile conditions for cooperation (larger c/b), cooperators form numerous small compact clusters. Typically, none of these clusters host specks of defectors because they would readily split the cluster into smaller ones.

Figure 2.

Typical snapshots of the invasion of cooperators (blue) in a world of defectors (red) for a small cost-to-benefit ratio (c/b = 0.02) and b for c/b closer to the extinction threshold (c/b = 0.12). Along the interface separating cooperators and defectors, some individuals recently switched from defection to cooperation (green) or vice versa (yellow). a Cooperators expand as a single contiguous cluster with embedded specks of defectors, and a few isolated tiny cooperator formations along the invasion front. In this snapshot there is one large cluster of size 23187 accompanied by 14 single, isolated cooperators and the average weighted cluster shape is γ = 0.078. The fraction of cooperators is f_c = 0.58 and q_c\c = 0.89. b Cooperators form numerous small compact clusters. There are 143 clusters ranging from a single cooperator to a cluster of size 1987, with a weighted average size of 537 and shape γ = 0.356. The fraction of cooperators is f_c = 0.37 and q_c\c = 0.76. The snapshots are shown for an initial 15 × 15 cluster on a 200² lattice and can be reproduced using the VirtualLabs (Hauert, 2006b).

For increasing c/b-ratios, the cluster size decreases, while the number of clusters increases (see Fig. 3a). Note that for small c/b, the tiny cooperator formations along the invasion front lead to a bimodal distribution of the cluster size. In order to determine the typical average cluster size and eliminate the effects of isolated cooperators without introducing an arbitrary threshold size, the average cluster size is weighted such that the weight of each cluster corresponds to its size. The cluster size and cluster count delineate two distinct regimes: for c/b < 0.1 (cf. Fig. 2a), few rather big clusters dominate the expansion process whereas for 0.1 < c/b < λ ≈ 0.15 (cf. Fig. 2b), numerous compact clusters minimize exploitation by defectors. As noted before (cf. Fig. 1), λ marks the extinction threshold of cooperators such that for c/b > λ the clustering advantages of cooperators are no longer sufficient to offset exploitation by defectors.

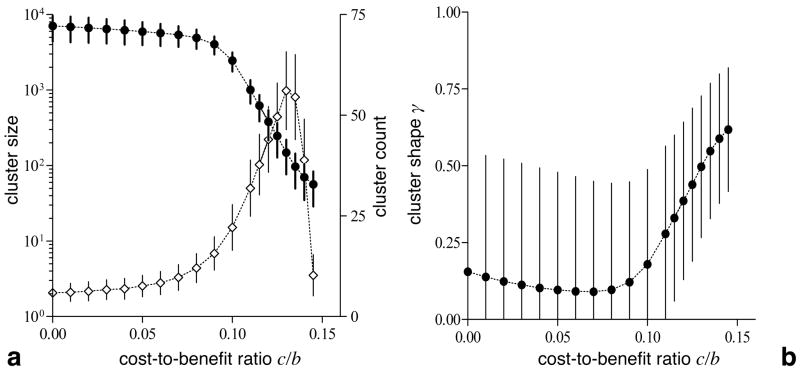
Figure 3.

Macroscopic features of the invasion of cooperators: a cluster size (•) and count (⋄) as well as b cluster shape γ for increasing cost-to-benefit ratios c/b. a As suggested by the snapshots in Fig. 2, the cluster size decreases with c/b, while the number of clusters increases. For c/b < 0.1, few sizeable clusters dominate the expansion, which means that the cluster size keeps increasing as invasion continues. In contrast, the big clusters break up and numerous small clusters are formed for c/b > 0.1. b The same two distinct regimes are reflected in the mean cluster shape γ weighted by the cluster size. For c/b < 0.1, γ is very low because of numerous embedded specks of defectors but displays a large variance due to their variable numbers. In contrast, compact clusters with convex shapes form for c/b > 0.1 such as to minimize interactions with defectors. For an initial cluster of 15 × 15 cooperators, the cluster size, count and shape are determined when cooperators reach the boundary of a 115² lattice and averaged over 1000 runs. Cluster size and shape are weighted by the cluster size (see text). Vertical bars indicate the standard deviation (the standard error lies within the size of the symbols).

Note that for small c/b, the cluster size keeps increasing as invasion progresses, but this is not true for larger c/b-ratios, where cooperators break up into smaller clusters of similar size. As c/b increases and approaches λ, the cluster size steadily decreases, but it cannot become arbitrarily small. In our case, cluster sizes of at least 50 cooperators seem to be required to sustain cooperation. The decrease in cluster size is accompanied by an increase in the cluster count. Interestingly, the cluster count exhibits a peak near c/b = 0.13. For larger c/b, the cluster size keeps decreasing at a slow rate, while the cluster count drops quickly, which leads to an increase in the distance between adjacent clusters. This repulsion between clusters of cooperators arises from those fortunate defectors that are able to exploit several clusters simultaneously. Their high payoffs increase their chances to invade and usually destroy some clusters. Increasing the typical distance between clusters reduces this risk.

The small variance in the size of contiguous clusters indicates that a typical cluster size exists as c/b approaches λ. This is remarkable because in closely related equilibrium systems, this limit leads to diverging fluctuations in the frequency of cooperators (Szabó & Hauert, 2002a,b). Hence, the fluctuations are caused by variations in the number of clusters rather than their sizes. For c/b < 0.1 no typical cluster size exists and cooperators usually expand as a single large cluster. The cluster size distribution is bi-modal due to a number of tiny runaway clusters along the periphery (see Fig. 2a).

For 0.1 < c/b < λ a typical cluster size exists, which defines the relevant spatial scale for local processes. This means that as the invasion progresses, the typical cluster size becomes much smaller than the overall area covered by the invading cooperators (see Fig. 2b). In this case, the system can approach local equilibrium in areas behind the invasion front. This is supported by the conditional probability that a neighbour of a cooperator is another cooperator, q_c\c, which quickly reaches its equilibrium value during the first growth phase (not shown). In contrast, if cooperators expand as a single cluster with embedded specks of defectors (see Fig. 2a), these specks are not in proper equilibrium because their background keeps expanding. Nevertheless, q_c\c rapidly changes during the first phase and increases only slowly during the second phase (not shown). The time when q_c\c ceases to change rapidly coincides with the transition from the first to the second growth phase; this further supports that the first phase constitutes a local equilibration process.

3.4 Cluster Shape

Under increasingly hostile conditions for cooperators (larger c/b-values), the cluster shape becomes more and more important. Compact and convex cluster shapes maximize interactions with other cooperators and minimize exploitation by defectors. The shape of a single cluster γ_s can be defined as the ratio of interactions within the cluster, A, to interactions with the surrounding defectors, P. Thus, γ_s is reminiscent of an area-to-periphery ratio (A/P ). In continuous two dimensional space the ratio A/P² is invariant with respect to the cluster size. Unfortunately, this invariance no longer holds in discrete lattice space. In order to take this into account, the shape γ_n of each cluster is normalized such that a single line of cooperators (minimal A, maximal P) yields γ_n = 0 whereas a square of cooperators (close to the maximum for A and minimum for P) returns γ_n = 1, irrespective of the cluster size. The mean (normalized) cluster shape γ is weighted by the cluster size to eliminate distortions due to renegade cooperators along the invasion front (see Fig. 3b). γ exhibits the same two distinct dynamical regimes as the cluster size and count (cf. Fig. 3a). For c/b < 0.1, γ is surprisingly small due to the embedded specks of defectors and exhibits large variations because of their variable numbers. For c/b > 0.1, γ quickly increases as numerous small compact clusters of cooperators form.

4 Conclusions

Under favourable conditions, i.e. for low costs and high benefits, cooperators are able to invade a spatially extended world of defectors. The ability to form clusters enables cooperators to persist, because spatial aggregation enables more frequent interactions with other cooperators while reducing exploitation by defectors. The invasion of cooperators occurs in two phases: During the first phase, the number of cooperators increases slowly because the expansion of cooperators is partly offset by defectors invading the initial cluster of cooperators. The first phase thus establishes a local equilibrium between cooperators and defectors. Consequently, the duration of this phase depends on the size of the initial cluster and can be neglected if the invasion was initiated by few cooperators. During the second phase, cooperators uniformly expand into defector territory. Under increasingly hostile conditions (larger c/b), the expansion speed decreases but the number of cooperators always increases according to a quadratic function. Interestingly, cooperators and defectors readily find themselves in a local equilibrium in the wake of the invasion front. Such local equilibration is a fast process compared to the invasion dynamics (or in contrast to global equilibration), a finding that has also been recognized in analytical studies using the technique of pair approximation (Le Gaillard et al., 2003, Matsuda et al., 1992, van Baalen & Rand, 1998). Due to the fast equilibration, good estimates of the equilibrium frequencies of cooperators and defectors can be obtained already from the invasion process (see Table 1). In fact, the dynamics in early stages already predicts the evolutionary fate of cooperators and defectors.

The difference between local and global dynamics suggests a natural separation of time scales. This is used to calculate the fixation probability of cooperators, ρ_C, in the limit of weak selection (Ohtsuki et al., 2006). Note that for the update rule chosen here, ρ_C < 1/S²always holds (S²denotes the population size). Thus, the probability that a single cooperator takes over is always less than that of a neutral mutant. This remains true if several cooperators attempt to invade as compared to an equal number of neutral mutants. However, even though evolutionary dynamics never favours cooperation, cooperators and defectors may co-exist for an exceedingly long time. In the absence of mutations, any finite system with a stochastic update rule must eventually reach a homogeneous absorbing state with all defectors or all cooperators, but whether these states can be reached within reasonable time is a rather different question (Taylor et al., 2006, Traulsen et al., 2007). The outcome not only strongly depends on the population size, but also on the existence and stability of (local) equilibria where cooperators and defectors can co-exist (Traulsen et al., 2006a,b). Thus, whether cooperators manage to invade a population of defectors is largely independent of whether they take over the population and displace defectors.

The invasion of cooperators can essentially unfold according to two distinct scenarios: under benign conditions (small c/b-ratios), cooperators expand and form a single large contiguous and continuously growing cluster interspersed with little specks of defectors (see Fig. 2a). In contrast, under hostile conditions (large c/b-values), cooperators split up and form numerous smaller compact clusters of a typical size and the embedded specks disappear (see Fig. 2b). The typical size decreases with increasing values of c/b, but once it drops below a threshold size, cooperation can no longer be sustained and disappears. Under hostile conditions, cooperators break up and form numerous isolated clusters of increasingly convex shape (see Fig. 3b), which reduces interactions with defectors and thus minimizes exploitation.

Spatial structures, or limited local interactions, lead to assortment. The strength and type of assortment depends on the geometry, the payoffs as well as on the update rules. In the spatial prisoner’s dilemma, the formation of clusters generates positive assortment of cooperator-cooperator interactions, which is crucial for their survival. Under harsher conditions (larger c/b), positive assortment becomes more important, as reflected in the increasingly convex shapes. At some point (c/b > λ), the assortment required to offset exploitation by defectors can be no longer achieved and cooperators disappear. Pair approximation deals analytically with assortment up to first order, but cannot be easily extended to account for macroscopic features such as cluster count, size and shape. The present study provides a first numerical attempt to link macroscopic features and microscopic mechanisms.

The characteristics of the invasion process are robust with respect to variations of the system size or modifications of the update rules. Changing from asynchronous to synchronous population updates (overlapping versus non-overlapping generations) and adopting different rules for strategy propagation – e.g. based on the Moran process (Moran, 1962, Nowak et al., 2004) or referring to situations where errors or uncertainties may lead to the adoption of worse performing strategies (Hauert & Szabó, 2005, Szabó & T oke, 1998) – introduce only minor corrections to quantitative features such as the invasion speed, equilibrium estimates or the maximum c/b-ratio for which cooperators can persist.

The macroscopic spatio-temporal patterns emerging through the invasion of cooperators in a spatially extended world of defectors reveal characteristic features of the underlying microscopic interactions and provide an outlook on the long-term behaviour of the system. The cluster size of cooperators reflects the cost-to-benefit ratio of cooperation, and the local equilibrium of cooperators and defectors behind the invasion front provides good estimates for the global equilibrium frequencies of the two strategies at a much later evolutionary stage.