Energetic considerations of ciliary beating and the advantage of metachronal coordination

Abstract

The internal mechanism of cilia is among the most ancient biological motors on an evolutionary scale. It produces beat patterns that consist of two phases: during the effective stroke, the cilium moves approximately as a straight rod, and during the recovery stroke, it rolls close to the surface in a tangential motion. It is commonly agreed that these two phases are designed for efficient functioning: the effective stroke encounters strong viscous resistance and generates thrust, whereas the recovery stroke returns the cilium to starting position while avoiding viscous resistance. Metachronal coordination between cilia, which occurs when many of them beat close to each other, is believed to be an autonomous result of the hydrodynamical interactions in the system. Qualitatively, metachronism is perceived as a way for reducing the energy expenditure required for beating. This paper presents a quantitative study of the energy expenditure of beating cilia, and of the energetic significance of metachronism. We develop a method for computing the work done by model cilia that beat in a viscous fluid. We demonstrate that for a single cilium, beating in water, the mechanical work done during the effective stroke is approximately five times the amount of work done during the recovery stroke. Investigation of multicilia configurations shows that having neighboring cilia beat metachronally is energetically advantageous and perhaps even crucial for multiciliary functioning. Finally, the model is used to approximate the number of dynein arm attachments that are likely to occur during the effective and recovery strokes of a beat cycle, predicting that almost all of the available dynein arms should participate in generating the motion.

1. Introduction

On an evolutionary scale, cilia are among the oldest and most frequently occurring locomotion organelles. Powered by a sliding filaments mechanism, they beat in periodical two-phase patterns. During the effective stroke they move approximately as a straight rod and during the recovery stroke they bend, roll close to the cell surface in a mostly tangential direction, and return to a ready position to initiate the next beat cycle. The primary function of cilia is to generate fluid flow in a preferred direction. Such flow can be utilized for propelling a cell through a fluid medium, for moving particles in a desired direction, or for moving mucus layers (see ref. 1 for a detailed description).

Cilia operate in a low Reynolds number environment where inertia is negligible. The evolution of asymmetrical beat patterns can thus be explained by the reversal property of Stokes flows, i.e., symmetrical beats create a zero average flow. Qualitative understanding of the two phases of the ciliary beats suggests [e.g., Sleigh (1)] that for optimal functioning they are designed to (i) take advantage of the large viscous resistance during the effective stroke to generate maximal thrust and (ii) minimize viscous resistance during the return to a “ready position” by using a relatively slow and mainly tangential recovery stroke.

In this report we introduce a method for computing the work done (hereafter referred to as energy expenditure) against viscous forces by a model cilium as an additional feature of our recently developed modeling framework [Gueron et al. (2) and Gueron and Levit-Gurevich (3)]. This model accounts for three-dimensional fluid dynamics, including interactions with fixed and moving boundaries, although the actual motion of the cilia is restricted to one plane.

Metachronal coordination between cilia is a situation where they beat with a constant phase difference between adjacent rows in such a way that their tips form a moving wave pattern. The reason why and how arrays of cilia beat in a metachronal pattern is not fully understood [Machemer (4); Tamm (5); Gheber et al. (6)], but there is evidence that metachronism may occur in part as the result of hydrodynamic coupling. Because our model accounts for the interactions between cilia in multiciliary configurations, we can assess the energetic cost of such interactions, and thus provide answers to the following questions. (i) How much work is done by the cilia against the viscous forces during a beat cycle? In particular, what portion of this energy is spent during the effective stroke (E_eff) and the recovery (E_rec) stroke? (ii) How does energy expenditure depend on the hydrodynamic interactions between neighboring cilia? Does it pay energetically for one cilium to synchronize with an adjacent cilium? Does metachronal coordination save energy in a multiciliary configuration, and, if so, to what extent?

Up to the present, one could not consider these questions quantitatively because an appropriate model that takes into account the effects of the hydrodynamic interactions between the cilia and the flat surface from which they emerge, and generates realistic beat patterns that may evolve dynamically as the result of external effects, has become available only recently.

Perhaps the first model indicating that synchrony is energetically efficient is early work of Taylor (7), who showed that when a pair of two-dimensional infinite sheets move in a sinusoidal pattern in a viscous fluid, minimal energy dissipation occurs when they are in synchrony. Beside the obvious fact that cilia are not two-dimensional infinite sheets, Taylor’s result cannot be directly related to cilia for another reason: the model did not discuss dynamical motions, because the wave patterns were assumed to be fixed a priori and were not allowed to change as a result of hydrodynamical coupling, as the case is for real cilia. A more recent study [Fauci (8)] used the Immersed Boundary Method for simulating the motion of waving two-dimensional infinite sheets. The results indicate that phase locking may occur. However, this particular implementation of the Immersed Boundary Method requires a great deal of computations (performed at that time on a supercomputer), and is restricted to investigating only two-dimensional infinitely long objects. The Immersed Boundary Method has been applied for simulations of a variety of problems such as three dimensional heart motion [Peskin and McQueen (9, 10)], sperm motility [Fauci and McDonald (11)], and ciliary motion [Dillon and Fauci (12)]. Because of the involved computational burden, only two-dimensional implementations and thus infinite objects were considered in most implementations, in particular the two latter works mentioned above.

Another approach for modeling the motion of slender bodies, called often the Resistive Force Theory, pioneered by Gray and Hancock (see ref. 2), is based on an asymptotic linear relation between the local drag forces and the local velocity. It is simple to implement and has been used extensively for modeling (planar) flagellar motion [e.g., Brokaw (13)], but it is not applicable for modeling multicilia configurations, as discussed in ref. 3.

2. The Modeling Framework for Simulation of Ciliary Motion

The modeling framework that we use here was introduced in ref. 2 and an updated version of this model was published in ref. 3. The latter report includes all the model’s equations, discusses their derivation, and provides the numerical procedures necessary for implementing it. We thus provide here only a brief description.

Our ciliary modeling framework consists of three building blocks that are linked together: (a) the hydrodynamic description of the ciliary system; (b) the geometric equations for the motion of the cilia; and (c) the internal bend-generating mechanism which we call here the “engine.” We outline each of these building blocks below.

(a) The hydrodynamic equations are based on a refined slender body theory for cilia moving in Stokes flow, which were developed by Gueron and Liron (14). Their equations relate the drag force exerted on the cilium by the surrounding fluid to its local velocity. These equations account for three-dimensional flow fields and are suitable for modeling three-dimensional cilia. This was the first proposed modeling tool that enabled simulations of multicilia configurations while taking the hydrodynamic interactions into account. Further details are provided in Section 2.1.

(b) The geometric equations describe the motion of the inextensible ciliary centerline as a function of its local velocity. When the motion is restricted to be planar, these dynamic equations can be solved numerically in a rather straightforward manner. To that end, we assume that the cilia (i.e., their centerlines) are initially found in one plane, aligned in a row. We also assume that the internal forces act in that plane—that is, the internal engine does not generate twist. This assumption guarantees that the motions remains planar, and we can therefore use the two-dimensional geometric equations to describe them (see Section 2.2 for details).

(c) Gueron et al. (2) and Gueron and Levit-Gurevich (3) developed a simple model for the internal bend-generating mechanism of cilia, whose parameters were obtained from analyzing ciliary beat data. The transitions between the two phases of the motion are controlled by a “geometric switch” that depends on the momentary shape of the cilia. This eliminated the need for using a biologically unmotivated “internal clock” in the model. The model was shown to capture the essential features of the motion, including properties that are not built in explicitly. Multicilia configurations consisting of rows of cilia were investigated with this model, and it was shown that when two adjacent model cilia start beating at different phases, they tend to synchronize within two cycles, as observed in experiments. Also, antiplectic metachronal patterns evolve autonomously in these multicilia configurations. These results provided the first modeling evidence in support of the conjecture that metachronism may occur autonomously, due to hydrodynamical interactions between the cilia.

2.1. The Hydrodynamical Equations of the Ciliary Model.

We use here the equations and notations that were introduced by Gueron and Liron (14). The cilium is considered as a slender cylindrical filament of length L and radius a. The variable s denotes the centerline’s arclength parameter measured from the anchor, and t denotes time. The subscripts _t and _s denote differentiation with respect to time and arclength s, respectively. The subscripts _T and _N denote the tangential and normal components of vectors, respectively. We denote the drag force per unit length, exerted by the cilium on the surrounding fluid by φ(s, t), the fluid viscosity by μ, and the cilium’s velocity by V(s, t). The following relations between the drag force and the velocity were derived in ref. 14:

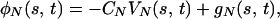1

where g_T = C_TG_T, g_N = C_NG_N and the vector G = (G_N, G_T) denotes the velocity field induced at s by “far segments” of the cilium, neighboring cilia, or external flow. For three-dimensional models, a binormal component, φ_B(s, t) = −C_BV_B(s, t) + g_B(s, t) is added, and C_B = C_N. The components of G are expressed in terms of appropriate singular solutions of the Stokes equations. The expressions for the tangential (C_T) and the normal (C_N) resistance coefficients are

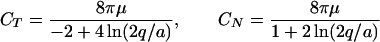2

for any q such that a ≪ q and q ≪ L. These coefficients are not the well known Gray–Hancock resistance coefficients and the ratio C_N/C_T ≈ 1.43 is lower than the value of 2 used in the GH approximation and lower than the value of 1.8 which was used for modeling flagella [Brokaw (13)]. Further discussion on the difference between the resistive force and the slender body theories is presented in ref. 14 and in ref. 3. The expression for G at the point s₀ along the centerline and at time t is

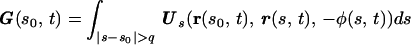3

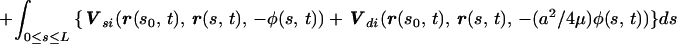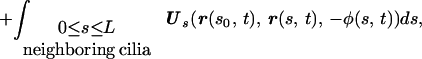where U_s(r, r₀, φ) is the velocity induced at r by a Stokeslet with intensity φ located at r₀, V_si(r, r₀, φ) is the velocity induced by the image system of the Stokeslet alone, and V_di is the velocity induced by the image system of the Doublet alone. Note that, as expected, the particular choice of the parameter q determines the value of the resistance coefficients C_T and C_N and, correspondingly, affects G.

2.2. Dynamic Equations and the Model for the Internal Engine.

Because we restrict the motion of the cilia to one plane, we consider only the two-dimensional time evolution of their centerlines. For each cilium, we denote the angle between its tangent and the horizontal axis of a fixed coordinate system by α(s, t), and if κ denotes the curvature of the centerline, then κ(s, t) = α_s(s, t). With this parametrization it is easy to satisfy inextensibility requirements, relate the normal and tangential components of the velocity, and derive appropriate equations for propagating the curve in time (see ref. 14).

The normal component F_N of the shear force induced within the cilium is modeled (in nondimensional form) by

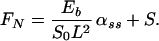4

An equation for the tangential component F_T, obtained from inextensibility condition, is

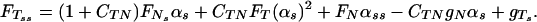5

Here, S = S(s, t) is the active shear force due to the internal sliding filaments mechanism and the radial spokes system. S₀ is a typical fixed magnitude of the internal shear force (used for scaling), E_b is its elastic bending resistance, C_TN = C_T/C_N, and C_NT = C_N/C_T. Propagation in time is implemented by

6

The part of our modeling framework that represents S(s, t), the active shear force (engine) that is generated within the cilium, was developed in refs. 2 and 3, and the equation for S(s, t) reads

7

Here, ω_eff/rec is a typical velocity during the effective and the recovery strokes, respectively. The parameters C̄_N ≡ C_NL²/S₀, A₁, A₂ and B_eff/rec attain different values during the effective and the recovery strokes (see the Appendix). The coefficient ±1 indicates the direction of S during the effective and recovery strokes, respectively. The transitions between these strokes are modeled by our geometric switch hypothesis which, for the effective stroke, depends on reaching a desired inclination angle (α_left = 130°, α_right = 20° with respect to the flat surface).

2.3. Computation of Energy Expenditure During a Beat Cycle.

To compute the mechanical energy that is being spent during any desired time interval, we add a new feature to our model. The power exerted by the cilium at any moment in time is given by

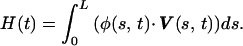8

The scalar product in Eq. 8 can be expressed by

Thus, the energy spent (mechanical work done) by the cilium during the time interval [t₁, t₂] can be written as

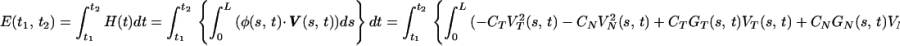9

It is important to note that the expression for E(t₁, t₂) depends only on the velocity of the cilium (though in a complicated manner) since G is implicitly a function of this velocity. This relation can be used in two different ways: (i) Observed positions of a cilium at different stages of its beat cycle yield an approximation of its velocity, which can then be used in Eq. 9 to compute E(t₁, t₂). Note that Eq. 1 approximate the drag force directly from the observed velocities and the ciliary shape [i.e., α(s, t)]. It thus follows that E(t₁, t₂) can be computed independently of any model for the ciliary engine. (ii) An equation for S(s, t) can be used for modeling the internal shear forces. These translate to appropriate drag forces Φ, then to velocities (through Eq. 1) and to the resulting motion. The energetic cost of this motion can be computed concurrently by Eq. 9. This procedure allows us to simulate different multicilia configurations at varied viscosities.

3. Results

3.1. Energy Expenditure Calculated from Observed Beats.

We used the positions of the cilium of Paramecium during a beat cycle [Sleigh (15)] to compute the drag forces induced on the cilium. The work done by the cilium against the viscous resistance during parts of the beat cycle was then obtained by using Eq. 9. Our model enables us to compute the energy expenditure at any desired time interval, whenever the ciliary positions are given. This can therefore provide additional information which is not available from experiments. We computed that the energy expenditure is ≈9⋅10⁻¹⁶ Joules during the effective stroke and ≈2⋅10⁻¹⁶ Joules during the recovery stroke. The ratio of the work done during the reconstructed effective and the recovery strokes, for an isolated cilium, is E_rec/E_eff ≈ 0.22. This roughly 5-fold difference highlights the gain in energy expenditure that is achieved by having the recovery stroke occur more slowly than the effective stroke and close to the cell’s surface.

Note that our result is appreciably larger than Sleigh’s (15) estimate for the energy expenditure of the cilia of Paramecium during the effective stroke. Sleigh estimated that if the cilium exerts a bending couple of 5 × 10⁻¹⁷ N⋅m to overcome the viscous resistance during the effective stroke, and sweeps an angle of ≈90° within ≈0.008 sec during this phase, then work is done at a rate of ≈1.25 × 10⁻¹⁴ Joules/cilium/sec. The overall work (per cilium) during the effective stroke is therefore approximately 10⁻¹⁶ Joules. Sleigh’s simplistic approximation is based on a rough estimate of the bending couple and does not take into account the effects of the flat surface from which the cilia emerge. Further, this estimate can be made only for the effective stroke. We emphasize at this point that the discussion of an isolated cilium is merely theoretical, because what we see in nature is already of the overall result of the interaction of this cilium with many neighboring cilia.

3.2. Energy Expenditure Obtained with a Model Internal Engine.

The computations performed in Section 3.1 used data obtained from observations on a cilium during its beat cycle and are independent of any model for its internal engine. We now repeat these computations, but this time we use the model engine equations presented in refs. 2 and 3. Fig. 1 (top left panel) shows the beat pattern produced by this model engine. The computation of energy expenditure by this model cilium in water agreed within a few percent with the energy expenditure computed by using the observed ciliary velocities (which were initially used to estimating the engine’s parameters). Thus, this model engine is suitable for investigating the energy expenditure in multiciliary configurations and at different fluid viscosities.

Figure 1.

Ciliary beats in different cilia configurations. The top line displays three isolated cilia beating in different viscosities (μ_water, 2μ_water and 3μ_water, correspondingly, from left to right). The solid and dashed lines represent the recovery and effective stroke, respectively. The time interval between snapshots is 3 msec. The middle line displays one snapshot of the 2-, 5-, and 10-cilia configurations in the viscosity of water. The bottom line displays eight snapshots of the 100-cilia configuration. Note that coordination similar to metachronism occurs in the multicilia configurations. The axes are in units of ciliary length. These figures are reproduced from Gueron and Levit-Gurevich (3).

3.2.1. Effects of increased viscosity on energy expenditure.

Using our model engine we found that the overall energy, as well as the ratio E_rec/E_eff, hardly change in the viscosity range μ_water ≤ μ ≤ 5μ_water (see Fig. 1, top line, for the beat patterns in different viscosities). This robust behavior occurs because of the particular changes in the beat pattern and frequency that result from the changed external conditions. It is important to point out that this robust behavior is actually the result of the modeling paradigm that underlies our model engine. The forces that generate the motion are quite accurately reconstructed by our hydrodynamic equations. However, there are various ways to model their control, which affect the response of the engine to external load. Our modeling assumption is that the internal mechanism does not change its properties because of a changed load. Therefore, the load dependence is reflected here only implicitly, through the geometric switches between the effective and the recovery strokes.

A different modeling approach would be, for example, to replace our configuration-dependent engine with a velocity-dependent one, such as Brokaw’s (16) model engine, which includes an assumption as to how the dyneins generate more force when the viscous drag is increased [see also ref. (13)]. Such an approach is likely to produce a different response to changes in viscosity than the present configuration-dependent engine.

3.2.2. The effects of cilia interactions.

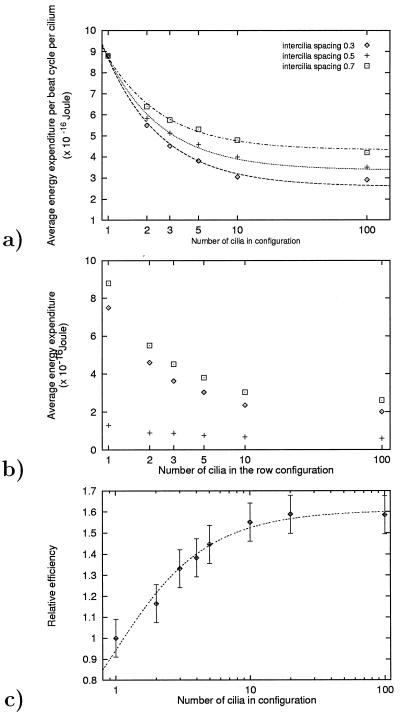
Beat patterns of model multicilia configurations having 2, 5, 10, and 100 cilia in a row are shown in Fig. 1. The intercilia spacing is 0.3 ciliary length (3.6 μm). Computation of the energy expenditure per cilium per cycle shows that as the number of the cilia in the row increases there is an approximately 3-fold decrease in the energetic cost of a beat cycle, the maximum decrease being attained for a row of ten cilia (Fig. 2a). Similar results with different intercilia spacings of 0.5 and 0.7 ciliary length, are also displayed in Fig. 2a. Obviously, as the intercilia spacing is increased, the interactions between the cilia weaken. Our computations show that, as a result, the savings in the average energy expenditure per cilium per cycle decreases.

Figure 2.

(a) The average per-cilium energy expenditure during the beat cycle, as a function of the number of cilia in multicilia configurations. The interciliary spacing is 0.3, 0.5, and 0.7 ciliary length. The horizontal axis is a logarithmic scale. The computations are done for the viscosity of water. (b) The average energy spent per cilium per cycle in multicilia configurations. Results for configurations of 1, 2, 3, 5, 10, and 100 cilia are shown. The interciliary spacing is 0.3 ciliary lengths. The computations are done for the viscosity of water. The horizontal axis displayed is a logarithmic scale. The diamond, plus, and square symbols represent the effective stroke, the recovery stroke, and the whole beat cycle, respectively. The average number of moles of ATP hydrolyzed, and of the number of dynein arm attachments are indicated by the same symbols, but the units of the ordinate would be 0–16⁻²⁰ moles and 0–10,000 attachments, respectively. (c) The relative efficiency of fluid propulsion, as a function of the number of the cilia in the row. Efficiency is defined here as the net fluid mass moved in the direction of the effective stroke through a test area near the ciliary array, per unit of spent energy (see explanation in text). The results are scaled with respect to those obtained for a single cilium. The horizontal axis displayed is a logarithmic scale.

In addition to ascertaining that increasing the number of the cilia in a row decreases the overall energy expenditure, it was of interest to determine the effect of row length on the energy expenditure during the effective stroke as compared to the recovery stroke. As shown in Fig. 2b, the energy used during the recovery stroke decreases by approximately a factor of two as the number of cilia in a row increases. We point out that the position of the cilium within the row has a relatively small effect on the energy expenditure during the recovery stroke. The energy expenditure during the effective stroke, however, decreases by a factor of four with increasing row length, and the cilia at the leading edge of the row (i.e., if the effective stroke is toward the left, then cilium number 1 is at the left end of the row) expend more energy during their effective stroke than do the cilia further inside. The ratio E_rec/E_eff varies between 0.18 and 0.3, depending on the number of cilia in the row and their spacing.

As noted earlier (2, 3) multicilia configurations reach their steady-state beat patterns within a few cycles from their initial resting state. When two closely spaced cilia start beating, they synchronize completely within two cycles, and when many cilia are aligned in a row a beat pattern resembling a metachronal wave rapidly evolves autonomously, as shown in Fig. 1. Our results indicate that the energy expended per cilium decreases very rapidly during this transition from a resting state to an actively beating state. As suggested in the next section, this decrease in energy expenditure per cilium may be crucial for enabling motion.

3.2.3. Does interciliary coupling increase the overall efficiency of the ciliary system?

It is interesting to investigate the energetic effect of the hydrodynamic coupling between the cilia, and in particular, to assess efficacy of metachronal coordination that the cilia interactions develop autonomously. It was already shown (3) that the beats that emerge in multicilia configurations change in pattern and frequency as a function of the number of cilia in the row (e.g., from 29.5 Hz for a single cilium in water to 42 Hz for a 10-cilia configuration). Further, our current computations show that the energy required per cilium per cycle decreases when the number of cilia is increased. However, this result alone does not reflect directly on the efficiency of the system, and a target quantity must first be defined. When the swimming of Paramecium is considered, for instance, the energy required for swimming a unit distance would be a most appropriate measure of efficiency. However, such computation is currently beyond the capability of the present model, and we settle with a more modest attempt. Recalling that the primary function of cilia is to generate fluid flow in a preferred direction, we compute the net fluid mass moving in the direction of the effective stroke through a test area near the beating ciliary array, per unit of spent energy. If this quantity increases with the number of cilia in the row configuration, it would give some indication that the interactions between the cilia are beneficial. To that end, we take advantage of the fact that our model allows us to compute the velocity of the fluid at any point in space.

We now define the test area that we use for this presentation. Suppose that the cilia are located along the line y = 0 in the x − y plane, the effective stroke is in the positive direction of the x axis, the anchor of the leftmost cilium is at the origin, and that of the rightmost cilium is at (d × (n_cilia − 1), 0, 0), where n_cilia is the number of cilia in the configuration and d is the interciliary spacing. For the present study, we define our test area as the rectangle R of dimensions 2d × 1.5 (in units of ciliary length), whose vertices have the coordinates (D, 0, −d), (D, 0, d), (D, 1.5, d), (D, 1.5, −d), where D = d × (n_cilia − 1) + 1.

Fig. 2c displays the result of the calculation of the fluid mass per energy spent for different ciliary row configurations. It demonstrates that the ciliary interactions that evolve contribute to an appreciable increase in the fluid propulsion per unit of energy spent, for rows of cilia with more than about 10 cilia per row.

4. Estimating the Rate of Dynein Arm Attachments

Satir et al. (17) proposed a stochastic model relating the present understanding of the internal ciliary structure to the formation and propagation of bends along a cilium. They concluded from their model that only a small proportion (about 1%) of the dynein arms need to be active at any one moment to generate ciliary motion. From an evolutionary perspective, it would be surprising if evolution conserved such a redundant structure. However, their conclusions are possibly the result of the fact that they do not take into account the hydrodynamic interactions of the each cilium with its neighbors and the surrounding fluid. Our model, which includes these considerations, can be used to obtain some insight into the number of dynein arms that must be activated per beat to obtain the observed ciliary beats. We therefore propose the following computations.

The hydrolysis of ATP by the dynein arms located along the length of the cilium provides the energy for ciliary motility. The sequence of attachments along individual doublets generates filament sliding and hence bend formation. Although the precise details of bend formation and propagation are not fully understood, one can nevertheless use the present model to estimate, indirectly, the number of dynein arms required for motion generation.

Let E_ATP = 6.02⋅10⁴ Joule be the energy produced by the hydrolysis of one mole of ATP [Brokaw and Johnson (18)]. The number of molecules in one mole is given by Avogadro’s constant N_av = 6.022⋅10²³. Thus, the hydrolysis of one ATP molecule releases E_ATP/N_av ≈ 10⁻¹⁹ Joule/molecule. We now consider the cilium of Paramecium whose typical length is L = 12 μm. The distance between two adjacent dyneins is approximately d = 24 nm [Satir (19)], and therefore the number of dynein arms along one doublet is L/d = 500, or 2L/d = 1,000 dyneins if we count inner and outer arms. We assume here that during the effective stroke, filaments 1–4 are actively sliding and filaments 5–9 are passive, and that during the recovery stroke, filaments 6–9 are active and filaments 1–5 are passive [Sleigh and Barlow (20); Satir (19)]. Therefore, only 2,000 dynein pairs (i.e., 4,000 dynein arms) can be reactivated during each phase. Satir (19) estimated that the duty phase of the dynein mechanochemical cycle is about 1–2 msec, whereas the whole cycle is about 33–34 msec. Since the beat duration of the cilia of Paramecium is ≈35 msec (beat frequency is ≈28 Hz), it follows that each dynein arm can be reactivated at most once during the beat cycle.

The attachment of one dynein arm “costs” one ATP molecule (two molecules for a pair, assuming only one active ATPase per dynein arm). If we denote the energy spent during some time interval by E, the amount of ATP consumed at the same interval by A, and the number of dynein arms attachments by N_att, we have:

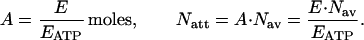10

We use the relations in 10, together with the results concerning ciliary energy expenditure. Fig. 2b displays the average amount of energy spent, the average amount of hydrolyzed moles of ATP, and the average number of dynein arms attachments, during the effective and the recovery strokes for several multicilia configurations.

Under the assumptions made here, an interesting interpretation arises when we compare our results for an isolated cilium to the results for a 100-cilia configuration. For the isolated cilium, our computations show that roughly 7,500 attachments are required during the effective stroke, which implies that each arm (of doublets 1–4) should attach twice during the effective stroke that lasts ≈8 msec. The conclusion is that this theoretical isolated cilium cannot beat—at least not at the observed pattern and frequency—unless it has neighboring cilia. On the other hand, note that in the 100-cilia configuration, which is energy-wise less costly (per cycle), only ≈2,000 arm attachments are required during the effective stroke. This number is feasible as it requires only one attachment per arm of doublets 1–4 during this phase. Note also that to achieve ≈2,000 arm attachments, practically all of the available dynein arms must participate.

We point out that our crude computations assume perfect mechanical efficiency, whereas the actual efficiency must be smaller. Indeed, Rikmenspoel (21) speculated that the efficiency of the energy conversion is roughly 20%. Taking into account imperfect efficiency, this would require that there are either more dynein arm attachments per beat (which, as argued above, is physically impossible) or that cilia interactions that would occur in closely packed two-dimensional arrays decrease the required energy.

We thus speculate that activity of most of the dynein arms is likely to be required to generate the observed motions. Moreover, according to the model, ciliary interactions and metachronal coordination markedly reduce the energy expenditure per beat cycle, and in this sense appear to play an important role in the functioning of large arrays of cilia.

5. Discussion

We have used our model to examine various aspects of the ciliary beating, to make several observations concerning the efficiency of the interciliary interactions and of the internal ciliary engine. However, we re-emphasize that part of our results depend on our modeling assumption of the internal control mechanism, in particular, on the geometric switch hypothesis. Further, the estimated number of the reactivated dynein arms may change in case there is more than one dynein per arm, if the dynein arms do not cycle from filaments 1–5 during the effective stroke to 6–9 during the recovery stroke [see e.g., Wolczak and Nelson (22)], or if one considers the inner and outer arms to have different mechanical functions [e.g., Brokaw (23)]. Finally, we point out that although our modeling framework is currently the most advanced one, the present study is still restricted to planar ciliary motion (with three-dimensional fluid dynamics). However, we are currently developing a suitable mathematical representation and feasible computational procedure that will allow us to model ciliary motion in three dimensions. This would the subject of future studies.

Appendix

Boundary and Initial Conditions.

The boundary conditions used in the model correspond to a cilium that is pinned at its basal end and free at its distal end:

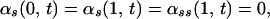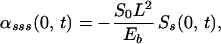A.1

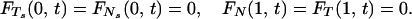A.2

The initial conditions correspond to an erect cilium is α(s, 0) = π/2 for all 0 ≤ s ≤ 1.

Parameter Values.

The values of the parameters used in our model are: S₀ = 10⁻¹² Newton, L = 12 μm, E_b = 25⋅10⁻²⁴Newton m², C_N = 0.0035 kg/m⋅sec, C_T = 0.0025 kg/m⋅sec.

The parameters of model engine are: ω_eff = 11,000°/sec, ω_rec = 2,290°/sec, α_left = 130° and α_right = 20°. During the effective stroke A₁ = 0.26, A₂ = −0.17, and during the recovery stroke A₁ = 2 for 0 ≤ s ≤ 0.1L and A₁ = 1 for 0.1L ≤ s ≤ L, A₂ = −2, and B_eff = 0, B_rec = 2.