Abstract
Pairs of discharges of single motor units recorded in the same or different muscles often show synchronisation above chance levels. If large numbers of units are synchronous within and between muscles then the synchrony will be measurable in population recordings such as surface EMG. Measuring synchrony between surface EMG recordings has a number of practical and scientific advantages compared with single motor units recorded from intramuscular electrodes. However, the measurement of such synchrony in the time domain between surface EMGs is complicated because the recordings are contaminated by electrical cross-talk. In this study we recorded surface EMG simultaneously from five hand and forearm muscles during a precision grip task. Using a novel ‘blind signal separation’ algorithm, we were able to remove electrical cross-talk. The cross-talk-corrected EMGs could then be used to assess task-dependent modulation in both oscillatory (15-30 Hz) and non-oscillatory synchrony (all other frequencies). In agreement with previous studies, the oscillatory component was maximal during steady holding but abolished during movement. By contrast, the non-oscillatory component of the EMG synchrony appeared remarkably constant throughout all phases of the task. We conclude that surface EMG recordings can be of considerable use in the assessment of population synchrony changes, providing that electrical cross-talk between nearby channels is removed using a statistical signal processing technique. Our results show a striking difference in the task-dependent modulation of oscillatory and non-oscillatory synchrony between muscles during a dynamic precision grip task.
Synchronisation of neural activity above the levels expected by chance is a commonly reported phenomenon within the central nervous system; however, there is still considerable debate over its function (Shadlen & Newsome, 1994; Softky, 1995). Within the motor system, synchrony has been reported within the cerebellum (Welsh et al. 1995), basal ganglia (Raz et al. 1996) and motor cortex (Smith & Fetz, 1989; Baker et al. 2001). In addition, synchrony can be seen in the periphery between pairs of discharges of single motor units recorded in the same (Sears & Stagg, 1976; Datta & Stephens, 1990) or different (Bremner et al. 1991) muscles.
A considerable component of the synchrony observed in activity recorded from muscles and from motor cortical areas is oscillatory in nature, at frequencies in the ‘beta’ band of approximately 15–30 Hz (Farmer et al. 1993; Conway et al. 1995; Murthy & Fetz, 1996; Baker et al. 1997; Donoghue et al. 1998). One likely source of synchrony between motor units is common input to motoneurones from branched axons (Bremner et al. 1991).
If large numbers of units are synchronous within and between muscles then the synchrony will be measurable in population recordings such as surface EMG, and this is indeed the case (Maier & Hepp-Reymond, 1995; Gibbs et al. 1997; Kilner et al. 1999). Measuring synchrony between different surface EMG recordings has a number of advantages compared with single motor units recorded from intramuscular electrodes. First, the experiments are technically simpler and allow measurement of muscle activity during periods of finger or limb movements, when needle electrode recordings prove particularly unstable. Secondly, surface EMG recordings are more representative of the activity of the whole muscle, and therefore are better related to the actual mechanical output (Bigland & Lipold, 1954).
Whilst several studies have reported how 15–30 Hz oscillatory synchrony measured between surface EMGs modulates with performance of a motor task (Baker et al. 1997; Kilner et al. 1999), less is known about the modulation of non-oscillatory components. Such components lead only to a central peak in cross-correlations without accompanying subpeaks. The measurement of synchrony in the time domain between surface EMGs is complicated by the contamination of the recordings by electrical cross-talk. Surface EMG electrodes do not only record the activity of the muscle over which they are placed, but also from other nearby muscles due to tissue volume conduction. This contamination is greatest when the different muscles are close together, as in the hand. Electrical cross-talk may contaminate measures of synchrony, both in the spectral and temporal domain, artificially increasing measures of the coupling.
In this study we recorded surface EMG simultaneously from five hand and forearm muscles during a precision grip task. Using a novel ‘blind signal separation’ algorithm, we were able to remove electrical cross-talk. The cross-talk corrected EMGs could then be used to assess task-dependent modulation in both oscillatory and non-oscillatory synchrony. We confirmed our previous finding that the oscillatory component is maximal during steady holding but abolished during movement (Baker et al. 1997; Kilner et al. 1999, 2000). By contrast, the non-oscillatory component of the EMG synchrony appears remarkably constant throughout all phases of the task.
METHODS
Behavioural data
The results reported here were gathered from 12 healthy human subjects (4 male and 8 female) all right handed by self report, and aged between 19 and 33 years. The same dataset formed the basis of our previous paper (Kilner et al. 1999) on frequency domain analysis of synchronisation. All subjects gave informed consent; the studies had local ethical committee approval and the experiments were conducted according to the Declaration of Helsinki. The subjects gripped two spring-loaded levers between the thumb and index finger of their right hand. A force of 1.5 N was required to overcome the initial spring tension before the levers moved and then a further force of 0.07 N was needed per millimetre of lever displacement. Visual feedback of the lever positions was provided via cursors on a computer video screen. Subjects began each trial with the hand relaxed. A trial was initiated when the cursors appeared. Subjects then moved the levers so that the cursors were positioned inside target boxes. The targets initially were stationary at a 2.1 N force level for 3 s. The target force then increased linearly to 2.6 N over 2 s. The trial was completed by a further 3 s hold at the higher force level. This is the RAMP task reported by Kilner et al. (1999).
Recordings
Bipolar surface EMGs were recorded from abductor pollicis brevis (AbPB), first dorsal interosseous (1DI), abductor digiti minimi (AbDM), flexor digitorum superficialis (FDS) and extensor digitorum communis (EDC). The electrodes used were rectangular Arbo Ag-AgCl electrodes (20 mm × 30 mm). For each intrinsic hand muscle the recording electrode was placed over the belly of the muscle and the reference electrode was placed over the metacarpophalangeal joint, of the thumb, index finger and auriculaire for AbPB, 1DI and AbDM muscles, respectively. For the intrinsic hand muscles the electrodes were placed 10 mm apart. For FDS the reference electrode was placed ∼60 mm from the wrist joint and the recording electrode was placed over the muscle ∼20 mm more proximal. For EDC the reference electrode was placed ∼40 mm from the elbow joint and the recording electrode was placed over the muscle ∼20 mm more distal. For the 1DI muscle, the task required ∼9 % of the maximum voluntary contraction. EMGs were amplified (gain 1-10K), high-pass filtered at 30 Hz, and then sampled at 5 kHz by a PC-compatible computer fitted with a 1401+ interface (CED Ltd, Cambridge), together with finger and thumb lever positions and markers indicating task events.
Analysis
Off-line, finger and thumb lever position signals were examined by eye; trials in which the subject had failed to move the levers as required were excluded. The first 50 correctly performed trials were used in subsequent analysis. EMG signals were smoothed and down-sampled by averaging successive sets of five points using a non-weighted average. The resultant EMG time series was therefore effectively sampled at 1 kHz.
Blind signal separation
In order to remove the component of correlation between the surface EMG recordings due to electrical cross-talk, we used a ‘blind signal separation’ algorithm developed by Chan et al. (1996). The problem of blind signal separation has received much attention in the engineering literature in recent years. The problem is illustrated in schematic form in Fig. 1 and may be expressed as follows. Assume there are N original signal waveforms (here EMGs), which are independent and each have zero mean; represent these as xi(t) (i = 1…N). Instead of recording these signals directly, we record N mixtures yi(t), generated by:
| (1) |
where h are mixing filters of order L, and Δ is the sampling interval between data points. Because this mixing process introduces dependency between the measured signals, they will not now in general be independent. Blind signal separation algorithms seek to determine a set of unmixing filters w such that:
| (2) |
Figure 1. Schematic diagram of the ‘blind signal separation’ algorithm.

The figure shows the problem and process of the ‘blind signal separation’ algorithm used. On the left of the figure are shown the original signals which are mixed by some mixing filter (h), in this case electrical cross-talk between muscles, to produce the observed signals, in this case the EMG recordings. The algorithm used calculates an unmixing filter (w) that when applied to the observed data produces the recovered original signals, in this case the EMG activity minus the electrical cross-talk.
This allows reconstruction of the original, but unobserved, signals. The algorithms are said to be ‘blind’, since this is achieved with no prior knowledge of the mixing filters h.
The standard statistical method of principle components analysis is an example of such a separation algorithm; however, it is limited to the case where only zero lag filters are considered (L = 0), and assumes that the original signals are uncorrelated at time lag zero; the principle components calculated are hence always orthogonal. Independent component analysis (Bell & Sejnowski, 1995; Lee, 1998) is also limited to consideration of zero lag filters, but makes the more general assumption that the signals are independent (i.e. contain no mutual information). The independent components so found are not necessarily orthogonal, which may give more satisfactory solutions for a range of problems (Bell & Sejnowski, 1996, 1997).
The algorithm we have used here (Chan et al. 1996) is capable of designing unmixing filters which depend on lags greater than zero (L > 0). Additionally, the filters are designed to minimise the cross-correlation between the separated signals over a range of cross-correlation lags, not just at lag zero. For further mathematical details of the algorithm, the paper of Chan et al. (1996) should be consulted. We used Chan et al.'s implementation of their algorithm, which is freely available over the internet:(http://www-sigproc.eng.cam.ac.uk/oldusers/dcbc1/research/separate.html)and runs in MATLAB (The MathsWorks Inc). A third-order unmixing filter was specified, and the cross-correlations were minimised up to lags of ± 10 ms. These parameters were chosen after preliminary analyses because they produced reliable separation.
The algorithm to calculate the unmixing filters was run on a section of data consisting of the first correctly performed trial for a given recording session. The unmixing filters so found were then applied to the entire recording to give the separated EMGs. One of the features of the blind signal separation algorithm is that the output signals are generated in arbitrary order. Thus, for example, if EMG from the 1DI muscle was recorded on channel 1, in the separated signals it could appear as any one of channels 1-5. In practice, however, this did not create difficulties, since the separated waveforms were sufficiently similar to the original EMG to allow straightforward assignment by eye of which EMG was on which channel (see Fig. 2B). A second feature of the algorithm is that the unmixing filters are of arbitrary scale, such that the units of the separated signal are meaningless. This is unimportant for surface EMG recordings, where the amplitude can anyway be greatly affected by a variety of uncontrolled factors such as skin resistance, muscle size and precise electrode location. In addition, EMG studies are usually concerned with the modulation of the EMG, rather than its absolute size. Calibration bars for separated EMG traces are therefore given in arbitrary units.
Figure 2. Effect of differentiation on EMG signal of a patient with Kallman's syndrome.

The effect of differentiation of the EMG on the cross-correlation of EMG signals from right and left 1DI muscles in a subject with Kallmann's syndrome. The subject performed abductions of the right 1DI muscle over a 25 min period.
The original and the separated EMG signals were further analysed in both the frequency and temporal domains.
Frequency domain analysis
Power and coherence spectra were calculated between all smoothed, down-sampled and rectified EMGs over the entire data set using a non-overlapping FFT window of 1024 points, permitting a frequency resolution of 0.97 Hz. All data were detrended prior to analysis using linear regression techniques (Kilner et al. 1999). Differences between the separated and non-separated spectra were assessed using both the arctanh transform (Rosenberg et al. 1989) and by comparing the maximum value of the coherence in the 15–30 Hz range using Student's paired t test.
Temporal domain analysis
Analogue cross-correlations were calculated between pairs of rectified EMGs. If r(τ) is the cross-correlation function, then:
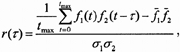 |
(3) |
where f1 and f2 are the two signals to be analysed, −f1 and −f2 are their mean values and σ1 and σ2 are their standard deviations. r is bounded between −1 and 1. In addition, in order to determine how synchrony changed during the task, time-resolved cross-correlograms were calculated using non-overlapping time bins 250 ms-wide aligned relative to the onset of the task. If ρi(τ) is the cross-correlation for bin i,
 |
(4) |
where f^1n(t) and f^2n(t) the two signals, aligned to the onset of the nth trial, and the means and standard deviations are now calculated over the same section of data from each signal which contributes to the cross-product inside the summation. Note that using this formula, the correlation calculated for bin i uses data only within the 250 ms duration of this bin for signal 1. However, for signal 2, data is taken from a wider region, extending either side of the bin edges by a time equal to the maximum cross-correlation lag which is calculated. This ensures that the same amount of data contributes to all lags of the correlation.
It was of interest to determine the proportion of the calculated cross-correlation which was due to oscillatory synchrony in the 15–30 Hz range (Farmer et al. 1993; Conway et al. 1995; Baker et al. 1997). This was effected using a similar technique to that of Baker et al. (2001). The cross-correlations were digitally filtered in the lag direction to remove all frequency components between 15 and 30 Hz. The subtraction of this cross-correlation from the original gave the fraction due to 15–30 Hz components. We will refer to these cross-correlations as ‘non-oscillatory’ and ‘oscillatory’, in a similar fashion to Baker et al. (2001).
In order to allow combination of data across subjects and muscle pairs, the cross-correlation at a given lag and time was transformed to make it normally distributed using the Fisher's Z transformation (Snedecor & Cochran, 1989):
| (5) |
where ln is the natural log. The values of Z were then averaged across subjects and muscle pairs, and the average was then retransformed to a correlation coefficient by:
| (6) |
The amplitude of the near-synchronous correlation was assessed by averaging values of Z within 5 ms of zero lag. These were transformed back to correlation coefficients for display (Fig. 5D–F); differences between phases of the task were tested for significance using Student's paired t test on the Z values.
Figure 5. Effect of ‘blind separation’ on frequency domain analysis.
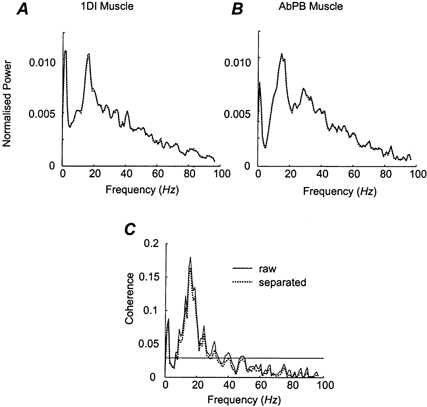
Spectral domain analysis from the 1DI and AbPB EMG from a healthy single subject calculated across the entire task, a period of ∼510 s. A, normalised power spectra of the rectified 1DI EMG, calculated from the raw data (continuous line) and separated data (dotted line). B, normalised power spectra of the rectified AbPB muscle, calculated from the raw data (continuous line) and separated data (dotted line). C, coherence spectra between the rectified 1DI-AbPB muscle pair, calculated from the raw data (continuous line) and separated data (dotted line). The horizontal continuous line indicates the 95 % significance level (P < 0.05).
RESULTS
Distinguishing physiological synchronisation from electrical cross-talk
As described above, blind signal separation algorithms are capable of removing contamination due to electrical cross-talk between signals. A critical assumption of these algorithms is that the original signals prior to contamination are uncorrelated. At first sight, this is not in general the case for EMG recordings from nearby muscles, since motor units are often synchronised (Bremner et al. 1991). However, as noted by Milner-Brown et al. (1975), such synchronisation may not manifest itself in measures calculated from unrectified EMG. This is because the motor unit action potentials (MUAPs) are biphasic, and the synchronisation exhibits some jitter in its timing. On some occasions, the positive phase of the MUAP in one muscle will coincide with the positive phase in the other; on other occasions, a positive phase will overlap with a negative. The cancellation so caused could lead to zero correlation between unrectified EMGs even though motor units in the two muscles recorded from show synchronisation.
We were able to test whether this might occur using data recorded from a patient with Kallman's syndrome, and supplied by M. Mayston and J. Stephens (see Mayston et al. 1997). Surface EMG recordings had been made from left and right 1DI muscles during a maintained bilateral index finger abduction. Due to abnormal branching of corticospinal tract fibres, such patients show marked ‘mirroring’ of hand and finger movements, and there is pronounced short-term synchrony between surface EMGs recorded from homologous muscles in the left and right hands (Mayston et al. 1997). However, since the two recordings are made from physically distant locations, electrical cross-talk will be negligible. It is then possible to assess what effect motor unit synchronisation will have on EMG correlation.
Figure 2A (‘Raw’ trace) shows a short period of one of the EMG recordings from this patient, in which a MUAP can be clearly seen. Figure 2B shows a cross-correlation calculated between the unrectified EMGs from left and right 1DI. There is a large central peak (height, 0.178 mV ms−1). Cancellation of synchrony effects by the biphasic MUAPs does not therefore lead to uncorrelated EMGs, presumably because the jitter of the synchronisation is not considerably larger than the width of the MUAPs (around 10 ms as judged from Fig. 2A). It would therefore be invalid to apply a blind signal separation algorithm to EMGs to remove electrical cross-talk, since the assumption of uncorrelated original sources is violated.
However, it is possible to meet the requirements of the algorithm if a pre-processing step is used. Figure 2A shows the effect of successively differentiating the EMG signal. This operation renders the MUAP polyphasic, and each phase is much reduced in duration. Figure 2B shows the cross-correlation calculated between the two EMGs recorded from the Kallman's patient after they have been differentiated. The reduction in MUAP width causes greater cancellation of the temporally imprecise synchronisation, until the cross-correlation peak is of negligible amplitude if third-order differentiated signals are used.
We conclude that if EMG signals are firstly differentiated several times, there will be sufficient cancellation of positive and negative phases of the MUAPs to produce negligible correlation between EMGs even when there is clear physiological synchrony. Any remaining correlation can then be confidently assigned to electrical cross-talk, which can be removed using a blind separation algorithm.
Effect of differentiation and separation on EMG
Figure 3 illustrates the application of these signal processing methods to EMGs recorded from a normal subject. Figure 3A shows the progression of a 50 ms section of EMG from the 1DI muscle through the three stages of the separation process. The raw data contains a waveform which was probably produced either by a single motor unit, or by a few units discharging together. After third-order differentiation this MUAP shape was rendered polyphasic. Following application of the separation algorithm, the general form and shape was conserved although there were small alterations in the amplitude, reflecting the removal of cross-talk. If desired, the separated signal can then be integrated three times to restore a signal comparable with the original data (see record at far right of Fig. 3A).
Figure 3. Effect of differentiation and separation on EMG signals.
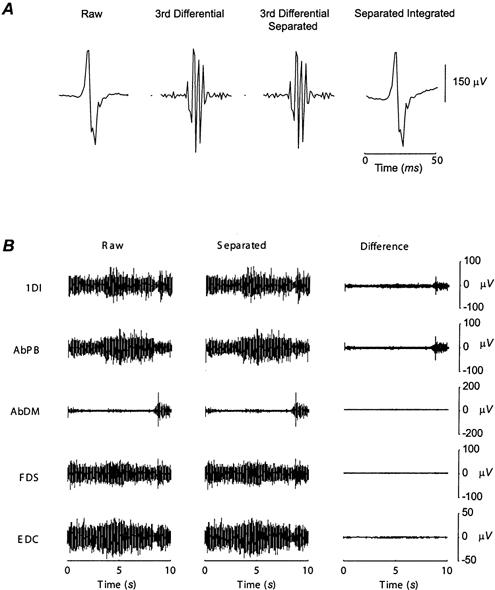
A. the effect of the process of differentiation and separation on a 50 ms window of EMG data from the 1DI muscle of a healthy subject. Moving from left to right the EMG is rendered polyphasic by third-order differentiation, then the common component due to electrical cross-talk is removed by separation, finally the polyphasic, separated EMG is reintegrated. Note the similarity between the original EMG signal and the final processed EMG signal. B, the effect of the separation algorithm on the five EMGs recorded from a single subject. The data shown is the average of the unrectified signals, pooled across trials. Note that the EMGs with the largest amount of electrical cross-talk, shown in the difference plot, are the intrinsic hand muscles.
Figure 3B shows the effect of the blind separation algorithm on the five surface EMGs recorded from a single subject. The left column shows the raw EMG recorded from each muscle for a single trial of the task. The middle column shows the output of the separation algorithm. After separation each EMG shows the same gross pattern of EMG modulation with the task as in the raw recordings. However, when the difference between the raw and separated signals is calculated (Fig. 3B, right panel) the effect of the separation is clear. The largest change is to the EMGs from 1DI and AbPB. A waveform has been removed from each of these, which appears to have a similar modulation with the task as the AbDM muscle, and is presumably due to cross-talk from this source. Only negligible changes have been made to EMGs recorded from the spatially distant electrodes, which is expected since electrical cross-talk between them should be small.
Figure 4 shows the effect of the separation algorithm on the cross-correlations between the 1DI and AbPB EMG recorded from a single subject. Figure 4A illustrates the correlation between the unrectified, third-order differentiated EMGs. Unlike the bilateral data from the Kalman's patient in Fig. 2, a large narrow central peak is seen, caused by electrical cross-talk between these two spatially close electrode pairs. There are also several narrow peaks either side of zero lag, presumably reflecting the autocorrelations of the single motor units from each EMG after they have been rendered polyphasic by differentiation. Figure 4B shows the cross-correlation between the separated EMGs. The blind separation algorithm has successfully abolished the peak, indicating that cross-talk has been removed from the separated signals.
Figure 4. Effect of ‘blind separation’ single subject data.
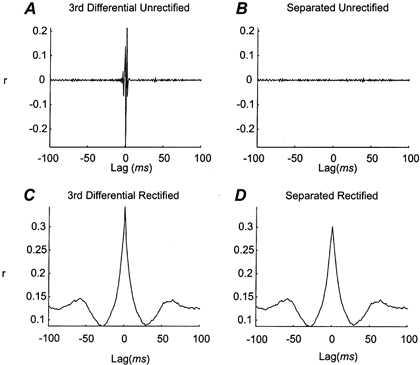
The cross-correlation between the non-separated and separated third-order differential of the EMGs recorded from AbPB and 1DI of a healthy subject during a precision grip task. A, cross-correlation for the non-separated unrectified signals. B, cross-correlation of the separated unrectified signals. C, cross-correlation of the non-separated rectified signals. D, the cross-correlation of the separated rectified signals. All the cross-correlations were calculated across the entire time of the ramp task, a period of ∼510 s.
As shown above, physiological synchrony makes no contribution to the cross-correlation between pairs of unrectified EMGs after they have been third-order differentiated. However, as noted by Milner-Brown et al. (1975), cancellation will not occur if the EMGs are first rectified before correlation. Figure 4C shows the cross-correlation between the rectified differentiated EMGs. A tall, broad peak can now be seen, reflecting physiological synchrony. There are clear side-bands around 60 ms, indicating a considerable component of this synchrony at ∼17 Hz, as previously reported (Farmer et al. 1993; Baker et al. 1997). Figure 4D presents the correlation between the rectified separated signals. It has a similar shape to that in Fig. 4C, showing that the properties of the synchrony between the EMGs have been preserved through the separation algorithm. However, the size of the peak is reduced (0.302 compared with 0.343 in Fig. 4C). This is as expected, since the peak of Fig. 4C reflects both motor unit synchronisation and cross-talk, whereas in Fig. 4D the contribution of cross-talk has been removed. The figure therefore illustrates how important it is to remove cross-talk in this way if an accurate assessment is to be made from surface EMG recordings of the strength of zero-lag physiological synchronisation.
Data from all the subjects showed an abolition of the central peak in the unrectified separated EMGs and also showed similar oscillatory synchrony in the 15–30 Hz range between rectified separated EMGs, with a mean lag of the side peaks of 50.7 ms (s.d., 2.8 ms; range, 36–70 ms).
Effect of electrical cross-talk on coherence estimates
The effect of the cross-talk on the estimates of coherence between muscle EMGs was assessed. Figure 5 shows the spectral analysis data for the 1DI-AbPB muscle pair from a single healthy subject. Figure 5A and B shows the power spectra for the two muscles before and after the removal of electrical cross-talk. As the separated EMGs are of arbitary units, due to the separation procedure, all of the power spectra were normalised so that they were a fraction of their total power. Both power spectra were almost identical before and after separation and showed only small differences in amplitude after separation. This was also true for the coherence spectra calculated between the two muscles (Fig. 5C). Although the two spectra did not overlie exactly, indicating that there were differences between the two spectra, these differences were not significant at any frequency (arctanh comparison P > 0.05, and Student's paired t test P > 0.05). Across all subjects no EMG-EMG coherence showed a significant difference at any frequency as a result of the separation even though the signals were contaminated by electrical cross-talk (see Fig. 4A). We therefore conclude that contamination by electrical cross-talk is of negligible effect when computing coherence estimates.
Different components of synchrony
Figure 6 shows an example of a time-resolved cross-correlation calculated between separated and rectified AbPB and 1DI EMGs in a single subject. Figure 6A shows the target lever position which the subjects were required to match (yellow shading), and overlain are the averaged actual finger and thumb traces for this subject. Figure 6B shows the averaged rectified EMG from these two muscles; both muscles show a pronounced modulation in activity level with performance of this task.
Figure 6. Task-dependent changes in oscillatory and non-oscillatory synchrony: single subject.

A shows the performance of the subject. The yellow line indicates the position of the yellow target boxes and the red line indicates the subject's average performance over all correctly performed trials. B shows the unseparated rectified EMGs for 1DI and AbPB averaged over all correctly performed trials. The EMG traces shown were down-sampled to an effective sampling rate of 100 Hz and low-pass filtered at 10 Hz. C-E, time-lag maps showing variation in cross-correlation during performance of the task, calculated between separated AbPB and 1DI EMGs for a single subject, across 50 trials. The ramp phase of the task occurred at time 3–5 s. A shows the time-lag maps for the raw data and B for the raw data notch filtered to exclude data in the 15–30 Hz range. C shows the time-lag map produced by the subtraction of the filtered from the raw map. F-H shows the modulation in the amplitude of the central peak with respect to the time.
Figure 6C shows the time-resolved cross-correlation; the lever target position is reproduced beneath, as below all time-resolved cross-correlations illustrated, to allow comparison of features with task phase. There is a peak at zero lag, which occurs predominantly during the two hold phases of the task. During these periods of steady holding, there are also subpeaks at approximately ± 50 ms; these correspond to the 15–30 Hz coherence shown earlier. Figure 6F shows the mean size of the central peak (within 5 ms of zero lag) as a function of time during task performance. This makes clear that not only is synchrony greater during the hold phases, but also that it is larger in the second hold period than the first. We have previously reported a similar result for 15–30 Hz coherence between EMGs in this task (Kilner et al. 1999).
Figure 6D and E shows the time-resolved cross-correlation filtered selectively to exclude, or to include, frequencies in the 15–30 Hz range. Figure 6G and H illustrate the corresponding time course of the amplitude of the central peak. It is clear that the majority of the synchronisation seen in Fig. 6A is oscillatory in nature, and that this component almost exclusively accounts for the modulation with the task.
The brief, large peaks seen at the end and beginning of the task in the non-oscillatory plot (Fig. 6D) relate to periods when the two muscles have near-zero levels of EMG, and should thus be considered unreliable. Figure 6D also shows weak subpeaks at around ± 20 ms lag. It is possible that these reflect oscillatory activity at approximately 40 Hz which has been described in non-maximally contracting muscles (the ‘Piper rhythm’; Brown, 2000). Alternatively, these peaks may simply be harmonics of the 15–30 Hz oscillations which remain after the narrow-band filter is applied. The magnitude of these faster oscillations was generally small in comparison with the central peak and was therefore unlikely to affect the subsequent analysis of the central peak height. Such higher frequency oscillatory side-bands have also been seen following a similar analysis of cortical data by Baker et al. (2001).
Time-resolved cross-correlations were calculated for each subject and each muscle pair. These measures were firstly combined across subjects separately for each pair of muscles and examined. However, no clear differences were seen between the different muscle pairs, so that it was decided to combine time-resolved cross-correlations both across subjects and muscle pairs. Kilner et al. (1999) also pooled coherence across muscle pairs in this way. The results of this analysis are shown in Fig. 7. Figure 7A–C shows the raw plots, and those filtered to include or exclude the 15–30 Hz signals respectively. Similar results are seen as in the single subject data of Fig. 6. There is a clear zero-lag peak, which is strongest during the hold periods of the task. On decomposition, it is seen that this modulation is mainly caused by the oscillatory component of the synchrony (Fig. 7C), with the non-oscillatory component remaining relatively constant.
Figure 7. Task-dependent changes in oscillatory and non-oscillatory synchrony: pooled data.
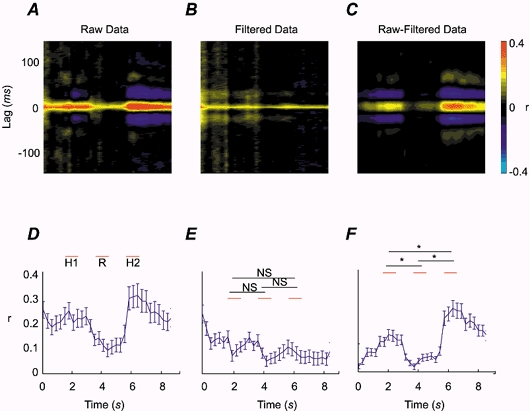
A-C, time-lag maps showing variation in cross-correlation during performance of the task, calculated and combined across all 12 subjects and 10 muscle pairs. The ramp phase of the task occurred at time 3–5 s. A shows the time-lag maps for the raw data and B for the raw data notch filtered to exclude data in the 15–30 Hz range. C shows the time-lag map produced by the subtraction of the filtered from the raw map. D-F shows the modulation in the amplitude of the central peak with respect to the time, error bars indicate s.e.m. Student's paired t tests were carried on the magnitude of the central peak in discrete 1 s sections between the H1, R and H2 periods of the task, as indicated by the red lines. Asterisks indicate significant differences at P < 0.001 and N.S. differences which are not significant (P > 0.05).
Figure 7D–F show the modulation of the central peak size (± 5 ms) during the task measured from the plots of Fig. 7A–C pooled across subjects and muscle pairs; the error bars are ± 1 s.e.m. In order to test the significance of the changes seen, three periods 1 s long were defined, as shown in Fig. 7D. These corresponded to the middle of the first hold (H1), second hold (H2) and the linear ramp phase (R). The Z values for these periods were compared using Student's paired t tests (see Methods). For the oscillatory correlation (Fig. 7C and F), synchrony was significantly greater during H2 than H1 and the synchrony during both hold periods was significantly greater than during the ramp period (P < 0.001, corrected for multiple comparisons). This was in contrast to the non-oscillatory correlations (Fig. 7B and E) where there were no significant differences between the three sections (P > 0.1, corrected for multiple comparisons).
DISCUSSION
The results presented in this study are important in two ways. First, we have shown that it is possible to remove contamination of nearby EMG recordings by electrical cross-talk using a statistical signal processing technique. Secondly, with this contaminant removed, we have shown that there is a striking difference in the task-dependent modulation of oscillatory and non-oscillatory synchrony between muscles during a dynamic precision grip task. Oscillatory synchrony in the 15–30 Hz range was only present during the steady hold periods and reduced during a slow linear tracking movement, whereas the non-oscillatory synchrony was not significantly modulated by the different phases of the task.
Removal of electrical cross-talk from surface EMGs
The ‘blind signal separation’ algorithm used in this study was able to remove electrical cross-talk between two EMG recordings successfully. A related algorithm has previously been used to remove eye movement artefacts from EEG recordings (Makeig et al. 1996), and to investigate task-related fMRI activity in the human brain (McKeown et al. 1998). As far as we are aware, this is the first report to apply this approach to EMG. As shown in Fig. 2, raw EMG recordings violate a central basic assumption of the algorithm, that the original signals should be uncorrelated, since motor units from different muscles are often weakly synchronised together (Bremner et al. 1991; Huesler et al. 2000). Like electrical cross-talk, synchronisation is stronger the closer together muscle pairs are (Bremner et al. 1991). However, cross-talk is deterministic, and results in a faithful reproduction, although possibly attenuated and filtered, of one EMG in the recording from another. By contrast, physiological synchronisation has stochastic temporal jitter. We have shown that this difference can allow the two effects to be isolated, and the cross-talk then removed.
Although this technique has been successful, it is important to stress its limitations. The signals produced following separation do not contain solely the activities of the muscles which were intended to be recorded. There are at least 39 muscles used to control the hand; in this study we have recorded from just five. The algorithm can only produce as output the same number of signals as are input. Each recording is therefore likely to contain EMG from multiple muscles; all that the algorithm guarantees is that no two recordings will contain common activity. Contamination from additional muscles in this way will in general vary between different behavioural tasks. The unmixing filters estimated for optimal separation in one task may not therefore generalise to other tasks.
Task-dependent modulation of oscillatory and non-oscillatory synchrony between EMGs
The task-dependent modulation of the oscillatory (15-30 Hz) and non-oscillatory synchrony between hand and forearm EMGs both extends and supports previous studies of synchrony in the motor system. The two types of synchrony showed different task modulations. Oscillatory synchrony was greatest during the hold periods, and was largest of all in the second hold phase. It was abolished during movement. This confirms our previous findings on the same data set using coherence analysis (Kilner et al. 1999). By contrast, the non-oscillatory synchrony showed no significant differences between the three main phases of the task.
A major source of the 15–30 Hz synchrony between EMGs is likely to be synchronisation at this frequency between corticospinal neurones which provide mono-synaptic inputs to motoneurones. Such synchrony has been demonstrated directly in monkey (Baker et al. 1997; Baker et al. 2001), and field potential measures of motor cortical activity are coherent with contralateral EMGs in this frequency band in both humans (Conway et al. 1995; Salenius et al. 1997; Kilner et al. 2000) and monkey (Baker et al. 1997). Single motor unit coherence at 15–30 Hz is abolished in stroke patients with damage to their contralateral motor cortex (Farmer et al. 1993).
The non-oscillatory synchronisation described here could be attributed to two sources. First, it is known that for several classes of motoneurone inputs, single fibres branch and innervate cells from multiple motoneurone pools. This is the case for cortico-motoneuronal cells (Shinoda et al. 1981; Buys et al. 1986) and probably for Ia afferents (Scott & Mendell, 1976; Nelson & Mendell, 1978; Fritz et al. 1989). It would also seem a likely arrangement for spinal interneurone inputs (Perlmutter et al. 1998; Maier et al. 1998). Several authors have suggested that central peaks in cross-correlograms calculated between single motor units arise from such branched fibre common input (Datta & Stephens 1990; Datta et al. 1991; Bremner et al. 1991; Farmer et al. 1993; Marsden et al. 1999; Huesler et al. 2000). Whilst these anatomical connections are fixed, it is still possible that the level of synchrony which they cause could modulate with task phase, if the activity in the branched fibres changed as a proportion of the total input to the motoneurones.
Secondly, non-oscillatory synchrony between EMGs could also arise from pre-synaptic synchronisation between motoneurone inputs. Baker et al. (2001) calculated time-resolved cross-correlations between identified corticospinal neurones in monkey primary motor cortex during a precision grip task. Using a similar technique of filtering the cross-correlation as implemented here, they showed that motor cortical cells exhibited both oscillatory and non-oscillatory synchrony. At the point when the total synchrony was largest, only around half of the synchronisation was contributed by 18–37 Hz frequency components. Both the oscillatory and the non-oscillatory synchrony modulated with the task, and were both maximal during the hold phase.
A puzzling feature of the present study is therefore the relative lack of modulation of the non-oscillatory motoneurone synchrony with the task. A possible explanation may be that this non-oscillatory synchrony is indeed caused both by branched fibre common input, and by pre-synaptic synchronisation. The firing rate of corticospinal cells is known to be greater during movements than during steady contractions (Lemon et al. 1986), so that the proportion of input to the motoneurones from branched corticospinal axons could be greater during movement. By contrast, as noted above, non-oscillatory synchrony between motor cortical neurones has been shown to be greater during holding (Baker et al. 2001). At least for the corticospinal system, therefore, the two sources of synchrony could modulate in an opposite manner during task performance, leading to the observed lack of apparent net change.
We have previously suggested that synchrony amongst the inputs to motoneurones could act as an efficient means of driving them at a given firing rate with as low an input firing rate as possible (Baker et al. 1999). Both oscillatory and non-oscillatory pre-synaptic synchrony in the motoneurone inputs will contribute to this effect. By contrast, although branched fibre common inputs are capable of causing synchrony between motor unit pairs, from the viewpoint of a single motoneurone they are no different from other inputs. They will show no more temporal summation than expected by chance, and will not therefore contribute to the ‘efficient’ motoneurone recruitment which we have previously proposed. If it is the case that our measure of non-oscillatory synchrony between EMGs is produced by both pre-synaptic synchrony and fibre branching, it is therefore a poor indicator of the extent to which motoneurone recruitment is being achieved by input synchrony versus total input rate.
Acknowledgments
The authors thank M. Mayston, L. Harrison and J. Stephens for the use of their data recorded from a patient with Kallman's syndrome, and Bill Fitzgerald and Alijah Ahmed for their expert knowledge of the blind separation algorithm. This work was funded by the Wellcome Trust and the Brain Research Trust.
REFERENCES
- Baker SN, Kilner JM, Pinches EM, Lemon RN. The role of synchrony and oscillations in the motor output. Experimental Brain Research. 1999;128:109–117. doi: 10.1007/s002210050825. [DOI] [PubMed] [Google Scholar]
- Baker SN, Olivier E, Lemon RN. Coherent oscillations in monkey motor cortex and hand muscle EMG show task-dependent modulation. Journal of Physiology. 1997;501:225–241. doi: 10.1111/j.1469-7793.1997.225bo.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baker SN, Spinks R, Jackson A, Lemon RN. Synchronization in monkey motor cortex during a precision grip task. I. Task-dependent modulation in single-unit synchrony. Journal of Neurophysiology. 2001;85:869–885. doi: 10.1152/jn.2001.85.2.869. [DOI] [PubMed] [Google Scholar]
- Bell AJ, Sejnowski TJ. An information-maximization approach to blind separation and blind deconvolution. Neural Computation. 1995;7:1129–1159. doi: 10.1162/neco.1995.7.6.1129. [DOI] [PubMed] [Google Scholar]
- Bell AJ, Sejnowski TJ. Learning the higher-order structure of a natural sound. Network: Computation in Neural Systems. 1996;7:261–266. doi: 10.1088/0954-898X/7/2/005. [DOI] [PubMed] [Google Scholar]
- Bell AJ, Sejnowski TJ. The ‘independent components’ of natural scenes are edge filters. Vision Research. 1997;37:3327–3338. doi: 10.1016/s0042-6989(97)00121-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bigland B, Lippold OCJ. The relation between force, velocity and integrated electrical activity in human muscles. Journal of Physiology. 1954;123:214–224. doi: 10.1113/jphysiol.1954.sp005044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bremner FD, Baker JR, Stephens JA. Effect of task on the degree of synchronization of intrinsic hand muscle motor units in man. Journal of Neurophysiology. 1991;66:2072–2083. doi: 10.1152/jn.1991.66.6.2072. [DOI] [PubMed] [Google Scholar]
- Brown P. Cortical drives to human muscle: the Piper and related rhythms. Progress in Neurobiology. 2000;60:97–108. doi: 10.1016/s0301-0082(99)00029-5. [DOI] [PubMed] [Google Scholar]
- Buys EJ, Lemon RN, Mantel GWH, Muir RB. Selective facilitation of different hand muscles by single corticospinal neurones in the conscious monkey. Journal of Physiology. 1986;381:529–549. doi: 10.1113/jphysiol.1986.sp016342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chan DCB, Godsill SJ, Rayner PJW. Multi-Channel Multi-Tap Signal Separation by Output Decorrelation. 1996. pp. 0951–9211. CUED/F. INFENG/TR.250, Department of Engineering, Cambridge University. ISSN.
- Conway BA, Halliday DM, Shahani U, Maas P, Weir AL, Rosenberg JR. Synchronization between motor cortex and spinal motoneuronal pool during the performance of a maintained motor task in man. Journal of Physiology. 1995;489:917–924. doi: 10.1113/jphysiol.1995.sp021104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Datta AK, Farmer SF, Stephens JA. Central nervous pathways underlying synchronization of human motor unit firing studied during voluntary contractions. Journal of Physiology. 1991;432:401–425. doi: 10.1113/jphysiol.1991.sp018391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Datta AK, Stephens JA. Synchronization of motor unit activity during voluntary contraction in man. Journal of Physiology. 1990;422:397–419. doi: 10.1113/jphysiol.1990.sp017991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donoghue JP, Sanes JN, Hatsopoulos NG, Gaal G. Neural discharge and local field potential oscillations in primate motor cortex during voluntary movements. Journal of Neurophysiology. 1998;79:159–173. doi: 10.1152/jn.1998.79.1.159. [DOI] [PubMed] [Google Scholar]
- Farmer SF, Bremner FD, Halliday DM, Rosenberg JR, Stephens JA. The frequency content of common synaptic inputs to motoneurones studied during voluntary isometric contraction in man. Journal of Physiology. 1993;470:127–155. doi: 10.1113/jphysiol.1993.sp019851. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fritz N, Illert M, dela Motte S, Reeh P, Saggau P. Pattern of monosynaptic Ia connections in the cat forelimb. Journal of Physiology. 1989;19:321–351. doi: 10.1113/jphysiol.1989.sp017875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gibbs J, Harrison LM, Stephens JA. Cross-correlation analysis of motor unit activity recorded from two separate thumb muscles during development in man. Journal of Physiology. 1997;499:255–266. doi: 10.1113/jphysiol.1997.sp021924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huesler EJ, Maier MA, Hepp-Reymond M-C. EMG activation during force production in precision grip. III Synchronisation of single motor units. Experimental Brain Research. 2000;134:441–455. doi: 10.1007/s002210000484. [DOI] [PubMed] [Google Scholar]
- Kilner JM, Baker SN, Salenius S, Hari R, Lemon RN. Human cortical muscle coherence is directly related to specific motor parameters. Journal of Neuroscience. 2000;20:8838–8845. doi: 10.1523/JNEUROSCI.20-23-08838.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kilner JM, Baker SN, Salenius S, Jousmaki V, Hari R, Lemon RN. Task-dependent modulation of Hz coherence between rectified EMGs from human hand and forearm muscles. Journal of Physiology. 1999;516:559–570. doi: 10.1111/j.1469-7793.1999.0559v.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee T-W. Independent component analysis, Theory and Applications. Boston: Kluwer Academic; 1998. [Google Scholar]
- Lemon RN, Muir RB, Mantel GWH. Corticospinal facilitation of hand muscles during voluntary movement in the conscious monkey. Journal of Physiology. 1986;381:497–527. doi: 10.1113/jphysiol.1986.sp016341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKeown M, Makeig S, Brown G, Jung T-P, Kindermann S, Bell AJ, Sejnowski TJ. Analysis of fMRI by blind separation into independent spatial components. Human Brain Mapping. 1998;6:1–31. doi: 10.1002/(SICI)1097-0193(1998)6:3<160::AID-HBM5>3.0.CO;2-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maier MA, Hepp-Reymond MC. EMG activation patterns during force production in precision grip. II. 5Muscular synergies in the spatial and temporal domain. Experimental Brain Research. 1995;103:123–136. doi: 10.1007/BF00241970. [DOI] [PubMed] [Google Scholar]
- Maier MA, Perlmutter SI, Fetz EE. Response patterns and force relations of monkey spinal interneurons during active wrist movement. Journal of Neurophysiology. 1998;80:2495–2513. doi: 10.1152/jn.1998.80.5.2495. [DOI] [PubMed] [Google Scholar]
- Makeig S, Bell AJ, Jung T, Sejnowski TJ. Independent component analysis of electroencephalographic data. Advances in Neural Information Processing Systems. 1996;8:145–151. [Google Scholar]
- Marsden JF, Farmer SF, Halliday DM, Rosenberg JR, Brown P. The unilateral and bilateral control of motor unit pairs in the first dorsal interosseous and paraspinal muscles in man. Journal of Physiology. 1999;521:553–564. doi: 10.1111/j.1469-7793.1999.00553.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mayston MJ, Harrison LM, Quinton R, Stephens JA, Krams M, Bouloux PM. Mirror movements in X-linked Kallmann's syndrome. I. A neurophysiological study. Brain. 1997;120:1199–1216. doi: 10.1093/brain/120.7.1199. [DOI] [PubMed] [Google Scholar]
- Milner-Brown HS, Stein RB. The relation between the surface electromyogram and muscular force. Journal of Physiology. 1975;246:549–569. doi: 10.1113/jphysiol.1975.sp010904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murthy VN, Fetz EE. Oscillatory activity in sensorimotor cortex of awake monkeys: synchronization of local field potentials and relation to behaviour. Journal of Neurophysiology. 1996;76:3349–3967. doi: 10.1152/jn.1996.76.6.3949. [DOI] [PubMed] [Google Scholar]
- Nelson SG, Mendell LM. Projection of single knee flexor Ia fibers to homonymous and heteronymous motoneurons. Journal of Neurophysiology. 1978;41:778–787. doi: 10.1152/jn.1978.41.3.778. [DOI] [PubMed] [Google Scholar]
- Perlmutter SI, Maier MA, Fetz EE. Activity of spinal interneurons and their effects on forearm muscles during voluntary wrist movements in the monkey. Journal of Neurophysiology. 1998;80:2475–2494. doi: 10.1152/jn.1998.80.5.2475. [DOI] [PubMed] [Google Scholar]
- Raz A, Feingold A, Zelanskaya V, Vaadia E, Bergman H. Neuronal synchronization of tonically active neurons in the striatum of normal and parkinsonian primates. Journal of Neurophsiology. 1996;76:2083–2088. doi: 10.1152/jn.1996.76.3.2083. [DOI] [PubMed] [Google Scholar]
- Rosenberg JR, Amjad AM, Breeze P, Brillinger DR, Halliday DM. The fourier approach to the identification of functional coupling between neuronal spike trains. Progress in Biophysics and Molecular Biology. 1989;53:1–31. doi: 10.1016/0079-6107(89)90004-7. [DOI] [PubMed] [Google Scholar]
- Salenius S, Portin K, Kajola M, Salmelin R, Hari R. Cortical control of human motoneuron firing during isometric contraction. Journal of Neurophysiology. 1997;77:3401–3405. doi: 10.1152/jn.1997.77.6.3401. [DOI] [PubMed] [Google Scholar]
- Scott JG, Mendell LM. Individual EPSPs produced by single triceps surae Ia afferent fibers in homonymous and heteronymous motoneurons. Journal of Neurophysiology. 1976;39:670–692. doi: 10.1152/jn.1976.39.4.679. [DOI] [PubMed] [Google Scholar]
- Sears TA, Stagg D. Short-term synchronization of intercostal motoneurone activity. Journal of Physiology. 1976;263:357–381. doi: 10.1113/jphysiol.1976.sp011635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shadlen MN, Newsome WT. Noise, neural codes and cortical organization. Current Opinion in Neurobiology. 1994;4:569–579. doi: 10.1016/0959-4388(94)90059-0. [DOI] [PubMed] [Google Scholar]
- Shinoda Y, Yokota J, Futami T. Divergent projection of individual corticospinal axons to motoneurons of multiple muscles in the monkey. Neuroscience Letters. 1981;23:7–12. doi: 10.1016/0304-3940(81)90182-8. [DOI] [PubMed] [Google Scholar]
- Smith WS, Fetz EE. Effects of synchrony between cortico-motoneuronal cells on postspike facilitation of primate muscles and motor units. Neuroscience Letters. 1989;96:76–81. doi: 10.1016/0304-3940(89)90246-2. [DOI] [PubMed] [Google Scholar]
- Snedecor GW, Cochran WG. Statistical Methods. (8) 1989 [Google Scholar]
- Softky WR. Simple codes versus efficient codes. Current Opinion in Neurobiology. 1995;5:239–247. doi: 10.1016/0959-4388(95)80032-8. [DOI] [PubMed] [Google Scholar]
- Welsh JP, Lang EJ, Sugihara I, Llinas R. Dynamic organization of motor control within the olivocerebellar system. Nature. 1995;374:453–457. doi: 10.1038/374453a0. [DOI] [PubMed] [Google Scholar]


