Abstract
The effect of temperature on isometric tension with and without the regulatory proteins tropomyosin and troponin was studied in bovine myocardium using a thin filament removal and reconstitution protocol. In control bovine myocardium, isometric tension increased linearly with temperature in the range 5–40 °C: isometric tension at 10 and 30 °C was 0.65 and 1.28 times that at 20 °C, respectively, with a Q10 of about 1.4. In actin filament-reconstituted myocardium without regulatory proteins, the temperature effect on isometric tension was less: isometric tension at 10 and 30 °C was 0.96 and 1.17 times that at 20 °C, respectively, with a Q10 of about 1.1. The temperature dependence of the apparent rate constants was studied using sinusoidal analysis. The temperature dependence of 2πb (rate constant of delayed tension phase) did not vary significantly with the regulatory proteins under the standard activating condition (5 mm MgATP, 8 mm Pi, 200 mm ionic strength, pCa 4.66, pH 7.00). Q10 for 2πb in control and actin filament-reconstituted myocardium was 3.8 and 4.0, respectively. There were two phases to the temperature dependence of 2πc (rate constant of quick recovery). In control and thin filament-reconstituted myocardium, Q10 for 2πc was approximately 5.5 in the low temperature range (≤ 25 °C) and 2.7 in the high temperature range (≥ 30 °C). In actin filament-reconstituted myocardium, Q10 for 2πc was 8.5 in the low temperature range and 3.6 in the high temperature range. The above results demonstrate that regulatory proteins augment the temperature dependence of isometric tension, indicating that the regulatory proteins may modify the actomyosin interaction.
Force generation and concomitant shortening in muscle is achieved by a cyclic interaction of two macromolecules: myosin, the main component of the thick filament, and actin, the main component of the thin filament. In the presence of actin, myosin cross-bridges hydrolyse ATP and convert its free energy to generate useful work. This process involves chemical reactions that are strongly influenced by ambient temperature. In skeletal and cardiac muscles on the one hand, it was shown that active isometric tension is highly temperature dependent (Ranatunga, 1982; Ranatunga & Wylie, 1983). This observation suggests to us that elementary steps of the cross-bridge cycle are not equally affected by the temperature change. Examination of isometric tension after a rapid temperature increase (T-jump) yielded information on the temperature dependence of apparent rate constants, demonstrating that the force-generation step is an endothermic reaction in rabbit psoas fibres (Goldman et al. 1987), in frog semitendinosus muscle fibres (Tsaturyan et al. 1999) and in rat myocardium (Ranatunga, 1999). Studies using the sinusoidal analysis technique also demonstrated that the force-generation step is an endothermic reaction, and is the most temperature-sensitive step of all elementary steps of the cross-bridge cycle (Zhao & Kawai, 1994; Wang & Kawai, 2001). In smooth muscles on the other hand, a study demonstrated that the temperature dependence of isometric tension is small (Jaworowski & Arner, 1998). Furthermore, a study using the in vitro motility assay system demonstrated that force between a single actin filament and heavy meromyosin (HMM) molecules does not depend on temperature (Kawai et al. 2000). Because both smooth muscle and the in vitro motility assay system lack troponin, a question arose as to the role of regulatory proteins in the temperature dependence of striated muscles.
In this study, we use the actin filament-reconstitution protocol to examine whether the regulatory proteins tropomyosin (Tm) and troponin (Tn) affect the temperature dependence of isometric tension. The thin filament in myocardium can be selectively removed by treatment with the plasma protein gelsolin (Funatsu et al. 1993). Gelsolin-treated myocardium loses the ability to generate active tension because of the absence of actin. By adding purified G-actin in the polymerizing condition to this thin filament-extracted myocardium, the actin filament can be reconstituted (Fujita et al. 1996). This actin filament-reconstituted myocardium develops force depending on the degree of reconstitution in the presence of MgATP, and this force is not Ca2+ sensitive. Further reconstitution with Tm and Tn results in full recovery of the Ca2+ sensitivity and isometric tension (Fujita et al. 1996, 2002) as well as the rate constants of the elementary steps of the cross-bridge cycle (Fujita et al. 2002). The present study demonstrates that, in actin filament-reconstituted myocardium, the temperature dependence of isometric tension was much less than that of control myocardium or thin filament-reconstituted myocardium, indicating that regulatory proteins augment the temperature effect on isometric tension.
METHODS
Chemicals and solutions
Creatine phosphate (CP), ATP, Mops and EGTA were purchased from Sigma Chemical Co. (St Louis, MO, USA); CaCO3, Mg(OH)2, NaOH, KOH, KH2PO4, K2HPO4, NaN3 and propionic (Prop) acid were purchased from Fisher Scientific Co. (Hanover Park, IL, USA); creatine kinase (CK) was purchased from Boehringer Mannheim (Indianapolis, IN, USA).
The composition of each solution used was as follows. Relaxing solution: 6.0 mm K2H2EGTA, 2.2 mm Na2MgATP, 5.0 mm Na2K2ATP, 8.0 mm phosphate (K1.5H1.5Pi), 41 mm NaProp, 74.5 mm KProp, 10 mm Mops, 40 mm 2,3-butanedione 2-monoxime (BDM). Wash solution: 6.0 mm K2H2EGTA, 2.2 mm Na2MgATP, 5.0 mm K2H2ATP, 41 mm NaProp, 93.1 mm KProp, 10 mm Mops. Standard activating solution: 6.0 mm K2CaEGTA (pCa 4.66), 5.8 mm Na2MgATP, 1.36 mm K2Na2ATP, 15 mm Na2CP, 8.0 mm K1.5H1.5Pi, 0.7 mm NaProp, 73.1 mm KProp, 10 mm NaN3, 10 mm Mops, 320 unit ml−1 CK (0.64 mg ml−1). Rigor solution: 8.0 mm K1.5H1.5Pi, 55 mm NaProp, 122.0 mm KProp, 10 mm Mops. The pH was adjusted to 7.00, the Mg2+ concentration to 0.5 mm, the total Na+ concentration to 55 mm, and ionic strength adjusted to 200 mm by NaProp and KProp. EGTA, CaEGTA and Pi were added as neutral potassium salts, MgATP and CP as neutral sodium salts, and free ATP as Na2K2ATP. Individual concentrations of ionic species were calculated with our computer program using the following association constants (log values at pH 7.0): CaEGTA, 6.28; MgEGTA, 1.61; CaATP, 3.70; MgATP, 4.00; CaCP, 1.15; MgCP, 1.30.
Muscle bundles and proteins
Bovine hearts were obtained from a slaughterhouse and immediately cooled with crushed ice. The muscle bundles (approximately 2 mm in diameter, 10 mm in length) were excised from a straight portion of papillary muscles (right or left ventricle) and incubated in Na-skinning solution containing (mm): 2.0 dithiothreitol (DTT), 30 BDM, 10 K2H2EGTA, 5.0 Na2H2ATP, 2.0 Na2MgATP, 122 NaProp and 10 Mops (pH 7.0) for 3 h at 0 °C. Na-skinning solution was used to minimize initial contraction. For further skinning, the solution was replaced with K-skinning solution containing (mm): 2.0 DTT, 30 BDM, 10 K2H2EGTA, 5.0 Na2K2ATP, 2.0 Na2MgATP, 122 KProp and 10 Mops (pH 7.0), and stored overnight at 0 °C. BDM and EGTA were used to minimize force generation. The solution was then further replaced with one containing 50 % (v/v) glycerol, 2.0 mm DTT, 30 mm BDM, 10 mm K2H2EGTA, 5.0 mm Na2K2ATP, 2.0 mm Na2MgATP, 122 mm KProp and 10 mm Mops (pH 7.0) followed by storage at 0 °C. The solution was replaced once again the following day, and the muscle bundles were then stored at −20 °C.
Actin acetone powder was prepared according to the method of Kondo & Ishiwata (1976) from skeletal muscle of rabbits humanely killed in accordance with NIH guidelines. Actin was extracted from the acetone powder according to the method of Spudich & Watt (1971). Purified G-actin was stored at 0 °C and used within 2 weeks of extraction. The tropomyosin-troponin complex was prepared from bovine cardiac muscle according to the method of Ebashi & Endo (1968). Bovine plasma gelsolin was prepared according to the method of Kurokawa et al. (1990). Bovine plasma was obtained from a slaughterhouse.
Experimental procedure
A strip of bovine myocardium (80–150 μm in diameter and ∼2 mm in length) was dissected from the skinned muscle bundle and each end was attached to a stainless-steel wire (210 μm in diameter) with nail polish. One end of the strip was attached to a length driver and the other end to a tension transducer. The myocardium was stretched until small passive tension was visible. The length (L0) of the myocardium was determined at this time by measuring the end-to-end distance. The diameter was also measured with a dissection microscope. The myocardium was treated in relaxing solution containing 1 % (v/v) Triton X-100 for 20 min to further dissolve internal membrane systems. Triton X-100 was then washed out using relaxing solution.
Removal of the thin filament and its stepwise reconstitution
To remove the thin filament, a freshly prepared myocardium was treated with solution containing gelsolin at 2 °C for 80 min (composition: 117 mm KCl, 4.25 mm MgCl2, 1.9 mm CaCl2, 2.2 mm Na2K2ATP, 2.0 mm K2H2EGTA, 20 mm Mops (pH 7.0), 40 mm BDM and 0.3 mg ml−1 gelsolin). The gelsolin-treated myocardium did not develop active tension when tested at 25 °C. To reconstitute the actin filament, the gelsolin-treated myocardium was immersed in a solution containing 80 mm KI, 4.0 mm MgCl2, 4.0 mm Na2H2ATP, 4.0 mm K2H2EGTA, 20 mm BDM, 20 mm K1.5H1.5Pi (pH 7.0) and 1 mg ml−1 G-actin at 0 °C for 7 min; this procedure was repeated four times to avoid nucleation of actin. G-actin in the polymerizing solution was freshly prepared each time, just before use. The actin filament-reconstituted myocardium developed active tension irrespective of Ca2+ as expected, so that relaxation was achieved by 40 mm BDM and at 0 °C. Further reconstitution of the thin filament was achieved by immersing the actin filament-reconstituted myocardium in relaxing solution containing 4 mg ml−1 Tm-Tn complex for 12 h at 0 °C.
Deduction of the apparent rate constants 2πb and 2πc
Three muscle models (control, actin filament-reconstituted, and thin filament-reconstituted myocardium) were maximally activated in activating solution in a temperature-controlled bath at eight discrete temperatures as described above. The 0.25 % L0 peak-to-peak sinusoidal wave at 18 frequencies (f, 0.13–100 Hz) was synthesized in a PC with 386 CPU (Industrial Computer Source, San Diego, CA, USA) that controlled the length driver via a D/A converter. Tension and length signals were digitized by two 16-bit A/D converters and complex modulus data Y(f) were calculated as the ratio between the stress change (in N m−2) and the strain change (no unit) in the frequency domain. The complex modulus data obtained during relaxation were subtracted to correct for the pick-up at high frequencies. The complex modulus data were resolved into two exponential processes (B and C) by fitting the data to eqn (1) (Kawai & Brandt, 1980; Wannenburg et al. 2000):
| (1) |
where i = √−1, and f is the frequency of length oscillation. Lowercase letters b and c represent the characteristic frequencies of the respective processes, while uppercase letters B and C represent their magnitudes. Process B is a low-frequency exponential delay (b ≈ 1.5 Hz at 25 °C) at which muscle generates oscillatory work. Process C is a high-frequency exponential advance (c ≈ 5 Hz at 25 °C) at which the muscle absorbs work from the length driver. H is the elastic modulus extrapolated to the zero frequency. The elastic modulus extrapolated to the infinite frequency is calculated as Y∞ = H - B + C. This quantity is called [stiffness] in our reports, because of the ease of terminology. Process B corresponds to [phase 3′, process C corresponds to ]phase 2′, and Y∞ corresponds to [phase 1′ of tension transients in response to step length changes (Huxley & Simmons, 1971). In relaxed and rigor muscle fibres, these exponential processes were absent. 2πb and 2πc are the apparent rate constants of the respective processes. Details of the sinusoidal analysis technique have been published previously (Kawai & Brandt, 1980).
Laser scanning confocal microscopy
The myocardium was removed from the stainless-steel wires, and both ends of the myocardium were attached to a glass slide between two layers of double-sided adhesive tape. A coverslip was placed over the double-sided adhesive tape, so that a solution could be introduced from one end and removed from the other, and so that the myocardium was suspended in the solution without touching the glass surface. The myocardium was stained with 8 μm rhodamine-phalloidin (RhPh; Molecular Probes, Eugene, OR, USA) in relaxing solution overnight at 0 °C; unbound RhPh was then washed out with relaxing solution. For microscopic observation, 20 mm DTT was added to the solution. The preparation was observed using an inverted microscope (Axiovert 100M, Carl Zeiss, Oberkochen, Germany) equipped with a confocal scanning unit (LSM 510, Carl Zeiss) with Ar laser (543 nm wavelength).
RESULTS
Standard experiments
To determine the temperature dependence of isometric tension, the myocardium was first activated in the standard activating solution at 25 °C (see Fig. 2). Then the myocardium was relaxed, the temperature was lowered to 5 °C and active tension was measured. The temperature was then gradually elevated to 10, 15, 20, 25, 30, 35 and 40 °C, and active tension was measured at each temperature. At the end of the experiment, the temperature was brought back to 25 °C and active tension was measured again to detect any deterioration in the preparation. Any preparation that developed 85 % or less tension was discarded. After the last activation at 25 °C, the myocardium was brought into the rigor condition to detect the rigor stiffness. The standard activating solution contained 8 mm rather than 0–2 mm Pi, because cross-bridges are more populated in the states AM, AM.ATP, M.ATP, M.ADP.Pi (M, myosin; A, actin with or without Tm and Tn) at this concentration, hence the rate constants 2πb and 2πc can be resolved more accurately (Kawai et al. 1993; Fujita et al. 2002).
Figure 2. Slow pen trace of isometric tension at different temperatures in the three muscle models.
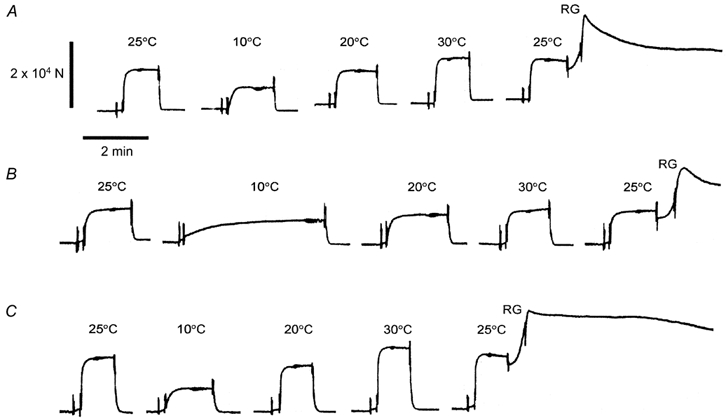
A, control bovine myocardium; B, actin filament-reconstituted myocardium; C, thin filament-reconstituted myocardium. Activation was achieved by immersing the myocardium in the standard activating solution. Before activation, the myocardium was washed in solution without BDM and Pi. The myocardium was first activated at 25 °C. The temperature was then increased in 5 °C steps and active tension was measured. In this figure, active tension at 10, 20 and 30 °C is shown. Active tension at 25 °C was then measured again to detect any deterioration in the preparation. The preparation was discarded when more than a 15 % tension decrease was noticed. At RG, the myocardium was brought to the rigor condition with two solution changes. Relaxation was obtained in solution containing 40 mm BDM at 0 °C. The diameter of the muscle fibres in A, B and C was 90, 120 and 90 μm, respectively.
Confocal images of tension development in control, actin filament-reconstituted and thin filament-reconstituted myocardium
Figure 1 shows a laser scanning confocal microscope image of control, gelsolin-treated and actin filament-reconstituted myocardium stained with RhPh, which selectively stains the actin filament. In the control myocardium (Fig. 1A), the thin filament is visible as a white band, the centre of which is the Z-line. The dark band is the H-zone where the thin filament is absent. In the gelsolin-treated myocardium (Fig. 1B), the dark band is widened, indicating that much of the actin filament has been removed. The remaining actin is limited to the Z-line level, as shown by the narrow white band. We confirmed that active tension did not develop after 80 min of gelsolin treatment. In the actin filament-reconstituted myocardium (Fig. 1C), the fluorescence image is almost identical to that of control myocardium (Fig. 1A). The isometric tension of actin filament-reconstituted myocardium was 9.7 ± 0.8 kN m−2 (n = 10) with the standard activating solution at 25 °C. This tension is approximately 0.6 times that of control myocardium (16.7 ± 1.7 kN m−2; n = 11). This result is in close agreement with a previous report that the actin filament-reconstituted myocardium develops less tension than the control myocardium (Fujita et al. 2002). In thin filament-reconstituted myocardium, isometric tension at 25 °C was 19.5 ± 2.0 kN m−2 (n = 8), which is close to that of control myocardium. Rigor stiffness at 25 °C in control, actin filament-reconstituted and thin filament-reconstituted myocardium was 1.18 ± 0.09 (n = 11), 1.19 ± 0.06 (n = 10) and 1.15 ± 0.10 MN m−2 (n = 8), respectively; these values were not significantly different. In the rigor condition, all cross-bridges which can attach to the actin filament are attached, so rigor stiffness may represent the length distribution of the actin filament. The finding that rigor stiffness did not change much between the three muscle models suggests that the length distribution of the actin filament after reconstitution was not very different from that of the control myocardium. As expected, rigor tension or stiffness did not develop when gelsolin-treated myocardium was soaked in the rigor solution.
Figure 1. Confocal fluorescence micrograph of control (A), gelsolin-treated (B) and actin filament-reconstituted (C) myocardium.

The actin filament was stained using rhodamine-phalloidin. Calibration bar, 4 μm.
Temperature effect on isometric tension and stiffness
Slow pen trace records of isometric tension at different temperatures in the three muscle models are shown in Fig. 2. Only active tension at 10, 20 and 30 °C is shown in the figure to avoid crowding of the data. After the final activation, the myocardium was brought to the rigor condition and rigor stiffness was measured. In the control myocardium (Fig. 2A) and in the thin filament-reconstituted myocardium (Fig. 2C), active tension increased in proportion to the increase in temperature. In the actin filament-reconstituted myocardium (Fig. 2B), the increase in active tension was much less.
The temperature dependence of isometric tension in the three muscle models is summarized in Fig. 3A. In the control myocardium, isometric tension increased almost linearly with temperature. This is in close agreement with previous results using mammalian skeletal and cardiac muscles (Ranatunga & Wylie, 1983; Goldman et al. 1987; Zhao & Kawai, 1994; Wang & Kawai, 2001). The slope of the temperature-tension relationship, ΔF/ΔT, was 0.46 kN m−2 °C−1. Isometric tension at 25 °C in control myocardium was 16.7 ± 1.7 kN m−2. In actin filament-reconstituted myocardium without regulatory proteins, the slope of the temperature-tension relationship became much less, being 0.16 kN m−2 °C−1. Isometric tension at 25 °C in the actin filament-reconstituted myocardium was 9.7 ± 0.8 kN m−2. In the thin filament-reconstituted myocardium, the slope was 0.62 kN m−2 °C−1, and isometric tension was 19.4 ± 2.0 kN m−2 at 25 °C. Isometric tension was almost the same in the three muscle models in the low temperature range (5–10 °C). The difference in isometric tension became larger at higher temperatures, and at 40 °C the isometric tension of the actin filament-reconstituted myocardium was 0.56 times that of the control myocardium.
Figure 3. Isometric tension (A), stiffness (B) and tension/stiffness (C) plotted against temperature.
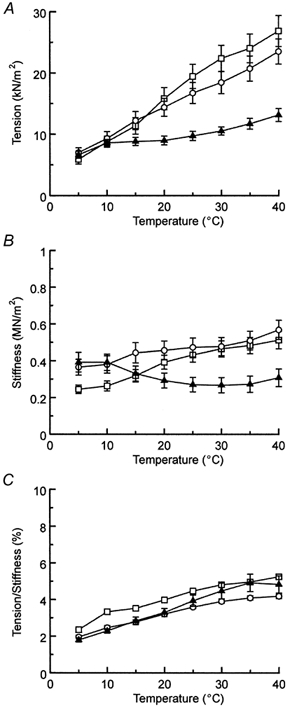
○, bovine control myocardium (n = 11); ▴, actin filament-reconstituted myocardium (n = 10); □, thin filament-reconstituted myocardium (n = 8). The initial tension before gelsolin treatment in the standard activating solution at 25 °C was 17.8 ± 1.9 kN m−2 for control, 20.6 ± 1.5 kN m−2 for actin filament-reconstituted, and 25.8 ± 3.2 kN m−2 for thin filament-reconstituted myocardium. Experiments were performed in the presence of 8 mm Pi and 5 mm MgATP. Error bars represent s.e.m., and error bars smaller than the symbol size are not shown.
The temperature dependence of stiffness during activation is shown in Fig. 3B. In the control and the thin filament-reconstituted myocardium, stiffness increased somewhat with an increase in the temperature. In the actin filament-reconstituted myocardium, stiffness decreased slightly with temperature. However, this stiffness change is not significant, because the effect is not very much larger than the error bars. Stiffness during activation at 25 °C was 0.47 ± 0.05, 0.27 ± 0.04 and 0.43 ± 0.04 MN m−2 for control, actin filament-reconstituted and thin filament-reconstituted myocardium, respectively. The temperature dependence of tension/stiffness during activation was similar in the three muscle models (Fig. 3C).
Effect of temperature on the apparent rate constants 2πb and 2πc
The temperature dependence of the apparent rate constants 2πb and 2πc were studied in the three muscle models using sinusoidal analysis during maximal activation. Figure 4 illustrates the frequency dependence of the complex modulus plotted in the elastic modulus (Fig. 4A, C and E) and viscous modulus (Fig. 4B, D and F) at three different temperatures (20 °C (○), 30 °C (▵) and 40 °C (□)). In all muscle models, an increase in temperature shifted both plots to the right, indicating that the cross-bridge kinetics became faster with temperature. The viscous modulus had a maximal value at 3–35 Hz, which approximates the characteristic frequency c. The elastic modulus had a minimal value at 1–16 Hz (≈fmin), which approximates the geometric average (√bc) of characteristic frequencies b and c. The complex modulus data were fitted to eqn (1), and the apparent rate constants 2πb and 2πc were deduced. Because we could not resolve process B at 15 °C, the complex modulus data were fitted with one exponential process C at 15 °C. The rate constants were averaged for eight to eleven experiments and plotted on a logarithmic scale in Fig. 5. This figure demonstrates that the rate constants increased exponentially with an increase in temperature.
Figure 4. The effects of temperature on the complex modulus Y(f).
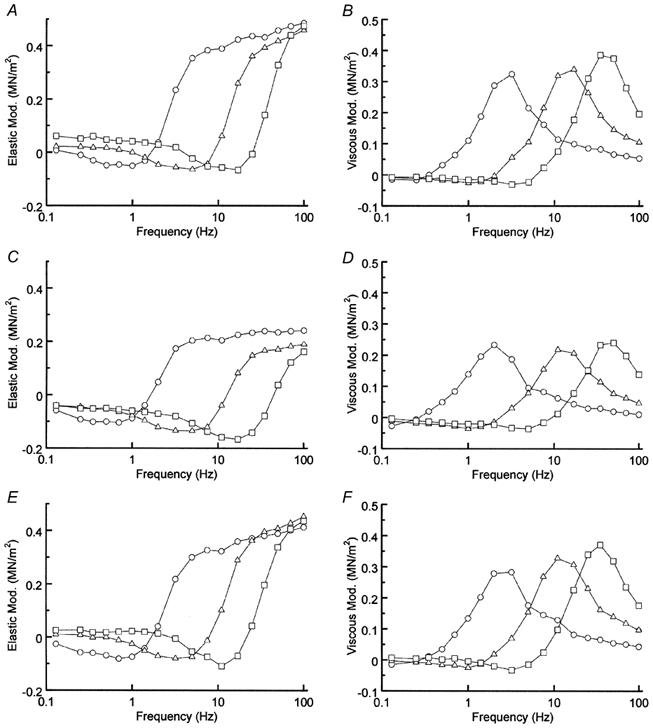
A and B, control myocardium; C and D, actin filament-reconstituted myocardium; E and F, thin filament-reconstituted myocardium. Elastic modulus (A, C and E) and viscous modulus (B, D and F) are plotted against frequency. ○, 20 °C; ▵, 30 °C; □, 40 °C. The phosphate concentration was 8 mm and the MgATP concentration was 5 mm. Peak-to-peak amplitude: 0.25 % L0. Average of 8–11 experiments.
Figure 5. The rate constants 2πb (A) and 2πc (B) as a function of temperature.
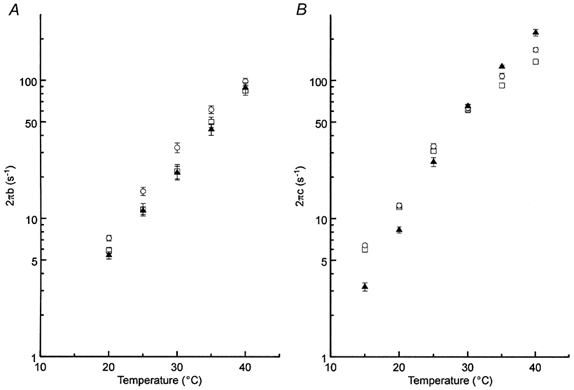
○, control myocardium (n = 11); ▴, actin filament-reconstituted myocardium (n = 10); □, thin filament-reconstituted myocardium (n = 8). Experiments were performed in the presence of 8 mm Pi and 5 mm MgATP. Error bars represent s.e.m., and error bars smaller than the symbol size are not shown.
The temperature dependence of 2πb did not differ much in the three muscle models. The Q10 of 2πb in the range 20–40 °C was 3.8, 4.0 and 3.9 in the control, the actin filament-reconstituted and the thin filament-reconstituted myocardium, respectively (Fig. 5A). The respective activation energy (Ea) was 101, 106 and 104 kJ mol−1. The temperature dependence of 2πc had two phases in all three muscle models with a break point at around 25–30 °C (Fig. 5B). In the low temperature range (15–25 °C), the Q10 of 2πc in the control myocardium was 5.5, with a corresponding Ea of 118 kJ mol−1. In the high temperature range (30–40 °C), the Q10 decreased to 2.7 with a corresponding Ea of 77 kJ mol−1. The actin filament-reconstituted myocardium had a higher Q10 value both in the low (Q10, 8.5; Ea, 149 kJ mol−1) and the high (Q10, 3.6; Ea, 97 kJ mol−1) temperature range. Thin filament-reconstituted myocardium regained the control temperature- 2πc relationship, with a Q10 of 5.4 (Ea, 117 kJ mol−1) in the low temperature range, and a Q10 of 2.3 (Ea, 63 kJ mol−1) in the high temperature range. Q10 and Ea values of the apparent rate constants are summarized in Table 1.
Table 1.
Temperature sensitivity of the apparent rate constants
| 2πb (20–40 °C) | 2πc (15–25 °C) | 2πc (30 –40 °C) | ||||
|---|---|---|---|---|---|---|
| Q 10 | Ea(kJmol−1) | Q10 | Ea(kJmol−1) | Q10 | Ea(kJmol−1) | |
| Control myocardium | 3.8 | 101 | 5.5 | 118 | 2.7 | 77 |
| Actin filament-reconstituted myocardium | 4.0 | 106 | 8.5 | 149 | 3.6 | 97 |
| Thin filament-reconstituted myocardium | 3.9 | 104 | 5.4 | 117 | 2.3 | 63 |
Ea, activation energy.
DISCUSSION
In this report, we describe the effect of temperature on isometric tension in skinned bovine myocardium when it is activated by saturating Ca2+ (pCa 4.66). There was a significant increase in isometric tension (Fig. 2A and Fig. 3A) when the temperature was elevated in the control myocardium. This result is consistent with those reported by others in myocardium (Ranatunga, 1999) as well as in skeletal muscle fibres (Goldman et al. 1987; Zhao & Kawai, 1994; Wang & Kawai, 2001). However, the temperature effect was much less in smooth muscle preparations (Jaworowski & Arner, 1998). This disparity led to the suggestion that the large temperature effect in striated muscle may be caused by regulatory proteins, because smooth muscles lack Tn, although smooth muscle-specific Tm is present. In an attempt to answer this question, we selectively removed the thin filament using the plasma protein gelsolin, and reconstituted the actin filament without Tm or Tn. In this myocardial model, we have a unique opportunity to study the temperature effect of isometric tension and compare the results in the presence and absence of regulatory proteins. Our results (Fig. 2 and Fig. 3A) demonstrate that the large temperature effect is abolished in the absence of Tm and Tn and enhanced in their presence.
To rule out a possibility that the diminished temperature effect is based on abnormal reconstitution of the actin filament, we further reconstituted this model with purified Tm and Tn to produce a total thin filament reconstitution. When we studied the temperature effect after the total reconstitution, isometric tension showed a sharp increase with temperature, which was close to that of the control myocardium (Fig. 2C and Fig. 3A). The frequency plots of the control and the thin filament-reconstituted myocardium were virtually identical (Fig. 4A and B vs. E and F). These observations rule out the possibility of abnormal reconstitution of the actin filament, and they confirm the finding that the diminished temperature effect is based on the absence of Tm and Tn in the actin filament-reconstituted myocardium.
It is interesting to speculate why the temperature effect is enhanced in the presence of Tm and Tn and diminished in their absence. Our previous investigations demonstrated that the large temperature effect is caused by an increase in the equilibrium constant (K4) of the force-generating step. An increase in K4 would result in an increase in the AM*ADP.Pi and AM*ADP states, without changing the force generated by each cross-bridge, and this fact was demonstrated in rabbit psoas (Zhao & Kawai, 1994) and soleus slow-twitch (Wang & Kawai, 2001) fibres. The states AM*ADP.Pi and AM*ADP are primary force-generating (or force-bearing) states. The reason for the steep increase in K4 with temperature is that the hydrophobic interaction between residues of actin and myosin molecules underlies the mechanisms of force generation. In such interaction, the standard enthalpy change (ΔH °) and the standard entropy change (ΔS °) are large positive numbers, and the heat capacity change (ΔCP) is a large negative number as observed in solution (Highsmith, 1977; Kodama, 1985) and in fibres (Zhao & Kawai, 1994; Wang & Kawai, 2001). Because ΔH ° > 0 (endothermic reaction), the increased temperature favours the states that generate force, as seen in many studies that changed temperature (Ranatunga, 1982; Ranatunga & Wylie, 1983; Goldman et al. 1987; Zhao & Kawai, 1994; Ranatunga, 1999; Tsaturyan et al. 1999; Wang & Kawai, 2001). Our observation that the temperature effect is much reduced in the absence of regulatory proteins implies that the hydrophobic interaction is much reduced when Tm and Tn are absent. This fact further implies that regulatory proteins change the conformation of actin so as to increase the hydrophobic interaction between actin and myosin.
Another important point in the isometric tension shown in Fig. 3A is that, if an experiment is carried out at a low temperature in the range 5–10 °C, then there is little change in tension as Tm and Tn are added to the actin filament. However, if the experiment is carried out at a temperature in the range 15–40 °C, tension increases by a factor of 1.3–1.9 times when Tm and Tn are added to the actin filament. This latter finding is consistent with our earlier study at 25 °C, in which isometric tension increased by a factor of 1.5 times as Tm and Tn were added (Fujita et al. 2002). These results are also consistent with those in single molecule experiments that used an in vitro motility assay. VanBuren et al. (1999) reported a 2-fold increase in force when Tm was added to a system that consisted of the actin filament and HMM molecule at 30 °C. Bing et al. (2000) reported a 1.8-fold increase in [the index of retardation] (≈force) when Tm was added at 27 °C. Similarly, Homsher et al. (2000) reported a 1.5-fold increase in force when Tm and Tn were added at 22–23 °C.
The effect of temperature on stiffness was not as remarkable as that on tension (Fig. 3B) and has been observed previously (Zhao & Kawai, 1994; Galler & Hilber, 1998; Tsaturyan et al. 1999; Wang & Kawai, 2001). This observation could be taken as evidence that tension per cross-bridge increases with temperature. However, stiffness may not be a good way to index the number of attached cross-bridges, because of the presence of in-series compliance in both thick and thin filaments (Huxley et al. 1994; Wakabayashi et al. 1994) in addition to cross-bridges. The fact that the tension/stiffness ratio increases linearly with the temperature (Fig. 3C; see also Zhao & Kawai, 1994; Galler & Hilber, 1998; Wang & Kawai, 2001) is consistent with the hypothesis that more cross-bridges are recruited into the tension-generating states at higher temperatures and that series compliance plays a significant role in fibre stiffness so that the overall increase in stiffness is not as significant as the increase in tension. The temperature dependence of tension/stiffness was almost the same in the three muscle models (Fig. 3C), further supporting the hypothesis that the series compliance makes an equally significant contribution in all three muscle models.
An additional mechanism that may account for the observed stiffness vs. temperature plot in actin filament-reconstituted myocardium (Fig. 3B, ▴) is as follows. In this myocardium, the number of cross-bridges in tension-generating states may remain the same when the temperature is raised. This can occur if the temperature effect is similar between the force-generation step (k4) and the ADP-isomerization step (k6):
where k indicates the rate constant of the elementary step. If k4 and k6 have the same temperature dependence, the population of cross-bridges in the primary tension-generating states (AM*ADP.Pi and AM*ADP) remains the same when the temperature is raised. The intervening Pi release step 5 is not very temperature sensitive in skeletal muscle fibres, as has been demonstrated (Zhao & Kawai, 1994; Wang & Kawai, 2001). Step 6 may be a mechanical step in which muscle performs external work (Kawai & Zhao, 1993), and it does not change much with temperature based on the observation in rabbit psoas (Zhao & Kawai, 1994). In the absence of regulatory proteins, the temperature sensitivity of step 4 is likely to be reduced, so the temperature sensitivity of k4 may be the same as that of k6.
Since no direct interactions have been demonstrated between myosin and Tm or Tn in solution, it is not likely that Tm and Tn modify the conformation of myosin directly. However, this possibility cannot be ruled out entirely, because it has been demonstrated that the S1 portion of myosin and Tm come to a close proximity in 3-D image-reconstruction studies using cryo electronmicrosopy (Milligan et al. 1990; Vibert et al. 1997). In contrast, numerous lines of evidence demonstrate the presence of interaction between regulatory proteins and actin molecules (Ebashi & Endo, 1968; Ishiwata & Fujime, 1972). Thus, the most likely scenario is that Tm and Tn in the presence of Ca2+ interact with actin and alter the actin conformation to modify the stereospecific interaction between actin and myosin. Such a possibility has been suggested based on structural studies (Rosol et al. 2000) and a binding study between Tm, actin, and myosin in solution (Cassell & Tobacman, 1996). It is possible that the alteration of actomyosin interaction further modifies myosin conformation so as to change the cross-bridge kinetics. In fact, we reported that the kinetic constants of elementary steps were significantly changed when Tm and Tn were added to the actin filament in bovine myocardium (Fujita et al. 2002), implying that actin and myosin interaction and concomitant cross-bridge kinetics are significantly altered with regulatory proteins.
We also performed sinusoidal analysis on the three muscle models, and detected the temperature effect on 2πb and 2πc (Fig. 4 and Fig. 5). The apparent rate constants 2πb and 2πc presumably correspond to phase 2b and phase 2a, respectively, of T-jump experiments (Ranatunga, 1999). Our earlier analysis on myocardium demonstrated that 2πb is closely correlated with the step that generates force, while 2πc is closely correlated with ATP binding and subsequent rapid detachment of cross-bridges (Kawai et al. 1993; Zhao & Kawai, 1994). The apparent rate constant 2πb increases with an increase in temperature with a Q10 of 3.8; the corresponding activation energy (Ea) is 101 kJ mol−1. The effect of temperature on 2πb is similar in the control and the actin filament-reconstituted myocardium with a Q10 of 4.0 (Ea= 106 kJ mol−1).
The effect of temperature on 2πc is larger than that on 2πb, and the plot of 2πc vs. temperature has a break point at 25–30 °C (Fig. 5B). In the control myocardium, 2πc increases with a rise in temperature with a Q10 of 5.5 (Ea= 118 kJ mol−1) in the low temperature range (≤ 25 °C), and with a Q10 of 2.7 (Ea= 77 kJ mol−1) in the high temperature range (≥30 °C). In the thin filament-reconstituted myocardium, similar values were observed. In the actin filament-reconstituted myocardium, the effect of temperature on 2πc is larger with a Q10 of 8.5 (Ea= 149 kJ mol−1) in the low temperature range (≤25 °C) and a Q10 of 3.6 (Ea= 97 kJ mol−1) in the high temperature range (≥30 °C). The temperature effect on 2πc of the control myocardium is reminiscent of an earlier report; a similar break point was observed at ∼20 °C in the rate constant of phase 2b of a T-jump experiment in rat myocardium (Ranatunga, 1999). The fact that there is a significant temperature effect on 2πc implies that there is a large temperature effect on the ATP-binding and/or cross-bridge detachment step(s), as demonstrated in rabbit psoas (Zhao & Kawai, 1994) and soleus slow twitch (Wang & Kawai, 2001) muscle fibres.
Acknowledgments
We would like to thank Dr Shin'ichi Ishiwata for useful comments on this manuscript. This work was supported by grant IBN 98–14441 from the National Science Foundation. H. Fujita is a recipient of a Postdoctoral Fellowship award from the Japan Society for Promotion of Science.
REFERENCES
- Bing W, Knott A, Marston SB. A simple method for measuring the relative force exerted by myosin on actin filaments in the in vitro motility assay: evidence that tropomyosin and troponin increase force in single thin filaments. Biochemical Journal. 2000;350:693–699. [PMC free article] [PubMed] [Google Scholar]
- Cassell M, Tobacman LS. Opposite effects of myosin subfragment 1 on binding of cardiac troponin and tropomyosin to the thin filament. Journal of Biological Chemistry. 1996;271:12867–12872. doi: 10.1074/jbc.271.22.12867. [DOI] [PubMed] [Google Scholar]
- Ebashi S, Endo M. Calcium ions and muscle contraction. Progress in Biophysics and Molecular Biology. 1968;18:123–183. doi: 10.1016/0079-6107(68)90023-0. [DOI] [PubMed] [Google Scholar]
- Fujita H, Sasaki D, Ishiwata S, Kawai M. Elementary steps of the cross-bridge cycle in bovine myocardium with and without regulatory proteins. Biophysical Journal. 2002;82:915–928. doi: 10.1016/S0006-3495(02)75453-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fujita H, Yasuda K, Niitsu S, Funatsu T, Ishiwata S. Structural and functional reconstitution of thin filaments in the contractile apparatus of cardiac muscle. Biophysical Journal. 1996;71:2307–2318. doi: 10.1016/S0006-3495(96)79465-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Funatsu T, Kono E, Higuchi H, Kimura S, Ishiwata S, Yoshioka T, Maruyama K, Tsukita S. Elastic filaments in situ in cardiac muscle: Deep-etch replica analysis in combination with selective removal of actin and myosin filaments. Journal of Cell Biology. 1993;120:711–724. doi: 10.1083/jcb.120.3.711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galler S, Hilber K. Tension/stiffness ratio of skinned rat skeletal muscle fibre types at various temperatures. Acta Physiologica Scandinavica. 1998;162:119–126. doi: 10.1046/j.1365-201X.1998.0272f.x. [DOI] [PubMed] [Google Scholar]
- Goldman YE, McCray JA, Ranatunga KW. Transient tension changes initiated by laser temperature jumps in rabbit psoas muscle fibres. Journal of Physiology. 1987;392:71–95. doi: 10.1113/jphysiol.1987.sp016770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Highsmith S. The effects of temperature and salts on myosin subfragment-1 and F-actin association. Archives of Biochemistry and Biophysics. 1977;180:404–408. doi: 10.1016/0003-9861(77)90054-6. [DOI] [PubMed] [Google Scholar]
- Homsher E, Lee DM, Morris C, Pavlov D, Tobacman LS. Regulation of force and unloaded sliding speed in single thin filaments: effects of regulatory proteins and calcium. Journal of Physiology. 2000;524:233–243. doi: 10.1111/j.1469-7793.2000.00233.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huxley AF, Simmons RM. Proposed mechanism of force generation in striated muscle. Nature. 1971;233:533–538. doi: 10.1038/233533a0. [DOI] [PubMed] [Google Scholar]
- Huxley HE, Stewart A, Sosa H, Irving T. X-ray diffraction measurements of the extensibility of actin and myosin filaments in contracting muscle. Biophysical Journal. 1994;67:2411–2421. doi: 10.1016/S0006-3495(94)80728-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ishiwata S, Fujime S. Effect of calcium ions on the flexibility of reconstituted thin filaments of muscle studied by quasielastic scattering of laser light. Journal of Molecular Biology. 1972;68:511–522. doi: 10.1016/0022-2836(72)90103-9. [DOI] [PubMed] [Google Scholar]
- Jaworowski Å, Arner A. Temperature sensitivity of force and shortening velocity in maximally activated skinned smooth muscle. Journal of Muscle Research and Cell Motility. 1998;19:247–255. doi: 10.1023/a:1005377016177. [DOI] [PubMed] [Google Scholar]
- Kawai M, Brandt PW. Sinusoidal analysis: A high resolution method for correlating biochemical reactions with physiological processes in activated skeletal muscle of rabbit, frog and crayfish. Journal of Muscle Research and Cell Motility. 1980;1:279–303. doi: 10.1007/BF00711932. [DOI] [PubMed] [Google Scholar]
- Kawai M, Kawaguchi K, Saito M, Ishiwata S. Temperature change does not affect force between single actin filaments and HMM from rabbit muscles. Biophysical Journal. 2000;78:3112–3119. doi: 10.1016/S0006-3495(00)76848-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kawai M, Saeki Y, Zhao Y. Crossbridge scheme and the kinetic constants of elementary steps deduced from chemically skinned papillary and trabecular muscles of ferret. Circulatory Research. 1993;73:35–50. doi: 10.1161/01.res.73.1.35. [DOI] [PubMed] [Google Scholar]
- Kawai M, Zhao Y. Cross-bridge scheme and force per cross-bridge state in skinned rabbit psoas muscle fibers. Biophysical Journal. 1993;5:638–651. doi: 10.1016/S0006-3495(93)81109-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kodama T. Thermodynamic analysis of muscle ATPase mechanisms. Physiological Reviews. 1985;65:467–551. doi: 10.1152/physrev.1985.65.2.467. [DOI] [PubMed] [Google Scholar]
- Kondo H, Ishiwata S. Uni-directional growth of F-actin. Journal of Biochemistry. 1976;79:159–171. doi: 10.1093/oxfordjournals.jbchem.a131043. [DOI] [PubMed] [Google Scholar]
- Kurokawa H, Fujii W, Ohmi K, Sakurai T, Nonomura Y. Simple and rapid purification of brevin. Biochemical and Biophysical Research Communications. 1990;168:451–457. doi: 10.1016/0006-291x(90)92342-w. [DOI] [PubMed] [Google Scholar]
- Milligan RA, Whittaker M, Safer D. Molecular structure of F-actin and location of surface binding sites. Nature. 1990;348:217–221. doi: 10.1038/348217a0. [DOI] [PubMed] [Google Scholar]
- Ranatunga KW. Temperature dependence of shortening velocity and rate of tension development in rat skeletal muscle. Journal of Physiology. 1982;329:465–483. doi: 10.1113/jphysiol.1982.sp014314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ranatunga KW. Endothermic force generation in skinned cardiac muscle from rat. Journal of Muscle Research and Cell Motility. 1999;20:489–496. doi: 10.1023/a:1005509731881. [DOI] [PubMed] [Google Scholar]
- Ranatunga KW, Wylie SR. Temperature-dependent transition in isometric contraction of rat muscle. Journal of Physiology. 1983;339:87–95. doi: 10.1113/jphysiol.1983.sp014704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosol M, Lehman W, Craig R, Landis C, Butters C, Tobacman LS. Three-dimensional reconstruction of thin filaments containing mutant tropomyosin. Biophysical Journal. 2000;78:908–917. doi: 10.1016/S0006-3495(00)76648-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spudich JA, Watt S. The regulation of rabbit skeletal muscle contraction. I. Biochemical studies of the interaction of the tropomyosin-troponin complex with actin and the proteolytic fragments of myosin. Journal of Biological Chemistry. 1971;246:4866–4871. [PubMed] [Google Scholar]
- Tsaturyan AK, Bershitsky SY, Burns R, Ferenczi MA. Structural changes in the actin-myosin cross-bridges associated with force generation induced by temperature jump in permeabilized frog muscle fibers. Biophysical Journal. 1999;77:354–372. doi: 10.1016/S0006-3495(99)76895-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- VanBuren P, Palmiter KA, Warshaw DM. Tropomyosin directly modulates actomyosin mechanical performance at the level of a single actin filament. Proceedings of the National Academy of Sciences of the USA. 1999;96:12488–12493. doi: 10.1073/pnas.96.22.12488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vibert P, Craig R, Lehman W. Steric-model for activation of muscle thin filaments. Journal of Molecular Biology. 1997;266:8–14. doi: 10.1006/jmbi.1996.0800. [DOI] [PubMed] [Google Scholar]
- Wakabayashi K, Sugimito Y, Tanaka H, Ueno Y, Takezawa Y, Amemiya Y. X-ray diffraction evidence for the extensibility of actin and myosin filaments during muscle contraction. Biophysical Journal. 1994;67:2422–2435. doi: 10.1016/S0006-3495(94)80729-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang G, Kawai M. Effect of temperature on elementary steps of the cross-bridge cycle in rabbit soleus slow-twitch muscle fibres. Journal of Physiology. 2001;531:219–234. doi: 10.1111/j.1469-7793.2001.0219j.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wannenburg T, Heijne GH, Geerdink JH, Van den Dool HW, Janssen PML, De Tombe PP. Cross-bridge kinetics in rat myocardium: Effect of sarcomere length and calcium activation. American Journal of Physiology - Heart and Circulatory Physiology. 2000;279:H779–790. doi: 10.1152/ajpheart.2000.279.2.H779. [DOI] [PubMed] [Google Scholar]
- Zhao Y, Kawai M. Kinetic and thermodynamic studies of the cross-bridge cycle in rabbit psoas muscle fibers. Biophysical Journal. 1994;67:1655–1668. doi: 10.1016/S0006-3495(94)80638-1. [DOI] [PMC free article] [PubMed] [Google Scholar]


