Openings in frog microvascular endothelium at different rates of increase in pressure and at different temperatures

Abstract

Experiments were carried out on single mesenteric capillaries and venules of pithed frogs to determine whether the rate of increase in intravascular pressure (dP/dt) influenced the critical pressure (P_B) which increases wall permeability. Vessels, microperfused with frog Ringer solutions containing 0.1 % bovine serum albumin and red cells, were occluded downstream before pressure was raised either as a ramp or in a series of 13.6 cmH₂O steps. By varying step duration, the mean dP/dt could be matched to dP/dt applied as a steady ramp. P_B was recorded as the pressure at which there was an abrupt increase in filtration with red cells passing to and through one or more sites in the vessel wall. In all vessels, increasing dP/dt raised P_B, with no differences between steps and ramps. The relation between P_B and dP/dt was linear, consistent with a latent period, T (the slope), between a critical pressure being reached and the abrupt increase in permeability being observed. Direct observation confirmed this latent period. Between 12 and 20 ^oC, T was 8.5 ± 0.47 s; between 0 and 5 °C, T was 11.5 ± 0.97 s. Tissue cooling did not influence the time constant, τ, describing the rate of stretch of wall following a step increase in pressure and used to measure wall visco-elastic properties. Nor was the value of τ (1.15 ± 0.06 s, n = 42) consistent with T being accounted for by visco-elasticity. It is suggested that the latent period may indicate an active response of the endothelium.

The walls of capillaries and venules sustain differences in hydrostatic pressure between the plasma and the surrounding tissues which, as a consequence of postural changes in larger animals and venous occlusion, may rise well over 50 cmH₂O. For example, when a human subject of moderate height stands still, microvascular pressures in the feet are raised to 130 cmH₂O or more (Levick & Michel, 1978). The integrity of microvascular walls under these circumstances is essential for the continuity of the local circulation. The maximum stresses that can be sustained by microvascular walls and an understanding of how such stresses are borne by the components of the wall are of considerable significance to the normal working of the circulation. It is not clear just how the thinness of the wall, which so greatly facilitates microvascular exchange, limits wall strength. Nor is it known how wall strength may be compromised by certain diseases.

It is usually considered that the endothelial basement membrane carries the stresses on the walls of these vessels and that the apparent loss of integrity of microvessels subjected to high intravascular pressures (with passage of cells as well as plasma into the tissues) represents stress failure of the basement membrane. This interpretation has been followed by West, Mathieu-Costello and their colleagues in a series of elegant studies on the strength of the alveolar capillary barrier of the lung (see West & Mathieu-Costello, 1999, for review). These authors, however, drew attention to the rapid recovery of vessel integrity once intravascular pressure was lowered, an observation which might not be anticipated to follow stress failure of the basement membrane (West et al. 1991).

Work in our laboratory on single frog mesenteric capillaries subjected to high intravascular pressures has also yielded some surprises for the stress failure interpretation (Neal & Michel, 1996, 2000). Permeability and wall strength are recovered within a few minutes if the intravascular pressure is lowered immediately after the walls of these vessels have appeared to show stress failure at one or more points. Furthermore, electron micrographs of serial sections of the vessel walls at sites of failure show that the majority of openings pass through the bodies of the endothelial cells rather than between them (Neal & Michel, 1996). While the compliance of intact microvessels is similar to that of the basement membrane after removal of the endothelium, in three experiments where the pressure was raised to 150–250 cmH₂O, compliance of the basement membrane continued to decrease (with no indication of a yield point) as trans-membrane pressure was raised well above values which would cause the ‘stress failure’ of intact vessels (Neal & Michel, 2000). While the compliance of intact vessels (and their basement membranes) appears to be relatively insensitive to cooling to between 0 and 5 °C, this degree of cooling raised the pressure at which openings could be induced in vessel walls by over 50 %. These observations led Neal & Michel to suggest that the endothelium rather than the basement membrane might determine the sudden opening in microvascular walls of pores, large enough to allow the passage of red cells into the tissues. The opening of these very large pores would be responsible for the abrupt increase in fluid filtration with the passage of red cells through the vessel walls, an appearance which has been interpreted as wall stress failure.

The experiments described in this paper set out to answer two questions: (a) is the critical value of the pressure, P_B, which induces the openings in microvascular walls, influenced by the rate at which the pressure is raised? and (b) is the value of P_B when the pressure is raised in steps different from its value when the pressure is raised continuously? We have therefore compared the values of P_B estimated when the intravascular pressure is raised as a continuous ramp at a series of different rates (dP/dt) with values of P_B estimated when the pressure was raised in steps of 13.6 cmH₂O (10 mmHg) at similar mean rates of increase in pressure.

There were several reasons for conducting these experiments. First, prior to this study, all estimates of P_B have been made with pressure raised in steps. Second, it seemed possible that if the opening of pores in the vessel wall is an active process, the endothelial cells might rearrange their attachments to the underlying basement membrane, if pressure is raised slowly, so as to minimise the fraction of the wall stress that was transmitted to them. In this way, the critical stress equivalent to P_B might be reached at much higher values of total wall stress if pressure was raised slowly than if it were raised rapidly. We will refer to this hypothesis as endothelial adaptation.

An alternative hypothesis arose from our observation that the appearance of pressure-induced openings was heralded by a series of short-lived increases in localised hydraulic permeability (Neal & Michel, 1996). These phenomena were interpreted as transient opening and closing of transendothelial channels. They suggested that there might be a period between the endothelium ‘sensing’ a critical wall stress (or strain) and the development of stable openings in the vessel wall. We will refer to this as the latent period hypothesis.

Whereas the endothelial adaptation hypothesis predicts that estimates of P_B in a given microvessel should increase as pressure is raised more slowly, the latent period hypothesis predicts that P_B should decrease as the pressure inside the vessel is raised more slowly. The latter can be readily seen if we assume the latent period, T, is independent of the rate of increase of intravascular pressure, dP/dt. Then the apparent P_B is related to a constant threshold value, P_B0, through the relationship:

(1)

A relationship of the general form of equation (1) might also arise if the microvascular wall were visco-elastic and opening the pores did represent stress failure. In this hypothesis, the vessel wall would fail once a critical strain had been reached. With a visco-elastic wall, the strain would lag behind dP/dt and the lag itself would appear as a latent period. Thus when results consistent with the latent period hypothesis were obtained, an investigation was carried out of the visco-elastic properties of the vessel walls and their sensitivity to tissue temperature.

Preliminary reports of the results described in this paper have been communicated to the British Microcirculation Society (Savla et al. 2001) and the European Society for Microcirculation (Savla et al. 2000).

METHODS

Animal preparation and general protocol

The experiments were carried out on mesenteric microvessels of male Rana temporaria or Rana pipiens (Blades; Edenbridge, Kent, UK). The frog was stunned by a blow to the head and the brain and upper spinal cord were destroyed by pithing, which was carried out following a protocol approved by the (UK) Home Office Inspector. The mesentery was delivered through an incision in the abdominal wall. A loop of the intestine was arranged over a polished Perspex pillar to allow transillumination of the microvasculature. The upper surface of the mesentery was continuously superfused with frog Ringer solution at 12–20 ^oC or 0–5 ^oC. The flow of the superfusate was set between 3 and 5 ml min⁻¹ to maintain a layer of fluid at a constant depth. The tissue was viewed through a Wild M8 stereomicroscope with a Hitachi CCTV camera attached to the camera tube. The output from the camera was displayed on video monitors and recorded.

Single venular capillaries (diameter 15–30 μm) were cannulated and perfused via sharpened glass micropipettes containing frog Ringer with bovine serum albumin (BSA) and a few human red cells to act as markers. The micropipette was connected to a water and mercury manometer so that the pressure applied to the vessel could be varied (Levick & Michel, 1973). After occluding the vessel downstream at a pressure of 20 cmH₂O, the pressure was increased to a baseline pressure of 40 cmH₂O. As shown in Fig. 1, the pressure applied through the micropipette was then raised either in a series of 10 mmHg steps lasting 2.5, 5, 10 or 20 s, or continuously at a rate of 0.6, 1.5, 3, 6, 9, 12 or 15 cmH₂O s⁻¹ until P_B was reached. To achieve a steady increase in pressure, a perfusion pump was used to raise the fluid levels in the manometer. The pressure in the lead from the manometer to the micropipette was monitored by a pressure transducer a few centimetres before it joined the micropipette holder, and the output from the transducer was recorded on a flat bed recorder. By varying the time that pressure was applied at each step, step increases and steady ramps of pressure were matched to give approximately the same mean values of dP/dt (Fig. 1). P_B was determined from direct observation of the vessel at the time of the experiment and from video recordings. At pressures less than P_B, the red cells within the vessel segment moved steadily towards the occluder due to filtration of fluid. When an opening developed, the red cells abruptly accelerated to this site, often passing through the wall into the surrounding tissue. The pressure in the vessel at this time was defined as P_B (Neal & Michel, 1996), recorded and a note made of the position of the site.

Figure 1. Steady and step increases in pressure at equivalent rates.

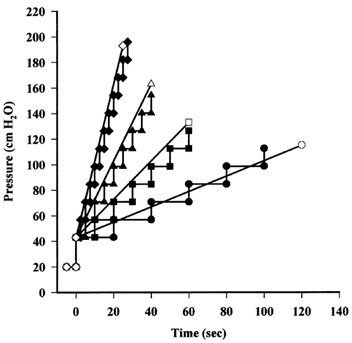
After occluding the vessel downstream, the pressure applied through the micropipette was raised either in steps of 13.6 cmH₂O (10 mmHg) lasting 2.5 (♦), 5 (▴), 10 (▪) or 20 s (•) or as a steady ramp. Steady increases in pressure were applied at rates of 6 (⋄), 3 (▵), 1.5 (□) and 0.6 cmH₂O s⁻¹ (○) equivalent to the mean rates achieved by the steps. Steady increases were also applied at 9, 12 and 15 cmH₂O s⁻¹ (not shown).

The occluder was then raised and the vessel was perfused freely at 20 cmH₂O for 5 min. The vessel was occluded again and the pressure raised for a second estimate of P_B to be made. Preliminary experiments showed that if, after an initial determination of P_B, the vessel was perfused freely for 5 min with a perfusion pressure of 20 cmH₂O or less, a second (or third) estimate of P_B on that vessel did not differ significantly from the initial estimate. The site of apparent rupture, however, was often different. Thus microvessels appear to recover their normal permeability and wall strength within 5 min of an estimation of P_B providing the intra-vascular pressure is kept low (see also Neal & Michel, 1996).

Estimation of the retardation time (τ) as a measure of visco-elastic properties of the microvascular wall

If the microvascular wall behaves as a simple visco-elastic material such that the strain, x, resulting from its extension by a step increase in transmural pressure of ΔP, initially changes with time in a manner determined by the Young's modulus (E), the viscosity (η) and the thickness (θ) of the wall and the vessel radius (r):

(2)

Thus following a step increase in pressure:

(3)

The time constant of the exponential, η/E, is known as the retardation time, τ, and may be used as a measure of visco-elasticity (e.g. Alexander, 1983).

To determine τ, we have adapted the red cell technique for estimating the compliance of microvascular walls (Kendall & Michel, 1995; Neal & Michel, 2000). With the pressure constant, a marker red cell within a closed section of vessel drifts slowly towards the occlusion site as fluid is filtered through the vessel wall from the intervening fluid column. Following a step increase in pressure, the red cell immediately jumps forward (towards the occlusion site) as the vessel expands and then decelerates to a rate determined by the new level of fluid filtration. If l is the distance of a marker red cell from the occlusion site, then when the perfusate oncotic pressure is low (as in the present experiments) under conditions of steady fluid filtration, the logarithm of l decreases linearly with time (Michel et al. 1974). Following a step increase in pressure, l drops from one linear relation of slope S₁ to a second linear relation of slope S₂ (Fig. 2). Extrapolation of the initial slope of log l against t to the time at which pressure was increased (t_o) yields a value l₁ and backward extrapolation of the second slope to the same time yields the value l_2. The difference (l₁ - l₂) is the step reduction in l which would have occurred if the expansion of the vessel had been instantaneous and the volume of the column of fluid between the red cell and the occlusion site remained constant. If the initial value of vessel radius (r₁) is known, the final value of the vessel radius (r₂) at the new pressure can be calculated from:

Figure 2. Estimation of changes in vessel radius following a step increase in pressure.

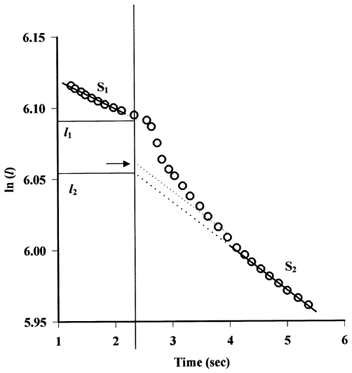
In this experiment, a marker red cell was followed before and after a step increase in pressure from 57 to 71 cmH₂O. The logarithm of the distance of the red cell from the occlusion site, l, decreases linearly with time until the step increase in pressure (indicated by the vertical line at t = 2.34 s), when l drops from one linear relation of slope S₁ (-0.021) to a second linear relation of slope S₂ (-0.031). Extrapolation of S₁ to the time at which pressure was increased yields a value l₁ and backward extrapolation of the second slope to the same time yields the value l_2. If r₁, the vessel radius prior to the increase in pressure is known, r₂, the new equilibrium value of vessel radius after pressure has been increased, can be calculated from l₁ and l₂ (equation (4)). Also illustrated is the estimation of an intermediate length (using S₂) from which an intermediate value of r can be calculated (horizontal arrow).

(4)

Values for r which existed as the radius increased from r₁ to r₂ can be estimated by drawing lines of slope S₂ through the points representing values of l at times immediately after pressure was increased and extrapolating these lines to t_o (Fig. 2). Equation (4) is then used to calculate the corresponding values of r.

Solutions

The Ringer solutions used as perfusate and superfusate were made from the same stock solution (mm): NaCl, 111.1; KCl, 2.4; MgSO₄, 1.0; NaHCO₃, 10; CaCl₂, 1.1; glucose, 5.5. The superfusates were bubbled with 3 % CO₂ in O₂ and pH was adjusted with HCl and NaOH. BSA at 1 mg ml⁻¹ was added to the perfusate. Prior to using the perfusate, washed human red blood cells were added at a haematocrit of 2–4 %.

Statistics

Data are presented as means ± s.e.m. for the indicated number of experiments (n). Comparisons between mean values were made using one-way ANOVA and t tests when comparing two means. P < 0.05 was considered to be significant. Trends between variables were described by linear regression. The significance of the correlation was assessed by the value of the correlation coefficient, and the significance of the difference between two regression coefficients was determined using a t test (Bailey, 1959).

RESULTS

Estimates of P_B with step and ramp increases in pressure: importance of dP/dt

In an initial series of experiments, estimates of P_B were made in the same microvessel as the pressure was raised in a series of steps, each of 10 mmHg (13.6 cmH₂O), and also when pressure was raised in a steady ramp at approximately the same mean rate as the step increases. The order in which vessels were exposed to step and ramp increases in pressure was alternated from experiment to experiment. Thus in comparing the effects of step and ramp increases in pressure, each vessel acted as its own control. In most vessels it was possible to compare the effects of step and ramp increases at more than one mean value of dP/dt. In five microvessels it proved possible to estimate P_B for both steps and ramps at four different mean values of dP/dt. The results from these experiments, supplemented by data from other vessels in which comparisons were possible at fewer values of dP/dt, are shown in Fig. 3 where values of P_B have been plotted against dP/dt. It is seen that at similar mean values of dP/dt, P_B appears to be independent of whether the pressure is raised steadily or in steps and this was confirmed by one-way ANOVA. Higher values of P_B, however, were found with higher values of dP/dt (when dP/dt > 2.5 cmH₂O s⁻¹, mean P_B was greater than mean P_B when dP/dt = 0.6 cmH₂O s⁻¹, P < 0.05, n ≥ 5).

Figure 3. The effects of step and steady increases in pressure on P_B at different rates of increase in pressure.

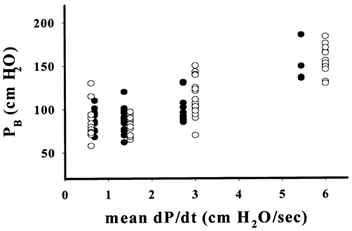
Values for P_B observed when pressure was increased stepwise (•) are plotted against the mean rate of increase in pressure (dP/dt) and compared with values of P_B when dP/dt was achieved as a steady ramp (○). There was no significant difference between values of P_B at similar mean values of dP/dt, but mean P_B was significantly increased at the two higher levels of dP/dt (n≥ 5, P < 0.05).

These findings appear to be contrary to the adaptation hypothesis but consistent with the latent period hypothesis. To examine this further, additional experiments were carried out at the values of dP/dt shown in Fig. 3 and also at the higher rates of 9, 12 and 15 cm H₂O s⁻¹. For each vessel, the mean value of P_B was plotted against the corresponding value of dP/dt. These results are shown in this form in Fig. 4, where it is seen that, in accordance with equation (1), P_B shows a linear trend with dP/dt, the regression equation for which is:

Figure 4. Relationship between P_B and dP/dt.

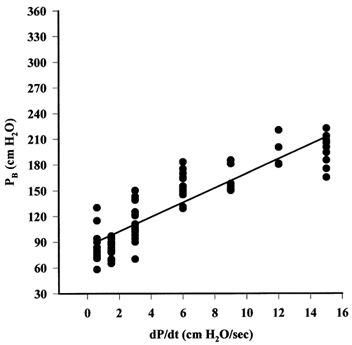
The increase in P_B with the rate of increase in pressure for measurements made between 12 and 20 °C is shown. Each point represents a measurement from one vessel (for each value of dP/dt, n > 4). The continuous line is the regression line through the points. P_B0 (the intercept) for these data is 85.46 cmH₂O. These observations are consistent with the latent period theory where the slope of the regression line is interpreted as the latent period, T.

(5)

Although there are suggestions of non-linearities in the relationship at high and low values of dP/dt, the scatter in the data does not justify a more sophisticated interpretation. Furthermore, a linear relationship between P_B and dP/dt is predicted by equation (1) which we can use to interpret the data. According to equation (1), the slope of the relationship (8.45 s) is the latent period, T, between a critical stress or strain being detected by the endothelium and the appearance of openings in the endothelium. The intercept represents the pressure at which that critical response is triggered. Thus the data in Fig. 4 indicate that as the pressure in a microvessel is raised, openings appear in the vessel wall approximately 8.5 s after the critical pressure of 86 cmH₂O has been exceeded.

The existence of a latent period is supported by a re-examination of the experiments where pressure was raised in steps. At the slowest rate of increase in pressure (step duration = 20 s) openings were observed 7–10 s after the step, consistent with T = 8.45 s. At higher mean rates of dP/dt, the latent period was more difficult to define as it was now comparable to or greater than the duration of each step.

Effect of temperature on the P_B-dP/dt relationship

Because previously it has been found that P_B is raised when the tissues are cooled below 5 °C, we carried out experiments to determine whether the effect of cooling was on the threshold pressure, P_B0, or on the latent period, T. Estimates of P_B were made on single vessels in cooled tissues with ramp increases of pressure of 1.0, 1.5, 3.0, 6.0 and 15 cmH₂O s⁻¹. Values of P_B for five different vessels were determined at each value of dP/dt.

P_B was found to be greater in cooled tissue than at room temperature. When the values for P_B were plotted against dP/dt, the slope of the relationship was greater than that for measurements made at room temperature. Thus the increase in P_B appeared to be the result of an increase in the latent period when the tissues were below 5 °C (Fig. 5). The regression line through the data below 5 °C is described by:

Figure 5. Effect of temperature on the relationship between P_B and dP/dt.

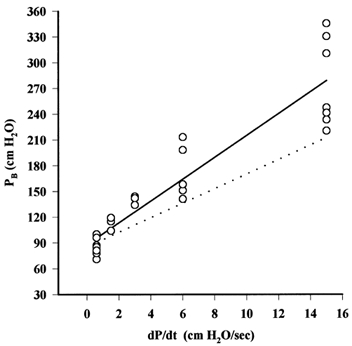
○, measurements of P_B at different values of dP/dt in microvessels cooled to 0–5 °C. The continuous line is the regression line through these points. The dotted line is the regression line for the relation in microvessels at 12–20 °C. While the relationship between P_B and dP/dt has a greater slope at 0–5 °C than at 12 –20 °C, the intercepts, P_B0, are not significantly different. A similar trend was seen when pressure was increased in a series of steps (data not shown).

(6)

A t test indicated that the regression coefficient for the data from cooled tissues was significantly greater than that for data obtained at room temperature (P < 0.02). Thus it would appear that cooling the tissues increases the latent period by approximately 35 %. If P_B0 is fixed at 88.4 cmH₂O, T calculated for all but the lowest ramp was 15.15 s.

Effect of temperature on the visco-elastic properties of the microvascular wall

If the microvascular wall has significant visco-elasticity, then it is possible that the latent period is a function of the retardation time, τ (i.e. the ratio of the viscosity of the wall to its Young's modulus). To explore this possibility, we have estimated τ at room temperature and at tissue temperatures below 5 °C. Since cooling the tissues below 5 °C increases the apparent latent period for P_B by approximately 35 %, a similar increase in τ should be observed if the latent period is a consequence of wall visco-elasticity.

Figure 6A shows the changes in the radius of a single vessel with time after a step increment in pressure of 13.6 cmH₂O. It is seen that the rate of increase in radius attenuates exponentially, in approximate agreement with equation (3). This is confirmed in Fig. 6B where values of the logarithms of the difference between the final value of the radius (R_inf) and its value immediately after pressure was increased have been plotted against time. The data approximate closely to a straight line of negative slope and the reciprocal of this slope yields a value for τ which in this experiment was 1.16 s.

Figure 6. Evaluating the changes in visco-elasticity.

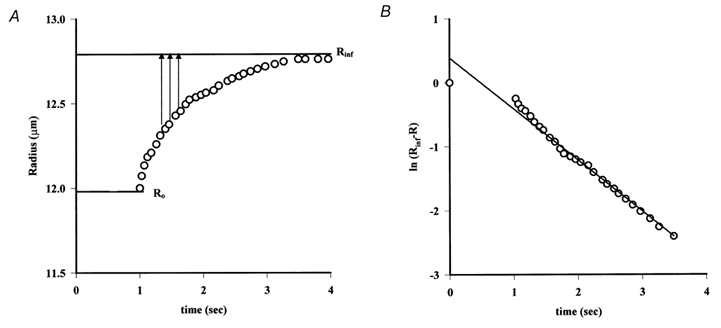
A, the changes in capillary radius, calculated from the movements of a marker red cell, after a step increase in pressure from 57 to 71 cmH₂O are plotted against time (progression of the same cell in Fig. 2). The radius increases approximately exponentially with time from an initial radius R₀ to a final radius, R_inf. B, semi-logarithmic plot of the changes in vessel radius against time (same data as in A) is linear. The slope of the relationship is the reciprocal of the time constant τ.

Mean values of τ from at least four determinations on each of four vessels at room temperature and at least four determinations on each of another four vessels in tissues cooled below 5 °C are shown in Table 1. Measurements were made at the following step changes in pressure: from 43 to 57 cmH₂O, from 57 to 71 cmH₂O and from 71 to 85 cmH₂O, with periods between successive steps of 5 and 10 s. One-way ANOVA indicated that the small differences between groups of measurements at each pressure step and at each temperature, were not significant (P = 0.685). Student's t test was used to compare the means of groups of measurements made over the same pressure step at different temperatures and indicated no significant difference (t = 0.869, n = 90, P = 0.387). Thus it would seem that the latent period between a critical pressure being reached and the appearance of openings in the endothelium is unlikely to be accounted for by the visco-elastic properties of the vessel wall.

Table 1.

Retardation time (τ) in frog mesenteric microvessels at 12–20 °C and 0–5 °C

Gradient of step	τ(s), 12–20 °C	τ(s), 0–5 °C
10mmHg (10s)−1	1.18 ± 0.06	1.24 ± 0.07
10mmHg (5s)−1	1.12 ± 0.11	1.18 ± 0.06
Mean ±s.e.m.	1.15 ± 0.06	1.21 ± 0.04

Mean values (±s.e.m.) of τ are calculated from four or more measurements on at least four vessels (n > 21).One-way ANOVA revealed that there were no significant differences between values of τ at any pressure step (43 to 57cmH₂O, 57 to 71cmH₂O, or 71 to 85cmH₂O).When values of τat 12–20 °C were compared with those for the same pressure step at 0 –5 °C, there was no significant difference (t =0.869 with 88 degrees of freedom, P = 0.387).

DISCUSSION

The observations reported in this paper show that the critical intravascular pressure, P_B, which induces openings in the wall of a microvessel, increases with the rate at which the pressure is raised. The picture is consistent with the hypothesis that the apparent stress failure of the vessel wall really represents the reversible opening of large pores in the endothelium once a critical wall stress is reached. The dependence of P_B upon the rate at which pressure is increased is consistent with a latent period between the critical wall stress being attained and the appearance of openings. Cooling the tissues increases the latent period without significantly changing the value of the critical stress that triggers the openings to form (represented by P_B0).

Before discussing how these observations might be interpreted, we will first consider the experimental approach that we have used. We estimated T indirectly from the slope of the relationship between P_B and dP/dt. It might be argued that T could be estimated more directly by raising the pressure in small steps, holding it constant for many seconds between each step until P_B0 is exceeded. T would then be the time interval between last rise in pressure and the appearance of openings in the vessel wall. Such an approach has the disadvantage that, at the start of any one experiment, neither P_B0 nor T are known. Thus if the pressure is raised in steps of 5 cmH₂O and each step is applied for 10 s, the appearance of openings 3 s after pressure was raised from 80 to 85 cmH₂O could mean that T has a value of either 3 or 13 s, or even 23 s. Similarly P_B0 could have a value of 85, 80 or even 75 cmH₂O. The experimental design that we adopted avoided these ambiguities and yielded mean values for T and P_B0 for a population of vessels. Once the value of T had been estimated indirectly, it was possible to go back to the records of experiments where pressure had been raised in steps and see that openings appeared approximately T s after a step increase in pressure.

There are several interpretations of our observations. Let us first consider those in which openings in the vessel wall represent stress failure. If the stress-bearing components of the wall are made of purely elastic material, the latent period might reflect the time between a critical stress being exceeded when pores appear and the time when the pores have grown large enough to be detected. This hypothesis can be dismissed on two grounds. Firstly, it predicts there should be a continuous increase in hydraulic permeability of the vessel during the latent period. Increases in hydraulic permeability do occur during this time but these are short-lived (< 1 s) with very rapid onset and offset as if pores were opening and closing rather than if pores were growing in size. Secondly, in this hypothesis one might expect the growth of the pores to increase with the rise in wall stress. Thus T might be expected to diminish as dP/dt increases. Our observations suggest that T is largely independent of dP/dt.

A more reasonable hypothesis, consistent with stress failure is that the stress-bearing components of the wall have visco-elastic properties. With a visco-elastic wall exposed to a steadily increasing stress, the strain lags behind the stress and the lag would be seen as T. While our measurements of the changes in vessel radius following step increments in intravascular pressure are entirely consistent with visco-elasticity of the wall, both qualitative and quantitative arguments militate against T being accounted for by visco-elasticity. First, our observation that T is increased by cooling contrasts with the apparent insensitivity of the retardation time, τ, to similar falls in tissue temperature. Since τ is the ratio of η, the viscosity coefficient of the vessel wall, to E, the Young's modulus of the wall, and as we know that E is insensitive to cooling (Neal & Michel, 2000), η is also relatively insensitive to cooling and is unlikely to be responsible for the temperature-sensitive T.

So far, however, the relationship between τ and T have not been defined and it is conceivable that a small change in τ might have a disproportionately large effect upon T. This relationship can be derived from a consideration of equation (2). In any one experiment, dP/dt has a constant value of α and αt can be substituted for ΔP in equation (2) to represent the transmural pressure at time = t. Integration of this form of equation (2) provides an expression for x, the strain in the vessel wall, as:

(7)

where τ = η/E.

If x_o is the critical strain that triggers the appearance of openings in the vessel wall, then Ex_o is the stress which, if applied for infinite time, is able to induce this critical strain. Ex_o is therefore the stress applied to the vessel wall by an intravascular pressure of P_B0 and P_B0= E θ x_o/r. If the vessel wall is visco-elastic and the pressure is raised at a steady rate of α cmH₂O s⁻¹, x will be less than x_o when P = P_B0 and will reach x_o at a later time, t_B. If the visco-elastic properties of the vessel wall are to account for the latent period, T, then the interval between the time at which P reaches P_B0 and x reaches x_o should be T. During the latent period, P will have risen from P_B0 to P_B. Rearranging equation (1) we see that:

(8)

which, from equation (7), is seen to be equivalent to:

(9)

Since αt_B is equal to P_B, comparison of equation (9) with equation (8) reveals that T should have a value of τ (1 - e^−tB/τ). T, however, has a value of approximately 10 s, whereas τ, which sets the upper limit for the value T on the visco-elastic theory, has a value of approximately 1 s. Thus relative magnitudes of τ and T are inconsistent with the visco-elastic properties of the microvascular wall accounting for more than 10 % of the latent period.

It may be argued that the absolute values of our estimates of τ are uncertain because they include the visco-elastic properties of the perfusion system as well as those of the vessel wall. Our estimates of τ, however, are consistent with the data of Swayne & Smaje (1989) for the dynamic compliance of the walls of frog and rat mesenteric capillaries. These authors minimised the influence of visco-elastic properties in their perfusion system by referring the transient changes in vessel radius to the pressure changes within an occluded microvessel (measured directly with a micropipette servo-nul system) after a step increase in the pressure was applied to the vessel. Furthermore, in our experiments, the visco-elastic properties of the perfusion system would contribute in a similar way to our estimates of both T and τ. It is the difference in magnitude between these parameters and the difference in the effects of temperature upon them that are so striking and suggest that they are quite different in nature.

In our discussion of visco-elasticity we have assumed that the compliance of the microvascular wall is linear, whereas it is known to be non-linear. This simplification does not, however, endanger our conclusions. A numerical solution of equation (2), which incorporates the non-linear compliance of vessel walls, differs only marginally from the linear model for a vessel of radius 10 μm over a range of pressure between 30 and 150 cmH₂O. Twenty- to fiftyfold increases in η with increasing wall stress (and with falling temperature) are necessary if the visco-elastic properties of the vessel wall are to be responsible for T. At this stage, it would seem more sensible to look for other causes of the latent period than the retardation time.

This brings us to the initial hypothesis that the openings in the endothelium induced by high intravascular pressure are the consequence of an active response of the endothelial cells rather than the result of stress failure. Our initial detailed study of the morphology of these openings (Neal & Michel, 1996) revealed that they were very similar to those present in frog mesenteric microvessels in acute inflammation and after treatment with the ionophore A23187 (Neal & Michel, 1992, 1995). The endothelial cell membranes were intact and although the endothelium adjacent to the openings was attenuated and occasionally fenestrated, the cell contents appeared to have been retained. The majority (28/36) of those openings which were completely reconstructed from ultrathin serial sections, passed through rather than between the endothelial cells. This was similar to the proportion of transcellular to intercellular openings that we reported in inflamed frog microvessels (Neal & Michel, 1992). These transcellular openings may be described more appropriately as very large pores rather than gaps in the endothelium.

If the opening of these large pores by high intravascular (transmural) pressure is an active process, the latent period may represent the time interval between the endothelium detecting a critical stress and the pores opening with the appearance of fluid and cells leaking rapidly into the interstitium. The sensitivity of the latent period to temperature is consistent with this view and one might expect that it could also be increased by agents that interfere with intracellular signalling processes. In this context, the reports of Parker and his colleagues (Parker & Ivey, 1997; Parker et al. 1998) are of considerable interest. They observed that the increased microvascular permeability seen in isolated rat lungs resulting from positive pressure ventilation could be attenuated by treatment with isoprenaline. It is presumed that the isoprenaline acted by raising intracellular cAMP levels, a manoeuvre that is known to attenuate agonist-induced increases in microvascular permeability (Michel & Curry, 1999). Although it is by no means certain that increases in permeability in rat lungs during positive pressure ventilation have a similar mechanism to that of pressure-induced openings in single frog capillaries, it would nevertheless be most interesting to investigate whether the appearance of pressure-induced openings in microvascular walls could be delayed or inhibited by raising intraendothelial levels of cAMP.

Finally we might speculate on why an active response of the endothelial cells might lead to the apparent rupture of the vessel wall while the wall can still sustain the load placed upon it. A clue to answering this question could be the rapid recovery with restoration of normal permeability and wall strength within a few minutes of pressure being lowered. An active process relieving wall stress before the wall fails might permit a rapid recovery, whereas stress failure of the wall may not be so rapidly reversible. While at present this is no more than a speculative hypothesis, it is one that is amenable to experimental investigation.