pH and rate of ‘dark’ events in toad retinal rods: test of a hypothesis on the molecular origin of photoreceptor noise

Abstract

Thermal activation of the visual pigment constitutes a fundamental constraint on visual sensitivity. Its electrical correlate in the membrane current of dark-adapted rods are randomly occurring discrete ‘dark events’ indistinguishable from responses to single photons. It has been proposed that thermal activation occurs in a small subpopulation of rhodopsin molecules where the Schiff base linking the chromophore to the protein part is unprotonated. On this hypothesis, rates of thermal activation should increase strongly with rising pH. The hypothesis has been tested by measuring the effect of pH changes on the frequency of discrete dark events in red rods of the common toad Bufo bufo. Dark noise was recorded from isolated rods using the suction pipette technique. Changes in cytoplasmic pH upon manipulations of extracellular pH were quantified by measuring, using fast single-cell microspectrophotometry, the pH-dependent metarhodopsin I-metarhodopsin II equilibrium and subsequent metarhodopsin III formation. These measurements show that, in the conditions of the electrophysiological experiments, changing perfusion pH from 6.5 to 9.3 resulted in a cytoplasmic pH shift from 7.6 to 8.5 that was readily sensed by the rhodopsin. This shift, which implies an 8-fold decrease in cytoplasmic [H⁺], did not increase the rate of dark events. The results contradict the hypothesis that thermal pigment activation depends on prior deprotonation of the Schiff base.

Rod photoreceptor cells are capable of reliably signalling the absorption of a single photon. The response to a photon appears as a discrete quantal event (the single-quantum response, SQR) clearly discernible from ‘continuous’ electrical fluctuations. Even in absolute darkness, however, the rod current exhibits not only continuous fluctuations symmetrical around the mean level, but also occasional larger unipolar ‘dark’ events, transient current decreases that are similar to the SQR in both amplitude and waveform (Baylor et al. 1980, 1984). These randomly occurring photon-like events constitute an intrinsic background noise that appears to set an ultimate limit to the capacity of the visual system to detect weak light in darkness (cf. Barlow, 1956; Aho et al. 1988).

Given the high initial amplification as well as the complex network of reactions that determine the shut-off of the response, the similarity of SQRs and dark events is strong evidence that the latter originate at the very input to the transduction cascade, i.e. in spontaneous (thermal) activation of the rhodopsin molecule. The SQR depends on serial activation of some 100 transducins by photoactivated rhodopsin and subsequent suppression of rhodopsin catalytic activity by multiple phosphorylation and arrestin binding (see Leskov et al. 2000; Pugh & Lamb, 2000). It is extremely improbable that waves indistinguishable from the SQR repeatedly arise e.g. from concerted spontaneous activation of hundreds of transducins followed by quenching that just happens to follow the kinetics of rhodopsin shutdown.

This seemingly inevitable conclusion, however, is faced with a serious discrepancy in the apparent energy barrier of thermal events compared with the photon-driven process. Estimates of the photoactivation barrier by photocalorimetry (Cooper, 1979; Birge & Vought, 2000) as well as less direct methods (Srebro, 1966, Koskelainen et al. 2000) converge on values around 40–50 kcal mol⁻¹, whereas measurements of the temperature dependence of dark event rates suggest not more than 20–24 kcal mol⁻¹ (Baylor et al. 1980; Matthews, 1984; Firsov & Govardovskii, 1990). To reconcile these, it is necessary to assume that thermal activation and light activation of rhodopsin follow different molecular paths. The most cogent hypothesis for a separate low-energy thermal pathway is that of Barlow et al. (1993), who proposed that the discrete dark events arise in a small subpopulation of rhodopsins, where the Schiff base linking the chromophore to the protein part has been deprotonated. Molecular computations indicate that the unprotonated form has a much lower energy barrier for chromophore isomerization, giving for the whole deprotonation-isomerization reaction an apparent activation energy consistent with those found for the ‘dark’ events (Barlow et al. 1993; Birge & Barlow, 1995; Birge & Vought, 2000).

Under this hypothesis, the dark event rate should be strongly pH dependent. The pK of the Schiff base of vertebrate rhodopsin is very high, a consensus estimate being pK_P >15 (Steinberg et al. 1993; see Ebrey, 2000 for a recent review). This means that the overwhelming majority of the molecules are in the protonated state, Rh_H⁺, at physiological pH:

where Rh_t denotes total rhodopsin concentration, and K_p is the protonation constant. Taking into account that [H⁺] >> K_p, the concentration of the unprotonated form, [Rh], is:

i.e. the small number of unprotonated molecules is expected to change in inverse proportion to intracellular [H⁺]. For example, one unit of alkaline shift in intracellular pH (pH_i) should increase the number of unprotonated molecules by a factor of 10, and if thermal activations occur only in the pool of unprotonated rhodopsin molecules, this should be evident as a 10-fold increase in the frequency of electrophysiological dark events. Barlow et al. (1993) recorded effects of extracellular pH (pH_o) on dark noise in the Limulus lateral eye and found changes in the predicted direction, although in fact much larger than expected.

The purpose of the present work was to test the hypothesis that rhodopsin with unprotonated Schiff base is the molecular source of discrete dark events in vertebrate rods. We did this by studying the effect of pH on the frequency of dark events, using the suction-pipette technique to record the dark current of single rods of the common toad Bufo bufo exposed to manipulations of extracellular pH. To quantify the resulting pH changes ‘seen’ by the pigment molecules, we measured the pH-dependent interconversion of rhodopsin photolysis products (metarhodopsins I, II and III, abbreviated MI, MII, MIII) using fast single-cell microspectrophotometry (MSP). These measurements show that pH in the immediate environment of the rhodopsin molecules would, on average, increase over a 0.9 pH unit range under our experimental changes of pH_o. The hypothesis then predicts an 8-fold increase in the rate of thermal rhodopsin activation when going from our lowest to highest pH values. Instead, we detected a small but statistically significant decrease in the dark event rate. Thus our results indicate that visual-pigment dark noise in vertebrate rods does not specifically originate from a subpopulation of molecules with unprotonated Schiff base.

METHODS

Animals

The experiments were done on common toads Bufo bufo caught in the wild in northwestern Russia or southern Finland. Animals were treated in accordance with the Finland Animal Welfare Act 1986 with guidelines of the Russian Physiological Society. Dark-adapted animals were decapitated, double-pithed, and enucleated under dim red light. All further manipulations were done under infrared video viewing. The eyes were cut open along the equator and the anterior part and vitreous were removed. A piece of eyecup with attached retina was cut off and the corresponding piece of retina was isolated for immediate use. The rest of the eyecup was put into a light-tight chamber in Ringer solution and stored at +7 °C for no longer than the following day.

Microspectrophotometry

To assess the intracellular pH shifts ‘seen’ by the rhodopsin molecules upon changes in perfusion pH, we measured the pH-dependent interconversion of MI, MII and MIII by fast MSP after short bleaching exposures. Absorbance spectra were recorded from single rods with an instrument basically similar to that described earlier (Govardovskii et al. 2000) but modified to allow brief bleaching and fast recordings of the absorbance spectra (Govardovskii & Zueva, 2000). Rhodopsin was bleached with a short (200–500 ms) pulse of light from a high-intensity green (525 nm) light-emitting diode (no. 110104, Marl International Ltd, Ulveston, Cumbria,UK). Nominally, as extrapolated from shorter exposures, a standard 500 ms light pulse would result in 99.6 % bleach. However, due to photoreversal reactions the final bleaching products contained, in addition to MI and MII and depending on pH, 3–5 % of a photoequilibrium mixture of rhodopsin and isorhodopsin. The mechanism of fast spectral scanning allowed the recording of a complete absorbance spectrum from 340 to 700 nm in 400 ms; recording of the first spectrum was started within 20 ms after the cessation of the bleaching light. The measuring beam was linearly polarized in the direction parallel to the disk plane, i.e. perpendicular to the rod outer segment (ROS) axis.

Two sorts of samples were used. To calibrate the pH dependence of the MI-MII-MIII conversion, measurements were made on detached ROSs supposedly lacking active pH regulation. Small pieces of retina were incubated for 10–15 min in the suitable solution (see below), and then gently shaken in a drop of the same solution, to obtain a suspension of detached outer segments. A small amount of the suspension was transferred to a fresh drop of the solution on a coverslip, covered with another coverslip, sealed by vaseline and used for measurements. For calibration measurements on detached ROS, a pseudointracellular solution was used. It contained (mm): KCl, 100; NaCl, 10; glucose, 10; MgSO₄, 1.0 or 10; buffered to desired pH by a 10 mm buffer. Between pH 6.5 and 8.0, buffering was achieved by Na-Hepes; at more acidic pH, by sodium phosphate buffer; at more alkaline pH, by Tris-HCl. The concentration of free Ca²⁺ was buffered to 50 nm, a value in the range of cytoplasmic levels, either by EGTA or EDTA with a calculated amount of CaCl₂ added. Mg²⁺ (10 mm) and EGTA (10 mm) were used at pH 7.5 and higher, when the chelator had sufficient affinity to Ca²⁺. At more acidic pH, EGTA was inefficient due to the traces of the cation in all chemicals, taking into account that total [Ca²⁺] in nominally calcium-free solution was 10 μm. Thus to achieve 50 nm free [Ca²⁺] at pH 6.5–7.0, we used 5 mm EDTA and reduced [Mg²⁺] to 1 mm. The concentration of free Ca²⁺ in the solution was computed with the program BAD (Brooks & Storey, 1992).

For measurements on intact rods, small pieces of retina were prepared in the same way as for the electrophysiological recordings. The pieces were placed in an MSP chamber formed by a narrow (∼200 μm) gap between coverslips with gravity-driven perfusion with a solution identical to that used for electrophysiological recordings at the same pH. The recordings were performed on the outer segments of intact rods protruding from the edge of the retinal pieces.

All MSP measurements were made at a standard temperature of 20 ± 0.5 °C.

Suction pipette recordings

The rod membrane current was recorded with the suction-pipette technique (Baylor et al. 1979). Isolated cells having intact outer and inner segments and cell bodies, but lacking synaptic processes were used in most cases. In successful experiments, they could be held for up to three hours without significant changes in response properties. Each cell was recorded at only one single pH value. All isolated cells were recorded in the inner segment in configuration to ensure that the outer segment containing the visual pigment (and generating the conductance changes recorded) was effectively exposed to the perfusion pH. A few recordings were made from rods still attached to small retinal pieces, so the outer segment was inside the pipette filled with the same solution as in the bath. No significant difference in the dark events rate was found between the two recording configurations, so these six cells are included in the analysis.

The cells were continuously superfused with a Hepes-based regular Ringer solution of composition (mm): NaCl, 90; KCl, 2.5; MgSO₄, 1; CaCl₂, 1; glucose, 10; Hepes, 10; NaHCO₃, 5; EGTA, 0.05; plus bovine serum albumin, 10 mg l⁻¹. After preparation the pH of the Ringer solution was adjusted to chosen values by adding either 1 m NaOH or HCl. pH was also always checked after the measurements were completed. The difference compared with the initial value in the experiments, after 4 to 6 h of perfusion, was less than 0.2 pH units. The temperature in most experiments was 16.5 ± 0.5 °C; four cells were recorded at 21.5 ± 0.5 °C.

The intensity of light stimuli (20 ms flashes) was controlled by neutral density filters interposed in the beam from a tungsten lamp. Interference filters were used to control wavelength: 532 nm for regular stimulation and the same together with 442 nm for rod identification (‘red’ 502 nm or ‘green’ 432 nm rod). Nominal calibration of light intensities was made with a calibrated photodiode, but a more precise value for photons absorbed was obtained for each individual cell using the statistics of rod responses to nominally identical dim flashes (see Baylor et al. 1979; Donner et al. 1990).

Light stimulation and data recording were under computer control (LabView, National Instruments, Austin, TX, USA). Light responses and dark records were low-pass filtered (0–10 Hz), digitized at a frequency of 100 Hz (10 ms per point) for light responses and 25 Hz (40 ms per point) for dark records and stored on the computer hard disk. In most cells the intensity-response curve was measured.

Each cell recorded was imaged before and after recordings with an infrared CCD camera attached to the microscope and a framegrabber computer card. The volume of the outer segment that had been recorded from was determined from these images. To calculate the number of rhodopsin molecules in the outer segment, the rhodopsin concentration was assumed to be 3 mm (Liebman, 1972; Hárosi, 1975).

Estimation of the rate of dark events

In 15 of 22 cells used for analysis, the ratio of SQR amplitude (‘signal’, S) to the standard deviation of the continuous noise (‘noise’, N), after appropriate filtering (usually DC to 1 Hz), was high enough to allow counting discrete dark events by eye (cf. Fig. 3A). However, in seven cells (mostly at low pH), S/N was insufficient for reliable identification of discrete events (cf. Fig. 3B). To determine the average frequency of discrete events in these records, we analysed the current histogram as in Donner et al. (1990). In principle, the three parameters, namely variance of the continuous noise, amplitude of the discrete event, and the number of the events in the record, can be unambiguously determined from the first, second and third moments of the record. This estimate, however, is rather sensitive to random fluctuations and to uncertainties in the position of the zero line. Thus the result was checked by computing the expected probability density of Gaussian continuous noise plus discrete events, p(i), as a convolution of probability densities of the corresponding components (Donner et al. 1990):

Figure 3. Sample recordings of dark noise in isolated rods.

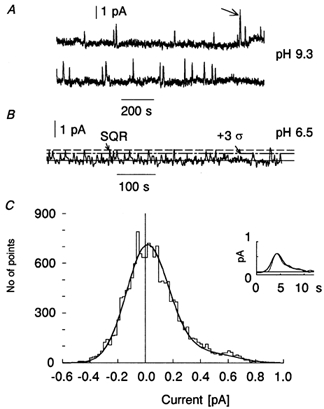
A, record with high discrete event/continuous noise amplitude ratio (high S/N): the discrete events can be counted by eye. The event marked with an arrow probably corresponds to two superimposed events. The record has been digitally low-pass filtered at 0.5 Hz. Temperature 16 °C. B, record with lower S/N: a direct count is unreliable. The dot-dash line marks a criterion level of 3 s.d. of the continuous noise. When peaks crossing this level are considered as discrete events, a total of 17 events during the 605 s record are counted. The dashed line shows the amplitude of the single-photon response (0.67 pA) estimated from amplitude fluctuations of 40 responses to about two-photon flashes (see Baylor et al. 1979). Temperature 16 °C. C, current amplitude histogram of the record shown in B, total 15125 points. The central peak is mostly due to the symmetrical continuous noise while the unipolar discrete events are responsible for the positive shoulder. The smooth line is an analytical fit to the histogram computed as a convolution of probability densities of continuous Gaussian noise and unipolar photon-like responses (see Methods). Estimated from the fit, 16.5 discrete events of 0.62 pA amplitude are present on a background of 0.145 pA s.d. continuous noise, in good agreement with the thresholding method in B. In the inset, the average of all dark events identified by the threshold-crossing method in panel B (thick line) are compared with the SQR (thin line). To facilitate comparison of waveforms, the SQR amplitude of 0.67 pA has been scaled down to the 0.61 pA amplitude of the average dark bump. The 10 % discrepancy between the two amplitude estimates is within statistical error. Note that the dark events rate in B, as compared to A, is 3-fold higher. This is partly due to 50 % bigger ROS volume recorded at pH 6.5, and partly due to the statistical effect of sampling a random sequence of events. When averaged over total recording time and normalized to ROS volume, the cell in B shows 30 % higher activation rate than the cell in A. This reflects a true effect of acidic pH (cf. Fig. 4).

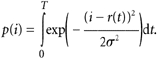Here r(t) is the waveform of the SQR estimated from the averaged response to a series of weak flashes, σ² is the variance of the continuous component, and T is the average interval between discrete dark events (= 1/f, where f is the event frequency). The expected probability density was normalized to the total number of points and compared with the experimental histogram (smooth vs. staircase line in Fig. 3C). Small adjustments of parameters can then be made to achieve the best fit.

Alternatively, discrete events can be defined as positive-going peaks that exceed a certain threshold level in the dark records. We applied a threshold of 3 × s.d., selected to make the probability level for the continuous noise to cross sufficiently low (Fig. 3B). The values thus obtained for T agreed within 10–15 % with those obtained by analysis of the current histogram as described above. The event rates from low-S/N records were always determined by both these methods. In three cells with intermediate S/N, all three methods (direct count, histogram analysis and threshold crossing) were applied, giving results that agreed within 10 %.

Since the cells were studied with different ROS volumes subject to recording, the averaging of results from different cells deserves some attention. The number of events counted from each cell was normalized to the standard number of rhodopsin molecules in an average ROS (3×10⁹). The normalized numbers from all cells were summed and divided by the total recording duration to obtain an average event frequency in a standard rod, and thus the activation rate per rhodopsin molecule. The relative s.d. was calculated as 1/√n, where n is the total number of events that had actually been counted (i.e. prior to any normalizations).

RESULTS

pH measurements

Figure 1A shows a set of MSP records from a single detached ROS in darkness and at various times after a 500 ms bleach. The flash bleached almost all the rhodopsin in the cell and the first scan (covering 20–420 ms after cessation of the bleaching exposure) reveals a spectrum with a sharp peak at 380 nm and a shoulder at 475–480 nm (the trace labelled 0 s). The main peak represents MII, and the long-wave sub peak is due to MI in equilibrium with MII, plus some amount of photoregenerated rhodopsin and isorhodopsin. In the subsequent scans the MII peak gradually decreases, and the peak at 480 nm first increases and then decays (traces recorded 30, 100, 200 and 600 s after the bleach). We tentatively call the emerging 480 nm product MIII (Baumann, 1972).

Figure 1. pH dependence of postbleach spectra of rod outer segments.

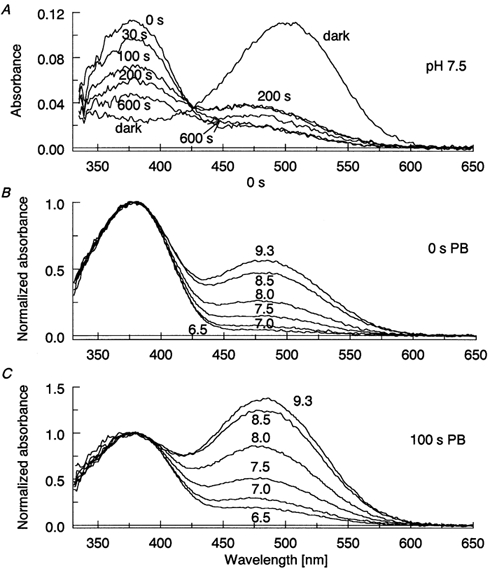
A, absorbance of a single detached ROS in pseudointracellular solution at pH 7.5, recorded in darkness and at different times after 500 ms complete bleach. The curve at 0 s postbleach demonstrates equilibrium between MI (shoulder at 480 nm) and MII (peak at 380 nm). Subesequent spectra, recorded at 30, 100, 200 and 600 s, show decay of MII and appearance of MIII. B, pH dependence of MI-MII equilibrium at 0 s postbleach. C, pH-dependence of MIII formation at 100 s postbleach. Each curve in B and C is an average from 10–12 isolated ROSs.

The MI-MII equilibrium is pH dependent, with high pH favouring MI (Matthews et al. 1963). High pH also facilitates MIII formation (Gyllenberg et al. 1974). Thus both the fraction of MI in the MI-MII mixture and the amount of MIII formed can be used as measures of pH_i. Panel B in Fig. 1 shows the pH_o dependence of postbleach spectra of isolated ROSs at 0 s after bleach, and panel C at 100 s after bleach, i.e. approximately at the time when the MIII content reaches its maximum. In Fig. 2A and B, averaged ratios of the absorbances at 480 and 380 nm (A₄₈₀/A₃₈₀) are plotted against the pH of the perfusion solution. For isolated ROSs (filled symbols) we assume that pH_i = pH_o. The basis for this assumption is that (i) observations on salamander rods loaded with the pH-sensitive dye BCECF show that pH regulation is weak or lacking in isolated ROSs (K. Donner, A. Koskelainen, E. Ruusuvuori and J. Saarikoski, unpublished results); (ii) isolated ROSs lack energy metabolism, which a priori excludes metabolic acid production on one hand, on the other hand ATP-dependent acid/base transport; (iii) in the isolated-ROS recordings we used a ‘pseudo-intracellular’ and nominally bicarbonate-free perfusion medium (see Experimental procedures). This eliminates any possibly remaining inward Na⁺ gradient that could drive proton extrusion and disables bicarbonate-dependent pH regulation (cf. Koskelainen et al. 1994). Thus we base our calibration of pH_ivs. the absorbance ratio A₄₈₀/A₃₈₀ on the data from isolated ROSs. The calibration curves shown as continuous lines in the figure are logistic fits to the data. (The logistic function was chosen so as to provide a smooth description of the data, appropriate for calibration, and has no theoretical meaning, see figure legend.)

Figure 2. Using the pH dependence of the MI-MII equilibrium and MIII accumulation for assessing intracellular pH in intact rods.

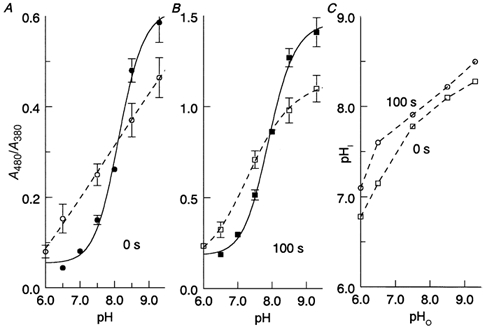
A, ratio of absorbances at 480 and 380 nm (A₄₈₀/A₃₈₀) at 0 s postbleach vs. pH of the perfusing solution in isolated ROS (•) and intact rods protruding from the edge of retinal pieces (○). Isolated ROS were perfused with a pseudointracellular solution while intact rods were perfused with a normal Ringer solution (see Methods). The continuous line is a logistic fit that is used as a calibration curve for A₄₈₀/A₃₈₀vs. pH_i. The formula of the fit is A₄₈₀/A₃₈₀= a + b/(1 +(pH/c)^−d) where a, b, c, d are constants. Error bars give ±s.d.B, same as in A, but for spectra recorded at 100 s postbleach, reflecting MIII accumulation. ▪, isolated ROS; □, intact rods. C, intracellular (pH_i) vs. extracellular (pH_o). pH in intact rods at 0 and 100 s postbleach obtained from the data shown in A and B.

Open symbols in Fig. 2 mark data from intact rods attached to retinal pieces, perfused with the same solutions as used in the electrophysiological experiments. At acidic pH the A₄₈₀/A₃₈₀ ratio was higher than in isolated ROSs, while the situation was reversed in the alkaline region. This expresses the ability of intact cells to regulate pH_i, i.e. to prevent it from changing as strongly as pH_o (Saarikoski et al. 1997). Using the calibration curve from isolated ROSs, we transform the measured A₄₈₀/A₃₈₀ ratios into estimates of pH_i and obtain a function relating pH_i to pH_o in intact rods (Fig. 2C). Both sets of points, obtained at 0 and 100 s postbleach, respectively, show that pH_i changes by 0.35–0.4 units per unit of pH_o change. In particular, when pH_o rises from 6.5 to 9.3 (the range used in the electrophysiological experiments), pH_i rises by 0.9–1.1 units. Thus, [H⁺]_i is expected to change over an 8- to 12-fold range in the conditions of our dark noise measurements.

It is worth noting that the pH_ivs. pH_o curve at 100 s postbleach is shifted by 0.2 to 0.3 units towards lower pH_i values compared with the curve at 0 s (Fig. 2C). The shift may reflect an acidification of the cytoplasm as a result of active hydrolysis of cGMP and GTP after bleaching (cf. Saarikoski et al. 1997).

Dark noise recordings

The dark current was recorded and completely analysed in a total of 22 ‘red’ (502 nm) rods at pH_o values of 6.5, 7.5, 8.5 or 9.3. The dark noise contains three components; instrumentation noise and continuous and discrete components of rod membrane current fluctuations. In the frequency band of our filtered recordings (0–1 Hz), instrumentation noise is significantly smaller than both the biological components. This was ascertained by comparing continuous noise in darkness and in the presence of a steady light, bright enough to shut off all rod current. The saturating light reduced continuous noise s.d. by more than 2.5-fold (range 2.5–5.6; data not shown). This means that the contribution of the instrumental noise to the s.d. of the ‘dark’ recordings in the worst case does not exceed 10 %.

Dark events in toad rods at room temperature are rare enough to be generally well separated from each other (cf. Baylor et al. 1980; Fyhrquist et al. 1998b) and under beneficial conditions they can just be counted by eye, which makes elaborate statistical analysis superfluous. Thus in most cases the numbers of dark events were counted by eye. However, in some recordings with a lower amplitude ratio of discrete events to continuous noise s.d. (which we shall refer to as the signal-to-noise ratio, S/N), a more sophisticated statistical procedure was used to estimate reliably the number of discrete events (see Methods). The observed dark event rate was recalculated to a rate of thermal activations per molecule of visual pigment on the basis of the volume of outer segment outside the pipette (i.e. recorded from) measured by video imaging, and the known packing density of rhodopsin in the rod.

Figure 3A shows a representative high-S/N record (at pH_i = 9.3) encompassing 43 min of dark current. Over this time, 22 positive-going quantal events can be counted, giving a frequency of one event per 116 s or 0.0085 events s⁻¹. This ‘raw’ count is clearly lower than the rate reported by Fyhrquist et al. (1998b) for the same species, one event per 50 s (0.02 s⁻¹) rod⁻¹, but the difference can be explained by the lower recording temperature (16 vs. 22 °C) and possible difference in the ROS volume. Figure 3B and C gives an example of the two types of analysis performed on low-S/N records, where counting by eye could not be relied upon (see Methods and Donner et al. 1990). In panel B, the threshold method is applied to a dark noise record with S/N = 4.2. Seventeen positive-going bumps cross the criterion level of 3 s.d. of continuous noise and are counted as dark events. Panel C shows the histogram of the current values of the record in B (staircase line). The histogram is fitted with the predicted probability density of Gaussian continuous noise plus dark events whose shape corresponds to the averaged dim-flash response (smooth bold line). The best fit indicates 16.5 events, in good agreement with the threshold method. To study further whether ‘dark events’ defined by threshold crossing in panel B are indeed similar to the SQR, they were excised, aligned on the time scale with respect to their peaks, and averaged. The amplitude of the average dark event, 0.61 pA, virtually coincides with the value obtained from histogram fitting (0.62 pA), and is consistent with the amplitude of the SQR estimated from the statistics of dim-flash responses (0.67 pA). The inset in panel C shows the averaged dark event (bold line) superimposed on the SQR scaled to the same amplitude for easier comparison of waveforms (thin line). The dark event averaged as described is seen to be slightly wider than the SQR, which is plausibly explained by imperfect (due to noise) temporal synchronization of individual events during averaging. Thus the threshold-crossing and histogram-fitting methods of analysis yield very similar results, and both are consistent with the idea that dark events and SQRs are identical. For the recording (at pH 6.5) shown in Fig. 3B, the two estimates of the dark event rate converge on a value of ∼0.027 events rod⁻¹ s⁻¹.

Seven of 22 cells were analysed with the threshold-crossing and histogram-fitting methods, and in three of these, a reliable direct count was also possible (see Fig. 5). The event frequencies obtained from the same record with the different methods agreed within 10 to 15 %. Average thermal activation rate at near-physiological pH_o = 7.5 and 16.5°C was 5 × 10⁻¹² s⁻¹.

Figure 5. pH dependence of the ratio of the SQR amplitude to the s.d. of continuous noise (S/N).

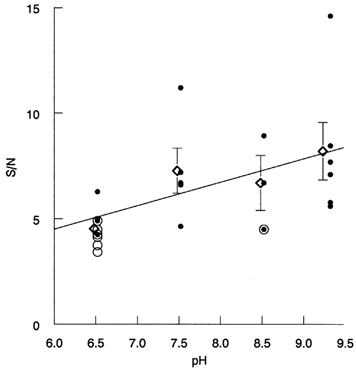
Each point represents one cell. •, cells in which the number of dark events was counted by eye. ○, cells analysed with the threshold-crossing and the histogram-fitting methods; overlapping • and ○ mark cells to which all three methods were applied. ⋄ with error bars give means ±s.e.m. The least-square straight line shows the general trend of the data.

The central result is summarized in Fig. 4. Here the frequencies of dark events per rhodopsin molecule, presumed to represent rates of thermal activation of the visual pigment, are plotted against pH_o (open circles and error bars give mean values ± 3 s.d.). The bold continuous line is a parabola fitted to the data points just to illustrate the general trend. The thin continuous line shows the prediction of the hypothesis that thermal activation rates are proportional to the number of available rhodopsin molecules with unprotonated Schiff base, assuming that this number varies in inverse proportion to [H⁺]_i and that pH_i follows the 0 s curve of Fig. 2C. It is immediately obvious that the data deviate strongly from the prediction and, in fact, do not even show any trend suggestive of increasing dark event frequencies with rising pH. On the contrary, there is a slight decline of the frequency at high pH (see Discussion).

Figure 4. Summary of the results on the rate of rhodopsin thermal activation as a function of pH.

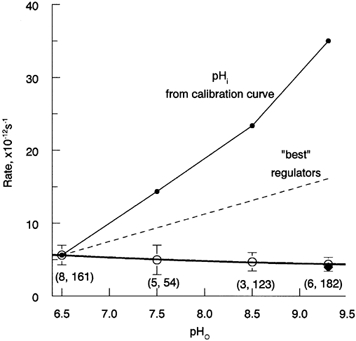
Open circles show the frequency of discrete dark events that has been converted into rates of activation per rhodopsin molecule using the volume of ROS recorded (see Methods). The number of cells and total number of discrete events counted for each data point are shown in parentheses. Error bars are ±3 s.d. The bold continuous line is a parabolic fit to the data. The thin continuous line shows relative concentrations of the deprotonated form of the chromophore expected from the average pH_i/pH_o relation taken from Fig. 2C (0 s curve). The dashed line (‘best regulators’) shows the lower limit for changes in the concentration of rhodopsin with deprotonated Schiff base over this range of pH_o, based on the difference between the most alkaline cell at pH_o = 6.5 and the most acidic cell at pH_o = 9.3. ♦ at pH 9.3 shows the activation rate corrected for higher recording temperature in part of pH 9.3 cells (see Discussion).

With respect to other possible effects of pH on rod properties, the only statistically significant pH dependence found was an increase in the ratio of the amplitude of discrete events to continuous noise, i.e. S/N with rising pH. This is illustrated in Fig. 5. The 1.8-fold difference in S/N between pH 6.5 and pH 9.3 is significant at P > 0.97 (Student's paired t test). In individual parameters of the quantal events (amplitude and time to peak of the SQR or dark events) or the s.d. of the continuous noise, no significant trends could be revealed in the collected data.

DISCUSSION

Calibration of intracellular pH changes

We measured the effect of pH_o on pH_i using the MI-MII transition and MIII formation after a bleaching exposure as pH indicator. On average, changing pH_o from 6.5 to 9.3 changed pH_i from 7.6 to 8.5 in intact rods. Our value ΔpH_i/ΔpH_o ∼ 0.35–0.40 for toad rods attached to pieces of retina is in reasonable agreement with the linear regression coefficients ΔpH_i/ΔpH_o ∼ 0.4–0.5 measured by Saarikoski et al. (1997) in isolated salamander (Ambystoma) rods loaded with the fluorescent pH-sensitive dye BCECF. However, the absolute level of pH_i in the retina-attached toad rods was clearly higher (by ∼0.6 pH units at pH_o = 7.5) than in the isolated salamander rods.

The capacity to regulate (stabilize) pH_i in the face of external pH changes will vary not only between individual rods, but also between different types of preparations and animal and photoreceptor species. If anything, the retina-attached rods in the MSP measurements are likely to have more effective pH regulation than the isolated rods we mostly used in the dark noise measurements. In the latter experiments, the average change in pH_i between pH 6.5 and pH 9.3 perfusion is therefore expected to have been ≥ 0.9 pH units. To get an absolute lower limit for the range of pH_i changes achieved in our noise recordings, we may take the values of the ‘best’ pH regulators among all rods encountered in the MSP recordings. The difference in pH_i between the most acidic cell recorded when pH_o = 9.3 and the most alkaline cell when pH_o = 6.5 was 0.46 units (at 0 s after bleach). This lower-limit pH_i change corresponds to a ∼3-fold change in [H⁺]_i and hence in predicted dark event rate, a difference that would have been readily detected in our experiments (dashed line in Fig. 4).

Is there an effect of pH opposite to that predicted?

Unexpectedly, the collected data in Fig. 4 indicate a small (22 %) but statistically significant (P > 0.97) decrease in event frequency between the lowest and the highest pH_o. Actual decline must be bigger, however, as it so happened that the temperature was 21.5 °C in the experiments that account for half of all dark events recorded at pH 9.3 (4 cells), whereas two cells at pH 9.3 and all the data at the lower pH (total 18 cells) were collected at 16.5 ± 0.5°C. Referring all to the common standard temperature 16.5°C results in a further relative downward shift of the data at pH 9.3 (♦ in Fig. 4, 30 % decline at pH 9.3 vs. pH 6.5) and an increase in the statistical significance of the decline (P > 0.99). The temperature correction was based on measurements in another toad species, Bufo marinus (activation energy of 22 kcal mol⁻¹; Baylor et al. 1980), and although B. bufo and B. marinus rhodopsins are very similar with respect to absorbance spectrum, amino acid sequence as well as dark event rates (Fyhrquist et al. 1998a, b and the present work), there remains in principle the possibility of a species difference that might have led us to ‘over-correct’ and exaggerate the decline. This said, it must be emphasized that possible uncertainties in the temperature correction can in no way change the main conclusion on the lack of increase of the thermal activation rate at high pH.

Does the Schiff base see the pH changes?

Our method of determining pH_i allowed us not only to measure cytoplasmic changes, it also showed that the changes really reach the visual pigment molecule, affecting its conformational states after a bleach. However, crucial for the test of the ‘pH-hypothesis’ is the question whether the cytoplasmic protons penetrate the chromophore binding pocket inside the membrane to affect the Schiff base. This is almost certainly the case. The binding pocket is known to contain several water molecules, and water trafficking between the interior of the molecule and the surroundings has been studied by Raman spectroscopy in conjunction with use of heavy water, D₂O. This technique has revealed fast penetration of D₂O to interact with the chromophore in bovine rhodopsin in disk membrane vesicles (Oseroff & Callender, 1974) as well as in several other vertebrate visual pigments (see e.g. Mathies, 1999). Thus, although direct data on toad rhodopsin are lacking, there is no reason to assume that the protonation state of the Schiff base specifically in Bufo bufo rhodopsin would be insensitive to pH changes around the molecule.

Lack of predicted pH effect on the frequency of dark events

The main result is that there was no increase in dark event rate with increasing pH (see Fig. 4). We conclude that the results are not compatible with the hypothesis that the main source of thermal activation of the rod visual pigment is a subpopulation of molecules with deprotonated Schiff base.

Before the present study, two abstracts have provided preliminary reports of experiments done to reveal possible pH effects on photoreceptor noise in rods of Bufo marinus and Xenopus laevis (Donner et al. 1997) and red-sensitive cones of salamander (Sampath & Baylor, 2001). In both these studies the actual changes in cytoplasmic pH remained unknown. However, the results are consistent with the present ones in that changes in external pH could not be shown to have any effect on rates of thermal activation of the visual pigment.

It seems that the mechanism for generation of discrete dark events in vertebrate rods differs from that in Limulus photoreceptors (Barlow et al. 1993), where pH had a big effect. We still lack a molecular theory that could provide a general explanation for the thermal activation of vertebrate rhodopsin. For example, although activation rates show a general correlation with the position of the absorbance maximum (λ_max) (Donner et al. 1990; Firsov & Govardovskii, 1990; Rieke & Baylor, 2000), significant differences in dark event rates have been observed between rods with spectrally similar rhodopsins (Bufo vs. Rana: Baylor et al. 1980; Donner et al. 1990; Fyhrquist et al. 1998b; present study). This suggests that subtle changes in the molecular structure of rhodopsin, not directly related to the chromophoric center, may have substantial effects on its thermal activation (cf. Fyhrquist et al. 1998a). The mechanisms of activation in rod and cone visual pigments are likely to differ even more strongly. The rate of thermal activation, if extrapolated from rod data (Firsov & Govardovskii, 1990) to salamander ‘red’ cone pigment, predicts a value of 4.4 × 10⁻⁹ s⁻¹, while Rieke & Baylor (2000) found approximately 1 × 10⁻⁴ s⁻¹. Thus there is a discrepancy of more than four orders of magnitude. It seems that the entire event frequency vs. λ_max relation is shifted to higher frequencies in cones. This notion is consistent with the fact that the dark event frequency of amphibian blue-sensitive (‘green’) rods (Matthews, 1984), whose pigment phylogenetically groups among the ‘blue’ cone pigments of other vertebrates (Hisatomi et al. 1999), is too high to fit the general frequency-λ_max relation for rods. Further, the >1 × 10⁵-fold difference in apparent thermal activation rate between amphibian L-cone and rod pigments (Vu et al. 1997; Rieke & Baylor, 2000) seems not to correlate with a corresponding difference in the energy barriers for light activation (Koskelainen et al. 2000).

The basic idea originally proposed by Barlow (1956, 1957) to explain the difference in sensitivity between rod and cone vision on the basis of different rates of thermal ‘dark’ activation of the visual pigments has received strong qualitative support from physiological data gathered in the two last decades (Baylor et al. 1980, 1984; Matthews, 1984; Donner et al. 1990; Firsov & Govardovskii, 1990; Fyhrquist et al. 1998b; Rieke & Baylor, 2000). However, we still have no comprehensive molecular understanding of this process that sets the ultimate limit to the sensitivity of vision.