Evidence for two distinct processes in the final stages of neurotransmitter release as detected by binomial analysis in calcium and strontium solutions

Abstract

The statistical parameters underlying acetylcholine (ACh) release were studied using Ca²⁺ and Sr²⁺ ions to promote ACh secretion. Experiments were performed at frog neuromuscular junctions using electrophysiological recording techniques. Increases in asynchronous ACh release, reflected as the frequency of occurrence of miniature end-plate potentials (MEPP_f), were evoked by high potassium depolarization in either Ca²⁺ or Sr²⁺ solutions. Increases in MEPP_f mediated by Ca²⁺ were of very low probability and well-described by a Poisson distribution whilst similar MEPP_f increases mediated by Sr²⁺ were best described as a simple binomial distribution. From the binomial distribution in Sr²⁺ solutions, values for the average probability of release (p) and the number of releasable ACh quanta (n) may be determined (whereby mean MEPP_f = np). In Sr²⁺ solutions, values of p were independent of both bin width and of the value of n, suggesting that both n and p were stationary. Calculations of p using the simple binomial distribution in Sr²⁺ solutions gave theoretical values for the third moment of the mean which were indistinguishable from the experimental distribution. These results, in conjunction with Monte Carlo simulations of the data, suggest that spatial and temporal variance do not measurably affect the analysis. Synchronous ACh release evoked by nerve impulses (end-plate potentials, EPPs) follow a simple binomial distribution in both Ca²⁺ and Sr²⁺ solutions. Similar mean levels of synchronous ACh release (m, where m =np) were produced by lower values of p and higher values of n in Ca²⁺ as compared to Sr²⁺. The statistical analyses suggest the presence of two different Ca²⁺-dependent steps in the final stages of neurotransmitter release. The results are discussed in accordance with (i) statistical models for quantal neurotransmitter release, (ii) the role of Sr²⁺ as a partial agonist for evoked ACh release, and (iii) the specific loci that may represent the sites of Ca²⁺ and Sr²⁺ sensitivity.

The skeletal neuromuscular junction has long been used as a model for neurotransmitter secretion as the electrophysiological correlates of both spontaneous and evoked transmitter release may be accurately quantified at this synapse (Katz, 1969; McLachlan, 1978; Silinsky, 1985). Previously, two different approaches for investigating the mechanisms of neurotransmitter release have been employed. One method has been to use mathematical analyses commonly employed to describe discrete statistical distributions, namely analyses of either Poisson or binomial distributions of quantal secretory events (McLachlan, 1978; Silinsky, 1985; Redman, 1990; Quastel, 1997). The other approach has been to compare the actions of the alkaline earth cations in order to dissect the Ca²⁺-dependent processes that mediate neurotransmitter secretion (Jenkinson, 1957; Dodge & Rahamimoff, 1967; Meiri & Rahamimoff, 1971; Silinsky, 1978, 1981, 1985). In this regard, Sr²⁺ is a weak, partial agonist when compared to Ca²⁺ for the process of neurally evoked ACh release, with maximal levels of ACh release considerably lower in Sr²⁺ than in Ca²⁺ solutions (Silinsky, 1981). It has been shown that differences in the abilities of Ca²⁺ and Sr²⁺ to promote spontaneous and evoked neurotransmitter release are unlikely to be due to differences in their entry via voltage gated Ca²⁺ channels (Augustine & Eckert, 1984; Silinsky, 1985), but rather reflect differences in the abilities of these two cations to activate the intraterminal release process (Mellow et al. 1982; Silinsky et al. 1995).

The secretion of ACh and other neurotransmitters at low levels of neurotransmitter release follows a Poisson process, which generally describes random events in space and time (Katz, 1969; Colquhoun, 1971; McLachlan, 1978; Silinsky, 1985). At higher levels of neurotransmitter release, binomial statistical analyses have been used to fit the data (Miyamoto, 1975; McLachlan, 1975; Bennett et al. 1975, 1976; McLachlan, 1978). Binomial analysis has often been performed in consort with morphological analysis as binomial distributions provide estimates of both p, the average probability of neurotransmitter quantum being released, and n, the total number of quanta available for release. The mean level of a neurotransmitter release or m = np (del Castillo & Katz, 1954; Colquhoun, 1971; McLachlan, 1978; Silinsky, 1985). The parameter n has been equated with structural correlates of the secretory apparatus such as the number of synaptic vesicles immediately available for release or with the total number of active zones of release (i.e. release sites) in the nerve ending (Silinsky, 1985; Markram et al. 1997). However, the observations that both n and p are dependent on the extracellular Ca²⁺ concentration prior to a nerve impulse (Miyamoto, 1975; Bennett et al. 1975; but see Bennett & Lavidis, 1979) would suggest that this latter interpretation for n might not be correct in its simplest form. An alternative model would suggest that n and p represent two different calcium-dependent steps in the neurotransmitter release process. According to this model it might be expected that different cations would have different abilities to act on the two components, n and p, of the release process.

The use of simple binomial analysis for synchronous evoked ACh release reflected as end-plate potentials (EPPs) has been questioned (Brown et al. 1976; Redman, 1990) as it has been suggested that EPPs may not follow a simple binomial distribution due to spatial variance in p. Indeed, a number of different mathematical methods have been used, providing alternative descriptions of n and p. However, these methodologies introduce new assumptions not present in the use of the simple binomial distribution - namely the assumption that n is a fixed entity (Clements & Silver, 2000).

To our knowledge, no attempt has been made to combine conventional binomial analysis with comparative studies of equi-active concentrations of the full agonist Ca²⁺ with the partial agonist Sr²⁺ for the neurotransmitter release process. The purpose of this paper is thus twofold. Firstly, we examined the validity of the simple binomial distribution as a description of the neurotransmitter release process. In order to achieve this, we investigated the frequency of occurrence of asynchronously released MEPPs (MEPP_f) in KCl-depolarised preparations. Under these conditions, temporal and spatial variations due to local changes in the intraterminal Ca²⁺ or Sr²⁺ concentrations are likely to be minimal (Miyamoto, 1986) and discrete quantal events may be counted. Secondly, we examined whether Ca²⁺ and Sr²⁺ differed in their abilities to act on the parameters n and p for both asynchronous ACh release and for synchronous ACh release evoked by action potentials (i.e. EPPs).

METHODS

General

Frogs (Rana pipiens) were killed by anaesthesia with 5 % ether, followed by double pithing, in accordance with guidelines laid down by our institutional animal welfare committee. Isolated cutaneous-pectoris nerve-muscle preparations were used in all experiments in conjunction with intracellular electrophysiological recording techniques. Briefly, microelectrodes used for intracellular recordings were filled with 3 m KCl and had resistances 3–10 MΩ. The signal from the microelectode was fed into a conventional high-input impedance microelectrode pre-amplifier (Axoclamp-2A, Axon Instruments). Responses were fed into a personal computer using either a Digidata 1200 or TL1–125 A/D converter (Axon Instruments). Solutions were delivered by superfusion with a peristaltic pump and removed by vacuum suction. All experiments were carried out at room temperature (22–24 °C).

In experiments where MEPPs were studied, the Ca²⁺ solutions contained (mm): NaCl, 115; KCl, 12; Hepes, 2; CaCl₂ 0.5 and the Sr²⁺ solutions contained: NaCl, 115; KCl, 10; Hepes, 2; SrCl₂ 0.5, unless otherwise stated (see Results). In order to aid the interpretation of the results, MgCl₂ was omitted from all solutions. To ensure steady-state levels of asynchronous release, preparations were equilibrated for 45 min in the elevated KCl solutions prior to experimentation. An additional 15 min equilibration time was employed when switching from solutions containing one divalent cation to another.

Records of MEPPs were analysed using CDR and WCP programs (DOS versions, Strathclyde University Superior Software; John Dempster). For each experiment, at least 4500 MEPPs were used for data analysis. The times of occurrence of the individual MEPPs were then used to construct continuous time histograms. For reasons described below, the entire data set was divided into a specified bin width (e.g. 10 or 100 ms). Because the description of the data is less detailed when the 100 ms bin width is used, non-overlapping arrays of bins were used. Briefly, starting at time zero, the data were first analysed with a 100 ms bin width to produce the first array of frequencies. The data were then re-binned with 10 ms increments between the starting points for each individual array (10 arrays total). Values for p (± 1 s.e.m.) were obtained from the estimates of p given by each individual array. This method maintains the accuracy of the description of the data, whilst avoiding the smoothing of the data resulting from the use of rolling bins. Records where there were detectable trends over the recording period, i.e. increases or decreases in MEPP_f, were discarded from the results presented here.

In experiments where EPPs were studied, nerve muscle preparations were paralysed with formamide treatment (2 m formamide, 20–30 min) (del Castillo & Motta, 1978) which allows the recording of MEPPs and EPPs simultaneously from the same end-plate. Recording solutions contained (mm): NaCl, 115; KCl, 12; Hepes, 2; and either CaCl₂, 0.3 or SrCl₂, 2.

For studies on evoked ACh release, EPPs were evoked at 0.2 Hz and collected using SCAN (DOS version, John Dempster, Strathclyde University Superior Software) or pCLAMP software (Axon Instruments). The data were analysed using a modified version of a computer program for evoked release (Mark Longerbeam, BME Systems; see also Christian & Weinreich, 1992).

The Poisson and binomial distributions

Overview

For the purposes of statistical analysis of neurotransmitter secretion, the skeletal neuromuscular junction has several distinct advantages over other systems (Edwards, 1995). In particular, with regard to evoked release, the potential number of release sites and the associated post-junctional receptors are in great excess over the actual number of quanta released in this study. As a consequence, the likelihood of more than one vesicle being released from a single release site is correspondingly low (which may not be correct in other systems). Thus, transmitter release is directly proportional to amplitudes of the EPPs.

The Poisson frequency distribution (which is frequently used to describe events of very low probability) is given by:

(1)

where f(x) represents the probability of observing 0, 1, 2, 3…x events per unit of time or space and m represents the average number of quanta released asynchronously (MEPPs) over a given interval of time period (e.g. MEPP_f in a 10 ms period) or synchronously in response to electrical stimulation (i.e. EPPs). An important property of the Poisson distribution is that the mean and the variance of the population m are equal (Colquhoun, 1971).

The simple binomial distribution, which assumes that the release of a quantum of ACh is independent of other quanta released, is given by:

(2)

In this equation, f(x) reflects the probability of observing 0, 1, 2, 3…n quanta released, p reflects the average probability of release and q the probability of a failure of release (where q = 1-p). As mentioned in the introduction, m is also equal to the product of n and p.

The conventional shorthand of eqn (2) can be rewritten as:

(3)

(see Colquhoun, 1971). For the sake of clarity, it is important to stress that p for a binomial distribution is not equivalent to the proportion of the total pool of transmitter released. For a binomial distribution, n represents the total number of possible events and p represents the individual probability that the event will happen. For example if 10 coins are all tossed at once, and this exercise is repeated a number of times, the frequency distribution of heads (i.e. the number of times that 1, 2, 3…9, 10 heads result from each toss of 10 coins) will be predicted by a binomial distribution with n = 10 coins, and p = 0.5 (probability of a head). Overall, the mean number of heads, m, will equal 5 (as m = np). Similarly for neurotransmitter release, the number of ACh quanta released in response to a sequence of nerve impulses (or during a series of fixed, non-overlapping time intervals) will be predicted by the binomial distribution where p = the average probability of a quantum being released and n = the number of available quanta (e.g. synaptic vesicles in a given interval of time). It should be noted that p is a constant, dimensionless and independent of n or the number of coins per throw (i.e. the number of quanta released per impulse). The reader is referred to Rees (2000) for a lucid description of the binomial distribution.

The binomial distribution is characterized by its moments about the mean. For the binomial distribution, the first moment μ'₁ is about the origin and equal to the mean itself. As presented in the introduction, this becomes:

(4)

The second moment about the mean (μ₂) is defined as the population variance (Var) whereby:

For a binomial distribution this becomes:

(5)

Hence:

(6)

Because p is dimensionless, when the events being studied are occurring over time (as with MEPPs), changing the duration of the bin will have no effect on p but will indeed change n. Hence, if the bin width analysed is changed from 10 ms bins to 100 ms for MEPPs (see Figs 1 and 2), p will remain constant whilst n increases in direct proportion to the interval length (i.e. 10-fold in this instance from 10 ms⁻¹ to 100 ms⁻¹) with the same unit as m (Provan & Miyamoto, 1993).

Figure 1. Poisson distribution of MEPPs in Ca²⁺ solutions and binomial distribution of MEPPs in Sr²⁺ for similar levels of asynchronous release in high K⁺ solutions (10 ms bin width).

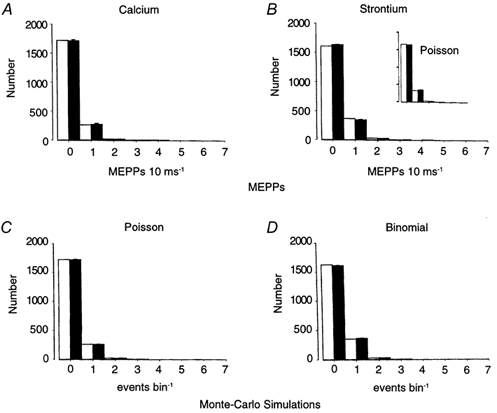
A, ▪, MEPP frequency distributions recorded in 0.5 mm Ca²⁺, with 12 mm KCl (± 1 s.e.m.). B, ▪, MEPP frequency distributions recorded in 0.5 mm Sr²⁺, with 10 mm KCl, from the same end-plate (± 1 s.e.m.). The MEPP frequencies obtained for both treatments were statistically indistinguishable (see Table 1 and text). Poisson distributions obtained from the mean frequency of MEPPs (eqn (1)) produced excellent descriptions of the Ca²⁺ MEPP data (A, □). The data in A are the averaged distributions from 4552 MEPPs. In contrast, the Poisson distribution did not produce good fits of the MEPPs recorded in Sr²⁺, but was well described by the binomial distribution (□). The theoretical binomial distribution in Sr²⁺ (□) was predicted by eqn (6) using the variance and mean of the MEPP distribution. The calculated value for p was 0.049 and n = 4.31 (χ² test, P < 0.05). The data in B are the averaged distributions from 5914 MEPPs. As can be seen from the inset, the differences between the Poisson distribution and these data are not readily apparent. The degree of significance results from the very small errors in the data (error bars are barely discernible on the graphs). See text for a further description of the statistical tests used in these experiments. C and D, results of Monte Carlo simulations. In C, the Monte Carlo simulation (▪) was generated using Poisson's equation (eqn (1)) and the mean value of the MEPP_f determined experimentally in A. In D, the Monte Carlo simulation (▪) was obtained using the estimates of n and p determined experimentally from B to generate a binomial distribution. Values of the variance and mean (as determined from the events generated by the Monte Carlo simulations (▪)) were then used to generate theoretical distributions (□). The population of events obtained by the Monte Carlo simulation of the Poisson distribution using the mean MEPP_f determined from the simulated data in C was well described by the theoretical Poisson distribution (This was similar to the data in Ca²⁺ solutions). Monte Carlo simulations of the binomial distribution were made by using values of p = 0.049 and n = 4.31 as determined experimentally in Sr²⁺ solutions, see B above). The estimates for p and n obtained from the Monte Carlo simulations were p = 0.067 and n = 3.15.

Figure 2. Poisson distribution of MEPPs in Ca²⁺ solutions and binomial distribution of MEPPs in Sr²⁺ for similar levels of asynchronous release in high K⁺ solutions (100 ms bin width).

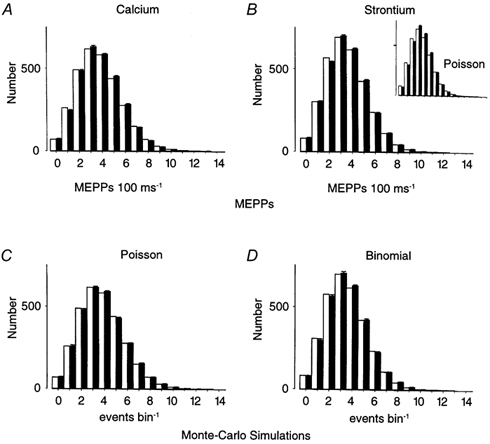
The results are similar to Fig. 1, only using a 100 ms bin width. A, MEPP frequency distributions recorded in 0.5 mm Ca²⁺, with 12 mm KCl (▪). B, MEPP frequency distributions recorded in 0.5 mm Sr²⁺, with 10 mm KCl, from the same end-plate (▪). The MEPP frequencies obtained for both treatments were similar. Poisson distributions obtained from the mean frequency of MEPPs (see Methods) produced good descriptions of the data in Ca²⁺ (□). The data in A are the averaged distributions from 11 291 MEPPs. In contrast, the Poisson distribution did not produce good fits of the MEPPs recorded in Sr²⁺ (inset) but was well described by the binomial distribution (□) predicted by the variance and mean of the MEPP distribution. The values obtained for B gave: p = 0.089 ± 0.004 and n = 37.9 (χ² test, P < 0.05). The data in B are the averaged distributions from 10 905 MEPPs. C and D, results of Monte Carlo simulations. In C, the Monte Carlo distribution (▪ ± s.e.m.) was obtained using the same mean frequency as the data recorded in A in conjunction with Poisson's equation (eqn (1)). In D, the Monte Carlo simulation was generated using the estimates of n and p from B to produce a binomial distribution (▪). Values of the variance and mean of the Monte Carlo distributions were then used to provide estimates of the Poisson and binomial distributions (□). The population of events obtained using Monte Carlo simulation of the Poisson distribution was well-described by the theoretical Poisson distribution (□). The Monte Carlo simulation of the binomial distribution ((D▪) using the estimates of p = 0.09 and n = 38 - see B above) was similar to the theoretical distribution generated using the variance and the mean of the Monte Carlo distribution (□). This simulation, using the variance and the mean of the Monte Carlo data, also yielded values of p = 0.095 and n = 37 (□).

The third moment of the mean μ₃ = Σ(x-x)³/n, often used as a measure of symmetry for statistical distributions. For the binomial distribution, the theoretical value for the third moment (eqn (3) in Miyamoto, 1986) is:

(7)

We used μ₃ as one of our measures for determining the validity of our results by comparing the calculated third moment of the mean of the data with the theoretical third moment as estimated by eqn (7).

Sources of error associated with non-stationarity and non-uniformity

A number of authors have suggested that the simple binomial distribution may not give truly accurate estimates of n and p when neurotransmitter release is evoked synchronously by action potentials. Three possible sources of error in the estimates of p derived by the simple binomial have been suggested: non-uniformity of p (spatial variance of p); non-stationarity of p (temporal variance of p); and non-stationarity of n (temporal variance of n). All three forms of variance have different effects on the estimates of p and n as given by the simple binomial distribution. (For any binomial distribution, the value of n in space is fixed at any one point. Hence non-uniformity of n is not possible (Brown et al. 1976; McLachlan, 1978; Miyamoto, 1986)).

Our reader should not be intimidated by these mathematical equations, as in reality they are conceptually relatively simple. For non-stationary variance, either p or n changes from impulse to impulse (or time period to time period). Non-stationarity thus results in a greater variance of release than would occur with fixed values of n and p. This greater degree of variance of transmitter release (Var) results in an underestimate of p, as can be seen from eqn (6). The specific equations for non-stationary and non-uniform release are as follows.

For non-stationarity of p, p varies between individual periods in the case of MEPPs or from impulse to impulse in the case of EPPs. Under these conditions, the estimate for p is (eqn (33), McLachlan, 1978):

(8)

For, non-stationarity of n, n varies from impulse to impulse in the case of EPPs or between individual periods in the case of MEPPs. Under these conditions, the estimate for p is (eqn (34), McLachlan, 1978):

(9)

In the cases of non-stationarity of p or non-stationarity of n, from eqns (8) and (9) it is evident that the error in the estimate of p is dependent on the value of n (see McLachlan (1978) and Stuart et al. (1994) for the derivations of the complex binomial distributions). Thus possible inaccuracies due to either non-stationarity of p or non-stationarity in n should be readily detectable by comparing values for p obtained from the use of different bin widths (and hence different values of n) for describing the MEPP records. Specifically, for non- stationarity of p (eqn (8)), as n decreases, the estimate of p becomes more accurate. For non-stationarity of n (eqn (9)), as n decreases, the estimate for p becomes less accurate.

In the case of non-uniformity of p (spatial variance in p), p is not uniform during an individual impulse (or during an individual period) but each releasable vesicle has a different release probability. The degree of contribution of individual events to the variance of release is proportionate to its contribution towards m. Thus the estimate for p is weighted towards those events which have high values of p. The estimate for p under these conditions is given by (eqn (32), McLachlan, 1978; eqn (11), Miyamoto, 1986):

(10)

At first glance, the case of non-uniformity of p is less easy to solve with simple data handling as the size of the error σ_p²/p in eqn (10) is dependent on p, not on n. One approach employs the use of the third moment about the mean to determine differences from the simple binomial distribution (Miyamoto, 1986) by comparing the value of μ₃ calculated from the data with that predicted by the binomial distribution. A closer inspection of eqn (10) reveals an alternative approach. If the bin width of the analysis is reduced such that n ∼ 1, then spatial variance is eliminated (and the σ_p²/p term in eqn (10) is eliminated as well) as n needs to be ≥ 2 for spatial variance in p to exist.

Hence by reducing n ∼ 1, we minimized the spatial variance of p. In addition, the effect of temporal variance of p (i.e. non-stationarity of p) is minimized as eqn (8) is reduced to eqn (6), i.e. that of the simple binomial distribution. In contrast, temporal variance of n (i.e. non-stationarity of n) is maximized (eqn (9)), leading to underestimates in p. Thus comparisons of the values of p, obtained by analyses using the 10 ms, the 100 ms and the very small bin width (n ∼ 1) should reveal inconsistencies between the simple binomial and the actual data. Hence by using these various bin widths, we can determine whether our estimates for p are affected by variance in either n or p. For each analysis of the data, time event histograms were constructed and distributions compared using the χ² test.

Binomial analysis of synchronous ACh release evoked by nerve action potentials and reflected as end-plate potentials (EPPs)

Binomial analysis was carried out using the conventional method described by McLachlan (1978, eqns (14) and (15)) and Christian & Weinreich (1992). The value of m was quantified as the ratio of the mean EPP amplitude (EPP) to the mean MEPP amplitude (MEPP) as follows:

(11)

Briefly, the EPPs and MEPPs were collected in Ca²⁺ and Sr²⁺ solutions. Each data set used between 300 and 575 EPPs for analysis. The values for m were then determined by eqn (1), correcting the EPPs for non-linear summation (McLachlan & Martin, 1981) when necessary. Next, p was determined from the following equation:

(12)

where EPP is the mean EPP amplitude, S²_EPP is the variance of EPP amplitudes, σ²_MEPP is the variance of MEPP amplitudes and MEPP is the mean amplitude of the MEPPs (Miyamoto, 1975; McLachlan, 1978).

Finally, n was determined by rearranging eqn (4):

(13)

Error estimates of m, n and p were calculated using eqn (18) in McLachlan (1978) and eqns (9) and (10) in Robinson (1976). MEPP amplitudes for analysis were obtained from spontaneous events occurring between the EPPs and fit a normal distribution (Miyamoto, 1975; McLachlan, 1978; Christian & Weinreich, 1992).

EPPs were binned into multiples of 0.1 mV and the expected frequencies of events were calculated from the compound Poisson equation (eqn (1)) and binomial equation (eqn (3)) for each interval (McLachlan, 1978). The expected frequencies were then added and an expected frequency plot generated. The theoretical frequencies of observing 0, 1, 2, 3…x quanta for the binomial or Poisson distributions were then compared with the actual data using the χ² squared statistic. For additional details, see McLachlan (1978) and Christian & Weinreich (1992).

Statistical comparisons

For comparisons of similar levels of release in Ca²⁺ and Sr²⁺ solutions or for comparing values in the tables, the data were first tested for normality and then comparisons made by either parametric statistics (e.g. Student's paired t test) or non-parametric statistics (Mann-Whitney rank sum test; Glantz, 1992). In the instance when more than two groups were compared (e.g. Table 4), an analysis of variance for the normally distributed data was followed by multiple comparisons using the Bonferroni inequality. This method is reasonable when three to four groups are compared and is the most conservative of the multiple comparisons procedures (Glantz, 1992, p. 93). Data are presented as mean ± 1 s.e.m.

Table 4.

Comparison of p using a 10 ms bin width (column 2) with p when n < 2 (column 3) in Sr²⁺solutions

m (10 ms)	p (10 ms)	p (n < 2)	n	bin (ms)
0.11	0.058	0.055	1.05	5.8
0.211	0.049	0.061	1.20	4
0.192	0.047	0.072	1.11	4.2
0.339	0.032	0.049	1.44	2
0.197	0.074	0.059	1.50	5
0.351	0.066	0.047	1.3	1.5
—	0.054 ±	0.057 ±	—	—
	0.006	0.003

Data for p (10 ms) was taken from Table 1, with experiment 1 excluded due to the inaccuracies in the measurements of MEPP_f for this experiment. The values in the bottom row are means ± 1 s.e.m.

RESULTS

Statistical analysis of asynchronous release evoked by high K⁺ depolarisation (MEPP_F) in Ca²⁺ and Sr²⁺ solutions

General description

The use of the simple binomial distribution to describe the neurotransmitter release evoked by action potentials has been questioned (Brown et al. 1976; Silinsky, 1985; Miyamoto, 1986). In particular, as discussed in the Methods, it has been suggested that spatial and temporal variance in both p and n would lead to incorrect estimates of p using the standard method for estimating p (eqn (3)).

As a way to reduce the spatial variance in p, we initially decided to investigate the distributions of asynchronous release (MEPP_f) in KCl-depolarised preparations. Under these conditions, the published data suggest that the concentration of Ca²⁺ or Sr²⁺ is constant throughout the length of the nerve terminal, thus reducing the possibility that non-uniformities in Ca²⁺ or Sr²⁺ concentrations contribute to spatial variance in p (Provan & Miyamoto, 1993; Xu-Friedman & Regehr, 2000). Indeed, such release does not appear to be restricted to discrete release sites at the neuromuscular junction, but occurs more uniformly along the terminal, adding support for this hypothesis (Ceccarelli & Hurlbut, 1980). Furthermore, transmitter release is likely to be at a steady state, with the rate of recycling and mobilisation of vesicles being constant, thus reducing temporal variance due to such vesicular turnover as a source of error. Finally, determining the MEPP_f allows for the direct counting of individual secretory events.

MEPP_f mediated by Sr²⁺ were in agreement with the theoretical data for a binomial distribution whilst MEPP_fs in Ca²⁺ were best fit by a Poisson distributions

MEPPs were recorded from single end-plates in Ca²⁺ and Sr²⁺ solutions. In initial experiments, the MEPP_f obtained in 12 mm KCl was two- to fourfold higher in 0.5 mm Ca²⁺ than in 0.5 mm Sr²⁺ solutions. We therefore reduced the KCl concentration of the Sr²⁺ solutions to 10 mm. This resulted in similar mean MEPP_f (in the range of 6 to 60 s⁻¹) recorded for the two divalent cations in the same cell, allowing a direct comparison of the statistical parameters of release for the two cations under conditions in which the levels of secretion were similar.

The Ca²⁺ and Sr²⁺ MEPP_f data, analysed using a 10 ms bin width, are summarized in Table 1. The mean MEPP_f (± 1 s.e.m.) in the 10 ms interval in Ca²⁺ solution (0.21 ± 0.05, n = 7 experiments) is not significantly different from that in Sr²⁺ solutions (0.28 ± 0.06, P ∼ 0.2). Despite these similar levels of secretion, Ca²⁺-dependent release in most cases was not significantly different from Poisson distributions, indicating extremely low values of p (Colquhoun, 1971) whilst Sr²⁺-dependent release at the same end-plates fit a binomial distribution. These differences in distribution were assessed using the χ² test and the calculated values for the mean and variance of the distributions (P < 0.005) - for a Poisson process, the mean equals the variance (Colquhoun, 1971; Glantz, 1992).

Table 1.

Comparison of n and p for similar mean levels of asynchronous ACh release (MEFF_f) in Ca²⁺ and Sr²⁺ solutions (10 ms bin width)

Calcium			Strontium
m (10 ms−1)	p	n (10 ms−1)	m (10 ms−1)	p	n (10 ms−1)
0.378	0.002 ± 0.007	188.50	0.351	0.066 ± 0.004	5.32
0.353	0.014 ± 0.007	25.21	0.602	0.053 ± 0.007	11.36
0.128	0.047 ± 0.007	2.72	0.100	0.058 ± 0.007	1.72
0.281	0.033 ± 0.008	8.52	0.211	0.049± 0.007	4.31
0.060	0.009 ± 0.007	6.67	0.192	0.044 ± 0.007	4.36
0.098	0.002 ± 0.007	49	0.339	0.032 ± 0.012	10.59
0.152	0.032 ± 0.007	4.75	0.197	0.071 ± 0.006	2.79
0.207 ± 0.048	0.0199 ± 0.007	40.743 ± 25.4	0.284 ± 0.06	0.054 ± 0.005	5.77 ± 1.41

The values in the bottom row are means ± 1 s.e.m.

For comparison between Ca²⁺ and Sr²⁺, however, we provide approximate values of n and p for Ca²⁺ (Table 1). Thus, for the experiment in Table 1 (row 1), the differences in MEPP_f (per 10 ms interval) in Ca²⁺ and Sr²⁺ were not statistically significant (P < 0.01). However, the value of p in the Sr²⁺ solution is well over an order of magnitude higher than in Ca²⁺ solution (and n is correspondingly lower than in the Ca²⁺ solution). The mean values in the table demonstrate that for equal levels of asynchronous release in Ca²⁺ and in Sr²⁺, p was significantly higher in Sr²⁺ solutions (P < 0.002) and n correspondingly lower in Sr²⁺ solutions than in Ca²⁺ solutions.

Figure 1 depicts a typical result in which the experimental data (filled bars) were compared with theoretical data (open bars) in equimolar Ca²⁺ (Fig. 1A) and Sr²⁺ solutions (Fig. 1B). The theoretical distributions in both Ca²⁺ and Sr²⁺ solutions are in good agreement with the observed data, suggesting that, under these conditions, the MEPPs obtained in Ca²⁺ are indistinguishable from the theoretical Poisson distribution calculated from the experimentally determined value of m in eqn (1). In contrast, the MEPPs recorded in Sr²⁺ obey a binomial distribution as predicted from eqns (6) and (4) using the variance and the mean of the MEPP frequencies (χ² test, P < 0.005).

It is of interest to compare our actual data in Ca²⁺ and Sr²⁺ with Monte Carlo simulations of the data in order to determine how well the actual data compare with the theoretical histograms at these particular levels of m, n and p. Figure 1C and D presents histograms of Monte Carlo simulations generated according to a Poisson distribution (Fig. 1C) and a simple binomial distribution (Fig. 1D) using the values of m, n and p obtained experimentally. The data are in good agreement with these simulations, namely the χ² values for the actual data are in agreement with χ² values for the Monte Carlo simulations.

Specifically, for the experiments in Sr²⁺ solutions (Fig. 1B) the χ² value for the fit to a Poisson distribution is 13.3 (n = 3 d.f., P < 0.005), suggesting that the hypothesis that the data follow a Poisson distribution can be rejected (the inset to Fig. 1B shows the predicted Poisson distribution). In contrast, the χ² value for the fit of the Sr²⁺ data to the binomial distribution is 4.7 (P ∼ 0.2), suggesting there is no justification for the hypothesis that the data deviate from a binomial distribution. For the Monte Carlo simulations (Figs 1C and D), the χ² values for the fit of the simulated data to a Poisson distribution = 15.5 (P << 0.005), whilst the χ² value for the binomial distribution = 3.4 (P > 0.25). With regards to the distinction between the mean and variance of the MEPP_f, for six consecutive 50 s periods of data acquisition in Sr²⁺ (analysed using a 10 ms bin width), the mean values were 0.199, 0.211, 0.196. 0.197, 0.188, 0.193 and the variances were 0.185, 0.193, 0.181, 0.187, 0.175, 0.175. The overall mean for the entire 300 s period was 0.197 ± 0.0031 whilst the variance for the entire period was 0.183 ± 0.0029. The differences between the mean and variance were highly significant (p = 0.006), demonstrating that the Sr²⁺ data do not obey a Poisson distribution.

Thus, despite the low values of p obtained in the presence of Sr²⁺, all of our tests failed to demonstrate any significant difference between the experimental results and a simple binomial distribution. Because the data in Sr²⁺ fit a binomial distribution, our subsequent analysis of MEPPs concentrated on Sr²⁺-mediated asynchronous ACh release.

As described in the Methods, one way to reduce the likelihood of non-stationary data is to change the size of the bin width and examine if p remains constant. To this end, we compared the values of n and p obtained using 10 ms bin intervals, with those obtained using 100 ms intervals. Figure 2 depicts experiments similar to those shown in Fig. 1 but using a 100 ms bin width. The data for Sr²⁺ with this longer bin width (Fig. 2B, filled bars) were also well fit by a binomial distribution (open bars) but not by a Poisson distribution (inset Fig. 2B) and that for Ca²⁺ was fit by a Poisson distribution (Fig. 2A). In addition, Monte Carlo simulations produced histograms that were similar to the experimental data (Fig. 2C and D). Finally, as Table 2 shows, values of p were unaffected by the bin interval used. Specifically, p for bin widths of 10 ms and 100 ms were indistinguishable both for each individual experiment and for the mean values of all the experiments (for the 10 ms bin, p = 0.053 ± 0.005; for the 100 ms bin, p = 0.056 ± 0.007, n = 7 experiments for both, P ∼ 0.8). Such a result is predicted for a simple binomial distribution with stationary data.

Table 2.

The value of p for asynchronous ACh release in Sr²⁺ solutions is independent of the interval used

m (10 ms)	p (10 ms)	p (100 ms)
0.602	0.053 ± 0.007	0.057 ± 0.004
0.100	0.058 ± 0.007	0.053 ± 0.007
0.211	0.049 ± 0.007	0.036 ± 0.005
0.192	0.044 ± 0.007	0.039 ± 0.007
0.339	0.032 ± 0.012	0.051 ± 0.004
0.197	0.071 ± 0.006	0.064 ± 0.004
0.351	0.066 ± 0.004	0.089 ± 0.004
—	0.053 ± 0.005	0.056 ± 0.007

The values in the bottom row are means ± 1 s.e.m.

In contrast, n was directly proportionate to the time interval used (also see below). These results underscore the fact that p is a fixed, dimensionless value; in contrast, n is a rate, dependent on the particular time interval used for the analysis when MEPPs are studied (eqns (3) and (4)) (Provan & Miyamoto, 1993).

Next, we examined the possibility that spatial variance contaminates the estimates of p in Sr²⁺ solutions by calculating the effects of spatial variance in p on the third moment about the mean (Table 3), using the method suggested by Miyamoto (1986) for the detection of non-uniform p. The observed value for the third moment (μ_3observed) was calculated using the traditional definition of this moment for any distribution, Σ(x-x)³/n (Table 3 column 2). Next, we took the our estimate of p (Table 3, column 1) and used it to calculate the ideal value for the third moment characteristic of the simple binomial distribution (eqn (7)), μ_3ideal = p(1 − p)(1 − 2p) (Table 3, column 3). Note that the observed and predicted data are in excellent agreement for each experiment (last column, μ_3observed/μ_3ideal ∼ 1) and for the mean values presented in the table (P ∼ 0.17).

Table 3.

Comparison of observed third moment of the mean (μ_3observed) with the ideal third moment (μ_3ideal) calculated from the measured p values for asynchronous release in Sr²⁺ solutions

p	μ3observed	μ3ideal	μ3observed/μ3ideal
0.0529	0.04515	0.0448	1.0078
0.0583	0.0484	0.0485	0.9979
0.0495	0.0429	0.0424	1.0117
0.0443	0.0384	0.0385	0.9964
0.032	0.0285	0.0288	0.9896
0.071	0.0568	0.0563	1.0089
0.066	0.0542	0.0535	1.0131
—	0.0449 ±	0.0447 ±	—
	0.004	0.004

The values in the bottom row are means ± 1 s.e.m.

As a final test of our data, we examined the effect of reducing the bin width such that n was less than 2. Under these conditions, the variance in p should be primarily temporal in nature, thus leading to an underestimate of p. As can be seen in Table 4, the values obtained for p in Sr²⁺ solutions at 10 ms (0.054 ± 0.006, n = 6 experiments) were statistically indistinguishable from the p values obtained at the smaller bin width (0.057 ± 0.004, P ∼ 0.71).

As can be seen from these results, we find no evidence for any variance in either p or n. The results thus suggest that the simple binomial analysis may be fruitfully applied to asynchronous ACh release resulting from the actions of Sr²⁺ and reflected as MEPP_f. In contrast, the Ca²⁺-dependent asynchronous release generally follows a Poisson process under the conditions of our experiments. These results demonstrate that similar levels of asynchronous release are produced with low p and high n in Ca²⁺ solutions when compared to Sr²⁺ solutions. It was thus of interest to test this under conditions in which both Ca²⁺ and Sr²⁺-dependent ACh release follow binomial distributions. We therefore decided to perform comparisons of n and p for EPPs of similar mean quantal content (m) stimulated by action potentials in Ca²⁺ and Sr²⁺ solutions.

The binomial analysis of synchronous ACh release evoked by action potentials (EPPs)

In these experiments, after making rough estimates of the concentrations of Ca²⁺ and Sr²⁺ that produced similar levels of evoked ACh release (EPPs), we recorded EPPs in the presence of 0.3 mm Ca²⁺ and in the presence of 2 mm Sr²⁺ in the same cell. In all 10 experiments depicted in Table 5, both evoked release in Ca²⁺ and in Sr²⁺ solutions fit a binomial distribution. Figure 3 illustrates the typical experimental result. For further details of the idealized curve fits of the data to the binomial distribution (black) and the Poisson distribution (grey), see Methods and legend to Fig. 3. In this experiment, despite the fact that the mean level of evoked ACh release (m) is slightly higher in Ca²⁺ than in Sr²⁺ solutions (m = 6.7 in Ca²⁺; m = 4.9 in Sr²⁺), p for Sr²⁺ was more than twofold higher than p for Ca²⁺ whilst n in Sr²⁺ is less than one-third of the value observed in Ca²⁺ solutions, with these differences being highly statistically significant (P < 0.001; see also Table 5). In the averaged data from these 10 experiments (Table 5), whilst the mean m in Ca²⁺ (6.4 ± 1.11) was only slightly higher than m in Sr²⁺ (4.7 ± 0.576), n in Ca²⁺ was greater than twofold higher than n in Sr²⁺ (P < 0.01) and p significantly lower in Ca²⁺ than in Sr²⁺ solutions (P < 0.01).

Table 5.

Comparison of binomial parameters of evoked ACh release (EPPs) in Ca²⁺ and Sr²⁺ solutions

Calcium			Strontium
m	p	n	m	p	n
6.67	0.12	57.3	4.89	0.27	17.9
6.0	0.69	8.6	4.3	0.61	7.1
5.7	0.49	11.6	5.0	0.53	9.5
4.3	0.32	13.4	3	0.39	7.5
5.3	0.38	14.1	2.0	0.39	5.1
4.6	0.32	14.5	5.4	0.41	13.2
16.3	0.38	42.8	8.9	0.64	13.7
5.4	0.30	18	4.7	0.37	12
5.0	0.11	52	3.6	0.25	14
5.1	0.13	39.2	5	0.31	16
6.44 ±	0.322 ±	27.15 ±	4.68 ±	0.417 ±z	11.61 ±
1.117	0.058	5.87	0.58	0.04	1.32

The values in the bottom row are means ± 1 s.e.m.

Figure 3. ACh release evoked by action potentials follows a binomial distribution in Ca²⁺ (A) and Sr²⁺ (B) solutions.

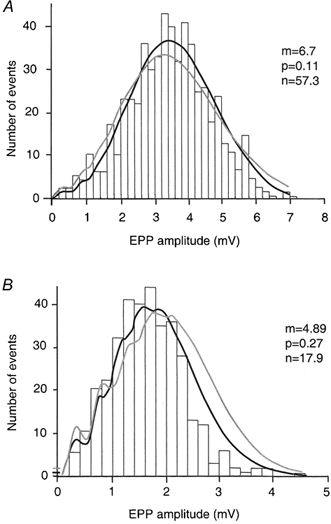
The concentrations of Ca²⁺ (0.3 mm) and Sr²⁺ (2 mm) were chosen to approximate equiactive concentrations of these ions for evoked released (m). The mean and variance of the EPP amplitudes (EPP and S²_EPP respectively) and the mean and variance of the MEPP amplitude (MEPP and σ²_MEPP, respectively) were used to in conjunction with eqn (12) to calculate p. The value of n was calculated by eqn (13). For calculation of error estimates for these parameters, see McLachlan (1978) and Methods. In Ca²⁺ (A), the values for m, n and p (± 1 s.e.m.) were respectively 6.7 ± 0.2, 57.3 ± 39 and 0.11 ± 0.08. In Sr²⁺ (B), values for m, n and p (± 1 s.e.m.) were respectively 4.9 ± 0.1, 17.9 ± 5.0 and 0.27 ± 0.06. The curved lines show expected frequency plot for the binomial distribution (dark line) and the Poisson distribution (grey line - see Methods). For the Ca²⁺ data (A), P > 0.05 for the χ² fit to the binomial distribution and P < 0.005 for the χ² fit to the Poisson distribution. For the Sr²⁺ data (B), P > 0.5 for the fit to the binomial distribution and P < 0.001 for the fit to the Poisson distribution. The statistical analyses thus demonstrate that there is no justification for the hypothesis that the data deviate from a binomial distribution. For all seven experiments (Table 5), the binomial distributions provided a better fit to these data than the Poisson distribution (χ² squared statistic). These data depict experiment 1 in Table 5.

DISCUSSION

In this paper we had two aims. Firstly, we wished to determine whether the simple binomial distribution provides a valid description of the neurotransmitter release process. Secondly, we wanted to determine whether there were differences between the binomial parameters n and p for equivalent levels of ACh release in Ca²⁺ and in Sr²⁺ solutions, as might be expected for a two-step release process. In order to achieve our first aim, we carried out a detailed analysis of asynchronous release reflected as MEPP_f. With the use of Sr²⁺, we were able to determine values for both n and p. In addition, by reducing the bin width, we were able to reduce the degree to which spatial variance in p might affect the calculated values for p. Despite the low values of p obtained in these experiments, we could find no evidence for a deviation from the simple binomial distribution. With regards to our second aim, results from both experiments on asynchronous release and nerve-evoked release demonstrate that, at similar levels of release, Sr²⁺ has a reduced ability to support the binomial parameter n when compared to Ca²⁺. It thus appears that the partial agonist action of Sr²⁺ (Meiri & Rahamimoff, 1971; Silinsky, 1981) is likely to be due to a reduced ability of Sr²⁺ to support the binomial parameter n.

From these results, it seems reasonable to assume that differences in the relative abilities of Ca²⁺ and Sr²⁺ to act on the parameters n and p reflect real differences between the abilities of these divalent cations to activate two different components of the release process. It also suggests that these two sites are both distinct and conformationally different. In accordance with this suggestion of distinctly different sites, the parameters n and p are both related to extracellular Ca²⁺ but with different degrees of co-operativity (Miyamoto, 1975; Bennett et al. 1975; for review see McLachlan, 1978). Specifically, for evoked release n is related to a third power of the extracellular Ca²⁺ concentration whilst p has a first power relationship (Bennett et al. 1975; McLachlan, 1978). Hence the mean level of release (m = np) reflects a fourth power relationship at low levels of neurotransmitter output (Dodge & Rahamimoff, 1967). Thus descriptions of release that rely on n as being unrelated to extracellular Ca²⁺ are not consistent with most of the published statistical studies of evoked neurotransmitter release. Rather, it seems likely that the statistical parameter n is related to both the numbers of vesicles in the readily releasable store and to Ca²⁺ entry. In this regard, recent kinetic studies have demonstrated that several rapidly occurring, reversible, Ca²⁺-dependent changes in the conformation of the secretory apparatus have to occur after Ca²⁺ entry and before the exocytotic release of neurotransmitter, providing possible functional correlates for n and p (see Davis et al. 1999, and below).

In general, the notion that n represents a fixed number of activatable release sites may be misleading. For example, in some cases, far more quanta than the number of active zones can be released by a nerve impulse (e.g. in the presence of K⁺ channel blockers (Heuser et al. 1979; Katz & Miledi, 1979; Silinsky, 1985)). A more parsimonious description would be to simply define n as a releasable vesicle. Given this definition, n might be considered to represent a vesicle primed at the active zone, with adequate Ca²⁺ or Sr²⁺ bound to the appropriate calcium sensor in the vesicle, and p represents the probability that a further Ca²⁺ or Sr²⁺ will bind, i.e. a conditional probability, causing the vesicular contents to be released. This interpretation would suggest that the binomial distribution of transmitter release is a consequence of a two-stage release process. Firstly, Ca²⁺ has to bind to a binding site, the ‘synaptic vesicle sensor(s)’ (e.g. synaptotagmin, see below (Südhof, 1995; Augustine et al. 1999; Augustine, 2001)) in order for it to be ‘releasable’ (step ‘n’). Then, in a final step, a further Ca²⁺ is required to bind for exocytosis to take place (step ‘p’). For a given level of release, Sr²⁺ proved to be much less effective at making vesicles available for release (n) than Ca²⁺.

This model for the release process may have important implications in the interpretation of a number of studies in which the assumption is made that n is fixed, and apparent changes in n and p represent changes in the spatial variance of p (Redman, 1990). Indeed, our two-step model for release has a major advantage over other suggested models, as in this model there is no necessity for a complex relationship between Ca²⁺ concentration and the spatial variance in p. This complex relationship requires an unusual and apparently discontinuous distribution of p. Furthermore, the alternative models proposed (e.g. eqns (10) and (11) in Redman, 1990) do not account for the relative differences in efficacies between Ca²⁺ and Sr²⁺ in the ACh release process (data in this paper and Meiri & Rahamimoff, 1971; Silinsky, 1981).

From our statistical analysis of the release process, it is clear that the processes n and p have different requirements. Specifically, for n, the Ca²⁺-binding domain of the Ca²⁺ sensor should: bind multiple Ca²⁺ ions (McLachlan, 1978), be reversibly activated by Ca²⁺ or Sr²⁺ in a submillisecond time frame and have a relatively greater affinity for Ca²⁺ than for Sr²⁺. In contrast, p saturates at a lower concentrations of Ca²⁺ than n (Miyamoto, 1975; Bennett et al. 1976; McLachlan, 1978). Thus, p should represent a higher affinity binding site than n in the final stage of vesicular fusion; this is indeed borne out by the published data (Bennett et al. 1976).

It is tempting to speculate as to which synaptic proteins might confer the properties of n and p on the release process. In this regard, the family of synaptic proteins known as synaptotagmins has recently attracted a lot of attention (Südhof, 1995; Geppert & Südhof, 1998; Davis et al. 1999; Augustine et al. 1999; Augustine, 2001). Synaptotagmins have two calcium binding domains, the C2A and C2B regions. The C2A Ca²⁺ binding region is nearest to the vesicle membrane, binds two to three calcium ions and also interacts with both the core plasma membrane protein syntaxin and acidic phospholipids in the nerve terminal membrane (Südhof, 1995; Geppert & Südhof, 1998; Davis et al. 1999; Chapman & Davis, 1999; see also discussion in Xu-Friedman & Regehr, 2000). The C2B region is involved in the obligate oligomerization of synaptotagmins (Chapman et al. 1996; Desai et al. 2000; Augustine, 2001) that occurs early after Ca²⁺ entry and prior to interaction with syntaxin and the other members of the SNARE complex (Davis et al. 1999). Later in the process of release, the C2B domain has been implicated in the switching of phospholipids from the vesicle to the plasma membrane (Schiavo et al. 1996) and possibly with the dilation of the fusion pore that proceeds exocytosis (Bai et al. 2000).

From the above description, it is noteworthy that the C2A domain of synaptotagmin fulfils all of the criteria for n. Specifically, Ca²⁺ binding to the C2A domain is co-operative and rapid, both in onset and offset (Davis et al. 1999). Furthermore, Ca²⁺ has a higher affinity than Sr²⁺ at the C2A regions of all the isoforms of synatotagmin that have been studied (Li et al. 1995; Fukuda et al. 1997). With respect to the various isoforms, synaptotagmin I is generally believed to the Ca²⁺ sensor for evoked neurotransmitter release whilst synaptotagmin III is purported to mediate asynchronous release reflected as MEPP_f (Li et al. 1995). This suggestion, that n is related to the relative affinity of Ca²⁺ or Sr²⁺ for the C2A domain (as well as the number of vesicle available within the readily releasable pool), by no means excludes other Ca²⁺ sensors with C2 domains as an important determinant of the parameter n (for an excellent recent review on the properties of calcium sensors, see Augustine, 2001).

The parameter p is dependent upon Ca²⁺ entry and the relative proximity of the Ca²⁺ sensors to the sites of Ca²⁺ entry, as well as the kinetics by which the exocytotic machinery responds to alkaline earth cations (Kasai, 1999). Candidates for the molecular correlates of p are, thus, less easy to identify. Indeed, our present results suggest that the relative potencies of Ca²⁺ and Sr²⁺ for p differ between asynchronous and synchronous release (see Kishimoto et al. (2001) for an interesting corollary in another secretory system). One possibility is that p represents the binding of Ca²⁺ or Sr²⁺ to a site that appears only after the initial interaction of Ca²⁺ with synaptotagmin (e.g. the binding of a single divalent cation to the C2A domain of calcium-primed synaptotagmin). Alternatively, p could represent the binding of Ca²⁺ or Sr²⁺ to some other strategic plasma membrane Ca²⁺ binding protein (e.g. an interaction between the Ca²⁺ channel and the SNARE protein syntaxin) or to another domain of the same Ca²⁺ binding protein. In this regard, the C2B domain is both a high affinity Ca²⁺-binding site and may not distinguish well between Ca²⁺ and Sr²⁺ in relation to interactions of this domain with membrane lipids (Popoli et al. 1997).

Whilst not excluding other sites, differential binding of cations and substrates to C2B domains could indeed explain the different effects of Ca²⁺ and Sr²⁺ on p for the two forms of release. For example for asynchronous release, Sr²⁺ is better than Ca²⁺ at supporting p (see Results). Sr²⁺ appears to bind as well as Ca²⁺ to the C2B domain of synaptotagmin as measured by the ability of synaptotagmin to bind to anionic phospholipid (Popoli et al. 1997). It is thus possible that p for asynchronous release is related to the binding of Ca²⁺ or Sr²⁺ to the C2B domain of synaptotagmin III with the greater p for asynchronous release reflecting a higher intraterminal concentration of Sr²⁺ than Ca²⁺ near the C2B domain responsible for asynchronous release in KCl-depolarized preparations (see Xu-Friedman & Regehr (2000) for justification). In contrast, Ca²⁺ is better than Sr²⁺ at equivalent extracellular molarity in supporting p for action potential evoked release (p approaches to 1 for evoked release with 0.5–1 mm extracellular Ca²⁺ - data not shown here). It is of interest that Ca²⁺ is preferred over Sr²⁺ for the binding to the C2B domain and promoting the oligomerization of synaptotagmin I that serves as an obligatory prelude to evoked release (Chapman et al. 1996). Thus if isomerization of synaptotagmin 1 is the step that determines p for evoked release, then this would explain the relative selectivity of Ca²⁺ over Sr²⁺ for p in the process of evoked, as opposed to asynchronous, release, which is likely to be mediated by synaptotagmin III.

Our current studies do suggest that, in combination with the recent advances in molecular biology, the use of binomial statistics at the skeletal neuromuscular junction will allow us to determine the specific proteins or processes which contribute to both p and n in the release process. We hope that this will give us the ability to probe precisely these penultimate steps of the process underlying Ca²⁺-dependent exocytosis of neurotransmitter from synaptic vesicles.