Titin-based contribution to shortening velocity of rabbit skeletal myofibrils

Abstract

The shortening velocity of skeletal muscle fibres is determined principally by actomyosin cross-bridges. However, these contractile elements are in parallel with elastic elements, whose main structural basis is thought to be the titin filaments. If titin is stretched, it may contribute to sarcomere shortening simply because it can recoil ‘passively’. The titin-based contribution to shortening velocity (V_p) was quantified in single rabbit psoas myofibrils. Non-activated specimens were rapidly released from different initial sarcomere lengths (SLs) by various step amplitudes sufficient to buckle the myofibrils; V_p was calculated from the release amplitude and the time to slack reuptake. V_p increased progressively (upper limit of detection, ∼60 μm s⁻¹ sarcomere⁻¹) between 2.0 and 3.0 μm SL, albeit more steeply than passive tension. At very low passive tension levels already (< 1–2 mN mm⁻²), V_p could greatly exceed the unloaded shortening velocity measured in fully Ca²⁺-activated skinned rabbit psoas fibres. Degradation of titin in relaxed myofibrils by low doses of trypsin (5 min) drastically decreased V_p. In intact myofibrils, average V_p was faster, the smaller the release step applied. Also, V_p was much higher at 30 °C than at 15 °C (Q₁₀: 2.0, 3.04 or 6.15, for release steps of 150, 250 or 450 nm sarcomere⁻¹, respectively). Viscous forces opposing the shortening are likely to be involved in determining these effects. The results support the idea that the contractile system imposes a braking force onto the passive recoil of elastic structures. However, elastic recoil may aid active shortening during phases of high elastic energy utilization, i.e. immediately after the onset of contraction under low or zero load or during prolonged shortening from greater physiological SLs.

The maximum velocity of sarcomere shortening is a useful parameter for estimating the contractile function of muscle fibres (Moss, 1992; Josephson & Edman, 1998; Gordon et al. 2000). This parameter can be obtained experimentally either by extrapolating force-velocity curves to zero load (Hill, 1938) or by using the ‘slack test’ method (Edman, 1979). In such experiments, care is usually taken to avoid a large influence of passive (or resting) tension (PT) on shortening velocity, as elastic recoil of non-contractile structures can accelerate the speed of shortening if PT is significant (Edman, 1979; Claflin et al. 1989; Galler & Hilber, 1994). Many experiments demonstrating the effect of PT level on unloaded shortening velocity (V_o) had been performed some time before the origin of PT in vertebrate skeletal muscle was established. Today it is clear that most of this PT originates in the intrasarcomeric titin (also known as connectin) filaments (Wang, 1996; Maruyama, 1997; Linke & Granzier, 1998; Trinick & Tskhovrebova, 1999). Although the involvement of titin in determining the viscoelasticity of muscle fibres has been studied thoroughly in recent years, no attempt has been made, to our knowledge, to take a fresh look at the function of titin as a contributor to shortening velocity. Here we describe experiments on single isolated rabbit psoas myofibrils aimed at quantifying the contribution of titin to the passive shortening of skeletal muscle sarcomeres at physiological lengths.

Titin molecules span the length of a half-sarcomere, connecting the Z-line to the M-line, but only the titin section located in the I-band is functionally elastic (Fürst et al. 1988). A-band titin is bound to the thick filament and therefore is inextensible at normal sarcomere lengths (SLs) (Labeit et al. 1997; Trinick & Tskhovrebova, 1999). In a single myofibril consisting solely of sarcomeres connected in series, titin is thought to be responsible for essentially all of the PT response to stretch (Linke et al. 1994; Bartoo et al. 1997). Previously it was shown that psoas muscle sarcomeres develop very little passive force over a SL range from 2.1 to ∼2.5 μm; only above this range, PT rises more steeply (Linke et al. 1996a, 1998b). This scenario can be explained by the sequential extension of structurally distinct molecular subsegments within I-band titin (Linke et al. 1996a; Gautel & Goulding, 1996; Trombitas et al. 1998), which may act as serially linked entropic springs behaving according to wormlike-chain polymer elasticity theory (Linke et al. 1998a; Trombitas et al. 1998). In the present work, we used the single myofibril as an ideal preparation to test how titin-based passive force translates into elastic recoil of sarcomeres that are free to contract in a non-activated state.

To determine the ‘passive’ shortening velocity (V_p) of a relaxed myofibril, we adopted a modified slack test protocol. Instead of measuring force during the experiment, we recorded the lengths of individual sarcomeres along the myofibril by using a custom-built, quick-scan, CCD-line camera to obtain a time resolution of 2 ms − 20 times higher than normal video rate. Single myofibrils were rapidly released from a pre-stretched SL by varying step amplitudes sufficient to buckle the specimens; sarcomeres thus went out of focus for a characteristic period of time. This approach revealed reproducible time-to-slack-reuptake values, which together with the corresponding release step values could be used to calculate V_p. Besides measuring the SL dependence of passive shortening velocity, we also determined the effect of variations in both temperature and step release size on V_p. Further, V_p was compared with the unloaded shortening speed of fully activated myofibrils, V_o, measured in conventional slack test experiments on skinned rabbit psoas fibres. From these results, we estimated to what degree passive elastic recoil of titin filaments might play a role in the overall shortening characteristics of mammalian skeletal muscle fibres. Our findings are consistent with an earlier proposal (Edman, 1979) suggesting that the contractile system is able to impose a substantial braking force onto the passive recoil of elastic structures, except at longer physiological SLs, at which both V_p and V_o rise steeply with passive force. However, even at shorter SLs, the titin-based contribution to shortening velocity may be important in aiding rapid shortening particularly during the very early phase of a contraction under low or zero load. During prolonged shortening, the impact of elastic recoil on overall shortening speed becomes progressively smaller, most probably because the passive shortening is opposed by viscous forces.

METHODS

Specimen preparation

Single myofibrils

Myofibrils were isolated from freshly excised rabbit psoas skeletal muscle as described previously (Linke et al. 1996a). Rabbits were killed by the method of captive bolt according to the recommendations of the institutional animal care committee (Medical Faculty, University of Heidelberg, Germany). Muscle fibre bundles were removed and thin muscle strips were dissected in a solution containing (mm): NaCl 132; KCl 5; EGTA 5; MgCl₂ 1; glucose 7; pH 7.1. The muscle strips were tied to thin glass rods and skinned in ice-cold rigor solution, containing (mm): KCl 75; Tris 10; EGTA 2; MgCl₂ 1 (pH 7.1) in the presence of 0.5 % Triton X-100 for 4 h. To obtain single myofibrils, the skinned strips were minced and homogenized in rigor solution. All solutions were supplemented with the protease inhibitor leupeptin to minimize titin degradation (Linke et al. 1998b).

Skinned fibres

For active shortening velocity measurements, rabbit psoas fibre bundles 200–300 μm in diameter and 4–6 mm long were dissected manually from muscle strips skinned in ice-cold relaxing solution containing (mm): magnesium methanesulphonate 46; potassium methanesulphonate 12; Mops 130; EGTA 15.5; KOH 50; Na₂ATP 3; 2,3-butanedione monoxime (BDM) 20 (pH 7.1; ionic strength 200 mm) in the presence of 0.25 % Triton X-100 for 8 h.

Passive shortening velocity measurements on single myofibrils

A drop of the myofibril suspension was placed on a coverslip on the stage of an inverted microscope (Zeiss Axiovert 135). A single myofibril was picked up by two micromanipulator-controlled glass microneedles, one of which was attached to a piezoelectric micromotor (Physik Instrumente, Waldbrunn, Germany). To anchor the specimen ends, the needle tips were coated with silicone adhesive in a 2:1 (v/v) mixture of Dow Corning 3145 RTV and 3140 RTV. In a previous study, we found that the silicone adhesive made no significant contribution to overall compliance of the system (Minajeva et al. 2001).

All experiments were performed in relaxing buffer supplemented with 20 mm BDM to suppress any possibly remaining contractile activity. Measurements were done at 15, 30 or 23 °C (room temperature). Temperature control was achieved by means of four Peltier elements fitted around the experimental chamber. The temperature of the buffer adjacent to a mounted myofibril was monitored with a thermosensor.

Single myofibrils were imaged by the conventional method (Linke et al. 1996a) using a video camera (Völker, Maintal, Germany), video recorder, frame grabber board (Vision-EZ; Data Translation) and image processing software (GlobalLab Image, Data Translation; Scion Image, based on NIH Image, NIH, Bethesda, MD, USA). However, the time resolution of this method (video rate: 25 full images s⁻¹) is insufficient to measure the high shortening speed of a passively contracting myofibril. To increase the time resolution of the SL detection method, a custom-built, linear 2048-element, CCD-array camera was attached to the camera port of the microscope and was scanned at 1 MHz to obtain a full myofibril image every 2 ms. CCD-data collection and motor control were performed using a PC, data acquisition (DAQ) board (PCI 6110E, 5 Msamples s⁻¹; National Instruments, Austin, TX) and custom-written LABVIEW software.

Only single myofibrils were used for measurements of passive shortening velocity (V_p); specimens containing more than one myofibril were discarded. In a typical experimental protocol, the single myofibril was stretched in 50 nm sarcomere⁻¹ steps from slack SL (average, 2.0 ± 0.1 μm, n = 57) to a desired SL between 2.15 and 3.0 μm. After each step, a 3 min rest period was observed to wait for stress relaxation. Then, specimens were released by steps of 150, 250 or 450 nm sarcomere⁻¹, completed within 1 ms. Myofibrils at long SLs needed to be released by greater amounts than those at shorter SLs, in order to buckle the specimen. During buckling, the myofibril went out of focus. The time elapsed before the myofibril came back into focus, and the release amplitude measured as the difference between initial SL and SL after shortening, were used to calculate V_p. This approach thus resembles the slack test method introduced by Edman (1979), but instead of detecting active force redevelopment after quick release, refocusing of the passively contracting myofibril is measured. Rapidly shortening myofibrils came back into focus suddenly (from one CCD frame to the next), whereas more gradual refocusing (lasting over several CCD frames) took place in less rapidly shortening specimens. In the latter case, the myofibril was considered to be back in focus when the peak height in the intensity profiles (see Fig. 1) was 30 % of the peak height before shortening. For a given release amplitude commencing from the same SL, the time to focus redevelopment was quite reproducible in repeated measurements. Nevertheless, to improve signal quality further, three recordings were taken at a given SL (rest interval, 3 min) and were later averaged.

Figure 1. Method used to measure the passive shortening velocity of single myofibrils.

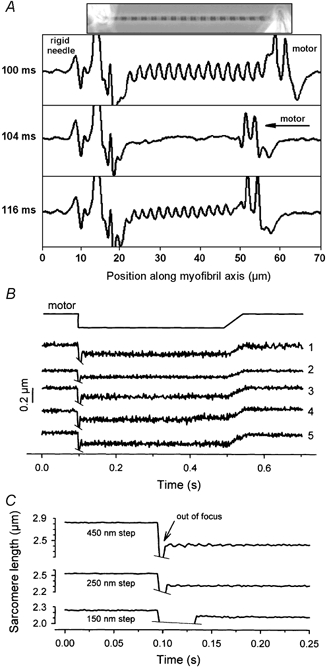
A, phase-contrast image of a single rabbit psoas myofibril suspended between glue-coated needle tips (top) and three representative intensity profiles recorded along the myofibril's length axis using a CCD-line camera. At 100 ms, the myofibril was held at a SL of 2.9 μm; at 104 ms, a quick motor step (450 nm sarcomere⁻¹) was applied to buckle the myofibril, which thus went out of focus; at 116 ms, the sarcomere pattern was restored as the myofibril took up the slack. B, motor movement and corresponding length change in five consecutive sarcomeres (1–5) of a single myofibril (average SL, 2.5 μm; step size, 150 nm sarcomere⁻¹). SL was measured, using LABVIEW software, from the distance between successive peaks in the intensity profile. While the myofibril was out of focus, a noise signal was recorded by the CCD array, which is cut for clarity. Four hundred milliseconds after the release, the myofibril was slowly (within 50 ms) stretched back to the initial SL. C, average SL of a myofibril during releases from three different initial SLs: ∼2.85 μm (release step, 450 nm sarcomere⁻¹; n = 9 sarcomeres), ∼2.55 μm (250 nm sarcomere⁻¹; n = 9) and 2.25 μm (150 nm sarcomere⁻¹; n = 8). From the time to focus redevelopment and the release amplitude, passive shortening velocity was calculated.

Active shortening velocity measurements

Active unloaded shortening velocity (V_o) was measured using a commercial system for muscle fibre mechanics (Scientific Instruments, Heidelberg, Germany). The ends of a skinned fibre bundle were clipped between stainless-steel holders, one attached to a micromotor and the other to a force transducer. Non-activated specimens were slowly stretched to a desired SL measured by laser diffraction. The fibre bundle was left to equilibrate for 5 min in a solution containing (mm): imidazole 20; EGTA 2; MgCl₂ 10; ATP 7.5; NaN₃ 1; creatine phosphate 10 (pH 7.0). Then, the preparation was transferred to activating solution, which had the same composition, but also contained 4 mm CaCl₂ (pCa 4.5). SL was again measured by laser diffraction. V_o was estimated by the slack test method (Edman, 1979) at temperatures of 15 and 23 °C.

Titin digestion by trypsin

Mild trypsin digestion has been used to selectively degrade titin in skinned skeletal muscle fibres (Higuchi, 1992). We adopted this method to extract titin in single skeletal myofibrils. With a myofibril suspended between needles, leupeptin was washed out from the buffer by changing the solution six times. Then, relaxing solution containing 0.05 μg ml⁻¹ trypsin was applied for 5 min at room temperature. Digestion was stopped by exchanging the solution for one containing leupeptin but no trypsin. V_p was determined before and after trypsin treatment.

Low percentage SDS-polyacrylamide gel electrophoresis

Titin degradation by trypsin was monitored in myofibril suspensions on the coverglass by low-percentage (2.8 %) SDS-PAGE. The samples were exposed to 0.05 μg ml⁻¹ trypsin for 5, 15 and 30 min. At the end of each time period, the myofibrils were transferred to Eppendorf tubes and washed extensively to remove the trypsin. The samples were solubilized and separated on 2.8 % SDS-polyacrylamide gels (cf. Linke et al. 1998b). Solubilization buffers and agarose-strengthened gels were prepared as described by Tatsumi & Hattori (1995).

RESULTS

Slack test to measure the passive shortening velocity of non-activated single myofibrils

To estimate the shortening velocity of single psoas myofibrils in a non-activated state, we modified the slack test method described by Edman (1979). The approach is explained in Fig. 1. The myofibril image was focused onto a linear CCD array (Fig. 1A). Within the first 100 ms of the CCD read-out, the stretched myofibril was held at a constant SL, here 2.9 μm. The sarcomere pattern appeared as a regular repeat of peaks and valleys in the intensity profile. Irregular patches at the ends arose from the projection of the needles. Then, the myofibril was released within 1 ms to a shorter SL, here 2.45 μm. The myofibril went out of focus as it buckled, and the regular intensity-profile pattern disappeared (Fig. 1A, middle trace). After a characteristic time period, the focus of the image was spontaneously restored as the myofibril took up the slack (Fig. 1A, bottom trace). The distance between consecutive peaks in the intensity profiles was determined by a centre-of-mass detection analysis (Linke et al. 1994) performed using LABVIEW software, and was taken as a measure of SL. Figure 1B indicates the lengths of five consecutive sarcomeres (1–5) in a myofibril (initial SL, 2.5 μm) that was released by a 150 nm sarcomere⁻¹ step. The time course of SL change was found to be quite uniform along the myofibril axis. Depending on the degree of myofibril prestretch, it was necessary to apply 150, 250 or 450 nm sarcomere⁻¹ step sizes, in order to slacken the myofibril to such an extent that the regular sarcomere pattern disappeared for at least two CCD frames (4 ms). Figure 1C shows average SLs of the same myofibril released from ∼2.85, 2.55 and 2.25 μm SL by steps of 450, 250 and 150 nm sarcomere⁻¹, respectively. From the time to slack reuptake and from the release amplitude, V_p was calculated.

Some additional aspects of the measurements should be pointed out. First, we measure average V_p recorded during shortening over a certain SL range. For instance, the V_p value derived from an initial SL of 2.85 μm in Fig. 1C is actually the average velocity recorded when the myofibril is released to shorten over the whole interval ∼2.85–2.40 μm SL (step release, 450 nm sarcomere⁻¹). As will be shown later (Fig. 5), the passive elastic recoil is greatly slowed down by forces opposing the shortening. Thus, during initial phases of shortening the speed should be higher than during late phases of shortening. The dependence of V_p on step release size, for releases commencing from the same SL (Fig. 2A), reflects this property. Furthermore, one can assume that shortening includes an initial, very rapid, phase during which the myofibril remains straight while passive force is reduced. Only then, a second phase should begin during which the myofibril is slack and sarcomeres are subjected to a continuously declining passive force, before the specimen begins to buckle. These initial phases of shortening are likely to be completed within one CCD scan interval (2 ms) and therefore are not detected by the system.

Figure 5. Passive shortening velocity and average energy (derived from elastic recoil) per shortening time depend on release step size.

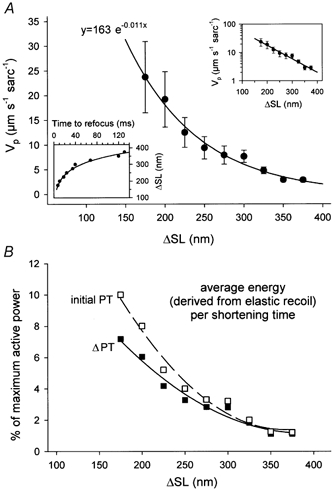
A, V_pversus release step size (ΔSL) measured on single rabbit psoas myofibrils shortening passively at room temperature from an initial SL of 2.5 μm. Data are means ± s.e.m. (n = 5 myofibrils). The fit is a two-parameter exponential decay function of the type indicated. Inset (upper right), half-logarithmic representation of the same data. Inset (bottom left), relationship between step release size and time to focus redevelopment. B, from the data in A and from corresponding passive tension (PT) values (see Fig. 3A; 1.2 mN mm⁻² initial PT at 2.5 μm SL), the average energy (derived from elastic recoil) per shortening time was calculated. This parameter is shown relative to the maximum power output of an actively shortening rabbit psoas muscle fibre, which was estimated to generate 600 W m⁻² (for further details, see text).

Figure 2. Dependence of passive shortening speed on sarcomere length, step release size and temperature.

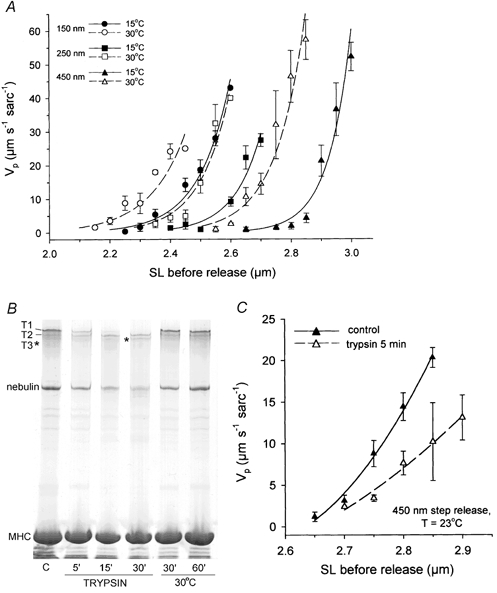
A, passive shortening velocity, V_p (means ± s.e.m.), calculated for release steps of 150, 250 or 450 nm sarcomere⁻¹, and temperatures of 15 or 30 °C. Under each experimental condition, 9–11 myofibrils were analysed. SL bin size, 50 nm. The SL-dependent increase in V_p was fitted with a simple two-parameter exponential growth function. Continuous lines represent fits for 15 °C data and dashed lines those for 30 °C data. B, example of a 2.8 % SDS-polyacrylamide gel to separate high molecular weight proteins in a suspension of skinned rabbit psoas myofibrils. Myofibrils were incubated for 1 h at room temperature in the presence of leupeptin (C, control) or without leupeptin in the presence of trypsin (0.05 μg ml⁻¹) for 5, 15 and 30 min. In addition, myofibrils were incubated without trypsin (in the presence of leupeptin) at 30 °C for 30 and 60 min. T1, intact native titin, T2 and T3, lower molecular weight titin bands, which appear due to proteolysis of native titin. Nebulin, ∼800 kDa protein. MHC, myosin heavy chain. C, titin proteolysis drastically reduces myofibrillar V_p. V_p (means ± s.e.m.) for 450 nm sarcomere⁻¹ release steps was measured in single psoas myofibrils before (n = 7) and after (n = 7) exposure for 5 min to low doses of trypsin (0.05 μg ml⁻¹) at room temperature.

Dependence of average V_p on sarcomere length, step release size and temperature

Figure 2A elucidates three different aspects of the measurements: the dependence of V_p on (1) the initial SL from which the release step was carried out; (2) the release step size (150, 250 or 450 nm sarcomere⁻¹); and (3) temperature. The filled symbols (pooled data for SL bins) and continuous lines (fits) represent V_p at 15 °C, the open symbols and dashed lines, V_p at 30 °C. The smallest release step used, 150 nm sarcomere⁻¹, was applicable within a range of initial SLs from 2.15 to 2.45 μm (30 °C) and 2.25 to 2.60 μm (15 °C). In myofibrils contracting passively from longer SLs, the time to slack reuptake was less than 2–4 ms, i.e. near or below the 2 ms time resolution limit of the CCD array. Thus, the speed of passive shortening was too fast to be detectable by our system. To slacken the myofibril for a longer period of time, we applied a larger motor step, 250 nm sarcomere⁻¹. Even greater release steps of 450 nm sarcomere⁻¹ were needed above ∼2.7 (15 °C) or ∼2.6 μm SL (30 °C). The maximum average V_p values thus obtained were near 60 μm s⁻¹ sarcomere⁻¹ (Fig. 2A) − 4 to 6 times higher than the values for maximum unloaded shortening velocity (V_o) typically measured in fully Ca²⁺-activated rabbit psoas fibres between 2.0 and 2.6 μm SL (see Fig. 4 and Moss, 1986). However, we point out that average V_p would reach values far greater than ∼60 μm s⁻¹ sarcomere⁻¹ if release steps were much smaller than those applied here for practical reasons (also see explanation to Fig. 5, below). Similarly, very high speeds of passive shortening were generally found for releases from SLs above 3.0 μm (15 °C) or 2.85 μm (30 °C). Under these conditions, the elastic recoil again was too fast (time to refocus < 2–4 ms) to allow reliable measurements of the slack reuptake time.

Figure 4. Maximum unloaded velocity of sarcomere shortening (V_o) of skinned rabbit psoas fibre bundles fully activated at pCa 4.5.

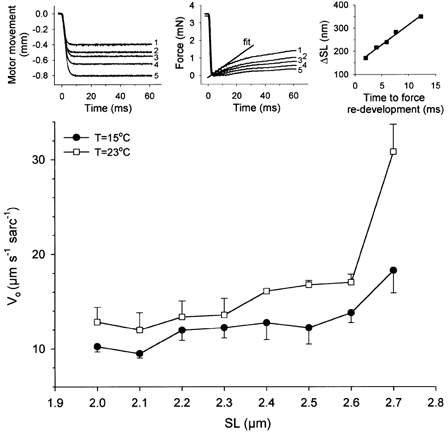
The Edman (1979) slack test method was employed. SL indicates sarcomere length during activation, measured by laser diffraction. Data are presented as means ± s.e.m. (n = 3–5 fibre bundles per point). The differences in V_o measured at 15 °C and 23 °C give an average Q₁₀ of ∼1.3, for SLs between 2.0 and 2.6 μm. Q₁₀ increases to ∼1.8 at 2.7 μm SL. Insets (upper panels), examples of slack test measurements showing raw data and V_o calculation for a representative muscle fibre preparation. Specimen length was 5.75 mm at a SL of 2.5 μm; diameter, 0.12 mm; V_o = 17 μm s⁻¹ sarcomere⁻¹.

V_p also exhibited a strong temperature dependence (Fig. 2A). To parameterize the temperature dependence, Q₁₀ values were calculated. The Q₁₀ was determined separately for the three different step release sizes. A value was obtained for each SL bin, and values were averaged. For 150 nm sarcomere⁻¹ steps, the average Q₁₀ was 2.0 ± 0.13 (mean ± s.d.); for 250 nm steps, 3.04 ± 0.29; and for 450 nm steps, 6.15 ± 0.50. Thus, the temperature sensitivity of the SL-V_p curves was strongly dependent on the step release size. For a given step size but different initial SLs, only little variation between Q₁₀ values was found - usually within the experimental error range. For 150 nm sarcomere⁻¹ step amplitudes, the range of Q₁₀ values was 1.83–2.25; for 250 nm steps, 2.55–3.51; and for 450 nm steps, 5.37–6.67. In sum, for one and the same step release size, Q₁₀ was unaffected by variations in initial SL, whereas Q₁₀ varied with the amplitude of the release step from a given initial SL.

As a control to test whether V_p indeed depends on an intact titin-filament system (as presumed in these experiments), titin was selectively digested by treatment with low doses of trypsin (0.05 μg ml⁻¹ in relaxing buffer). The time course of titin degradation was monitored on 2.8 % SDS- polyacrylamide gels (Fig. 2B). This analysis revealed that, following 5 min trypsin treatment at 23 °C, the ratio between intact titin (T1) and myosin heavy chain (MHC) was decreased by 80 %, compared with controls. Also, a titin degradation product (T2) became more prominent on the gels, confirming that partial digestion of titin had already occurred after 5 min of trypsin treatment. A 15 min incubation of myofibrils with trypsin reduced the amount of T1 by 93 % and significantly increased T2. In myofibrils treated with trypsin for 30 min, the T1 band disappeared completely and was replaced by T2 and a new T3 band (asterisk in Fig. 2B). For comparison, we investigated whether the integrity of titin might be affected by incubation of myofibrils at a temperature of 30 °C in the absence of trypsin, but in the presence of the protease inhibitor leupeptin (the two right lanes in Fig. 2B). These conditions were used for part of the V_p experiments described above. The gels showed that neither after 30 min, nor after 60 min, was the T1 band noticeably affected, although the faint T2 band tended to become slightly stronger after a 1 h long experiment. Passive shortening velocity was then measured both before and after 5 min exposure of single rabbit psoas myofibrils to 0.05 μg ml⁻¹ trypsin at room temperature (Fig. 2C). Following titin degradation, V_p was reduced by approximately 50 % at initial SLs between ∼2.7 and ∼2.85 μm. At this stage, no obvious changes in the sarcomere pattern in phase-contrast images of single myofibrils were detectable (data not shown). However, trypsin treatment for more than 7–8 min frequently caused breakage of stretched myofibrils. We conclude that measurements of V_p most probably reflect the passive elastic recoil of the (extensible I-band section of) titin filaments. Whether or not intermediate filaments contribute to the passive shortening speed remains to be seen; however, such contribution is expected to be small or absent, as these structures generate no measurable passive force in rabbit psoas muscle fibres at SLs below ∼3.5 μm (Wang et al. 1993).

Relation between V_p and passive tension

V_pversus SL curves of single psoas myofibrils (Fig. 2A) rose more steeply than the steady-state passive tension (PT)-SL curve (Fig. 3A; data compiled from previous work; Linke et al. 1996a, 1998a,b). V_p was also plotted against PT (Fig. 3B). Since PT is little sensitive to temperature - in the temperature range studied, the Q₁₀ for the stretch-dependent force generation of an entropic spring, such as titin, is ∼1.03 (Linke et al. 1998b) - the same PT data were used to construct V_p-PT curves for V_p data sampled at 15 and 30 °C. Both initial PT and the difference between initial PT and steady-state PT at the end of the release step (ΔPT) were considered. This distinction was made because titin filaments are viscoelastic (Wang et al. 1993; Bartoo et al. 1997) and, for a short period of time following the step, become unloaded to a higher degree than the value of ΔPT indicates (Minajeva et al. 2001). Therefore, the true V_pversus PT curve for a given experimental condition might lie in between the curves shown for the respective conditions in the upper and lower panels of Fig. 3B. What is clear from these graphs is that even minor changes in PT can accelerate the passive elastic recoil dramatically. Note that over the low-PT range between slack SL and ∼2.5 μm SL already, V_p could reach very high values if release steps were small (Fig. 3B).

Figure 3. Passive shortening velocity rises more steeply than passive tension.

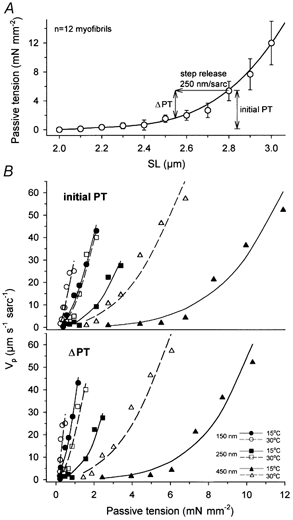
A, passive SL-tension relationship of single psoas myofibrils (data compiled from Linke et al. 1996a, 1998a, b). The graph also illustrates the parameters ‘ΔPT’ and ‘initial PT’ used in B. B, V_pversus PT curves, for both initial PT (top panel) and ΔPT (bottom panel). Data points and curves were assembled from Figs 2A and 3A. The same symbol codes and line types as in Fig. 2A were used.

Active unloaded shortening velocity

How do these numbers compare with the unloaded shortening velocity (V_o) of fully Ca²⁺-activated rabbit psoas fibres? A summary of results of conventional slack test experiments performed on actively shortening skinned fibre bundles is shown in Fig. 4. The insets (upper panels in Fig. 4) indicate recordings obtained from a typical experiment. The inset graph on the right shows that data measured at different release steps from ∼170 to 350 nm sarcomere⁻¹ could be fitted with a straight line - as expected from the work of others (Edman, 1979; Moss, 1992; Gordon et al. 2000) - to reveal V_o (here, 17 μm s⁻¹ sarcomere⁻¹). The summary data (Fig. 4, lower panel) indicate that, although there was a trend indicating a slight, continuous, increase in V_o from 2.1 to 2.6 μm SL, no statistically significant variations in V_o (Student's t test) were found over this SL range, at 15 or 23 °C. This result confirms earlier findings in frog skeletal muscle (Edman, 1979; Claflin et al. 1989). However, at both 15 and 23 °C, a statistically significant (P < 0.001; Student's t test) increase in V_o was seen when SL was raised from 2.6 to 2.7 μm (Fig. 4). Between 2.0 and 2.6 μm SL, average V_o was 11.8 ± 0.6 μm s⁻¹ sarcomere⁻¹ (mean ± s.e.m.) at 15 °C and 14.5 ± 0.8 μm s⁻¹ sarcomere⁻¹ at 23 °C. The Q₁₀ was ∼1.3 when averaged over the SL range 2.0–2.6 μm, but it increased to ∼1.8 at 2.7 μm SL. The V_o value of 11.8 ± 0.6 μm s⁻¹ sarcomere⁻¹ at 15 °C translates to ∼5 muscle lengths s⁻¹, close to the value of 4.4 muscle lengths s⁻¹ (Moss, 1986), but higher than the value of 2.3 muscle lengths s⁻¹ (Julian et al. 1981), reported elsewhere for skinned rabbit psoas fibres at the same temperature. Thus, V_o does not reach the high values obtainable for V_p even at shorter SLs (Fig. 2).

V_p decreases during prolonged passive shortening

The fact that V_o (of fully activated fibres) is independent of the step release size, whereas V_p is not, prompted us to further evaluate the passive shortening of single psoas myofibrils at a series of different step releases from the same SL of 2.5 μm (T = 23 °C). The lower left inset in Fig. 5A shows that the relationship between the time to focus redevelopment and step release size (ΔSL) was non-linear (compare with Fig. 4, right inset). Figure 5A demonstrates that the V_pversus step size data points could be fitted by a two-parameter exponential decay function with a coefficient of 163 μm s⁻¹ sarcomere⁻¹ and a decay ‘rate constant’ of −0.011 nm⁻¹. Consequently, a linear fit to the data in a half-logarithmic representation (Fig. 5A, upper right inset) intercepts the V_p axis at a theoretical value (for a zero release step) of 163 μm s⁻¹ sarcomere⁻¹. The negative slope of this curve indicates the slowing of passive myofibril shortening with increasing step release size. Most probably, this slow down in V_p results from viscous forces within the sarcomeres opposing the elastic recoil (see Discussion).

Contribution of elastic recoil to overall shortening characteristics

According to Edman (1979), passive tension may be seen as a negative, compressive, load imposed onto the muscle. During passive shortening, the potential energy of the stretched titin spring is converted to kinetic energy, but is partly dissipated as heat as viscous forces slow down the shortening. We wanted to know how the energy derived from the elastic recoil compares quantitatively with the energy generated during active shortening. From the data shown in Fig. 5A, we estimated the average elastic energy per shortening time measured in the modified slack test protocols, by calculating PT × V_p for each release step. For these calculations, we used the PT value measured before shortening (or the difference in PT before and after the step release, ΔPT), although PT probably decreases soon after the onset of passive shortening and reaches zero when the myofibril buckles. However, kinetic energy is present as long as shortening persists. This kind of calculation is useful to approximate how the elastic energy utilizable for passive recoil drops with prolonged shortening due to viscous drag. Since the values calculated (energy per shortening time) have a power unit that is normalized to cross-sectional area, they could be expressed relative to the maximum power output of active muscle (Fig. 5B), by taking 600 W m⁻² as an approximation for the latter. This value was estimated for a rabbit psoas fibre bundle - the one used in the experiments of Fig. 4 (insets) - by making the reasonable assumption that maximum active power is 1/3V_o × 1/3 maximum active force. The value compares well with values reported in the literature (e.g. Ameredes et al. 2000).

It appeared that average energy (derived from elastic recoil) per shortening time, for step releases between 175 and 375 nm sarcomere⁻¹ from an initial SL of 2.5 μm, is at most 10 % of active maximum power output (Fig. 5B). The analysis also predicts, if the curves shown in Fig. 5B are extrapolated to the power axis, that average elastic energy per time interval is much higher at smaller step releases, e.g. 35–50 % of maximum active power for 20 nm sarcomere⁻¹ steps from 2.5 μm initial SL. This is expected, as the slow down of elastic recoil by viscous forces is less if shortening is terminated earlier. Furthermore, for SLs >> 2.5 μm, the average energy derived from elastic recoil would be quite high also for larger release steps, as both PT and V_p rise steeply. In fact, for 450 nm sarcomere⁻¹ releases from 2.95 μm SL (initial PT, ∼10 mN mm⁻²; ΔPT, ∼9 mN mm⁻², T = 15 °C; see Fig. 3B), the average energy per shortening time was estimated to be in excess (125–140 %) of maximum active power.

DISCUSSION

Over the past decade, the structural and functional properties of titin in muscle have been studied extensively (see reviews by Wang, 1996; Maruyama, 1997; Labeit et al. 1997; Linke & Granzier, 1998; Horowits, 1999; Trinick & Tskhovrebova, 1999). Such work has established a number of important mechanical roles for this giant protein in skeletal muscle: titin (1) keeps the thick filament centred in the sarcomere during activation; (2) provides a structural framework for other sarcomere proteins; and (3) functions as a molecular spring responsible for the development of a retractive force upon stretch of non-activated muscle. Although the spring-like behaviour of titin implies that the protein is somehow involved in determining the shortening characteristics of stretched muscle, we know of no attempt aimed at quantifying the titin-based contribution to shortening velocity. The present study was initiated to measure this contribution in the single myofibril preparation, in which passive elastic recoil should essentially reflect the properties of no other structures than the titin filaments. Intermediate filaments may contribute somewhat to the passive recoiling, but their contribution is likely to be miniscule or absent in the SL range studied (2.1–3.0 μm), as these filaments generate no passive force in rabbit psoas muscle at SLs below ∼3.5 μm and very little passive force between 3.5 and 4.5 μm SL (Wang et al. 1993). To quantify the passive (titin-based) shortening speed (V_p) we modified the slack test protocol of Edman (1979), conventionally used to determine the active unloaded shortening velocity (V_o) of muscle fibres. Two main goals were pursued in these experiments. First, we wanted to know how V_p is affected by parameters such as initial SL, passive tension level, step release size and temperature. Second, we wanted to compare V_p with V_o to obtain more information about the physiological relevance of passive elastic recoil in skeletal muscle.

Factors affecting the passive elastic recoil of skeletal muscle sarcomeres

V_p rose steeply with SL (Fig. 2A) but was readily reduced when myofibrils were exposed to low doses of trypsin to partially degrade the titin filaments (Fig. 2B and C). Thus, titin may indeed be the principal determinant of myofibrillar passive elastic recoil. Results showed that V_p could be already quite fast at very low PT levels of < 1–2 mN mm⁻² (Fig. 3). Because of the great impact of small changes in PT on V_p, and because of our 2 ms resolution limit for measuring slack-reuptake time, V_p could be studied only over a relatively small SL range at a given step release amplitude. However, application of different sized release steps allowed the measurement of average V_p over a much broader SL range, from ∼2.1 to 3.0 μm. Additional analysis revealed that, for releases from a given initial SL, longer step amplitudes were associated with smaller average V_p values (Fig. 5A). This dramatic slow down of passive recoil with prolonged shortening would be difficult to explain with the mechanical properties of titin itself. Rather, we propose that the observed behaviour mainly results from viscous forces counteracting the passive shortening.

Viscous forces have long been known to affect the shortening velocity of skeletal muscle (e.g. Hill, 1968; Ford et al. 1977; Chase et al. 1998) As reviewed by Gordon et al. (2000), several factors may potentially limit active unloaded shortening, such as (1) cytoskeletal elements that resist sliding, (2) intrinsic viscous drag on the filaments, and (3) resistive drag produced by strongly attached cross-bridges. Since in the present study, myofibrils shortened passively in BDM-containing relaxing buffer, force-generating cross-bridges should not form and hence, should play no role in opposing the elastic recoil. Also viscous drag, produced when thin filaments slide past the thick filament through the cytosol, should not limit shortening, as the forces generated by these processes are too low to have a significant impact on shortening speed (Chase et al. 1998; Gordon et al. 2000). This leaves structural or cytoskeletal factors as the possible elements limiting shortening. Among these, weakly bound cross-bridges (Brenner et al. 1991) could constitute a resistive, although miniscule (Hill, 1968), force. In contrast, much greater resistance to filament sliding may come from weak and/or transient interactions involving actin filaments and titin (Funatsu et al. 1993; Soteriou et al. 1993; Jin, 1995; Kellermayer & Granzier, 1996; Linke et al. 1997; Stuyvers et al. 1997). Indeed, weak binding between I-band titin regions and actin was confirmed recently and shown to cause viscous effects in isolated cardiac myofibrils (Kulke et al. 2001a). Because there is no reason to suppose that such interactions are absent in skeletal muscle sarcomeres, we conclude that the most likely scenario is one in which passive elastic recoil is opposed by viscous forces originating in weak actin-titin associations.

In this context, it is interesting to note that V_p changed strongly with temperature (Fig. 2A and Fig. 3B). Such a response cannot be caused by titin itself, as the wormlike-chain model of entropic elasticity (Bustamante et al. 1994; Marko & Siggia, 1995), which has been successfully applied to explain titin elasticity in skeletal muscle (Linke et al. 1998a,b; Trombitas et al. 1998), predicts that a temperature rise of 10 °C (from 25 °C) increases passive force by only 3 %. A recent study reported a rise in steady-state PT of non-activated skeletal muscle fibres with temperature (Ranatunga, 1994), although in another study from the same laboratory, increasing temperature actually decreased the passive force parameters measured during quick-stretch protocols (Mutungi & Ranatunga, 1998). In our experience, the temperature effect on titin-based PT of myofibril preparations is very small (W. A. Linke, unpublished data). In contrast, the high Q₁₀ values measured here for V_p, ranging from 2 to ∼6 (depending on step release size), indicate that passive shortening velocity is determined by something in addition to titin's spring force. A potential contributor to the temperature dependence of V_p again could be viscous drag. Since actin-titin interactions give rise to viscosity in the sarcomere (Kulke et al. 2001a), it is possible that these interactions are modified by temperature. To prove that actin-titin interactions play a role in the temperature-sensitive passive shortening speed, it will be useful to measure the effect of temperature on V_p in actin-extracted single myofibrils. Although in the past, we used a Ca²⁺-independent gelsolin fragment to extract actin from cardiac myofibrils (Kulke et al. 2001a) or insect flight muscle (Kulke et al. 2001b), this fragment was shown to be much less effective at removing actin from vertebrate skeletal myofibrils, where thin filaments are stabilized by nebulin (Gonsior & Hinssen, 1995). Cardiac myofibrils may be better suited than skeletal myofibrils to test whether actin-titin interactions underlie the high Q₁₀ value of V_p.

Finally, we point out that temperature had a much greater effect on V_p than on V_o. The main determinant of V_o affected by temperature is cross-bridge kinetics, which play no role in the passive elastic recoil. Cross-bridge kinetics are likely to dominate the temperature sensitivity of V_o in the SL range between 2.0 and 2.6 μm, at which the average Q₁₀ was ∼1.3 (Fig. 4) - near the lower end of the range of Q₁₀ values reported in the literature for fast-twitch muscles (i.e. 1.8–2.4; Ranatunga, 1984). In comparison, Q₁₀ for V_p could be as high as 6.15 at release steps of 450 nm sarcomere⁻¹ commencing from SLs of 2.6–2.8 μm. Interestingly, the Q₁₀ for V_o at 2.7 μm SL (rising V_o with elevated passive force) increased to 1.8. We speculate that this rise may be due to a stronger effect of temperature changes on average V_p than on V_o.

Comparison between passive and maximum active shortening velocities

The impact of passive tension on active unloaded shortening velocity, measured by the slack test method, has been studied previously in frog (Edman, 1979; Claflin et al. 1989; Morgan et al. 1990; Edman, 1993) and mammalian (Galler & Hilber, 1994) skeletal muscle fibres. In the frog muscle experiments, V_o stayed relatively constant over a SL range between 1.7 and 2.7 μm, at which PT is low. Above ∼2.7 μm SL, V_o progressively increased (Edman, 1979), at least for releases performed to the same final SL in the presence of PT (Claflin et al. 1989; Edman, 1993). In skinned rabbit psoas fibres, V_o increased continuously as PT rose substantially between 2.5 and 3.0 μm SL (Galler & Hilber, 1994). In the present study, a steep increase in V_o was found in sarcomeres stretched to a length of 2.7 μm. The active and passive shortening characteristics of rabbit psoas sarcomeres measured here warrant a comparison.

First, we confirm that V_o is unaltered as long as PT stays low. This is so despite the high V_p values (detectable up to ∼60 μm s⁻¹ sarcomere⁻¹) measured already at very low initial PT levels and small release steps (Fig. 3). These results strongly support Edman's conclusion that the cross-bridges impose a substantial braking force onto the passive recoil of elastic structures (Edman, 1979). However, at SLs above 2.6 μm, at which skinned rabbit psoas fibres showed steeply increasing V_o (Fig. 4), passive elastic recoil adds significantly to the active power output. We estimated that, for a relatively long step release of 450 nm sarcomere⁻¹ from an initial SL slightly above 2.9 μm, the average energy (derived from elastic recoil) per shortening time may equal active maximum power. This implies that passive elastic recoil is an important contributor to isotonic shortening commencing from higher physiological SLs. Moreover, our calculations indicated that high elastic energy utilization is also expected for small releases from shorter initial SLs as low as 2.5 μm (Fig. 5). This is a consequence of the fast passive shortening immediately after the onset of a quick release, when elastic recoil is not yet slowed down greatly by viscous drag. Thus, even at modest physiological SLs, passive elastic recoil may aid active shortening during the very early phase of isotonic contraction (see Edman, 1979; Claflin et al. 1989).

Another point to be discussed concerns the observation that ‘resting viscosity’ or ‘dynamic PT’ seems to disappear when a muscle fibre is activated (Ford et al. 1977; Morgan et al. 1990). This phenomenon was suggested earlier to be possibly related to cross-bridge function (Morgan et al. 1990), since cross-bridges had been thought to play a role in PT (Hill, 1968). However, these interpretations may not hold up in light of more recent results pointing at titin filaments as the main source of PT. Titin is viscoelastic (Wang et al. 1993; Higuchi, 1996; Bartoo et al. 1997; Minajeva et al. 2001), and it is conceivable that the mechanical properties of this protein are changed during Ca²⁺-dependent activation. Although this issue is not settled yet, preliminary results do not support a direct effect of Ca²⁺ on the stiffness of titin (Linke et al. 1996b). In contrast, Ca²⁺ modulates the above-mentioned interaction between I-band titin and actin filaments in cardiac muscle specimens (Stuyvers et al. 1997; Kulke et al. 2001a.) In these studies, the actin-titin association was less strong at elevated [Ca²⁺], resulting in lowered viscous forces. The findings, if true also for skeletal muscle, may explain why part of the viscosity seen in passive fibres is not present in active fibres. Independent of this, titin's spring-like properties would continue to play a role in the overall shortening characteristics of activated muscle: passive elastic recoil should be even faster when viscous forces counteracting the shortening are lower in the presence of Ca²⁺.

In summary, we showed that the passive shortening velocity of single psoas myofibrils steeply increases with SL and passive tension level and that V_p could reach values greatly exceeding the velocity of active unloaded shortening. In contrast to V_o, V_p strongly depends on the step release amplitude applied in the slack test protocols. Further, V_p was highly temperature sensitive. Most probably, viscous forces oppose the passive shortening and are largely responsible for the dependence of V_p on temperature and step size. Results also suggest that the passive recoil of elastic structures is significantly slowed down by the contractile elements. However, the retractive force of stretched titin filaments, which underlies the elastic recoil, may be important in that it acts as an additional driving force on the contractile system at short release steps and during shortening from longer physiological SLs.