Abstract
Using human Kv1.5 channels expressed in HEK293 cells we assessed the ability of to mimic the previously reported action of Zn2+ to inhibit macroscopic hKv1.5 currents, and using site-directed mutagenesis, we addressed the mechanistic basis for the inhibitory effects of and Zn2+. As with Zn2+, caused a concentration-dependent, -sensitive and reversible reduction of the maximum conductance (gmax). With zero, 5 and 140 mm the pKH for this decrease of gmax was 6.8, 6.2 and 6.0, respectively. The concentration dependence of the block relief caused by increasing [K+]o was well fitted by a non-competitive interaction between and , for which the KD for the K+ binding site was 0.5-1.0 mm. Additionally, gating current analysis in the non-conducting mutant hKv1.5 W472F showed that changing from pH 7.4 to pH 5.4 did not affect Qmax and that charge immobilization, presumed to be due to C-type inactivation, was preserved at pH 5.4. Inhibition of hKv1.5 currents by or Zn2+ was substantially reduced by a mutation either in the channel turret (H463Q) or near the pore mouth (R487V). In light of the requirement for R487, the homologue of Shaker T449, as well as the block-relieving action of , we propose that H+ or Zn2+ binding to histidine residues in the pore turret stabilizes a channel conformation that is most likely an inactivated state.
We have previously shown in human Kv1.5 (hKv1.5) channels that external Zn2+ ions caused a depolarizing shift of the activation curve, an effect referred to as the gating shift, as well as a reduction of the current amplitude, which we termed block, that was relieved by external permeant ions such as K+ and Cs+ (Zhang et al. 2001b). Although a gating shift is very often associated with a change of the external concentration of divalent cations, as first detailed by Frankenhaeuser & Hodgkin (1957), the block of voltage-gated K+ channels by divalent cations, in particular Zn2+, is not a general finding and its mechanistic basis is therefore of some interest. In a follow-up study of the effects of Zn2+ on gating currents (Zhang et al. 2001a) we found that Zn2+ ions caused a rightward shift of the voltage dependence of on-gating charge movement or the Qon(V) relationship. This Zn2+-induced shift of the Qon(V) was approximately two-fold greater than that observed for the conductance-voltage (g(V)) relationship and implied that Zn2+ binding at a site in the outer channel pore could inhibit the ionic current as well as the movement of the voltage sensor. The latter effect is consistent with recent evidence for a close proximity of the outer pore mouth and the S4 segment, which comprises a major part of the voltage sensor (Blaustein et al. 2000; Li-Smerin et al. 2000; Cha & Bezanilla, 1998; Loots & Isacoff, 1998), and with the view that the voltage-sensing domain wraps around the outer rim, i.e. the turret of the pore (Loots & Isacoff, 2000).
Identifying the potential site(s) of action of Zn2+ is facilitated by the fact that Zn2+ shows high affinity binding to the imidazole ring of histidine (H) or to the sulphur atom of cysteine (C) residues. Lower affinity binding of Zn2+ can also occur at the side chain carboxyl group of the acidic amino acid residues glutamate (E) and aspartate (D) (Vallee & Auld, 1990). In the six transmembrane segment (6TM) α-subunit of hKv1.5 there is, in the pore-forming (P-) region and the extracellular segments linking it to S5 (S5-P) and S6 (P-S6), only one high affinity Zn2+ ligand - H463 - which, based on the crystal structure of KcsA channels (Doyle et al. 1998), is found in the turret. Other potential Zn2+ binding sites include, at the NH2-terminal end of S5-P, a glutamate residue, E456, that is strictly conserved in voltage-gated channels (Ortega-Saenz et al. 2000) and which appears to interact with S4 (Loots & Isacoff, 2000). E456 is, however, an unlikely Zn2+ binding site, at least in part because its side chain carboxyl group is believed to form hydrogen bonds with residues in the P-S6 region (Larsson & Elinder, 2000). Two aspartate residues are also found in the outer pore mouth of hKv1.5: D469 in the outer pore helix and D485, which forms part of the ‘GYGD’ motif in the pore signature sequence.
Interestingly, the inhibition of rat Kv1.5 (rKv1.5) currents by extracellular protons () (Steidl & Yool, 1999) has features similar that of the Zn2+ block of hKv1.5. Although not evident with Zn2+ during 300 ms pulses (Zhang et al. 2001b), an acceleration by of current inactivation during long-lasting (> 1 s) depolarizations raised the possibility that the current inhibition was due to an accumulation of channels in the C-type inactivated state (Steidl & Yool, 1999). The term ‘C-type inactivation’ originated with the observation that Shaker splice variants with different carboxy-terminal regions (including S6) showed different rates of slow inactivation (Hoshi et al. 1991). Subsequently it was reported that mutations in the pore (P) region of Kv2.1 channels increased the inactivation rate by a process having different characteristics than C-type inactivation, and the term ‘P-type inactivation’ was coined (De Biasi et al. 1993). A growing body of evidence now suggests that slow inactivation in Shaker-related channels such as Kv1.5 is in fact a complex process involving either multiple and independent inactivation mechanisms or a single inactivation process that involves multiple steps (Olcese et al. 1997; Yang et al. 1997; Kiss et al. 1999; Loots & Isacoff, 2000; Wang & Fedida, 2001). P-type inactivation appears to involve a partial constriction of the outer pore mouth that eliminates K+ currents but has no effect on gating currents, including their ability to undergo charge immobilization following the ‘closed to open’ transition (Yang et al. 1997). C-type inactivation might be coupled to P-type inactivation and has been proposed to involve a further conformational change of the outer pore that stabilizes the S4 segments in the activated or outward position. This ‘stabilization’ contributes to a voltage-dependent slowing of return or off-gating charge movement, an effect that is also known as charge immobilization (Olcese et al. 1997; Wang & Fedida, 2001). The possibility that a common mechanism of action, possibly involving an inactivation process, might account for the inhibition of Kv1.5 current by Zn2+ and H+, also pointed to the potential for a common site of action. In this connection it is known that Zn2+ and H+ bind to histidine residues and an rKv1.5 mutant in which histidine residues in the pore turret are replaced by glutamine (Q) (rKv1.5 H452Q) has a substantially reduced acid sensitivity (Steidl & Yool, 1999).
Against this background the experiments described here had two major goals. The first goal was to determine the concentration dependence of the inhibition of hKv1.5 channels by protons and to discover if, as with Zn2+, the inhibition by was affected by changes of . After confirming a -sensitive inhibition of hKv1.5 currents by , the second goal was to gain at least a preliminary insight into the molecular basis for that inhibitory action by assessing the effects of point mutations. We provide evidence that the binding of H+ or Zn2+ to histidine residues (H463) in the channel turret is a necessary but not sufficient condition for the inhibitory effect. Instead, H463s appear to function as sensors, such that H+ or Zn2+ binding permits a conformational change that involves an arginine (R) residue near the pore mouth (R487). An examination of gating currents revealed that (pH 5.4) has no effect on the total gating charge movement (Qmax) and that charge immobilization persists following strong depolarizations. Based on these observations we propose that protons and Zn2+ ions inhibit hKv1.5 currents by affecting channel availability. The possibility that the inhibition of hKv1.5 currents arises by the facilitation of a transition to a non-conducting state, possibly the P-type inactivated state, is discussed.
METHODS
Cell preparation
Wild type (wild-type) hKv1.5 channels were studied in a human embryonic kidney cell line (HEK293; American Type Culture Collection), as reported previously (Wang et al. 2000). Cells were dissociated for passage by using trypsin-EDTA and were maintained in minimum essential medium (MEM), 10 % fetal bovine serum, penicillin-streptomycin and 0.5 mg ml−1 gentamicin in an atmosphere of 5 % CO2 in air. All tissue culture supplies were obtained from Invitrogen (Burlington, ON, Canada).
Point mutations of the wild-type hKv1.5 α-subunit in the plasmid expression vector pcDNA3 were made using the Quikchange Kit (Stratagene, La Jolla, CA, USA) to convert the histidine (H) residue at position 463 to glutamine (Q) (H463Q) or glycine (G) (H463G). The double mutant H463Q,R487V was created by subcloning a cassette of hKv1.5 H463Q into hKv1.5 R487V (Wang et al. 2000) using BstEII and ClaI restriction enzymes (New England BioLabs, Beverly, MA, USA). Stable transfections of HEK293 cells were made using 0.8 μg of hKv1.5 H463Q, hKv1.5 H463Q, R487V or hKv1.5 H463G cDNA and 2 μl of Lipofectamine 2000 (Invitrogen). Geneticin (0.5 mg ml−1) was added 48 h after transfection.
Recording solutions
The standard bath solution contained, in mm: 140 NaCl, 3.5 KCl, 10 Hepes, 2 CaCl2, 1 MgCl2, 5 glucose and its pH was adjusted to 7.4 with NaOH. Where the effect of the external concentration of potassium () on the proton block was examined, zero solution was made by substituting NaCl for KCl and, for greater than 3.5 mm, NaCl was replaced by KCl. Caesium-containing solutions were prepared by substitution of CsCl for KCl (3.5 mm ) or for both KCl and NaCl (20 mm and 140 mm ). In experiments addressing the effect of on the current inhibition, N-methyl-d-glucamine (NMG+) replaced Na+ and the pH was adjusted with HCl. The external concentration of H+ () was adjusted with 10 mm buffer, where the buffer was Hepes for the pH range 6.8-7.4, Mes for pH 5.4-6.7 or Taps for pH 8.4. Zinc-containing test solutions were made by the addition of ZnCl2 from 0.1 or 1 m stock solutions. The low solubility of Zn(OH)2 limits the maximum concentration of Zn2+ that can be used at pH 7.4 to less than 5 mm. Our standard patch pipette solution for recording K+ currents contained, in mm: 130 KCl, 4.75 CaCl2 (pCa2+ = 7.3), 1.38 MgCl2, 10 EGTA, 10 Hepes and was adjusted to pH 7.4 with KOH.
For gating current recordings the bath solution contained, in mm: 140 NMGCl, 1 MgCl2, 10 Hepes (pH 7.4) or Mes (pH 5.4), 2 CaCl2, 10 glucose and the pH was adjusted with HCl; the patch pipette solution consisted of 140 NMGCl, 1 MgCl2, 10 Hepes, 10 EGTA and was adjusted to pH 7.2 with HCl. Chemicals were from the Sigma Aldrich Chemical Co. (Mississauga, ON, Canada).
In an experiment, a section of glass coverslip with cells attached to it was placed in the recording chamber (0.5 ml volume) and perfused with 5-10 ml of control solution. After recording control currents the chamber was flushed with 5-6 ml of test solution to ensure complete replacement of the bath solution before treated responses were recorded. If after perfusing 5-6 ml of control solution the post-treatment currents did not recover to within ± 10 % of the pre-treatment amplitudes the entire data set was discarded. In most cells, however, virtually complete recovery was observed. We found no difference between experiments done with discontinuous perfusion, as described above, and experiments where the cells were continuously perfused (not shown).
Signal recording and data analysis
Macroscopic currents were recorded at room temperature (20-25 °C) using the patch clamp technique primarily in the whole cell configuration. In some of the cell lines expressing mutant hKv1.5 channels at a high level, i.e. the H463Q and some of the R487V mutants, the large amplitude of the whole cell currents necessitated recording macroscopic currents from outside-out patches. Voltage clamp experiments were done with an EPC-7 patch clamp amplifier and Pulse + PulseFit software (HEKA Electronik, Germany). Patch electrodes were made from thin-walled borosilicate glass (World Precision Instruments, FL, USA) and had a resistance of 1.0-2.5 MΩ measured in the bath with standard internal and external saline. Capacitance and series resistance compensation (typically 80 %) were used. An on-line P/N method, for which the holding potential was −100 mV and the scaling factor was 0.25, was used to subtract leak and any uncompensated capacitive currents. Current signals filtered at 3 kHz (-3 dB, 8-pole Bessel filter) were digitized (16 bit) at a sampling interval of 100 μs (10 kHz). Voltages have been corrected for the liquid junction potentials.
To quantify the inhibition of currents, tail currents were recorded at −50 mV following a depolarizing pre-pulse. Peak tail current amplitudes were then obtained by extrapolation of a single exponential function fitted to the tail current decay to the start of the step to −50 mV. After normalization of tail currents either to the maximum current of the control or the treated response, data points were fitted to a single Boltzmann function:
| (1) |
where, when y is the current normalized with respect to the control response, A is the proportion of the control gmax. When y is the current normalized with respect to the maximal treated current, A is the best-fit value for the normalized maximal response and ideally has a value of unity. V1/2 is the half-activation potential or mid-point of the activation curve, V is the voltage during the pre-pulse and s is the slope factor, in millivolts, reflecting the steepness of the voltage dependence of gating.
To quantify gating charge movement during activation or deactivation, charge-voltage (Q(V)) curves were generated by time integration of on- or off-gating currents, as described previously (Chen et al. 1997). Activation gating in hKv1.5 is best fitted by the sum of two Boltzmann functions, where the larger component, known as Q2, represents ≈80 % of the total charge movement (Hesketh & Fedida, 1999). However, for simplicity, Q(V) data obtained at pH 7.4 and 5.4 were fitted to eqn (1), where y is the charge moved, A is the maximal charge (Qmax) and V is the voltage at which the on-gating charge (Qon) or off-gating charge (Qoff)is evoked. V1/2 and s remain as described above.
Concentration-response data for Zn2+ were fitted to the Hill equation:
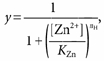 |
(2) |
where y is the proportion of the control gmax, KZn is the equilibrium dissociation constant for Zn2+ binding and nH is the Hill coefficient reflecting the number of Zn2+ ions binding per channel. For protons, eqn (2) was modified to account for the fact that the data points were normalized to the response at pH 7.4:
| (3) |
where KH is the equilibrium dissociation constant for proton binding.
The equation used to model the binding interaction between , and the hKv1.5 channel has been described previously (Zhang et al. 2001b) and is also known as the ternary-complex model of interaction that is used to describe the binding of two ligands to the same receptor:
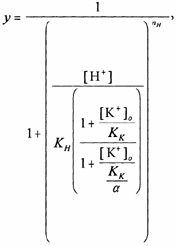 |
(4) |
where KH is the equilibrium dissociation constant for proton binding in zero , KK is the equilibrium dissociation constant for K+ binding at pH 7.4 and the parameter α is known as the co-operativity factor or the coupling constant/factor. A value for α greater than unity indicates negative co-operativity. To reduce the number of parameters in the model the Hill coefficient for K+ binding was assumed to be unity.
Data are expressed as the mean ± the standard error of the mean (s.e.m.) except for the values obtained by non-linear least-squares fitting routines (Igor, Wavemetrics, OR, USA), which are expressed as the mean ± the standard deviation (s.d.). The paired-sample t test (control versus treated) was used to assess the actions of protons and Zn2+ on the inactivation rate. A P-value of 0.05 or less was considered significant.
RESULTS
Increasing [H+]o causes a gating shift and reduces the maximum conductance (gmax)
Representative traces in Fig. 1 show the effect of changing pHo from 7.4 to 6.4 in nominally K+-free medium (zero ) in which Na+ was the major extracellular cation. For the control currents the voltage protocol consisted of a 300 ms pulse command to between −40 and 40 mV in 5 mV increments followed immediately by a 300 ms command to −50 mV to record the tail current. The robust pulse and ensuing tail currents, shown at a higher gain in the inset, obtained during or following strong depolarizations in pH 7.4 medium (Fig. 1A), are consistent with a failure of hKv1.5 currents to disappear or ‘collapse’ in zero (Jäger & Grissmer, 2001). After switching to pH 6.4 medium the range of the pulse voltages was changed from −30 to 60 mV to compensate for a small rightward shift of the voltage dependence of gating: the so-called gating shift. As noted by Steidl & Yool (1999), there appeared also to be a slight slowing of the activation kinetics with extracellular acidification but this was not systematically studied and was certainly not as pronounced as the slowing caused by Zn2+ (Zhang et al. 2001b). A more profound effect of the increased extracellular acidity, and the main focus of this report, was a large reduction of pulse and tail current amplitudes. Figure 1C, which was derived in part from the traces shown in Fig. 1A and B, plots the tail current amplitudes at −50 mV measured as described in the Methods and fitted to a Boltzmann function. In this cell, increasing caused V1/2 to shift from −6.2 mV to 4.3 mV and the maximal tail current amplitude at pH 6.4 was 14 % of that measured at pH 7.4. Both the gating shift and the current reduction reversed completely and rapidly (e.g. Fig. 9) after returning to pH 7.4.
Figure 1. Extracellular acidification decreases the maximum conductance (gmax) and causes a rightward shift of the conductance-voltage (g(V)) relationship for hKv1.5 currents.
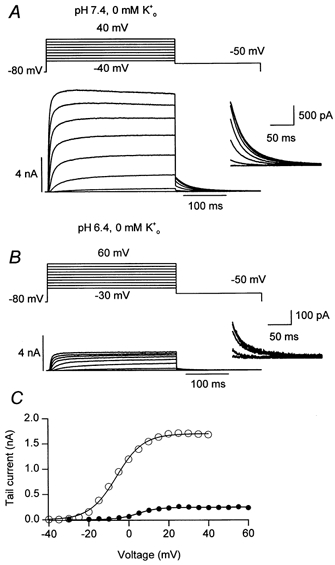
Panels A and B show, respectively, representative control (pH 7.4) and treated (pH 6.4) currents evoked by the voltage protocol shown above each family of traces. Successive pulse command voltages were incremented by 5 mV but for clarity only alternate traces are shown. The change of the range of pulse voltages at pH 6.4 was necessary to compensate for the gating shift. The holding potential in this and other figures was −80 mV, except where noted. Inset traces show the tail currents at a higher gain. Tail current amplitudes, obtained by extrapolating the fit of a single exponential function to the start of the step to −50 mV, are plotted in C and fitted to a Boltzmann function to obtain the equivalent of the g(V) relationship. Acidification shifted the V1/2 from −6.2 mV to 4.3 mV and the maximum current decreased from 1.7 nA to 0.24 nA, which corresponds to a gmax relative to that at pH 7.4 (relative gmax) of 0.14.
Figure 9. The effect of the stimulus frequency and holding potential on the inhibition of wild-type hKv1.5 currents by .
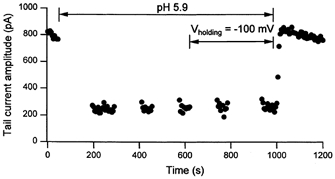
This graph, which is representative of the results obtained from six such experiments, three at pH 5.9 and three with 1 mm Zn2+, plots the amplitude of tail currents measured at −50 mV following a 300 ms step to 60 mV to maximally activate channels. After 10 consecutive control responses in standard external saline (pH 7.4, 3.5 mm ) and evoked at 5 s intervals from a holding potential of −80 mV, pulsing was stopped and 5 ml of test solution was perfused to change the extracellular pH to 5.9 for the duration indicated by arrows. Resumption of the step commands approximately 2 min after extracellular acidification showed an immediate ≈75 % reduction of the tail current amplitude. The identical effect was obtained for each of two subsequent pulse trains confirming that the inhibition was not affected by a period without stimulation. Changing the holding potential to −100 mV also had no effect on the current amplitude. Returning to pH 7.4 medium while pulsing shows the effect rapidly (within 15 s) and completely reverses, implying that a change of the internal pH is not involved.
External protons have been reported to reduce the amplitude of rKv1.5 currents (Steidl & Yool, 1999), but the reduction (≈40 %) was substantially less than shown in Fig. 1 (-85 %) and in the left column of Fig. 2, which summarizes the results obtained in 12 such experiments. Since our previous work showed that the reduction of hKv1.5 currents by Zn2+ was affected by , we next addressed the possibility that this apparently greater potency of the inhibition by protons of hKv1.5 currents shown in Fig. 1 was due to the use of a zero K+ bathing solution.
Figure 2. Increasing reduces the inhibition of hKv1.5 current by protons.
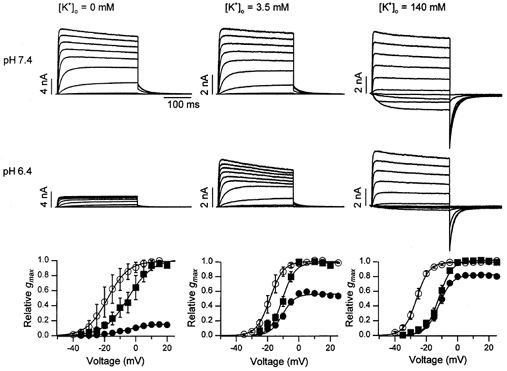
Traces obtained from three different cells showing the current at pH 7.4 (control, top row) and pH 6.4 (treated, lower row) in, from left to right, zero, 3.5 and 140 mm . In zero , control and treated pulse currents were evoked by 300 ms pulses from −50 to 45 mV in 5 mV steps; in 3.5 mm , the pulse command range was −50 to 45 mV at pH 7.4 and −30 to 65 mV at pH 6.4; in 140 mm , the range for pulse voltages was −40 to 55 mV. For clarity, only alternate current traces are shown. The corresponding control (○) and treated g(V) relationships, obtained from a number of similar experiments, are shown in the graph at the bottom of each column. Treated data were normalized with respect both to the gmax at pH 6.4 (▪) and to the control gmax (•). The relative gmax at pH 6.4 in zero, 3.5 and 140 mm was 0.19 ± 0.02 (n = 12), 0.56 ± 0.01 (n = 6), and 0.81 ± 0.12 (n = 6), respectively. In zero , V1/2 and s changed from −21.4 ± 4.3 and 4.7 ± 0.5 mV at pH 7.4 to −8.2 ± 4.0 and 7.1 ± 0.3 mV at pH 6.4, respectively. In 3.5 mm , the corresponding values were −18.3 ± 1.9 mV and 3.9 ± 0.4 mV at pH 7.4 and −10.5 ± 1.2 mV and 3.9 ± 0.4 mV at pH 6.4; and, in 140 mm , −26.2 ± 1.1 mV and 3.8 ± 0.3 mV at pH 7.4 and −12.3 ± 1.1 mV and 3.8 ± 0.4 mV at pH 6.4.
Increasing [K+]o inhibits the reduction of gmax by extracellular acidification
Current traces in the left, centre and right columns of Fig. 2 were recorded from cells in which was zero, 3.5 and 140 mm, respectively, and the pHo was changed from 7.4 (upper row of traces) to 6.4 (lower row of traces). The voltage protocol was similar to that described for Fig. 1. Graphs at the foot of each column show the tail currents from a number of similar experiments for control (○) and treated responses normalized either with respect to the maximum control tail current (•) or to the maximum treated tail current (▪). That inhibits the proton-induced current reduction is shown by the increase of the relative gmax from 0.19 ± 0.02 (n = 12) in zero , to 0.56 ± 0.01 (n = 6) in 3.5 mm and finally to 0.81 ± 0.12 (n = 6) in 140 mm . As with the Zn2+ block, the gating shift at pH 6.4 was not significantly affected by changes of (see Fig. 2 legend for V1/2 and s values) suggesting that the proton-induced gating shift and current inhibition are independent effects.
Data obtained by repeating experiments of the type shown in Fig. 2 over a range of pHs were fitted to the Hill equation to generate the concentration-response curves shown in Fig. 3. In zero medium in which Na+ was the predominant metal cation (•) the best fit to the data gave a KH of 153 ± 13 nm (pKH ≈ 6.8) and a Hill coeffcient (nH) of 1.5 ± 0.2, which suggests that inhibition requires protonation of at least two sites. To determine if Na+ ions affect the current inhibition by protons, the zero experiments were also done with NMG+ as the major extracellular cation. With the KH was 128 ± 53 nm (pKH ≈ 6.9) and nH was 1.2 ± 0.5 (○ and dashed line of Fig. 3). This suggests that external Na+ ions do not affect the current inhibition by protons. With 5 mm the KH increased to 590 ± 85 nm (pKH ≈ 6.2) but the value for nH of 1.6 ± 0.4 was not significantly different from that with zero . In comparison with the substantial rightward shift caused by increasing from zero to 5 mm, a much smaller increase of the KH to 1.1 ± 0.11 μM (pKH ≈ 6) was obtained when was increased from 5 to 140 mm. The nH in 140 mm was 1.8 ± 0.3.
Figure 3. The concentration dependence of the inhibition of Kv1.5 currents by protons in zero (•), 5 (▪) and 140 mm (▴) .
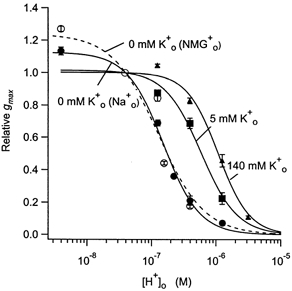
Data for zero were obtained with either 143.5 mm Na+ (•) or 143.5 mm NMG+ (○) as the major extracellular cation. The lines represent the best fit to eqn (3). The fitted values for the equilibrium dissociation constant for protons (KH), the pKH and nH were, in zero and 143.5 mm NMG+: 128 ± 53 nm (mean ± s.d.), 6.9 and 1.2 ± 0.5; in zero and 143.5 mm Na+: 153 ± 13 nm, 6.8 and 1.5 ± 0.2; in 5 mm : 590 ± 85 nm, 6.2 and 1.6 ± 0.4; and in 140 mm : 1.1 ± 0.11 μM, 6.0 and 1.8 ± 0.3. Although the pKH estimates with either Na+ or NMG+ as the extracellular cation are similar, the increase of the relative gmax with NMG+ at pH 8.4 was significantly greater. Consistent with a non-competitive versus competitive interaction between and (see Fig. 4), the increase of KH going from zero to 5 mm was greater than that going from 5 mm to 140 mm.
relief of the effect of protons is fitted by a model of non-competitive inhibition
As noted with Zn2+ block of hKv1.5 channels (Zhang et al. 2001b), the greater relief of the proton-induced current inhibition when was changed from zero to 5 mm compared with when it was changed from 5 to 140 mm , suggested that K+ ions and protons were not competing for a common site. For that reason we modelled the interaction between and as an allosteric inhibition (eqn (4)), by which we mean that the interaction is mediated via separate binding sites and is therefore non-competitive.
For this analysis (Fig. 4) we focused in particular on the current inhibition at pH 6.4 with concentrations of zero, 1, 3.5, 5, 10, 20, 80 and 140 mm. The fit of these data to eqn (4) gave mean values (± s.d.) of 150 ± 1900 nm for KH, 1.33 ± 17 for nH, 0.68 ± 9 for KK and 6.2 ± 14.9 for α, the factor by which bound H+/K+ inhibits the binding of K+/H+. To reduce the s.d. of the estimates for KK and α, we fixed the values for KH and nH in the fitting routine at 153 nm and 1.5, respectively, based on the data of Fig. 3 (zero , 143.5 mm ). This was justified on the basis of the similarity to the values for KH and the nH from Fig. 3 and the preliminary fit (i.e. with the four parameters free) of the data at pH 6.4. With KH and nH fixed, the fit of the data at pH 6.4 gave estimates for KK and α of 0.65 ± 0.27 mm and 5.5 ± 0.7, respectively.
Figure 4. The concentration dependence of the antagonism by and of the inhibition of hKv1.5 currents by .
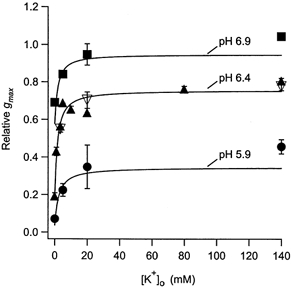
The relative gmax at different concentrations is plotted for pH 6.9 (▪), pH 6.4 (▴) and pH 5.9 (•). The data for pH 6.9 and 5.4 were obtained with zero, 5, 20 and 140 mm . At pH 6.4, was zero, 1, 3.5, 5, 10, 20, 80 and 140 mm. Assessment of the block-relieving effect of (▿) was done with concentrations of 3.5, 20 and 140 mm. The lines represent the best fit of the data to eqn (4) (see Methods). With the values for KH and nH fixed to those obtained directly from the data in Fig. 3 (153 nm and 1.5, respectively) the best-fit values for KK and α were 0.65 ± 0.27 mm and 5.5 ± 0.7. appears to be equivalent to in its antagonism of the proton block. The best fit of the data at pH 6.9 was obtained with 0.93 ± 2.8 mm for KK and 6.2 ± 9.1 for α; at pH 5.9 the corresponding values were 0.66 ± 0.48 mm and 6.2 ± 1. These estimates for KK are very near those estimated for the relief of the Zn2+ block (≈0.5 mm; Zhang et al. 2001b).
At pH 6.9 and pH 5.9 the relative gmax was measured with zero, 5, 20 and 140 mm . For the data at pH 5.9 the best-fit values for KK and α, with KH and nH constrained as above, were 0.66 ± 0.48 mm and 6.2 ± 1, respectively; at pH 6.9 the corresponding values were 0.93 ± 2.8 mm and 6.2 ± 9.1.
External Cs+ ions mimic the block-relieving effect of K+
In hKv1.5 channels the permeability of Cs+ ions relative to K+ ions is approximately 0.2 (Fedida et al. 1999) and the KD for the relief by (KCs) of the Zn2+ block is some five- to six-fold higher than the KK (Zhang et al. 2001b). Surprisingly, with the same experimental protocol but using Cs+ at concentrations of 3.5, 20 and 140 mm (▿, Fig. 4) the ability of to antagonize the current inhibition by protons was indistinguishable from that of .
Sensitivity to and Zn2+ inhibition is reduced in hKv1.5 H463Q
The range of pKHs for the inhibition of hKv1.5 is consistent with the titration of one or more histidine residues and, as noted above, in rKv1.5 channels in which glutamine (Q) is substituted for H452, the homologue of H463 in hKv1.5, there is a substantially reduced proton sensitivity (Steidl & Yool, 1999). Based on the crystal structure of KcsA (Doyle et al. 1998), H463 is presumed to be located in the outer rim or ‘turret’ of the pore mouth (Fig. 5B). Since Zn2+ ions also bind avidly to histidine residues this raised the possibility that the current inhibition caused either by Zn2+ or involves binding to one or more of the H463s in the turret of the homotetrameric hKv1.5 assembly. To test that hypothesis we examined the concentration dependence of the conductance decrease by and Zn2+ in the mutant hKv1.5 H463Q. These experiments were done in zero so that the interpretation of the results would not be complicated by a change, if any, of the affinity of the site at which K+ ions bind to produce an allosteric inhibition of the actions of Zn2+ and H+.
Figure 5. The structure of the S5, S6 and the pore (P) loop of Kv1.5 inferred from the crystal structure of KcsA.
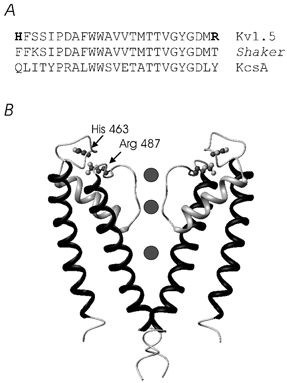
A, the sequence alignment for Kv1.5, Shaker and KcsA between the turret and the outer pore mouth. B, a side view of the KcsA channel in which the foreground and background α-subunits have been removed for clarity. The α-subunit of voltage-gated K+ channels has an additional four transmembrane segments (S1-S4) that are not illustrated. Sites at which mutations were made, namely H463 and R487, are shown at their homologous positions in the KcsA crystal structure. The orientation of the side chains of these two residues is tentative.
The g(V) relationships (Fig. 6A) and concentration- response curves (Fig. 6B) for the proton sensitivity of hKv1.5 H463Q, confirmed the results reported for rKv1.5. Thus, the gating shift was apparently intact but the decline of gmax was seen only with much higher proton concentrations. Fitting of the concentration-response data (Fig. 6B) to the Hill equation gave an estimate for KH of 4.7 ± 1.9 μM (pKH = 5.3) and an nH of 1 ± 0.4 versus the corresponding values of 0.15 μM (pKH = 6.8) and 1.5 in wild-type hKv1.5. The acid sensitivity of hKv1.5 H463Q is therefore quite comparable to that of rKv1.5 H452Q, where the pKH is ≈5.2 (Steidl & Yool, 1999).
Figure 6. A point mutation in the turret (S5-P loop), H463Q, reduces the inhibition but not the gating shift caused by and Zn2+.
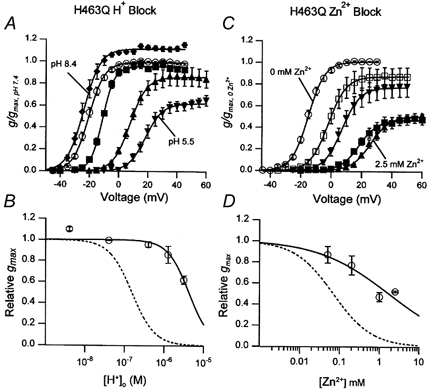
A, the g(V) relationship in zero at pH 8.4 (♦), pH 7.4 (○), pH 6.4 (▪), pH 5.9 (▴) and pH 5.5 (▾) after normalization with respect to the gmax at pH 7.4. Values for the relative gmax, V1/2 and s were: at pH 8.4, 1.1 ± 0.02, −23.9 ± 1.3 mV and 5.4 ± 0.5 mV (n = 5); at pH 7.4, 1, −20.1 ± 1.0 mV and 4.6 ± 0.2 mV(n = 28); at pH 6.4, 1.06 ± 0.03, −13.0 ± 0.5 mV and 4.0 ± 0.5 mV (n = 3); at pH 5.9, 0.86 ± 0.08, 7.6 ± 0.7 mV and 5.6 ± 0.4 mV (n = 8); and, at pH 5.5, 0.63 ± 0.04, 19.2 ± 1.7 mV and 5.7 ± 0.4 mV (n = 7). B, the concentration dependence of the reduction of gmax by protons. Fitting of the data to the Hill equation gave a KD of 4.7 ± 1.9 μM (pKH ≈ 5.3) and nH of 1.0 ± 0.4. The gmax- concentration relationship for wild-type hKv1.5 is represented by the dashed line. C, the g(V) relationship as described for A but with zero (○), 50 μM (□), 200 μM(▾), 1 mm (▪) and 2.5 mm (▴) of Zn2+. The relative gmax, V1/2, and s were 1, −14.9 ± 0.9 mV and 4.8 ± 0.3 mV for the control (n = 27); 0.87 ± 0.08, −1.9 ± 0.9 mV and 6.2 ± 0.9 mV for 50 μM Zn2+ (n = 5); 0.77 ± 0.09, 7.1 ± 1.1 mV and 5.9 ± 0.2 mV for 200 μM Zn2+ (n = 6); 0.47 ± 0.04, 18.5 ± 2.0 mV and 6.0 ± 0.7 mV for 1 mm Zn2+ (n = 10); and 0.52 ± 0.009, 27.2 ± 2.3 mV and 6.4 ± 0.8 mV for 2.5 mm Zn2+ (n = 5). D, as described for B but with Zn2+. The best-fit values for KZn and nH were 1.7 ± 1 mm and 0.5 ± 0.2. The dashed line indicates the concentration-response relationship for wild-type Kv1.5 in zero (KZn = 69 μM, nH = 0.9; Zhang et al. 2001b).
Tests of the effects of Zn2+ on the H463Q mutant showed that the outcome (Fig. 6C and D) mirrored that seen with protons. Because of the limited solubility of Zn(OH)2 the highest concentration of Zn2+ we tested was 2.5 mm and consequently a full concentration-response curve could not be obtained. From the limited concentration range over which data were collected the extrapolated KZn was 1.7 ± 1 mm or roughly 25-fold higher than for wild-type hKv1.5 (Zhang et al. 2001b). The nH for the inhibition by Zn2+ of wild-type hKv1.5 and hKv1.5 H463Q currents was 0.9 (Zhang et al. 2001b) and 0.5 (Fig. 6), respectively.
In the course of this series of experiments we became aware of a report that currents through hKv1.5 H463G channels were completely suppressed upon changing from 4.5 mm to zero medium at pH 7.4 (Jäger & Grissmer, 2001). This result was surprising since no such effect is apparent with the hKv1.5 H463Q mutant under the same recording conditions (Fig. 6 and Fig. 7A). Our experiments with hKv1.5 H463G confirmed this conductance collapse in zero at pH 7.4 (Fig. 7C) and we also noted that there was a striking increase in the inactivation rate in 3.5 mm (Fig. 7B) that was not previously reported. Thus, in contrast to wild-type hKv1.5 (Fig. 1) and hKv1.5 H463Q (Fig. 7A) where there is little or no current decay evident during 300 ms pulse commands, in hKv1.5 H463G the current decay at 40 mV is well fitted by a single exponential function with a time constant of 73 ± 8 ms (n = 4; Fig. 7B).
Figure 7. In hKv1.5 H463G slow inactivation is greatly accelerated and the conductance collapses in zero at pH 7.4.
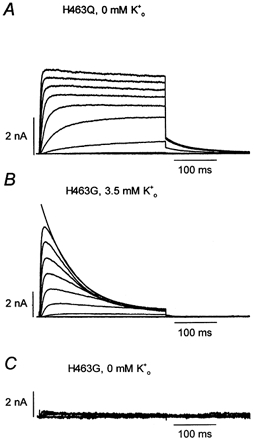
A, shown for comparison are the currents from hKv1.5 H463Q evoked in zero by 300 ms pulses to between −40 and 40 mV in 10 mV increments. B, hKv1.5 H463G currents recorded using the same stimulus protocol but with 3.5 mm . The solid line superimposed on the current at 40 mV represents the best fit of the current decay to a single exponential function. The mean time constant for inactivation at 40 mV was 73 ± 8 ms (n = 4). C, from the same cell as in B and using the same voltage command protocol after switching to zero at pH 7.4. Unlike either wild-type Kv1.5 H463 (Fig. 1) or Kv1.5 H463Q, is required for hKv1.5 H463G channels to function normally at pH 7.4. Complete recovery was obtained after returning to K+-containing bath solution (not shown).
and Zn2+ accelerate inactivation
In rKv1.5 has been shown to accelerate inactivation, an effect that was evident only with long depolarizing commands (Steidl & Yool, 1999). Similarly, in hKv1.5 there was no obvious change of inactivation kinetics during 300 ms depolarizations but an increased inactivation rate was evident with as well as Zn2+ during depolarizations lasting for several seconds (not shown). Fitting a single exponential function to the current decay during a 7-10 s depolarization at 60 mV in external medium with 5 mm K+ at pH 7.4 gave a time constant for inactivation (τinact) of 2.63 ± 0.11 s (n = 4). In the same cells, extracellular acidification to pH 6.4 caused a roughly 50 % reduction of τinact to 1.19 ± 0.04 s (P < 0.05). Using the identical stimulation protocol we found that the changeover from Zn2+-free medium at pH 7.4 to medium at the same pH and containing 1 mm Zn2+ reduced τinact by approximately 30 %, from 3.0 ± 0.18 s to 2.14 ± 0.16 s (n = 4, P < 0.05). Although these results confirm that current inhibition by and Zn2+ is associated with a moderately increased rate of inactivation, we suggest below that this cannot account for the reduction of gmax.
Current inhibition by protons and Zn2+ is reduced in hKv1.5 R487V
To more directly address the possibility that the reduction of gmax reflected an effect on one or more inactivation processes we next examined the actions of and Zn2+ in a hKv1.5 mutant in which an arginine (R) residue in the P-S6 region (Fig. 5A) was mutated to valine (V) (R487V, Fig. 8). This was motivated by the fact that mutations at the homologous site (T449) in N-type (fast) inactivation-removed Shaker channels (ShakerIR) either accelerates (T449E, T449K, T449A) or slows (T449Y, T449V) inactivation (Lopez-Barneo et al. 1993). A previous study of hKv1.5 R487V showed that inactivation was indeed dramatically slowed when channel currents were carried by Na+ but, curiously, the time course of K+ currents was relatively unchanged (Wang et al. 2000). It has also been proposed that a charged residue at position 487 is critical for the current inhibition by (Jäger & Grissmer, 2001).
Figure 8. A mutation near the pore mouth, R487V, substantially reduces the sensitivity to inhibition by and Zn2+.
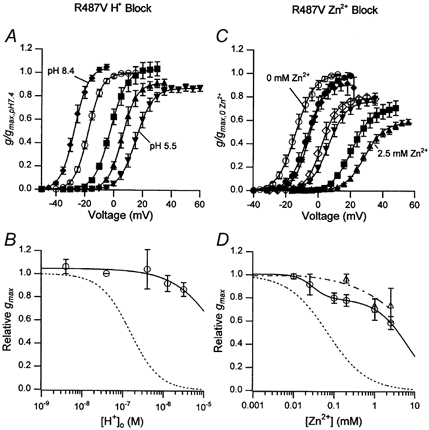
A, the g(V) relationship in zero at pH 8.4 (♦), pH 7.4 (○), pH 6.4 (▪), pH 5.9 (▴) and pH 5.5 (▾) after normalization with respect to gmax at pH 7.4. The values for the relative gmax, V1/2 and s were, respectively, 1.04 ± 0.02, −28.5 ± 1.1 mV, 4.6 ± 1.0 mV at pH 8.4 (n = 3); 1, −18.1 ± 0.9 mV, 4.5 ± 0.2 mV at pH 7.4 (n = 17); 1.04 ± 0.06, −1.8 ± 1.3 mV, 5.6 ± 0.4 mV at pH 6.4 (n = 5); 0.92 ± 0.03, 6.4 ± 1.3, 4.9 ± 0.4 at pH 5.9; and 0.87 ± 0.03, 15.5 ± 1.6 mV, 5.5 ± 0.2 mV at pH 5.5 (n = 5). B, the concentration-response relationship for the reduction of gmax by protons. The continuous line, representing the best fit of the data to the Hill equation, was obtained with KH = 23 μM (pKH of 4.6) and nH = 0.8. C, the g(V) relationship in zero and with Zn2+ concentrations of 10 μM (•), 25 μM (♦), 100 μM (⋄), 200 μM (▾), 1 mm (▪) and 2.5 mm (▴) after normalization with respect to the control (○) gmax. The relative gmax, V1/2 and s were, respectively, 1, −13.4 ± 1.5 mV, 4.5 ± 0.3 mV for the control (n = 15), 0.99 ± 0.01, −5.9 ± 1.5 mV, 5.4 ± 0.4 mV in 10 μM Zn2+ (n = 4); 0.92 ± 0.05, −5.7 ± 0.1 mV, 4.7 ± 0.5 mV in 25 μM Zn2+ (n = 3); 0.80 ± 0.02, 2.8 ± 1.8 mV, 4.8 ± 0.5 mV in 100 μM Zn2+ (n = 4); 0.78 ± 0.02, 5.2 ± 1.6 mV, 5.3 ± 0.3 mV in 200 μM Zn2+ (n = 5); 0.70 ± 0.05, 21.0 ± 1.2 mV, 5.9 ± 0.3 mV in 1 mm Zn2+ (n = 3); and 0.59 ± 0.02, 28.9 ± 1.1 mV, 5.9 ± 0.3 mV in 2.5 mm Zn2+ (n = 5). D, as described for B but with Zn2+. The continuous line represents the best fit of the hKv1.5 R487V data to the sum of two Hill equations. Binding at the higher affinity site (KZn = 29 ± 0.2 μM) accounted for ≈20 % of the inhibition. The apparent elimination of the higher affinity site in the double mutant Kv1.5 R487V, H463Q (▵ and dashed line) suggests that it may reflect Zn2+ binding to H463. The extrapolated KZn for the lower affinity site in the R487V mutant was 6.4 ± 0.07 mm. Again, the dotted lines in B and D represent the corresponding concentration-response curves for wild-type hKv1.5 (Zhang et al. 2001b).
Figure 8 summarizes the results of experiments assessing the inhibition of hKv1.5 R487V by protons and Zn2+ ions in zero (143.5 mm Na+) medium. The g(V) relationships derived from tail current measurements (Fig. 8A) show that the gating shift was apparently intact in the R487V mutant. However, there was a dramatic change of the concentration dependence of the -induced conductance decline. For example, whereas in wild-type hKv1.5 the relative gmax at pH 5.9 was 0.07 ± 0.01 (n = 9; Fig. 4), in hKv1.5 R487V the relative gmax at the same pH was 0.92 ± 0.03 (n = 5; Fig. 8A and B). An extrapolated pKH of 4.6 obtained from the best fit of the concentration- response data of Fig. 8B suggests a shift of ≈2 pH units from the pKH of wild-type hKv1.5 channels.
Tests of the sensitivity of hKv1.5 R487V channels to Zn2+ (Fig. 8C and D) showed that the gating shift was, again, substantially unaffected and, as with , there was a clear increase of the Zn2+ concentration required to cause 50 % inhibition. Thus, whereas wild-type hKv1.5 currents were half-inhibited by 0.07 mm Zn2+ (Zhang et al. 2001b), in the R487V mutant 41.2 ± 1.7 % (n = 5) of gmax persisted in 2.5 mm Zn2+. Closer inspection of the concentration- response data of Fig. 8D suggested that two Zn2+ binding sites might be involved in the inhibition of hKv1.5 R487V currents. Subsequent experiments with the double mutant hKv1.5 H463Q, R487V (▵, Fig. 8D) implied that the higher affinity site (KZn = 29 μM) that accounted for approximately 20 % of the conductance decline in the R487V mutant, was apparently eliminated. The latter observation could be accounted for in many ways, perhaps the simplest being that the higher affinity site in the R487V mutant reflects the binding of Zn2+ to one or more H463 residues. The concentration dependence of the reduction of gmax in the double mutant was best fitted by a single Hill function with a KZn of 2.2 mm, representing an approximately 30-fold increase over that measured in wild-type hKv1.5 under the same recording conditions.
Current inhibition by and Zn2+ is apparently not use-dependent
If, as has been proposed to account for the block of rKv1.5 currents by (Steidl & Yool, 1999), the inhibition of hKv1.5 currents by Zn2+ or extracellular acidification were due to an accumulation of inactivation, then the degree of inhibition would be expected to show use-dependence. Figure 9 shows the results of a representative experiment addressing this issue. Peak tail current amplitudes following 300 ms depolarizations from −80 mV to 60 mV at pH 5.9 are bracketed by control and recovery responses at pH 7.4. was 3.5 mm. Two features of the current behaviour at pH 5.9 are significant. First, inhibition of the current is apparent with the first pulse and is more or less constant for each of the subsequent pulses during a train of 10 pulses delivered at 5 s intervals. Second, a 2 min stimulus-free interval in which the membrane was held at either −80 mV or −100 mV had no block-relieving effect. Consequently, despite the fact that both Zn2+ and slightly enhance the rate of inactivation of residual hKv1.5 currents, there is no support for the hypothesis that accumulation of inactivation accounts for the reduction of gmax. Finally, Fig. 9 also demonstrates the rapid reversal, i.e. within the time course of fluid exchange in the bath, of the current inhibition after beginning the perfusion with pH 7.4 solution. The latter observation argues against a mechanism involving a change of the internal pH concomitant to extracellular acidification.
Protons cause a depolarizing shift of the Q(V) relationships but do not affect Qmax
Because gating currents can provide useful evidence on the conformational states available to a channel we recorded gating currents in a stable HEK293 cell line expressing hKv1.5 W472F mutant channels (Chen et al. 1997). This mutant is analogous to the Shaker W434F non-conducting mutant in that it has no measurable K+ current, perhaps because of permanent or greatly accelerated P-type inactivation (Yang et al. 1997).
Representative examples of gating current traces from hKv1.5 W472F recorded at pH 7.4 and pH 5.4 in the same cell are shown in Fig. 10A–D. To prevent contamination of gating currents by endogenous HEK293 ionic currents, these recordings were made in symmetrical 140 mm NMG+. At pH 7.4, on-gating currents were evoked between −60 and 100 mV from a holding potential of −100 mV and at pH 5.4 the voltage range was from −60 to 150 mV to compensate for the proton-induced gating shift. As reported previously (Chen et al. 1997), on-gating currents at pH 7.4 were first apparent at −60 mV and as the strength of the depolarization increased both the peak amplitude and decay rate of the on-gating current increased. Following depolarizations up to 0 mV the return- or off-gating currents decayed rapidly as channels deactivated at −100 mV. In contrast, following depolarizations to 0 mV or more the off-gating currents are superimposable and have a clear rising phase that is followed by a slow decay. This slowing of charge return is such that integration of the off-gating current over a 15 ms period produces a Qoff that is reduced relative to Qon. This decrease of Qoff/Qon or charge immobilization has been attributed to the conformational change underlying C-type inactivation (Chen et al. 1997; Yellen, 1997) since it is affected by the presence of permeant metal cations, much as C-type inactivation of ionic currents is affected by extracellular cations (Lopez-Barneo et al. 1993; Baukrowitz & Yellen, 1995). C-type inactivation is greatly accelerated in the recording conditions used here because there are no permeant metal cations on either side of the membrane. The transition of the voltage sensor from its outward ‘immobilized’ position to the inward position remains voltage dependent but stronger hyperpolarizations are required to overcome the stabilizing interaction between the sensor and the C-type inactivated state. This accounts for the leftward shift, relative to the Qon(V) relationship, of the voltage dependence of charge return (Olcese et al. 1997; Wang & Fedida, 2001; and see Fig. 10E).
Figure 10. Extracellular acidification to pH 5.4 causes a depolarizing shift of the Qon(V) and Qoff(V) relationships but does not reduce Qmax.
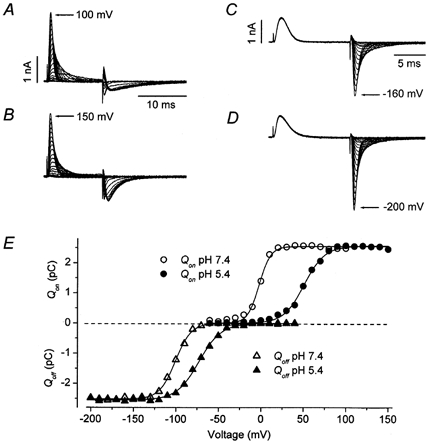
Panels A and B show at pH 7.4 and 5.4, respectively, the on- and off-gating currents recorded when the membrane was depolarized for 12 ms from a holding potential of −100 mV to between −60 and 100 mV (A) or −60 and 150 mV (B) in 10 mV increments before stepping back to −100 mV. Outward charge movement (Qon) induced by the depolarization was determined by integrating the on-gating currents at pH 7.4 (○) and 5.4 (•), and is plotted in panel E. For the Qon(V) relationship in E, the fitted values for V1/2 and s were, respectively, −2.2 mV and 6.5 mV at pH 7.4 and 50.2 mV and 11.8 mV at pH 5.4. Qmax was not significantly affected by extracellular acidification. C and D, from the same cell as in A and B, these panels show the off-gating currents following a 12 ms step from −80 mV to 50 mV in pH 7.4 (C) or to 100 mV at pH 5.4 (D) to move Qmax. Off-gating current was recorded in 10 mV increments between −200 and −10 mV at pH 7.4 and between −200 and 40 mV at pH 5.4. Charge return at pH 7.4 (▵) and pH 5.4 (▴) is plotted against the repolarization voltage in E to obtain the Qoff(V) relationship. Extracellular acidification changed the V1/2 of Qoff(V) from −100.5 mV to −72.9 mV and s increased from 9.4 mV to 13.1 mV. Both at pH 7.4 and pH 5.4 there is a leftward shift of the voltage dependence of Qoff relative to Qon(V).
Figure 10B shows that changing the external pH from 7.4 to 5.4 caused a rightward shift of the voltage dependence of the on-gating currents such that the on-gating current evoked at 150 mV at pH 5.4 was comparable to that at 100 mV at pH 7.4. At pH 5.4 there was also a substantial increase of the peak amplitude and an increase of the decay rate of off-gating currents following strong depolarizations. To quantify the effects of changes of pHo on activation gating, the on-gating currents in Fig. 10A and B were integrated to obtain the voltage dependence of on-gating charge movement shown in Fig. 10E. A fit of the Qon(V) relationship at pH 7.4 (○) to a single Boltzmann function gave a maximum charge movement Qmax of +2.5 pC, V1/2 = −2.2 mV and s = 6.5 mV. At pH 5.4 (•, Fig. 10E) Qmax, V1/2 and s were +2.5 pC, 50.2 mV and 11.8 mV. In the six cells examined V1/2 was 4.3 ± 2.2 mV at pH 7.4 and 48.9 ± 1.2 mV at pH 5.4; s increased from 7.1 ± 0.5 mV at pH 7.4 to 10.5 ± 0.4 mV at pH 5.4; and the relative Qmax (Qmax,pH5.4/Qmax,pH7.4) was 1.0 ± 0.003. Thus, changing pHo from 7.4 to 5.4 caused a ≈45 mV rightward shift of the V1/2 of the Qon(V) relationship and a decrease of the voltage sensitivity of activation. Both of these effects are replicated by Zn2+ (Zhang et al. 2001a) and interestingly, as with Zn2+, the shift of V1/2 of the Qon(V) relationship is roughly twice that measured for the g(V) curve. For example, at pH 5.9 the V1/2 of the g(V) relationship was shifted by ≈21 mV (not shown).
Panels C and D of Fig. 10 illustrate the outcome of experiments to determine if the change of off-gating current in Fig. 10B was due to a shift of the voltage dependence of off-gating charge movement (Olcese et al. 1997). The voltage clamp protocol consisted of a 12 ms step from the holding potential of −80 mV to 50 mV at pH 7.4 (C) or 100 mV at pH 5.4 (D) to evoke maximal charge movement. This was followed immediately by a pulse to between −10 and −200 mV at pH 7.4 or to between 40 and −200 mV at pH 5.4. Integration of the off-gating currents yielded the Qoff(V) curves shown in Fig. 10E at pH 7.4 (▵) and pH 5.4 (▴). Considering first the data at pH 7.4, it can be seen that, as in the Shaker non-conducting mutant (Olcese et al. 1997), the voltage dependence of return charge movement was shifted leftward (V1/2 = −100.5 mV) by ≈100 mV relative to the Qon(V) curve. Of particular importance is that a similar effect is seen at pH 5.4 where the V1/2 of the Qoff(V) curve was −72.9 mV, representing a leftward shift of ≈124 mV from the V1/2 of the Qon(V) relationship.
The values, respectively, for V1/2 and s of the Qoff(V) relationship in three such experiments were, at pH 7.4, −102.8 ± 1.4 mV and 11.4 ± 1.0 mV and, at pH 5.4, −75.3 ± 1.4 mV and 14.8 ± 1.1 mV. Thus, at pH 7.4, there was, following a depolarization that moved Qmax, a ≈107 mV leftward shift of the voltage dependence of return gating charge movement. A comparable leftward shift of ≈124 mV of the voltage dependence of gating charge movement was seen at pH 5.4.
DISCUSSION
The first series of experiments (Figs 1–4) described in this paper show that, as with Zn2+ ions, external protons cause a concentration-dependent and reversible inhibition of hKv1.5 currents. Although this effect is associated with a depolarizing shift of the activation (g(V)) curve, the two actions appear to be mechanistically unrelated. Both effects have been reported for rKv1.5 channels (Steidl & Yool, 1999) but we have extended the previous work by showing that external ions such as K+ and Cs+, but not Na+, are able to relieve the inhibition but not the gating shift caused by protons. In zero the apparent pKH of the protonation site is 6.8 and this decreases to 6.2 with 5 mm . The latter pKH accords well with the pKH of 6.2 for rKv1.5 responses recorded in 2 mm (Steidl & Yool, 1999) and the pKH of 6.1 in N-terminal-deleted ferret Kv1.4 with 3 mm (Claydon et al. 2000). The influence of on this inhibition of hKv1.5 currents was modelled as a non-competitive interaction between K+ and protons (Fig. 4) and the estimated KD for this antagonism by is very near that estimated for the Zn2+ block (Zhang et al. 2001b), i.e. KK = 0.5-1.0 mm. This implies that the same K+ binding site is involved in both cases and is perhaps homologous to the site (KD ≈ 0.75 mm) at which K+ binds to lock Ba2+ ions within the pore of Shaker B-channels (Harris et al. 1998). Binding sites with a similar affinity for K+ have also been shown to influence the availability of Shaker T449A channels (KD = 0.8 mm; Lopez-Barneo et al. 1993) and to competitively inhibit C-type inactivation in ShakerIR channels (KD = 1-2 mm; Baukrowitz & Yellen, 1996). Interestingly, the external lock-in site of Shaker B-channels, and the site at which K+ binds to antagonize the inhibitory actions of Zn2+ or in hKv1.5, also share the property of having a low affinity for Na+ ions.
One of two clear differences between the actions of and Zn2+ is that while the KD for the relief by of the Zn2+ block is roughly five-fold higher than that for (Zhang et al. 2001b), is as effective as in antagonizing the current inhibition by protons (Fig. 4). In the case of Zn2+ the higher KD for Cs+ was assumed to reflect the lower permeability of Cs+ in the pore. With it is conceivable that protonation of a negatively charged, cation-binding site decreases that site's negativity and alters the selectivity sequence to one favouring Cs+ binding (Hille, 1992). If so, the selectivity sequence of a binding site in the outer pore mouth must be involved since we have no evidence of a change of the reversal potential with extracellular acidification. The nH of ≈1.5 for the proton block suggests that at least two sites, most likely H463 residues in the tetrameric channel assembly, must be protonated. Although the nH for Zn2+ block is near unity (Zhang et al. 2001b) this might still involve co-ordinated binding of histidine residues of two or more subunits.
Evidence against a pore-blocking mechanism
The block of cardiac voltage-gated Na+ (NaV) channels by Zn2+ occurs by occlusion and is eliminated by the mutation of a cysteine residue in the pore (Backx et al. 1992). Similarly, the block by external protons of NaV channels in nerve and skeletal muscle has a voltage-dependence suggesting a site of action within the pore (Woodhull, 1973). It seems unlikely, however, that the inhibition of hKv1.5 current by and Zn2+ is due to pore block. First, in the voltage range where the open probability is maximal there is no indication of a voltage-dependent decline of the inhibition by Zn2+ (Zhang et al. 2001b) or , e.g. Fig. 1C, as would be expected were these ions binding at a pore site within the electric field. The latter observation is consistent, however, with an interaction with one or more H463 residues which, being in the channel's turret, are outside the electric field. It is well established that Zn2+ and H+ bind to histidine residues and we have shown directly that the H463Q substitution shifts the pKH measured in zero from 6.8 to approximately 5.4 (Fig. 6). The acid sensitivity that persists in this mutant and in hKv1.5 R487V (Fig. 8) is similar to that reported for Shaker (pKH ≈ 5.4) (Perez-Cornejo et al. 1998) and Kv1.2 channels (pKH ≈ 4.9; Ishii et al. 2001). Exactly where protons and Zn2+ act in these mutants is not known, but given their typical pKH values of 4-5, likely candidates are the aspartate residues in the outer pore mouth (see Introduction).
Since each of the H463s is approximately 14-16 Å from the central axis of the pore (Aiyar et al. 1995; Doyle et al. 1998) it is very unlikely that binding of either ion to H463 residues would directly occlude the permeation pathway since Zn2+ has an ionic radius of 0.74 Å and H+ is orders of magnitude smaller. Assuming that the site at which external K+ binds to antagonize the current inhibition by Zn2+ and is in the outer pore mouth, our observation that this interaction is best described by a non-competitive versus a competitive model of inhibition also argues against direct pore block as a mechanism of action of either cation. It appears therefore that protonation or ‘zincification’ of H463 residues indirectly leads to current inhibition. From this view of H463 as sensor arises the next question: what is the nature of the effector?
A connection between current inhibition and an inactivation process
Though it is clear from this study and that of rKv1.5 currents (Steidl & Yool, 1999) that inactivation is faster at acidic pHs, our simulation studies (not shown) indicate that this increased rate of inactivation cannot itself account for the reduction of gmax. Furthermore, although increasing can speed recovery from C-type inactivation of Kv1.3 currents (Levy & Deutsch, 1996), an explanation for the inhibition that involves a slowing of recovery from inactivation and an accumulation of inactivation can be rejected since a 2 min period without voltage pulsing has no effect on the degree of inhibition (Fig. 9). Nonetheless, a simple interpretation of the effect of (or ) on the reduction of gmax caused by or Zn2+ is that, by a ‘foot-in-the-door’ mechanism, acts as a competitive antagonist of a conformational change at the pore mouth that is believed to underlie inactivation. In this connection we think it is significant that a point mutation at a site (position 487; T449 in Shaker) that has been implicated in the regulation of inactivation (Lopez-Barneo et al. 1993) dramatically affects the proton block (Fig. 8). In the studies of mutant Shaker channels the terms ‘potentiation’/ ‘conductance collapse’ were used to describe the increase/decrease of gmax when was increased/decreased. It is likely that potentiation/ collapse in ShakerIR is analogous to block-relief/block in hKv1.5, but there are some differences. Foremost among these is that, in contrast to the Shaker mutants, in Kv1.5 the block (conductance collapse) is and pH sensitive. That is to say at pH 7.4 removing has little or no effect on wild-type hKv1.5 currents, whereas at pH 6.4 decreasing causes a substantial conductance decline. Additionally, although the tendency for the conductance of Shaker mutants to collapse in zero is strongly correlated with an accelerated inactivation rate, this does not extend to hKv1.5 where wild-type hKv1.5 is much more prone to block at pH 6.4 than is hKv1.5 R487V, even though both inactivate at approximately the same rate at pH 7.4 (Fedida et al. 1999). Nonetheless, the fact that current inhibition by is substantially reduced by increasing or by the R487V mutation implies that an inactivation process is involved. Additional insight into the possible basis for the proton block and, in particular, the role of C-type inactivation was provided by gating current results (Fig. 10).
External acidification and on-gating charge movement
Based on the data of Fig. 10 we can immediately exclude a mechanism of action in which protonation of H463 residues impedes on-gating charge movement and consequently prevents the opening of the activation gate since at pH 5.4 there is no significant reduction of Qmax. This is a second major distinction between the actions of and Zn2+. At a concentration that reduces gmax by more than 90 %, Zn2+ decreases Qmax by 10-15 % as though it were preventing the late, weakly voltage-dependent transitions in the activation pathway (Zhang et al. 2001a). However, even though Qmax is unchanged by extracellular acidification, we cannot rule out the possibility that opening of the activation gate becomes uncoupled from the outward movement of the voltage sensor. Interestingly, as with Zn2+ (Zhang et al. 2001a), the proton-induced depolarizing shift of V1/2 for the Qon(V) relationship is roughly two-fold greater than that measured from the g(V) relationship. We have attributed this differential effect on the g(V) and Q(V) curves to the presence of two distinct binding sites. In our view the protonation of an as yet unidentified site on the channel surface affects the movement of the voltage sensor and culminates in a rightward shift both of the g(V) and the Q(V) curves. The protonation of a second site, which is probably H463, has two direct or indirect effects: it decreases gmax and it causes a rightward shift of the voltage dependence of activation gating. The latter effect possibly reflects the close proximity of S4 and H463 in the S5-P loop (Loots & Isacoff, 2000). Since H463-protonated and therefore non-conducting channels can report the gating shift in gating current measurements, but not in ionic current measurements, the gating shift attributed to protonation of this second site is evident only in the Q(V) curve.
External acidification and off-gating charge movement
At pH 7.4 and pH 5.4 the mid-point of the Qoff(V) relationship was shifted leftward, relative to the corresponding Qon(V) curve, by 107 mV and 124 mV, respectively (Fig. 10).That this shift occurs at both pH values is significant because it has been attributed to a stabilization of S4s in the outward position by a conformational change linked to C-type inactivation (Olcese et al. 1997; Wang & Fedida, 2001). We take this to mean that at pH 5.4 channels are not C-type inactivated prior to a depolarizing pulse but are able to become so when sufficiently depolarized. In other words, at a low pH, wild-type hKv1.5 apparently behaves like the non-conducting mutant hKv1.5 W472F. That is to say, the gating shift notwithstanding, on- and off-gating charge movement is relatively normal but the channels are never or, at best, only very briefly in a conducting state. We speculate, as proposed for homotetrameric ShakerIR W434F (Yang et al. 1997), that in wild-type hKv1.5 protonation of, or Zn2+ binding to, H463s allows an inactivation process to occur, either from one or more of the closed states or at a greatly accelerated rate following the outward movement of the voltage sensor and channel opening. Since our data indicate that the transition to the C-type inactivated state is intact even at low pHs, this leaves P-type inactivation as a possible basis for the -induced current inhibition. Some support for this suggestion comes from a study of the ShakerIR FWFW mutant (Yang et al. 1997) where, as described for P-type inactivation (De Biasi et al. 1993), peak FWFW current was increased by external TEA+ and where there was also an enhancement of FWFW current when was increased. In a similar manner, in hKv1.5 the block-relief by would be due to the occupancy of a site, presumably near the outer pore, that inhibits P-type inactivation. The co-operativity factor, α, of eqn (4) would then be interpreted to mean that protonation of H463s, by virtue of a conformational change, inhibits the binding of K+ at its site, and vice versa.
This proposed scheme, which remains to be tested by single channel analysis, is at least functionally equivalent to closed-state inactivation proposed to account for the loss of current in ShakerIR T449 mutants (Lopez-Barneo et al. 1993), to the decrease of channel availability proposed for the current loss in zero in Kv1.4 (Pardo et al. 1992), and to the non-conducting ‘open’ state proposed for Kv1.3 (Jäger et al. 1998) and hKv1.5 (Wang et al. 2000) channels.
What is the connection between H463 and R487?
To reiterate, our view is that H463 acts as a sensor and R487 is a required component in the effector mechanism, e.g. inactivation. Concerning the nature of the coupling between H463 and R487, it has been proposed that the charge of H463 reduces the pKH of R487 by an electrostatic effect (Jäger & Grissmer, 2001). However, a number of our observations argue against such an electrostatic interaction. First, a strong, mutual electrostatic interaction between R487 and H463 would be expected to affect the pKH of H463. In this connection, a histidine residue substituted at the same position in the turret of Shaker channels (F425H) has a pKH of 6.4 in 2 mm (Perez-Cornejo et al. 1998), that is similar to that for wild-type hKv1.5 (pKH ≈ 6.2 in 5 mm , Fig. 3). This suggests that the pKH of a histidine in the turret is weakly influenced, if at all, by the nature of the residue apposed to it in the tertiary structure (Doyle et al. 1998), be it either charged as with R487 in hKv1.5, or polar and uncharged as with T449 in Shaker. This also implies that an effect of the R487V mutation on the binding equilibrium for H+ or Zn2+ at H463 does not account for the decreased sensitivity of hKv1.5 R487V currents to inhibition by either cation. Another argument against an electrostatic interaction between a protonated H463 and R487 is that the proposed shift of the pKH of R487 by ≈6 units would require that these two residues be in much closer apposition (Elinder et al. 2001) than the 8 Å (Cα to Cα) suggested by the crystal structure of KcsA (Doyle et al. 1998). We have also found, contrary to the expectation of an electrostatic mechanism, that increasing the Debye length by decreasing the ionic strength of the external solution does not substantially affect the block of wild-type hKv1.5 by Zn2+ (L. J. Minshall & S. J. Kehl, unpublished). On these grounds, an electrostatic interaction between protonated H463 and R487 seems unlikely, but the pH sensitivity of hKv1.5 R487H (Jäger & Grissmer, 2001) does imply that a positive charge near the pore mouth is necessary for the virtually complete suppression of outward current seen in zero .
An alternative view of the coupling between H463 and R487 is that, perhaps because of the change of its charge and a consequent increase of its hydrophilicity, the protonation of H463 permits a conformational change requiring R487. Although we have no direct evidence for such a conformational change, it is intriguing that studies of Kv2.1 have shown that the distribution of channels between two outer vestibule conformations is regulated by (Immke et al. 1999). Additionally, a lysine residue (K356) which is positively charged at neutral pH, and which is homologous in position and charge to a protonated H463 of hKv1.5, is crucial in this K+-dependent conformational change (Immke et al. 1999). The K356 residue is also involved in the enhancement of Kv2.1 currents by (Wood & Korn, 2001).
Inactivation and the influence of the charge on and size of the residue at position 463
Jäger & Grissmer (2001) recently reported, and we have confirmed here, that in the mutant hKv1.5 H463G the conductance collapses at pH 7.4 after switching to zero (Fig. 7). We also found that this mutant inactivates much faster than wild-type hKv1.5, which underscores the association in Shaker, noted above, between an increased inactivation rate and a tendency for the current to collapse in zero . The differences in the properties of wild-type hKv1.5 and the H463Q and H463G mutants also imply that both the charge on and the size of the residue at position 463 influence the structural rearrangement leading to a conductance collapse in zero . The importance of charge is evident in wild-type hKv1.5 at pH values where, when H463 residues are protonated, the conductance collapses in zero . An influence of the size of the residue at position 463 is suggested by different behaviours of the H463Q and H463G mutants. Thus, there is no conductance collapse in zero at pH 7.4 in hKv1.5 H463Q, where the substituted glutamine is uncharged, but polar, and occupies only a slightly smaller volume than histidine (≈150 Å3). In contrast, in the H463G mutant the uncharged but much smaller glycine residue (≈60 Å3) does allow the conductance to collapse in zero at pH 7.4. Additional indirect support for the idea that the size of the residue at this position in the turret affects inactivation comes from the report that substitution of glutamine for glycine at the homologous position in Kv1.3 (G380Q) slows inactivation roughly seven-fold (Nguyen et al. 1996).
Finally, the results of voltage clamp fluorimetry in Shaker suggest that, rather than being restricted to a structural collapse at the selectivity filter, slow inactivation may involve a co-ordinated movement extending to the outer rim (turret) of the pore (Loots & Isacoff, 2000). This is consistent with our results that in hKv1.5 both the charge on and the volume of the residue at position 463 in the turret influences a co-ordinated movement to an inactivated state.
Acknowledgments
This work was supported by a grant to S.J.K. from the Natural Sciences and Engineering Research Council and by grants to D.F. from the Canadian Institutes for Health Research and the Heart and Stroke Foundation (HSF) of British Columbia and Yukon. S.Z. was in receipt of a Research Fellowship from the HSF of Canada and D.C.H.K. was supported by a Trainee Award from the Michael Smith Foundation for Health Research. We thank Qin Wang who prepared the cells and Dr Simon Baudrexel who assisted with some of the experiments.
REFERENCES
- Aiyar J, Withka JM, Rizzi JP, Singleton DH, Andrews GC, Lin W, Boyd J, Hanson DC, Simon M, Dethlefs B. Topology of the pore-region of a K+ channel revealed by the NMR-derived structures of scorpion toxins. Neuron. 1995;15:1169–1181. doi: 10.1016/0896-6273(95)90104-3. [DOI] [PubMed] [Google Scholar]
- Backx PH, Yue DT, Lawrence JH, Marban E, Tomaselli GF. Molecular localization of an ion-binding site within the pore of mammalian sodium channels. Science. 1992;257:248–251. doi: 10.1126/science.1321496. [DOI] [PubMed] [Google Scholar]
- Baukrowitz T, Yellen G. Modulation of K+ current by frequency and external [K+]: A tale of two inactivation mechanisms. Neuron. 1995;15:951–960. doi: 10.1016/0896-6273(95)90185-x. [DOI] [PubMed] [Google Scholar]
- Baukrowitz T, Yellen G. Two functionally distinct subsites for the binding of internal blockers to the pore of voltage-activated K+ channels. Proceedings of the National Academy of Sciences of the USA. 1996;93:13 357–13 361. doi: 10.1073/pnas.93.23.13357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blaustein RO, Cole PA, Williams C, Miller C. Tethered blockers as molecular ‘tape measures’ for a voltage-gated K+ channel. Nature Structural Biology. 2000;7:309–311. doi: 10.1038/74076. [DOI] [PubMed] [Google Scholar]
- Cha A, Bezanilla F. Structural implications of fluorescence quenching in the Shaker K+ channel. Journal of General Physiology. 1998;112:391–408. doi: 10.1085/jgp.112.4.391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen FS, Steele D, Fedida D. Allosteric effects of permeating cations on gating currents during K+ channel deactivation. Journal of General Physiology. 1997;110:87–100. doi: 10.1085/jgp.110.2.87. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Claydon TW, Boyett MR, Sivaprasadarao A, Ishii K, Owen JM, O'Beirne HA, Leach R, Komukai K, Orchard CH. Inhibition of the K+ channel Kv1. 4 by acidosis: protonation of an extracellular histidine slows the recovery from N-type inactivation. Journal of Physiology. 2000;526:253–264. doi: 10.1111/j.1469-7793.2000.00253.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Biasi M, Hartmann HA, Drewe JA, Taglialatela M, Brown AM, Kirsch GE. Inactivation determined by a single site in K+ pores. Pflügers Archiv. 1993;422:354–363. doi: 10.1007/BF00374291. [DOI] [PubMed] [Google Scholar]
- Doyle DA, Morais CJ, Pfuetzner RA, Kuo A, Gulbis JM, Cohen SL, Chait BT, MacKinnon R. The structure of the potassium channel: molecular basis of K+ conduction and selectivity. Science. 1998;280:69–77. doi: 10.1126/science.280.5360.69. [DOI] [PubMed] [Google Scholar]
- Elinder F, Mannikko R, Larsson HP. S4 charges move close to residues in the pore domain during activation in a K channel. Journal of General Physiology. 2001;118:1–10. doi: 10.1085/jgp.118.1.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fedida D, Maruoka ND, Lin S. Modulation of slow inactivation in human cardiac Kv1. 5 channels by extra- and intracellular permeant cations. Journal of Physiology. 1999;515:315–329. doi: 10.1111/j.1469-7793.1999.315ac.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frankenhaeuser B, Hodgkin AL. The action of calcium on the electrical properties of squid axons. Journal of Physiology. 1957;137:218–244. doi: 10.1113/jphysiol.1957.sp005808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris RE, Larsson HP, Isacoff EY. A permanent ion binding site located between two gates of the Shaker K+ channel. Biophysical Journal. 1998;74:1808–1820. doi: 10.1016/s0006-3495(98)77891-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hesketh JC, Fedida D. Sequential gating in the human heart K+ channel incorporates Q1 and Q2 charge components. American Journal of Physiology. 1999;277:H1956–1966. doi: 10.1152/ajpheart.1999.277.5.H1956. [DOI] [PubMed] [Google Scholar]
- Hille B. Ionic Channels of Excitable Membranes. Sunderland, MA, USA: Sinauer Associates; 1992. [Google Scholar]
- Hoshi T, Zagotta WN, Aldrich RW. Two types of inactivation in Shaker K+ channels: Effects of alterations in the carboxy-terminal region. Neuron. 1991;7:547–556. doi: 10.1016/0896-6273(91)90367-9. [DOI] [PubMed] [Google Scholar]
- Immke D, Wood M, Kiss L, Korn SJ. Potassium-dependent changes in the conformation of the Kv2. 1 potassium channel pore. Journal of General Physiology. 1999;113:819–836. doi: 10.1085/jgp.113.6.819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ishii K, Nunoki K, Yamagishi T, Okada H, Taira N. Differential sensitivity of Kv1. 4, Kv1.2, and their tandem channel to acidic pH: involvement of a histidine residue in high sensitivity to acidic pH. Journal of Pharmacology and Experimental Therapeutics. 2001;296:405–411. [PubMed] [Google Scholar]
- Jäger H, Grissmer S. Regulation of a mammalian Shaker-related potassium channel, hKv1. 5, by extracellular potassium and pH. FEBS Letters. 2001;488:45–50. doi: 10.1016/s0014-5793(00)02396-6. [DOI] [PubMed] [Google Scholar]
- Jäger H, Rauer H, Nguyen AN, Aiyar J, Chandy KG, Grissmer S. Regulation of mammalian Shaker-related K+ channels: evidence for non-conducting closed and non-conducting inactivated states. Journal of Physiology. 1998;506:291–301. doi: 10.1111/j.1469-7793.1998.291bw.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiss L, Loturco J, Korn SJ. Contribution of the selectivity filter to inactivation in potassium channels. Biophysical Journal. 1999;76:253–263. doi: 10.1016/S0006-3495(99)77194-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larsson HP, Elinder F. A conserved glutamate is important for slow inactivation in K+ channels. Neuron. 2000;27:573–583. doi: 10.1016/s0896-6273(00)00067-2. [DOI] [PubMed] [Google Scholar]
- Levy DI, Deutsch C. Recovery from C-type inactivation is modulated by extracellular potassium. Biophysical Journal. 1996;70:798–805. doi: 10.1016/S0006-3495(96)79619-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li-Smerin Y, Hackos DH, Swartz KJ. A localized interaction surface for voltage-sensing domains on the pore domain of a K+ channel. Neuron. 2000;25:411–423. doi: 10.1016/s0896-6273(00)80904-6. [DOI] [PubMed] [Google Scholar]
- Loots E, Isacoff EY. Protein rearrangements underlying slow inactivation of the Shaker K+ channel. Journal of General Physiology. 1998;112:377–389. doi: 10.1085/jgp.112.4.377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loots E, Isacoff EY. Molecular coupling of S4 to a K+ channel's slow inactivation gate. Journal of General Physiology. 2000;116:623–636. doi: 10.1085/jgp.116.5.623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lopez-Barneo J, Hoshi T, Heinemann SH, Aldrich RW. Effects of external cations and mutations in the pore region on C-type inactivation of Shaker potassium channels. Receptors and Channels. 1993;1:61–71. [PubMed] [Google Scholar]
- Nguyen A, Kath JC, Hanson DC, Biggers MS, Canniff PC, Donovan CB, Mather RJ, Bruns MJ, Rauer H, Aiyar J, Lepple-wienhues A, Gutman GA, Grissmer S, Cahalan MD, Chandy KG. Novel nonpeptide agents potently block the C-type inactivated conformation of Kv1. 3 and suppress T cell activation. Molecular Pharmacology. 1996;50:1672–1679. [PubMed] [Google Scholar]
- Olcese R, Latorre R, Toro L, Bezanilla F, Stefani E. Correlation between charge movement and ionic current during slow inactivation in Shaker K+ channels. Journal of General Physiology. 1997;110:579–589. doi: 10.1085/jgp.110.5.579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ortega-Saenz P, Pardal R, Castellano A, Lopez-Barneo J. Collapse of conductance is prevented by a glutamate residue conserved in voltage-dependent K+ channels. Journal of General Physiology. 2000;116:181–190. doi: 10.1085/jgp.116.2.181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pardo LA, Heinemann SH, Terlau H, Ludewig U, Lorra C, Pongs O, Stühmer W. Extracellular K+ specifically modulates a rat brain K+ channel. Proceedings of the National Academy of Sciences of the USA. 1992;89:2466–2470. doi: 10.1073/pnas.89.6.2466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perez-Cornejo P, Stampe P, Begenisich T. Proton probing of the charybdotoxin binding site of Shaker K+ channels. Journal of General Physiology. 1998;111:441–450. doi: 10.1085/jgp.111.3.441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steidl JV, Yool AJ. Differential sensitivity of voltage-gated potassium channels Kv1. 5 and Kv1.2 to acidic pH and molecular identification of pH sensor. Molecular Pharmacology. 1999;55:812–820. [PubMed] [Google Scholar]
- Vallee BL, Auld DS. Zinc coordination, function, and structure of zinc enzymes and other proteins. Biochemistry. 1990;29:5647–5659. doi: 10.1021/bi00476a001. [DOI] [PubMed] [Google Scholar]
- Wang Z, Fedida D. Gating charge immobilization is caused by the transition between inactivated states in the Kv1. 5 channel. Biophysical Journal. 2001;81:2614–2627. doi: 10.1016/S0006-3495(01)75905-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Z, Zhang X, Fedida D. Regulation of transient Na+ conductance by intra- and extracellular K+ in the human delayed rectifier K+ channel Kv1. 5. Journal of Physiology. 2000;523:575–591. doi: 10.1111/j.1469-7793.2000.00575.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wood MJ, Korn SJ. Two mechanisms of K+-dependent potentiation in Kv2. 1 potassium channels. Biophysical Journal. 2001;79:2535–2546. doi: 10.1016/S0006-3495(00)76494-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woodhull AM. Ionic blockage of sodium channels in nerve. Journal of General Physiology. 1973;61:687–708. doi: 10.1085/jgp.61.6.687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Y, Yan Y, Sigworth FJ. How does the W434F mutation block current in Shaker potassium channels? Journal of General Physiology. 1997;109:779–789. doi: 10.1085/jgp.109.6.779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yellen G. Single channel seeks permeant ion for brief but intimate relationship. Journal of General Physiology. 1997;110:83–85. doi: 10.1085/jgp.110.2.83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang S, Kehl SJ, Fedida D. Modulation of Kv1. 5 potassium channel gating by extracellular zinc. Biophysical Journal. 2001a;81:125–136. doi: 10.1016/S0006-3495(01)75686-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang S, Kwan DCH, Fedida D, Kehl SJ. External K+ relieves the block but not the gating shift caused by Zn2+ in human Kv1. 5 potassium channels. Journal of Physiology. 2001b;532:349–358. doi: 10.1111/j.1469-7793.2001.0349f.x. [DOI] [PMC free article] [PubMed] [Google Scholar]


