Abstract
During precision grip, coherence between motor cortex and hand muscle EMG oscillatory activity in the 15-30 Hz range covaries with the compliance of the manipulated object. The current study investigated whether short-term synchrony and coherence between discharges of single motor units (SMUs) in the first dorsal interosseous (1DI) muscle were similarly modulated by object compliance during precision grip. Eight subjects used index finger and thumb to grip two levers that were under robotic control. Guided by visual feedback of the lever force levels, subjects held the levers against a steady force of 1.3 N for 8 s; they then linearly increased the force to 1.6 N over a 2 s period and held for a further 8 s before linearly decreasing the force back to the 1.3 N level over another 2 s period. Subjects performed the task at two different levels of compliance, each with identical grip force levels. Both surface EMG and SMU activity were recorded from the 1DI muscle. Short-term synchrony between the discharges of pairs of SMUs was assessed in the time domain by cross-correlation and in the frequency domain by coherence analysis. Coherence was seen in two frequency ranges: 6-12 Hz and 15-30 Hz. The compliance of the gripped object had a significant effect on both short-term synchronisation and coherence in the 15-30 Hz range between SMUs; both were greater for the more compliant condition. There was no change in the 6-12 Hz coherence.
A number of recent reports have investigated the possible function of synchronous oscillatory synchrony within the sensorimotor cortex of monkeys and humans (Murthy & Fetz, 1992, 1996; Sanes & Donoghue, 1993; Stancak & Pfurtscheller, 1996; Baker et al. 1997; Donoghue et al. 1998). These oscillations can be detected in global measures of cortical activity, including magnetoencephalography (MEG) and EEG in humans, and local field potential (LFP) in monkeys; the dominant characteristic frequency of these oscillations is in the beta range of 15-30 Hz, and they are thought to arise from the synchronous discharge of large numbers of cortical neurones. There are clear task-dependent changes in such 15-30 Hz oscillations, with oscillatory activity disappearing during a finger movement, but reappearing following movement completion (Jasper & Penfield, 1949; Gastaut, 1952; Salmelin & Hari, 1994; Stancak & Pfurtscheller, 1996; Baker et al. 1997).
At least a part of the sensorimotor oscillatory activity is known to influence the descending motor command to the upper limb. Cortical activity in the 15-30 Hz range has been shown to be coherent with oscillatory EMG activity in contralateral hand and forearm muscles (Murthy & Fetz, 1992; Conway et al. 1995; Baker et al. 1997; Salenius et al. 1997; Hari & Salenius, 1999; Kilner et al. 1999, 2000). This direct coupling of cortical oscillations with muscular output provides a useful method of assessing any functional significance of the oscillatory activity. Thus, cortico-muscular coherence established during prehensile actions has also been shown to vary in a task-dependent manner. It was most prominent during the steady hold period of the precision grip task, but was abolished during digit movement (Baker et al. 1997; Kilner et al. 1999, 2000; Feige et al. 2000). Coherence was shown to be largest when a steady hold period immediately followed movement, and covaried positively with the compliance of the object being gripped; it was smallest during isometric grip of a solid object (Kilner et al. 2000). This raised the possibility that 15-30 Hz cortico-muscular coherence may encode the ‘motor set’ needed to maintain steady grip of compliant objects; such tasks require precise co-ordination of both grip force and aperture (Johansson, 1996).
A number of earlier studies have implicated oscillatory drive from the cortex as a source of synchrony between discharges of single motor units (SMUs) recorded from human hand muscles (Milner-Brown et al. 1975; Datta & Stephens, 1990; Datta et al. 1991; Bremner et al. 1991a; Farmer et al. 1993; Marsden et al. 1999). In general, these studies have investigated synchrony and coherence between pairs of SMUs recruited during gentle isometric contractions. Farmer et al. (1993) showed that there is a strong positive correlation between the magnitude of short-term synchrony between two SMUs recorded from the same muscle and the degree of coherence between the same SMUs in both the 6-12 Hz and 15-30 Hz bandwidths.
The aims of the current study were twofold: firstly, we wanted to investigate the nature of the 15-30 Hz oscillatory activity present in hand muscle EMG during the precision grip task. In particular, we wanted to see if this activity is present in the discharges of individual SMUs or whether it arises as a result of the population of SMUs that contribute to the surface EMG signal. Secondly, to understand the possible function of such synchrony, we hypothesised that if the degree of cortico-muscular coherence at 15-30 Hz reflects the motor commands required to grip objects of different compliance, then the short-term synchrony and coherence between SMUs in 1DI should be similarly modulated by object compliance. To investigate this, we recorded SMU pairs during the precision grip task performed under two different compliant conditions and then measured the amount of synchrony between them.
METHODS
Subjects
The data in this study was collected from eight subjects (five male) aged 22-56 and all right handed by self report. All subjects gave informed consent and the study had local ethical committee approval. The experiments were in concordance with the Declaration of Helsinki.
Behavioural task
The precision grip task was similar to that used in previous studies (Kilner et al. 1999, 2000). The manipulandum consisted of two short metal levers mounted on the shafts of two DC motors. The force produced by each motor was a function of the position of each lever. The manipulandum was mounted on a table in front of the subject, who gripped the levers with the tips of the right thumb and index finger such that the finger and thumb were perpendicular to the table; the forearm was supported in the fully pronated position. The ulnar digits were flexed out of the way. Subjects were instructed to relax their left arm and hand during task performance. Visual feedback of the forces exerted on each lever was given by square cursors displayed on a VDU screen at eye level. Subjects were given instructions to exert forces on the thumb and index finger levers by means of two target boxes displayed on the screen. Subjects were instructed to keep the cursors inside the respective target boxes at all times.
In these experiments subjects gripped each lever with a gentle force (1.3 N) for 8 s (Fig. 2A, ‘HOLD 1’); they then tracked a linear increase of the force to 1.6 N over a 2 s period (‘ramp’), followed by a further hold at this force level for 8 s (‘HOLD 2’), before they then tracked a linear decrease of the force back to the 1.3 N force level over a 2 s period. This format of the task was chosen to avoid any rapid movements associated with initial grip or release of the levers that would destabilise SMU recordings; the 8 s hold period was used so as to be long enough for an adequate sample of SMU discharges, but short enough so avoid any decrease in coherence as has been seen during very long hold periods (Kilner et al. 2000). Finally, a two-step task was used to increase the likelihood of oscillatory activity in the 15-30 Hz range, as our previous studies have shown that EMG-EMG coherence was always greatest for a steady hold after a ramp movement (Kilner et al. 1999, 2000).
Figure 2. Modulation of a single motor unit discharge by task conditions.
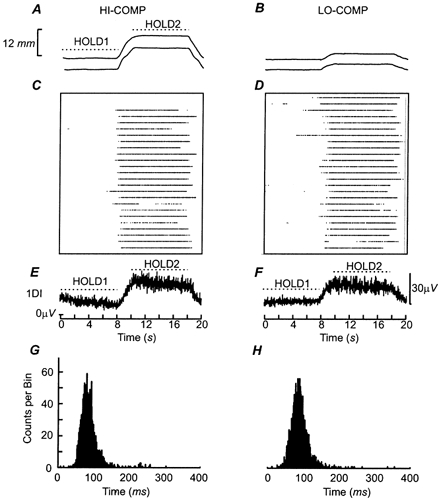
A and B, the position of the finger (upper trace) and thumb levers during precision grip task performance under the most compliant (HI-COMP) and least compliant (LO-COMP) conditions, averaged across 25 trials. The scale of the lever displacement at the tip of the digit is shown to on the left. C and D, the firing of a single motor unit (SMU) under the two task conditions. Each point represents a discriminated discharge from the SMU. Data are aligned to the onset of the first hold period. Trial number increases from the bottom up. E and F, the average rectified EMGs of the 1DI muscle recorded during the task conditions. G and H, the interspike interval histogram (ISIH) calculated across the entire task for the single motor units shown in C and D. The ISIH were calculated between 0 and 400 ms and had a binwidth of 1 ms.
Task conditions
Two task conditions were tested, HI-COMP and LO-COMP. In both of them, the motors opposed the subject's applied forces with a compliant or spring-like load but with different spring constants. These spring constants were identical to COMP1 and COMP3 tasks as described in Kilner et al. (2000). When the levers were most compliant (HI-COMP condition), a displacement of ≈12 mm was required to reach the high force target; the stiffer spring condition (LO-COMP) required a smaller displacement of ≈4 mm (Fig. 2A and B). The tasks were aligned to the onset of the increasing ramp period, producing a trial of 20 s and each trial was repeated 25 times. The order of presentation of the task conditions was randomised between subjects.
Recordings
Surface EMG from the 1DI muscle of the right hand was recorded with bipolar electrodes, with one electrode over the metacarpophalangeal joint of the index finger and the other over the belly of the muscle. Single motor unit (SMU) activity was recorded from the same muscle using custom-made bipolar intramuscular needle electrodes specially designed to maintain optimal recording stability and selectivity (Bawa & Lemon, 1993). These electrodes consisted of a pair of 50 μM diameter, insulated, stainless-steel wires (California Fine Wire Company Ltd, USA) embedded in a 25 gauge sterile hypodermic needle (Becton Dickinson, Ireland) filled with epoxy resin glue (Agar Scientific Ltd, UK). Electrodes had an impedance at 1 kHz of 0.8-1 MΩ between the two wires. Two needle electrodes were inserted about 1-1.5 cm apart and each needle positioned in the muscle so as to obtain recordings from at least one SMU that discharged steadily at the force level required by the task. Subjects received some audio feedback of the SMU recordings, and were asked to maintain a similar level of discharge throughout the different trials performed; subjects were not asked to fire a particular unit at any specified rate or modulate its firing in any particular way. The experimenter tracked a minimum of two SMUs through the recording session, monitoring their general waveform, interspike interval histogram and task-related pattern of activity. In addition, subjects were asked to minimise any extraneous hand and finger movements so as not to destabilise the recordings. Nevertheless, we have no independent proof that the same group of SMUs were sampled throughout the recording period, but this does not, in fact, materially affect our results (see Results and Discussion).
Both SMU and surface EMG activity were amplified (gain 1-10 K); SMU discharges were high-pass filtered at 30 Hz and then sampled at 20.83 kHz. EMG was high-pass filtered at 30 Hz, and then sampled at 2.083 kHz by a personal computer fitted with a 1401+ interface (CED Ltd, Cambridge), together with finger and thumb lever positions and markers indicating task events.
Analysis
Off-line SMU activity was discriminated from the needle electrode channels using custom-written software (Getspike, Dr S. N. Baker, Anatomy Department, University of Cambridge, UK). This software used principal component analysis to discriminate SMU discharges that crossed a set threshold level. The discriminated events were considered to derive from a single motor unit if there were no or very few counts at spuriously short intervals (< 10 ms) in the interspike interval histogram (ISIH) and if the shape of the motor unit was constant throughout the recording session. The resultant discriminated data was written at a sampling rate of 200 kHz (but with the resolution limited by the recording sampling rate) at the time the leading edge of the motor unit potential crossed a threshold level for each unit discriminated. Using this software, SMUs could be reliably discriminated and in many cases it was possible to discriminate discharges of more than one SMU on the same needle electrode. Prior to any further analysis, the resolution of the spike events was reduced to 1 ms, with, therefore, an effective sampling rate of 1 kHz.
Off-line finger and thumb lever position signals were examined by eye; trials in which subjects did not perform the task correctly were rejected (13.5 %). Before further analysis, the EMG was rectified and then both the rectified EMG and lever position channels were low passed filtered at 100 Hz and subsequently downsampled to an effective sampling rate of 200 Hz.
Selection criteria for SMUs
Of the eight subjects who participated in the experiments, the data for three were excluded from any SMU analysis because no more than one SMU could be reliably discriminated from both needle electrode channels in each task condition. The remaining five subjects had at least two motor units discriminated for each task condition with a minimum of 500 spikes discriminated during the HOLD1 and HOLD2 periods. To ensure that no erroneous measures of synchrony or coherence were included in the study, strict selection criteria were applied to these discriminated SMUs. Fifteen were rejected for having too few spikes (< 500). The maximum number of SMUs discriminated for a given task condition (HI-COMP or LO-COMP) was 6 with a mean of 3.8. Across both task conditions, 40 discriminated units were accepted for further analysis, with 20 units for HI-COMP and 20 units for LO-COMP. In many cases it is probable that the same SMU was sampled for both HI-COMP and LO-COMP conditions (similar waveform and discharge rate during the task) but because we could not be certain that an identical SMU was sampled during both conditions we have treated them as two separate populations. Half of the accepted sample of SMUs were recorded from different electrodes and the rest from the same electrode.
Time domain analysis
Synchronisation between discharges of pairs of simultaneously recorded SMUs was assessed by computing a cross-intensity function, the cross-correlogram, 150 ms pre-and post-trigger with a 1 ms bin width. The mean and standard deviation of the background activity was calculated from all bins excluding a section 10 ms either side of the central peak. Central peaks were considered significant if they exceeded the background mean level by more than two standard deviations for three consecutive bins. The magnitude of synchrony was assessed using two measures, the ‘k’ and the ‘b’ values. The ‘k’ value was equal to the maximum number of counts in the largest single bin divided by the mean background level (Kirkwood, 1979; Bremner et al. 1991a). The ‘b’ value was calculated from the cusum, the cumulative sum of the difference between the mean background level and the cross-correlogram (Ellaway, 1978). Central peaks in the cross-correlogram larger than the mean background level were represented as clear positive deflections in the cusum. The onset, t1, and offset, t2, of these deflections were assessed by eye. The duration of the central peak was calculated as t2-t1. The degree of synchronisation ‘b’ was equal to the area of the peak above the background level, e, divided by the sum of the response spikes, E, and reference spikes, T, i.e. b = e/(E + T) (Bremner et al. 1991a). This equation assumes that both the response and reference units were firing at all times throughout the time when e was calculated, as the area e is normalised by the sum of the response spikes and the reference spikes. Therefore, care was taken in selecting periods in the task where both units were discharging so as not to distort the measure of ‘b’.
Spectral analysis
Power spectra were calculated for each discriminated SMU, and coherence spectra were calculated between pairs of simultaneously recorded SMUs. Power spectra for the 1DI surface EMG were also calculated (Rosenberg et al. 1989). The downsampled and rectified surface EMGs were analysed using a 256 point fast Fourier transform (FFT) window, permitting a maximum frequency resolution of 0.76 Hz. 1DI power spectra were calculated from six consecutive 256 point disjoint sections (1536 points), from each HOLD period, aligned to the onset of each HOLD.
Coherence between single motor units
Prior to spectral analysis, the SMU event channels were converted to a binary waveform, with a 1 at the time of each event, and therefore with an effective sampling rate of 1 kHz. Each of these motor unit channels was low pass filtered at 100 Hz before spectral analysis to ensure no artefacts arose due to aliasing. Spectral analysis was performed on six disjoint 1024 points sections of data from each hold period where there were at least 10 events for each unit. The 1024 point FFT permitted a frequency resolution of 0.976 Hz (Rosenberg et al. 1989). Peaks in coherence spectra were only considered significant when three consecutive frequency bins were greater than the significance level (P < 0.05) (Marsden et al. 1999).
RESULTS
The level of synchrony in 1DI muscle showing 20 Hz oscillatory activity
The approach adopted in the current study allowed us to record discharges of small populations of single motor units during natural finger movements. Most of the SMUs had large signal-to-noise ratios and these units were reliably discriminated. However, inspection of the overall EMG activity during the task made it clear that the general level of synchrony prevented us from determining the contribution of SMUs with smaller signal-to-noise ratios. This is illustrated in Fig. 1, which shows a section of raw surface EMG data together with the recording from one of the needle electrode channels during the HOLD2 of the HI-COMP task (subject JL). The arrows on the needle channels indicate the event times of the different discriminated units (SMU 1, black arrows; SMU 2, dark grey arrows; SMU 3, light grey arrows). The open arrows show the time at which one would expect SMU 1 to have discharged given this unit's previous steady firing rate. No unit was discriminated at these times, because at least two other units were firing synchronously, and the waveforms were mixed in the needle electrode recording. Interestingly, this period of exactly synchronous firing of the units was reflected in the surface EMG recording as a large burst of activity (Fig. 1A). It is clear that when many active units are firing synchronously it seriously compromises the discrimination process. This is demonstrated in the ISIH of SMU 1 (Fig. 1B). Although the ISIH is dominated by a large peak around 80 ms, corresponding to the steady firing of the motor unit, the ISIH shows a second sub-peak at half the firing rate, which reflects events that have not been successfully discriminated. Motor units such as SMU 1 could not be included in our analysis.
Figure 1. Synchronous bursting of 1DI SMUs during precision grip.
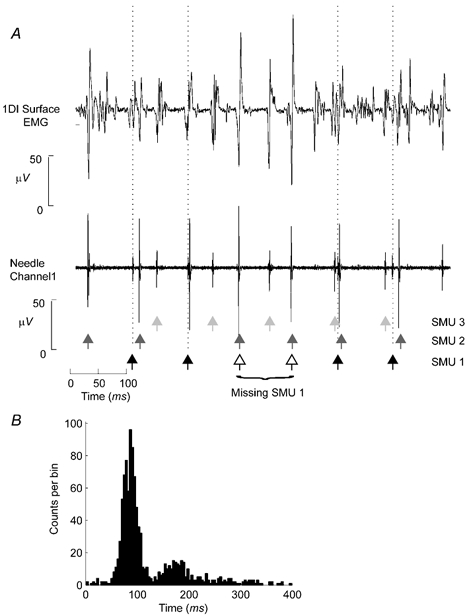
A, top panel, a section of surface EMG activity from the 1DI muscle during the HOLD2 period of the task. The bottom panel shows the corresponding section of one of the raw needle electrode channels. The dashed vertical lines indicate the time of discrimination for one of the SMUs discriminated from this electrode. The time of discharge of this SMU is also indicated by the black arrows. The dark and light grey arrows show the times of discrimination of two other discriminated SMUs. The open arrows show the time that would have been expected for discrimination of SMU1 based on its average firing rate over the entire task. For this section of data SMU1 would have been expected to fire twice. B, the ISIH for the unit identified by the black arrows in A. Note that there is a clear peak around intervals of ≈80 ms, reflecting the firing rate of the unit at 11 Hz, but also a sub-peak around 180 ms (5.5 Hz) as a result of missed units in the discrimination process, as shown by the open arrows in A.
Single subject data during the two different task conditions
Figure 2 shows the data for a single subject (JL) performing the task under the two different conditions tested. Figure 2C and D shows the raster plots for a single motor unit recorded during each of these tasks. The motor unit shown was only recruited during the second hold period of the task at the higher force level. The averaged rectified surface EMG recordings are plotted in Fig. 2E and F and show that overall muscle activity of the 1DI muscle mirrored the force requirements, being greater during the second hold period than the first hold period (Fig. 2A and B). Importantly, there were no clear changes in the overall 1DI EMG activity under the two task conditions, HI-COMP and LO-COMP, reflecting the identical force requirements of the conditions tested (see Methods).
Figure 2G–H shows the ISIH for discharges during the entire task for the two motor units shown in panels C and D. Each unit had a broad peak in the ISIH, ranging from 50-120 ms. Furthermore, for the units shown there were no clear sub-peaks at ≈180 ms that would correspond to the failure to discriminate all spikes correctly.
Single motor unit firing rates
Across the population of units recorded in all subjects and accepted for analysis, less than 2 % of events had an interspike interval (ISI) of less than 10 ms, indicating excellent discrimination. Only 7.6 % had an ISI between 33 and 66 ms (corresponding to firing at 15-30 Hz). The majority of intervals, 68.7 %, were in the 66-120 ms range (8-13 Hz). Figure 3A and B shows the mean firing rates of all accepted units during the HOLD 1 and HOLD 2 periods of the two task conditions. Figure 3A shows the mean of the mean firing rate whereas Fig. 3B shows the mean of the modal firing rate, both calculated from the ISIH. Both measures showed the same pattern of modulation across the task and across task conditions. For both conditions the firing rate was significantly faster during the higher force hold period (HOLD 2) than during the lower force hold (HOLD 1; P < 0.05 comparisons of two means). Note that changing the lever compliance did not result in a significant difference in firing rates for either hold period (P > 0.05 comparisons of two means).
Figure 3. Properties of motor unit discharge under different task conditions.
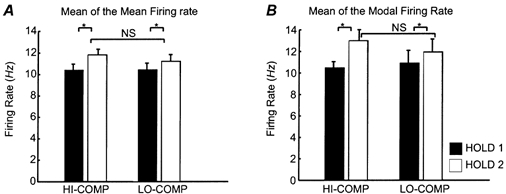
A, the mean of the mean firing rate of the analysed SMUs calculated from the ISIH for the first and second hold periods of the task for SMUs with more than 500 events per period. Error bars are s.e.m.s (n = 12 HI-COMP HOLD 1, n = 19 HI-COMP HOLD 2, n = 13 LO-COMP HOLD 1 and n = 20 LO-COMP HOLD 2). B, the same data using the mean of the modal firing rate calculated from the ISIH.
Synchrony between motor units
In order to make a quantitative comparison of the synchrony between pairs of SMUs, analysis was performed on events combined over the first hold period (0-8 s) and second hold period (10-18 s). These periods are indicated by the dashed horizontal lines in Fig. 2E and F. Figure 4 shows the cross-correlograms for a single subject (JL), constructed from the spike trains of the three 1DI motor units pooled across both hold periods of the HI-COMP task. Figure 4A-C show the cross-correlograms calculated with ± 150 ms window, while Fig. 4D-F show the same data up to a ± 50 ms lag. All cross-correlograms were dominated by a peak at zero-lag. Although this was more pronounced in the cross-correlograms constructed for SMU 1-SMU 2 (Fig. 4A, D) and SMU 1-SMU 3 (Fig. 4B, E), there was still a clear peak in the cross-correlogram for SMU 2-SMU 3 (Fig. 4C, F) but this was not significant.
Figure 4. Motor unit synchronisation: single subject data.
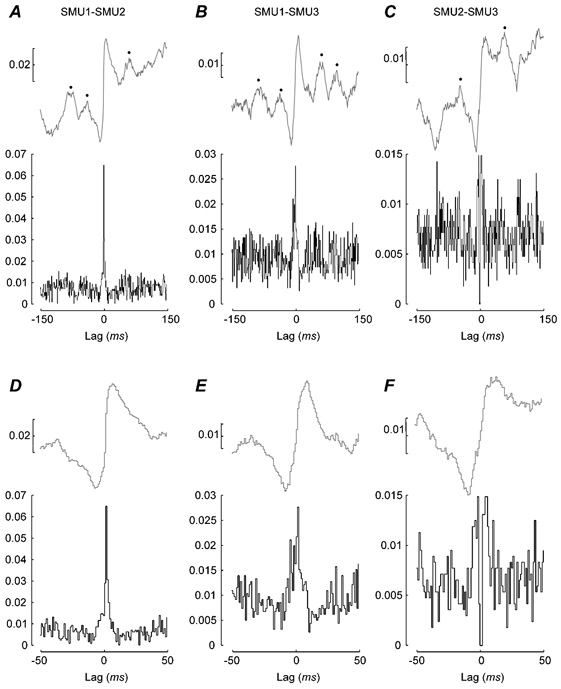
A-F, the synchrony measured in the time domain between three different units recorded from the right 1DI muscle during the HI-COMP task (subject JL). The data shown were pooled across both hold periods. A-C, the cross-correlations with a lag of 150 ms. D-F, the same data but only plotting the central 100 ms. A and D, the correlation between SMU1 and SMU2; B and E, the correlation between SMU1 and SMU3; and C and F, the correlation between SMU2 and SMU3. The black lines show the cross-correlograms calculated with a 1 ms resolution and the grey lines show the cusum. The ordinate on the cross-correlograms is the ratio of synchronous events to the total number of reference events. The scale of the cusum is the value ‘b’ (see Methods). Number of trials 25; number of events: n = 2038 for SMU1; 1314 for SMU2 and 1627 for SMU3.
In Fig. 4 the corresponding cusums are shown above the cross-correlograms. As well as showing a clear central peak in cross-correlograms and a large positive inflection in the cusums, the data shown in Fig. 4A-C also have marked sub-peaks at lags of approximately ± 50 ms. These were present, although more difficult to discern, in the cross-correlograms, but were clearly detectable in the cusums (indicated by •). The clearest example is that for the SMU 1-SMU 3 correlation (see Fig. 4B). These side peaks reflect an increase in the probability that the two units fire with defined lags and could arise due to a common periodic oscillatory drive. The side peaks in Fig. 4B reflect such oscillatory synchrony between the units at a frequency of approximately ≈20 Hz.
Figure 5 shows the data collected across all motor-unit pairs and across subjects. Figure 5A–B and C-F show results collected from the cross-correlation and cusum analysis, respectively. All subjects had at least one significantly synchronous motor unit pair in both task conditions. There was a slightly higher percentage of cross-correlograms showing a significant central peak (‘k’ value) in the HI-COMP (more compliant) compared with the LO-COMP (less compliant) condition (compare open and black bars Fig. 5A) and this was also reflected in the percentage of cusums with a clear central positive deflection (compare open and black bars Fig. 5C). However, these modest changes in the percentages were not significant (P > 0.05, χ-squared test). Across task conditions the percentage of cusums with a clear positive deflection was consistently greater than the percentage of significant central peaks in the cross-correlations (P < 0.05, χ-squared test) reflecting the ease of identifying positive deflections in the cusums (compare Fig. 5A and C).
Figure 5. Motor unit synchronisation: pooled subject data.
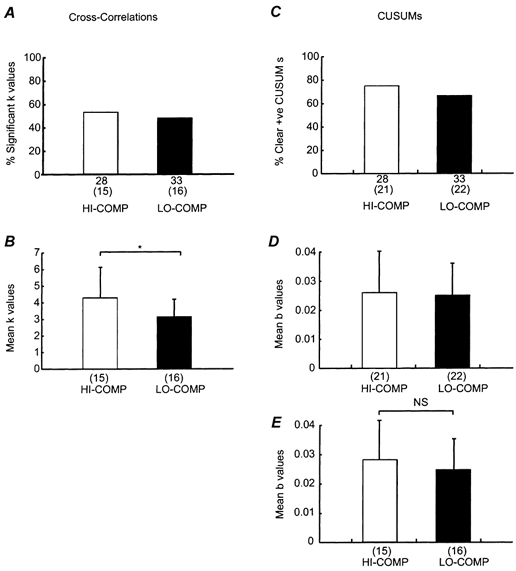
A and B, the cross-correlation data and (C-E) the cusum data for motor unit pairs from all five subjects analysed. A, the percentage of significant ‘k’ values for the HI-COMP (open bars) and LO-COMP (black bars). The total number of motor unit pairs is shown under each column, with the number significant shown in brackets. C, the corresponding data for the percentage of clear positive peaks in the cusum. B, the mean ‘k’ value for the two different task conditions. D shows the mean cusum ‘b’ value from all correlations with a clear positive deflection whereas in E the mean cusum ‘b’ value from correlations with significant ‘k’ values only are shown. The n number is shown under each column. Standard error bars are shown where possible. *= significant difference, P < 0.05 Mann-Whitney, NS = non-significant difference.
Figure 5B shows that the magnitude of the synchrony measured by the ‘k’ value was significantly higher for the more compliant condition (HI-COMP) (P < 0.05, Mann- Whitney U test). This difference was not paralleled in the ‘b’ value from the cusum measurements (Fig. 5D). A higher value of the mean ‘b’ value was observed for the HI-COMP condition compared with LO-COMP when only those SMU pairs with a significant ‘k’ value were considered (Fig. 5E), but this difference was not significant.
Coherence between spike trains of single motor units
Figure 6A-C (continuous lines) show the power spectra for the discharge of three 1DI SMUs recorded over both hold periods from subject JL under HI-COMP conditions. Figure 6D-F (continuous lines) plots the coherence between the activity of these three units; the dashed horizontal black line indicates the 95 % confidence interval for each coherence spectrum. The power spectrum of the rectified 1DI surface EMG recording (dotted trace) has been plotted in the background of all the plots in Fig. 6. The power spectra for all three motor units were dominated by a large peak at ≈12 Hz. This corresponded to the mean firing rate of the motor units as calculated from the ISIH. The power spectra for some units also showed a smaller but discernible peak in the 15-30 Hz range (see for example SMU 3 in Fig. 6C). Interestingly, neither the peak at ≈12 Hz nor the peak at ≈20 Hz in the power spectra of the single motor units corresponded to the peak in the power spectrum of the 1DI surface EMG (compare dotted and continuous traces in Fig. 6A-C).
Figure 6. Single subject data: power and coherence spectra during the HI-COMP task.
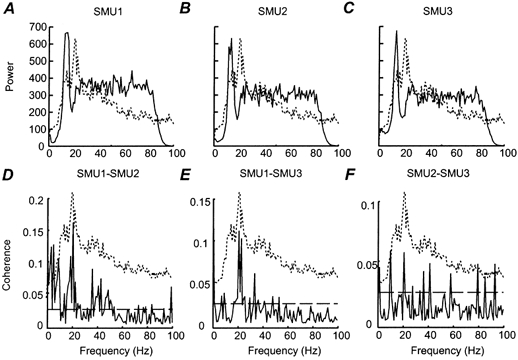
A-C, the power spectra calculated using a 1024 pt FFT window for three SMUs recorded from right 1DI and pooled over the two hold periods (subject JL). These SMUs are the same as those shown in Fig. 3. D-F, the coherence spectra calculated between pairs of the power spectra shown in A-C. The dashed horizontal line indicates the 95 % confidence limit. Peaks in the coherence spectra were only considered significant if three consecutive bins were above this confidence limit. Superimposed on each plot is the power spectrum of the 1DI surface EMG recording (dashed line) calculated over the two HOLD periods. The scale of these power spectra does not correspond to the scale given on the y axis, which only applies to the SMU data.
The form of the coherence spectra varied between SMU pairs. Although peaks were sometimes seen in the 6-12 Hz range, the most common feature was the presence of a peak in the 15-30 Hz range (e.g. in Fig. 6D and E). This peak corresponded exactly to the peak in the 15-30 Hz range in the power spectrum of the 1DI surface EMG in each case (compare dotted and continuous traces in Fig. 6D-F). The SMU1-SMU2 (Fig. 6D) coherence spectrum also showed significant coherence at low frequencies (< 4 Hz) and at higher frequencies, around 40 Hz.
Figure 7 shows the coherence spectra between SMUs in the two different task conditions tested. Two frequency ranges of coherence were analysed, the 6-12 Hz range (Fig. 7A and B) and the 15-30 Hz range (Fig. 7C and D). Coherence spectra were only accepted for further analysis if they were constructed from at least 48 disjoint sections with at least five discharges per SMU in each disjoint section. Each section was 1.024 s in duration. These strict criteria reduced the number of motor unit pairs studied in the coherence analysis compared with the time-domain studies (compare the numbers under the columns in Fig. 5A and C to those in Fig. 7A and C). The number of motor unit pairs with significant coherence was modulated with lever compliance in both frequency ranges, with a larger percentage in HI-COMP, the more compliant condition (Fig. 7A and C). In the 15-30 Hz range, 10/16 pairs were significant in the HI-COMP condition compared with 10/25 in the LO-COMP. However, these differences in the percentage were not significant in either frequency range (P > 0.05, χ-squared test). The mean level of the coherence in the 15-30 Hz range was also significantly greater for HI-COMP vs. LO-COMP (Fig. 7D; P < 0.05 Mann-Whitney U test). The mean level of coherence in the 6-12 Hz range did not show any systematic relationship with lever compliance of the task (Fig. 7B).
Figure 7. Task-dependent changes in SMU-SMU coherence.
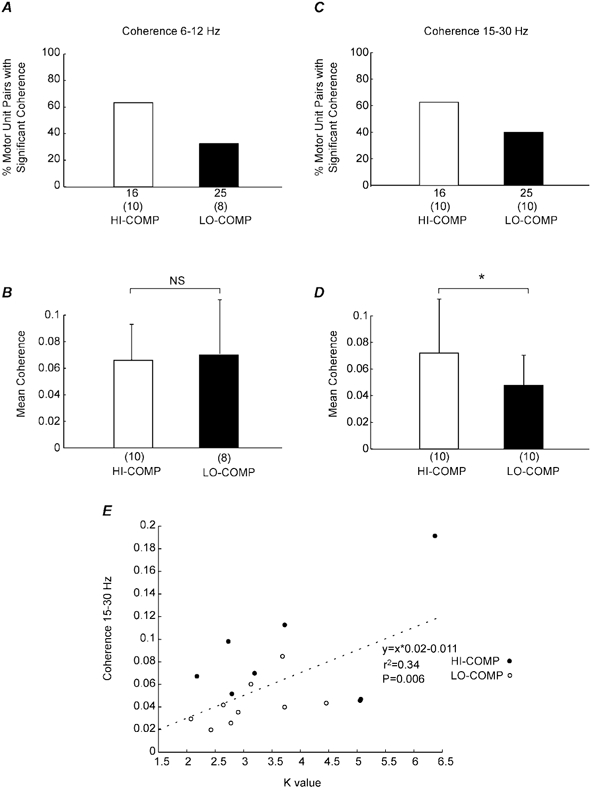
A, the percentage of motor units pairs that showed significant coherence in the 6-12 Hz range for the HI-COMP (open bars) and LO-COMP (black bars) task conditions. Motor unit pairs were considered significant if three consecutive bins were above the 95 % confidence level. The number of total motor unit pairs analysed for coherence is shown at the bottom of each column, with the number significant shown in the brackets. B, the mean level of the coherence in the 6-12 Hz range for each task condition as in A. The total number of significant motor units pairs is shown at the bottom of each column. The error bars indicate the standard error. C and D, the corresponding analysis for the 15-30 Hz range. E, the linear regression of the ‘k’ value against the mean coherence in the 15-30 Hz range for each subject and for each task condition.
The change in the level of coherence in the 15-30 Hz range with the task condition was very similar to the modulation of the ‘k’ value (compare Fig. 7D with Fig. 5B). Figure 7E shows the scatter of the ‘k’ value against the maximum coherence value in the 15-30 Hz range for those SMU pairs that showed significant changes for both measures. To increase the number of SMU pairs, data have been pooled across the two task conditions. There was a clear relationship between the degree of synchrony and the magnitude of the coherence (r2 = 0.34, P < 0.01); this regression was still significant if the outlying point with a ‘k’ value of 6.5 was removed from the analysis.
DISCUSSION
Our previous work has demonstrated that the level of coherent oscillatory activity between contralateral motor cortex and human hand muscles shows a positive covariation with the compliance of the gripped object (Kilner et al. 2000). The main objective of the present study was to determine whether synchrony between pairs of simultaneously recorded single motor units from the 1DI muscle covaried in a similar manner with the level of compliance in the gripped object. This was found to be the case: both time- and frequency-domain analysis showed that synchrony between discharges in pairs of 1DI units increased with the level of object compliance (Fig. 5B and Fig. 7D). Interestingly, this compliance-related synchrony was evident only in the 15-30 Hz frequency range, and not at the lower frequencies which characterise the firing rates of the motor units themselves.
Synchrony between SMUs during precision grip of a compliant load
Because of the technical need to maintain recording stability from the same group of SMUs, we concentrated on synchrony during precision grip under just two different levels of compliance. We used force levels similar to those used in our previous studies (Kilner et al. 1999, 2000), to allow a direct comparison between the results. Subjects concentrated on maintaining the required force levels during the task and were not given any feedback about SMU discharge rate. Although we took great care to ensure that we recorded from the same, small group of SMUs throughout the experiment (see for example the SMU in Fig. 2), we had no independent measure of whether identical units were recorded under both HI-COMP and LO-COMP conditions. For this reason, we have treated the SMU data in HI-COMP and LO-COMP conditions as separate, but representative, populations of activity in the 1DI motoneurone pool.
We found a significant increase in SMU synchrony with lever compliance, as measured in the time domain by the ‘k’ value of the cross-correlations (Fig. 5B). We observed a similar, but not significant, trend in the ‘b’ value of cusums from those SMU pairs with a clear and significant peak in the cross-correlation (Fig. 5E). Frequency-domain analysis also revealed a significant increase in synchrony with compliance; this was seen in the 15-30 Hz bandwidth (Fig. 7D), but not in the lower frequency range (6-12 Hz) analysed. This lower range spanned the firing rates of most SMUs sampled, suggesting that the fundamental firing rates of these units were not the source of the observed changes in synchrony. There may be important advantages in avoiding the use of a strong ≈10 Hz control signal, which might lead to excess tremor if the system were driven at its resonant frequency by corticospinal inputs.
The increase in synchrony with compliance was not rate-dependent, since the firing rate of the SMUs sampled did not show any significant difference between the two compliant conditions tested (Fig. 4). This is important since previous studies have demonstrated that the relative firing rates of the SMU pair can affect the level of synchrony (Ellaway & Murthy, 1985; Bremner et al. 1991b). The parallel changes in short-term synchrony and in coherence in the 15-30 Hz range confirms results from Farmer et al. (1993).
Origin of SMU-SMU synchrony
Our previous studies have shown that power spectra of surface EMG recordings of hand and forearm muscles during precision grip of a compliant load are characterised by prominent peaks in the 15-30 Hz range (Baker et al. 1997; Kilner et al. 2000). The central origin of this 15-30 Hz synchrony has been deduced from a number of different observations. First, such synchrony seems to be a common feature in EMG activity recorded from a wide variety of muscles in both upper and lower limbs. This is inconsistent with a peripheral or simple reflex origin, which would be sensitive to different biomechanical properties and conduction delays/loop times (Salenius et al. 1997). Second, a cortical oscillator coherent at 15-30 Hz with hand muscle EMG has been localised to the hand area of primary motor cortex (Kilner et al. 2000). Third, the phase delay between cortex and muscle may be appropriate to conduction over fast cortico-motoneuronal (CM) pathways (Gross et al. 2000).
The results of the current study show that such 15-30 Hz oscillatory EMG activity arises as a result of oscillatory synchrony between motor units and it is not related to the firing rate of motor units themselves. None of the SMUs sampled showed discharge with significant peaks in this frequency range, but this was consistently observed in the interactions between them (Fig. 7). This is in agreement with the hypothesis put forward by McAuley & Marsden (2000) where the discharges of individual motor units drift in and out of phase with the modulating 15-30 Hz rhythm. Such modulation is hard to see at the single motor unit level but is evident in the population recordings.
Short-term stochastic synchrony between pairs of motoneurones probably arises because of branching of input fibres, providing common input to both motoneurones (e.g. Datta & Stephens, 1990; Datta et al. 1991; Bremner et al. 1991a); one source of common drive are branched CM inputs. Oscillatory synchrony, on the other hand is thought to arise because of synchrony between populations of premotoneuronal inputs, including corticospinal neurones (e.g. Farmer et al. 1993; Conway et al. 1995; Baker et al. 1997; Kilner et al. 1999, 2000; Baker et al. 2001). We suggest that it is the centrally generated oscillatory synchrony at 15-30 Hz that varies according to the compliance of the object, and which causes the changes to SMU-SMU synchrony observed in this study. The different types of short-term synchrony may explain why compliance-related modulation appeared to be smaller for the time-domain data, ‘k’ and ‘b’ values, which measure both stochastic and oscillatory synchrony, than for the frequency domain data, which is not sensitive to changes in stochastic synchrony.
Possible functions of 15-30 Hz cortico-muscular coherence
The time and frequency domain measures of synchrony between SMUs in the 1DI muscle show the same pattern of modulation with compliance as was observed for coupling between surface EMG activity from different hand muscles, and between EMG and MEG recorded from the contralateral sensorimotor cortex (Kilner et al. 1999, 2000). The modulation of oscillatory synchrony between SMUs is consistent with our hypothesis that cortico-muscular synchrony during precision grip reflects an efficient control mechanism used to maintain steady grasp of a compliant object (Baker et al. 1997; Kilner et al. 2000). Although coherence is absent during movement itself, it is most marked just after the grasp of an object has been adjusted, and declines over long periods of stable grasp (1-3 min).
Compliant objects are commonplace, and include food items, such as fruit, springy objects such as plastic bottles or tubes, clothing, spring-loaded instruments, tools, etc. Such objects present considerable challenges for the manipulatory system compared to solid, incompressible objects, which can be handled efficiently by appropriate scaling and distribution of the grip force (Johansson, 1996; Flanagan et al. 1999). In order to hold and manipulate compliant objects, precise co-ordinated control of both grip force and grip aperture (i.e. digit position) is needed, and the need for such control becomes more demanding when very springy objects are handled because small changes in grip force will lead to large changes in grip aperture. Oscillatory synchrony may characterise a low-level control system which engages and then maintains the particular level of activity in the large number of synergistic muscles that are needed to exert efficient grip between the digits. Oscillatory activity in the descending corticospinal command could have a substantial effect on the extent of motoneurone recruitment and hence on the strength of a given contraction (Baker, 1997).
Acknowledgments
This work was supported by MRC, the Wellcome Trust and British Council. We should like to acknowledge the expert assistance of Dr Stuart Baker, Dr Chris Seers, Dr Kelvin Jones and Dr Parveen Bawa.
REFERENCES
- Baker SN. Quantification of the relative efficacies of asynchronous and oscillating inputs to a motoneurone pool using a computer model. Journal of Physiology. 1997;504:116. [Google Scholar]
- Baker SN, Olivier E, Lemon RN. Coherent oscillations in monkey motor cortex and hand muscle EMG show task-dependent modulation. Journal of Physiology. 1997;501:225–241. doi: 10.1111/j.1469-7793.1997.225bo.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baker SN, Spinks R, Jackson A, Lemon RN. Synchronization in monkey motor cortex during a precision grip task. I. Task-dependent modulation in single-unit synchrony. Journal of Neurophysiology. 2001;85:869–885. doi: 10.1152/jn.2001.85.2.869. [DOI] [PubMed] [Google Scholar]
- Bawa P, Lemon RN. Recruitment of motor units in response to transcranial magnetic stimulation in man. Journal of Physiology. 1993;471:445–464. doi: 10.1113/jphysiol.1993.sp019909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bremner FD, Baker JR, Stephens JA. Effect of task on the degree of synchronization of intrinsic hand muscle motor units in man. Journal of Neurophysiology. 1991a;66:2072–2083. doi: 10.1152/jn.1991.66.6.2072. [DOI] [PubMed] [Google Scholar]
- Bremner FD, Baker JR, Stephens JA. Variation in the degree of synchronization exhibited by motor units lying in different finger muscles in man. Journal of Physiology. 1991b;432:381–399. doi: 10.1113/jphysiol.1991.sp018390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conway BA, Halliday DM, Farmer SF, Shahani U, Maas P, Weir AL, Rosenberg JR. Synchronization between motor cortex and spinal motoneuronal pool during the performance of a maintained motor task in man. Journal of Physiology. 1995;489:917–924. doi: 10.1113/jphysiol.1995.sp021104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Datta AK, Farmer SF, Stephens JA. Central nervous pathways underlying synchronization of human motor unit firing studied during voluntary contractions. Journal of Physiology. 1991;432:401–425. doi: 10.1113/jphysiol.1991.sp018391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Datta AK, Stephens JA. Synchronization of motor unit activity during voluntary contraction in man. Journal of Physiology. 1990;422:397–419. doi: 10.1113/jphysiol.1990.sp017991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donoghue JP, Sanes JN, Hatsopoulos NG, Gaal G. Neural discharge and local field potential oscillations in primate motor cortex during voluntary movements. Journal of Neurophysiology. 1998;70:219–232. doi: 10.1152/jn.1998.79.1.159. [DOI] [PubMed] [Google Scholar]
- Ellaway PH. Cumulative sum technique and its application to the analysis of peristimulus time histograms. Electroencephalography and Clinical Neurophysiology. 1978;45:302–304. doi: 10.1016/0013-4694(78)90017-2. [DOI] [PubMed] [Google Scholar]
- Ellaway PH, Murthy KSK. The origins and characteristics of cross-related activity between gammamotoneurones in the cat. Quarterly Journal of Experimental Physiology. 1985;70:219–232. doi: 10.1113/expphysiol.1985.sp002905. [DOI] [PubMed] [Google Scholar]
- Farmer SF, Bremner FD, Halliday DM, Rosenberg JR, Stephens JA. The frequency content of common synaptic inputs to motoneurones studied during voluntary isometric contraction in man. Journal of Physiology. 1993;470:127–155. doi: 10.1113/jphysiol.1993.sp019851. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feige B, Aertsen A, Kristeva-Feige R. Dynamic synchronisation between multiple cortical motor areas and muscle activity in phasic movements. Journal of Neurophysiology. 2000;84:2622–2629. doi: 10.1152/jn.2000.84.5.2622. [DOI] [PubMed] [Google Scholar]
- Flanagan JR, Burstedt MK, Johansson RS. Control of fingertip forces in multidigit manipulation. Journal of Neurophysiology. 1999;81:1706–1717. doi: 10.1152/jn.1999.81.4.1706. [DOI] [PubMed] [Google Scholar]
- Gastaut H. Etude electrocorticographique de al reactivite des rythmes rolandiques. Review of Neurology. 1952;87:176–182. [PubMed] [Google Scholar]
- Gross J, Tass PA, Salenius S, Hari R, Freund HJ, Schnitzler A. Cortico-muscular synchronisation during isometric muscle contraction in humans as revealed by magnetoencephalography. Journal of Physiology. 2000;527:623–631. doi: 10.1111/j.1469-7793.2000.00623.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hari R, Salenius S. Rhythmical corticomuscular communication. Neuroreport. 1999;10:1–10. [PubMed] [Google Scholar]
- Jasper H, Penfield W. Electrocorticograms in man:Effect of voluntary movement upon the electrical activity of the precentral gyrus. Archiv für Psychiatrie und Zeitschrift. 1949;183:163–174. [Google Scholar]
- Johansson RS. Sensory control of dextrous manipulation in humans. In: Wing AM, Haggard P, Flanagan JR, editors. Hand and Brain. The Neurophysiology and Psychology of Hand Movements. San Diego: Academic Press; 1996. pp. 381–414. [Google Scholar]
- Kilner JM, Baker SN, Salenius S, Hari R, Lemon RN. Human cortical muscle coherence is directly related to specific motor parameters. Journal of Neuroscience. 2000;20:8838–8845. doi: 10.1523/JNEUROSCI.20-23-08838.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kilner JM, Baker SN, Salenius S, Jousmaki V, Hari R, Lemon RN. Task-dependent modulation of 15–30 Hz coherence between rectified EMGs from human hand and forearm muscles. Journal of Physiology. 1999;516:559–570. doi: 10.1111/j.1469-7793.1999.0559v.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirkwood PA. On the use and interpretation of cross-correlation measurements in the mammalian central nervous system. Journal of Neuroscience Methods. 1979;1:107–132. doi: 10.1016/0165-0270(79)90009-8. [DOI] [PubMed] [Google Scholar]
- McAuley JH, Marsden CD. Physiological and pathological tremors and rhythmic central motor control. Brain. 2000;123:1545–1567. doi: 10.1093/brain/123.8.1545. [DOI] [PubMed] [Google Scholar]
- Marsden JF, Farmer SF, Halliday DM, Rosenberg JR, Brown P. The unilateral and bilateral control of motor unit pairs in the first dorsal interosseous and paraspinal muscles in man. Journal of Physiology. 1999;521:553–564. doi: 10.1111/j.1469-7793.1999.00553.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milner-Brown HS, Stein RB, Lee RG. Synchronization of human motor units: possible roles of exercise and supraspinal reflexes. Electroencephalography and Clinical Neurophysiology. 1975;38:245–254. doi: 10.1016/0013-4694(75)90245-x. [DOI] [PubMed] [Google Scholar]
- Murthy VN, Fetz EE. Coherent 25-hz to 35-hz oscillations in the sensorimotor cortex of awake behaving monkeys. Proceedings of the National Academy of Sciences of the USA. 1992;89:5670–5674. doi: 10.1073/pnas.89.12.5670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murthy VN, Fetz EE. Oscillatory activity in sensorimotor cortex of awake monkeys: synchronization of local field potentials and relation to behaviour. Journal of Neurophysiology. 1996;76:3949–3967. doi: 10.1152/jn.1996.76.6.3949. [DOI] [PubMed] [Google Scholar]
- Rosenberg JR, Amjad AM, Breeze P, Brillinger DR, Halliday DM. The fourier approach to the identification of functional coupling between neuronal spike trains. Progress in Biophysics and Molecular Biology. 1989;53:1–31. doi: 10.1016/0079-6107(89)90004-7. [DOI] [PubMed] [Google Scholar]
- Salenius S, Portin K, Kajola M, Salmelin R, Hari R. Cortical control of human motoneuron firing during isometric contraction. Journal of Neurophysiology. 1997;77:3401–3405. doi: 10.1152/jn.1997.77.6.3401. [DOI] [PubMed] [Google Scholar]
- Salmelin R, Hari R. Spatiotemporal characteristics of sensorimotor neuromagnetic rhythms related to thumb movement. Neuroscience. 1994;60:537–550. doi: 10.1016/0306-4522(94)90263-1. [DOI] [PubMed] [Google Scholar]
- Sanes JN, Donoghue JP. Oscillations in local field potentials of the primate motor cortex during voluntary movement. Proceedings of the National Academy of Sciences of the USA. 1993;90:4470–4474. doi: 10.1073/pnas.90.10.4470. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stancak A, Pfurtscheller G. Mu-rhythm changes in brisk and slow self-paced finger movements. NeuroReport. 1996;7:1161–1164. doi: 10.1097/00001756-199604260-00013. [DOI] [PubMed] [Google Scholar]


