The presence of local osmotic gradients can account for the water flux driven by the Na⁺–glucose cotransporter

Since 1996, several articles have been published supporting the hypothesis that water is stoichiometrically cotransported with other solutes and ions in a secondary active manner (Loo et al. 1996, 2002; Zeuthen et al. 1997, 2001; Meinild et al. 1998). The main points supporting this intriguing hypothesis were that (1) addition of a cotransported substrate generated an apparently instantaneous cell swelling and (2) an ionophore-mediated ionic current failed to produce similar initial (i.e. in the first 30 s of transport) cell swelling. We have revisited the water cotransport hypothesis using the human Na⁺-glucose cotransporter (hSGLT1) expressed in Xenopus laevis oocytes and have reached the conclusion that all of the transport-related cell swelling can be quantitatively accounted for by the local accumulation of intracellular osmolytes and the passive transport of water through the endogenous and hSGLT1-dependent water permeabilities (Duquette et al. 2001). In this commentary, we will present two lines of evidence which clearly contradict the water cotransport hypothesis.

When 5 mm α-methyl-glucose (αMG, a non-hydrolysable glucose analogue) is presented to an hSGLT1-expressing oocyte clamped at -100 mV, an inward cotransport current of 1-2 μA is stimulated and the oocyte starts to swell with a time delay that closely matches the exchange time of the bath solution (10-20 s in the present case; see Fig. 1). After 60 s of cotransport, a steady-state swelling rate can be measured with some precision and was found to average 240 water molecules per αMG molecule transported, which is in excellent agreement with the proposed stoichiometry for water cotransport through hSGLT1 (Meinild et al. 1998; Zeuthen et al. 2001). If the membrane potential is rapidly (within 10 ms) stepped to 0 mV, the cotransport current is reduced by 94 ± 1 % (n = 6) but the swelling rate fails to follow the cotransport current. As determined by adjusting straight lines to the volume recording 20 s before and after the depolarisation, the swelling rate is indeed significantly reduced but by only 25 ±2 %. The fact that a large fraction of the cotransport-induced swelling rate appears to continue while the cotransport current is basically shut off is in contradiction with the water cotransport hypothesis.

Figure 1. Effect of a rapid reduction in cotransport current on the observed cell swelling.

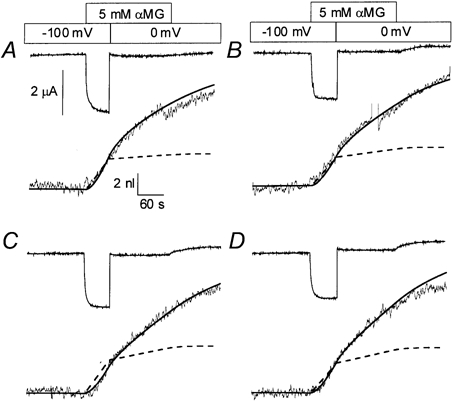
Superimposed onto the four experimental recordings are the predictions from the water cotransport model (dashed line) and from the osmolyte accumulation model (continuous line).

The absolute value of the intracellular diffusion coefficient is a central issue in testing the hypothesis that local osmotic gradients do occur and can account for the cotransport-stimulated cell swelling. We have developed a simple intracellular diffusion model using the oocyte geometry (Duquette et al. 2001) in which it is assumed that all small molecules and ions diffuse with a single intracellular diffusion coefficient (D_i). The intracellular aqueous space was assumed to be equal to the oocyte water content, i.e. 85 % of the oocyte volume. When a hypotonic shock of 50 mosmol l⁻¹ is applied to an oocyte, the ‘volume vs. time curve’ appears linear for a short time (≈30 s) before experiencing a significant reduction in slope. The most likely explanation for this non-linearity is that the osmolarity gradient experienced by the plasma membrane decreases with time as the cytosolic solution becomes diluted. This non-linear volume vs. time relationship during hypotonic shock is highly dependent on D_i and it was found that a value of (0.07 ± 0.03) × 10⁻⁵ cm² s⁻¹ (mean ± s.d.) was necessary to account for the observed swelling (n = 9). This value of D_i is about one order of magnitude lower than the aqueous diffusion coefficient for small molecules.

The diffusion model can be used to find a set of parameters that can fit the detailed cell swelling triggered by the addition of 5 mm αMG to an hSGLT1-expressing oocyte (see Fig. 2). In good agreement with the values needed to fit simple hypotonic shocks, it was found that a D_i of (0.11 ± 0.03) × 10⁻⁵ cm² s⁻¹ (n = 5) and an average of 4.1 ± 0.3 osmolytes per αMG molecule transported provided the best fit for the whole experiment. This indicates the early presence of transport-driven osmolyte accumulation and suggests that osmolyte accumulation can account for all of the cell swelling observed. The inset of Fig. 2 represents the osmolarity gradient built up by the cotransport current as a function of time for the experiment depicted in Fig. 2. It can be seen that the osmolarity gradient required to account for the cell swelling observed at t = 60 s is only 5 mosmol l⁻¹.

Figure 2. Cotransport-stimulated cell swelling.

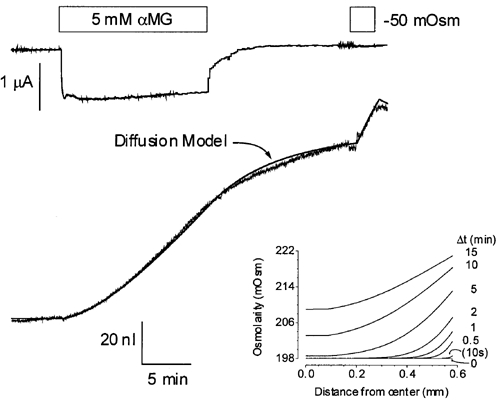
The continuous smooth line represents the fit provided by the diffusion model using the parameters described in the text. The inset shows the osmolarity profiles from the centre of the oocyte to the plasma membrane as a function of time after initiating the cotransport current.

It has been claimed that such an osmolarity gradient may not initially exist because current injection through a cation ionophore did not produce such early cell swelling (no swelling observed until t > 30.60 s; Zeuthen et al. 1997; Meinild et al. 1998). We have reproduced these observations using ROMK2 (Duquette et al. 2001) and we came to the conclusion that ionic flux does not accurately mimic cotransport involving neutral substrates. First of all, the diffusion coefficient for a neutral solute like glucose is about 2-3 times lower than the diffusion coefficient for NaCl in aqueous solution. In addition, a neutral substrate transported into the cell will accumulate directly under the oocyte membrane and initiate a slow diffusion process towards the oocyte centre. In the case of ionic influx, since the experiment is performed under voltage-clamp conditions, an identical net charge will be injected by the current electrode to maintain intracellular electroneutrality. Depending on the relative mobility of intracellular anions vs. cations, osmolyte (i.e. salt) accumulation will be split between the plasma membrane and the tip of the current electrode. This would make a pure ionic injection less efficient than a Na⁺-glucose cotransport in generating a local osmotic gradient.

In summary, it is our hope that the study outlined in this Perspective will contribute to the clarification of water transport across plasma membranes. The hypothesis of secondary active water transport has generated considerable interest within the transport physiology community and our initial goal was not to attack this interesting hypothesis but to test to what extent the ‘dogma’, that water movement across membranes is always passive, could explain the water movement observed. At this point, we have come to the conclusion that the dogma can fully explain the experimental observations.