Spatial heterogeneity of transmembrane potential responses of single guinea-pig cardiac cells during electric field stimulation

Abstract

Changes in transmembrane voltage (V_m) of cardiac cells during electric field stimulation have a complex spatial- and time-dependent behaviour that differs significantly from electrical stimulation of space-clamped membranes by current pulses. A multisite optical mapping system was used to obtain 17 or 25 μm resolution maps of V_m along the long axis of guinea-pig ventricular cells (n = 57) stained with voltage-sensitive dye (di-8-ANEPPS) and stimulated longitudinally with uniform electric field (2, 5 or 10 ms, 3–62 V cm⁻¹) pulses (n = 201). The initial polarizations of V_m responses (V_mr) varied linearly along the cell length and reversed symmetrically upon field reversal. The remainder of the V_m responses had parallel time courses among the recording sites, revealing a common time-varying signal component (V_ms). V_ms was depolarizing for pulses during rest and hyperpolarizing for pulses during the early plateau phase. V_ms varied in amplitude and time course with increasing pulse amplitude. Four types of plateau response were observed, with transition points between the different responses occurring when the maximum polarization at the ends of the cell reached values estimated as 60, 110 and 220 mV. Among the cells that had a polarization change of > 200 mV at their ends (for fields > 45 V cm⁻¹), some (n = 17/25) had non-parallel time courses among V_m recordings of the various sites. This implied development of an intracellular field (E_i) that was found to increase exponentially with time (τ = 7.2 ± 3.2 ms). Theoretical considerations suggest that V_ms represents the intracellular potential (φ_i) as well as the average polarization of the cell, and that V_mr is the manifestation of the extracellular potential gradient resulting from the field stimulus. For cells undergoing field stimulation, φ_i acts as the cellular physiological state variable and substitutes for V_m, which is the customary variable for space-clamped membranes.

The use of electrical shocks to bring a heart out of fibrillation, a potentially fatal self-sustaining reentrant cardiac rhythm, has been applied clinically for over 50 years (Beck, 1941). A series of events must transpire for electrical defibrillation to be successful. First, the electrical current must be disbursed throughout the tissue volume, such that a ‘critical mass’ or perhaps the entire mass of the tissue experiences a minimal level of current, or potential gradient necessary for it to become excited (Walcott et al. 1997; Dillon & Kwaku, 1998). Second, the current (and accompanying local interstitial electric field) then perturbs the transmembrane potential of the cells through putative biophysical mechanisms that have been identified from computational modelling (Sobie et al. 1997; Roth & Krassowska, 1998; Trayanova et al. 1998a) and experimental studies in tissue (Knisley et al. 1999). Detailed studies in experimentally designed networks of cardiac cells reveal that polarization develops at the cleft spaces (Fast et al. 1998), at the borders of linear or curved strands of cells (Fast et al. 2000; Tung & Kleber, 2000), in regions of fibre bends and expansions (Gillis et al. 2000), or at intercellular junctions (Sharma & Tung, 2001). All of these examples may be explained through the concept of the generalized activating function that defines the location and strength of ‘virtual’ electrodes (Sobie et al. 1997). A common feature among field responses is that dual regions of depolarization and hyperpolarization develop in close proximity to one another. This behaviour is captured at the level of a single isolated cell in which one end of the cell is depolarized by the field while the other end is hyperpolarized. Thus, a single isolated cell provides a prototypical model system to study responses of cardiac membranes with closely juxtaposed regions of opposite polarity.

In a different but related context, electrical field stimulation of single cardiac cells is commonplace in the laboratory, and it is often assumed that the mechanism for field stimulation is similar to that of space-clamped membranes that are depolarized by stimulus current (Jones et al. 1994). Theoretical studies suggest that while similarities can be found in the existence of a stimulus threshold or in the inverse relation between stimulus amplitude and duration required for excitation, substantive differences remain (Tung & Borderies, 1992). Most notable is that during field stimulation, the cell membrane is highly and non-uniformly polarized. As a result, the mechanism for field stimulation is more complex. For example, with the intracellular injection of stimulus current across space-clamped cell membranes, the depolarizing charge is supplied by the electrode but is diminished by cellular, outward potassium membrane currents. On the other hand, with field stimulation the depolarizing charge arises not at all from the stimulating electrode, but solely from cellular, inward membrane currents. In cardiac cells stimulated at rest these currents initially flow through the inwardly rectifying potassium channels in the hyperpolarized end of the cell and later through the fast sodium channels in the depolarized end of the cell (Tung & Borderies, 1992; Krassowska & Neu, 1994). Thus, it is clear that field responses are unlike the single polarity responses that result from stimulation by an intracellular unipolar electrode. Nevertheless, the vast majority of information about cellular electrophysiological behaviour has been obtained from conditions in which the cell membrane is space-clamped, from which characteristics of excitatory behaviour such as strength-duration or strength-interval relations have been derived, or ionic currents have been measured. Few if any experimental studies have been performed to characterize the behaviour of non-uniformly polarized membranes.

Optical methods that employ fast response voltage-sensitive dyes (Salama, 1988; Girouard et al. 1996) allow the monitoring of transmembrane voltage at a subcellular resolution, free from electrical artifact. In this study we used a multisite mapping system and voltage-sensitive dye to obtain one-dimensional spatial maps of transmembrane responses from adult guinea-pig ventricular myocytes stimulated at rest and during the action potential plateau. These maps allow the detailed quantification of the spatial and temporal heterogeneities of the transmembrane potential (V_m) responses of a cell to field stimuli applied during these two phases of the action potential. In addition to corroborating and extending the results of some of the theoretical and experimental studies already published, our ability to obtain high resolution spatial and temporal maps of V_m gives new insights into field-cell interactions. Portions of this study have been presented previously in abstract form (Sharma et al. 1999) and in preliminary short reports (Sharma & Tung, 1999, 2000).

METHODS

Cell isolation

All experiments were carried out under an animal use protocol approved by the Animal Care and Use Committee of The Johns Hopkins University. Single ventricular myocytes were enzymatically isolated from whole hearts of adult male guinea-pigs (Hartley strain, weight 200–300 g) as follows. The animals were anaesthetized with an intraperitoneal injection of sodium pentobarbital (0.1 ml (100 g)⁻¹, Abbott Labs, North Chicago, IL, USA), with 0.1-0.3 ml heparin to minimize clotting. Once the animal failed to respond to the paw pinch test, its chest was quickly opened via a radical medial thoracotomy. The heart was quickly excised and placed in a beaker containing ∼50 ml of oxygenated 1.8 mm Ca²⁺-containing Tyrode solution at room temperature (∼22 °C). The beating heart was gently massaged to eject blood from the heart cavity. The heart was then quickly mounted on a Langendorff column and perfused in a retrograde direction. The enzymatic dissociation was performed using the following sequence of solutions, all of which were oxygenated and maintained at 37 °C: (1) 1.8 mm Ca²⁺ Tyrode solution for 5 min; (2) Ca²⁺-free Tyrode solution for 7 min; (3) 50 ml Ca²⁺-free Tyrode with 1 U ml⁻¹ protease (Type XIV, Sigma Chemical, St Louis, MO, USA), 90 U ml⁻¹ collagenase (Worthington Biochemical Corp., Freehold, NJ, USA) and 1 mg ml⁻¹ bovine serum albumin (Type V, Sigma) for 7 min. (4) Ca²⁺-free Tyrode solution for 5 min. After perfusion the ventricles were chopped, gently stirred and filtered to obtain single cells. The cells were stored in 0.2 mm Ca²⁺ Tyrode solution and allowed to recover for approximately 30–40 min. After this period the cells were transferred into 1.8 mm Ca²⁺ Tyrode solution and used for experiments. All experiments were performed at room temperature. The composition of Ca²⁺-free Tyrode solution (mm) was: 135 NaCl, 5.4 KCl, 1 MgCl₂, 0.33 NaH₂PO₄, 5 Hepes, 5 glucose (adjusted to pH 7.4 with NaOH).

Cell staining

A stock solution of 135 mm pyridinium, 4-[2-[6[(dioctylamino)-2-naphthalenyl]ethenyl]-1-(3-sulfopropyl)-, inner salt (di-8-ANEPPS, Molecular Probes, Eugene, OR, USA) was prepared by dissolving the dye in (w/w) 75 % dimethyl sulfoxide (DMSO) and 25 % Pluronic-127 (BASF, Parsippany, NJ, USA). Pluronic-127 facilitated dissolution of the dye. The stock solution was stored in a light-tight bottle at room temperature. To minimize exposure of the dye stock to light, 10 μl aliquots were transferred to four to five light-tight centrifuge tubes during a single access of the stock. Before an experiment, 10 μl of dye stock from one centrifuge tube was further diluted in 1.8 mm Ca²⁺ Tyrode solution to yield a final concentration of 20–100 μm. For staining, 50–100 μl of diluted dye solution was added to 5–10 μl of solution containing cells. The cells were allowed to stain for ∼4-5 min, and thereafter 2–3 ml of normal Tyrode solution was added to further dilute the dye. The experiments were usually begun immediately after the cells were stained.

Experimental setup

The experimental setup (Fig. 1) was designed and built using an approach similar to those used for neuronal (Chien & Pine, 1991) and cardiac (Rohr & Kucera, 1998) studies. The system was assembled around an inverted microscope (Diaphot-TMD, Nikon Inc., NY, USA). An electronic shutter (Vincent Associates, Rochester, NY, USA) gated the light for a desired duration from a short arc 150 W xenon arc lamp (Opti Quip, Highland Mills, NY, USA) into the microscope via the epi-illumination pathway. The excitation light was filtered (ExF: 460–570 nm, Omega Optical Inc., Brattleboro, VT, USA) and deflected onto the sample using a dichroic mirror (DM: 570 nm, Omega Optical Inc.). The fluorescence emitted from the sample was long-pass filtered (EmF: 570 nm, Omega Optical Inc.) and focused onto a square bundle (∼12 mm × 12 mm) consisting of 149 hexagonally packed, plastic optical fibres. Each individual fibre (Boston Optical Fiber, Westborough, MA, USA) had a core of 980 μm with 20 μm cladding. At magnifications of × 40 and × 60 used for this study, each optical fibre collected fluorescence from a 25 μm and 17 μm diameter region, respectively, in the specimen plane.

Figure 1.

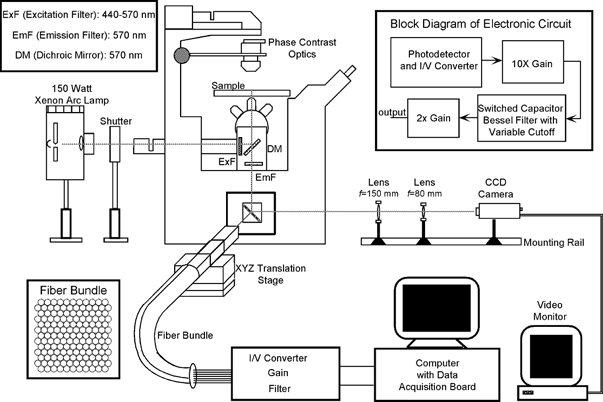
Schematic representation of the experimental setup

An optical fibre bundle-based system was used to record fluorescence signals (see text for details). The grey line traces the optical pathway. The insets on the top left and right give the details of the optical filters and the electronic circuits, respectively. The face of the fibre bundle consisting of 149 optical fibres is shown in the inset at the bottom left.

Depending on the length of the cell image, the fluorescence signals from 4 to 12 fibres were fed into equal numbers of custom built signal detection and conditioning circuits. Each circuit consisted of a first-stage photodiode and current-to-voltage (I/V) converter with a feedback resistor of 100 or 200 MΩ, followed by gain (× 20) and filtering stages. The filter was an 8 pole tunable switched-capacitor Bessel filter with −3 dB cutoff set at 1.5 kHz or higher. The step responses of all of the channels had a 10 to 90 % rise time of ∼250 μs with the 100 MΩ resistor and ∼300 μs with the 200 MΩ resistor, and were synchronous to within ∼5 μs. The final outputs were acquired into a 200 MHz Pentium industrial computer (ANT Computers, Walnut, CA, USA) using a 64 channel, 16-bit resolution, data acquisition board (SI-DSP6400-200, Sheldon Instruments, Provo, UT, USA) at a sampling rate of 10 kHz per channel. Also recorded were the current flow between the field stimulus electrodes, measured as the voltage drop across a 10 Ω series resistor, and the electric field in the chamber measured via field-monitoring electrodes (see below). The data acquisition programs were written in LabVIEW (National Instruments, Austin, TX, USA) using drivers supplied with the data acquisition board. All data were post-processed using MATLAB (The MathWorks Inc., Natick, MA, USA).

To obtain brightfield images of the cells, the camera port of the microscope was modified by using a pair of optical rail-mounted achromatic lenses (Edmund Scientific, Barrington, NJ, USA) to project the images onto a CCD camera (Model 4910, Cohu Inc., San Diego, CA, USA) that was connected to a monochrome frame grabber board (LG-3, Scion Corp., Frederick, MD, USA) installed in a desktop computer (Macintosh IIci, Apple Computers, Cupertino, CA, USA). By adjusting the distance between the two lenses the effective focal length of the lens pair could be varied, allowing the magnification and field of view to be adjustable. For the experiments reported in this study the field of view was ∼0.2 mm × 0.3 mm.

Experimental chamber, electrodes and electric field measurement

A 0.17 mm thick, 22 mm diameter glass coverslip containing cultured cardiac cells was mounted as the floor of the experimental chamber by using a stainless steel plate retaining ring and rubber gasket to form a water tight seal. Two parallel-plate (10 mm × 4 mm) platinum foil electrodes (the field electrodes) separated by 12 mm were used for field stimulation. The cells were stimulated using two stimulators (SD9 and S44, Grass Medical Instruments, Quincy, MA, USA) connected in parallel, and voltage pulses were applied to one field electrode while the other electrode was grounded. The field direction could be reversed by interchanging the role of the two electrodes. The electrodes were mechanically decoupled from the chamber so that the chamber could be rotated to align the long axis of a given cell to the field direction. The electric field in the chamber was monitored in terms of the total current applied to the field electrodes, and the voltage drop across a second pair of Ag-AgCl electrodes (the field-monitoring electrodes) separated by approximately 0.7 mm, mounted on a manipulator and placed in the bath. Each field-monitoring electrode was ∼250 μm in diameter and was insulated along its length except at the terminal 200–300 μm of the sensing end. During field stimulation with particularly high voltages (up to 100 V), a significant common-mode voltage was generated at the field-monitoring electrodes that sometimes saturated the field recording amplifiers. For such cases the field was estimated from the applied current by linear extrapolation of the current versus field calibration obtained at lower amplitude pulses. The electric field in the chamber was uniform to within 10 %.

Experimental procedure and data analysis

The cells were stimulated using a two-pulse (S1-S2) protocol. Both pulses were rectangular, with an S1 duration of 5 ms and S2 duration of 10 ms. For some experiments the S1 duration was reduced to 2 ms. The cells fired an action potential in response to S1, and the S2 pulse was applied during the action potential plateau, 20 ms after the onset of S1. To reduce dye-induced phototoxic damage to the cells (Schaffer et al. 1994) the light exposure duration was set at ∼100 ms. For a given cell, the excitation threshold was determined by gradually increasing the amplitude of S1 while S2 was off, and by visually monitoring the cell under the microscope for the contraction that occurred upon attainment of the excitation threshold. With S1 fixed at ∼1-2 V cm⁻¹ above this level, the S2 was turned on, and the transmembrane responses of the cell to S1-S2 stimuli were optically recorded from several (the exact number depending on the cell length) contiguous circular sites along the cell length. The experiments were conducted by varying the S2 amplitude (∼3 to 62 V cm⁻¹) and direction. The S1 amplitude was usually less than 10 V cm⁻¹. The number of stimuli applied and recordings obtained varied from cell to cell, but usually ranged from one to five. For a few cells (n = 7) in which the first field pulse was greater than ∼45 V cm⁻¹ any subsequent excitation of the cell was not possible (see Results and Discussion). In such cases only one set of recordings was obtained for each cell. Fields directed from left to right of the cell were defined to be positive (e.g. refer to Fig. 2A).

Figure 2.

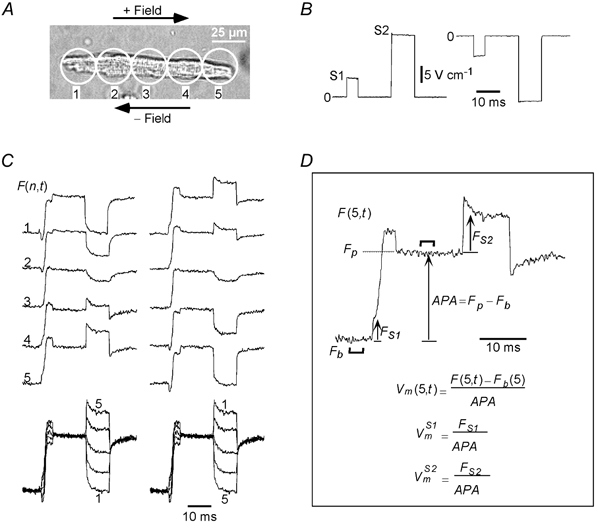
Typical S1-S2-induced V_m s

A, image of an adult guinea-pig cell that was stimulated with both positive and negative pairs of S1-S2 pulses. The field pulses were measured to be +5.5/+21.6 V cm⁻¹ and −5.6/-20.9 V cm⁻¹, and are shown in B. C, left and right columns show the V_m responses to the positive and negative fields, respectively, and demonstrate reversal in $V_{\text{m}}^{\text{S}1}$ and $V_{\text{m}}^{\text{S}2}$ at all sites with reversal of field polarity. The last row in C shows the V_m responses superimposed from all sites. The transitions between the uniformly polarized and non-uniformly polarized states of the cell at the onset and cessation of the S1 and S2 pulses are clearly visible. D, illustration of the method to define the S1- and S2-induced V_m responses from the fluorescence signals, using the signal recorded from site 5 (F(5,t)) for the positive field as an example. The action potential amplitude (APA) was computed as the difference between baseline fluorescence (F_b) and plateau fluorescence (F_p), each being averaged over a 3 ms duration (indicated by thick lines) during rest and plateau, respectively. The formulae for computing the S1- and S2-induced responses ($V_{\text{m}}^{\text{S}1}$ and $V_{\text{m}}^{\text{S}2}$) are also shown in D. Cell length: 128 μm.

In this study we represent the optically recorded transmembrane potential responses as V_m = V_m(n,t), where n is the site number and t is time. For a given n, V_m was obtained by normalizing the difference between the fluorescence signal (F = F(n,t)) and the baseline fluorescence (F_b) to the action potential amplitude (APA). APA was obtained by subtracting F_b from the plateau fluorescence (F_p), with both amplitudes averaged over a 3 ms duration (Fig. 2D illustrates the method for determining V_m). $V_{\text{m}}^{\text{S}1}$(n,t) and $V_{\text{m}}^{\text{S}2}$(n,t) denote V_m at site n during S1 and S2, respectively, measured with respect to the pre-pulse potential (resting for S1 and plateau for S2), and at time t from the onset of their respective pulses. For example, $V_{\text{m}}^{\text{S}2}$(3,1) represents V_m during the S2 pulse with the plateau potential as reference, and measured at site 3 with 1 ms delay from the onset of the S2 pulse. To reduce the effect of noise, $V_{\text{m}}^{\text{S}1}$ and $V_{\text{m}}^{\text{S}2}$ were averaged over a 0.3 ms window around the time of measurement.

For the purposes of discussion we partition V_m into rapid initial (V_mr) and slower residual (V_ms) components, where the initial component was generally measured at t = 0.3 ms (slightly greater than the rise time of our instrumentation) following the onset of the pulse, and the residual component was taken to be the remainder of the V_m response between t = 0.3 ms and the end of the pulse. The choice of 0.3 ms was the best compromise between the necessity of a short duration to capture only passive field responses of the membrane (see Discussion) and a long duration to maximize the measured signal. The nomenclature for representing the V_mr and V_ms components during S1 and S2 is similar to $V_{\text{m}}^{\text{S}1}$ and $V_{\text{m}}^{\text{S}2}$, and is elaborated in the Discussion section as the components are introduced. To compare S2 responses among cells of varying lengths, we determined the maximum $V_{\text{m}}^{\text{S}2}$ (${\hat{V}}_{\text{m}}^{\text{S}2}$) experienced by a cell, defined as the average of magnitudes of $V_{\text{m}}^{\text{S}2}$ at its two ends and measured 0.3 ms after the S2 onset. If V_m was not recorded directly from the cell ends, $V_{\text{m}}^{\text{S}2}$ was estimated by extrapolating the linear V_m response (refer to Fig. 4C) to the cell ends. ${\hat{V}}_{\text{m}}^{\text{S}2}$ is expressed in millivolts, assuming an action potential amplitude of 128 mV (Watanabe et al. 1985).

Figure 4.

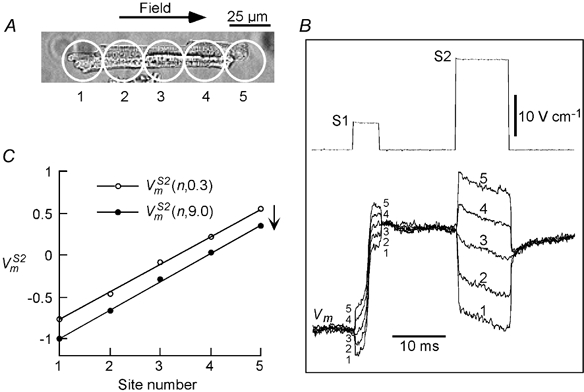
S2-induced V_ms

A, an adult guinea-pig cell that was stimulated with a +5.9 V cm⁻¹ S1 pulse and +22.0 V cm⁻¹ S2 pulse. $V_{\text{m}}^{\text{S}1}$ responses from the 5 recording sites are shown superimposed in B. C, plots of the $V_{\text{m}}^{\text{S}2}$ responses (normalized to APA) measured 0.3 and 9 ms ($V_{\text{m}}^{\text{S}2}$(n,0.3) and $V_{\text{m}}^{\text{S}2}$(n,9.0), respectively) from the onset of S2. $V_{\text{m}}^{\text{S}2}$(n,9.0) underwent a parallel hyperpolarizing shift with respect to $V_{\text{m}}^{\text{S}2}$(n,0.3). Cell length: 118 μm.

The statistical correlation between different parameters was determined by calculating Pearson's correlation coefficient (r), and conducting Student's two-tailed t test for rejecting the null hypothesis that the slope of the best fit line was zero and the parameters were not correlated (Pagano & Gauvreau, 1993). Values of P < 0.05 were considered to be significant for rejecting the null hypothesis.

RESULTS

Experiments were performed on n = 57 cells, with a total of 201 S1-S2 stimuli. The average length of cells used in this study was 142 ± 25 μm. All experiments were analysed in terms of the transmembrane potential responses during S1 ($V_{\text{m}}^{\text{S}1}$) and S2 ($V_{\text{m}}^{\text{S}2}$).

Field-induced transmembrane potential responses, V_m

The cell shown in Fig. 2A was stimulated twice, first with a positive (Fig. 2B, left trace) and then with a negative (Fig. 2B, right trace) S1-S2 pulse pair. Rows 1 to 5 in Fig. 2C show the fluorescence signals, F(n,t), recorded from corresponding sites on the cell for the positive (left column) and negative (right column) S1-S2 pairs. The cell polarized differently along its length, with the end facing the anode undergoing hyperpolarization and the end facing the cathode undergoing depolarization. The polarizations for sites 2–4 varied proportionally between those of sites 1 and 5. The polarization pattern reversed upon field reversal (compare left and right columns in Fig. 2C). However, for both field polarities V_m was spatially asymmetric along the cell length during the S1 and S2 pulses. For example, the V_m responses during the S1 pulse ($V_{\text{m}}^{\text{S}1}$) exhibited a depolarizing trend that remained invariant with field polarity, while the V_m responses during the S2 pulse ($V_{\text{m}}^{\text{S}2}$) exhibited a hyperpolarizing trend. The depolarizing and hyperpolarizing trends are clearly revealed in the V_m responses from the central site, F(3,t), which do not contain a discrete jump at the make or break of the respective pulses.

The fluorescence signals from all sites are shown superimposed at the bottom of Fig. 2C after normalizing all the traces to APA (refer to Fig. 2D and Methods). During the S1 pulse the responses were parallel to each other and merged smoothly into the upstroke of the action potential. During the S2 pulse the V_m responses were parallel as well. The S1- and S2-induced polarizations converged to a common potential upon termination of their respective field pulses. It is important to note that neither set of field responses is symmetric about its pre-pulse potential.

Field responses at rest ($V_{\text{m}}^{\text{S}1}$)

Figure 3A shows V_m responses at rest to an S1 field pulse of shorter duration (2 ms) and lower amplitude (4.1 V cm⁻¹) than that of Fig. 2. Under these conditions, the rapid upstroke of phase 0 depolarization occurs after the pulse, so that the slow depolarizing phase preceding the action potential upstroke can be clearly seen riding on the passive response of the cell. V_m signals were recorded from the five sites, and are shown superimposed in Fig. 3B. These signals show parallel time courses following the initial dispersion in polarization at the onset of the S1 pulse. When measured at t = 0.3 ms and t = 2.0 ms, the plots of $V_{\text{m}}^{\text{S}1}$(n,0.3) and $V_{\text{m}}^{\text{S}1}$(n,2.0) each varied linearly along the cell length as shown in Fig. 3C, and reversed symmetrically with a reversal in the field direction (not shown). Moreover, $V_{\text{m}}^{\text{S}1}$(n,2.0) was parallel to $V_{\text{m}}^{\text{S}1}$(n,0.3) and shifted in the depolarizing direction. Similar depolarizing $V_{\text{m}}^{\text{S}1}$ signals were observed in response to 14 other 2 ms duration S1 stimuli applied to five cells.

Figure 3.

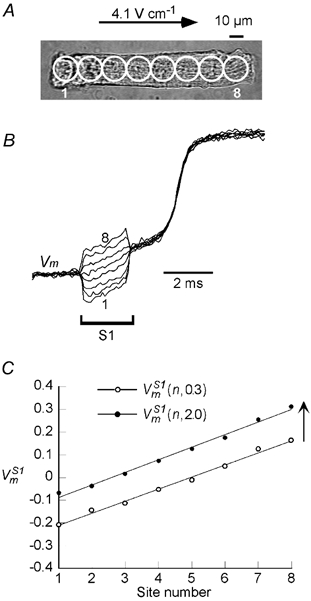
S1-induced V_m s

A, a cell stimulated with a 2 ms, 4.1 V cm⁻¹ S1 pulse. B, the field-induced changes in $V_{\text{m}}^{\text{S}1}$ (normalized to APA) at the 8 sites represented by circles overlaid on the cell image of A. C, plot of the $V_{\text{m}}^{\text{S}1}$ responses measured at 0.3 and 2 ms ($V_{\text{m}}^{\text{S}1}$(n,0.3) and $V_{\text{m}}^{\text{S}1}$(n,2.0), respectively) from the onset of S1. Cell length: 142 μm.

Field responses during the plateau ($V_{\text{m}}^{\text{S}2}$)

The cell shown in Fig. 4A was stimulated with a positive pair of S1 (+5.9 V cm⁻¹) and S2 (+22.0 V cm⁻¹) field pulses. The V_m signals from the five recording sites on the cell are superimposed in Fig. 4B. As was the case for $V_{\text{m}}^{\text{S}1}$ responses, there was a non-uniform polarization of the cell at the onset of the S2 pulse that varied monotonically from hyperpolarization at site 1 to depolarization at site 5. Following the initial dispersion in polarization, the $V_{\text{m}}^{\text{S}2}$ responses showed parallel time courses, but unlike the case with the S1 pulse, the time courses were in the hyperpolarizing direction. When measured at t = 0.3 ms and t = 9.0 ms, the plots of $V_{\text{m}}^{\text{S}2}$(n,0.3) and $V_{\text{m}}^{\text{S}2}$(n,9.0) each varied linearly along the cell length as shown in Fig. 4C, and reversed symmetrically with a reversal in the field direction (not shown). Furthermore, $V_{\text{m}}^{\text{S}2}$(n,9.0) shifted in the hyperpolarizing direction, parallel to $V_{\text{m}}^{\text{S}2}$(n,0.3).

To determine how the characteristics of $V_{\text{m}}^{\text{S}2}$ varied with S2 amplitude, multiple shocks were applied to the same cell. Control experiments were first performed to exclude the possibility that repeated exposures of a cell to the excitation light and any subsequent dye phototoxicity might cause changes in $V_{\text{m}}^{\text{S}2}$. Fig. 5A shows a cell stimulated with four successive S1-S2 pairs with constant S1 and S2 pulse amplitudes, and the upper set of traces shows the $V_{\text{m}}^{\text{S}2}$ responses to one of the pairs. The field responses from one of the central sites, $V_{\text{m}}^{\text{S}2}$(3,t), are superimposed in the lower set of traces for the four S1-S2 pairs and show that $V_{\text{m}}^{\text{S}2}$(3,t) remained unchanged with successive stimuli.

Figure 5.

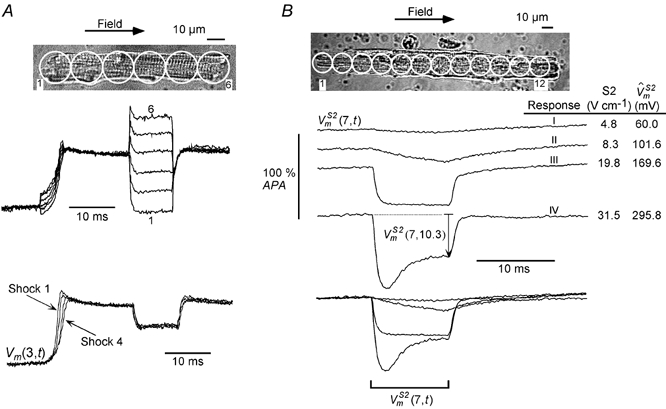
Dependence of $V_{\text{m}}^{\text{S}2}$ on S2 pulse amplitude

A, a cell (length: 101 μm) stimulated with four successive S1-S2 stimuli with identical S1 and S2 amplitudes (+4.5 and +31.4 V cm⁻¹, respectively). A, upper set of traces, the superimposed signals from all sites for one such pulse pair. A, lower set of traces, the superimposed $V_{\text{m}}^{\text{S}2}$ responses from site 3 for all 4 stimuli. $V_{\text{m}}^{\text{S}2}$ remained unaltered with successive stimuli. B, another cell (length: 210 μm) that was also stimulated with 4 successive stimuli but of increasing S2 amplitude. B, bottom portion, the resultant $V_{\text{m}}^{\text{S}2}$ responses from site 7 shown individually and also superimposed. The temporal behaviour (I–IV) of $V_{\text{m}}^{\text{S}2}$ response varied with S2 amplitude (see text for details).

Figure 5B shows a cell that was stimulated with four successive S1-S2 pairs with increasing S2 amplitudes. The $V_{\text{m}}^{\text{S}2}$ signals recorded from one of the central sites, $V_{\text{m}}^{\text{S}2}$(7,t), are shown individually and superimposed. $V_{\text{m}}^{\text{S}2}$ had four different characteristic responses, depending on the S2 amplitude. For an S2 of 4.8 V cm⁻¹, $V_{\text{m}}^{\text{S}2}$ remained essentially unperturbed (response I). On increasing S2 to 8.3 V cm⁻¹, $V_{\text{m}}^{\text{S}2}$ slowly hyperpolarized (response II). Further increases in S2 amplitude resulted in faster hyperpolarization. At an S2 amplitude of 19.8 V cm⁻¹, $V_{\text{m}}^{\text{S}2}$ hyperpolarized within ∼1 ms from the onset of S2 and then became flat for the remainder of the S2 pulse (response III). Finally, when the S2 amplitude increased to 31.5 V cm⁻¹, $V_{\text{m}}^{\text{S}2}$ exhibited a depolarizing trend after the initial rapid hyperpolarization (response IV). The corresponding $V_{\text{m}}^{\text{S}2}$ values for the various S2 pulses are also indicated in Fig. 5B. The superimposed traces facilitate a comparison of the magnitudes and relative speeds of the different $V_{\text{m}}^{\text{S}2}$ responses (Fig. 5B, lowermost traces).

We classified the responses of all 57 cells and 201 stimuli into the four types described above. A response was defined to be of type I if the mean V_m change at the end of the S2 pulse was less than 5 % of APA relative to V_m immediately after the S2 onset:

(1)

A response was considered to be of type II if ΔV₁ > 0.05, and V_m did not reach a peak in hyperpolarization during S2 duration. A response was classified to be of type III if ΔV₁ > 0.05 and V_m reached a peak in hyperpolarizization (V_mp) during the S2 pulse, but V_m at the end of the S2 pulse was depolarized by less than 5 % relative to V_mp :

(2)

If V_m reached a hyperpolarized peak during the S2 pulse and ΔV₂ > 0.05, the response was defined to be of type IV.

The numbers of occurrences for the various types of response over a broad range of ${\hat{V}}_{\text{m}}^{\text{S}2}$ are summarized as stacked column plots in Fig. 6A. The probability of occurrence of each response type was computed for each bin as the number of occurrences of that type divided by the total number of occurrences for all types in that bin. The results are plotted in Fig. 6B and can be used to estimate the ${\hat{V}}_{\text{m}}^{\text{S}2}$ corresponding to a 50 % probability of occurrence of a particular response type. In this manner, $V_{\text{m}}^{\text{S}2}$ threshold values for types II, III and IV behaviour were estimated to be 60, 110 and 220 mV, respectively. The corresponding electric field thresholds for the various response transitions can be estimated by performing an analysis similar to that of Fig. 6 with the applied field (scaled for a nominal cell length of 120 μm) as the x-axis, and were found to be 12, 22 and 44 V cm⁻¹, respectively.

Figure 6.

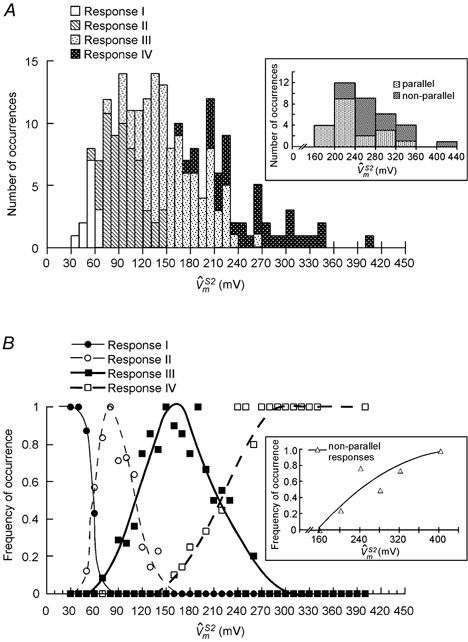
Summary of $V_{\text{m}}^{\text{S}2}$ response types for all cells (n = 57)

A, histogram summarizing the number of occurrences of various response types of $V_{\text{m}}^{\text{S}2}$ over the entire range of ${\hat{V}}_{\text{m}}^{\text{S}2}$ values. The inset shows sub-distribution of type IV responses into parallel and non-parallel time courses. The symbols in B represent frequency of occurrence of various response types for each bin. The curves drawn by eye through these symbols can be used to estimate the ${\hat{V}}_{\text{m}}^{\text{S}2}$ thresholds for occurrence of various response types. Inset in B is a frequency plot corresponding to inset of A, and depicts occurrence of non-parallel responses as a function of ${\hat{V}}_{\text{m}}^{\text{S}2}$. The curve is a second degree polynomial fit through the data. Note that a larger bin size was chosen for the insets to enhance the confidence in tracking the trend of non-parallel type IV responses with increasing ${\hat{V}}_{\text{m}}^{\text{S}2}$.

All of the S1 and S2 field responses described thus far consist of spatial patterns of polarizations that are distributed linearly along the length of the cell and parallel to each other during field pulses. However, at very high field intensities where response IV behaviour is observed, this pattern was sometimes altered. For 17 of the 25 stimuli that elicited response IV behaviour, the $V_{\text{m}}^{\text{S}2}$ responses were still distributed linearly along the cell but had non-parallel time courses. The sub-distribution of type IV responses into parallel and non-parallel time courses is shown in the inset of Fig. 6A, and the corresponding frequency plot is shown in Fig. 6B, inset. The threshold for occurrence of non-parallel responses was ∼200 mV, and their incidence increased with increasing S2 amplitude. Fig. 7 illustrates typical responses with non-parallel time courses. The cell shown in Fig. 7A was stimulated with two successive S1-S2 pulse pairs with increasing S2 amplitude. For the lower amplitude pulse (38.3 V cm⁻¹), the $V_{\text{m}}^{\text{S}2}$ responses from different sites showed parallel time courses (Fig. 7B, upper traces). However, for the higher amplitude pulse (56.2 V cm⁻¹), the time courses of the $V_{\text{m}}^{\text{S}2}$ responses became slightly convergent (Fig. 7B, lower traces). When the $V_{\text{m}}^{\text{S}2}$ responses were plotted at t = 1.0 ms and t = 9.0 ms (Fig. 7C), the slope of $V_{\text{m}}^{\text{S}2}$(n,9.0) was less than the slope of $V_{\text{m}}^{\text{S}2}$(n,1.0), unlike the parallel shift seen at lower field intensities (e.g. Fig. 4C). The change in slope is indicative of the development of an internal electric field (see Discussion). All 17 type IV responses with non-parallel time courses showed a post-S2 downward deflection (indicated by the arrow in Fig. 7B, lower traces) and a depression in the plateau potential. Moreover, all cells exhibited spontaneous contractions after the pulse, and either failed to fire or fired an abnormally slow action potential in response to a subsequent stimulus.

Figure 7.

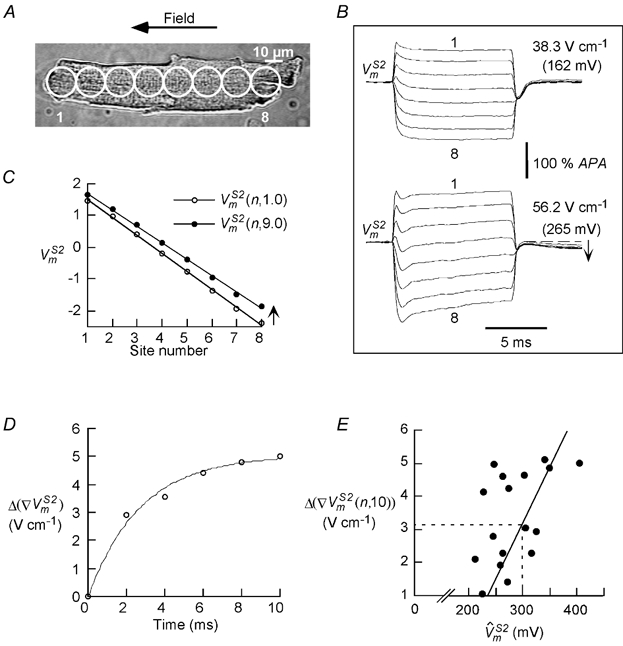
$V_{\text{m}}^{\text{S}2}$s with non-parallel time courses at high field intensities

A, a cell (length:143 μm)that was successively stimulated with S2 stimuli of 38.3 and 56.2 V cm⁻¹. B, upper and lower sets of traces, show the $V_{\text{m}}^{\text{S}2}$ responses for the two S2 stimuli,which change from a parallel behaviour (at 38.3 V cm⁻¹) to non-parallel behaviour (at 56.2 V cm⁻¹). Moreover,following the pulse a depression in the plateau potential was observed for the S2 of 56.2 V cm⁻¹, indicated by the arrow in B, lower set of traces. For comparison with other cells the ${\hat{V}}_{\text{m}}^{\text{S}2}$s are indicated in parentheses. C, the S2 response measured at 1 ms ($V_{\text{m}}^{\text{S}2}$(n, 1.0)) and 9 ms ($V_{\text{m}}^{\text{S}2}$(n, 9.0)). The $V_{\text{m}}^{\text{S}2}$(n, 9.0) decreased in slope, and shifted in the depolarizing direction from $V_{\text{m}}^{\text{S}2}$(n, 1.0). D, the slope reduction Δ (∇$V_{\text{m}}^{\text{S}2}$), which is equivalent to the internal field E_i, rises exponentially during S2 (τ = 2.7 ms). E, the slope reduction at the end of S2, Δ(∇$V_{\text{m}}^{\text{S}2}$(n, 10)), increases monotonically with ${\hat{V}}_{\text{m}}^{\text{S}2}$ (r = 0.66, P < 0.05, n = 17).The dashed lines indicate that E_i is 3.2 V cm⁻¹ for a ${\hat{V}}_{\text{m}}^{\text{S}2}$ of 300 mV.

We further characterized the non-parallel behaviour of the $V_{\text{m}}^{\text{S}2}$ responses by quantifying the changes in the slopes of the $V_{\text{m}}^{\text{S}2}$ responses as a function of time. The slope reduction (Δ(∇$V_{\text{m}}^{\text{S}2}$)) was determined by taking the difference in the slope of $V_{\text{m}}^{\text{S}2}$ along the cell length at time t (∇$V_{\text{m}}^{\text{S}2}$(n,t)) and the slope early after onset (t = 0.3 ms) of the S2 pulse (∇$V_{\text{m}}^{\text{S}2}$(n,0.3)). Δ(∇$V_{\text{m}}^{\text{S}2}$) was plotted as a function of time and found to rise exponentially to an asymptotic value with a time constant (τ) of ∼2.7 ms (Fig. 7D). A similar reduction in slope was observed for all type IV responses with non-parallel time courses (τ = 7.2 ± 3.2 ms, n = 17). The final slope reduction attained at the end of the S2 pulse, Δ(∇$V_{\text{m}}^{\text{S}2}$)(n,10), was found to increase monotonically with ${\hat{V}}_{\text{m}}^{\text{S}2}$ (Fig. 7E, r = 0.66, P < 0.05, n = 17). For type IV responses with parallel time courses, Δ(∇$V_{\text{m}}^{\text{S}2}$(n,10)) was unmeasurable and below our measurement sensitivity of 1 V cm⁻¹.

Not apparent from Fig. 6 is the net change in $V_{\text{m}}^{\text{S}2}$ polarization with increasing S2 amplitude and ${\hat{V}}_{\text{m}}^{\text{S}2}$. Following the S2 pulse, the $V_{\text{m}}^{\text{S}2}$ responses from all sites converged to a common hyperpolarized potential within ∼0.3 ms (e.g. refer to superimposed $V_{\text{m}}^{\text{S}2}$ responses in Fig. 2C and Fig. 4B, and inset in Fig. 5A). This post-shock common potential was measured with reference to the pre-S2 plateau potential (Fig. 8, inset) in all 57 cells for 201 applied stimuli and is plotted in Fig. 8. For ${\hat{V}}_{\text{m}}^{\text{S}2}$ < 220 mV (vertical dashed line), which is the transition point between responses III and IV, the magnitude of $V_{\text{m}}^{\text{S}2}$ hyperpolarization at time t = 10.3 ms ($V_{\text{m}}^{\text{S}2}$(n,10.3)) increased monotonically. For ${\hat{V}}_{\text{m}}^{\text{S}2}$ > 220 mV the $V_{\text{m}}^{\text{S}2}$(n,10.3) saturated and then decreased slightly with increasing ${\hat{V}}_{\text{m}}^{\text{S}2}$, presumably because the late depolarizing trend in type IV responses counterbalanced some of the early hyperpolarization during the S2 pulse. This decrease in $V_{\text{m}}^{\text{S}2}$(n,10.3) was particularly evident in type IV responses with non-parallel time courses (e.g. compare post-S2 potential for the two sets of traces in Fig. 7B).

Figure 8.

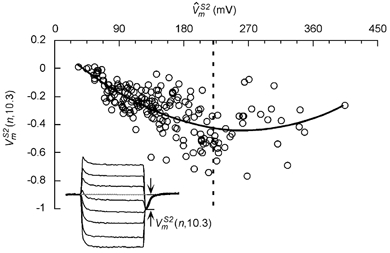
Net hyperpolarization at S2-break ($V_{\text{m}}^{\text{S}2}$(n,10.3))

$V_{\text{m}}^{\text{S}2}$(n,10.3) is plotted for 201 stimuli in 57 cells and increased montonically with ${\hat{V}}_{\text{m}}^{\text{S}2}$ up to a ${\hat{V}}_{\text{m}}^{\text{S}2}$ value of 220 mV (50 % transition point for the type III and IV responses). The thick line is a second degree polynomial fit through the data points. Inset shows the method for measuring post-S2 hyperpolarization.

DISCUSSION

This report is the first systematic study to quantify the field responses of single cardiac cells during different phases of the action potential and with varying field intensities. Previous studies of field stimulation of single cardiac cells have focused mainly on showing that the two ends of the cell polarize in opposite directions (Knisley et al. 1993; Windisch et al. 1995; Cheng et al. 1999). A multichannel optical mapping system was used here to perform detailed measurements of the spatial and temporal components of the electric field-induced transmembrane potential (V_m) responses in adult guinea-pig ventricular myocytes. The main results are as follows: (1) Uniform electric fields oriented along the long axis of the cell induce a spatial pattern of membrane polarization that is linearly distributed along the cell length. This pattern appears immediately after the onset of the field pulse and is independent of the phase of the action potential (rest or plateau) during which the field is applied. (2) Accompanying the linear spatial pattern is a time-varying response that is depolarizing during rest and hyperpolarizing during the action potential plateau. These temporal changes are common to all sites along the cell length, resulting in parallel shifts in the V_m responses during the field pulse. (3) The temporal components of the field responses vary according to field intensity. For pulses at rest, threshold pulses result in a slow depolarization followed after a latency delay by rapid phase 0 depolarization, whereas higher amplitude and longer duration pulses result in an immediate phase 0 depolarization during the field pulse. For pulses during the action potential plateau, four types of hyperpolarizing response behaviour can be observed, depending on the field amplitude. 4) At field strengths greater than ∼45 V cm⁻¹ (that result in V_m of 200 mV or larger), the V_m responses from different sites on the cell can have non-parallel time courses. This behaviour is accompanied by a post-pulse depression in the plateau potential, spontaneous contractions after the pulse, and abnormal excitatory behaviour in response to subsequent stimuli.

In the discussion that follows we interpret the field-induced V_m responses during S1 and S2 pulses in terms of their temporal components. We designate the initial, rapid component of the field response as V_mr and the remainder of the field response as V_ms.

State-invariant component of the field responses (V_mr)

The initial rapid component, V_mr, is in accord with the theoretical analysis of passive cylindrical cells stimulated by a uniform electric field (Bernhardt & Pauly, 1973; Klee & Plonsey, 1976; Jeltsch & Zimmerman, 1979). Following the initial 0.3 ms transient at the onset of an S1 pulse applied at rest, the $V_{\text{m}}^{\text{S}1}$ responses undergo linear shifts along the length of the cell. These shifts persist for the remainder of the S1 pulse (e.g. Fig. 3C), so that the $V_{\text{m}}^{\text{S}1}$ responses track one other in a parallel fashion. Maximum depolarization occurs at the cell end facing the cathode and maximum hyperpolarization at the end facing the anode. The polarization reverses symmetrically along the cell with a reversal in the field direction (Fig. 2C). A similar behaviour is seen for $V_{\text{m}}^{\text{S}2}$ immediately following the onset of an S2 pulse applied during the action potential plateau. If we designate the initial (t = 0.3 ms) components of the $V_{\text{m}}^{\text{S}1}$ and $V_{\text{m}}^{\text{S}2}$ responses as V^S1_mr and V^S2_mr, respectively, both V^S1_mr and V^S2_mr vary linearly along the cell length (Fig. 3C and Fig. 4C), irrespective of the field direction, and have similar slopes at the same field intensity. Moreover, they vary in direct proportion to the strength of the electric field (not shown). Thus, we deem the initial rapid response to be independent of the phase, or physiological state, of the action potential. One consequence of the heterogeneity in V_m along the length of the cell is that the flux of ions through voltage-gated ion channels and electrogenic transporters will be non-uniform. We have recently reported that spatial gradients in intracellular calcium exist during field stimulation (Sharma & Tung, 2002b).

State-dependent component of the field responses (V_ms)

Following the initial dispersion of the V_m responses at rest (V^S1_mr), the residual responses during S1 stimulation exhibit parallel time courses (Fig. 3B and Fig. 4B). Designating the slow, time-varying component of $V_{\text{m}}^{\text{S}1}$ as $V_{\text{m}}^{\text{S}1}$, we see that $V_{\text{m}}^{\text{S}1}$ exhibits depolarization and is the same for all of the recording sites. Hence, the $V_{\text{m}}^{\text{S}1}$ responses differ only by their initial V^S1_mr values. Moreover, there exists a central site at which V^S1_mr is zero (e.g. site 5 in Fig. 3B) and where the S1 response is smoothly continuous with the V_m signals before and after the S1 pulse. This observation suggests that $V_{\text{m}}^{\text{S}1}$ reflects an average depolarization of the cell response. A similar conclusion can be reached for the time-varying $V_{\text{m}}^{\text{S}2}$ component of the $V_{\text{m}}^{\text{S}2}$ signals during the action potential plateau (Fig. 2C and Fig. 4B), except that the average cell response is now hyperpolarizing. The dissimilarity between $V_{\text{m}}^{\text{S}1}$ and $V_{\text{m}}^{\text{S}2}$, and their variation with pulse duration, pulse amplitude, and phase (physiological state) of the action potential, support the notion that these components arise from active, voltage-dependent currents in the cell membrane. These observations are in accord with the theoretical field responses of cardiac cells with active membranes (Tung & Borderies, 1992; Leon & Roberge, 1993; Krassowska & Neu, 1994; Fishler et al. 1996; Cheng et al. 1999) and with previous experimental studies (Windisch et al. 1995; Cheng et al. 1999).

Four types of response behaviour can be observed, with transitions between the behaviours occurring at ${\hat{V}}_{\text{m}}^{\text{S}2}$ values of 60, 110 and 220 mV. The hyperpolarizing trend in $V_{\text{m}}^{\text{S}2}$ increases with ${\hat{V}}_{\text{m}}^{\text{S}2}$, and can occur within the first millisecond following the onset of S2 (response types III and IV in Fig. 5B). At the break of the S2 pulse, $V_{\text{m}}^{\text{S}2}$ remains hyperpolarized relative to the pre-S2 potential for all field amplitudes and response types, implying that depolarizing and hyperpolarizing currents are not balanced along the cell length, and that a net positive charge has been removed from the cell capacitance during the S2 pulse. Clearly, the current imbalance and magnitude of removed charge increase monotonically with the S2 amplitude (Fig. 8) up to a ${\hat{V}}_{\text{m}}^{\text{S}2}$ of ∼220 mV. Thereafter, the amount of hyperpolarization levels off, suggesting a saturation in net hyperpolarizing currents, or more likely an increase in net depolarizing currents (e.g. via electroporation).

Although this study focused mainly on guinea-pig cells, a few experiments were performed on rabbit ventricular myocytes. In these cells, a depolarizing $V_{\text{m}}^{\text{S}1}$ and hyperpolarizing $V_{\text{m}}^{\text{S}2}$ were also observed. The temporal behaviour of $V_{\text{m}}^{\text{S}2}$ and its change with S2 amplitude were similar to the guinea-pig results, suggesting that some combination of ionic currents that are preserved across different mammalian species is involved in shaping the field responses. Contrary to our results, Knisley et al. (1993) observed nearly symmetrical $V_{\text{m}}^{\text{S}2}$ responses with little hyperpolarizing shift. The difference may exist because of the longer S1-S2 interval (50 ms) used in their study, or the low signal-to-noise ratio (∼2.5) of their recordings that may have precluded an accurate measure of any asymmetry.

Physical interpretation of the two components of the field response

We present a simple physical interpretation of V_mr and V_ms based on theoretical considerations of a field-stimulated cell. For generality, variables that to this point have been written as a function of site number (n) are now replaced with their continuum forms; e.g. V_m(n,t) is replaced by V_m(x,t). In the most general case V_m can be expressed as,

(3)

where φ_i is the intracellular potential, and φ_o is the extracellular potential. In the right hand side of eqn (3), φ_o scales with the applied electric field (E_o) and in the steady-state varies linearly with position for a prolate spheroidal cell with a relatively non-conductive membrane (Klee & Plonsey, 1976; Tung & Borderies, 1992). The form factor f is approximately 1 when the ratio of major to minor axis is large, and between 1 and 1.5 otherwise. The time to reach steady state for a step change in external field is ultrarapid and much faster than the dynamics of physiological currents. It depends on the intracellular and extracellular conductivities, membrane specific resistance, membrane specific capacitance, and cell size, and has been estimated to be of the order of 10 μs (Cartee & Plonsey, 1992).

The polarization caused by the field pulse activates/ inactivates the membrane ionic currents in a non-uniform fashion along the cell length, resulting in a net charge transfer across the cell membrane. Because the intracellular space is small and conductive, this will produce a time-varying but spatially uniform change in φ_i (a sustained isopotential condition). Thus, eqn (3) can be rewritten as:

(4)

Hence, φ_i acts as the cellular physiological state variable during field stimulation, and substitutes for V_m, which is the customary variable for space-clamped membranes.

In our experiments, we separated V_m into rapid (V_mr) and slow (V_ms) components. V_mr is independent of the phase of the action potential. It reverses with field polarity and varies linearly along the length of the cell. V_ms varies with the phase of the action potential during which the field pulse is applied, changes as a function of time during the field pulse, and is identical for all of the sites in the membrane. Therefore, our observations imply that V_m(x,t) can be expressed as:

(5)

Comparing eqns (4) and (5) one can associate V_mr with fE_ox, and V_ms with φ_i. Therefore, in response to a step change in the external field, the cell initially polarizes in a passive fashion as a consequence of the extracellular potential gradient. The passive polarization, in turn, causes a spatially non-uniform change in activity of ion channels and electrogenic transporters along the cell length. Although the intracellular space remains isopotential, the net imbalance of ionic currents causes a net charge to be transferred across the cell membrane capacitance, and the intracellular potential to change with time. Consequently V_m will deviate by a time varying offset from that expected for a passive cell. Stimulation at rest results in a net inward flow of positive charge and membrane depolarization, while stimulation during the plateau results in a net outward flow of charge and membrane hyperpolarization. One can also use an alternative scheme to interpret V_m that uses the field response from the central site as a ‘common-mode’ component, which reflects the active response of the membrane, and the remainder of the field response as a ‘differential-mode’ component, which reflects the passive response of the membrane (Sharma & Tung, 2000; Sharma & Tung, 2002a).

Given the interpretation presented above, the slope of the V_mr responses (∇V_mr) should be proportional to fE_o. ∇V_mr can be obtained from data such as that of Fig. 4C by converting the abscissa into centimetres and the ordinate into volts by using a typical APA value of 128 mV. An analysis of all the S2 responses with parallel time courses (n = 184 from 50 cells) shows that ∇$V_{\text{m}}^{\text{S}2}$ increases monotonically with S2 amplitude with a slope of 0.85E_o (r = 0.83, P < 0.001), a value close to but somewhat less than the value of 1–1.5 expected for a prolate spheroidal cell with a non-conductive membrane. This effect might explain why the actual fields (12, 22 and 44 V cm⁻¹) required for various response transitions are greater than the fields that would be calculated (10.0, 18.3, 36.7 V cm⁻¹) if one assumes a linear, passive relationship between E_o and ${\hat{V}}_{\text{m}}^{\text{S}2}$ (i.e. E_o = 2${\hat{V}}_{\text{m}}^{\text{S}2}$/L, (Susil et al. 1999), where L = nominal cell length of 120 μm).

Several explanations may account for the less than expected slope between ∇$V_{\text{m}}^{\text{S}2}$ and S2 amplitude. A misalignment of the longitudinal axes of our cells with the field axis by ∼30 deg could give rise to the observed discrepancy, although our alignment accuracy was better than ∼10 deg on average. Alternatively, if the conductance of the ends of the cell were to increase substantially during field stimulation, an intracellular electric field could develop in the same direction as E_o, thus reducing the polarization at a given location and decreasing the slope of polarization along the cell length. However, evidence is lacking that suggests a plausible source for this conductance. Gap junction channels might remain functionally intact at the cell ends following cell isolation (Severs et al. 1989), but are presumably sealed in an isolated cell. There is as yet no data that their conductance increases significantly in a voltage-dependent manner. A third possibility is that the passage of any small current through the longitudinal and transverse segments of the transverse (T) tubule system (Ayettey & Navaratnam, 1978) could produce a decline in the V_m response from the surface to the core of the cell. Since the voltage-sensitive dye also binds to T tubular membranes, the fluorescence signal reflecting the volumeaveraged V_m signal at any site on the cell could be less than that at the sarcolemma.

Parallel versus non-parallel behaviour

For fields greater than ∼45 V cm⁻¹ some type IV responses have non-parallel and slightly convergent time courses (e.g. lower set of $V_{\text{m}}^{\text{S}1}$ traces in Fig. 7B). This may be achieved if the intracellular potential in eqn (3) is a function of both time and space, e.g.

(6)

E_i is an internal field that develops with time in the same direction as the applied field. Substituting eqn (6) into eqn (3) and taking the spatial gradient into account results in:

(7)

from which the decline of the spatial gradient of V_m(t) from its initial value at the S2 onset is:

(8)

(Figure 7D suggests that E_i increases exponentially with time. Assuming that E_i is zero at the beginning of the S2 pulse, it reaches a value of ∼5 V cm⁻¹ by the end of the S2 pulse, when the external field is 56.2 V cm⁻¹ and ${\hat{V}}_{\text{m}}^{\text{S}2}$ is 265 mV.

It is well known that V_m in the range of several hundred millivolts causes a many-fold increase in membrane conductance, presumably by the formation of non-specific nanometre-sized pores, a phenomenon commonly known as electroporation (Weaver, 1993). Electroporation is a graded process in cardiac cell membranes, but begins to occur at V_m of ∼200 mV and increases with increasing V_m (Tung, 1996). Since a typical 120 μm-long cell stimulated with a ∼45 V cm⁻¹ field is expected to develop a V_m of ∼230 mV at its ends, the electroporation and subsequent increase in membrane conductance at the cell ends would allow the longitudinal flow of intracellular current, the development of E_i, and type IV responses with non-parallel time courses. The increase in occurrence of non-parallel type IV responses with increasing ${\hat{V}}_{\text{m}}^{\text{S}2}$ (Fig. 6B, inset) is consistent with the stochastic nature of electroporation. Moreover, the magnitudes of electroporation and E_i are expected to increase monotonically with ${\hat{V}}_{\text{m}}^{\text{S}2}$ (Fig. 7E). Finally, post-S2 depression in plateau potential and excitability, together with spontaneous contractions, were observed for all 17 cells with non-parallel type IV responses and are consistent with the electroporation hypothesis, because an increase in membrane conductance would tend to shunt V_m towards zero.

Implications for cardiac tissue responses during defibrillation

Fluorescence V_m signals have been recorded from frog atrial tissue and show a depolarizing bias for point stimuli applied at rest (Neunlist & Tung, 1994; Tung et al. 1994). In contrast, V_m signals for stimuli applied during the early action potential plateau show a hyperpolarizing biased $V_{\text{m}}^{\text{S}2}$ in frog atrium (Neunlist & Tung, 1995), strands of cultured neonatal rat cells (Gillis et al. 1996), and guinea-pig papillary muscle (Zhou et al. 1998). Hence, in many instances the field responses of cells within the heart wall resemble those of isolated cells in terms of the average cellular response. Modelling studies suggest that virtual sources can arise from the resistive heterogeneities in the extracellular and intracellular spaces (Sobie et al. 1997; Fishler, 1998). The most ubiquitous inhomogeneities in the heart arise from the intercellular gap junctions. These are theoretically able to produce a sawtooth pattern of polarization (Plonsey & Barr, 1986) that has been demonstrated in isolated cell-pairs (Sharma & Tung, 2001) and is believed by some to play a role during defibrillation (Keener, 1998). The field causes a non-uniform polarization of each cell with an abrupt discontinuity in V_m at the intercellular junctions. The subsequent heterogeneous perturbations in ionic currents and net polarization change of the cell in the tissue proceeds in a manner similar to that of the isolated cell. The contribution of the sawtooth effect might be expected to be particularly important under pathophysiological conditions such as ischaemia (Huang et al. 1999), when the cells in the tissue become relatively uncoupled and intercellular resistance is elevated.

The similarities between single cell and tissue responses can be more than merely qualitative. When 110–150 μm-wide, linear strands of cultured neonatal rat ventricular cells were field stimulated in the transverse direction, the initial V_m responses were linear and symmetrical across the strand width following the onset of an S2 pulse (Fast et al. 2000; Tung & Kleber, 2000). The initial responses were followed by a slower hyperpolarizing component that activates in the range of 5–9 V cm⁻¹, and by a delayed depolarizing component that activates in the range of 25–27 V cm⁻¹. These strand responses are similar to those that we observed in the single cell (Fig. 5 and Fig. 6).

At the same time, tissue responses contain additional complexities not found in single cells. The tissue modelling results of Susil et al. (1999) suggest that the speed of polarization during field stimulation decreases with increasing tissue size, owing to the increased separation between the virtual sources at the two ends. Therefore, the rise time of V_mr in tissue may be substantially slower than in single cells. Indeed, the rapid component measured within the first 3 ms of the field onset in linear strands of cultured cardiac cells disappears when the strand width is increased from 150 to 500 μm (Fast et al. 2000). In curved strands of cells the V_m responses to transverse field stimulation can be separated into an initial, position-dependent polarization (like V_mr) and a time-dependent global component (like V_ms) whose characteristics are a function not only of field strength but also of strand curvature (Tung & Kleber, 2000).

Another difference between tissue and cellular responses can result from the intracellular current that flows from cell to cell within a tissue. The pathways for current flow will be dictated by the three-dimensional architecture and anisotropy of the tissue. Experiments with transversely stimulated strands of cultured cardiac myocytes have shown that field responses have markedly non-parallel time courses at intensities of 10 to 30 V cm⁻¹ even when the strand widths are comparable to the length of a typical cardiac cell (Fast et al. 2000; Tung & Kleber, 2000). This suggests that in multicellular tissue a time-dependent intracellular electric field, similar to our E_i, develops at lower field strengths. Since the V_m that develops at the strand boundaries is much lower than that required for electroporation, the E_i-producing current is likely to pass through existing membrane ion channels or electrogenic transporters.

Finally, it should be noted that a hallmark of field-induced polarizations in cardiac tissue is that they always occur in pairs, with regions of opposite polarity adjacent to one other. Using the single cell as a model system for paired polarizations that are closely coupled (∼120 μm scale), our study shows that for pulses applied during the early plateau, V_m slowly returns after the stimulus to the pre-pulse potential for type II responses (Fig. 5B). At higher field intensities that cause type III and IV responses, a rapid post-S2 reactivation of V_m can be seen. A similar post-excitatory response has been proposed as the mechanism for break excitation in tissue, that involves the reactivation of fast sodium channels in membranes that are hyperpolarized during their refractory period, followed by re-excitation of those membranes by neighbouring depolarized membranes (Roth, 1995). Recent experimental and computational modelling studies suggest that the excitation wave front emanating from the break response can interfere with reentrant activity underlying cardiac arrhythmias, and hence may be a mechanism for defibrillation (Trayanova et al. 1998b; Efimov et al. 2000). Although the initiation of a wave front may be mimicked at the cellular level, the pattern of post-excitatory propagation will depend strongly on the structural properties of the tissue.

Limitations of the study

All experiments reported in this study were carried out on cells with their long axis aligned along the field direction, and we attributed the V_ms response to an imbalance in ionic currents through membrane channels. It is possible that gap junctional channels at the ends of the cell may have contributed to V_ms. One way to address this issue would be to apply transverse stimulation to the cell, so that fewer gap junctions would experience large polarization. Although experiments were performed on transversely stimulated cells (n = 11) and showed qualitatively the same behaviour (data not shown), quantitative conclusions could not be drawn because of the limited spatial resolution in our measurements.

Since we always used low S1 amplitude pulses (< 10 V cm⁻¹) the S1 amplitude-dependent changes in temporal behaviour of $V_{\text{m}}^{\text{S}1}$ were not investigated thoroughly. Moreover, we focused primarily on the field responses at rest and during the early plateau, and any further dependence of these responses on action potential phase was not investigated. Although such data do not yet exist for single cells, Gillis et al. (1996) observed spatially symmetrical responses in cultured strands of cells for field pulses delivered transverse to the strand during the repolarizing phase of the action potential. This result suggests flat (constant) $V_{\text{m}}^{\text{S}2}$ responses. We also found $V_{\text{m}}^{\text{S}2}$ to be flat in some cells in which action potentials were abnormally short and where S2 occurred during the repolarization phase. Thus, one may expect $V_{\text{m}}^{\text{S}2}$ to be hyperpolarizing during the plateau phase, flat during the repolarizing phase, and depolarizing during the resting phase of the action potential.

Glossary

t

Time

n

Site number

F(n,t)

Fluorescence signal recorded from site n at time t

V_m(n,t)

Transmembrane potential for site n derived from F(n,t)

∇V_m

The spatial gradient (slope) of V_m along the cell length

Δ(∇V_m)

Changes in ∇V_m with time

APA

Action potential amplitude of F(n,t)

$V_{\text{m}}^{\text{S}1}$(n,t)

Response for site n measured with respect to the resting potential and at time t from the onset of S1

$V_{\text{m}}^{\text{S}2}$(n,t)

Response for site n measured with respect to the plateau potential and at time t from the onset of S2

V _mr

Initial, rapid component of the V_mresponse

V _ms

Late, slower component of the V_m response

${\hat{V}}_{\text{m}}^{\text{S}2}$

Maximum V_m experienced by a cell, measured at 0.3 ms after the S2 onset as the average of absolute polarizations at the two ends of the cell

φ_i

Intracellular potential

φ_o

Extracellular potential

E _i

Intracellular electric field

E _o

Extracellular electric field

f

Form factor accounting for cell shape