Abstract
We have tested whether the cardiovascular changes at the onset of exercise could be simulated only by an increase in the baroreflex set point and locally induced vasodilatation in the exercising muscles. The mathematical model consists of a heart, a linear elastic arterial reservoir and two parallel resistive vascular beds. The arterial baroreflex loop is modelled by three separate time domain processing objects, each with its own gain, time constant and delay. These are intended to simulate the action of a sympathetic signal to the peripheral vascular bed, a parasympathetic signal to the heart and a sympathetic signal to the heart. We used this model with previously published experimental data to estimate the unknown parameters in the reflex control loop. In all 10 subjects and in the global averaged response, the short-term cardiovascular responses were adequately simulated by using individual sets of parameters in the model. An increase in the baroreflex set point and locally induced vasodilatation in the exercising muscles can explain almost all of the cardiovascular changes in the recorded variables (mean arterial pressure, RR interval and stroke volume) at the onset of exercise.
In the present study we utilized physiological data (Toska & Eriksen, 1994) together with a mathematical model to test whether the cardiovascular changes at the onset of exercise could be simulated by an increase in the baroreflex set point and locally induced vasodilatation in the exercising muscles.
The central command probably makes a major contribution to the complex changes in both respiration and circulation at the onset of exercise, as reviewed by Raven et al. (1997), whereas vasodilatation in the exercising muscles is controlled by local mechanisms (Walløe & Wesche, 1988; Kiens et al. 1989; Laughlin et al. 1996).
The aim of the present study was to test whether the onset of moderate exercise could be simulated on the basis of these two control mechanisms, since a full and detailed model of the cardiovascular changes at the onset of exercise could become very complex. A number of mathematical models of the circulation have been presented (Green & Jackman, 1984; Melchior et al. 1992; ten Voorde, 1992; Lu et al. 2001), each of which is generally designed to shed light on one or a few specific physiological problems. The mathematical model presented here is a modified version of an earlier published model (Toska et al. 1996) and illustrates the potential of computer modelling. Minor changes to the earlier model, which was designed to explain the cardiovascular changes on thigh cuff inflation, make it possible to explain almost all of the cardiovascular changes at the onset of exercise by means of just two simple mechanisms. These are a rapid increase in baroreflex set point (Bevegård & Shepherd, 1966; Potts et al. 1993) and locally induced vasodilatation of the resistance vessels in the exercising muscles. The design of our model is very similar to the block diagram presented by Warner et al. (1964) in their Fig. 1.
Figure 1. Block diagram representing the mathematical model of baroreflex control of human arterial circulation.
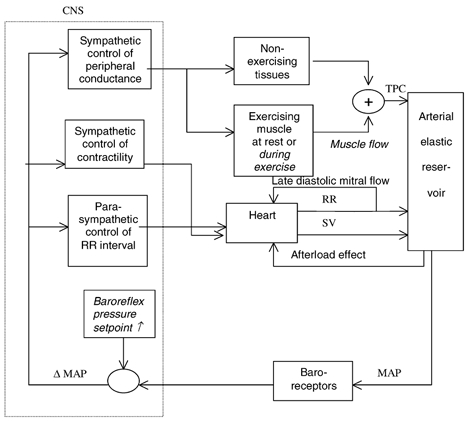
Arrows show information flow between blocks. CNS, central nervous system; TPC, total peripheral conductance; RR, RR interval; SV, stroke volume; MAP, mean arterial pressure. Equations (1) to (8) describe functional relationships between input and output of blocks. The text in italic font indicates the changes in the model from rest to exercise.
With the present model, we simulated both the global averaged response and each of the subject's responses, and thus obtained different sets of parameters for each individual. In repeated model simulations, the control parameters were systematically adjusted by an automated algorithm that minimized deviations between the time courses of the cardiovascular variables simulated by the model and the previously recorded responses in each individual.
The three main simulated time courses from the model and hence the variables that were adjusted to obtain the best fit to the experimental results, were mean arterial pressure (MAP), RR interval (RR) and stroke volume (SV). Total peripheral conductance (TPC) was then calculated by TPC = SV/(MAP × RR).
The present model includes a detailed description of the baroreflex control loop combined with a simple beat-to-beat model of the circulation, because our previous recordings were sampled on a beat-to-beat basis.
| Glossary | |
|---|---|
| B(t) | Baroreflex signal (mmHg) |
| Bph | Parasympathetic signal to the heart (mmHg) |
| Bsh | Sympathetic signal to the heart (mmHg) |
| Bsp | Sympathetic signal to the peripheral vessels (mmHg) |
| C | Aortic compliance (l mmHg−1; C= 0.00005 l mmHg−1 kg−1) |
| dph | Baroreflex delay, parasympathetic (s; dph= 0.25 s) |
| dsh | Baroreflex delay,sympathetic to the heart (s; dsh= 1.00 s) |
| dsp | Baroreflex delay,sympathetic to the peripheral vessels (s; dsp= 6.00 s) |
| dmf | Muscle flow delay (seconds; dmf= 1.8 s) |
| G | Conductance in a peripheral vascular bed (l s−1 mmHg−1) |
| Ge | Conductance in the exercising parts of the body (l s−1 mmHg−1) |
| G0 | Total peripheral conductance (TPC)before exercise (l s−1 mmHg−1) |
| Gr | Conductance in the non-exercising parts of the body (l s−1 mmHg−1) |
| Gp | TPC (l s−1 mmHg−1) |
| Ka | Sensitivity to afterload effect on stroke volume (ml mmHg−1; adjusted) |
| Kph | Sensitivity to parasympathetic signal to the heart (s mmHg−1; adjusted) |
| Ksh | Sensitivity to sympathetic signal to the heart (l mmHg−1; adjusted) |
| Ksp | Sensitivity to sympathetic signal to the peripheral vessels (l mmHg−1; adjusted) |
| ExCond | Fraction of TPC in the exercising parts of the body (fraction; ExCond = 0.15) |
| P ˙ | Time-differentiated pressure in the aorta (mmHg s−1) |
| P(t) | Time-dependent mean arterial pressure (mmHg) |
| P0 | Mean arterial pressure before exercise (mmHg) |
| Pa | Instantaneous pressure in the aorta (mmHg) |
| Pd | End-diastolic pressure (mmHg) |
| Ps(t) | Set point for arterial pressure control (mmHg) |
| Q ˙h | Flow out of the heart (l s−1) |
| Q ˙m | Mitral flow late in diastole (l s−1; adjusted) |
| Q ˙mf | Muscle flow (l s−1; adjusted) |
| Q ˙p | Total flow in the peripheral arteries (l s−1) |
| RR | RR interval (s) |
| RR0 | RR interval before exercise (s) |
| SV | Stroke volume (l) |
| SV0 | Stroke volume before exercise (l) |
| Tc,ph | Baroreflex time constant, parasympathetic to the heart (s; Tc,ph= 0.25 s) |
| Tc,sh | Baroreflex time constant,sympathetic to the heart (s; Tc,sh= 10s) |
| Tc,sp | Baroreflex time constant, sympathetic to the peripheral vessels (s; Tc,sp= 10s) |
| Tc,set | Set point time constant (s; adjusted) |
| Tc,mf | Muscle flow time constant (s; adjusted (constraint to less than 13.2 s)) |
| tcount | Time when countdown is started (s) |
| tex | Time when exercise is started (s) |
Methods
Experimental data
The methods used to record the responses in 10 healthy volunteers have been reported in detail elsewhere (Toska & Eriksen, 1994). Briefly, each subject rested supine before exercise. After a 10 s countdown, the subject performed moderate, dynamic exercise while supine. The cardiovascular responses were recorded beat-by-beat: SV by an ultrasound Doppler method (Eriksen & Walløe, 1990), MAP by a finger plethysmograph (Finapres) (Imholz et al. 1990) and RR interval by electrocardiogram. CO and TPC were then calculated beat-by-beat from these recorded data. In each of the 10 healthy subjects, coherent averaged responses were calculated from several identical experimental runs and these were called the individual responses. The global averaged response was calculated from a total of 63 sets of results from 10 subjects. All subjects gave written informed consent, and all procedures used conformed with the Declaration of Helsinki.
Mathematical model
A schematic representation of the model is shown in Fig. 1. The mathematical model is a simplified representation of the arterial cardiovascular system, including a non-distributed model of the peripheral arteries and baroreflex control of arterial pressure. The haemodynamic variables are calculated on a beat-to-beat basis, whereas the baroreflex time processing is modelled in a continuous time scale. Accordingly, the pulsatility of arterial pressure and flow is not modelled, and deviations of MAP from its set point serve as the input to the baroreflexes. The baroreflexes are divided into three parts: sympathetic heart contractility control, parasympathetic RR interval control and sympathetic control of the peripheral arteries. Each of the three parts has its own time processing with a preset gain, time constant, and delay. In several initial model simulation runs, the simulation of a sympathetic RR interval reflex did not improve the fit between the simulated and recorded time courses. This reflex was therefore omitted in all subjects and also because the sympathetic RR interval response is probably not involved when RR > 0.6 s (HR < 100 beats min−1) (Rowell, 1993). The arterial circulation is divided into sections representing the heart, the large arteries and the peripheral vessels, which are further divided into two parts representing the exercising part and the rest of the body. All cardiovascular variables are calculated beat-to-beat, and usually no beat-numbering indexes are used. Whenever the values from a previous beat are used, this is indicated by subscripts, i.e. RR(n - 1). The variables are usually calculated as deviations from the mean value before countdown to exercise, which is indicated by the index zero, i.e. RR0. The baroreflex processing objects operate in a continuous time scale, and this is denoted by the time variable (t). Details of the various parts of the model are described below.
Modelling the heart
For each cardiac cycle, new values of RR interval and SV are calculated. The RR interval depends of the baroreflex input of a parasympathetic signal (Bph). The signal can be compared with the firing frequency of the respective nerves, but the signal is expressed in mmHg. The heart has in itself a certain sensitivity (seconds per millimetre of mercury) to the parasympathetic influence, Kph. Kph is equivalent to gain in the reflex.
| (1) |
SV is dependent on afterload, preload and the sympathetic control of the contractility of the heart. The effect of afterload is calculated from the end-diastolic pressure of the previous beat (Pd(n - 1)) and afterload sensitivity (Ka). A linear relation between afterload and SV reduction is assumed. The influence of changes in the RR interval on the preload conditions of the heart is approximated by the late diastolic filling rate of the left ventricle. A constant flow through the mitral valve during the late stage of diastole is then assumed. This late diastolic filling, identical to the mitral flow before atrial systole, is 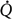 m. A perfect Frank-Starling mechanism is assumed, resulting in constant end-systolic ventricular volumes (Herndon & Sagawa, 1969). An increase in left ventricular filling will thus increase the ventricular output by the same amount. The sympathetic control of the contractility depends on the baroreflex input of a sympathetic (Bsh) signal, and Ksh is equivalent to the gain in the baroreflex.
m. A perfect Frank-Starling mechanism is assumed, resulting in constant end-systolic ventricular volumes (Herndon & Sagawa, 1969). An increase in left ventricular filling will thus increase the ventricular output by the same amount. The sympathetic control of the contractility depends on the baroreflex input of a sympathetic (Bsh) signal, and Ksh is equivalent to the gain in the baroreflex.
| (2) |
Modelling the large arteries
The central large arteries are represented as a linear elastic reservoir with a certain compliance, i.e. a one-element windkessel model. The windkessel receives blood from the heart during each simulated systole, and there is a continuous outflow to the peripheral vascular bed during the entire cardiac cycle. This flow is modeled as an exponential pressure-dependent volume decay with a time constant depending on the total peripheral conductance (Gp) and the windkessel compliance (C). After the onset of exercise the extra blood to the exercising muscles, denoted 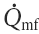 , is withdrawn from the reservoir during the whole cardiac cycle. For each cycle, windkessel MAP is calculated by integration, and the end-diastolic pressure is read just before the next systole.
, is withdrawn from the reservoir during the whole cardiac cycle. For each cycle, windkessel MAP is calculated by integration, and the end-diastolic pressure is read just before the next systole.
| (3) |
| (4) |
Modelling the peripheral resistance vessels
The peripheral circulation is represented by two parallel resistances, representing the exercising muscles (e) and the rest of the body (r). This division was chosen to permit the exercising muscles to be excluded from the baroreflex control of the peripheral resistance. This functional sympatholysis was assumed to operate at the level of moderate exercise, where local metabolites from the muscles may override any sympathetic nervous input. This simplified the algorithm, whereas any functional effect of a sympathetic vasoconstriction in the exercising muscle would be reflected only in a reduced muscle flow. This muscle flow is already adjusted in the model. The fraction of TPC representing the exercising muscles (ExCond) is in this leg exercise model estimated to be 0.15.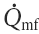 increases from the onset of exercise (Fig. 2B). The conductance in each part of the peripheral circulation is calculated beat-to-beat from the sympathetic signal to the peripheral vessels (Bsp) and the innervation sensitivity, or sympathetic peripheral gain, Ksp. The total peripheral conductance is the sum of the individual conductances, conductance in the exercising parts of the body (Ge) and conductance in the non-exercising parts of the body (Gr).
increases from the onset of exercise (Fig. 2B). The conductance in each part of the peripheral circulation is calculated beat-to-beat from the sympathetic signal to the peripheral vessels (Bsp) and the innervation sensitivity, or sympathetic peripheral gain, Ksp. The total peripheral conductance is the sum of the individual conductances, conductance in the exercising parts of the body (Ge) and conductance in the non-exercising parts of the body (Gr).
Figure 2. Baroreflex set point (A) and muscle flow (B).
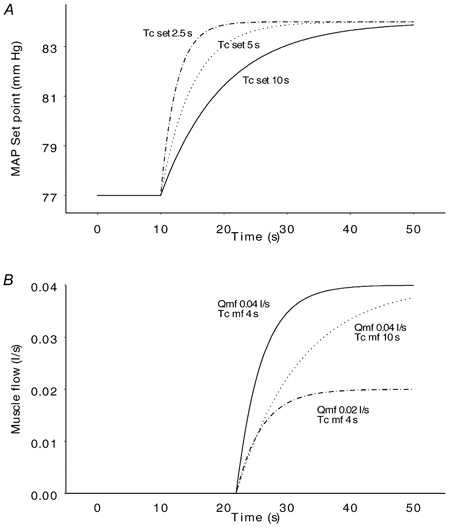
The upper panel shows the development of the baroreflex set point with three different time constants. The set point increases from 77 to 84 mmHg with baroreflex time constants (Tc,set) of 2.5 s (upper curve), 5 s (middle curve) and 10 s (lower curve). The changes in set point start at time 10 s when the countdown starts as an expression of a central command. The lower panel shows the development of muscle flow with combinations of two different maximal muscle flows (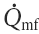 ) and two different muscle flow time constants (Tc,mf). In the upper and middle curves, muscle flow increases from 0 (the resting value) to a maximal value of 0.04 l s−1 with time constants of 4 s and 10 s respectively. In the upper and lower curves, the time constant is the same (4 s), but the maximal muscle flow is 0.04 l s−1 and 0.02 l s−1 respectively. The increase in muscle flow starts at time 20 s at the onset of exercise after a delay of 1.8 s (dmf).
) and two different muscle flow time constants (Tc,mf). In the upper and middle curves, muscle flow increases from 0 (the resting value) to a maximal value of 0.04 l s−1 with time constants of 4 s and 10 s respectively. In the upper and lower curves, the time constant is the same (4 s), but the maximal muscle flow is 0.04 l s−1 and 0.02 l s−1 respectively. The increase in muscle flow starts at time 20 s at the onset of exercise after a delay of 1.8 s (dmf).
| (5) |
| (6) |
| (7) |
Modelling the baroreflexes
The time processing of the input from the peripheral baroreflexes is modelled by three separate time domain processing objects, each with its own preset time constant and delay. The inputs to these elements are the actual MAP minus the set point for arterial pressure control, and the outputs are a sympathetic signal to the peripheral vascular bed (Bsp) and sympathetic (Bsh) and parasympathetic (Bph) signals to the heart, each representing the magnitude of the firing frequency of the respective nerves.
| (8) |
In this equation, t‘is an integration variable. This is equivalent to a combined time delay and time constant filter. Each of the three parts of the baroreflex is described by its own eqn (8) with separate values for d and Tc (dsh, Tc,sh, dph, Tc,ph, dsp, Tc,sp) representing the sympathetic (sh) and parasympathetic (ph) innervation of the heart and the sympathetic innervation of the peripheral vessels (sp) respectively.
The physiological parallels to these time processing objects are mainly nerve conduction, central processing and synaptic delays, and delays and inertia in the peripheral organs.
Simulation of the countdown preceding exercise
At the start of countdown to exercise the model increases the baroreflex set point by a simulated time constant towards a new value defined by the maximal value of MAP from the experiments. The different time courses of the increase in set point given different time constants are illustrated in Fig. 2A. Baroreflex resetting is a parallel shift of the baroreflex curve without change in gain.
Simulation of the onset of exercise
At the onset of exercise the increase in baroreflex set point is continued depending on its time constant. After a short delay (dmf) corresponding to the time needed to accumulate local metabolites in the exercising muscles, there is an increase in muscle flow  from 0 (defined as the resting value) towards a simulated maximal value with a simulated time constant. The different time courses of the increase in muscle flow given different maximum muscle flow and time constants are illustrated in Fig. 2B. Thus, the increase in muscle flow is controlled by local mechanisms.
from 0 (defined as the resting value) towards a simulated maximal value with a simulated time constant. The different time courses of the increase in muscle flow given different maximum muscle flow and time constants are illustrated in Fig. 2B. Thus, the increase in muscle flow is controlled by local mechanisms.
Simulation cycle
At the start of a new cardiac cycle, the difference between MAP in the previous cycle and the time-dependent set point for arterial pressure control is calculated. The next efferent reflex signal (B) from the three parts of the central baroreflexes is then calculated. The signal processing in the baroreflex objects (eqn (8)) is such that the magnitude of these efferent reflex signals may be influenced by the inputs from all of the preceding heartbeats, making it possible to represent the probable biologic reflex. The baroreflex signal depends on the magnitude of the time delays and time constants, which are set individually in the three parts. The next RR interval and TPC are then calculated from the reflex signals and the stage of the exercise cycle (i.e. rest, countdown, exercise). The volume and pressure in the windkessel are calculated in two steps. During the first 0.15 s of a new cycle, there is a pure exponential volume decay, according to eqn (4). At the end of this interval the end-diastolic pressure Pd is read, and is used in the calculation of the next SV (eqn (2)). SV is added to the reservoir in one step, and the exponential volume decay during the rest of the cycle is calculated. MAP is obtained by integration over the complete heart cycle. The instantaneous volume and pressure curve are distorted in comparison with a real arterial pressure curve, but this will have little effect on the integrated MAP.
Parameter estimation
The parameters in the model are by definition all quantities needed to specify the system (see Glossary). For a given set of parameter values, the time-varying variables MAP, RR interval and SV will have predetermined time courses during the simulation of exercise. Differences between the previously recorded responses and the time courses obtained by model simulation were reduced by adjusting the model parameters. The model was subjected to an automated parameter adjustment algorithm (Press et al. 1989) to find the set of parameters resulting in the best fit between simulated and measured time courses. This is explained previously (Toska et al. 1996).
For each subject, the steady-state values of MAP, RR interval and SV were found from the ten-second period immediately before countdown to exercise. To decrease the number of degrees of freedom in the parameter setting, we decided to run the model using a preset value of aortic compliance (C) of 0.00005 l mmHg−1 kg−1. This means that in a 70 kg person, an additional volume of 3.5 ml increases the arterial pressure by 1 mmHg (Rowell et al. 1996). For this small range of pressure change, a constant value of arterial compliance was used.
Constraints on the parameters
In preliminary simulations, automatic adjustment of all model parameters was allowed, and the solution was inspected for parameter values outside realistic physiological bounds. It was evident that non-physiological values could give simulated time courses similar to the recorded time series. Negative values for some of the parameters were therefore not permitted (time constants, delays, late diastolic mitral flow and autonomic sensitivity). There was also interdependence between some of the parameters. Some parameters were therefore set to a fixed value and only a subset of parameters was selected for adjustment in the final simulation run. These fixed values are given in the glossary.
The global averaged response was used to perform the minor modifications of the model and the selection of the set of parameters to be adjusted.
In the individual experimental runs the model was started twice using two different sets of starting values for the eight adjusted parameters. In the first run, the starting values used were the mean values from several previous model runs. In the second run, the adjusted parameters were set at other values, some above and some below those used in the first run, but still within a range that appeared to be physiologically reasonable.
Results
In the physiological recordings, countdown to exercise induced a decrease in RR interval, a corresponding increase in MAP and a small decrease in SV, while TPC was kept remarkably constant. The onset of exercise started a decrease in MAP, a large decrease in RR interval, a small increase in SV and an increase in TPC. After approximately 10 s of moderate, dynamic exercise, MAP started to increase again, RR interval and SV stabilized, while TPC fell to a new level, showing a peripheral vasoconstriction (Toska & Eriksen, 1994).
Figure 3 shows the recorded and simulated time courses of the cardiovascular responses as shown by the global averaged response of the 10 subjects. The parameters used for simulation of the global averaged response are given in the last row in Table 1.
Figure 3. Recorded (narrow lines) and simulated (thick lines) time courses of cardiovascular responses in the global averaged response of the ten subjects.
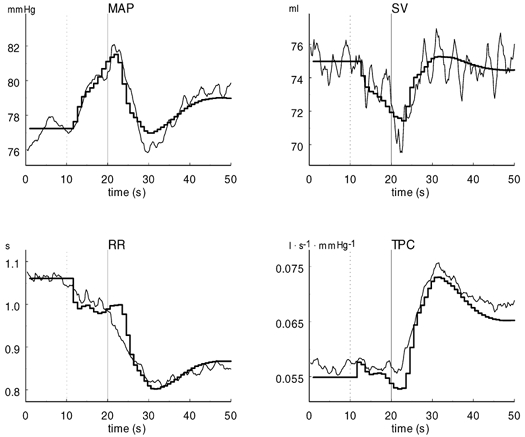
The dotted lines at 10 s indicate the start of countdown, and the continuous lines at 20 s indicate the onset of exercise. MAP, mean arterial pressure; RR, RR interval; SV, stroke volume; TPC, total peripheral conductance.
Table 1.
Best-fit set of parameters for each subject and the averaged response
| Subject no. | Height (cm) | Weight (kg) | Age (years) | Sex | Increase in baroreflex setpoint(mmHg) | Tc,set (s) | Kph (msmmHg−1) | Ksp (l mmHg−1) | Ksh (mlmmHg−1) |
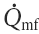 (ls−1) (ls−1) |
Tc,mf (s) |
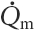 (ml s−1) (ml s−1) |
Ka (ml mmHg−1) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 173 | 73 | 22 | F | 5.0 | 6.96 | 26.8 | 0.0528 | 0.40 | 0.023 | 1.90 | 21.6 | −0.81 |
| 2 | 180 | 73 | 26 | M | 8.0 | 8.65 | 33.5 | 0.0775 | 0.21 | 0.035 | 3.51 | 6.8 | −0.89 |
| 3 | 165 | 57 | 22 | F | 7.5 | 1.73 | 24.2 | 0.0581 | 0.23 | 0.041 | 3.40 | 0.0 | −0.89 |
| 4 | 173 | 64 | 21 | M | 7.5 | 2.95 | 30.7 | 0.0675 | 0.36 | 0.057 | 6.41 | 0.0 | −0.98 |
| 5 | 167 | 61 | 23 | F | 8.5 | 5.33 | 39.8 | 0.0163 | 0.54 | 0.028 | 11.46 | 0.0 | −0.77 |
| 6 | 187 | 83 | 22 | M | 5.5 | 8.61 | 25.7 | 0.0898 | 0.06 | 0.027 | 6.64 | 0.0 | −0.47 |
| 7 | 174 | 65 | 21 | M | 13.5 | 16.28 | 55.2 | 0.1394 | 1.21 | 0.040 | 5.16 | 0.0 | −0.66 |
| 8 | 166 | 75 | 22 | F | 11.0 | 13.00 | 38.4 | 0.0226 | 1.13 | 0.012 | 0.90 | 0.0 | −0.67 |
| 9 | 166 | 56 | 24 | F | 5.0 | 1.79 | 40.7 | 0.0274 | 0.35 | 0.050 | 2.56 | 11.6 | −0.60 |
| 10 | 174 | 62 | 23 | F | 6.0 | 4.51 | 27.2 | 0.0754 | 0.02 | 0.042 | 13.20 | 3.4 | −0.98 |
| Mean | 172.5 | 66.9 | 22.6 | 7.8 | 6.98 | 34.2 | 0.0627 | 0.45 | 0.036 | 5.51 | 4.3 | −0.77 | |
| Median | 173.0 | 64.5 | 22.0 | 7.5 | 6.15 | 32.1 | 0.0628 | 0.35 | 0.038 | 4.34 | 0.0 | −0.79 | |
| S.D. | 7.0 | 8.7 | 1.5 | 2.7 | 4.80 | 9.6 | 0.0368 | 0.41 | 0.013 | 4.06 | 7.2 | 0.17 | |
| CV | 0.04 | 0.13 | 0.07 | 0.37 | 0.69 | 0.28 | 0.59 | 0.91 | 0.38 | 0.74 | 1.66 | −0.22 | |
| Global average response | 7.0 | 6.72 | 37.3 | 0.0832 | 0.35 | 0.040 | 5.95 | 1.8 | −0.80 |
This summarizes the best-fit set of parameters. Global average response, the coherent average response from the ten individuals; CV, coefficient of variation; see Glossary for definition of other abbreviations.
Figure 4 shows the recorded and simulated time courses of the cardiovascular responses in two subjects. The four upper panels belong to subject 1, from whom we obtained the best fit between the simulation run and the recorded data, defined as the lowest value obtained by the least squared method. The four lower panels belong to subject 9, from whom we obtained the poorest fit. Subject 9 showed a greater decrease in MAP and RR interval after the onset of exercise than subject 1. The individual parameters reflect some of the differences between the two subjects (Table 1). The increase in baroreflex set point was equal (5 mmHg). In subject 1, set point time constant was almost four times greater, parasympathetic RR sensitivity lower, sympathetic peripheral sensitivity larger, muscle flow lower, and late diastolic mitral flow twice as high as in subject 9.
Figure 4. Recorded (narrow lines) and simulated (thick lines) time courses of cardiovascular responses in subject 1 (four upper panels, best simulation run) and subject 9 (four lower panels, poorest simulation run).
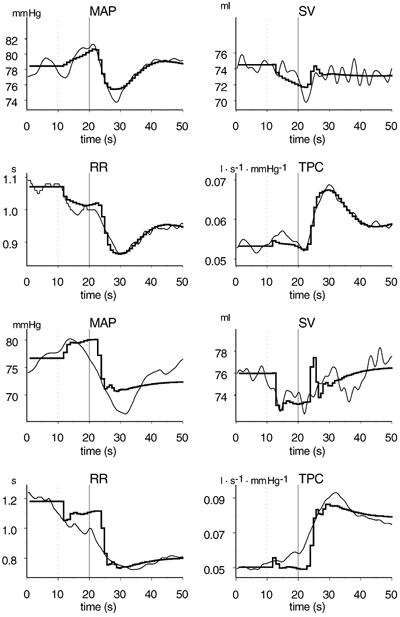
The dotted lines at 10 s indicate the start of countdown, and the continuous lines at 20 s indicate the onset of exercise. MAP, mean arterial pressure; RR, RR interval; SV, stroke volume; TPC, total peripheral conductance.
Simulations were performed for each of the 10 subjects and for the global averaged response using of a selected subset of eight parameters to be adjusted. Table 1 shows the individual values and the means and medians of these parameters in one simulation run. The parameters were identical in all but three individuals in the two simulation runs when model was started from different points.
Discussion
Our main finding was that the detailed time courses of the short-term cardiovascular changes at the onset of exercise were successfully simulated by an increase in baroreflex set point and vasodilatation in the exercising muscles. This very simple model of baroreflex control of the arterial circulation in humans was able to simulate previously recorded short-term cardiovascular responses at the onset of exercise in healthy humans. Individual variations in the recorded responses were simulated by individual variations in the parameters in the model. The baroreflex function in this model is thus capable of simulating the time course of MAP as shown by Toska et al. (1996).
The model is based on the assumption that all changes in arterial pressure are small and take place in the more linear part of the sigmoidal curve relating reflex responses to changes in receptor pressure (Sagawa, 1983). The slope of the curve in this part is the open-loop gain (Sagawa, 1983). We compared the simulations with beat-by-beat physiological recordings. Except for the article by Toska et al.( 1996) on a mathematical model, we have only found one paper that compare physiological recordings with simulated time courses (Linnarsson et al. 1996).
Parameter estimates
The parameters were identical in almost all subjects in the two different simulation runs using different starting values. In three of the simulations (subjects 2 and 10 and the global averaged response) there were only differences in values for two (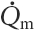 and Bsh) of the eight parameters. We concluded that this was due to some redundancy in our model, since both of these parameters influence stroke volume depending on RR interval.
and Bsh) of the eight parameters. We concluded that this was due to some redundancy in our model, since both of these parameters influence stroke volume depending on RR interval.
Values of several parameters not involved in the reflex control loop were estimated in each subject (e.g.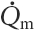 , Ka). Some of these may be compared with values from previous investigations.
, Ka). Some of these may be compared with values from previous investigations.
An increase in the set point of the baroreflexes was one of the two essential parts of our simulation. The baroreflex is progressively reset to a higher level (Walgenbach & Donald, 1983) during exercise. There is substantial evidence in the literature that the baroreflexes are reset at the onset of exercise, as reviewed by Raven et al. (1997). The increase in the baroreflex set point was set to the value obtained by measuring the maximal increase in MAP during the onset of exercise. This parameter was therefore not adjusted in the simulation runs. This was done in order to prevent a large increase in baroreflex set point from being combined with very low baroreflex sensitivity, which would produce the same results as in our model. In our model, the baroreflex set point increases gradually (Fig. 2A) and it is assumed that there is no change in gain. It has been proposed that it is reset either by central command or by input from the skeletal muscle receptors (Rowell et al. 1996). The baroreflex is simulated as a part of the response to a central command in our model, since it starts before exercise. We assume that the response from the skeletal muscle receptors requires time to develop. Many authors assume that arterial baroreceptors are essential in producing the cardiovascular responses evoked by exercise, but no definitive conclusion has been reached for humans. Walgenbach & Donald (1983) concluded that the baroreflex acts to balance the opposing effects of sympathetic vasoconstriction and metabolic vasodilatation in dogs during exercise.
The baroreflex set point time constant was allowed to vary freely between the simulation runs. Its mean value was ≈7 s. This means that 67 % of the baroreflex resetting was completed within 7 s.
Parasympathetic RR sensitivity was considered to be the main influence on the duration of the RR interval, since the exercise level was relatively moderate. If the sympathetic system has any influence on the RR interval, which it probably has, this will in our model be included in the parasympathetic signal to the heart. Simulation of the sympathetic RR reflex did not improve the fit between simulated and recorded time courses, and was therefore omitted in all subjects. Parasympathetic RR sensitivity has been extensively estimated in humans. Our model gain can best be compared with dynamic baroreflex sensitivity calculations. Saul et al. (1991) found the peak gain of the arterial HR baroreflex to be 8–16 ms mmHg−1, which is about half our values. This may be because the increase in baroreflex set point was fixed individually, and the values used may be lower than the physiological increase. Saul et al. (1991) also calculated the reflex from arterial blood pressure and not MAP as we have done.
Sympathetic peripheral vasoconstriction was the main regulator of the MAP at the onset of exercise. However, the full effect of this vasoconstriction became apparent only after ≈10 s both due to the delay in the reflex and to the immediate vasodilatation in the exercising muscles. This was hypothesized in the paper that our experimental data originate from (Toska & Eriksen, 1994).
Although we found that inclusion of the sympathetic effects on RR were unnecessary in order to simulate the responses to exercise, the same was not true regarding the sympathetic modulation of contractility. The effects on SV from changes in preload and afterload alone were insufficient to account for the observed changes in SV. Thus, sympathetic modulation of contractility was needed in order to accurately model the response of SV to exercise. The well documented ability of sympathetic nerves to alter contractility (Janicki et al. 1996) provides justification for the inclusion of this factor.
The values of muscle blood flow, and the dynamics of the changes in blood flow, we found compare well to the actual values measured by Eriksen et al. (1990). The rise in muscle vascular conductance, and the following rise in muscle blood flow, is probably the cause of the immediate reduction in MAP after the onset of exercise. Muscle flow was estimated to be ≈36 ml s−1 (compared to ≈40 ml s−1 in the study of Eriksen et al. 1990). The muscle flow time constant was ≈5 s. This means that 67 % of the muscle flow is reached within 5 s (compared to 80 % within 10 s in the study of Eriksen et al. 1990).
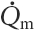 (late diastolic mitral flow), Ksh (sympathetic contractility) and Ka (afterload) are closely connected since all three influence SV. This redundancy was shown to be very important when the RR interval and the set point development showed any kind of time discrepancy.
(late diastolic mitral flow), Ksh (sympathetic contractility) and Ka (afterload) are closely connected since all three influence SV. This redundancy was shown to be very important when the RR interval and the set point development showed any kind of time discrepancy.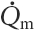 was therefore only necessary in four of the subjects, but because of the different input to these variables the redundancy proved to be necessary.
was therefore only necessary in four of the subjects, but because of the different input to these variables the redundancy proved to be necessary.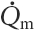 was ≈11 ml s−1 in the subjects where the parameter was needed to obtain a good simulation. Reported values in the literature are usually for peak flow and are therefore not comparable to our results.
was ≈11 ml s−1 in the subjects where the parameter was needed to obtain a good simulation. Reported values in the literature are usually for peak flow and are therefore not comparable to our results.
Ka was about −0.8 ml mmHg−1. This means that an increase in afterload of 10 mmHg would decrease SV by ≈8 ml. The afterload effect in dogs is reported to be −0.3 ml mmHg−1 (Janicki et al. 1996).
Arterial compliance was kept constant during the individual simulations as we assumed that changes in arterial compliance do not occur during the acute onset of exercise. Major changes in arterial compliance would cause alterations in arterial baroreflex function (Potts et al. 1996).
Potential limitations
The model presented here is a very simple one that includes very few physiological mechanisms. For example, the lack of a venous system is an oversimplification that results in a venous return with no upper limit in the model. However, during moderate, supine exercise as performed in our experiments venous return is probably not a limiting factor.
We also chose only to simulate the first 30 s after the onset of exercise to avoid the humoral influence and other possible neural reflexes with a long time delay. Major changes in the cardiovascular response usually occur within 30–60 s after the onset of exercise and even faster in the case of moderate exercise (Toska & Eriksen, 1994).
There is a great deal of literature regarding the carotid baroreflex. In our model, aortic and carotid baroreflexes are considered as one arterial baroreflex, which may interfere with the results obtained from the simulations. But since the exercise was performed in the supine position, the pressure at the two arterial receptors should be equal.
Noise in the transient phase from rest to exercise can have great impact on the adjustment of the delays in the nervous circuit. In turn, the delays will then have a great influence on the other parameters. Therefore we chose to fixate the delays prior to the simulation runs.
The short-term fluctuations in the recorded variables could probably be simulated at least partly by including respiration and the subsequent fluctuations in SV, RR interval and MAP.
Conclusions
Our most important finding was that despite its limitations and simplifications, including a very simple heart and a non-distributed model of the peripheral arteries, our model provided adequate simulations for all subjects and the global averaged curves when a few variables were adjusted. This means that an increase in the baroreflex set point and locally induced vasodilatation in the exercising muscles can explain almost all of the cardiovascular changes in the recorded variables (MAP, RR and SV) at the onset of exercise.
Acknowledgments
We would like to thank the Research Council of Norway for its financial support. A special thanks to Morten Eriksen for his important contributions in the initial construction of the model and valuable discussions.
References
- Bevegård S, Shepherd JT. Circulatory effects of stimulating the carotid arterial stretch receptors in man at rest and during exercise. Journal of Clinical Investment. 1966;45:132–142. doi: 10.1172/JCI105317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eriksen M, Waaler BA, Walløe L, Wesche J. Dynamics and dimensions of cardiac output changes in humans at the onset and at the end of moderate rhythmic exercise. Journal of Physiology. 1990;426:423–437. doi: 10.1113/jphysiol.1990.sp018147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eriksen M, Walløe L. Improved method for cardiac output determination in man using ultrasound Doppler technique. Medical and Biological Engineering and Computing. 1990;28:555–560. doi: 10.1007/BF02442607. [DOI] [PubMed] [Google Scholar]
- Green JF, Jackman AP. Peripheral limitations to exercise. Medicine and Science in Sports and Exercise. 1984;16:299–305. [PubMed] [Google Scholar]
- Herndon CW, Sagawa K. Combined effects of aortic and right atrial pressures on aortic flow. American Journal of Physiology. 1969;217:65–72. doi: 10.1152/ajplegacy.1969.217.1.65. [DOI] [PubMed] [Google Scholar]
- Imholz BP, Settels JJ, van der Meiracker AH, Wesseling KH, Wieling W. Non-invasive continuous finger blood pressure measurement during orthostatic stress compared to intra-arterial pressure. Cardiovascular Research. 1990;24:214–221. doi: 10.1093/cvr/24.3.214. [DOI] [PubMed] [Google Scholar]
- Janicki JS, Sheriff DD, Robotham JL, Wise RA. Cardiac output during exercise: contributions of the cardiac, circulatory, and respiratory systems. In: Rowell LB, Shepherd JT, editors. Handbook of Physiology, section 12, Exercise: Regulation and Integration of Multiple Systems. New York: Oxford University Press; 1996. pp. 649–704. [Google Scholar]
- Kiens B, Saltin B, Walløe L, Wesche J. Temporal relationship between blood flow changes and release of ions and metabolites from muscles upon single weak contractions. Acta Physiologica Scandinavica. 1989;136:551–559. doi: 10.1111/j.1748-1716.1989.tb08701.x. [DOI] [PubMed] [Google Scholar]
- Laughlin MH, Korthuis RJ, Duncker DJ, Bache RJ. Control of blood flow to cardiac and skeletal muscle. In: Rowell LB, Shepherd JT, editors. Handbook of Physiology,section 12, Exercise: Regulation and Integration of Multiple Systems. New York: Oxford University Press; 1996. pp. 705–769. [Google Scholar]
- Linnarsson D, Sundberg CJ, Tedner B, Haruna Y, Karemaker JM, Antonutto G, Di Prampero PE. Blood pressure and heart rate responses to sudden changes of gravity during exercise. American Journal of Physiology. 1996;270:H2132–2142. doi: 10.1152/ajpheart.1996.270.6.H2132. [DOI] [PubMed] [Google Scholar]
- Lu K, Clark JW, Jr, Ghorbel FH, Ware DL, Bidani A. A human cardiopulmonary system model applied to the analysis of the Valsalva maneuver. American Journal of Physiology - Heart and Circulatory Physiology. 2001;281:H2661–2679. doi: 10.1152/ajpheart.2001.281.6.H2661. [DOI] [PubMed] [Google Scholar]
- Melchior FM, Srinivasan RS, Charles JB. Mathematical modeling of human cardiovascular system for simulation of orthostatic response. American Journal of Physiology. 1992;262:H1920–1933. doi: 10.1152/ajpheart.1992.262.6.H1920. [DOI] [PubMed] [Google Scholar]
- Potts JT, Hatanaka T, Shoukas AA. Effect of arterial compliance on carotid sinus baroreceptor reflex control of the circulation. American Journal of Physiology. 1996;270:H988–1000. doi: 10.1152/ajpheart.1996.270.3.H988. [DOI] [PubMed] [Google Scholar]
- Potts JT, Shi XR, Raven PB. Carotid baroreflex responsiveness during dynamic exercise in humans. American Journal of Physiology. 1993;265:H1928–1938. doi: 10.1152/ajpheart.1993.265.6.H1928. [DOI] [PubMed] [Google Scholar]
- Press WH, Flannery BP, Teukolsky SA, Wetterling WT. Numerical recipes in Pascal, the art of scientific computing. Cambridge, UK: Cambridge University Press; 1989. pp. 326–330. [Google Scholar]
- Raven PB, Potts JT, Shi X. Baroreflex regulation of blood pressure during dynamic exercise. Exercise and Sport Sciences Reviews. 1997;25:365–89. [PubMed] [Google Scholar]
- Rowell LB. Human Cardiovascular Control. Oxford: Oxford University Press; 1993. [Google Scholar]
- Rowell LB, O'Leary DS, Kellogg DLJ. Integration of cardiovascular control systems in dynamic exercise. In: Rowell LB, Shepherd JT, editors. Handbook of Physiology, section 12, Exercise: Regulation and Integration of Multiple Systems. New York: Oxford University Press; 1996. pp. 770–838. [Google Scholar]
- Sagawa K. Baroreflex control of systemic arterial pressure and vascular bed. In: Shepherd JT, Abboud FM, editors. Handbook of Physiology, section 2, The Cardiovascular System, Peripheral Circulation and Organ Blood Flow. III. Bethesda, MD, USA: American Physiological Society; 1983. pp. 453–496. part 2. [Google Scholar]
- Saul JP, Berger RD, Albrecht P, Stein SP, Chen MH, Cohen RJ. Transfer function analysis of the circulation: unique insights into cardiovascular regulation. American Journal of Physiology. 1991;261:H1231–1245. doi: 10.1152/ajpheart.1991.261.4.H1231. [DOI] [PubMed] [Google Scholar]
- ten Voorde B. Amsterdam: Vrije Universiteit; 1992. Modeling the baroreflex. A systems analysis approach. PhD Thesis. [Google Scholar]
- Toska K, Eriksen M. Peripheral vasoconstriction shortly after onset of moderate exercise in humans. Journal of Applied Physiology. 1994;77:1519–1525. doi: 10.1152/jappl.1994.77.3.1519. [DOI] [PubMed] [Google Scholar]
- Toska K, Eriksen M, Walløe L. Short-term control of cardiovascular function: estimation of control parameters in healthy humans. American Journal of Physiology. 1996;270:H651–660. doi: 10.1152/ajpheart.1996.270.2.H651. [DOI] [PubMed] [Google Scholar]
- Walgenbach SC, Donald DE. Inhibition by carotid baroreflex of exercise-induced increases in arterial pressure. Circulation Research. 1983;52:253–262. doi: 10.1161/01.res.52.3.253. [DOI] [PubMed] [Google Scholar]
- Walløe L, Wesche J. Time course and magnitude of blood flow changes in the human quadriceps muscles during and following rhythmic exercise. Journal of Physiology. 1988;405:257–273. doi: 10.1113/jphysiol.1988.sp017332. [DOI] [PMC free article] [PubMed] [Google Scholar]


