Two forms of electrical resonance at theta frequencies, generated by M-current, h-current and persistent Na⁺ current in rat hippocampal pyramidal cells

Abstract

Coherent network oscillations in the brain are correlated with different behavioural states. Intrinsic resonance properties of neurons provide a basis for such oscillations. In the hippocampus, CA1 pyramidal neurons show resonance at theta (θ) frequencies (2-7 Hz). To study the mechanisms underlying θ-resonance, we performed whole-cell recordings from CA1 pyramidal cells (n = 73) in rat hippocampal slices. Oscillating current injections at different frequencies (ZAP protocol), revealed clear resonance with peak impedance at 2-5 Hz at ≈33 °C (increasing to ≈7 Hz at ≈38 °C). The θ-resonance showed a U-shaped voltage dependence, being strong at subthreshold, depolarized (≈-60 mV) and hyperpolarized (≈-80 mV) potentials, but weaker near the resting potential (-72 mV). Voltage clamp experiments revealed three non-inactivating currents operating in the subthresold voltage range: (1) M-current (I_M), which activated positive to -65 mV and was blocked by the M/KCNQ channel blocker XE991 (10 μm); (2) h-current (I_h), which activated negative to -65 mV and was blocked by the h/HCN channel blocker ZD7288 (10 μm); and (3) a persistent Na⁺ current (I_NaP), which activated positive to -65 mV and was blocked by tetrodotoxin (TTX, 1 μm). In current clamp, XE991 or TTX suppressed the resonance at depolarized, but not hyperpolarized membrane potentials, whereas ZD7288 abolished the resonance only at hyperpolarized potentials. We conclude that these cells show two forms of θ-resonance: ‘M-resonance’ generated by the M-current and persistent Na⁺ current in depolarized cells, and ‘H-resonance’ generated by the h-current in hyperpolarized cells. Computer simulations supported this interpretation. These results suggest a novel function for M/KCNQ channels in the brain: to facilitate neuronal resonance and network oscillations in cortical neurons, thus providing a basis for an oscillation-based neural code.

Coherent oscillatory activity of neuronal populations in the brain is correlated with different brain functions and behavioural states (Buzsaki et al. 1983; Singer, 1993; Steriade et al. 1993). In the hippocampus, slow oscillations in the theta (θ) frequency band (4-10 Hz) is a prominent feature of the network activity (Vanderwolf, 1988; Vinogradova, 1995; Buzsaki, 2002). The hippocampal θ oscillations are found in all mammals studied so far, including humans (Tesche & Karhu, 2000; Kahana et al. 2001). The θ rhythm can be recorded by EEG or magnetoencephalography (MEG), and as somatic and dendritic membrane potential variations of individual hippocampal pyramidal cells (Leung & Yim, 1986; Ylinen et al. 1995; Kamondi et al. 1998). In rodents, the hippocampal θ rhythm is prominent during exploration, locomotion and rapid eye movement (REM) sleep (Bland, 1986; Vanderwolf, 1988; Vinogradova, 1995; Buzsaki, 2002). In humans, θ band oscillations, recorded from the cerebral cortex and hippocampus by EEG or MEG, are particularly evident during working memory and maze navigation tasks (Sarnthein et al. 1998; Kahana et al. 2001; Raghavachari et al. 2001).

The θ rhythm is thought to represent the ‘on-line’ state of the hippocampus, and to be critical for temporal coding and modification of synaptic weights (Buzsaki, 2002). Thus, several lines of evidence suggest that the θ activity plays an important role in sensory-motor behaviour, learning and memory processes, and synaptic plasticity (Winson, 1978; Huerta & Lisman, 1993; Wilson & McNaughton, 1994; Buzsaki, 2002). The θ activity has been proposed to be necessary for place-specific discharge of hippocampal pyramidal cells, to be a mechanism for selective attention and a critical link in information selection, processing and memory trace formation (Vinogradova, 1995; Czurko et al. 1999). In particular, when a rat moves through a place field, single hippocampal place cells systematically change their phase of firing relative to the population θ rhythm, as if the θ rhythm provides a reference for a spike timing-based neural code for spatial information (O'Keefe & Recce, 1993).

Since it was first observed over 60 years ago (Jung & Kornmueller, 1938), the hippocampal θ rhythm has been intensively studied both in vivo, in vitro and ‘in silico’ (i.e. by computer modelling). Nevertheless, the underlying cellular and network mechanisms remain uncertain (Buzsaki, 2002). One complication is that there appear to be different forms of θ activity, such as atropine-sensitive and atropine-resistant forms (Vanderwolf, 1988; Buzsaki, 2002). In addition, the θ-like activities induced in brain slices by muscarinic or glutamatergic agonists differ in several respects from each other and from the θ rhythm observed in vivo (Buzsaki, 2002). These findings suggest that more than one θ mechanism exists.

In general, a neuronal population rhythm can (1) be caused by intrinsic pacemaker activity of certain neurons, (2) emerge as a network property, often involving mutual synaptic inhibition, or (iii) arise from a dynamic interplay between synaptic interactions and intrinsic electrical properties of the neurons. Several lines of evidence suggest that the latter mechanism underlies the hippocampal θ oscillations. This study focuses on certain intrinsic neuronal properties underlying the tendency of the membrane potential of individual neurons to resonate, i.e. to oscillate with maximal amplitude at a certain ‘preferred’ input frequency (Hutcheon & Yarom, 2000). It has already been reported that isolated hippocampal CA1 pyramidal neurons show resonance at low frequencies (2-7 Hz) corresponding roughly to the θ band (Leung & Yu, 1998; Pike et al. 2000). However, the ionic mechanisms underlying this θ-resonance remain to be determined.

Resonance generally results from an interplay between the passive membrane properties of the cell, i.e. capacitance and instantaneous ‘leak’ conductance, and time-dependent voltage-gated membrane currents (Hutcheon & Yarom, 2000). The hippocampal pyramidal cells are equipped with two slow voltage-gated ionic currents that seem promising candidates for contributing to slow subthreshold resonance and θ oscillations: the M-current (I_M) and the h-current (I_h or I_H, also called Q-current, I_Q). Both of these are non-inactivating currents that activate and deactivate slowly (τ ≈50-500 ms) at ‘subthreshold’ membrane potentials, i.e. negative to the spike threshold. However, functionally they are virtually mirror images of each other. Whereas I_M is a pure K⁺ current (reversing close to E_K ≈-90 mV) that is activated by depolarizations beyond ≈- 60 mV, I_h is a mixed cation (Na⁺, K⁺) current that reverses close to -20 mV and is activated by hyperpolarizations beyond ≈-60 mV (Brown & Adams, 1980; Halliwell & Adams, 1982; Brown et al. 1990; Storm, 1990). Because of their opposite voltage dependences and directions (I_M is outward over its entire activation range, whereas I_h flows inward over its entire activation range), they both function similarly as intrinsic, slow ‘voltage clamps’, tending to stabilize the membrane potential by opposing depolarizing or hyperpolarizing inputs. Thus, both I_M and I_h cause slow (≈100 ms) over- and undershoots and ‘sags’ in the voltage response to injected current pulses (Halliwell & Adams, 1982) and both I_M and I_h contribute to the medium afterhyperpolarization (mAHP) in hippocampal pyramidal neurons (Storm, 1989; Storm, 1990; Williamson & Alger, 1990). This behaviour already suggests a tendency to resonate at frequencies in the θ range. In addition, evidence suggesting that M-like currents may underlie slow oscillations and resonance has been reported from neocortical, amygdala and cerebellar neurons (Gutfreund et al. 1995; Pape & Driesang 1998; D'Angelo et al. 2001).

M-currents regulate the excitability of a variety of neurons (Brown & Adams, 1980; Halliwell & Adams 1982; Brown, 1988; Hille 2001). Data from various cell types indicate that the underlying potassium channels are encoded by the KCNQ gene family (Wang et al. 1998), which comprises five genes in mammals (Jentsch, 2000). Of these, KCNQ2, KCNQ3 and KCNQ5 are widely expressed in neurons of the CNS and PNS, whereas KCNQ4 expression is more restricted (Jentsch, 2000; Schroeder et al. 2000). I_M in rat sympathetic neurons is probably generated by KCNQ2/KCNQ3 heteromultimeric channels (Wang et al. 1998), and a recent report suggests that KCNQ2 and KCNQ5 underlie I_M in cultured rat hippocampal neurons (Shah et al. 2002). Mutations in either KCNQ2 or KCNQ3 in humans lead to a neonatal form of hereditary epilepsy (BFNC) attributed to a decrease in M-current (Jentsch, 2000).

The h-current is due to channels encoded by the HCN gene family (Ludwig et al. 1998), which comprises three genes in mammals, HCN1-3. I_h has been implicated in oscillations, pacemaking and resonance in several cell types, from cardiac pacemaker cells to thalamic neurons (Pape, 1996; Lüthi & McCormick, 1998; Neuhoff et al. 2002). So far it has been less clear whether h-currents play such roles in cortical neurons (Gutfreund et al. 1995; Hutcheon et al. 1996b). For example, although I_h was originally suggested to underlie the prominent oscillations of entorhinal stellate cells (Alonso & Llinas, 1989), this hypothesis was later rejected (Alonso & Klink, 1993). Recently, however, it was suggested that I_h, but not I_M underlies low-frequency θ-resonance in hippocampal neurons (Suckling et al. 2000).

In addition to the M- and h-currents, hippocampal and many other vertebrate central neurons are also equipped with a non-inactivating low-threshold sodium current (I_NaP; Llinas, 1988; French et al. 1990; Alzheimer et al. 1993; Crill, 1996) This tetrodotoxin (TTX)-sensitive current is probably due to a modal change in gating of conventional Na⁺ channels, or possibly a distinct type of non-inactivating channel (Crill, 1996). Persistent Na⁺ currents have been shown to contribute importantly to intrinsic oscillations of some central neurons (e.g. Klink & Alonso, 1993; Gutfreund et al. 1995; Hutcheon et al. 1996b; Pape & Driesang, 1998).

In this study, we sought to determine the mechanisms underlying the characteristic slow (θ) resonance of hippocampal pyramidal neurons. For the reasons outlined above, we focused on the roles of I_h, I_M and I_NaP. Our results indicate that there exist two forms of θ-resonance, with distinct mechanisms, in these neurons: one occurring mainly at depolarized membrane potentials, the other at hyperpolarized potentials. Using a mathematical model, we show that the proposed mechanisms are sufficient to generate the two forms of resonance. The existence of these two forms may help to explain why different types of θ oscillation are observed under different experimental conditions and behavioural states (Buzsaki, 2002).

Some of these results have been presented in abstract form (Storm et al. 2002; Storm & Hu, 2002).

Methods

Subjects

Thirty-one young (3-8 weeks of age) male rats (Møllergaard Wistar) were used. The experimental procedures were approved by the responsible veterinarian of the Institute, in accordance with the statute regulating animal experimentation given by the Norwegian Ministry of Agriculture, 1996.

Slice electrophysiology

The rats were deeply anaesthetized with halothane before decapitation. Transverse hippocampal slices (400 μm thick) were prepared with a vibratome (Campden Instruments, UK) and maintained in an interface chamber filled with artificial cerebral spinal fluid (ACSF) containing (mm): 125 NaCl, 25 NaHCO₃, 1.25 KCl, 1.25 KH₂PO₄, 1.5 MgCl₂, 1.0 CaCl₂, 16 glucose and saturated with 95 % O₂ - 5 % CO₂. During the recordings, the slices were kept submerged in a chamber perfused with ACSF of the composition described above, except that the CaCl₂ concentration was 2.0 mm. In voltage-clamp experiments for recording I_M and I_h, tetrodotoxin (TTX, 0.5-1 μm) was added to the extracellular medium and, to minimize the run-down of channel activity that can occur during voltage clamp (e.g. Lüthi & McCormick, 1999), a low calcium medium was used for voltage-clamp recording of I_M and I_h (mm): 125 NaCl, 25 NaHCO₃, 2.5 KCl, 1.5 MgCl₂, 0.2 CaCl₂, 1.8 MnCl₂, 16 glucose. In most of the current clamp experiments, 10 μm DNQX (6,7-dinitroquinoxaline-2,3-dione) and 10 μm bicuculline free base was added to the extracellular medium to block spontaneous synaptic transmission. The ACSF was saturated with 95 % O₂-5 % CO₂ and heated to 30.8-35.4 °C (32.9 ± 0.09 °C), except in a few experiments performed to test the temperature dependence of the resonance, when the medium was heated from ≈33 to ≈38 °C (see Fig. 2). In all other experiments, the temperature was kept constant within ± 0.5 °C during each recording.

Figure 2. Temperature dependence of the resonance frequency.

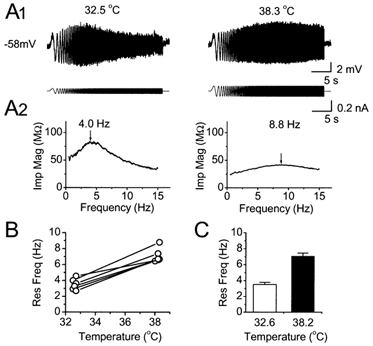
A1, voltage responses to ZAP current injection at 32.5 and 38.3 °C, from a cell maintained at -58 mV. The resonance (peak) frequency shifted from 4.0 to 8.8 Hz by warming the perfusion medium from 32.5 to 38.3 °C. A2, impedance magnitude plotted as a function of frequency, from the same traces as in A1. The peaks of the impedance magnitude profiles are marked with arrows. B, resonance frequency plotted as a function of the recording temperature for the six cells tested at ≈32.5 °C and again after warming to ≈38.0 °C. In all the cells, the resonance frequency was increased by warming. C, summary diagram showing the temperature effect on the mean resonance frequency. The resonance frequency at 38.20 ± 0.04 °C was significantly higher than at 32.62 ± 0.04 °C (7.09 ± 0.36 vs.3.50 ± 0.28 Hz, n = 6, P = 0.0002, Student's paired t test).

Whole-cell giga-seal recordings were obtained from CA1 pyramidal cells using the ‘blind’ method. The patch pipettes were filled with a solution containing (mm): 140 KMeSO₄ or potassium gluconate, 10 Hepes, 10 phosphocreatine sodium salt, 2 ATP sodium salt, 0.4 GTP sodium salt, and 2 MgCl₂, giving a pipette resistance of 4-7 MΩ. For current-clamp recordings, an Axoclamp 2A amplifier (Axon Instruments Inc., Foster City, USA) was used in bridge mode. The series-resistance was 10-40 MΩ. For voltage-clamp recordings, an Axopatch 1D amplifier (Axon Instruments Inc.) was used. In these recordings, the series-resistance was 10-20 MΩ. All potentials were corrected for the junction potential.

Only cells with a stable resting membrane potential more negative than -60 mV and stable action potential amplitudes were used for recording. To keep the conditions constant during the measurements, and comparable between cells, the cell membrane potential was manually clamped at a fixed potentials.

Numerous previous studies have demonstrated the usefulness of single-electrode/whole-cell voltage-clamp recordings of membrane currents of intact neurons in slices, including kinetic and pharmacological properties of I_M, I_h and I_NaP in hippocampal pyramidal neurons (e.g. Halliwell & Adams, 1982; Nicoll, 1988; Storm, 1990; Lüthi & McCormick, 1999; Franz et al. 2000; Neuhoff et al. 2002;). However, in all such recordings the voltage control is necessarily limited: good space-clamp control of the distal dendrites and axons is unattainable, and some currents are too large and fast to be effectively clamped even at the soma. In this study, our goal was limited to measuring largely somatic currents activated in the subthreshold voltage range, which are most relevant for somatic resonance behaviour and subthreshold oscillations. The currents I_M, I_h and I_NaP are well suited for this approach because of their small amplitude and their slow, non-inactivating kinetics. (e.g. Halliwell & Adams, 1982; Nicoll, 1988; Storm, 1990; Lüthi & McCormick, 1999; Franz et al. 2000; Neuhoff et al. 2002).

We used essentially the same experimental conditions for our voltage-clamp measurements of I_NaP as we used for our resonance tests in current clamp, with normal intra- and extracellular media, which is often employed to isolate Na⁺ currents (French et al. 1990). We did this for the following reasons. (1) K⁺ channel blockade would inevitably shift the Na⁺-spike threshold to a more negative level, thus precluding accurate measurements of I_NaP close to the physiological spike threshold where the effect of I_NaP is most prominent. (2) By making the cell electrotonically more compact, Cs⁺ or other K⁺ channel blockers would cause our somatic recording to include I_NaP also from more remote, non-somatic parts of the cell, which is not relevant for the somatic resonance behaviour under physiological conditions.

Recording and analysis of electrical resonance

The impedance (Z) amplitude profile (ZAP) method was used to characterize the electrical resonance behaviour of the cells (Puil et al. 1986; Pape & Driesang, 1998; Hutcheon & Yarom, 2000). During whole-cell bridge current-clamp recording, we injected through the recording electrode a sinusiodal current (the ZAP current) with constant amplitude and linearly increasing frequency (0-15 Hz for 20-30 s), and recorded the voltage response. Resonance was manifest as a distinct and reproducible peak in the voltage response at a certain position of the response, corresponding to a certain frequency. The ratio (called the Q value; Hutcheon et al. 1996b) of the impedance at the resonance peak to the impedance at 0.5 Hz, was used to quantify the strength of the resonance. The amplitude of the ZAP current was adjusted to keep the perturbation of the membrane potential close to 10 mV peak-to-peak, thus avoiding triggering of action potentials. In particular, when KCNQ channel blocker (XE991) was applied, the resulting increase in the cell's input resistance, necessitated a reduction amplitude of the ZAP current accordingly, in order to keep the peak voltage response constant (Fig. 6). The ZAP protocol was applied to the cells under two different conditions: (1) in normal saline, keeping the voltage responses subthreshold to avoid action potentials being triggered, and (2) after application of tetrodotoxin (TTX, 1 μm) to block action potentials.

Figure 6. XE991 blocked θ-resonance at depolarized but not at hyperpolarized membrane potential.

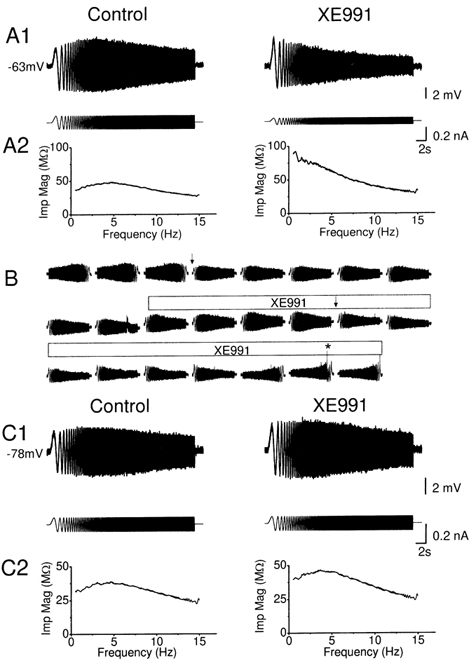
A1 and C1, typical voltage responses (upper traces) evoked from depolarized (-63 mV, in A1) and a hyperpolarized (-78 mV, in C1) membrane potentials by injecting a ZAP current (lower traces), before and after application of 10 μm XE991. After applying XE991, it was necessary to reduce the amplitude of the ZAP current in order to obtain a voltage response of similar peak-to-peak amplitude as before, because XE991 increased the input resistance. Note that XE991 abolished the resonance at -63 mV indicated by a typical ‘spindle-shaped’ voltage response to ZAP current injection, thus shifting the peak voltage response to the lowest frequency tested (n = 7, P = 0.02, Q = 1.13 ± 0.04 and 1.00 ± 0.00 before and after application of XE991), but had little effect on the resonance at -78 mV (n = 5, P = 0.13, Q = 1.16 ± 0.07 and 1.12 ± 0.06 before and after application of XE991). A2 and C2, impedance magnitude plotted as a function of input frequency before and after XE991, from the same traces as in A1 and A2. B, typical time course of the XE991 (10 μm; indicated by bar above the traces) effect on resonance at a depolarized level (-63 mV). In order to limit the variations in the peak-to-peak amplitude of the voltage response, the peak-to-peak amplitude of the ZAP current was changed at places marked with arrows. To test for time dependence of the responses (cf. Fig. 1B), the ZAP currents were inverted before and after XE991 application (first three and last three traces). No time dependence was detected. Note that the cell fired action potentials in one of the last traces (*).

To plot the magnitude of the cell impedance as a function of frequency, the magnitude of the fast Fourier transform (FFT) of the voltage response was divided by the magnitude of the FFT of the input current (ZAP current; Hutcheon & Yarom, 2000).

Although we routinely used a ZAP protocol rising from 0 to 15 Hz in 30 s (or 20 s in a few cases), we initially also compared it with other protocols, including ZAP protocols with a larger frequency span (0-30 Hz in 30 s) or a declining frequency (15-0 Hz in 30 s; see Fig. 1B). The results and Q values obtained with these alternative protocols were indistinguishable from those obtained with the standard ZAP protocol in the same cell (Fig. 1A and B).

Figure 1. Subthreshold resonance in CA1 pyramidal cells.

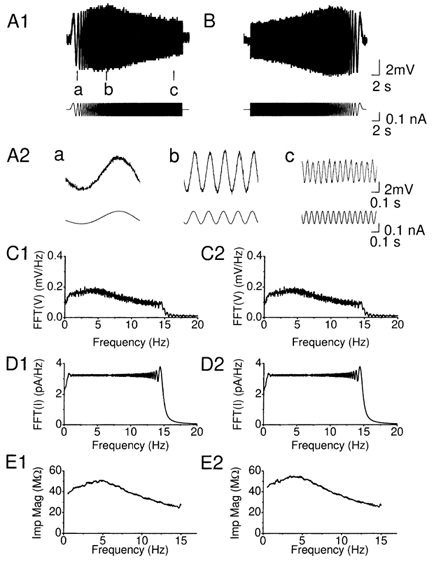
A1, membrane potential response of a hippocampal CA1 pyramidal cell (upper trace) to injection of a ZAP function current (lower trace) with linearly increasing frequency (0-15 Hz, over 30 s). The cell was depolarized to -63 mV by steady DC injection. Note that the peak in the voltage response at the point marked b. A2, samples (a-c) of voltage response (upper trace) and the ZAP current (lower trace) corresponding to the times a-c marked in A1, shown at an expanded time scale. B, to test whether the peak reflected frequency-dependent as opposed to time-dependent membrane properties, an inverted ZAP current was injected (1B, lower trace), i.e. with linearly decreasing frequency (15-0 Hz, over 30 s). C1 and 2, fast Fourier transform (FFT) of the membrane potential responses shown in A1 and B (FFT(V)). D1 and 2, FFT of the ZAP function input shown in C1 and C2 FFT(I). E1 and 2, impedance magnitude (Imp Mag) calculated by dividing FFT(V) with FFT(I) (impedance magnitude, Z = FFT(V)/FFT(I)] plotted as a function of input frequency, using the data in B and C. All data in this figure were obtained from the same cell.

Data acquisition, storage and analysis

The data were acquired using pCLAMP 7.0 (Axon Instruments), at a sampling rate of 0.5 KHz, and also digitized and stored on video tapes (Instrutec VR-10), and measured and plotted using pCLAMP 7.0 and Origin 5.0 (Microcal, USA). Values are expressed as means ± s.e.m.. Two-tailed paired Student's t test was used for statistical analysis (α = 0.05). Most of the n (i.e. number of cells), P and Q values are given in the figure legends.

Chemicals and drugs

The M-channel blocker XE991 was obtained from DuPont pharmaceutical company. DNQX and ZD7288 (4-ethylphenylamino-1,2-dimethyl-6-methylaminopyrimidinium chloride) was purchased from Tocris Cookson Ltd (UK). The remaining drugs were from Sigma-Aldrich Norway AS (Oslo). Substances were bath-applied by adding them to the superfusing medium.

Computational methods

Computer simulations were performed using the Surf-Hippo simulator, version 3.0 (Borg-Graham, 1999; Graham, 2002). Surf-Hippo is written in Lisp language and was run on a Linux workstation. For integrating the circuit equations, Surf-Hippo uses a variant of the Crank-Nicholson method described by Hines (1984). The variable time-step method was used to speed up the simulation.

The cell was represented by six compartments, comprising an isopotential soma (diameter 25 μm) and a dendrite cable (total length 1200 μm and diameter 6 μm) consisting of five segments of equal length. In keeping with previous simulations with Surf-Hippo (Borg-Graham, 1999; Shao et al. 1999), we used different membrane resistances in the soma and the dendrite for the simulations presented here (2.5 kΩ cm² and 40 kΩ cm², respectively). However, we also did simulations with a uniform membrane resistance in the soma and dendrite (40 kΩ cm²), and obtained qualitatively similar results. A uniform intracellular resistivity of 200 Ω cm and a specific membrane capacitance of 1.0 μF cm⁻² was assumed. With these values the model was able to account for the input resistance and whole-cell capacitance measured in experiments. The active conductances in the soma included a persistent Na⁺ current (I_NaP), three voltage-gated Ca²⁺ currents I_T, I_N, I_L, three voltage-gated K⁺ currents I_A, I_DR, I_M, a fast-inactivating BK-type Ca²⁺- and voltage-dependent K⁺ current I_CT (Shao et al. 1999), and a hyperpolarization-activated non-specific cation current I_h. The active conductances in the dendritic cable included I_NaP and I_h. The fast inactivating Na⁺ current, I_NaT, was left out of the simulations in order to avoid action potentials. The leak current was set with a reversal potential of -80 mV for both soma and the dendritic cable.

Calculations of all currents were based on the Hodgkin-Huxley formalism with rate constants derived from the Boltzmann equation (Borg-Graham, 1991). An exception is I_CT which was calculated from a Markov model with three states (Shao et al. 1999). The intracellular Ca²⁺ dynamics, which were confined to the soma, included Ca²⁺ influx, diffusion, instantaneous buffering and an extrusion mechanism (Borg-Graham, 1999; Shao et al. 1999). All Ca²⁺ compartments were initialized to 50 nm.

Each of the three currents I_M, I_h and I_NaP (Table 1) was described according to the parameterized Hodgkin-Huxley formalism (Borg-Graham, 1991). Except for these three currents, all channel kinetics were adapted from the ‘working model’ of Borg-Graham (1999). The I_NaP kinetics were adapted from French et al. (1990).

Table 1.

Model parameters of I_NaP, I_h and I_M

	INaP	Ih	Im
General parameters
Erev	30	−17	−80
Number of particles	1	1	2
Particle parameters*
z(valence)	5	−5	15
γ	0.5	1	0.45
Base rate (1/ms)	1	1	0.003
V1/2(mV)	−49	−95	−57.5
τ0(ms)	1	150	0.0043

^*‘Extended Hodgkin-Huxley’ description.

Simulation temperature: 31°C. V_½ gives the midpoint of the activation curve; z is the valence, setting the steepness of the activation curve; γ is the symmetry parameter determining the skew of τ(v); the base rate (K) is the leading coefficient of α(V) and β(V);τ_o represents a ratelimiting step in the state transition.

In order to adapt the model to the set of CA1 cells and recording conditions used in this study, we made adjustments of the parameters in the model setting the maximal conductance of I_h, I_NaP, I_NaP (Table 1) and the activation time constants of I_h and I_M so that the currents obtained in simulated voltage-clamp experiments (not shown) approximated our experimental voltage-clamp measurements of I_h, I_NaP, I_M (see Results, Fig. 4 and Fig. 5).

Figure 4. Selective elimination of M-current (I_M) and H-current (I_h) by the ion channel blockers XE991 and ZD7288.

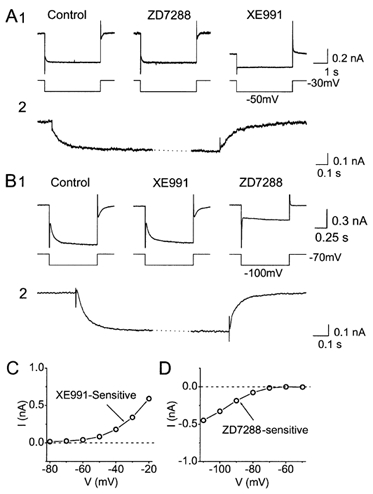
Whole-cell voltage-clamp recordings from CA1 pyramidal cells bathed in 1 μm TTX to block Na⁺ channels. A1, typical example showing that XE991, but not ZD7288, blocked I_M. I_M was recorded by giving 4 s-long -20 mV voltage-clamp steps to -50 mV from a holding potential of -30 mV. M-channel closure was seen as a slow inward relaxation (tail current) after stepping to -50 mV, and M-channel reopening as a slow outward relaxation after stepping back to -30 mV. Bath application of 10 μm ZD7288 had no detectible effect, whereas subsequent application of 10 μm XE911 fully blocked I_M, abolishing the relaxations and causing an inward shift of the holding current. A2, the XE991-sensitive current, calculated by subtracting the current traces before and after XE991, at an expanded time scale. Note the larger instantaneous jump in the current when stepping from -30 to -50 mV (when most M-channels are open), compared to stepping from -50 to -30 mV (when most M-channels are closed). The example shown in A2 is taken form a different cell than A1 because an A-current evoked by the step to -30 mV partly masked the time course of M-current opening in A1. B1, ZD7288, but not XE991, blocked I_h. The cell was maintained at -70 mV, and stepped to -100 mV for 1 s. I_h activation and deactivation were seen as slow inward and outward relaxations at the beginning and end of the step, respectively. I_h was highly resistant to 10 μm XE991, but was fully blocked by subsequent application of 10 μm ZD7288. B2, the ZD7288-sensitive current, calculated by subtracting the current traces before and after ZD7288, shown at an expanded time scale. C, XE991-sensitive difference current amplitude, obtained by subtraction of currents before and after the application of 10 μm XE991, plotted as a function of membrane potential (V). D, ZD7288-sensitive difference current amplitude, obtained by subtraction of currents before and after the application of 10 μm ZD7288, plotted as a function of membrane potential (V). In C and D, the difference currents were measured at the end of the negative-going voltage step (cf. panels A2 and B2). TTX (1 μm) was applied throughout all experiments (A-D) to block Na⁺ channels.

Figure 5. Blockade of the persistent Na⁺ current (I_NaP) by TTX.

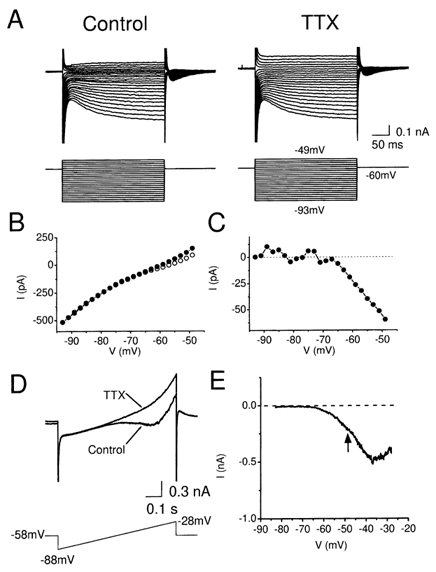
A, membrane currents in a CA1 pyramidal cell in response to voltage-clamp steps to different membrane potentials (-93 mV to -40 mV) from a holding potential of -60 mV, before and after bath application of 1 μm TTX. B, steady state current-voltage (I-V) plot of the data from A. The current (I) was measured at the end of the 300 ms voltage steps, before (○) and after (•) TTX application. C, TTX-sensitive current, calculated by subtracting the steady state currents before and after TTX in B, plotted as a function of membrane potential. Note that the TTX-sensitive current started to activate at about -65 mV. D, typical example of currents in response to a ramp voltage commands (from -88 to -28 mV, given once every 10 s) before and after application of TTX (1 μm). The holding potential between the ramp commands was -58 mV. E, TTX-sensitive current, obtained by subtracting the current in response the ramp command before and after application of TTX in D, plotted as a function of membrane potential.

We regard our simplified model with only five dendritic compartments as a model of the soma and proximal part of the dendrites - the parts of the cell that are most likely to participate in the resonance behaviour observed during somatic recording.

In the standard model used in this study (Figs 9-11), I_NaP was distributed at uniform density in the soma and all dendritic compartments (Table 2), for the following reasons: (1) cortical pyramidal cells show a uniform density of Na⁺ channels in the soma and primary apical dendrite (Huguenard et al. 1988); (2) I_NaP was detected in the apical dendrite at least 300 μm from the soma (Mittmann et al. 1997); (3) I_NaP probably represents largely a modal change in the inactivation properties of the fast Na⁺ channels and should therefore follow the uniform distribution of the latter (Crill, 1996).

Figure 9. Computer simulation of how M-, h- and NaP-currents contribute to the resonance at depolarized and hyperpolarized membrane potentials.

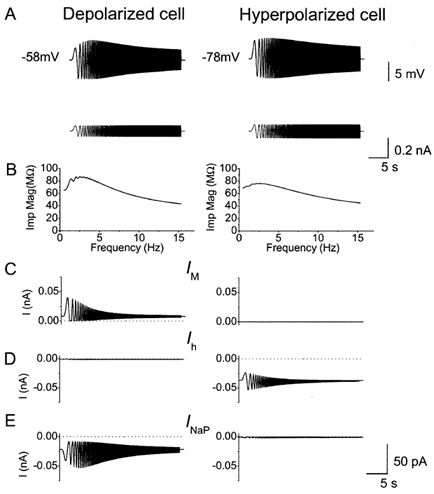
A, voltage response (upper traces) to ZAP current (lower traces) from the model cell maintained at -58 and -78 mV. B, impedance magnitude plotted as a function of input frequency from the traces in A. C-E, I_M, I_h and I_NaP during the response to ZAP current, shown in A. Note that I_M and I_NaP were significantly activated by the ZAP current only at -58 mV. In contrast, I_h was significantly activated by the ZAP current only at -78 mV. Note that I_M and I_h were most responsive at low frequencies, whereas I_NaP could follow the ZAP also at high frequencies.

Figure 11. Computer simulation showing U-shaped voltage dependence of the resonance strength.

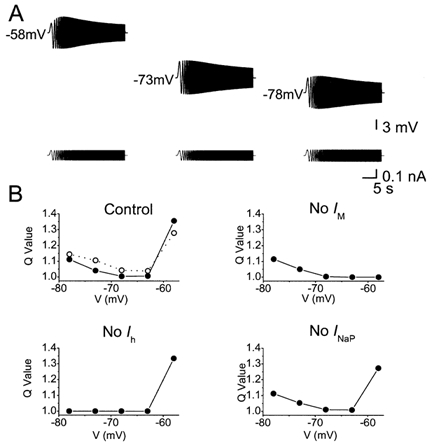
A, model simulations (with the same model as in Figs 9-10) of ZAP responses at three different membrane potentials: depolarized (-58 mV), resting potential (-73 mV), and hyperpolarized (-78 mV). B, plots of voltage dependence of resonance strength in the model. Comparison between results with the full model (Control) and with each of the three key ionic currents omitted from the model (No I_M, No I_h, No I_NaP). In each case, the Q value, which indicates strength of resonance, was plotted as a function of the membrane potential (filled circles). In the upper left panel (Control), the experimental data, replotted from Fig. 3C, are shown for comparison (open circles and broken line).

Table 2.

Distribution and densities of I_NaP, I_h and I_M

		Segment
	Soma	1	2	3	4	5
INaP	0.17	0.17	0.17	0.17	0.17	0.17
Ih	0.2	0.3	0.4	0.5	0.6	0.7
IM	6.7	—	—	—	—	—

Distribution unit: maximum conductance density (p^Sμm⁻²).

In the standard model, I_h was distributed at a linearly increasing density from the soma along the dendritic compartments (Table 2), in accordance with the results of Magee (1998). In contrast, I_M was confined to the soma, because so far no comprehensive information exists regarding the distribution of M-channels along the dendrites, but recently available data indicate that there are M-channels at least in the soma and very first part of the apical dendrite of CA1 pyramidal cells (Cooper et al. 2001). However, we do not expect that a distribution of M-channels further out in the dendrites would produce any significant changes in our results.

In addition to simulations with the standard model, we also performed some simulations using other distribution profiles of I_NaP, I_M and I_h, in order to explore the importance of these distributions. Although an extensive exploration of the parameter space was not performed, it appeared that the resonance phenomena described in this paper were not critically dependent on the distributions of I_M, I_NaP and I_h. Confining I_NaP and I_h only to the somatic compartment, leaving just a passive dendritic cable, did not produce qualitative changes.

Results

Recording of electrical resonance in the subthreshold voltage range

Whole-cell patch-clamp recordings were obtained from 73 CA1 pyramidal cells in rat hippocampal slices. The cells had resting potentials near -70 mV (72.6 ± 1.2 mV; n = 69) and action potential thresholds close to -50 mV (-47.7 ± 0.7 mV; n = 29). These values are in agreement with previous studies (Storm, 1990; Staff et al. 2000).

We first studied the resonance behaviour of the cells at membrane potentials just negative to the action potential threshold, i.e. in the subthreshold voltage range where neurons in an active network spend much of their time. To characterize the electrical resonance properties, we used the impedance (Z) amplitude profile (ZAP) method (Puil et al. 1986; Hutcheon & Yarom, 2000) during whole-cell bridge current-clamp recording (Fig. 1).

The membrane potential was first manually clamped at a constant subthreshold level close to -60 mV (-58 to -63 mV) by steady current (DC) injection through the recording electrode. To test for resonance, a sinusiodal current (the ZAP current) with constant amplitude and linearly increasing frequency (0-15 Hz during 20-30 s; Fig. 1A1, lower trace) was injected, and the voltage response recorded (Fig. 1A1, upper trace). The peak-to-peak amplitude of ZAP current was adjusted to keep the voltage response below the action potential threshold. Action potentials had to be avoided, since they and their after-potentials would distort the resonance response.

In all the cells tested at a depolarized subthreshold level (n = 23), resonance was manifest as a distinct and reproducible peak in the voltage response at a certain point, corresponding to a frequency of 3.0 ± 0.2 Hz (at -58 to -63 mV; n = 23) (Fig. 1A1). Sample traces from different parts of the ZAP response (marked a-c in Fig. 1A1) are shown below at an expanded time scale (Fig. 1A2).

To test whether the peak reflected frequency-dependent as opposed to time-dependent membrane properties, we also injected an inverted ZAP current, i.e. with linearly decreasing frequency (15-0 Hz, over 30 s; Fig. 1B). In all cells tested (n = 4), the resulting peak response occurred at a frequency that was indistinguishable from the one obtained with the regular ZAP current, confirming that the peak was essentially frequency-dependent.

To analyse the resonance response, we performed fast-Fourier transform (FFT) of both the membrane potential response (Fig. 1C) and the ZAP input current (Fig. 1D). The impedance profile was then calculated by dividing FFT(V) with FFT(I) (impedance magnitude (Imp Mag), Z = FFT(V)/FFT(I)) (Fig. 1E).

To quantify the strength of the resonance, we calculated the ratio (called the Q value; (Hutcheon et al. 1996b)) of the impedance at the resonant peak to the impedance at 0.5 Hz. All the cells tested showed some degree of resonance, as indicated by a Q value > 1.00 (Q = 1.32 ± 0.08, n = 23), and a peak resonance frequency near 3 Hz (3.0 ± 0.2 Hz; n = 23) when tested at subthreshold potentials (-58 to -63 mV; Fig. 3C and D). These Q values are similar to those found to produce subthreshold resonance in rat neocortical neurons (1.4 ± 0.3 and 1.3 ± 0.3, for two different groups of cells, respectively; Hutcheon et al. 1996b). About 40 % of our cells showed particularly strong resonance (Q = 1.58 ± 0.16; 9 of 23 cells) with a peak resonance frequency of 4.1 ± 0.2 Hz (9 of 23 cells).

Figure 3. Voltage dependence of resonance behaviour.

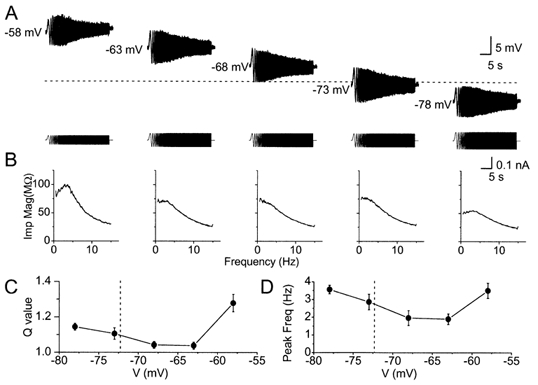
A, voltage responses of a CA1 pyramidal cell to ZAP current injections at different membrane potentials (-58 to -78 mV). The different membrane potentials were obtained by different amounts of steady current injection. In order to make the peak-to-peak voltage response similar at different membrane potentials, it was necessary to adjust the amplitude of the ZAP current (lower traces), because of differences in input resistance at different membrane potentials. Note the stronger resonance at depolarized (-58 mV) and hyperpolarized (-78 mV) potentials compared to potentials near the resting level (-72.6 ± 1.2 mV). B, impedance magnitude plotted as a function of input frequency at different membrane potentials of the same cell as in A. C, summary diagram of Q values plotted as a function of membrane potential for all the six cells tested. The Q value indicates the strength of the resonance, and is 1.0 when there is no resonance. D, summary diagram of peak resonance frequency plotted as a function of membrane potential for all the six cells tested. The Q value at -58 mV was significantly higher than that at -78 mV (P = 0.04), indicating stronger resonance at -58 mV. In C and D, each of the six neurons were tested at five different membrane potentials (i.e. n = 6 for each point). When we also included the data from our all other experiments (Figs 1-3 and 6-8), in which each cell was tested only at some potentials, the resulting plots (not shown) were virtually identical to the plots (C and D) for the six completely tested cells.

Temperature dependence of the resonance frequency

Our experiments were routinely performed at temperatures close to 33 °C (32.9 ± 0.09 °C; see Methods), i.e. a subphysiological level, as is commonly used in brain slice experiments in order to promote recording stability. However, the resonance frequency is likely to be higher at the normal body temperature, which is close to 38 °C in the rat. To measure the temperature dependence of the resonance, we warmed the bathing medium while recording from a cell, repeatedly probing its resonance properties. Figure 2A shows an example of such an experiment, where the temperature was raised from 32.5 to 38.3 °C, causing the resonance frequency to increase from 4.0 to 8.8 Hz in this cell. Figure 2B and C shows summaries of the data from all six cells tested in this way. By warming the bath from 32.6 ± 0.04 to 38.2 ± 0.04 °C, the resonance frequency increased significantly, from 3.50 ± 0.28 to 7.09 ± 0.36 Hz (n = 6, P = 0.0002, Student's paired t test), i.e. roughly a doubling in frequency for a 5 °C change. These results give an extrapolated Q₁₀ value of 4.22 for the resonance frequency of CA1 pyramidal cells at -58 mV.

Two forms of θ-resonance with distinct voltage dependencies

To determine the voltage dependence of the electrical resonance, we shifted the membrane potential to different levels by DC current injection before applying the ZAP current (which was added to the DC current). As shown in Fig. 3, the resonance showed a dual voltage dependence: it was prominent at depolarized, just subthreshold potentials near -60 mV, declined to a minimum when approaching the resting potential (-72.6 ± 1.2 mV; n = 69), and increased again at hyperpolarized potentials beyond -75 mV.

This U-shaped voltage dependence was seen more clearly in the impedance plots. Thus, in Fig. 3B, the impedance magnitude (Imp Mag) plots obtained at -58 and -78 mV showed a peak near 4 Hz, which was weaker or missing at intermediate potentials. Such a dual voltage dependence was evident in the summary plots of both peak frequency and Q value for all the cells tested (Fig. 3C and D; n = 6, see figure legend). Thus, the average frequency of the resonance peak was close to 3.5 Hz at both depolarized (-58 mV) and hyperpolarized (-78 mV) potentials, but was only about 2 Hz near the resting potential. The voltage dependence of the strength of the resonance (Q value) was also U-shaped, but asymmetrical, reaching a higher value (P = 0.04) at depolarized (Q = 1.28 ± 0.05 at -58 mV; n = 6) compared to hyperpolarized membrane potentials (Q = 1.14 ± 0.01 at -78 mV; n = 6). In between, at potentials closer to the resting level, the Q value approached 1.0, indicating only weak resonance (Fig. 3D; a Q value of 1.0 indicates no resonance).

Thus, there appear to be two different voltage ranges where the θ-frequency resonance is prominent, and the strength of the resonance shows opposite voltage dependence within the two ranges. As will be described below, the subsequent pharmacological analysis showed that these two forms of θ-resonance are also mechanistically different.

Voltage-clamp recording and blockade of M- and h-currents

In order to determine the ionic mechanisms underlying the two forms of θ-resonance we used highly selective ion channel blockers. For the reasons outlined in the Introduction, our prime candidates for ionic mechanisms were the M-current (I_M), h-current (I_h) and persistent Na⁺ current (I_NaP). To assess the possible contribution of each of these currents, we first needed to determine whether they were stably present under our whole-cell recording conditions, and determine their pharmacological properties. Therefore, we performed a series of whole-cell voltage-clamp experiments under conditions that were essentially identical to those used to record the resonance behaviour in current clamp (see Methods).

To measure I_M in relative isolation, a holding potential of -30 mV was used. At this potential, I_M is steadily activated, whereas most other voltage-gated ion channels are largely inactivated, thus eliminating the K⁺ currents I_A, I_D and delayed rectifier current (I_K) as well as Ca²⁺ currents (Brown & Adams, 1980; Halliwell & Adams, 1982; Storm, 1990). Negative-going steps (-20 mV) from a holding potential of -30 mV evoked a slow inward relaxation and the step back to -30 mV caused a similarly slow outward relaxation (Fig. 4A1; n = 6) characteristic of I_M deactivation and activation, respectively (Halliwell & Adams, 1982).

To measure I_h, we applied negative-going steps (-30 mV) from a hyperpolarized holding potential, -70 mV, where other channel types are not active. These steps also evoked slow inward relaxations (Fig. 4B; n = 5) representing typical I_h activation (Halliwell & Adams, 1982; Pape 1996).

We next tested the effects of two channel blockers: XE991 - a selective blocker of M-/KCNQ-type K⁺ channels (Wang et al. 1998), and ZD7288 - a selective blocker of h-/HCN-type channels (Pape, 1994; Harris & Constanti, 1995). At -30 mV, bath application of 10 μm XE991 abolished the slow relaxations in response to negative steps, produced an inward shift in the holding current and reduced the input conductance, consistent with blockade of I_M (Fig. 4A; n = 6). The XE991-sensitive current was isolated by digital subtraction of records obtained before and after the application (displayed at an expanded time scale in Fig. 4A2) and showed characteristic M-current kinetics. In contrast to the effects seen at -30 mV, no effect of XE991 was observed at the holding potential of -70 mV (Fig. 4B).

Conversely, ZD7288 had effects only at hyperpolarized potentials. Thus, bath application of 10 μm ZD7288 blocked the slow relaxations during hyperpolarizing steps from -70 mV, caused an outward shift in the holding current, and reduced the input conductance at -70 mV, consistent with h-channel blockade. The ZD7288-sensitive current, isolated by digital subtraction (Fig. 4B2) showed characteristic h-current kinetics.

In contrast to at -70 mV, ZD7288 had no effect at -30 mV, either on the slow I_M relaxations observed during negative steps, or on the holding current (Fig. 4A1, middle trace). In agreement with previous results with these blockers, we found that the effects of XE991 and ZD7288 could not be reversed by washout (Harris & Constanti, 1995); therefore the blockers were applied cumulatively to demonstrate their distinct effect in the same cell (as shown in Fig. 4A1 and B1). Identical results were obtained also when each blocker was applied alone.

During long-lasting voltage-clamp recordings, both I_Mand I_h showed a slow gradual rundown (2-30 % reduction in 10-30 min), as has also been reported by others (see e.g. Fig. 4 in Lüthi & McCormick, 1999). Nevertheless, currents maintained most of their amplitude for the time needed to perform the experimental protocols, and the effects of blockers could clearly be distinguished by their characteristic time course.

These results indicate that I_M and I_h can be reliably recorded under our experimental conditions, are activated over distinct voltage ranges, and can be selectively blocked by 10 μm XE991 and 10 μm ZD7288, respectively.

Voltage-clamp recording and blockade of the persistent Na⁺ current

To measure the voltage dependence of I_NaP, a series of different voltage steps from a holding potential of -58 or -60 mV (Fig. 5A, left) was delivered repeatedly while applying tetrodotoxin (TTX, 1 μm) to block voltage-gated Na⁺ channels (n = 8; Fig. 5A, right). The steady state current, measured at the end of the 300 ms long steps, showed a TTX-induced difference at all potentials beyond about -65 mV, while there was no effect at more negative potentials. This is shown in the current-voltage (I-V) plot in Fig. 5B. The plot of the TTX-sensitive difference current, obtained by subtraction, revealed an inward current at potentials positive to -65 mV (Fig. 5C).

However, the voltage range that could be explored by this approach was limited by the occurrence of unclamped Na⁺ action currents at potentials beyond -50 mV. To measure I_NaP at more depolarized potentials, we applied a slow ramp voltage command, rising from -88 to -28 mV in 750 ms (n = 7; Fig. 5D). This slow depolarization caused inactivation of the fast transient Na⁺ current underlying the action potentials, leaving only the non-inactivating I_NaP. (In this study we do not distinguish between I_NaP and a possible contribution of a ‘window current’ component generated by inactivating Na⁺ channels; cf. French et al. 1990; Crill, 1996). Application of TTX again blocked a persistent inward current, I_NaP, which started to activate between -70 and -65 mV and increased steeply with depolarization (n = 7; Fig. 5D and E; an arrow marks the action potential threshold).

Effects of M-channel blockade on resonance at different potentials

After using voltage clamp to study the three main persistent voltage-gated ionic currents operating in the subthreshold voltage range, we next proceeded to investigate which roles these currents play in the resonance behaviours observed in the current-clamp mode.

First, to test the role of M/KCNQ-type K⁺ channels in resonance behaviour, we bath-applied 10 μm XE991 while repeatedly injecting the ZAP current into the cell. To avoid spontaneous action potentials after the application, XE991 was tested while holding the cell at -63 mV by steady current injection (‘manual voltage clamp’). Figure 6A shows that XE991 virtually abolished the resonance at -63 mV. Figure 6B illustrates a typical time course of the XE991 effect by showing the complete series of records obtained before and during XE991 application. Although the peak-to-peak amplitude of the ZAP response showed some fluctuation, a clear resonance peak was always present before XE991, but disappeared gradually during the XE991 application (horizontal bar). In the three first and three last traces shown, the ZAP current was reversed in order to demonstrate that the resonance was not time-dependent (cf. Fig. 1B). Note that, because of the increased input resistance caused by M-channel blockade, the amplitude of the ZAP current amplitude had to be reduced after XE991 application (see Fig. 6A, lower traces, and arrows in Fig. 6B), in order to obtain a peak-to-peak voltage response comparable to the control traces and to avoid triggering action potentials (see Methods). In a few cases, an action potential was triggered at the end of the ZAP response (* in Fig. 6B).

In contrast to the blocking effect of XE991 on the resonance at depolarized potentials (Fig. 6A and B), this substance had no detectable effect on the resonance observed at hyperpolarized potentials (Fig. 6C). Thus, when the cells were tested at -78 mV, a clear resonance peak (at about 4 Hz) remained in the presence of 10 μm XE991, but could readily be blocked by ZD7288, as shown in Fig. 7. In many cells, a slow increase in the amplitude of the ZAP response was observed (Fig. 6C1 and Fig. 8C2), reflecting a time-dependent increase in R_input (probably due to ‘washout’ of ion channel activity). Such a change was also seen during recording in control medium and, hence, was not due to the application of blockers, and it did not alter the resonance. Another M-channel blocker, linopirdine (30 μm), mimicked the effects of XE991; it suppressed the resonance at -58 mV, but not at -78 mV (n = 1; data not shown).

Figure 7. ZD7288 blocked θ-resonance at hyperpolarized but not at depolarized membrane potential.

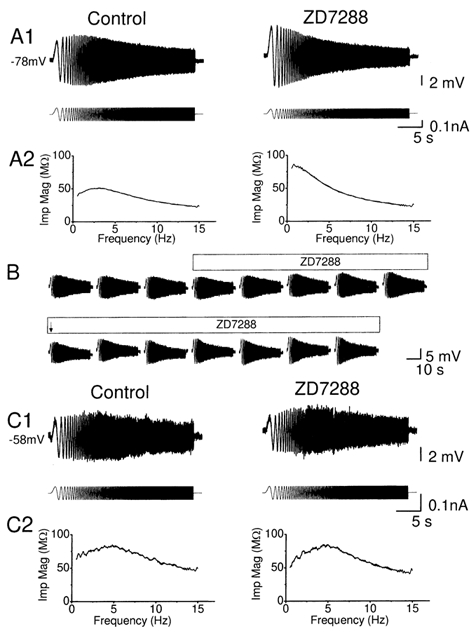
A1 and C1, typical voltage response (upper traces) evoked from hyperpolarized (-78 mV, in A1) and depolarized (-58 mV, in C1) membrane potentials by injecting a ZAP current (lower traces), before and after application of 10 μm ZD7288. The resonance at hyperpolarized level (-78 mV) was blocked by ZD7288 (n = 7, P = 0.004, Q = 1.12 ± 0.03 and 1.00 ± 0.00 before and after application of ZD7288), while the resonance at the at depolarized level (-58 mV) was resistant to ZD7288 (n = 4, P = 0.36, Q = 1.19 ± 0.08 and 1.29 ± 0.17 before and after application of ZD7288). A2 and C2, the impedance magnitude, calculated from the data in A1 and C1, is plotted against input frequency before and after ZD7288 application. B, typical time course of blockade of resonance, evoked from a hyperpolarized level. The steady state DC current had to be adjusted before and after ZD7288, due to the hyperpolarization caused by ZD7288. The peak-to-peak amplitude of ZAP current was reduced after ZD7288, at the time marked with an arrow.

Figure 8. Effect of TTX on the resonance at different membrane potentials.

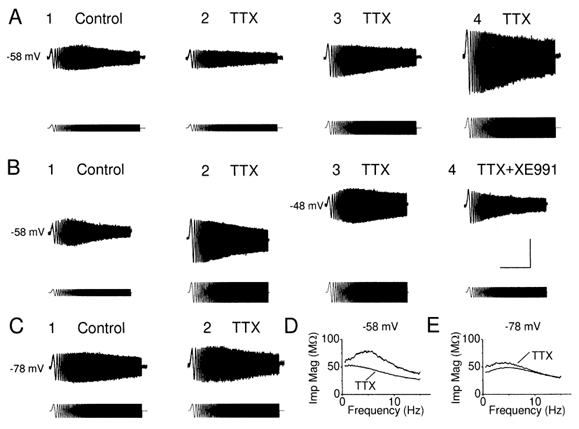
A, voltage responses to ZAP current before (A1) and after (A2-4), in a cell maintained at subthreshold level. The resonance at depolarized membrane potential was largely reduced by TTX at this membrane potential (n = 5, P = 0.03, Q = 1.17 ± 0.06 and 1.00 ± 0.00 before and after application of TTX). The peak-to-peak amplitude of voltage deflections in response to same ZAP current injection was reduced after TTX (A2), when compared to the control period (A1), due to the ‘amplifying’ effect of I_NaP. A3, resonance was absent after increasing the peak-to-peak amplitude of ZAP current, so that the peak-to-peak amplitude to voltage deflection was comparable before and after TTX. Resonance was not rescued by increasing the peak-to-peak amplitude of ZAP current to make the voltage response (A4) much larger than control. B1-3, in the presence of TTX, resonance was restored by depolarizing the cell further to -48 mV, whereas it was blocked by XE991 (B4, n = 4). C, voltage response to ZAP current injection from a hyperpolarized membrane potential before (C1) and after TTX (C2), in the same cell shown in A. Note that the resonance at -78 mV was resistant to TTX (n = 5, P = 0.22, Q = 1.17 ± 0.04 and 1.14 ± 0.04 before and after application of TTX). D, impedance magnitude plotted against input frequency, from the traces in A1 and A2. Note that distinct ‘hump’ of impedance magnitude profile close to 5 Hz in control condition disappeared in the presence of TTX. E, impedance magnitude plotted against input frequency, from the traces in C1 and C2. The small increase of the impedance magnitude could be due to rundown of the ‘leak’ current. The scale bars in B4 apply to all records in A-C: 10 s, 10 mV, 420 pA.

Effects of h-channel blockade on resonance at different potentials

The h-channel blocker ZD7288 was used to test the role of this channel type in electrical resonance. Figure 7A shows that bath-application of 10 μm ZD7288 abolished the resonance at -78 mV. Figure 7B shows a typical time course of the effect as a complete series of records obtained before and during application of the blocker. A clear resonance peak was always present in normal medium, in spite of some variation in the peak-to-peak amplitude of the ZAP response, but disappeared after ZD7288 was applied. As expected, ZD7288 increased the input resistance at hyperpolarized potentials, presumably by blocking h-channels. Consequently, the ZAP current again had to be reduced to obtain a voltage response of comparable amplitude to the control (Fig. 7A1, lower trace, and arrow in Fig. 7B). In contrast to its effect on the resonance at hyperpolarized membrane potential, ZD7288 caused little or no change of resonance at depolarized potentials (Fig. 7C).

Effects of the Na⁺ channel blockade on resonance at subthreshold potentials

To test the role of the persistent Na⁺ current, I_NaP, on resonance behaviour, we applied the Na⁺ channel blocker TTX (1 μm). Figure 8 shows that bath-application of 1 μm TTX nearly abolished the resonance at -58 mV (A and D) but not at -78 mV (C and E). Under otherwise constant conditions, TTX also caused a hyperpolarization of the cell (not shown), as would be expected when the I_NaP that is persistently activated at this potential is blocked (cf. Fig. 5C and E). Even when the TTX-induced hyperpolarization was compensated (prevented) by DC injection (as was routinely done, e.g. in Fig. 8A2-4), the voltage response to the ZAP current was much reduced in amplitude, presumably due to elimination of the amplifying effect of I_NaP (Hutcheon & Yarom, 2000). Furthermore, even when the voltage response amplitude was increased to match (Fig. 8A3) or exceed (Fig. 8A4) the control amplitude, by increasing the injected ZAP current (lower traces in A), there was still little or no resonance. In contrast, when we depolarized the cell further (to about -48 mV) by DC current injection, we found that a strong resonance reappeared (Fig. 8B3), and could be fully blocked by 10 μm XE991 (Fig. 8B4), showing that the resonance at this depolarized potential was also dependent on M-current.

This observation appears to differ from results reported by others. Thus, Gutfreund et al. (1995) found, in neocortical pyramidal cells, that I_NaP merely amplifies the resonance, so that TTX would only reduce its amplitude without fully blocking the resonance. A possible explanation for this discrepancy will be suggested in the Discussion.

Table 3 summarizes our results with ion channel blockers. Taken together, these data indicate that M-current, persistent Na⁺ current and h-current all contribute to resonance at θ frequencies in CA1 pyramidal cells. It appears that I_M and I_NaP produce resonance at depolarized, just subthreshold potentials, whereas I_h apparently is essential at hyperpolarized potentials. At in-between membrane potentials, near the resting level, there is less θ-resonance, presumably because the three essential currents, I_M, I_NaP and I_h, are all too weakly activated in this voltage range.

Table 3.

The effect of ion channel blockers on the strength of resonance, as indicated by the Q values before and after applying the blockers

	Depolarized	Hyperpolarized
Control	1.13 ± 0.04	1.16 ± 0.07
XE991	1.00 ± 0.00	1.12 ± 0.06
P value (n)	0.02(7)	0.13(5)
Control	1.19 ± 0.08	1.12 ± 0.03
ZD7288	1.29 ± 0.17	1.00 ± 0.00
Pvalue (n)	0.36(4)	0.004(7)
Control	1.17 ± 0.06	1.17 ± 0.04
TTX	1.00 ± 0.00	1.14 ± 0.04
Pvalue (n)	0.03(5)	0.22(5)

In the following discussion of the two forms of θ-resonance, we will for convenience use the shorthand terms ‘M-resonance’ for the M-current-dependent form occurring at depolarized potentials and ‘H-resonance’ for the h-current-dependent form occurring at hyperpolarized potentials.

Mathematical modelling of electrical resonance in CA1 pyramidal cells

The above experimental results strongly suggest that M-, h- and NaP-currents each contribute substantially to electrical resonance behaviour in CA1 pyramidal cells. However the experiments do not answer the question of whether these three currents, combined with the passive membrane properties of the cell, are alone sufficient to cause the two types of resonance behaviour that we observed. In principle it is not possible to prove experimentally that certain mechanisms are sufficient to cause a certain phenomenon, because there is always a possibility that an inconspicuous but essential mechanistic factor went undetected. In pharmacological experiments, there is also, in principle, a possibility that the substances used, however specific they appear to be from extensive experimental testing, could have unexpected direct or indirect side effects.

To test for these possibilities, and to gain deeper insight into the roles of the different currents in such resonance behaviour, we performed mathematical simulations of electrical resonance in CA1 pyramidal cells.

Computer simulations were performed using a reduced compartmental model of a CA1 pyramidal cell, which has been developed by Lyle Graham in collaboration with our laboratory (see Methods; Borg-Graham 1999; Shao et al. 1999) and incorporates 11 active currents and intracellular Ca²⁺ dynamics. In order to adapt the model to the set of CA1 cells and recording conditions used in this study, we adjusted the whole-cell capacitance and the maximal conductance of I_M, I_NaP (French et al. 1990) and I_h, and the activation time constants of I_M and I_h to approximate our voltage-clamp measurements of these currents (Fig. 4 and Fig. 5), and omitted I_NaT, I_D and I_sAHP (see Methods).

Using this modified model, we simulated the responses to ZAP currents like those used experimentally (Fig. 9), i.e. with linearly increasing frequency, rising from 0 to 15 Hz within 30 s (lower traces in Fig. 9A). The resulting voltage responses at -58 and -78 mV (Fig. 9A, upper traces) resembled those obtained experimentally at the same potentials under control conditions, and showed similar resonance peaks in the impedance plots (Fig. 9A and B; compare with left- and right-hand panels in Fig. 3A and B).

We next used the model to reveal the expected contribution of the different ionic currents to the resonance behaviour at depolarized and hyperpolarized potentials. Figure 9C-E shows the main currents underlying these responses to ZAP currents at -58 mV (left) and -78 mV (right): I_M, I_h and I_NaP. It is evident that the M-current provides a large contribution to the M-resonance at -58 mV, but virtually no contribution to the H-resonance at -78 mV (Fig. 9C). Conversely, the h-current provides a large contribution to the H-resonance at -78 mV, but is little activated at -58 mV (Fig. 9D). The persistent Na⁺ current is active at -58 mV, but not at -78 mV (Fig. 9E). However, there is a difference between I_M and I_NaP. I_M shows a strong frequency-dependent modulation of its amplitude: the larger I_M at low frequencies preferentially depresses the amplitude of the voltage response at those frequencies, thus generating resonance, in concert with the passive membrane properties of the cell (Hutcheon & Yarom, 2000). In contrast, the amplitude of I_NaP shows largely voltage-dependent as opposed to frequency-dependent modulation (Fig. 9E), so that I_NaP merely follows the amplitude of the voltage response (Fig. 9A) and amplifies it at all frequencies (See also Discussion).

All other currents included in the model (the Ca²⁺ currents, and the K⁺ currents I_K(DR), I_A and I_C) showed negligible amplitudes during these simulations (data not shown). Furthermore, omitting all of these other currents did not introduce any noticeable change in the results of the simulation (data not shown). These results demonstrates that I_M, I_NaP and I_h are sufficient for producing M- and H-resonance, respectively.

To test whether the dendritic conductances or the dendritic cable were important for the resonance, we performed simulations also with just a passive dendritic cable, or a single somatic compartment (i.e. no dendritic cable) with just I_M, I_NaP and I_h. In both cases, robust θ-resonance at depolarized and hyperpolarized potentials was obtained, indicating that the dendrites played no essential role in the resonance behaviour (data not shown).

Furthermore, when pharmacological blockade of I_M was simulated by removing I_M from the model (Fig. 10A, No I_M) the resonance peak was abolished at -58 mV but not at -78 mV, thus resembling the effect of blockade of I_M by XE991 (Fig. 6A). Conversely, when blockade of I_h was simulated by removing I_h from the model (Fig. 10A, No I_h), the resonance peak was abolished at -78 mV but not at -58 mV, thus mimicking the effect of blockade of I_h by ZD7288 (Fig. 7A).

Figure 10. Computer simulation showing that resonance at depolarized and hyperpolarized membrane potential is due to different mechanisms.

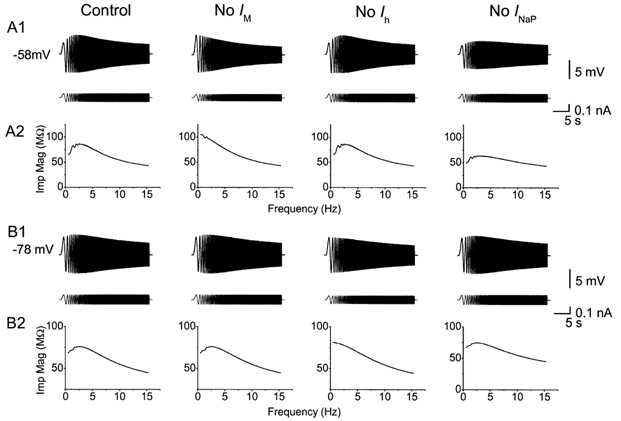
A1, voltage responses (upper trace) to ZAP current (lower trace) from the model cell at -58 mV, before and after removal of I_M, I_hor I_NaP. Resonance at depolarized level was fully blocked by removal of I_M, but was resistant to removal of I_h. Removal of I_NaP reduced the peak-to-peak amplitude of the resonance, but caused little change of resonance frequency at -58 mV. B1, voltage response (upper trace) to ZAP current (lower trace) from the model cell at -78 mV, before and after removal of I_M, I_h or I_NaP. Resonance at -78 mV was resistant to removal of I_NaP and I_M, but was blocked by removing I_h. A2 and B2, impedance magnitude plotted as a function of input frequency, from the traces in A1 and B1, respectively.

These results show that I_M is essential for producing resonance at the depolarized potential -58 mV (M-resonance), whereas I_h is essential for producing resonance at the hyperpolarized potential -78 mV (H-resonance). Thereby, the simulations exclude the possibility that the experimental results obtained with XE991 and ZD7288 were due to pharmacological side effects on other channel types.

To simulate blockade of I_NaP by TTX, we removed this current from the model (Fig. 10A, No I_NaP). This reduced the peak-to-peak amplitude of the response at -58 mV, but not at -78 mV. However, the M-resonance observed at -58 mV, was not abolished, as indicated by the peak in the impedance plot (Fig. 10A2, No I_NaP) and the peak occurred at about the same frequency as before omitting I_NaP from the model. This limited effect on the resonance peak in the simulations was also seen when the amplitude of the ZAP current was increased to make the peak-to-peak voltage response match that of the control response (data not shown), as was done in the experiments (Fig. 8A3 and 4). Thus, these simulation results differ from what we observed experimentally (Fig. 8). A possible reason for this apparent discrepancy is suggested in the Discussion. In accordance with previous studies (Hutcheon et al. 1996a), these simulation results predict that a persistent Na⁺ current amplifies the oscillatory response, but does not determine the resonance frequency.

For each experimental situation, several different simulations were performed, over a range of different parameter values, in order to test whether the simulation results were specific to a particular set of parameter values. These explorations showed that the main results were robust, i.e. not dependent on a particular set of values (data not shown).

Figure 11 shows model simulations of the voltage-dependence of the resonance behaviour. The ZAP responses at different membrane potentials (A) and the plots of the Q value for the full model (B, upper left panel, filled circles) showed a U-shaped voltage dependence for the model, resembling our experimental results (the data from Fig. 3C were replotted in Fig. 11B, upper left panel: open circles and broken line). When, I_M or I_h was omitted from the model, the resonance strength (Q value) was strongly and selectively reduced at depolarized or hyperpolarized potentials, respectively, resulting in monotonic voltage dependence plots (Fig. 11B). When I_NaP was omitted from the model, the Q value was only reduced at depolarized potentials (Fig. 11B, lower right panel).

These results indicate that both the M- and h-current contribute to resonance at θ frequencies in CA1 pyramidal cells. Furthermore, the simulations predict that a persistent Na⁺ current can amplify the slow oscillatory response, without being necessary for resonance to occur and without determining the resonance frequency.

Discussion

Main results

The results of the present study indicate that the CA1 pyramidal cells are endowed with two different mechanisms for slow electrical resonance at theta frequencies. One form of θ-resonance, M-resonance, operates at depolarized, subthreshold membrane potentials, between the resting potential and the spike threshold (-70 to -50 mV). This form is dominated by the M-current and the persistent Na⁺ current. The second form of θ-resonance, H-resonance, is most prominent at hyperpolarized membrane potentials (-75 to -95 mV) and is dominated by the h-current. These intrinsic properties coexist with, and presumably interact with, network level mechanisms of oscillation (Buzsaki, 2002).

Our conclusions are based on several lines of evidence. (1) Current-clamp recordings of resonance behaviour demonstrated two forms of slow (θ) resonance: M- and H-resonance, occurring at different membrane potential ranges (Fig. 3); (2) each of these two forms of resonance was specifically suppressed by selective channel blockers: the M-resonance was abolished by XE991 or TTX, whereas the H-resonance was abolished by ZD7288 (Figs 6-8); (3) voltage-clamp recordings demonstrated that I_M and I_NaP were activated at the membrane potentials where the M-resonance occurred and that I_h was activated at potentials where the H-resonance occurred (Fig. 4 and Fig. 5); (4) the voltage-clamp recordings also showed that XE991, ZD7288 and TTX acted as selective blockers of I_M, I_h and I_NaP, respectively, under our recording conditions; (5) finally, computer simulations with a simplified mathematical model of a CA1 pyramidal cell demonstrated that currents with the observed properties of I_M, I_h and I_NaP are sufficient to explain the main features of the M- and H-resonance (Figs 9-11). Taken together, these results strongly suggest that I_M, I_NaP and I_h are both necessary and sufficient for the M- and H-resonance, respectively, in CA1 pyramidal cells.

Most of our experiments were performed at about 33 °C (32.9 ± 0.09 °C), i.e. about 5 °C below the normal physiological brain temperature of rats (≈38 °C). This low experimental temperature, which was chosen for technical reasons, seems to largely account for the relatively low resonance frequency observed in most of our experiments: mean ≈3 Hz at both hyperpolarized (-75 to -80 mV) and depolarized (-60 mV) potentials (see Fig. 3D). Accordingly, when warmed from 33 to 38 °C, the cells roughly doubled their resonance frequency, from 3.5 to 7.1 Hz (Fig. 2), thus reaching frequencies that are typical of θ oscillations in the rat hippocampus in vivo (Vanderwolf, 1988; Buzsaki, 2002). Furthermore, the estimated temperature dependence of resonance frequency (Q₁₀ = 4.22) seems to fit reasonably well those estimated for both I_M and I_h kinetics in CA1 cells (Q₁₀ ≈ 5 for both currents; Halliwell & Adams, 1982). Hence, the ionic mechanisms described here are likely to generate resonance well within the physiological θ-frequency band observed in vivo.

How do the M- and h-currents cause resonance?

We suggest that the M-resonance at depolarized potentials can be explained as follows. For the sinusoidal depolarizations occurring at the lowest frequencies of the ZAP protocol (0-3 Hz), the M-channels have time to open before the peak depolarization is reached, thus causing an outward current which depresses the peak. During the imposed low-frequency hyperpolarizations, I_M will have time to turn off before the peak hyperpolarization is reached, thus causing a depolarizing influence that reduces the peak negative amplitude.

To explain the H-resonance at hyperpolarized potentials, we hypothesize the following effects of I_h. At -80 mV I_h is already substantially activated. During the sinusoidal depolarizations at low frequencies (0-2 Hz), the h-channels have time to close before the peak is reached, thus causing a hyperpolarizing influence (due to reduced inward I_h) that depresses the peak. Likewise, during low-frequency hyperpolarizations, the h-channels have time to open before the peak hyperpolarization, thus causing a depolarizing influence (more inward I_h) near the peak, which reduces the negative peak amplitude.

It may perhaps seem surprising that the presence of I_M and I_h, which both contribute to the medium after-hyperpolarization (mAHP; Storm, 1989, 1990, 1993; Williamson & Alger, 1990), can cause an apparent attenuation of the hyperpolarizing half-cycle of the ZAP response at low frequencies. This is because the apparent attenuation is only relative to the amplitudes seen at higher frequencies. Secondly, it occurs at frequencies that are too low for I_M and I_h to produce significant mAHP-like effects, i.e. when the M-channels have sufficient time to close, and the h-channels have time to open, during the slow ‘downstroke’ of each hyperpolarizing half-cycle. Near the resonance frequency, however, the ‘downstroke’ is fast enough to allow I_M and I_h to produce more of their mAHP-like effects: I_M by its outward tail current following the opening of M-channels during the depolarizing half-cycle, I_h by the reduction of its inward tail current caused by the closing of h-channels during the preceding depolarizing half-cycle (Storm, 1989).

At the higher frequencies of the ZAP current, the influence of both M- and h-channel gating will approach zero because the gating will not have time to follow the rapid potential changes. Hence, the response will increasingly be determined by the passive membrane properties of the cell. Consequently, the briefer the sinusoidal current deflections, the less will be their charging of the membrane capacitance (i.e. a larger proportion of the injected current will be shunted as capacitative current C_m × (dV/dt) and therefore not contribute to the voltage deflections determined by the current flowing through the ohmic resitance; ΔV = ΔI_ohmic × R).

Thus, when progressing from low to high frequencies in the ZAP protocol, the resonance peak will occur at intermediate frequencies where the attenuating influences of M-and h-channel have declined (because their slow gating cannot follow the faster oscillations), while the passive capacitative shunting occurring at high frequencies is still not maximal. Our computer simulations largely confirmed these hypotheses (Fig. 9 and Fig. 10).

How does the NaP-current contribute to the resonance?

Since I_NaP is known to have fast activation and deactivation kinetics (time constants < 5 ms, French et al. 1990; Crill, 1996), it is not expected to generate low-frequency resonance (Hutcheon & Yarom, 2000). However, I_NaP can amplify the resonance generated by other mechanisms (e.g. I_M) in the following way. During depolarizations, I_NaP will activate and cause further depolarization, whereas hyperpolarizations will turn off I_NaP, thus causing more hyperpolarization. Because I_NaP is fast compared to the passive membrane time constant and the kinetics of I_M, it will not alter the time course of the responses or the resonance frequency.

Our computer simulations, as well as those of others (Gutfreund et al. 1995; Hutcheon et al. 1996a), support the prediction outlined above. Also experimental results reported from neocortical and enthorinal neurons (Klink & Alonso, 1993; Gutfreund et al. 1995; Hutcheon et al. 1996b) support this notion, by showing that TTX only reduces the amplitude of the ZAP response without fully blocking the M-resonance or changing its frequency dependence (Hutcheon & Yarom, 2000).

In contrast, we found surprisingly that the resonance observed at -58 mV virtually disappeared after applying TTX, but returned when the cell was depolarized further to -48 mV (Fig. 8B3). When XE991 was added, however, the resonance at -48 mV was fully blocked also at depolarized potentials (Fig. 8), indicating that this is also a form of M-resonance. How can these observations be reconciled with the prediction that I_NaP merely amplifies the resonance?

We suggest the following hypothesis. When studying resonance at -58 mV, we injected a depolarizing current at the soma, producing a local depolarization there, whereas more distal part of the cell (in particular the distal apical dendrites) would be expected to be less influenced by the somatic current injection and, therefore, have a more negative membrane potential, closer to the resting potential (about -70 mV).

We hypothesize that I_NaP may help this locally imposed depolarization to spread further out into the dendrites than would be the case without I_NaP. Thus, I_NaP, due to its regenerative (positive feedback) properties, may produce something like a ‘spatial plateau depolarization’ stretching relatively far out from the soma. Application of TTX would cause this ‘plateau depolarization’ to collapse, making the depolarization imposed by the somatic current injection more local. Consequently, as the dendritic membrane potential falls back to a more negative level, the M-channels close and the I_M-dependent M-resonance there disappears. Even if the soma is kept depolarized, providing a local basis for M-resonance, this tendency will be swamped by the large regions that cannot resonate because their M-channels are closed. Thus, the overall voltage response, as recorded at the soma, will be dominated by the large non-resonating membrane. However, when the cell is further depolarized, by injecting stronger DC current at the soma (still in TTX), even the dendrites will be depolarized back into the M-current activation range, causing them to resonate again as they did before TTX was added.

This hypothesis needs further testing, preferably by combining new experiments with more elaborate modelling. In particular, for improved simulations one would need more complete information regarding M-channel distribution in the dendrites than is currently available (Cooper et al. 2000), and a more realistic dendritic geometry.

Do other ion channels contribute to the two forms of θ-resonance?

The three currents involved in the M- and h-forms of θ-resonance, I_M, I_NaP and I_h, have two properties in common: they activate at potentials negative to the spike threshold, and they do not inactivate. In contrast, all of the other known voltage-dependent ionic conductances in the CA1 cells are likely to be excluded from contributing strongly to the subthreshold ZAP response and θ-resonance. This is because they either activate strongly only at more depolarized potentials (transient Na⁺ current, high-threshold Ca²⁺ currents and K(DR)-type and Ca²⁺-activated K⁺ currents) or inactivate at the depolarized holding potential (D- and A-currents) or during the slow sinusoidal depolarizations during the ZAP (A-currents). In thalamic relay neurons, slow oscillations are generated through interplay between I_h and the low-threshold Ca²⁺ current (I_CaT) (Pape 1996; Lüthi & McCormick, 1999). According to our experimental results, this appears not to occur in the CA1 hippocampal pyramidal cells, probably because the somatic I_CaT and I_h are relatively smaller in this cell type (Halliwell & Adams, 1982; Thompson & Wong, 1991). This intuitive reasoning was supported by our computer simulations, which showed that the transient Na⁺ current, the Ca²⁺ currents, and the K⁺ currents I_K(DR), I_A, I_D and I_C are all close to zero throughout the ZAP responses. Furthermore, a simplified model containing only I_M, I_NaP and I_h, was able to reproduce the resonance behaviour at both depolarized (M-resonance) and hyperpolarized (H-resonance) membrane potentials, equally well as the complete model containing all the conductances. This result demonstrates that the three currents I_M, I_NaP and I_h, are sufficient to explain the θ-resonance of CA1 pyramidal cells at depolarized and hyperpolarized membrane potentials.

Comparison with previous results

Voltage dependence of the θ-resonance

The U-shaped voltage dependence of the θ-resonance, i.e. the fact that the resonance was larger at both depolarized and hyperpolarized membrane potentials than at the resting potential (Fig. 3), appears not to have been reported previously. So far, only resonance with a monotonic voltage dependence seem to have been found. For example, pyramidal cells from guinea-pig frontal cortex show a resonance and oscillations that are maximal in amplitude at depolarized potentials (near -55 mV), and absent at the most hyperpolarized potentials tested (< -79 mV) suggesting that those cells lack h-type resonance (Gutfreund et al. 1995), in contrast to CA1 cells. Similarly, the prominent θ-like oscillations in stellate cells of the entorhinal cortex were found to be maximal at depolarized potentials near -55 mV, and absent at more negative potentials (Alonso & Llinas, 1989; Alonso & Klink, 1993). Interestingly, however, a slightly (Leung & Yim, 1986) or clearly (Ylinen et al. 1995) U-shaped voltage dependence of θ oscillation amplitude has been recorded in CA1 pyramids during hippocampal θ activity in vivo. It therefore seems likely that the dual M-and h-type mechanisms described here may contribute to the θ oscillations of CA1 pyramids in vivo, although the situation is then far more complex and rhythmic input from the network is the main source of the θ activity (Ylinen et al.1995).

Involvement of M-current

Evidence that M-like currents may underlie slow oscillations and resonance has previously been reported from three types of neuron. Gutfreund et al. (1995) found that a model with a slow K⁺ current with I_M-like kinetics could reproduce resonance and oscillations resembling those observed in neurons from the guinea-pig frontal cortex. The resonance was abolished by applying a mixture of 15 mm TEA and 5 mm Cs⁺, but specific M-channel blockers were not tested. In amygdala neurons, Pape & Driesang (1998) found that Ba²⁺ ions reduced θ band-resonance and carbachol (but not 20 mm TEA) blocked low-threshold oscillations, but they cautiously pointed out that these antagonists also affect several currents other than I_M. In cerebellar granule cells, D'Angelo et al. (2001) found a Ca²⁺-independent and TEA-insensitive K⁺ current with I_M-like kinetics that was inhibited by Ba²⁺ and could induce bursting and θ band-resonance in a model.

However, to our knowledge, involvement of M-current in θ-resonance or θ oscillations has not previously been clearly demonstrated by use of selective M-channel blockers or other specific tools. The subthreshold oscillations of entorhinal stellate neurons were blocked by Ba²⁺ ions (Alonso & Klink, 1993), but the possible involvement of I_M was rejected because carbachol did not block the oscillations and the I_M hypothesis could not explain the effect of Ba²⁺ on the I-V plot (Klink & Alonso, 1993, 1997a). Likewise, in rat sensorimotor cortex neurons, the role of an M-current in subthreshold membrane resonance was excluded by the finding that the resonance was not blocked by Ba²⁺ ions, but by Cs⁺ (Hutcheon et al. 1996b). A recent preliminary report concluded that θ-resonance in rat CA1 pyramidal cells is due to I_h, but not I_M, because the M-channel blocker linopirdine had no apparent effect (Suckling et al. 2000). The reason for the discrepancy between their results and ours is not clear, but may be related to the fact that they used younger animals (12-18 days, O. Paulsen, personal communication 16th July 2002). In young cells, I_M may be expressed at low levels, and/or may be rapidly lost by ‘washout’ during whole-cell recording because the cells are smaller.

To our knowledge, the M-current is also missing in the numerous computer models made to simulate θ rhythm and other forms of hippocampal network oscillations (e.g. Wallenstein & Hasselmo, 1997; Denham & Borisyuk, 2000; Traub et al. 2000), except for one (Bibbig et al. 2001). The latter model included an M-current, but it was not added to produce θ rhythm or resonance; instead it was added to provide medium afterhyperpolarizations (mAHPs), firing accommodation and a transition from α to β oscillations (by ad hoc changes e.g. in M-conductance density (⁻g_M)). Likewise, the h-current is also missing from most hippocampal network models (e.g. Traub et al. 2000). As mentioned above, an I_M-like conductance was included in a previous model of membrane potential oscillations in neurons from guinea-pig frontal cortex (Gutfreund et al. 1995), but such a conductance is absent from more recent models of neocortical neurons (Hutcheon et al. 1996a).

Involvement of I_h and I_NaP

As outlined in the introduction, I_h and/or I_NaP have already been implicated in membrane potential oscillations and resonance in several cell types, including neurons in the thalamus (Pape, 1996; Lüthi & McCormick, 1998), entorhinal cortex (Alonso & Llinas, 1989) neocortex (Gutfreund et al. 1995; Hutcheon et al. 1996b) and hippocampus (Suckling et al. 2000). However, in entorhinal stellate cells, where I_h was first suggested to underlie subthreshold oscillations (Alonso & Llinas, 1989), this hypothesis, as well as involvement of I_M, were later rejected (Klink & Alonso, 1993, 1997b). The reasons for these differences remain to be determined, but may be related to differences between cell types, experimental conditions or developmental changes.

A new function for the M-current

Previously, the M-current has been found to have the following four functions in neurons: (1) stabilization of the resting potential, (2) effector mechanism for neuromodulation by acetylcholine and peptides, including generation of slow synaptic potentials; (3) generation of the mAHP and (4) early spike frequency adaptation (Brown et al. 1990; Storm, 1990; Hille, 2001). The present data indicate that the neuronal M-current also has another functional role: (5) generation of slow subthreshold resonance in the θ frequency band. When embedded in an active network, this neuronal M-resonance will facilitate neuronal and network oscillations and action potential discharges in the same preferred frequency band.

It seems plausible that the function of the M-current in generating oscillations may actually represent the main raison d’être of the M-current (i.e. KCNQ channels) in the brain. This seems particularly probable in hippocampus and other parts of the cortex, where oscillations in the θ frequency band appear to play such vital functional roles for neuronal coding, synaptic plasticity, learning and memory (Buzsaki, 2002). Thus, KCNQ channels in the CNS may have evolved under a selection pressure favouring properties suitable for certain neural oscillations, thereby contributing to the evolution of an oscillation-based neural code (O'Keefe & Recce, 1993; Hopfield, 1995).

The present data also strongly support a central role for the h-current in brain oscillations (Hutcheon et al. 1996b; Pape, 1996; Suckling et al. 2000). As for I_M it seems plausible that this may actually be a principal function of the h-/HCN-type channels in the hippocampus and cortex. This would be in accordance with of the role of h-currents in oscillations and pacemaking already described in some other cells (e.g. Pape, 1996; Lüthi & McCormick, 1998). The striking similarity between the functional effects of I_M and I_h, i.e. that they both generate θ-resonance and mAHPs albeit at different potentials, may be more than a coincidence. The two channel types may have been selected in evolution and co-evolved as ‘partners’ sharing a common task within different voltage ranges or at different functional states of the network. Since I_M and I_h are differentially modulated, their functional roles may be overlapping when their voltage ranges are shifted by neuromodulation (Pedarzani & Storm, 1995; Pape, 1996; Storm, 2000).

Contribution of the two forms of resonance to network oscillations in the θ range

The extracellular currents underlying the θ waves recorded by EEG are mainly generated by the entorhinal input, CA3 (Schaffer) axons and voltage-dependent calcium currents in pyramidal cell dendrites (Buzsaki, 2002). In contrast to these large currents ‘expressing’ the θ rhythm, small low-threshold currents operating in the subthreshold voltage range may be important for determining the rhythm. Thus, although the M-, h- and NaP-currents are small compared to those underlying action potentials, these modest low-threshold currents can have a decisive impact on the initiation and timing of action potentials, because they operate in the subthreshold voltage range, where the larger currents are not active and the input resistance is high. The resonance properties of the CA1 pyramidal cells described here imply that the neurons will respond more strongly to synaptic input at θ frequencies (Cobb et al. 1995; Buzsaki, 2002). Thus, the neurons will act as frequency selectors or bandpass filters, promoting population activity at the preferred θ frequencies (Gutfreund et al. 1995). In particular, rhythmic input from single GABAergic interneurons (basket or axo-axonic interneurons) can synchronize θ frequency oscillations in CA1 hippocampal pyramidal cells, causing entrainment of their subthreshold oscillations and phase locking of their firing (Cobb et al. 1995). The mechanism underlying this inhibitory phasing of the pyramidal cells was found to be a subthreshold rebound depolarization following the inhibitory synaptic potentials, presumably due to intrinsic membrane conductances (Cobb et al. 1995). The present study strongly suggests that the intrinsic currents underlying this inhibitory phasing, entrainment and synchronization are I_M, I_NaP and I_h, and that they may engage in this function differently, depending on the prevailing membrane potential and the modulatory state of the cell. However, our results do not address the question of whether intrinsic neuronal properties or network-level mechanisms are most important for θ oscillations in vivo.

Why is the θ-resonance minimal near the resting potential? Possible consequences and effects of neuromodulation

The strength of the θ-resonance appeared to be minimal near the resting potential (Fig. 3C). The reason for this is that the depolarization-activated I_M and I_NaP are necessary for producing resonance at depolarized potentials, whereas the hyperpolarization-activated I_h is essential at more negative potentials. At in-between membrane potentials, near the resting level, the θ-resonance is reduced because the three essential currents, I_M, I_NaP and I_h, are all weakly activated. Our current-clamp and voltage-clamp data (Figs 1-8), as well as the computer simulations (Figs 9-11), support this idea.

A functional consequence of its minimum near the resting potential, is that θ-resonance will require a certain level of synaptic activity to be strongly expressed. Thus, excitatory (EPSPs) or inhibitory (IPSPs) potentials of sufficient amplitude and duration, or more persistent neuromodulatory shifts in the membrane potential, could bring the cell into the voltage ranges where θ-resonance mechanisms are strong. For example, trains of glutmatergic EPSPs or depolarizing modulation by monoaminergic, metabotropic glutamatergic or cholinergic input (Madison & Nicoll, 1986; Charpak et al. 1990; Pedarzani & Storm, 1995) may activate the M-resonance. (Of relevance here is the observation that leak conductance-mediated depolarization requires lower agonist concentrations than I_M suppression, and may therefore occur more often under physiological circumstances; Nicoll, 1988). Conversely, the H-resonance may be brought into play by transmitter-induced hyperpolarizations induced by, e.g. GABA or monoamines (see, e.g. Madison & Nicoll, 1986).

In addition, the direct effect of the membrane conductance changes induced by the chemical signals will also affect the cell input resistance (R_input) and passive membrane time constant (τ_m), thereby shifting the resonance frequency. For example, adenosine or GABA_B agonists, which open inward rectifier K⁺ channels, would be expected to reduce R_input and τ_m, thus shifting the resonance peak to somewhat higher frequencies.

Stronger and more direct effects are expected through modulation of the three main players in the θ-resonance, I_M, I_NaP and I_h. Each of these currents are known targets of neurotransmitters and modulator substances. Ascending cholinergic pathways from the basal forebrain (medial septum/diagonal band) and monoaminergic input from the brainstem (locus coerulus, raphe nuclei, ventral tegmental area) are known to mediate changes in the functional state of the forebrain, from sleep and drowsiness to arousal, wakefulness and attention (Steriade et al. 1993). Accordingly, monoamine transmitters such as noradrenaline, serotonin, histamine or dopamine, by shifting the activation curve of I_h to more a depolarized voltage range (Pedarzani, 1995; Pape, 1996; Storm et al. 2000), could cause this current to participate in the generation of resonance near the resting potential, or even at depolarized potentials, together with I_M. Acetylcholine could have a similar effect by shifting the voltage dependence of I_h (Lüthi & McCormick, 1998) while having an opposite effect at depolarized potentials, suppressing the M-resonance by blocking I_M (Halliwell & Adams, 1982). Thus, the dual mechanism of θ-resonance reported here implies multiple possibilities for tuning of the rhythmic network activity through neuromodulation.