Photosynthetic maximum quantum yield increases are an essential component of the Southern Ocean phytoplankton response to iron

Abstract

It is well established that an increase in iron supply causes an increase in total oceanic primary production in many regions, but the physiological mechanism driving the observed increases has not been clearly identified. The Southern Ocean iron enrichment experiment, an iron fertilization experiment in the waters closest to Antarctica, resulted in a 9-fold increase in chlorophyll (Chl) concentration and a 5-fold increase in integrated primary production. Upon iron addition, the maximum quantum yield of photosynthesis (φ_m) rapidly doubled, from 0.011 to 0.025 mol C·mol quanta⁻¹. Paradoxically, this increase in light-limited productivity was not accompanied by a significant increase in light-saturated productivity (P_max^b). P_max^b, maximum Chl normalized productivity, was 1.34 mg C·mg Chl⁻¹·h⁻¹ outside and 1.49 mg C·mg Chl⁻¹·h⁻¹ inside the iron-enriched patch. The importance of φ_m as compared with P_max^b in controlling the biological response to iron addition has vast implications for understanding the ecological response to iron. We show that an iron-driven increase in φ_m is the proximate physiological mechanism affected by iron addition and can account for most of the increases in primary production. The relative importance of φ_m over P_max^b in this iron-fertilized bloom highlights the limitations of often-used primary productivity algorithms that are driven by estimates of P_max^b but largely ignore variability in φ_m and light-limited productivity. To use primary productivity models that include variability in iron supply in prediction or forecasting, the variability of light-limited productivity must be resolved.

A dozen iron enrichment experiments in high-nutrient low-chlorophyll (Chl) regions of the world ocean have unequivocally shown that iron limits primary production and that the addition of iron has significant biogeochemical consequences (1, 2). Although it has been shown that enhanced iron supply increases biomass, photosynthetic efficiency and primary production within the entire phytoplankton assemblage (3–6), the photophysiological mechanism driving the increased productivity has not been analytically linked to the observed changes in protein expression and photochemistry (7). On the most basic level, phytoplankton photosynthesis can be categorized as either light-limited photosynthesis or light-saturated photosynthesis (8). At low irradiances, the rate of phytoplankton photosynthesis is light limited and proportional to the supply of irradiance. As irradiance increases, photosynthesis increases proportionally until the photosynthetic capabilities of the phytoplankton begin to become saturated. Light-saturated photosynthetic rates then remain constant as irradiance levels increase.

Here, we show that iron addition results in a doubling of light-limited photosynthesis rates but has no statistically significant impact on light-saturated photosynthesis rates. These results shed light on the mechanistic response to iron addition. Iron limitation decreases light-limited photosynthesis primarily by reducing the ability of phytoplankton to synthesize functional proteins for de novo creation or repair of damaged reaction centers (7). In particular, photosynthetic reaction center core and electron transport chain proteins that require iron cannot be formed or repaired, resulting in a reduced ability to process absorbed light energy into chemical energy. Under iron limitation, damaged photosystem II reaction centers manifest as decreased variable fluorescence, and a lesioned electron transport results in a decreased reaction center turnover rate (7, 9). Both processes directly reduce light-limited photosynthesis, ultimately resulting in a reduction in the quantum yield of photosynthesis (10).

In this context we explore (i) the strong ecological importance of light-limited photosynthesis, (ii) the implications of these results for primary production models that are primarily modulated by parameters that describe light-saturated photosynthesis, and (iii) the need for models to have the ability to represent changes in light-limited photosynthesis. We briefly describe the Southern Ocean iron enrichment experiment (SOFeX). We then introduce standard primary production models, the photosynthetic efficiency results from SOFeX, and an example of a primary production model that has the capacity to resolve increases in primary productivity caused by iron-dependent changes in the efficiency of light-limited photosynthesis.

Results and Discussion

SOFeX.

The SOFeX group conducted an in situ iron fertilization in January and February 2002 in the Pacific Sector of the Southern Ocean, one of a series of experiments designed to test the Martin Iron Hypothesis (11). The southern of the two SOFeX patches (1) was in the waters nearer Antarctica and poleward of the southern boundary of the Antarctic circumpolar current (≈66°S, 172°W). One of three major high-nutrient, low-Chl regions of the world ocean, these waters were characterized by high levels of macronutrients (≈28 μM nitrate, 60 μM silicic acid) (12), extremely low iron concentrations (13, 14), iron-limited production (15), well defined mixed layers (45 m), and cold surface temperatures (−0.5°C) (1). Acidified iron sulfate was mixed with ambient seawater and introduced just below the sea surface into a ≈15-km × 15-km patch over 2 days, resulting in a surface iron concentration of ≈0.7 nM dissolvable Fe. The patch was fertilized three additional times (Fig. 1, gray bars) and responses were monitored for 27 days.

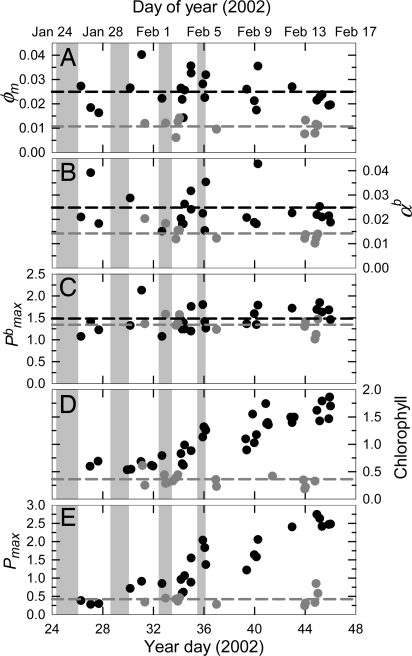
Fig. 1.

Time series of phytoplankton physiological parameters [φ_m, maximum quantum yield (A); α ^b, maximum Chl-specific light utilization coefficient (B); P _max^b, Chl-specific maximum primary productivity (C)], biomass [HPLC-derived Chl (D)], and primary productivity [P_max, maximum primary productivity (E)]. Black circles and black dotted lines represent discrete samples and the mean value inside the iron-enriched patch, respectively. Dark gray circles and dark gray dotted lines represent discrete samples and mean values outside the iron-enriched patch, respectively. Gray bars indicate periods of iron fertilization. Physiological units are as in Table 1: P_max (mgC · m⁻³ · h⁻¹), chlorophyll (mg m⁻³).

Primary Productivity Models.

Primary productivity models have appeared in the literature on average once every 2 years over the past four decades (16). Recent reviews conclude that after reconciling numerous aliases for similar parameters and differing complexities of spectral light integration, primary productivity models are fundamentally the same (16–18). Behrenfeld and Falkowski (16) described a standard depth-integrated model (DIM),

where total daily primary productivity within the euphotic zone (PP_eu) is equal to surface Chl (Chl₀) scaled to the depth of the euphotic zone (Z_eu) multiplied by the Chl-specific optimal photosynthetic rate (P _opt^b) scaled to day length (DL) times a light limitation term (F). Note that P _opt^b is operationally distinct from P _max^b, which describes the Chl-normalized light-saturated rate of photosynthesis as controlled by the cellular concentration and activity of dark reaction enzymes and can be measured in the laboratory with 2-h photosynthesis versus irradiance (PvsE) experiments. P _opt^b, which is measured in the field, is the optimal Chl-normalized, light-saturated rate of photosynthesis as governed by the counterbalancing effects of light limitation, light saturation, and photoinhibition over a 24-h period. Although P _opt^b and P _max^b are operationally distinct, they are functionally similar in that they predominantly describe light-saturated photosynthesis.

The variables in Eq. 1 are ranked in importance according to their ecological variability in Behrenfeld and Falkowski's consumer's guide to phytoplankton primary productivity models (16). Most of the three orders of magnitude change in PP_eu (≈30–10,000 mg C·m⁻²·d⁻¹) is the result of 250-fold depth-integrated changes in phytoplankton biomass, Chl₀* Z_eu (≈2–500 mg Chl·m⁻²). P _opt^b varies within a factor of 40 (≈ 0.5–20 mg C·mg Chl⁻¹·h⁻¹), and estimates of the dimensionless F indicate it can potentially cause PP_eu to change by a factor of ≈4. DL has only a minor effect on the variability of PP_eu.

This ranking has been demonstrated statistically. In a compilation of >11,000 ¹⁴C measurements of primary productivity, 38% of the observed variability in PP_eu was accounted for solely by the product of surface Chl (Chl₀) and euphotic depth (Z_eu) (17). When measured values of P _opt^b were used in Eq. 1 the correlation improved to 86% (17). Alternatively, in that study the light-limitation variable F in Eq. 1 made little difference to the model output. In their study, Behrenfeld and Falkowski (16) developed and used a simple light-dependent equation to represent F:

where F is dimensionless and ranges between 0.45 and 0.61 for E_d (0⁺), total daily irradiance just above the surface of the ocean, values from 9 to 60 mol quanta·m⁻²·d⁻¹. With this empirical representation of F and observed measures of Chl_0, Z_eu, and P_opt^b, the correlation between modeled and measured productivity was 86%. Furthermore, model performance decreased by only 3% (r² = 0.83) when F was held constant at an average value of 0.55 (16).

This robust analysis marginalizes the use of light-limited photosynthesis parameters within production algorithms. Behrenfeld and Falkowski (16, 17) argued that productivity algorithm performance primarily depends on the accuracy to which P_opt^b can be modeled. Furthermore, they argued that adding computational overhead in the form of complex light propagation models adds limited, if any, increase in model performance. In a recent primary-productivity-algorithm-testing round robin there were 23 of 24 algorithms within the study that included variable phytoplankton physiology (19). Only six of those 23 algorithms included a light-limitation term that was based on physiology rather than scaled to daily mean irradiance (i.e., Eq. 2). In 13 of the algorithms, variations in phytoplankton physiology were limited to variations in P_opt^b or P _max^b. It was also noted that one of the most widely used algorithms is the vertically generalized production model (17), a combination of Eqs. 1 and 2, in which P_opt^b is obtained as a seventh-order polynomial of sea surface temperature.

In this article we revisit the importance of light-limited productivity. We show that in this Southern Ocean iron enrichment 5-fold integrated primary productivity and 9-fold Chl concentration increases (4) were not accompanied by a significant increase in P _max^b. Instead, productivity and biomass increases were driven by 2-fold increases in α ^b and φ_m, measures of the efficiency of light-limited productivity and components of the productivity model variable F. The standard DIM proposed by Behrenfeld and Falkowski (16, 17), a combination of Eqs. 1 and 2, would fail to model the development of an iron-enriched bloom because the proximal physiological drivers of the productivity increase (α ^b, φ_m) are not model inputs. By showing that productivity increases observed during SOFeX were driven by increases in α^b and φ_m, we underscore the limitations of using light-saturated (P _max^b- or P_opt^b-based) production models and the importance of using the family of models that resolve light-limited production (e.g., refs. 20–22). Models that account for variability in light-limited photosynthesis will better reproduce the effects of natural background and episodic iron input.

SOFeX Results.

There was an immediate and sustained increase in the maximum quantum yield (φ_m) of total phytoplankton in response to iron addition (Fig. 1A). φ_m is the fundamental quotient of the moles of carbon incorporated in the phytoplankton cell divided by the moles of light that the phytoplankton cell absorbs and is a key indicator of the photosynthetic efficiency of phytoplankton. The >2-fold mean increase in φ_m (Table 1) was driven by a nearly 2-fold increase in the maximum light utilization coefficient, α ^b (Table 1 and Fig. 1B), and a 28% decrease in the mean absorption normalized to incubator irradiance, (ā_φINC*) (Table 1). The increases in photosynthetic efficiency of light-limited production, α ^b and φ_m, were not accompanied by a statistically significant increase in P _max^b (Fig. 1C and Table 1).

Table 1.

Phytoplankton physiological parameters and single factor ANOVA significance test of out vs. in of the iron-enriched patch (25 in samples, 11 out samples)

Parameter	Units	Location	Mean	SE	Min	Max	P value	Significance
φm	mol C·mol quanta−1	Out	0.011	± 0.001	0.006	0.014	3.9E-8	***
		In	0.025	± 0.001	0.014	0.040
Pmaxb	mg C·mg Chl−1·h−1	Out	1.34	± 0.05	1.01	1.58	0.1190	ns
		In	1.49	± 0.05	1.07	2.13
αb	mg C·mg Chl−1·h−1/μmol     quanta·m−2·s−1	Out	0.014	± 0.001	0.010	0.020	0.0011	**
		In	0.025	± 0.002	0.015	0.056
Ek	μmol quanta·m−2·s−1	Out	97	± 4	67	111	3.8E-6	***
		In	65	± 3	36	92
āφINC*	m2 mg Chl−1	Out	0.032	± 0.002	0.024	0.045	0.0022	**
		In	0.023	± 0.001	0.016	0.049

ns = not significant. Significance: *, 0.01 < P ≤ 0.05; **, 0.001 < P ≤ 0.01; ***, P ≤ 0.001.

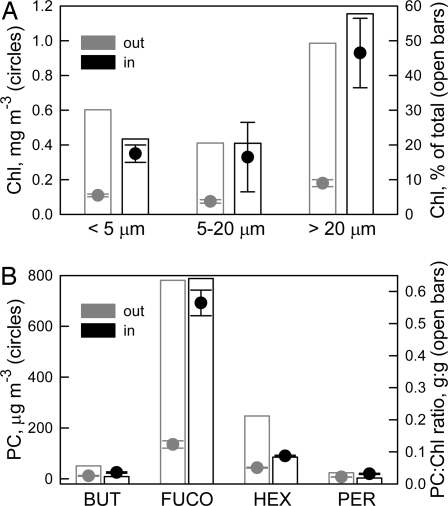
Throughout the iron enrichment experiment, Chl accumulated and primary productivity increased (Fig. 1 D and E). It is important to note that the increases in Chl resulted from a proportionally similar increase within the pico-, nano-, and micro-phytoplankton size classes (Fig. 2A). Iron addition did not markedly change the proportional makeup of the phytoplankton size-fraction assemblage. Likewise, whereas the absolute concentrations of the photosynthetic carotenoids (PCs) peridinin, 19′-butanoyloxyfucoxanthin, fucoxanthin, and 19′-hexanoyloxyfucoxanthin increased ≈2-fold with iron addition, the PC:Chl quotients were similar inside and outside the iron-enriched patch (Fig. 2B). Fucoxanthin, a marker for diatoms, was the dominant PC inside and outside the iron-enriched patch, and the Chl-normalized relationships among the PCs changed very little (Fig. 2B).

Fig. 2.

PC pigments and size-fractionated Chl. (A) Size-fractionated fluorometrically derived Chl concentrations outside (gray circles) and inside (black circles) the iron-enriched patch. Gray and black open bars are a proportional representation of each of the three size classes outside and inside the iron-enriched patch, respectively. (B) HPLC-determined PC concentrations (circles) and PC:Chl quotients (open bars). Out values (gray) are means for the entire experimental period. In values (black) represent means of the three, inside the patch, stations with the highest primary productivity (4). Error bars are SEM. <5 μm, picoplankton; 5–20 μm, nanoplankton; >20 μm, microplankton; PER, peridinin; BUT, 19′-butanoyloxyfucoxanthin; FUCO, fucoxanthin; HEX, 19′-hexanoyloxyfucoxanthin.

Because there was no significant increase in the performance of light-saturated maximum productivity (P _max^b) and the proportion of pigments and size classes within the phytoplankton assemblage changed very little, we argue that the observed increases in Chl and productivity were primarily the result of increased photosynthetic efficiency in light-limited productivity (α ^b). Primary productivity models that do not include light-limited photosynthesis parameters such as α ^b and φ_m cannot model this productivity response to iron addition. The following light-limited-photosynthesis-resolving productivity model demonstrates that, by primarily increasing the efficiency of light-limited photosynthesis, significant increases in primary productivity can be achieved.

Productivity Model Using SOFeX Results.

There is a diversity of primary productivity models that build in complexity on the standard DIM presented in Eq. 1. With some minor exceptions (i.e., changes in Chl and P_opt^b with depth) the overriding difference between the DIM presented in Eq. 1 and more complicated depth-, time- and wavelength-resolved models is the treatment of the propagation of light through the water column and the expression of the efficiency of light-limited productivity (φ_m, α ^b). In Eq. 1 the treatment of irradiance, α ^b and φ_m is expressed within the dimensionless variable F. Because it is thought that F plays a relatively minor role in the overall global variability of PP_eu, most models of primary productivity use an average value of F or vary F as a function of light, as in Eq. 2. However, to resolve the observed iron-dependent 2-fold changes in α ^b and φ_m it is necessary to use a productivity model that expresses F and light-limited primary productivity more fully.

A typical light-limited, photosynthesis-resolving productivity model resolves the quantity and quality of irradiance throughout the water column and throughout the day (see review in ref. 18). In this case the resolution is 1 m and ≈30 s:

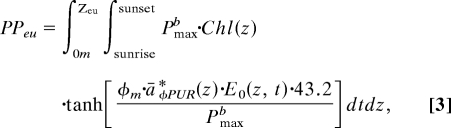where PP_eu is the daily primary productivity integrated to the depth of the euphotic zone (mg C·m⁻²·d⁻¹); P _max^b is the maximum Chl-specific productivity (mg C·mg Chl·h⁻¹); Chl(z) is the depth-dependent Chl concentration (mg Chl·m⁻³); φ_m is the maximum quantum yield (mol C·mol quanta⁻¹); E₀(z, t) are 30-s and 1-m intervals of irradiance (μmol quanta·m⁻²·s⁻¹); 43.2 converts micromols and milligrams to moles and hours to seconds; and ā_φPUR*(z) is the mean Chl-specific absorption coefficient (m²·mg Chl⁻¹) defined in relation to the actual spectral composition of in situ light, photosynthetically usable radiation (PUR):

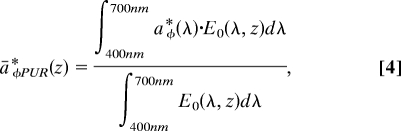where a*_φ(λ) (m²·mg Chl⁻¹) is lipid-soluble absorption by phytoplankton pigments (Fig. 3A), and E₀(λ,z) (μmol quanta·m⁻²·s⁻¹) is modeled depth- and spectrally dependent scalar in situ irradiance (Fig. 3B, black lines). Scalar irradiance is calculated from downwelling photosynthetically active radiation (PAR) that is measured above the surface of the ocean [E_d (0⁺), μmol quanta·m⁻²·s⁻¹] and propagated through the water column by using spectrally resolved light attenuation models dependent on date, location, and Chl concentration (23–25). This productivity model (Eq. 3) performed well in comparisons with 24-h simulated in situ ¹⁴C primary productivity measurements in which 24-h productivity, φ_m, P _max^b, and ā_φPUR*(z) were measured from identical sample bottles (r² = 0.95, slope = 0.92).

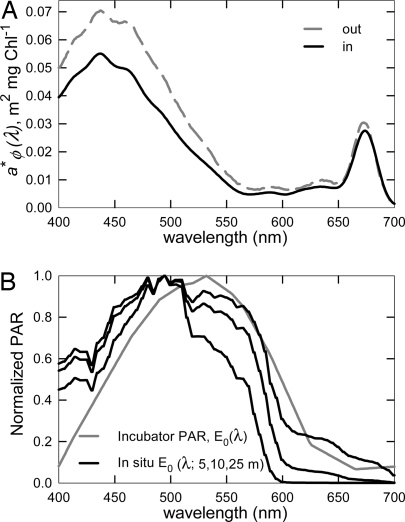
Fig. 3.

Absorption coefficient and modeled PAR. (A) Mean wavelength-dependent Chl-specific absorption coefficient, α*_φ (λ), from 400 to 700 nm inside and outside the iron-enriched patch. (B) Modeled individually normalized spectral quality of in situ PAR on February 2, 2002, 66°S, 172°W at local noon with a uniform 1 mg Chl·m⁻³ from 0-Z_eu and PvsE incubator irradiance. The black lines represent modeled PAR, E₀ (λ, z), at 5, 10, and 25 m representing 60%, 35%, and 9% light levels, respectively. The spectral quality of PAR used for the PvsE incubations, E₀^inc (λ), is represented by a gray solid line.

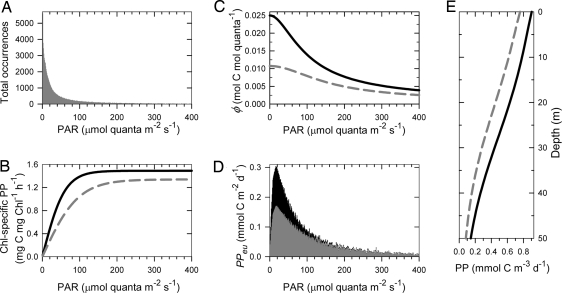
We use the light-limited, photosynthesis-resolving primary productivity model in Eq. 3 to demonstrate the importance of light-limited productivity in response to enhanced iron supply. Approximately 30-s intervals of measured surface PAR from sunrise to sunset on a typical day during the SOFeX cruise were propagated through a 50-m water column (approximate mixed layer depth) at 1-m intervals using light attenuation models (23–25) to produce the family of 100,000 discrete PAR occurrences shown in the histogram in Fig. 4A. Using Eq. 3, the mean values in Table 1, and the histogram of PAR occurrences (Fig. 4A), the absolute amount of primary productivity (mmol C·m⁻²·d⁻¹) were calculated for each discrete PAR wavelength (Fig. 4D). The same variables were used to plot primary productivity versus depth (Fig. 4E). Fig. 4B shows the mean PvsE curve inside and outside the iron-enriched patch for the mean values in Table 1. The difference between the light-limited vs. light-saturated portion of the PvsE curve is clear in Fig. 4B; light-saturated photosynthesis begins at irradiances of ≈100 μmol quanta·m⁻²·s⁻¹ outside the iron-enriched patch. Approximately 83% of the family of PAR occurrences in Fig. 4A occur at light levels <100 μmol quanta·m⁻²·s⁻¹. As a result, the majority of PP_eu occurs at low-light intensities (Fig. 4D). For this example, ≈58% of the PP_eu outside of the iron-enriched patch (total = 19.8 mmol C·m⁻²·d⁻¹) and 66% of the PP_eu inside the patch (total = 27.7 mmol C·m⁻²·d⁻¹) occur at light intensities <100 μmol quanta·m⁻²·s⁻¹ (Fig. 4D). More importantly, the large majority of the difference in primary productivity outside and inside the iron-enriched patch occurs at very low light intensities; 50% of the difference occurs at irradiances <37 μmol quanta·m⁻²·s⁻¹ and 84% of the difference occurs at irradiances <100 μmol quanta·m⁻²·s⁻¹ (Fig. 4D).

Fig. 4.

Modeled productivity and irradiance. (A) Histogram of ≈100,000 total occurrences of PAR at a given PAR. Less than 3% of the total discrete PAR measurements are >400 μmol quanta·m⁻²·s⁻¹. (B) Average Chl-specific primary production vs. irradiance inside (black solid line) and outside (gray dashed line) the iron-enriched patch generated from parameters in Table 1. (C) Quantum yield (φ_m) vs. PAR inside (black solid) and outside (gray dashed) the iron-enriched patch. (D) Total primary productivity within the euphotic zone (PP_eu) at given PAR values inside (black) and outside (gray) the iron-enriched patch. (E) Primary productivity in D plotted vs. depth. Light attenuation and primary productivity was modeled with Chl = 0.5 mg·m⁻³ from 0 to 50 m for both the control and iron-replete model run to isolate the effect of Chl on primary production; 0.5 mg·m⁻³ was chosen as an approximation of the mean Chl concentration in the Southern Ocean poleward of the southern boundary of the Antarctic Circumpolar Current. A 50-m water column was chosen because it represents a typical mixed layer depth and euphotic zone depth in the study area.

The relative importance of light-limited productivity only weakly depends on daily irradiance. In Fig. 4, productivity is modeled by using an integrated daily surface irradiance of 16 mol quanta·m⁻²·d⁻¹, which represents a typical irradiance for the SOFeX cruise (range = 9 to 44 mol quanta·m⁻²·d⁻¹). Modeled with the cruise maximum of 44 mol quanta·m⁻²·d⁻¹, 50% of the productivity outside of the iron-enriched patch and 57% of the productivity inside the patch would occur at light intensities <100 μmol quanta·m⁻²·s⁻¹. Fully 50% of the difference in productivity from inside the patch to outside the patch would occur at light intensities <48 μmol quanta·m⁻²·s⁻¹. Regardless of the quantity of total daily irradiance, most photosynthesis in the water column occurs at light-limited irradiances.

Although maximum quantum yield, φ_m, has not previously been reported in Southern Ocean iron experiments, all five Southern Ocean bloom-forming mesoscale iron additions conducted between 1999 and 2004 resulted in increased photosynthetic competency as measured by variable fluorescence (1, 2, 26–28). The PvsE experiment results reported here are similar to those made during a 2000 mesoscale iron enrichment experiment in the Atlantic sector of the Southern Ocean (EisenEx; ref., 28). “During EisenEx, we observed no general inside/outside difference in P _max^b, whereas α^b was slightly higher inside the Fe-enriched patch” (28). Also, one of the first iron-enrichment experiments conducted in the equatorial Pacific saw similar results; iron-induced increases in φ_m were not accompanied by significant increases in P^b, Chl-normalized primary production (mmol C·mg Chl⁻¹·d⁻¹) (29).

The 5-fold increases in PP_eu and 9-fold increases in Chl measured during the SOFeX iron addition were not accompanied by a significant increase in P _max^b. Instead, biomass and productivity increases were driven by 2-fold increases in φ_m and α ^b. Any primary productivity model that does not incorporate variability in light-limited production will fail to reproduce the development of an iron-induced bloom because the physiological driver of the productivity increase (φ_m and α ^b) in such a model is a constant rather than a variable. Primary productivity algorithms that resolve the variability of light-limited photosynthesis are necessary to model iron effects in the Southern Ocean and, we hypothesize, other iron-regulated regions of the world ocean. Primary productivity models that account for variability in light-limited photosynthesis will better reproduce the effects of natural background and episodic iron inputs.

Materials and Methods

Chl was determined by fluorometric methods and HPLC. Water samples were filtered in parallel onto 25-mm Whatman glass fiber filters (GF/F, nominally a 0.7-μm size fraction) and 5- and 20-μm Poretics polycarbonate filters. Fresh samples were extracted in 90% acetone at −20°C for 24–30 h (30) and quantified by using a Turner Designs fluorometer (31, 32). A complete suite of phytoplankton pigments were also analyzed from frozen samples following the procedures described by Bidigare et al. (33).

Maximum quantum yield was determined with measurements of phytoplankton absorption and PvsE experiments. Particulate matter was collected by filtering 0.5–4 liters of upper mixed layer sample water through 25-mm GF/F glass fiber filters, with greater volumes filtered for low biomass waters. Spectral absorption coefficients were measured with a dual beam spectrophotometer. Diffuse coefficients for total particulate matter were calculated by using the equations described in the National Aeronautics and Space Administration Ocean Optics Protocols (34) and by Mitchell (35). Methanol was used to extract pigments from the filtered sample, and the depigmented filter was then measured to estimate detrital absorption (36). The difference between the two measurements nominally represents lipid-soluble absorption by phytoplankton pigments [a_φ*(λ)] (Fig. 3A). The mean Chl-specific absorption coefficient normalized to incubation irradiance (ā_φINC*, m²·mg Chl⁻¹) is calculated as in Eq. 4 with the exception that E₀ (λ, z) is replaced with E₀^inc (λ). E₀^inc (λ) is the spectrally dependent scalar irradiance of incubation and does not include UV radiation (Fig. 3B, gray solid line).

PvsE curves were derived from ¹⁴C uptake measurements after 2-h incubations in temperature-controlled blue light incubators, modified from the design of Jassby and Platt (37). Each incubator held 12 22-ml polyethylene scintillation vials in which natural seawater samples were exposed to different light treatments of PAR. Irradiance was supplied from the bottom of incubation vessels by using a 250-W tungsten-halogen slide projector lamp (Gray ENH), spectrally modified by using a heat mirror, a broad band cool mirror (Optical Coating Laboratory), and blue stage-lighting screens (Cinemills M144). Light intensity was modified by using neutral density screening. Samples were inoculated with 10–50 MBq of NaH¹⁴CO₃ and incubated for 2 h. The incubator vials were cleaned and ¹⁴C was prepared according to Fitzwater et al. (38).

The Chl-specific maximal photosynthetic rate (P _max^b) was estimated by using a nonlinear, least-squares routine (39). The maximum Chl-specific light utilization coefficient [α ^b, mg C·mg Chl⁻¹·h⁻¹·(μmol quanta·m⁻²·s⁻¹)⁻¹] was determined following Johnson and Barber (40). The light-saturation index (E_k, μmol quanta·m⁻²·s⁻¹) is the quotient of P _max^b and α ^b. Maximum quantum yield of carbon uptake (φ_m, mol C·mol quanta⁻¹) was calculated from α ^b and ā_φINC*:

where 43.2 converts seconds to hours, milligrams to mols, and micromols to mols. It is important to note that φ_m can be used to describe the φ_m of a single phytoplanktor cell, in which case the theoretical φ_m is 0.125. Here, we use φ_m to describe the φ_m of the in situ mixed phytoplankton assemblage that depends on irradiance, nutrients, and temperature and is unlikely to approach the theoretical maximum of 0.125 mol C·mol quanta⁻¹. The range of φ_m in this study (0.006 to 0.040 mol C·mol quanta⁻¹; Table 1) is in line with near surface φ_m measurements made in the Atlantic Sector of the Southern Ocean (0.006–0.027 mol C·mol quanta⁻¹) (41).