A two-step nucleotide-flipping mechanism enables kinetic discrimination of DNA lesions by AGT

Abstract

O⁶-alkylguanine-DNA alkyltransferase (AGT) repairs damage to the human genome by flipping guanine and thymine bases into its active site for irreversible transfer of alkyl lesions to Cys-145, but how the protein identifies its targets has remained unknown. Understanding molecular recognition in this system, which can serve as a paradigm for the many nucleotide-flipping proteins that regulate genes and repair DNA in all kingdoms of life, is particularly important given that inhibitors are in clinical trials as anticancer therapeutics. Computational approaches introduced recently for harvesting and statistically characterizing trajectories of molecularly rare events now enable us to elucidate a pathway for nucleotide flipping by AGT and the forces that promote it. In contrast to previously proposed flipping mechanisms, we observe a two-step process that promotes a kinetic, rather than a thermodynamic, gate-keeping strategy for lesion discrimination. Connection is made to recent single-molecule studies of DNA-repair proteins sliding on DNA to understand how they sense subtle chemical differences between bases efficiently.

Many proteins flip nucleotides from the DNA base stack into their active sites to remove or chemically modify bases for gene regulation and repair (1–4). Based on an x-ray crystallographic structure of uracil-DNA glycosylase (UDG) (2), it was proposed that, as the protein compresses the DNA backbone, the nucleotide that flips is “pushed” by a finger residue and “pulled” by specific interactions in the active site (5, 6). Alternatively, more passive mechanisms in which the protein shifts the equilibrium for base pair opening have been suggested (7, 8). Evaluating these mechanisms for different proteins in physiologically relevant contexts is important for understanding how nucleotide-flipping proteins identify their targets (4). Here, we study O⁶-alkylguanine-DNA alkyltransferase (AGT), which repairs alkylated guanine and thymine DNA bases by transferring the alkyl lesions irreversibly to an active-site cysteine (Cys-145; Fig. 1a). This uncommon direct damage reversal mechanism makes AGT of fundamental interest, although understanding its behavior is also of medical significance because inhibitors are in clinical trials as anticancer therapeutics (9).

Fig. 1.

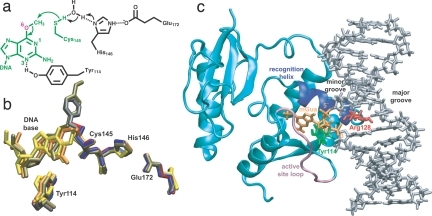
Structure of AGT. (a) Chemical mechanism (21). (b) Comparison of active-site structures: blue, unmodified wt (PDB entry 1EH6) (17); red, wt with methylated Cys-145 (1EH7) (17); gray, wt with benzylated Cys-145 (1EH8) (17); orange, C145S mutant with DNA containing mGua (1T38) (21); yellow, wt with DNA containing N¹,O⁶-ethanoxanthine (1T39) (21); tan, wt bound to N4-alkylcytosine (1YFH structure C) (22). (c) Wild-type–mGua complex constructed for the simulations; water molecules and counterions are not shown. The extrahelical mGua nucleotide (orange; with 5′ and 3′ phosphate groups marked) binds within the enzyme active site buried by an active-site loop [Gly-153–Gly-160 (mauve)]. The “arginine finger” [Arg-128 (red)], at the beginning of the recognition helix [Ala-127–Gly-136 (royal blue)], is positioned inside the DNA duplex (silver) where it intercalates via the minor groove; Tyr-114 is shown in green.

In principle, molecular dynamics simulations can provide atomic-resolution pathways for nucleotide flipping and the forces that promote them, but they are limited to tens of nanoseconds at present. Because instances of spontaneous base flipping are estimated to be separated by milliseconds even in the presence of a protein (4), it is not possible to harvest a statistically meaningful number of such events in simulations without restraints. Free energy projections along selected coordinates can be obtained from simulations in which harmonic “umbrella” potentials are used to enhance sampling of low probability states; such simulations showed that the cytosine-5-methyltransferase of the HhaI bacterium stabilizes a fully flipped state and a major groove pathway that leads to it (4, 10). Nevertheless, the information obtained from such simulations is thermodynamic, not kinetic, and different projections can lead to qualitatively different conclusions.

Here, we exploit recent advances in computational approaches (11–14) to obtain explicit dynamic trajectories for protein-catalyzed nucleotide flipping and translate them into a physically understandable mechanism. The simulations of AGT reveal a two-step mechanism consistent with existing data for mutants. The finger residue (Arg-128) captures spontaneous base pair fluctuations to stabilize an intermediate in which the lesion is extrahelical; a loop (residues Gly-153 to Gly-160) gates the active site, and these motions determine the kinetics of the second step. Comparison of free energies for flipping guanine (Gua) and O⁶-methylguanine (mGua) suggests that the extrahelical intermediate identified enables kinetic discrimination between damaged and undamaged bases. We relate this mechanism to molecular parameters estimated in recent experimental studies that track single DNA-repair proteins sliding on DNA (15) (Y. Lin, T. Zhao, Z. Farooqui, X. Qu, C. He, A.R.D., and N. F. Scherer, unpublished data).

Results

Path Sampling Simulations Reveal a Two-Step Mechanism.

Because of its medical relevance (9), AGT has been the focus of many biochemical (16–19) and structural (17, 20–22) studies, making it an attractive system for computational investigation. For the calculations, we constructed a complex between the wild type (wt) and a DNA duplex containing mGua from the structure of the catalytically inactive C145S mutant bound to that ligand (21). Comparison of structures for the protein pre- and postrepair and in complex with various oligomers (Fig. 1b) shows that the active-site geometry and thus the mode of recognition is the same in all cases, which suggests that our results do not depend on the choice of starting structure. The protein binds the DNA through a helix–turn–helix motif with the second (“recognition”) helix (Ala-127–Gly-136) buried deeply within the minor groove (Fig. 1c). The “arginine finger” (Arg-128) is located at the N-terminal end of this helix, and its side chain intercalates in the DNA base stack to make hydrogen bonds with the orphaned cytosine.

Although lesion detection cannot be studied by straightforward molecular dynamics simulations, it can be simulated with transition path sampling (TPS), a Monte Carlo procedure that harvests trajectories that are constrained to go from one stable state (e.g., the base in the stack) to another (e.g., the base in the active site) but are otherwise unbiased (11, 12). In practice, such simulations consist of repeatedly “shooting”: selecting a phase space point from an existing trajectory with a flipping event, perturbing it, integrating the equations of motion to the stable states (basins), and accepting the resulting trajectory if and only if it still contains a flipping event. By eliminating the time required to wait for spontaneous fluctuations that give rise to flipping from a stable state, TPS enables the efficient study of the dynamics of interest. However, at least one trajectory with a flipping event is needed to initiate the procedure.

To overcome this last problem, we recently introduced bias annealing (14), in which a path for a molecularly rare event is initially generated with targeted molecular dynamics (23) and the resulting bias is removed by shooting with progressively lower force constants for the harmonic restraints used to drive the transition of interest, while enforcing the TPS basin constraints. This method was shown to be an order of magnitude faster than gradually shifting the path ensemble by changing the TPS basin definitions for a two-dimensional model potential (14). We believe that the computational savings is even greater for larger systems, such as that studied here, because the simulations are accelerated exponentially with the bias strength. In addition to the advantage that fewer total integration steps are required to obtain an unbiased path of full length, this feature permits an investigator to explore different possible basin definitions rapidly during the early phase of a project to select those that result in the greatest shooting efficiency. We discuss the strengths and weaknesses of the bias annealing procedure in more detail in ref. 14.

Bias annealing now makes possible the study of the kinetics [rather than simply the thermodynamics (4, 10)] of protein-promoted nucleotide flipping with TPS. Our application of the bias annealing method to the AGT-DNA system (Fig. 1c) revealed that mGua flips through the major groove via a metastable state outside both the DNA base stack and the protein active site. We then used TPS to harvest >100 unbiased trajectories for each of the two transitions: to this extrahelical intermediate from the base stack and from the intermediate to the active site. This number of trajectories is statistically significant given that paths were found to decorrelate within approximately three shooting moves, as estimated by a procedure adapted from ref. 24 [supporting information (SI) Fig. 5].

Dynamics of Flipping from the DNA Base Stack.

Objective description of the paths requires the identification of physically meaningful coordinates that are capable of distinguishing (meta)stable states from transition states defined dynamically by their probabilities to commit to a basin (p). Because of the large number of degrees of freedom in complex systems, relating p to structural and energetic properties of the system by trial-and-error is very costly in terms of both human and computational resources and thus has been achieved for only a handful of relatively simple systems (12, 25). We previously introduced the idea that informatic methods can be used to efficiently search an otherwise prohibitively large number of candidate physical variables for those combinations that can predict p (13), and we apply these methods here to achieve a level of description unprecedented for a large biomolecular system.

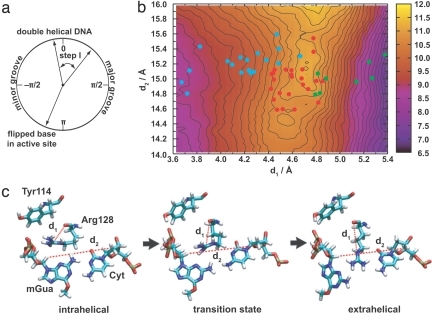
For the unstacking step, the informatic method paired the distance between the carbonyl oxygen and C^ζ atoms of Arg-128 (d₁) with the distance between the H1′ atom of mGua and the H3′ atom of its Watson–Crick partner (d₂). Projection of the dynamics onto these coordinates (Fig. 2 and SI Fig. 6a) shows that they are indeed capable of separating the unflipped state (cyan) from the extrahelical intermediate (green) and the transition states that connect them (red). This choice of coordinates was validated by comparison of the dynamics with an independent umbrella sampling calculation restricted to the predicted transition state region (Fig. 2b). The stable and transition states fall on well defined basins and saddlepoints, respectively, in this projection of the free energy. Such a high correspondence is not expected for arbitrary coordinates (see ref. 25 for a discussion), and we thus feel confident that these coordinates adequately describe the dynamics.

Fig. 2.

Flipping from the base stack to the extrahelical intermediate. (a) Range studied in terms of the pseudodihedral angle. (b) Free energy as a function of the coordinates identified by the informatic approach (contours are spaced every 0.2 kcal·mol⁻¹). Colored points indicate structures for which commitment probabilities (p) were calculated: cyan, mGua intrahelical; green, extrahelical; red, at a transition state. (c) Representative structures for the transition (see SI Movie 1 for animation).

The coordinates d₁ and d₂ measure the extension of the arginine finger and the flipping of the base (as the backbone sugars become closer). The transition states for the process occur with d₁ ≈ 4.6 Å and d₂ ≈ 15.1 Å compared with 3 < d₁ < 4 Å and 11.5 < d₂ < 16.5 Å for the intrahelical state and 5 < d₁ < 7 Å and 12 < d₂ < 16 Å for the extrahelical state (SI Fig. 6a). The fact that d₂ must fluctuate to the top of its range before d₁ can increase indicates that the insertion of Arg-128 follows the loss of base pairing. This analysis, together with visual inspection of trajectories, suggests the following sequence of molecular events (Fig. 2c). The mGua and Cyt bases fluctuate apart by shifting their pattern of hydrogen bonds while maintaining the orientation of the planes containing their aromatic rings. Arg-128 captures this transient motion to form a structure in which it interacts comparably with both bases. It then shifts its interaction to Cyt, which enables mGua to diffuse into solution to form the extrahelical intermediate. This mechanism explains the experimental observation that side chain length at this position is directly proportional to the rate of DNA repair (17) more readily than does one in which Arg-128 pushes (longer side chains are floppier). Other highly ranked combinations of coordinates for this step yield qualitatively similar conclusions.

Dynamics of Insertion into the Active Site.

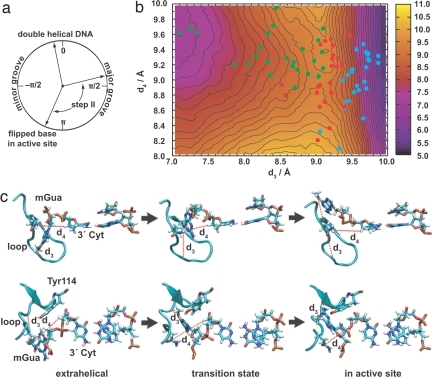
The coordinates selected to describe the transition from the extrahelical intermediate to the active site were the distance between the methyl carbon of mGua and the C^α atom of Ala-154 (d₃) and the distance between the H3′ atom in the deoxyribose ring of the nucleotide sequentially 3′ to the flipping base and the C^γ atom of Asn-157 (d₄) (Fig. 3 and SI Fig. 6b). These coordinates were validated as above by comparison of the predicted commitment probabilities with an independently calculated free energy projection (Fig. 3b). Physically, these coordinates reflect the position of the flipping base and DNA backbone relative to a loop (Gly-153 to Gly-160) that gates the active site. For the base to enter the active site, this loop must undergo fluctuations in position (e.g., the nonhydrogen atoms of Gly-156 move ≈3 Å compared with 1–2 Å for other atoms in the protein); ≈30 ps are required for the system to relax to the fully flipped state from the transition state for this step because of minor local free energy minima, but the base is committed to that stable state once past the loop.

Fig. 3.

Same as Fig. 2 for flipping from the extrahelical intermediate into the active site. In b, colors indicate the extrahelical intermediate (green), transition states (red), and the base in the active site (cyan). Upper and Lower in c are two views of the same structures (see SI Movies 2 and 3 for animation).

Tyr-114 Acts Electrostatically Rather than Sterically.

It is important to emphasize that the coordinates selected by the informatic procedure are not wholly unique and concern only the base-flipping dynamics. Others are likely to be important for repair, which involves protein binding and catalysis as well. Given these facts, we examined the behavior of Tyr-114, mutations of which impact the overall kinetics of repair to some degree (16). In the simulations, Tyr-114 hydrogen-bonds to the phosphate group 3′ of mGua in the intrahelical conformation and then sequentially transfers its interactions to the N7 and the N3 atoms of the base during flipping (Fig. 3c). The first two of these interactions occur in transient structures and thus were not observed crystallographically (21, 22). In contrast to the suggestion that Tyr-114 interacts sterically with the 3′ phosphate group during flipping (21), we believe that it affects repair in three ways: by stabilizing binding before flipping, by providing hydrogen bonds during flipping, and by influencing the reactivity of the damaged base. All of these are likely to be modest electrostatic effects. That the interactions are of this nature rather than steric is consistent with the mutant data because hydrophobic residues still have substantial partial charges. In structures from the simulations in which we replaced Tyr-114 with phenylalanine (Phe), even without any relaxation, the interaction of Phe with the base was −3.2 kcal·mol⁻¹ compared with −5.6 kcal·mol⁻¹ for Tyr and that with the 3′ phosphate group was −1.2 kcal·mol⁻¹ compared with −1.8 kcal·mol⁻¹ for Tyr.

Comparison of the Energetics for Flipping Gua and mGua Suggests a Kinetic Gate-Keeping Strategy for Lesion Detection.

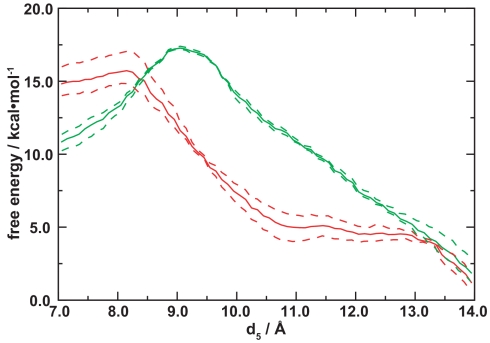
To determine the functional significance of the base-flipping mechanism elucidated, we compared the free energies for flipping Gua and mGua (Fig. 4 and SI Fig. 7). The free energies projected onto d₁ and d₂ (the unstacking step) were essentially the same for the two bases, with the extrahelical conformation somewhat lower in free energy than the intrahelical conformation. That the protein significantly stabilizes a base separated state (compare with SI Fig. 8) is consistent with findings for other DNA-repair proteins (4, 7, 8, 10, 26). For the active-site entry step, it was necessary to substitute the distance between the O⁶ atom of the flipping base and the C^α atom of Ala-154 (d₅) for d₃ because Gua lacks the methyl carbon. In that case, the free energies differed significantly: the barrier to Gua flipping is much higher (Fig. 4).

Fig. 4.

Comparison of free energies for flipping Gua (solid green) and mGua (solid red) from the extrahelical intermediate into the active site. Curves shown are linear cuts through the saddlepoint from two-dimensional free energy surfaces for d₄ and d₅ (SI Fig. 7): d₄ = −0.0857d₅ + 10.0 Å for Gua and d₄ = −0.0857d₅ + 10.2 Å for mGua. The dashed curves connect the highest and lowest free energy estimates for each (d₄, d₅) pair obtained from partitioning the data for each umbrella sampling window into three separate 20-ps intervals and re-performing the weighted histogram analysis; similar procedures were used to estimate the uncertainty in refs. 10 and 24.

These data suggest a “gate-keeping” strategy for lesion discrimination. Both Gua and mGua would flip to the extrahelical state, but only the latter would have a significant chance to continue on to the active site before flipping back to the intrahelical state. In contrast to that proposed for hOGG1 (3), this gate-keeping mechanism is kinetic rather than thermodynamic in nature: there is only a 3-fold preference for mGua over Gua once in the active site of AGT (18). A gate-keeping mechanism was also suggested for AGT based on a secondary binding site observed in one of the crystal structures (22), but the extrahelical nucleotide in the simulations differs significantly in structure from the partially flipped one observed crystallographically.

Discussion

Transition path sampling (TPS) has transformed the computational study of rare events in molecular systems over the last decade (11, 12), but its application to complex, biological systems has been limited (24, 25, 27–29). Efficient means for generating initial paths (14) together with informatic methods (13) that we introduced now enable us to harvest a statistically significant number of trajectories of a biomedically important stochastic process in its entirety and identify the features that characterize the ensemble of transition states. In contrast to the “push–pull” mechanism once proposed for nucleotide flipping (2, 5), we observe a two-step process that promotes a kinetic, rather than a thermodynamic (3, 7, 8), gate-keeping strategy for lesion discrimination.

Comparison of the simulation results with experimental data is needed to validate this recognition mechanism and refine it as needed. As already discussed, biochemical data for mutants of Tyr-114 (16) and Arg-128 (17) are consistent with the observed dynamics. The simulations also point to the importance of the active-site loop (Gly-153 to Gly-160). In support of this idea, mutants of many of these residues were recently obtained during directed evolution of AGT to maximize activity toward O⁶-benzylguanine derivatives (bGua) (30). In particular, A154T by itself was found to give a 4-fold increase in activity; this is of interest because Ala-154 interacts directly with the methyl group of mGua in the extrahelical intermediate in the simulations. At the same time, care must be used in interpreting these data. Although our simulations concern only nucleotide flipping, changes to the protein sequence are likely to affect both binding and catalysis, and the available data do not enable one to distinguish between these processes. Moreover, the binding mechanism for bGua in the absence of DNA, as in ref. 30, could be very different from that in its presence.

Perhaps the strongest prediction of our simulations is the existence of the extrahelical intermediate. As noted above, there is precedent for extrahelical intermediates in other DNA-repair systems. Base analogs have been used to obtain crystal structures of complexes of UDG and hOGG1 with partially flipped bases (3, 8). Although it is possible for base analogs to stabilize off-pathway intermediates, complementary data from NMR imino proton exchange experiments on UDG with a variety of DNA duplexes (7) suggest that these structures are meaningful representations of the unperturbed systems. Although a terminal overhanging thymine was fortuitously observed to be partially flipped in a structure of two AGT molecules with one bound to a modified cytosine (22), it is not clear that such a structure could be accessed by a nonterminal nucleotide; therefore, additional studies of AGT with alternate DNA constructs are needed. Because AGT can accommodate fluorescently active groups (31), it may also be possible to determine the number of states a base analog populates and the rates for transition between them from single-molecule fluorescence resonance energy transfer experiments with labeled wt and mutant AGTs.

Using the methods in ref. 32, we estimate (SI Table 1) the rate for partial flipping for mGua and Gua to be ≈10⁻³ to 10⁻² ps⁻¹; mGua proceeds rapidly to the active site (≈10⁻¹ ps⁻¹), whereas Gua is much slower (≈10⁻⁶ ps⁻¹). Assuming a diffusive step size of 1 bp, single-molecule tracking studies of the C-terminal domain of Ada, a bacterial homolog of AGT, yield a (helical) sliding rate of 2.6 × 10⁻⁴ steps ps⁻¹ (Y. Lin, T. Zhao, Z. Farooqui, X. Qu, C. He, A.R.D., and N. F. Scherer, unpublished data), which is comparable with that measured previously for hOGG1 (15). Comparison of the rates for sliding with those for flipping suggests that the kinetic gate-keeping mechanism of lesion discrimination would be operative and would allow the protein to scan the sequence rapidly compared with one requiring full flipping. At higher concentrations and in physiological contexts, it is likely that the DNA will be crowded with proteins (18, 19, 21, 22). Then, there will be more chance that undamaged bases enter the active site, but this possibility is not dangerous because the protein directly removes alkyl groups rather than excising bases. Overall, these considerations illustrate how a dialogue between theory and experiment can provide a quantitative understanding of how DNA-repair proteins can search DNA efficiently to maintain genomic integrity.

Methods

Obtaining Reactive Trajectories.

The molecules were represented by the CHARMM all-hydrogen force field (33–36); parameters for the mGua base were generated in a consistent fashion (see SI Methods, SI Fig. 9, and SI Tables 2 and 3). Simulations were performed with the TPS and bias annealing implementations in CHARMM (14, 25). Because TPS and bias annealing both construct new trial trajectories from existing ones (i.e., make local Monte Carlo moves in the space of paths), it is impossible to guarantee that all possible mechanisms are represented in the sampled paths; this issue is discussed further for this system in ref. 14. Measures of the quality of sampling (SI Figs. 5 and 10) suggest that the simulations explore the space efficiently and converge.

Attempts to drive flipping through the minor groove were unsuccessful because of steric clashes, and that pathway was not considered further. For steering the base from the active site through the major groove, a single harmonic restraint based on a pseudodihedral angle (θ) was used. The angle is defined by the centers-of-mass of nonhydrogen atoms in the flipping base, its sugar, the sugar of the 3′ nucleotide, and the base of the 3′ nucleotide together with its Watson–Crick partner (SI Fig. 11). During bias annealing, the target value of θ was advanced following natural fluctuations in the “forward” direction in steps of −0.06 rad from θ = −2.6 rad (the active site) through θ = −π rad to θ = 1.4 rad (the extrahelical intermediate) (SI Table 4). The trajectories harvested with TPS for this step were 80 ps in length and spanned the basins −2.7 ≤ θ ≤ −2.5 rad and 1.2 ≤ θ ≤ 1.6 rad. We believe that this length is more than adequate for sampling the reaction of interest because the actual transition times observed were typically <4 ps (SI Fig. 10a).

To obtain trajectories for forming an intrahelical conformation with Watson–Crick base pairing (θ = −0.2 rad), alternative harmonic restraints were needed. We used three separate restraints (SI Fig. 12): a pseudodihedral angle based on the C^ζ atom of Arg-128 and the centers-of-mass of heavy atoms in the Cyt base, the base 5′ of Cyt, and its Watson–Crick partner (a₁); a pseudodihedral angle based on the C^ζ atom of Arg-128 and the centers-of-mass of heavy atoms in the Cyt base, the base 3′ of Cyt, and its Watson–Crick partner (a₂); and the average of the distance between the N1 atom of mGua and the N4 atom of Cyt and the distance between the N2 atom of mGua and the N3 atom of Cyt (d₀). Bias annealing was performed with the target value of a₁ advanced by −0.02 rad from 0.0 rad to −0.5 rad, a₂ by 0.02 rad from −0.8 rad to −0.1 rad, and d₀ by 0.1 Å from 3.0 Å to 10.0 Å (SI Table 5). The final trajectories harvested with TPS were 60 ps; one basin was defined as −0.2 ≤ a₁ ≤ 0.2 rad, −1.0 ≤ a₂ ≤ −0.6 rad, and 2.8 ≤ s ≤ 3.2 Å, and the other basin was defined as −0.6 ≤ a₁ ≤ −0.4 rad, −0.3 ≤ a₂ ≤ 0.1 rad, and 8.0 ≤ s ≤ 12.0 Å. Again, the time spent between basins was typically a few picoseconds, which suggests that the choice of trajectory length did not restrict the paths sampled (SI Fig. 10b).

Identification of Reaction Coordinates.

To define the stable and transition states, we used p, the likelihood that additional trajectories initiated from a configuration with momenta drawn isotropically from a Maxwell–Boltzmann distribution commit to the forward basin before the backward basin (see SI Methods for details). The combinations of physical variables that predict p were identified by a genetic neural network (GNN) approach (13, 37). For both steps of the reaction of interest (unstacking and active-site entry), four classes of variables were considered: (i) intra- and intermolecular pairwise distances for the DNA and protein molecules, (ii) interaction energies between protein residues and DNA fragments surrounding the flipping base, (iii) accessible surface areas of protein residues at the protein–DNA binding interface, and (iv) fragment center-of-mass-based pseudodihedral angles that measure the relative positions of the flipping base. In total, we tested 3,558 coordinates for the unstacking step and 8,693 coordinates for the active-site entry step. The respective databases comprised the values of these variables and the commitment probabilities for 53 and 75 representative structures. These databases were found to be sufficient to obtain two-descriptor models that predicted the commitment probabilities in a jackknife cross-validated fashion with root-mean-square (rms) errors of 0.1 (compared with a range of 0–1 for p; SI Fig. 13). Because there is some confusion in the literature (38), it is important to emphasize that the structures in the databases were sampled independently of the reaction coordinates, p is calculated only once for these structures, and the GNN procedure does not require the performance of the standard histogram test. These features result in substantial computational savings, as described in ref. 13. Analyses conducted after the completion of this work suggest that there is some advantage to using an alternate scoring function for evaluating the fit and computational resources are better allocated such as to sample more structures with fewer trajectories (39), but these variations were not explored because adequate coordinates had already been identified. Free energy calculations and rate estimations are discussed in SI Methods.