MAKING QUANTAL ANALYSIS MORE CONVENIENT, FAST, AND ACCURATE: USER FRIENDLY SOFTWARE QUANTAN

Abstract

Quantal analysis of synaptic transmission is an important tool for understanding the mechanisms of synaptic plasticity and synaptic regulation. Although several custom-made and commercial algorithms have been created for the analysis of spontaneous synaptic activity, software for the analysis of action potential evoked release remains very limited. The present paper describes a user-friendly software package QUANTAN which has been created to analyze electrical recordings of postsynaptic responses. The program package is written using Borland C++ under Windows platform. QUANTAN employs and compares several algorithms to extract the average quantal content of synaptic responses, including direct quantal counts, the analysis of synaptic amplitudes, and the analysis of integrated current traces. The integration of several methods in one user friendly program package makes quantal analysis of action potential evoked release more reliable and accurate. To evaluate the variability in quantal content, QUANTAN performs deconvolution of the distributions of amplitudes or areas of synaptic responses employing a ridge regression method. Other capabilities of QUANTAN include the analysis of the time-course and stationarity of quantal release. In summary, QUANTAN uses digital records of synaptic responses as an input and computes the distribution of quantal content and synaptic parameters. QUANTAN is freely available to other scholars over the internet.

1. Introduction

Neurotransmitters are packed in presynaptic vesicles and released from axonal terminals as multimolecular packages termed neurosecretory quanta. Neuronal secretion is stochastic in origin (for review: Redman, 1990; Bennett and Kearns, 2000; Atwood and Karunanithi, 2002; Sakaba et al., 2002; Stevens, 2003), and the number of quanta released in response to an action potential, as well the amount of transmitter released by a single vesicle, varies from trial to trial. The probabilistic nature of neurosecretion considerably complicates investigation of synaptic regulation and plasticity. At the same time, statistical analysis of quantal release proved to be a powerful tool in understanding the regulation of the release probability, the number of releasable quanta, and quantal size (Van der Kloot and Molgo, 1994; Oleskevich et al., 2000; Uteshev et al., 2000; Meyer et al., 2001; Bykhovskaia et al., 2001; Searl and Silinsky, 2002; Tsvetkov et al., 2002; Neher and Sakaba, 2003; Sargent et al., 2005; Biro et al., 2005).

Spontaneous release events can be detected as miniature excitatory postsynaptic potentials (mEPSP) or currents (mEPSC) using amplitude thresholds for the recorded or differentiated signal. Several custom made (Cochran, 1993; Ankri et al., 1994) and commercial (SynaptoSoft) program packages have been created for the automatic detection and analysis of mEPSPs. A more challenging problem is to determine how many quanta are released in response to a presynaptic action potential, since these quantal events usually overlap and cannot be reliably discerned. At the same time, extracting the number of quanta released in response to an action potential from the recordings of excitatory postsynaptic currents (EPSCs) or potentials (EPSPs) is an ultimate condition for the statistical analysis of quantal release. The problem of the detection of evoked quantal events can be solved differently for different synapses at different experimental conditions. Under the conditions when multiquantal responses are infrequent and the instrumental noise is sufficiently low, quanta can be detected visually (Katz and Miledi, 1965; Wernig, 1972; Zucker, 1973) as inflections or multiple peaks of EPSP traces. A software package that performs this procedure automatically by analyzing differentiated signals has been created (Bykhovskaia et al., 1996).

However, quantal events often occur synchronously or nearly synchronously, and at these conditions quantal events cannot be reliably discerned. In addition, measured synaptic responses may include variable contributions of noise or may be intrinsically variable. Therefore, deconvolution algorithms have been developed to extract the distribution of quantal content from the noisy distribution of EPSP sizes (Van der Kloot, 1988, 1997; Korn et al., 1993; Stricker et al., 1994; Vorobieva et al., 1999; Bekkers, 2003; Stricker and Redman, 2003). Deconvolution methods usually rely on the information about quantal events obtained from the analysis of mEPSPs or unitary evoked EPSP. Thus, there is a need for a software package that could be universally suitable for the analysis of spontaneous synaptic activity, counting quantal events at low-output synapses, and evaluation of quantal content at high-output synapses by a deconvolution method.

This manuscript describes user-friendly software QUANTAN that has been created to perform quantal analysis of synaptic currents or potentials at various experimental conditions. The software performs multiple tasks required for statistical analysis of transmitter release, including filtering of electrical recordings, event detection, analysis of the release time-course, separation of synchronous and asynchronous release components, calculation of quantal content and its variability, and fitting the quantal release by binomial and Poissionian statistical models. QUANTAN combines our previously developed algorithms for direct quantal counts at low-output synapses (Bykhovskaia et al., 1996) and deconvolution of the distribution of EPSC sizes at high-output synapses (Vorobieva et al., 1999); further, it incorporates an algorithm for evaluation of the accuracy of direct quantal counts, which facilitates the choice for the appropriate detection method. Furthermore, it employs several different methods to calculate quantal content, thus possible errors can be assessed. The software has been extensively tested for the analysis of EPSCs recorded focally from the lobster (Bykhovskaia et al., 2001, 2004; Kapitsky et al., 2005), mouse (Samigullin et al., 2004; Coleman et al., 2007), and drosophila (Akbergenova and Bykhovskaia, 2007) neuromuscular junctions (nmj). QUANTAN is freely available to other scholars over the internet.

2. Methods and Results

2.1 Electrophysiology

EPSCs were recorded focally from the mouse and the lobster nmjs (Fig.1). Dissection procedures, solutions compositions, and visualization of synaptic terminals are described elsewhere (Bykhovskaia et al., 2004; Samigullin et al., 2004; Kapitsky et al., 2005). Briefly, the axon was stimulated electrically via suction electrode, and synaptic activity was recorded focally from visualized (2-Di-4-Asp or FM1−43, Molecular probes) synaptic terminals (Fig 1. A) using fire-polished macropatch electrodes of 5−15 μm diameter. Recordings (Fig 1 B) were digitized using PClamp 6.2 or PClamp 8.0 (Axon Instruments) with 10−50 μs resolution.

1. Focal recordings from the mouse diaphragm nmj.

A. Recording site: an endplate stained with 2-Di-4-Asp. B. Examples of EPSCs recorded at physiological conditions (2 mM Ca²⁺) and at the reduced Ca²⁺ (0.5 mM). Recordings at 2 mM Ca²⁺ demonstrate multiquantal EPSCs followed by asynchronous quanta. Recordings at 0.5 mM Ca²⁺ demonstrate a unitary EPSC (top), a transmission failure followed by an asynchronous mEPSC (middle), and a double quantal EPSC (bottom).

2.2. General organization of the program package QUANTAN

Software QUANTAN is written using C++ Builder (Borland) and operates under Windows platform. It includes the modules for quantal detection, the analysis of average EPSC traces and evaluation of the detection accuracy, evaluation of the quantal size (q), calculation of the distribution of quantal content (m) employing direct counts or deconvolution, and fitting the obtained distribution of m by binomial or Poissonian statistical model (Fig.2). In addition, QUANTAN includes a module for transformation of data files (Fig. 2B, “File transformation”), which allows cutting or rearranging episodes in the original data files. Input data files contain recordings of synaptic responses digitized by PClamp (Axon Instruments, version 6 or higher).

2. General organization of QUANTAN software.

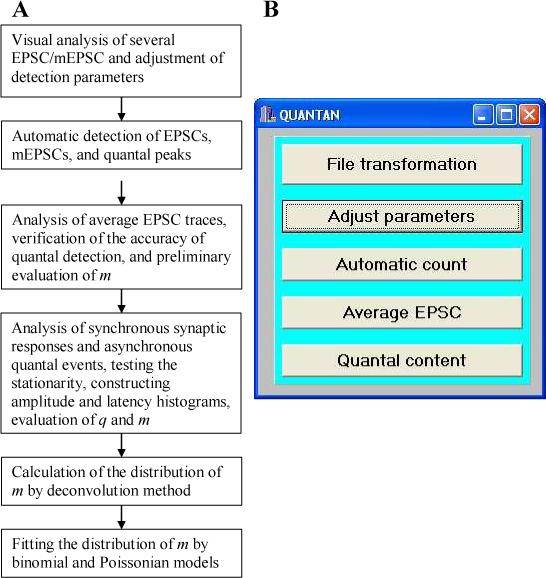
A. Summary of the QUANTAN modules involved in different steps of quantal analysis B. Starting QUANTAN: the initial dialog window.

2.3.Event detection

To accurately detect EPSCs, mEPSCs, or multiple quantal peaks in a single EPSC, we improved and further developed an earlier version of our detection software (Bykhovskaia et al., 1996). Digitized and differentiated recordings are analyzed to determine the following parameters for each EPSC or mEPSC (a response): 1) onset; 2) duration; 3) latencies and amplitudes of multiple quantal peaks or inflections, if they are present (Fig. 3 A,B).

3. Visual quantal detection.

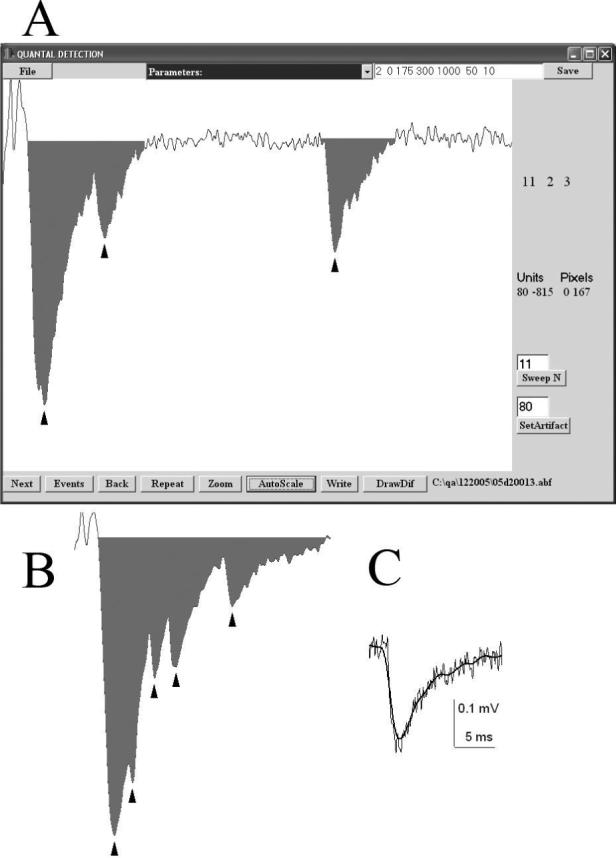
A. A dialog window for the visual quantal detection. The recorded episode is displayed, the EPSC area is marked, arrowheads point to the detected events. Detection parameters are displayed in the top right corner, and they can be edited and saved. A user can inspect all the sweeps in succession (“Next” button), only non-failure sweeps (“Events” button), or enter a sweep number (“Sweep N” button). A click on a screen displays the corresponding time-point and the value of the signal (Units). B. An example of multiple quantal peaks (arrowheads) detected in a single EPSC recorded from the mouse neuromuscular junction (extracellular Ca²⁺ was reduced to 0.5 mM, stimulation frequency was 15 Hz). C. Gaussian filtering does not change the shape of the signal while reducing the noise. Thin line – recorded signal; thick line – the same signal after filtering with 1/f_c=75 time points at the digital resolution of 50 μs.

A response is tentatively detected if a rising phase and a subsequent falling phase are detected. A rising phase is defined as five consecutive time-points where a signal differential is negative, and the first of these points is considered an onset. To detect the falling phase, we analyze the differentiated signal over a time interval of 1 ms. At each time-point (i) following the rising phase we calculate a total differentiated signal over a 1 ms interval as a sum of signal differentials over all the time points from i to i+1 ms. If this total differentiated signal exceeds a parameter selected by a user (MS/2, Table 1) then i is assumed to represent the beginning of a falling phase. This approach makes the detection algorithm sufficiently universal and independent of the stability of the recording baseline. A relative baseline is computed as an average signal at a millisecond temporal interval preceding the onset of the response. The response is considered terminated when the deviation of the signal from the baseline becomes less than a parameter selected by a user (Noise, Table 1). The response is accepted only if its amplitude (the maximal deviation from the baseline) exceeds a threshold (MS, Table 1) selected by a user.

Table 1.

Parameters utilized for the detection of quantal events and multiquantal responses

Parameter	Description	Units	Range used in our studies
Channel	Output channel to be analyzed. If a single channel was employed for recordings, Channel is set 0.		0−2
Polarity	Intracellular (1) or extracellular (0) recordings		0 or 1
Noise	Base-line S.D. (after filtering)	r.u.1	50−300
Minimal Signal, MS	Amplitude threshold for detected events	r.u.	300−2000
Filter	1/f, where f is the cut-off frequency for the Gaussian digital filter	Time-points2	15−70
Resolution	Temporal interval between subsequent points in a digitized signal	μs	10−50

¹Relative units used by acquisition software to digitize the signal

²Time-points of the digitized signal

This detection algorithm works efficiently only if the amplitude threshold (MS) exceeds the baseline noise (Noise). Otherwise, digitized signals are filtered to reduce the noise (Fig. 3 C). QUANTAN employs Gaussian digital filtering (Colcuhoun and Sigworth, 1995) which is controlled by a parameter Filter (Table 1). Filtering and compensation for the recording noise precedes signal differentiation, detection of the rising and falling phases of a response, and computation of the relative baseline. After a response is detected, it is analyzed to determine all the peaks and inflections, which represent peaks of single quanta (Fig. 3 A, B, arrowheads). QUANTAN incorporates an earlier developed procedure (Bykhovskaia et al., 1996) for accurate detection of inflections and peaks of current traces.

At the first stage, an investigator analyzes visually 20−30 sweeps and adjusts the parameters (Table 1) to optimize the accuracy of the event detection. After a selection of an input file (*.pfl, Table 2), a dialog window for the event detection (Fig. 3 A) opens. A binary file containing digitized recordings can be opened (button “File”), and synaptic responses can be visualized (Fig. 3 A,B). The detection parameters are adjusted so that the events detected by QUANTAN (Fig.3A, B, arrowheads) match the events detected visually. Once the detection parameters are adjusted, the event detection is performed in an automatic mode (“Automatic count”, Fig. 2B). A dialog window allows opening multiple data files and analyzing them automatically with the same set of detection parameters. Two text output files are created for each input data file (Table 2).

Table 2.

Files used and created by QUANTAN

Name	Created by	Content
File1.pfl	Created by a user; modified by “Adjust parameters” and “Automatic count” modules	A list of detection parameters is followed by a list of the files analyzed
Data1.txt	“Automatic count” module	Each line represents a single EPSC or mEPSC and includes: number of detected quantal events; onset; termination; amplitude; integrated signal; latencies of all the quantal peaks
Data.av	“Automatic count” module	Each of the six columns represents: an average failure of transmission; an average EPSC classified as unitary; an average EPSC classified as double quantal; an average EPSC classified as triple quantal; an average mEPSP; an average sweep
File.res	“Quantal Content” module	All the calculated parameters of synaptic activity (Table 3)
File.mqc	“Quantal Content” module	Distribution of countal content obtained by direct counts
File.qaa	“Quantal Content” module	Distribution of quantal sizes
File.tam	“Quantal Content” module	Distribution of EPSC sizes
File.lat	“Quantal Content” module	Latency distribution

¹The filename “File” is selected by user

² The filename “Data” corresponds to the name created by acquisition software (PClamp, Axon Instruments)

2.4. Evaluation of quantal content m and parameters of synaptic activity

Direct counts of quantal peaks provide an accurate evaluation of quantal content only if the release rate is low, and multiquantal responses are infrequent. When several quanta are released in response to a stimulus, it is likely that postsynaptic quantal events would overlap and that some quantal peaks would be missed. Thus, as synchronous release component increases, the method of direct counts tends to significantly underestimate quantal content. The ratio between the EPSC size and quantal size serves as a reasonable estimate of m when multiquantal releases are frequent. The size of EPSCs or mEPSCs can be represented either by their amplitudes or by the integrated current traces (area). A disadvantage of amplitude measurements is that quantal latencies in a multiquantal EPSC are not precisely synchronized, and thus, amplitude of a multiquantal EPSC might be smaller than the sum of the amplitudes of comprising quanta. Generally, area measurements give a more accurate estimation of quantal content at the nmj than amplitude measurements (Cooper et al., 1995; Van der Kloot, 1997). However, amplitude measurements are less sensitive to the baseline noise than area measurements (Iansek and Redman, 1973). Thus, each method has his its relative advantages and disadvantages depending on the experimental conditions, and, therefore, it is beneficial to compare how quantal content varies when it is calculated by different ways: direct counts, amplitude measurements, or area measurements. QUANTAN evaluates quantal content by all the three methods.

To test the accuracy of the method of direct quantal counts, QUANTAN employs the following procedure. During the automatic event detection, sweeps are grouped according to the number of detected quantal peaks. At the end of the detection procedure, all the sweeps of each group are superimposed and averaged, and all the average sweeps are saved in an output file Data.av (Table 2). Thus, the output file Data.av contains an average failure, an average single quantal EPSC trace, an average double quantal EPSC trace, an average triple quantal EPSC trace, and an average of all the sweeps. In addition, an average mEPSC is obtained by superposition of all the detected mEPSCs, which are aligned relative to the latencies of their peaks. If all the quantal peaks were identified correctly, we expect that the integrated double quantal EPSC would be twice larger than the integrated single quantal EPSC, while the average failure would not significantly derive from the baseline. Furthermore, we expect that the average unitary EPSC would be similar to the average mEPSC (Fig. 4 B). We test whether this is true using the module “Average EPSC” (Fig 4 A).

4. Average quantal and multiquantal EPSCs.

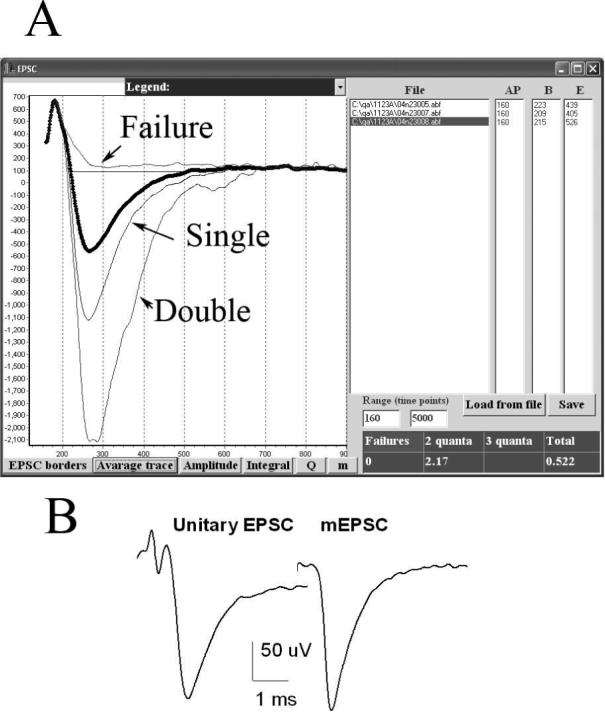
A. A dialog window for the visualization of the average quantal and multiquantal EPSCs. The list of the files analyzed appears in the “File” window. The onset and the end points of the average EPSCs are determined in response to the “EPSC borders” button, and, thus, the time window for synchronous release is defined. The latencies of the action potential, the onset, and the end of the average EPSC appear in the windows “AP”, “B”, and “E”, respectively. These values can be edited and saved by a user (“Save” button). The graph (appears in response to “Average trace” button) shows the average single and double EPSCs (thin lines, color coded), as well as the average of all the EPSCs in a highlighted file (thick dotted line). The table (right bottom corner) shows the ratios of the sizes (integrated traces) of multiple EPSCs to the size of the unitary EPSC. In this experiment, EPSCs were recorded from the mouse nmj at 15 Hz stimulation frequency at the reduced (0.5 mM) extracellular Ca²⁺. The area of the average double EPSC was 2.17 times larger than the average area of the unitary EPSC; triple quantal EPSCs were not detected; the average failure ran above the baseline, its size being equal 0. Thus, in this example quantal detection could be considered accurate, since the EPSCs detected as doubles are approximately twice (2.17 times) larger than the EPSCs detected as unitary. The ratio of the area of the average EPSC to the unitary EPSC (0.522) can be considered a reasonable estimate of m. The amplitudes and the areas of the average EPSCs can be plotted in this window and saved in the *.pfl file (“Amplitude” and “Integral” buttons), as well as the amplitudes of the average unitary EPSCs (“Q” button) and the estimates of m (“m” button). B. The average unitary EPSC and the average mEPSC obtained from the same dataset are similar, which confirms that that multiple quantal EPSCs were not classified as single quanta. Note that the average mEPSC has a slightly larger amplitude than the average unitary EPSC, and it is slightly sharper. The reason is that mEPSCs were superimposed according to their peak latencies, while EPSCs were always superimposed according to the action potential latencies, thus some asynchrony of synaptic latencies was present in the superposition of unitary EPSCs.

The example presented in Fig. 4 illustrates an accurate detection of quantal events by the method of direct counts. The area of the average double quantal EPSC is approximately twice (by 2.17 times) larger than the area of the average unitary EPSC, and the trace of the average failure runs above the baseline (Fig. 4A). Furthermore, the average unitary EPSC and the average mEPSC are similar (Fig. 4 B). In contrast, if the ratio between the area of the average double quantal EPSC and the area of the average unitary EPSC is significantly less than two, we conclude that direct counts are inacurate. In this case, amplitude or area measurements should be employed to calculate quantal content.

At this stage we also determine whether EPSCs and mEPSCs were detected correctly or some of the events were undetectable because of the instrumental and/or intracellular noise. If some of the events are below the detection threshold, then the average failure deviates noticeably from the baseline and its area is significantly different from zero. If this proves to be the case, one should go back to the detection procedure and attempt optimization of the detection parameters. Subsequent analysis can only be applied to the recordings where EPSCs and mEPSCs are reliably detected.

Analysis of the average EPSC allows us to determine the time window for the synchronous release component (Fig. 4 A, horizontal line). When tens or hundreds of the recorded sweeps are aligned, the asynchronous events do not affect noticeably the average signal. Thus, we consider the temporal interval between the onset of the average EPSC and its decay to the baseline as a time window for the synchronous release component. All the uniquantal signals outside of this time window are regarded as mEPSCs.

At the next step (Fig. 5), detailed analysis of synchronous and asynchronous release components is performed, and quantal content of synchronous release component is accurately evaluated. This procedure allows us to compare different methods of the evaluation of quantal content. Quantal content m can be evaluated: 1) by direct counts; 2) as a ratio of the average EPSC amplitude and quantal amplitude; 3) as a ratio of the average EPSC area and quantal are. Area measurements are, generally, preferable (Cooper et al., 1995; Vander Kloot 1997), since this method accounts for a possible asynchrony of quantal events in EPSCs (Bykhovskaia et al., 1999), while amplitude measurements are likely to underestimate quantal content if quantal peaks are not precisely synchronized. On the other hand, area measurements are more sensitive to the recording noise, and thus, may have larger errors than amplitude measurements.

5. Evaluation of quantal content m.

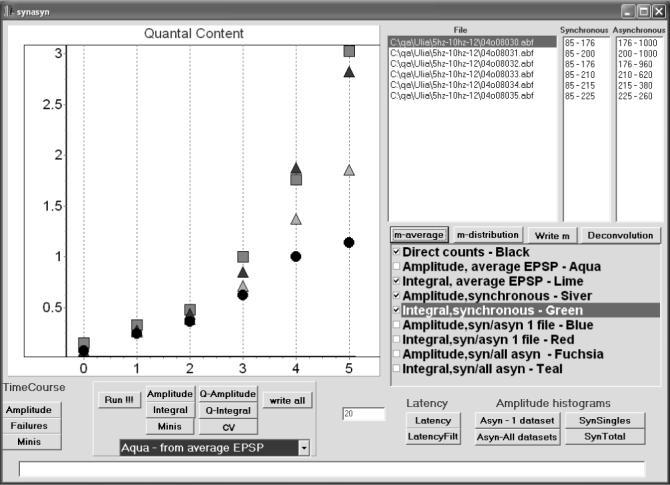
In this experiment, EPSCs (300 sweeps per file) were recorded from the lobster nmj at stimulation frequencies of 5, 10, 20, 30, 40, and 50 Hz (points 0−5). Quantal content was evaluated by four methods (checked): direct counts (circles); the average EPSC amplitude divided by the average amplitude of the unitary EPSC from the highlighted file (light triangles); the average EPSC area divided by the average area of the unitary EPSC from the highlighted file (dark triangles); the area of the average superimosed EPSC divided by the area of the average superimposed unitary EPSC from the highlighted file (squares). At the points 0−2 (5−20 Hz stimulation frequency) the results of all the methods agree, thus direct counts can be considered accurate. At the points 3−5 (30−50 Hz) the area measurements (squares and dark triangles) give the highest quantal content. Since these two m estimates obtained by area measurements are in a good agreement, area measurements can be considered accurate. In contrast, amplitude measurements (light triangles) and direct counts (circles) underestimate quantal content at high stimulation frequencies (30−50 Hz, points 3−5). Other methods available for m evaluation (listed) are: 1) the amplitude of the average superimposed EPSC divided by the amplitude of the average superimposed unitary EPSC in the highlighted file; 2) the average EPSC amplitude or area divided by the average amplitude or area of mEPSCs collected from either the highlighted file or throughout the experiment.

To evaluate the errors introduced in the area measurements by the recording noise, we employ two methods to calculate the EPSC area (integrated current trace): 1) superposition of all the recorded traces and calculation of the area of the average EPSC, as described in the previous section; 2) calculation of the area of each EPSC and finding the average. The advantage of the first method is that it not sensitive to the recording noise, since the noise is largely eliminated in the average signal. The advantage of the second method is that it provides us with the size variability. An agreement between the values of m obtained by these two methods indicates that the area measurements are accurate. This is the case for the example presented in Fig. 5 (squares and dark triangles). Thus, in the experiment presented in Fig. 5 area measurements would be the correct method to evaluate m, while amplitude measurements and direct counts underestimate m as quantal release increases (Fig. 5, light triangles and circles).

The evaluation of quantal amplitudes or areas, q, can be obtained in the following ways: 1) from mEPSCs recorded from the same site in the same experiment; and 2) from unitary EPSCs recorded from the same site under conditions where quantal output is low and direct counts are accurate (Table 3). The distributions of the quantal size obtained by these two ways can be constructed and compared. In the experiment presented here (Fig. 5), unitary EPSCs recorded at the lowest stimulation frequency were selected for quantal size evaluation.

Table 3.

Procedures implemented in the “Quantal Content” module

Parameter	Methods
EPSC size	Amplitude of the average superimposed EPSC
	Area of the average superimposed EPSC
	Distribution of EPSC amplitudes, mean, S.D., and C.V
	Distribution of EPSC areas, mean, S.D., and C.V
Quantal size	Amplitude of the average superimposed unitary EPSC
	Area of the average superimposed unitary EPSC
	Amplitude of the average superimposed mEPSC
	Area of the average superimposed mEPSC
	Distribution of the amplitudes of unitary EPSCs, mean, S.D., and C.V
	Distribution of mEPSC amplitudes, mean, S.D., and C.V
	Distribution of unitary EPSC areas, mean, S.D., and C.V
	Distribution of mEPSC areas, mean, S.D., and C.V
Quantal content	Area measurements
	Amplitude measurements
	Direct counts
Frequency of asynchronous quantal events	Average number of mEPSCs per sweep
Latency	Distribution of latencies of detected quantal events
	Filtered latency histogram
Synaptic activity as a function of a stimulus trial	EPSC amplitude
	mEPSC frequency

In this module we can also calculate other parameters of synaptic activity (Table 3), such as: 1) the rate of asynchronous release; 2) the distribution of synaptic latencies; 3) synchronous and asynchronous synaptic activity as a function of the stimulus number. The results of all the calculations can be saved in ASCII files (Table 2).

2.5. Distribution of quantal content obtained by deconvolution of the distribution EPSC sizes

The algorithms described above allow us to evaluate the average quantal content m and to obtain the distribution of m at the synapses with a low quantal output, where direct counts are accurate. The distribution of quantal content in high-output synapses has to be derived by a deconvolution method. Our goal here is to deconvolve the distribution of EPSC sizes and to obtain the distribution of quantal content without relying on any a priori assumptions about the variability of quantal size or the release model. We have previously developed a model-independent deconvolution algorithm (Vorobieva et al., 1999), which uses experimentally obtained distributions of EPSCs and quanta and computes the distribution of quantal content by solving a system of regression equations. The method is based on 1) constructing the distribution of quantal sizes from either mEPSCs or unitary EPSCs recorded under low-release conditions; 2) constructing distributions of multiquantal EPSCs employing bootstrap; 3) applying multiple linear regression (Seber and Lee, 2003) to derive the distribution of m.

Our deconvolution method has been extensively tested (Vorobieva et al., 1999; Bykhovskaia et al., 2001) by analyzing simulated datasets of EPSCs, as well as by the comparison of the distributions of m obtained for low-output synapses employing the deconvolution procedure and the method of direct counts. We demonstrated that the results of deconvolution were in a good agreement with the distribution of m that was either simulated or obtained by direct counts at low-output synapses (Vorobieva et al., 1999). However, we also demonstrated that the accuracy of the method critically depends on the selection of input parameters (Table 4). The selection of the input parameters is best performed under a visual control. QUANTAN incorporates the deconvolution algorithm and a module which enables us to examine quickly and conveniently how the distribution of m depends on the parameters selected. The major stages of this procedure are presented in Figure 6.

Table 4.

Inputs and outputs of the deconvolution procedure.

Inputs and outputs	Example (presented at the Fig. 6)
Inputs
The measure of size: amplitudes or integrated signals	Integrated signals
A source of EPSCs	A file containing 300 sweeps recorded at 0.5 Hz stimulation frequency from the mouse nmj (2 mM Ca2+)
A source of quanta	Asynchronous mEPSPs collected from the same recording
Number of bins in the distribution of quantal sizes	8
Ridge regression coefficient	0.03
Outputs
Qunatal counts, their expected frequencies with the confidence intervals	Fig. 6 D
Restored distribution of EPSC sizes	Fig. 6 E
Fit between the restored and original distributions of EPSC sizes	χ2=23.5, P<0.95
Optimized binomial and Poissonian distributions	Fig. 6 F
Goodness of fit for the Poissonian model	χ2=66.4
Goodness of fit for the binomial model	χ2=8.4, P<0.9
Binomial parameters	p=0.57, n=9

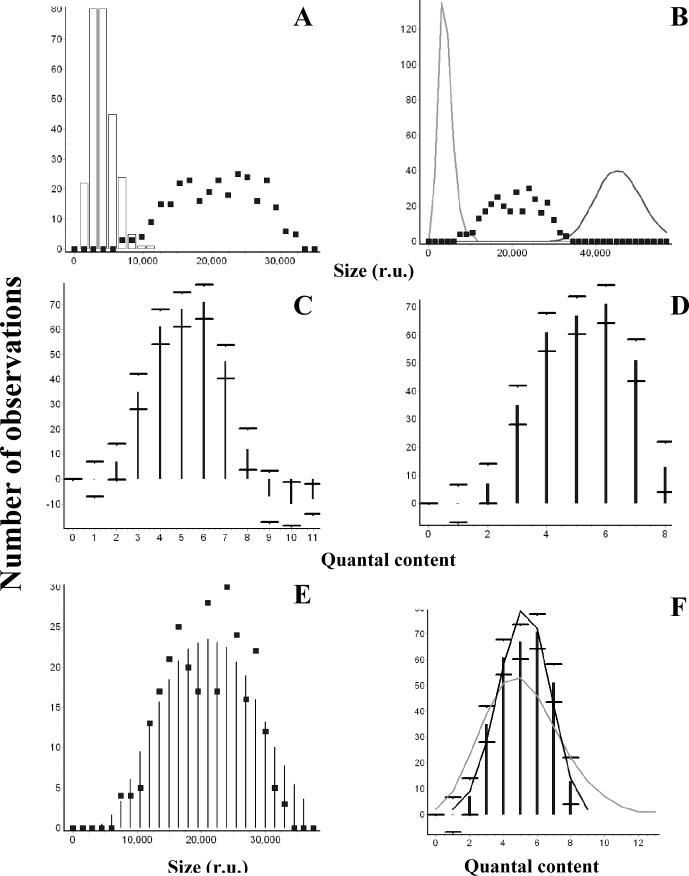
6. Deriving the distribution of quantal content m by the deconvolution method.

All the graphs were created within the “Deconvolution” dialog window. A. The distribution of sizes as areas (integrated current traces) of EPSCs (squares) and quantal events (mEPSCs, columns) recorded from the same site at the mouse nmj. B. The distribution of EPSC sizes (squares) is enclosed between simulated distributions of unitary and 11-quantal events (lines). C. Deconvolution performed with the maximal number of quanta released in a trial m_max=11. Negative frequencies were obtained for m=9, m=10, and m=11. D. Deconvolution performed with the maximal number of quanta released in a trial m_max =8, which corresponds to the maximal number of quanta in a trail which had a positive frequency at the previous step (panel C). E. Original (squares) and restored (bars) distributions of EPSC sizes. F. Fit of the distribution of m by binomial (black line) and Poissonian (gray line) statistical models.

First, the source file(s) of EPSCs and quanta (synchronous or asynchronous, Table 4) are selected, and the distributions of EPSC sizes and quantal sizes are constructed (Fig. 6A). Either area or amplitude can serve as a measure of the size, and the width of the bin is adjusted to provide the maximal number of bins with the distribution of quantal size being smooth and unimodal.

The deconvolution algorithm can be successfully applied even if the distribution of quantal size is not unimodal. In this case, however in would be beneficial to consider the potential sources for the multiple modes. If additional peaks in the quantal distribution result from the instrumental noise, the solution of the deconvolution algorithm would be more stable if the bin size is increased to eliminate the extra modes resulting from noise. In our experience, 5−10 entries in the quantal size distribution proved to be sufficient to obtain a stable solution of the regression equations. Another source of polymodality may be several synapses responding to a stimulus, each generating its own mode in the quantal distribution. In this case, the obtained multimodal distribution of the quantal size can be used, although it is important to ascertain that evoked EPSCs and quanta result from the same population of synapses. Finally, extra modes in the distribution may indicate that some of the events classified as unitary are, in fact, multiquantal. In this case, we have to optimize either recording conditions or event detection parameters, so that the distribution of the quantal size is constructed exclusively from single quantal events.

At the next step (Fig. 6B), we determine the minimal and maximal number of quanta which could be possibly released in a trial in this experiment. We adjust the minimal and maximal number of quanta in such a way that simulated multiquantal distributions obtained by a bootstrap method would lie at the borders of the EPSC distribution. For example, the EPSC distribution presented in Fig. 6B (squares) in enclosed between single quantal and 11-quantal distributions (lines). We conclude, therefore, that in this experiment the maximal number of quanta released in a trial does not exceed eleven, while the minimal number of quanta is one or higher. Next, the distribution of m (Fig. 6 C) is derived by ridge regression method (Vorobieva et al., 1999) with the ridge regression coefficient (Table 4) adjusted to provide desired confidence intervals. Sometimes the resulting distribution of m has negative components (for example, 9, 10, and 11 quanta have negative frequencies, Fig. 6 C). This means that the maximal number of quanta released in a trial (m_max) was overestimated. At the next step, we exclude the entries in the distribution of m which have negative frequencies, adjust m_max, and repeat the deconvolution procedure (Fig. 6 D, m_max=8). This corrected distribution of m is validated by calculating the restored distribution of EPSC sizes (Fig. 6 E, columns) and comparing it with the original distribution of EPSC sizes (Fig. 6 E, squares) employing chi-square test (Table 4).

Finally, the obtained distribution of m can be fit by either Poisson or binomial model (Fig. 6 F). Binomial model of the transmitter release with the parameters (n) and (p) (and the Poissonian model, as its limiting case with a large n and a small p) assumes that each of n releasable units can produce a release of a neurotransmitter quantum with a probability p (McLachian, 1978). Although basic assumptions of the simple binomial model can be affected by non-uniformity of release probabilities among the releasable units (Smith et al., 1991; Wojtowicz et al., 1991; Quastel, 1997) and by non-stationarity of the release process from trial to trial (Brown et al., 1976), this model is widely used (Searl and Silinsky, 2002, 2003; Sola et al., 2004; Biro et al., 2005; Kirischuk et al., 2005; Bremaud et al., 2007) and can be helpful for understanding of neurosceretory mechanisms and regulation.

Binomial parameters (Table 4) are optimized in QUANTAN by the a chi-square minimization procedure. The initial approximations for the parameters n and p can be obtained from the mean and variance of the distribution of m. However, sometimes the number of releasable units, n, obtained this way, is smaller than the maximal number of quanta released in a trial, m_max. Since, by the nature of a binomial process, the number of quanta released in a trail cannot exceed n, in the latter case we optimize n and p starting from n=m_max and p=<m>/m_max. During the optimization procedure, n is not allowed to drop below the maximal number of quanta which produced a significant number of observations. The number of observations is considered significant if zero lies outside its confidence interval. For example, for the distribution presented in Fig. 6D, we have a significant number of observations for the number of quanta m=8, but not for m=1 and m=2. Thus, in this example n would not be allowed to drop below eight.

3. Discussion

Here I presented a user-friendly program package QUANTAN which incorporates multiple steps of quantal analysis, from measuring EPSC parameters to deriving the distribution of m and fitting it by statistical models. The methods incorporated in QUANTAN were illustrated by applying them to quantal analysis of focal extracellular recordings of EPSCs. However, all the described procedures can be applied to EPSPs recorded intracellularly. This software was extensively tested using the neuromuscular preparation (Bykhovskaia et al., 2004; Samigullin et al., 2004; Coleman et al., 2007; Kapitsky et al., 2005; Bykhovskaia and Akbergenova, 2007.). With certain limitations, it can be also employed for quantal analysis at other synapses.

3.1 Main features of software QUANTAN

The major advantage of this program package is that it incorporates a number of algorithms for evaluation of quantal content m and operates under the visual control. Having several different algorithms, as well as the ability to compare them, incorporated in a single user friendly package tremendously facilitates quantal analysis and, most importantly, minimizes potential errors. Another advantage of QUANTAN is that it combines extraction of signals from the recordings of synaptic activity with subsequent statistical analysis, evaluation of quantal content, and deconvolution. To the best of my knowledge, this is the only software package which uses a recorded signal as an input and produces the distribution of m obtained by several methods, including deconvolution, as an output.

The main stages of the analysis incorporated in QUANTAN are 1) identification of EPSCs and mEPSCs in the recordings and calculation of their parameters, including synaptic delays, amplitudes, areas, the number of peaks, and their latencies; 2) separation of the quantal release into synchronous and asynchronous components; 3) calculation of the average quantal content by direct counts, amplitude measurements, and area measurements; 4) deconvolution of the distribution of the EPSC size.

Combining multiple algorithms in QUANTAN allows us to overcome some limitations of quantal analysis. One of these limitations is the accuracy of the method of direct counts. Although direct counting is a very convenient and widely used approach, this method sometimes produces errors because multiple quanta released synchronously or nearly synchronously can be counted as a single quantal event (Zucker, 1973; Bykhovskaia et al., 1999). The verification of the accuracy of direct quantal counts can be easily performed in QUANTAN by employing the area measurements of the detected single and multiple quantal responses.

At high-output synapses, where direct counts cannot be employed, quantal content is often calculated as a ratio between EPSC and mEPSC size (amplitude or area). QUANTAN performs this procedure quickly and conveniently in an automatic mode. Furthermore, it evaluates the accuracy of area measurements, which are generally preferable but can be strongly affected by the recording noise. Finally, it allows the extraction of the variability and distribution of the quantal content employing a deconvolution of EPSC and mEPSC sizes.

The advantage of the deconvolution technique incorporated in QUANTAN is that it is completely model-independent and does not make any assumptions about the distribution of quantal size. It operates with the distribution of quantal size obtained experimentally. This approach is critical for the synapses where the distribution of quantal size has a significant variance and a skew (discussed below). This approach contrasts to earlier deconvolution techniques, where variations in quantal size were neglected (Aumann and Parnas, 1991), approximated by a Gaussian (Korn et al., 1993), or assumed to result from the instrumental and intracellular noise with a relatively small variance and approximated by a mixture of Gaussians (Stricker and Redman, 1994, 2003; Stricker et al., 1994). Furthermore, the technique employed here does not require any a priori assumptions about the release model, such as that the release process obeys either binomial or Poissonian law (Bekkers and Sevens, 1995; Bekkers, 2003). Although in many cases this assumption is valid, the distribution of m can deviate from these statistical models because the release probability and/or the number of releasable quanta can vary from trial to trial. It should also be noted that deconvolution methods do not always provide unique solution for the distribution of m, therefore all the distributions of m obtained by deconvolution should be examined and validated by comparison of the observed and restored distributions of EPSC sizes. The comparison of different solutions and their validation is greatly facilitated in QUANTAN because of its graphical capabilities.

3.2. Quanta and their variability

Unless the rate of quantal release is very low and direct counts are accurate, a reasonable estimate of quantal size is required for any method of quantal analysis. Several approaches have been employed to evaluate the quantal size. The most direct approach is to obtain the distribution of quantal size experimentally from the recordings of spontaneous or asynchronous activity. However, in many cases mEPSCs may not be an appropriate measure of the quantal size.

First, the distribution of mEPSCs might not adequately reflect the distribution of action potential evoked quanta, since mEPSCs and EPSCs might arise from different sets of synapses. To overcome this problem, various methods have been used to record single quantal responses, including focal recordings of EPSCs under conditions when quantal release is reduced and multiquantal responses are infrequent (Cooper et al., 1995; Bykhovskaia et al., 2001; Kapitsky et al., 2005), focal recordings of mEPSCs (Samigullin et al., 2004), local applications of hypertonic solutions (Bekkers and Stevens, 1995) or strontium (Oliet et al., 1996; Bekkers and Clements, 1999), and recordings of mEPSCs from the synapses with few inputs (Isaakson and Walmsley, 1995). When one of these strategies is chosen, QUANTAN facilitates separation of synchronous and asynchronous release components, classification of synaptic responses as uniquantal or multiquantal, and comparison of quantal distributions obtained from synchronous and asynchronous release components.

Second, some of asynchronous events might be multiquantal, probably, due to spontaneous fluctuations of calcium concentration, as was observed for inhibitory postsynaptic responses in the goldfish Mauthner cell (Korn et al., 1993). In this case, the distribution of quantal events can be approximated by a Gaussian function, and the distribution of EPSCs can be analyzed as a mixture of normal distributions. Although this approach can be applied to the synapses where quanta were demonstrated to have a Gaussian distribution (Korn et al., 1987, 1993; Korn and Faber, 1990), in many experimental systems this is not the case. Thus, it was demonstrated that generally the distribution of quantal size in excitatory synapses is unimodal and skewed (Van der Kloot, 1991; Calister and Walmsley, 1996; Isaakson and Walmsely, 1996; Frerking et al., 1997; Liu et al., 1999) and can be accurately described by a log-normal function (Van der Kloot, 1989; Rossi et al., 1994). The large variance and the positive skew in the distribution of quantal size can be reasonably ascribed to the variation in transmitter concentration (Frerking et al., 1995; Pothos et al., 2000) or to the variation in postsynaptic receptor concentration (Nusser et al., 1997; Liu et al., 1999). Thus, the assumption about the normal distribution of the quantal size cannot be considered universally applicable, and to ensure the accuracy of quantal analysis the quantal distribution has to be investigated experimentally. QUANTAN is designed for the application of quantal analysis to the recording conditions where a reasonable measure of quantal size can be obtained experimentally.

Third, the parameters of the mEPSC distribution can be inaccurately measured because of the noise contamination, and small events can missed because of being below the detection threshold, as it is often the case in central synapses. High-pass filtering, in particular the digital Gaussian filter incorporated in QUANTAN, sometimes enables overcoming the problem. Nevertheless, in central synapses quantal parameters often cannot be measured directly, and the intracellular and instrumental noise has to be deconvolved from the probability density function of the postsynaptic current (Redman, 1990 for review). An elegant approach to the noise deconvolution was developed by Stricker and coauthors (Stricker and Redman, 1994; 2003; Stricker et al., 1994, 1996), who described the baseline noise by a mixture of Gaussians. More recently, intracellular noise was taken into account more directly by evaluating the noise of postsynaptic channels and glutamate concentration in the cleft (Neher and Sakaba, 2001b).

Finally, the rate of asynchronous release may be so high that single quantal events would not be distinguishable in the asynchronous release component. This situation may be further complicated by a non-stationarity of asynchronous release. Solving these problems requires fluctuation analysis of postsynaptic currents (Segal et al., 1985; Fesce et al., 1986; Rossi et al., 1994) and taking into account non-stationary synaptic activity (Neher and Sakaba, 2001a, 2003), which is beyond the capabilities of the QUANTAN package.

3.3 Summation of quantal units in evoked multiquantal responses

The classical quantal model of neurotransmission assumes that a multiquantal postsynaptic response results from a linear summation of individual qunatal currents (del Castillo and Katz, 1954). Many approaches to quantal analysis, including the one described here, rely on this assumption. However, it is now clear that this assumption is not universal, and postsynaptic current can be shaped not only by the release of neurotransmitter but also by a number of postsynaptic factors. Thus, it is important to discuss the deviations from the linear summation of quantal currents in a multiquantal postsynaptic signal.

Nonlinear summation of synaptic currents occurs when a synaptic response significantly alters the membrane potential of a postsynaptic cell. This condition implies that EPSCs are sufficiently large and synaptic potentials are comparable to the resting membrane potential of the postsynaptic cell. This would be the case for EPSCs which are comprised out of tens or hundreds of quanta, since changes in a membrane potential produced by a single quantal EPSC are negligibly small. The average amplitude of synaptic potential calculated by QUANTAN can be corrected for non-linear summation (Martin, 1995), and the correction factor is roughly proportional to the relative change in the membrane potential caused by the synaptic response. The corrected amplitude of the evoked synaptic response can be used to calculate the average quantal content.

Saturation and desensitization of postsynaptic receptors are additional factors which could influence the magnitude and shape of the postsynaptic current. Although it was demonstrated (Harzell et al., 1975; Magleby and Pallotta, 1981) that postsynaptic acetylcholine receptors are neither saturated nor desensitized by a quantum, and quantal currents add linearly, this may not be the case for glutamate receptors. Both desensitization (Trussell et al., 1993; Otis et al., 1996) and saturation (Tang et al., 1994) of AMPA glutamate receptors was observed during synaptic transmission in the CNS. Furthermore, comparison of the mEPSC time-course (Heckmann and Dudel, 1998) with desensitization kinetics of glutamate receptor channels (Heckmann and Dudel, 1997) at the Drosophila nmj suggested that the release of a single quantum might possibly cause the receptor desensitization at this synapse. If postsynaptic receptors become saturated, quantal currents would not add up linearly in a postsynaptic response. Furthermore, if multiple quanta are released in a slightly asynchronous way, the receptor desensitization may affect the amplitudes of delayed quantal currents. Thus, some of these factors can affect the applicability of the approach to quantal analysis presented here. Below we discuss the applicability of the QUANTAN software package.

3.4 Applicability and limitations of software QUANTAN

QUANTAN is designed for the analysis of synaptic activity in the electrical recordings where signal to noise ratio is sufficiently low, so after digital filtering the events can be reliably detected. The quantal detection procedure was developed based on the visual analysis of postsynaptic records, therefore the accuracy of automatic detection is comparable that the accuracy of the visual analysis. Thus, QUANTAN is a fast and convenient tool for the detection and counting of the evoked and spontaneous synaptic currents and constructing the distributions of their amplitude, area, and latency. It incorporates convenient tools for the verification of quantal detection accuracy, including 1) a comparison of evoked and spontaneous quantal events, and 2) a comparison of evoked responses which have been classified as transmission failures, singles, doubles, and triples. Thus, QUANTAN would be a useful tool in all the studies of synaptic activity in peripheral and central synapses which rely on event detection, the probability of transmission failures, or measurements of the EPSCs or mESPCs amplitude, area, or latency.

Under the conditions when the rate of the evoked release is high and quantal events are not discernable in an evoked response, QUANTAN can be used to derive the distribution of quantal content by deconvolution of the distribution of EPSC sizes. The validity of the quantal content calculation is based on the following assumptions: 1) postsynaptic responses, whether uniquatal or multiquantal, can be detected and reliably discriminated from the instrumental and intracellular noise; 2) quantal events arise from the same population of synapses as evoked multiquantal responses; and 3) the area (or amplitude) of a multiquantal response is a sum of the areas (or amplitudes) of comprising quanta. These assumptions have been justified for the neuromuscular synapse, and QUANTAN has been extensively tested at the nmjs of crustacean (Kapitsky et al., 2005), mice (Samigullin et al., 2004; Coleman et al., 2007) and Drosophila (Akbergenova and Bykhovskaia, 2007). QUANTAN would be also applicable to the analysis of the release rate at neursecretory cells when release events are detected using cathechoamine amperometry (Elhamdani et al., 2001; Grabner and Fox, 2006)

The calculation of quantal content described here would have many limitations at central synapses, since postsynaptic responses are often affected by saturation (Tang et al., 1994) and desensitization (Trussell et al., 1993; Otis et al., 1996) of AMPA receptors and by residual glutamate current (Barbour et al., 1994; Kinney et al., 1997; Carter and Regehr, 2000). Furthermore, individual quantal events may not be detectable because of a high rate of asynchronous release and baseline noise. This situation may be further complicated by a non-stationarity of asynchronous release. Thus, fluctuation analysis of postsynaptic currents has been developed (Segal et al., 1985; Fesce et al., 1986; Rossi et al., 1994) to estimate the release rate and mEPSC parameters under conditions when the rate of asynchronous release is high and individual quantal events are not detectable. This approach has been adapted and further developed by Neher and Sakaba (2001a,b, 2003) who took into account non-stationary synaptic activity, which could result from postsynaptic receptor desensitization or residual glutamate in the synaptic cleft and residual postsynaptic current.

However, under certain recording conditions quanta and EPSCs can be recorded from the same population of central synapses, and the basic assumptions of quantal analysis described above appear to be applicable. This was achieved, for example, by local application of sucrose (Bekkers and Stevens, 1995) or Sr²⁺ (Bekkers and Clements, 1999) to hippocampal synapses. Direct measurements of mEPSCs and EPCS arising from a limited number of synaptic connections were obtained in slices of rat anteroventral cochlear nucleus (Isaacson and Walmsely, 1995), and it was demonstrated that desensitization of AMPA receptors in this cells is not significant (Isaacson and Walmsely, 1996). Inhibitory synaptic currents and asynchronous quanta have been recorded from single contacts at striatal neurons (Behrends and Bruggencade, 1998). Finally, NMDA receptor – mediated EPSCs and mEPSCs were recorded from autaptic synapses at cerebellar neurons, and at this synapse quantal content was assessed as a ratio between the EPSC and mEPSC amplitude (Lu at al., 2006). QUANTAN would be a useful tool for the analysis of such experiments.