Abstract
In response to the need of establishing a high-resolution spatiotemporal neuroimaging technique, tremendous efforts have been focused on developing multimodal strategies that combine the complementary advantages of high-spatial-resolution functional magnetic resonance imaging (fMRI) and high-temporal-resolution electroencephalography (EEG) or magnetoencephalography (MEG). A critical challenge to the fMRI-EEG/MEG integration lies in the spatial mismatches between fMRI activations and instantaneous electrical source activities. Such mismatches are fundamentally due to the fact that fMRI and EEG/MEG signals are generated and collected in highly different time scales. In this paper, we propose a new theoretical framework to solve the problem of fMRI-EEG integrated cortical source imaging. The new framework has two principal technical advancements. First, by assuming a linear neurovascular coupling, a method is derived to quantify the fMRI signal in each voxel as proportional to the time integral of the power of local electrical current during the period of event related potentials (ERP). Second, the EEG inverse problem is solved for every time instant using an adaptive Wiener filter, in which the prior time-variant source covariance matrix is estimated based on combining the quantified fMRI responses and the segmented EEG signals before response averaging. A series of computer simulations were conducted to evaluate the proposed methods in terms of imaging the instantaneous cortical current density (CCD) distribution and estimating the source time courses with a millisecond temporal resolution. As shown in the simulation results, the instantaneous CCD reconstruction by using the proposed fMRI-EEG integration method was robust against both fMRI false positives and false negatives while retaining a spatial resolution nearly as high as that of fMRI. The proposed method could also reliably estimate the source waveforms when multiple sources were temporally correlated or uncorrelated, or were sustained or transient, or had some features in frequency or phase, or had even more complicated temporal dynamics. Moreover, applying the proposed method to real fMRI and EEG data acquired in a visual experiment yielded a time series of reconstructed CCD images, in agreement with the traditional view of hierarchical visual processing. In conclusion, the proposed method provides a reliable technique for the fMRI-EEG integration and represents a significant advancement over the conventional fMRI-weighted EEG (or MEG) source imaging techniques, and is also applicable to the fMRI-MEG integrated source imaging.
Keywords: multimodal neuroimaging, functional magnetic resonance imaging, blood oxygen level dependent, electroencephalography, cortical source imaging, adaptive Wiener filter, inverse problem
INTRODUCTION
Neural activities elevate electromagnetic signal changes accompanied by hemodynamic and metabolic changes. These changes are the basic sources for most noninvasive neuroimaging techniques. For example, electroencephalography (EEG) and magnetoencephalography (MEG) monitor the electrophysiological activity inside the brain by measuring the induced electromagnetic field using electric or magnetic sensors over the scalp surface (Nunez and Srinivasan, 2005; He, 2004; Hämäläinen et al., 1993). Both EEG and MEG have an intrinsic high temporal resolution that allows tracking rapid neurophysiologic processes at the neuronal time scale of milliseconds. However, the EEG (or MEG) source imaging often suffers from ambiguities in defining the anatomical locations of underlying electrical sources due to the need of solving highly ill-posed inverse problems (for reviews, see He, 1999; Pascual-Marqui, 1999; Darvas et al., 2004). On the other hand, functional magnetic resonance imaging (fMRI) (Bandettini et al., 1992; Kwong et al., 1992; Ogawa et al., 1992) is capable of mapping neural activations across the entire brain by utilizing a so-called blood oxygen level dependent (BOLD) contrast derived from a combination of hemodynamic and metabolic responses (Ogawa et al., 1990). Functional MRI has rapidly gained a prominent position in neuroscience research owing to its excellent spatial resolution and specificity. However, it is also generally accepted that fMRI is not suitable for studying the temporal aspect of rapid neuronal events since the hemodynamic response evolves in seconds rather than milliseconds (Boynton et al., 1996). In the past decade, the complementary advantages of EEG/MEG and fMRI have attracted great interests to integrate these modalities in an attempt to provide a multimodal neuroimaging technique with millimeter spatial and millisecond temporal resolutions (Liu et al., 1998; Dale and Halgren, 2001; Liu et al., 2006a). Furthermore, the feasibility of simultaneously recording EEG and fMRI makes EEG more preferable than MEG in terms of being integrated with fMRI (Allen et al., 1998, 2000; Goldman et al., 2000; Bonmassar et al., 2001; Gotman et al., 2002; Im et al., 2006).
The principle of fMRI-EEG integration lies in the linkage between hemodynamic response and neural activity. Early studies (Rees et al., 2000; Heeger et al., 2000) have found a linear relationship between human fMRI response and primate neuronal spike activity in the visual areas (V5 and V1). Nevertheless, important findings obtained from simultaneously recorded BOLD and intracranial electrical signals on primates suggest that the BOLD response is linearly correlated with the power of local field potential (LFP), which represents the synchronized synaptic inputs of a given neural population (Logothetis et al, 2001; Logothetis, 2002). Since then, evidence has increasingly suggested that the BOLD fMRI signal primarily reflects synaptic activity rather than neuronal spike activity (Arthurs and Boniface, 2002; Lauritzen and Gold, 2003; Martindale et al., 2003). This is also in light of the fact that the hemodynamic response is driven by the metabolic energy demand, nearly all of which is imposed by synaptic activity instead of action potential firing (Mathiesen et al., 1998; Arthurs and Boniface, 2002). The observed correlation between the BOLD signal and the neuronal spiking rate (Rees et al., 2000; Heeger et al., 2000) might be explained by the post-synaptic current flow in correlation with the spike activity of the pre-synaptic neurons (Heeger and Ress, 2002; Arthurs and Boniface, 2002). In addition, the energy contained in the synaptic current flow (proportional to the square of current density or LFP) can be further thought of as the physical energy correlate of metabolic energetics. In line with the pioneering work done by (Logothetis et al. 2001), another recent study using the visual stimulation with different contrasts and frequencies suggests that the BOLD fMRI response varies linearly with the power (instead of the magnitude) of the current source activity summed over the entire stimulus duration (Wan et al., 2006). In consideration of the above evidences together, it is reasonable to assume that regions in the brain that show increased BOLD responses are also on average more electrically active over time (Dale and Sereno, 1993).
Under this assumption, fMRI activation maps resulting from statistical analyses of fMRI time series are typically used as a priori information regarding where the EEG sources are likely located. Depending on different EEG source models, the fMRI map can be used to constrain the locations of multiple current dipoles, namely the fMRI-constrained dipole fitting (Ahlfors et al., 1999; Korvenoja et al., 1999; Fujimaki et al., 2002; Vanni et al., 2004), or to constrain the distributed source distribution over the folded cortical surface or in the 3-D brain volume, namely the fMRI-constrained current density imaging (George et al., 1995; Liu et al., 1998; Dale et al., 2000; Wagner et al., 2000; Babiloni et al., 2005; Ahlfors and Simpson, 2004; Sato et al., 2004; Phillips et al., 2005; Liu et al., 2006b; Mattout et al., 2006).
While applications of dipole fitting techniques are often questionable when brain activities are spatially distributed and not confined to focal regions, the distributed source imaging has relative wider applicability. Existing methods for the fMRI-constrained current density imaging have been implemented under different frameworks such as Wiener estimation (Dale and Sereno, 1993; Liu et al., 1998; Dale et al., 2000), weighted minimum norm (Wagner et al., 2000; Babiloni et al., 2005; Ahlfors and Simpson et al., 2004), Bayesian estimation (Sato et al., 2004; Phillips et al., 2005; Mattout et al., 2006) and Twomey regularization (Liu et al., 2006b).
All these approaches have limitations in two important aspects. First, there is no generalized method to quantify the fMRI signals such that the resulting quantification has an explicit physical interpretation in the context of EEG source imaging (Liu et al., 2006b). It is perhaps such limitation that makes it difficult to develop a principled way of using the fMRI data in solving the EEG inverse problem. Moreover, when the prior spatial constraint is derived from the fMRI activation map after applying a statistical threshold as in most existing methods, the fMRI-constrained source reconstruction is also subject to the choice of threshold as well as various methods of fMRI analysis (Ahlfors and Simpson, 2004). Secondly but more importantly, an fMRI-derived “time-invariant” spatial constraint (Lin et al., 2006) is applied when imaging the temporally variable current source distribution that accounts for the event-related potentials (ERP) during the entire period of interest. However, such a time-invariant spatial constraint may entail both fMRI false positives and false negatives, as a result of possible mismatches between locations of fMRI activations and instantaneous source activities, namely the fMRI-EEG mismatches.
Most of the fMRI-EEG mismatches are fundamentally caused by the highly different temporal scales in which the fMRI and EEG data are generated and collected. Neural activities evolve so fast that the brain function is always carried out readily. In response to a single “event”, the evoked neural activity is most substantial within a very short period of time ranging from tens to hundreds milliseconds. Since neuronal events are accompanied with instantaneous electrical responses, the scalp EEG signals collected with a sufficiently fast sampling rate carry the information about the “current” status of underlying neural activities (Nunez and Srinivasan, 2005). On the other hand, the neuronal activity also induces delayed and sluggish hemodynamic responses measured by fMRI. It has been shown that the change of BOLD fMRI signals only happens about 3 seconds after the event onset (Boynton et al., 1996). Since such a delay is significant relative to the short duration of neural activity, one can only infer from the fMRI data the “past” status of neural activity. The sluggish hemodynamics may also be appreciated by considering the neurovascular coupling system as a low-pass filter (or a temporal point spread function) (Logothetis et al., 2001; Friston et al., 1994). The rapid neural dynamics is effectively smoothed out, and the fMRI response accordingly reflects the energetic effect of neural activity averaged (or accumulated) over time (Boynton et al., 1996; Mathiesen et al., 1998; Martindale et al., 2003; Wan et al., 2006). Lastly, the fMRI data acquisition is also limited by the scanning speed (typically up to 50 ms per slice), which is often too slow to probe the temporal aspect of neural activity. In short, the spatial locations of fMRI activations cannot be simply equated with those of electrical activities at every millisecond considering that the fMRI has much lower temporal resolution and specificity than the EEG.
The fMRI-EEG mismatches can be further categorized into two types, namely fMRI extra sources and fMRI invisible sources (Liu et al., 1998; Wagner et al., 2000; Liu et al., 2006b). The fMRI extra sources represent the source regions deemed as active in fMRI but are not the EEG sources at certain time instants. During a short period of interest following the event onset, the fMRI activations have to be thought of as “static” (or time-invariant) while the EEG signals are variable and the source imaging is carried out instant by instant. Electrical source activities at certain time instants may only involve a subset of the activated fMRI areas, whereas other areas may appear as false positives if including them all as time-invariant spatial constraints (Liu et al, 2006b). The fMRI invisible sources are the real EEG sources but not deemed as active by fMRI. A transient current source may generate observable EEG signals whereas it may last too briefly to induce a sustained BOLD response. Under this condition, the fMRI-derived time-invariant spatial constraint includes false negatives, which often result in the underestimation of fMRI invisible sources as reported in several independent studies (Liu et al., 1998; Liu et al., 2006b). Therefore, dealing with such unavoidable spatiotemporal mismatches is essential to establishing a reliable fMRI-EEG integrated neuroimaging.
In this paper, we introduce a new theoretical framework on the integration of fMRI and EEG. This new framework distinguishes itself from other existing approaches by 1) using a unified quantification of BOLD-fMRI responses that can be interpreted as proportional to the time integral of EEG source power (or source variance with respect to a zero mean), and 2) deriving a set of “time-variant” spatial constraints in the form of source covariance matrices by fusing data from both fMRI and EEG. The derived time-variant source covariance matrices are incorporated into solving the instantaneous EEG inverse problem by means of the Wiener filter. In contrast to the conventional Wiener filter method with a time-invariant source covariance matrix (Dale and Sereno, 1993; Liu et al., 1998; Dale et al., 2000; Lin et al., 2006), we shall refer to the proposed approach as the “adaptive Wiener filter”, considering the time-variant source covariance matrix is derived in a data-driven manner.
In both computer simulation and experimental settings, we evaluated the performance of the proposed method, as opposed to the inverse solution based on the EEG alone (Hämäläinen and Ilmoniemi, 1984) and the fMRI-constrained inverse solution based on the Wiener estimation with a constant spatial prior (Liu et al., 1998; Dale et al., 2000). In our simulations, effects of both fMRI false positives and false negatives were investigated. The estimation accuracy under typical or complicated source temporal dynamics was also assessed. In our experimental investigation, the spatiotemporal cortical activity responding to a unilateral visual stimulus was imaged by using three algorithms in comparison, i.e. the minimum norm estimation (Hämäläinen and Ilmoniemi, 1984) based on the visual evoked potential (VEP) alone, or using the proposed adaptive Wiener filter and the conventional 90% fMRI weighted algorithm (Liu et al, 1998) based on both fMRI and EEG.
METHODS
Quantification of BOLD-fMRI signals
Since an fMRI experiment is often conducted in a block-design manner, we first derive a quantification method based on the BOLD-fMRI response evoked by a block of repeated stimuli, and then generalize the method to other experimental designs such as the event-related design.
Assume a single stimulus at time 0 evokes synaptic current sources s⃑(r,t) (where r indicates location in the brain and t indicates time) that last for a very short period Ts typically ranging from several tens to several hundreds milliseconds. Then the source activity evoked by a block of N stimuli, denoted as g⃑(r,t), can be written as Eq. (1).
| (1) |
where δ(t) is a delta function, TISI is the inter-stimulus-interval (ISI) and * denotes convolution. Eq. (1) is valid when the ISI is longer than the neuronal refractory period. It is particularly so in most ERP studies, in which the ISI is designed to be even longer than Ts in order to ensure that the electrical activity responding to preceding stimuli recovers to the resting state (or the baseline) before the response to next stimulus is elicited.
Assume the induced BOLD-fMRI response f(r,t) relates to the power of local synaptic current by a linear system that is characterized by the hemodynamic impulse response function (HRF) h(t), plus noise. Such a linear system is illustrated in Fig. 1 and mathematically expressed as Eq. (2) to Eq. (4):
| (2) |
| (3) |
| (4) |
where g(r,t) and s(r,t) are the magnitudes of g⃑(r,t) and s⃑(r,t) respectively, fs(r,t) is the “signal” part of the fMRI response and fn(r,t) is the “noise” part.
Figure 1.
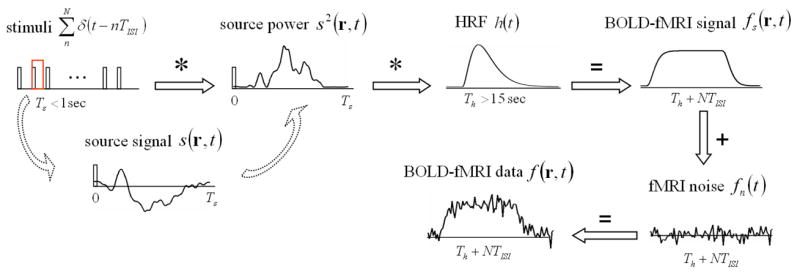
Illustration of the linear system that describes the relationship between electrophysiological signals and BOLD-fMRI responses under a train of repeated stimuli. See the detailed description in the text.
In terms of describing the relationship between the neural activity and the BOLD fMRI response, the model being assumed as Eq. (2) is similar to a linear transform model that serves as the theoretical core of the widely used fMRI statistical parametric mapping (Friston et al, 1994; Boynton et al, 1996; Dale and Buckner, 1997). It should be noted that here we input the neural activity assessed by the power of synaptic current flow to the linear system (i.e. HRF) (Logothetis et al., 2001; Wan et al., 2006; also see Introduction), instead of using the stimulus function.
Note that Eq. (3) can be re-organized as Eq. (5):
| (5) |
We define a predictor signal p(t) as Eq. (6).
| (6) |
Then, Eq. (5) can be further re-written as Eq. (7) and Eq. (8).
| (7) |
| (8) |
Since the hemodynamic impulse response h(t) evolves much slower than the electrophysiological impulse response, it keeps approximately constant over the duration of the electrical source signal evoked by a single stimulus. Mathematically, we assume p(t) ≈ p(t − τ) for 0 ≤ τ ≤ Ts. Then Eq. (8) can be simplified as Eq. (9)
| (9) |
We define β(r) as Eq. (10) and re-write Eq. (9) as Eq. (11)
| (10) |
| (11) |
For a time series of fMRI response with Nf discrete samples over time, it immediately follows from Eq. (4) and Eq. (11) that an over-determined linear regression model can be described using a vector notation as Eq. (12).
| (12) |
where F(r) = [f(r,1) f(r,2)… f(r, Nf]T and Fn(r) = fn(r,1) fn(r, 2)… fn(r, Nf)]T are a vector of the fMRI time series and its “noise” part respectively, and P = [p(1) p(2)… p(Nf)]T is a vector of the predictor signal.
Based on Eq. (12), the minimum least-squares estimate of β(r), denoted as β̂(r), can be computed from Eq. (13)
| (13) |
As expressed in Eq. (13), β̂(r) is a quantity that exclusively depends upon the BOLD response, the experimental protocol and the hemodynamic impulse response function. More importantly, β̂(r) can be interpreted, by the definition of β(r) in Eq. (10), as an estimate of the time integral of current source power over the period of Ts. This interpretation is meaningful in the context of electrical source imaging and is explicitly used later when incorporating the fMRI into solving the EEG inverse problem.
The above method can also be applied to the quantification of the event-related fMRI response, simply by changing the predictor function in Eq. (6) to Eq. (14).
| (14) |
The above method can be further generalized to more complicated experimental designs with multiple or mixed tasks. Correspondingly, multiple predictor functions need to be defined by convolving the mathematically expressed experimental protocol with the HRF. If the quantification of BOLD responses has a multivariate nature, the regression parameters should be defined for each stimulus or task independently. And we can set up a general linear model (GLM) (Friston et al., 1995) similarly as Eq. (12) and compute the regression parameters using a multivariate linear algorithm.
EEG inverse problem of cortical source imaging
As originally proposed in (Dale and Sereno, 1993), the EEG source space is constrained to a realistically-shaped cortical surface extracted from high-resolution T1-weighted magnetic resonance (MR) images. For the source modeling, the folded cortical surface can be extracted from the segmented boundary between the gray matter and the white matter. The cortical current density distribution is modeled by thousands of current dipoles evenly placed on the folded cortical surface, and the orientation of each dipole is constrained to be perpendicular to the local cortical patch (Dale and Sereno, 1993; Liu et al., 2006b). For the volume conductor modeling, the head model contains 3 compartments (scalp, skull and brain) and the electrical conductivity is assumed to be piece-wise homogeneous. After tessellating 3 surfaces that separate these compartments, the boundary element method (BEM) (Hämäläinen and Sarvas, 1989) can be employed to solve the EEG forward problem.
As a result, a transfer matrix A can be numerically computed to link the underlying current source distribution, s(t), to the recorded scalp potentials, x(t), under the existence of measurement noise, b(t), for every time instant t.
| (15) |
where A is a Nx-by-Ns matrix (Nx is the number of EEG sensors, Ns is the number of current sources), s(t) is a Ns-by-1 vector, x(t) and b(t) are Nx-by-1 vectors.
At any time instant, the spatial vectors s(t), x(t) and b(t) can be viewed as stochastic processes with their index sets over source or sensor locations. Assuming both s(t) and b(t) have zero means, we define the source auto-covariance matrix and the noise auto-covariance matrix as Eq. (16) and Eq. (17), respectively.
| (16) |
| (17) |
If a priori information is given to both Cs(t) and Cb(t), a linear inverse operator G(t) as Eq. (18) can be used to estimate s(t) from x(t), denoted as ŝ(t).
| (18) |
| (19) |
In practice, the noise covariance matrix, Cb(t), can be estimated directly from the EEG data (Fuchs et al., 1998), whereas a priori knowledge of Cs(t) is usually unavailable and hence it is typically assumed to be proportional to an identity matrix (Hämäläinen and Ilmoniemi, 1984) or a spatial Laplacian operator (Pascual-Marqui et al., 1994). It has also been demonstrated that the Wiener filter in Eq. (18) has an equivalent formulation of weighted minimum norm (Hauk, 2004; Liu et al., 2006a).
It is worthwhile to emphasize that in the Wiener filter formulation as Eq. (18), the stochastic process is referred to the spatial domain instead of the time domain and the source covariance matrix is accordingly assumed to be time-variant.
fMRI-EEG integrated adaptive Wiener filter
Assuming there is no a priori cross-correlation between different source locations, the time-variant source covariance matrix can be expressed as a diagonal matrix as Eq. (20).
| (20) |
Recall that, at any source location, the quantification of BOLD-fMRI response as previously described represents an estimate of the time integral of source variance (see definition in Eq. (16)) over the ERP time period. Therefore, we introduce the fMRI-derived spatial constraints to the sum of source variances, as expressed by Eq. (21).
| (21) |
where β̂i is the quantified fMRI response at the i-th source location.
However, Eq. (21) alone is insufficient to obtain the time-variant source covariance matrix at every time instant. The reason is obvious because the temporal variation of source variance cannot be resolved by fMRI due to its lack of temporal resolution.
We further use a data-driven approach described as below to retrieve the temporal variation of the source variances based on the segmented EEG data before response averaging. This approach is based on a common practice in ERP experiments that the electrical response is repeatedly induced by a train of stimuli (or tasks). The EEG response in each repetition is referred to as an epoch that is usually time-locked to the onset of the stimulus.
Denote x(t,k), s(t,k) and b(t,k) as the random column vectors of EEG recordings (Nx-by-1), source signals (Ns-by-1) and measurement noise (Nx-by-1) at the time t and in the k-th epoch. A valid assumption is that source signals in different epochs represent independent observations of the identical stochastic process, s(t), for any specific time t, as illustrated in Fig. 2. Accordingly, we can compute an inverse estimate of the instantaneous source auto-covariance if the number of epochs is sufficiently large.
Figure 2.
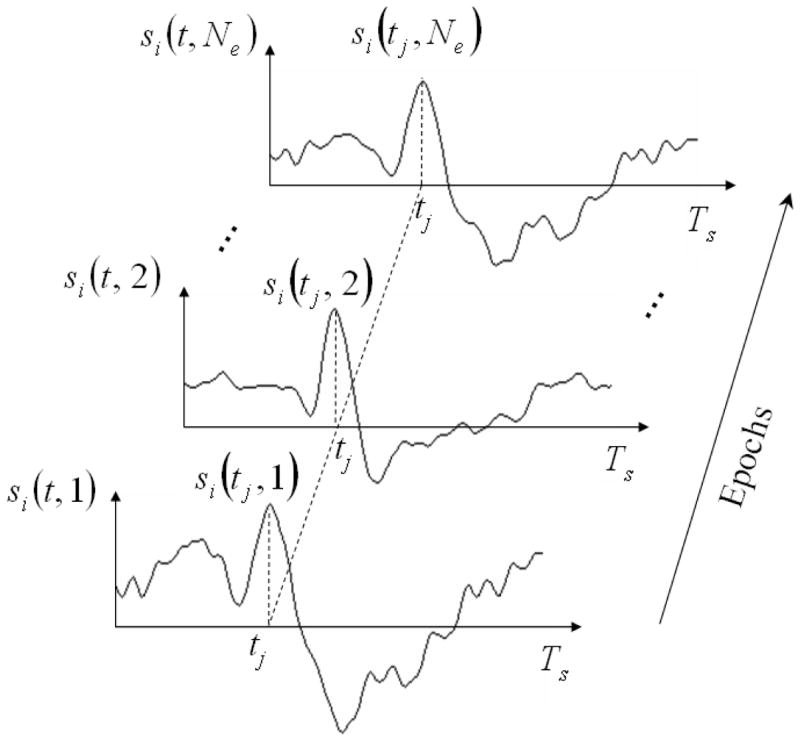
The source signal at any i-th location si(t) is not a stationary stochastic process over time, but its values at any give time tj sampled in different epochs are i.i.d. Therefore s(t,k), for 1 ≤ k ≤ Ne, represents an independent observation of a stochastic process s(t) for each individual time t(note that s(t) is a stochastic process with its index sets over source locations).
By collecting signals at the time t from all Ne epochs, we define Eq. (22) to (24):
| (22) |
| (23) |
| (24) |
Then, we re-write the forward model in Eq. (15) in a matrix notation as Eq. (25).
| (25) |
The singular value decomposition (SVD) of X(t) is written as Eq. (26)
| (26) |
where Nq = min(Nx,Ne ), the singular vector Uq(t) is the q-th column vector in the matrix U(t) that represents a spatial component of scalp potentials at the time t, the singular vector Vq(t) is the q-th column vector in the matrix V(t) that represents the variation (over epochs) of the corresponding spatial component Uq(t).
We truncate the spatial components that do not satisfy the discrete Picard condition (Hansen, 1990), since the truncated spatial components are not sufficiently smooth to be associated with any source activity and hence are dominated by noise perturbation.
After the truncation, we compute the maximum likelihood estimates (MLE) of distributed sources that account for each of the Q remaining spatial components, written as Eq. (27).
| (27) |
where s̃q(t) is an Ns-by-1 vector that represents the estimated source distribution underlying the q-th spatial component Uq(t) at the time t, and the regularization parameter rq can be obtained by using the “L-curve” method (Hansen, 1992).
Combining the MLE for all Q components, we can obtain a set of source estimates for the time t in all Ne epochs, collectively denoted as S̃(t).
| (28) |
where S̃(t) is an Ns-by-Ne matrix with each row representing the variation of estimated source signals over epochs.
Following the definition in Eq. (16), the variance of source estimates at the i-th location for the time t, denoted as σ̃i(t), can be written as Eq. (29).
| (29) |
where S̃i(t) is the i-th row vector in the matrix S̃(t).
Substitute S̃(t) by Eq. (28) and re-write Eq. (29) as Eq. (30).
| (30) |
Since and for any p ≠ q, Eq. (30) can be simplified as Eq. (31).
| (31) |
Repeat the above procedures for all the time points during the period Ts, a time course of source variance estimates can be computed for every source location i, collectively denoted as a vector σ̃i as Eq. (32).
| (32) |
Clearly, Eq. (32) contains the temporal information regarding the variation (over time) of the source variance inversely estimated from the EEG epochs, and Eq. (21) represents the spatial information regarding the time integral of source variance as quantified from independent fMRI measurements. Combining Eq. (32) and Eq. (21), we derive the prior estimates of source variance from both fMRI and EEG data, as expressed by Eq. (33).
| (33) |
Once σi(t) is calculated for every source location i and every time point t, it becomes immediately straightforward to compute the time-variant source covariance matrices based on Eq. (20) and estimate the cortical source distribution based on Eq. (18) and Eq. (19) for every time point individually. Qualitatively speaking, a larger value of source variance at a specific location means that the inverse solution is more preferentially located at that location.
In contrast to the conventional Wiener filter approach (Liu et al., 1998; Dale et al., 2000) based on time-invariant spatial constraints, the method described as above is called the “adaptive Wiener filter” in the sense that the time-variant source covariance matrix is derived from the combination of fMRI and EEG in a data driven manner.
Computer simulations
The performance of the proposed method was evaluated in a series of computer simulations. The simulation setting was based on a realistically-shaped head volume conductor and cortical surface models that were constructed from high resolution T1-weighted MR images of a human subject (256 slices, matrix size: 256×256, voxel size: 1×1×1 mm3). The electrical conductivities of the scalp, skull and brain were set to be 0.33, 0.0165, and 0.33 S/m, respectively (Lai et al, 2005; Oostendorp et al, 2000; Zhang et al, 2006). The cortical current density source model consisted of around 7,000 current dipoles evenly placed on the cortical surface. 128 electrodes with a standard montage were co-registered to the boundary element head model. Fig. 3 shows the head model, cortical surface model and the electrodes used in the simulation setting.
Figure 3.
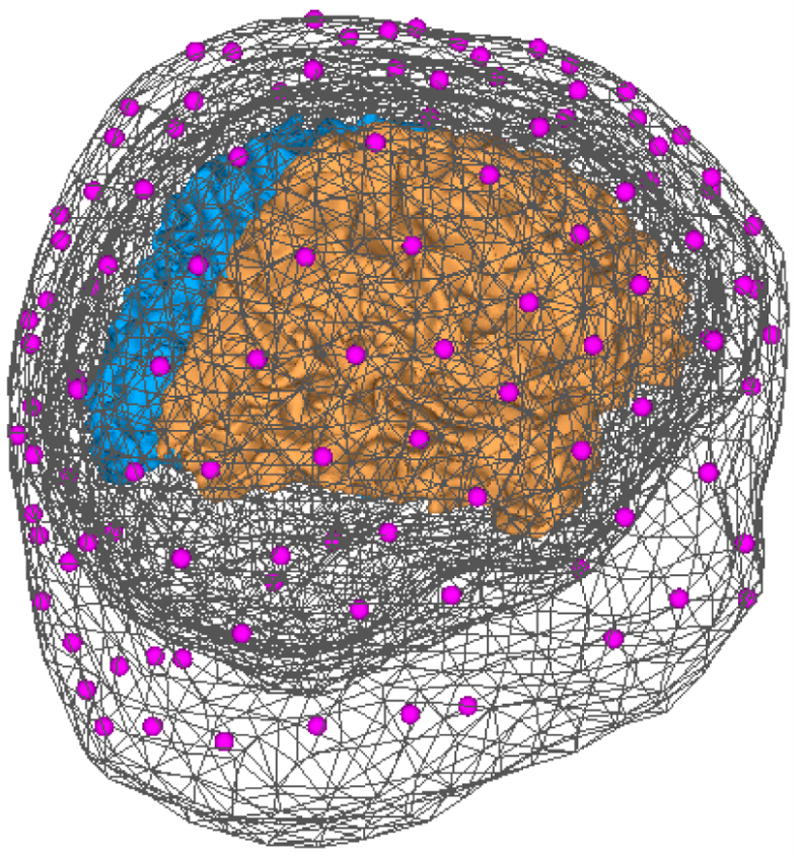
Realistic cortical source model and head volume conductor model. The head model consists of 3 triangulated boundary meshes (shown in dark gray). 128 electrodes (shown in purple) are coregistered to be over the scalp surface. The cortical source model is on the folded cortical surfaces (the left hemisphere shown in blue and the right hemisphere shown in brown).
Based on the above settings, we simulated current source signals, BOLD fMRI signals and EEG recordings. We computed the inverse solutions from the simulated data using three algorithms. The detailed procedures are described step by step as follows.
1) Current source activities. 3 current dipoles were placed on 3 selected locations on the folded cortical surface. To simulate the source activity, representative waveforms were assigned to these dipole sources such that the source signals were simulated to be temporally uncorrelated or correlated, or to be transient or sustained, or to have the same frequency but different phases or the same phase but different frequencies, or to have time courses obtained in a real experiment.
-
2) BOLD-fMRI responses. The BOLD-fMRI signals were generated from the simulated current sources. The source waveforms were repeated every 500 ms for a total of 30 s. For each source location, the BOLD signal was simulated by convolving the time course of source power with a gamma-function HRF suggested by (Boynton et al., 1996), written as Eq. (34).
where n = 3, τ = 1.25 sec and ε = 2.5 sec as in the default settings of a widely used fMRI analysis software - BrainVoyager QX (BrainInnovation, Netherlands).(34)
The spatial distribution of the simulated BOLD signals was then convoluted with a gaussian spatial kernel with a given full-width-half-maximum (FWHM). Here the FWHM was chosen to be 4 mm, which represented a reasonable value consistent with the known spatial resolution of fMRI according to previous experimental studies (Engel et al., 1997). Gaussian white noise (GWN) was added into the simulated BOLD time courses so that the BOLD response had a signal-to-noise ratio (SNR) equal to 10.
3) EEG recordings. From the simulated spatiotemporal current source distributions, we further simulated scalp EEG signals at 128 electrodes using the BEM-based forward calculation (Hämäläinen and Sarvas, 1989; He et al., 1987). 250 trials of EEG data were simulated as the summation of the forward solution and GWN. The SNR in each trial was around 0.6 and the ERP signal averaged from all the trials had a SNR equal to 10.
4) Source imaging. Finally, we reconstructed the spatiotemporal source distribution based on the simulated EEG alone using the minimum-norm algorithm (Hämäläinen and Ilmoniemi, 1984), or based on both the simulated fMRI and EEG using time-invariant (Liu et al., 1998; Dale et al., 2000) or time-variant spatial constraints (as proposed in this paper).
Visual Stimulation Experiment
To assess the applicability of the proposed adaptive Wiener filter algorithm, we also employed real fMRI and EEG data collected during a preliminary experiment with a unilateral checkerboard visual stimulus.
The experiment was conducted with a healthy subject (male, age 22) under the approval of the institutional review board (IRB) at the University of Minnesota. Informed consent was obtained from the subject before the experiment. The experiment included 2 separate sessions with the identical visual stimuli for the EEG and fMRI data collection respectively. The visual stimulation was a rectangular checkerboard within the lower left quadrant of the visual field; the checkerboard pattern was reversed at 2 Hz. In the EEG experiment, 6-second breaks without stimulation were randomly inserted into the otherwise 4-minute continuous visual presentation, such that the subject had a break about every 20 seconds on average to avoid the neural adaptation. In the fMRI experiment, the visual stimuli were presented in six 30-second blocks separated by seven 30-second resting blocks without stimulation. The stimuli delivered through a DLP projector were back-mirrored to the subject inside the MRI scanner. For both EEG and fMRI experiments, the subject was instructed to always gaze at a central fixation point.
The EEG signals collected from a 64-channel system (BrainAmp MR 64 plus, BrainProducts, Germany) with a 1000-Hz sampling rate were sequentially subject to the ocular artifact rejection, band-pass filtering (0.3 – 40 Hz), segmentation with respect to the stimulus onsets, pre-stimulus baseline correction, linear trend removal. After these preprocessing steps, the data in 380 segmented epochs was averaged to yield the visual evoked potentials (VEP). The anatomical MRI and fMRI data were collected in a 3-T MRI system (Siemens Trio, Siemens, Germany). The whole-head T1-weightd MR images (matrix size 256×256, 1mm slice thickness) were acquired using the Turboflash sequence (TR/TE = 20 ms/5 ms). The T2*-weighted fMRI data was acquired from 16 axial slices (matrix size 64×64, 5mm thickness) covering the visual cortex using the echo planar imaging (EPI) sequence (TR/TE = 1000 ms/35 ms). The MRI and fMRI data were analyzed using BrainVoyager QX (Brain Innovation, Netherlands). The EPI volumes underwent several preprocessing steps including three-dimensional motion correction, slice scan time correction and linear trend removal. Then, the fMRI data was aligned with the anatomical MR images. The fMRI activation map was obtained by statistical analysis using a general linear model (Friston et al., 1994).
Three cortical current density imaging algorithms were applied to image the cortical responses on the hemisphere (right) contralateral to the stimulation (left). The 90% fMRI-weighted Wiener estimation (Liu et al., 1998; Dale et al., 2000) and the proposed algorithm used both EEG and fMRI data, whereas the minimum-norm algorithm used the VEP data lone.
RESULTS
BOLD-fMRI simulation and quantification
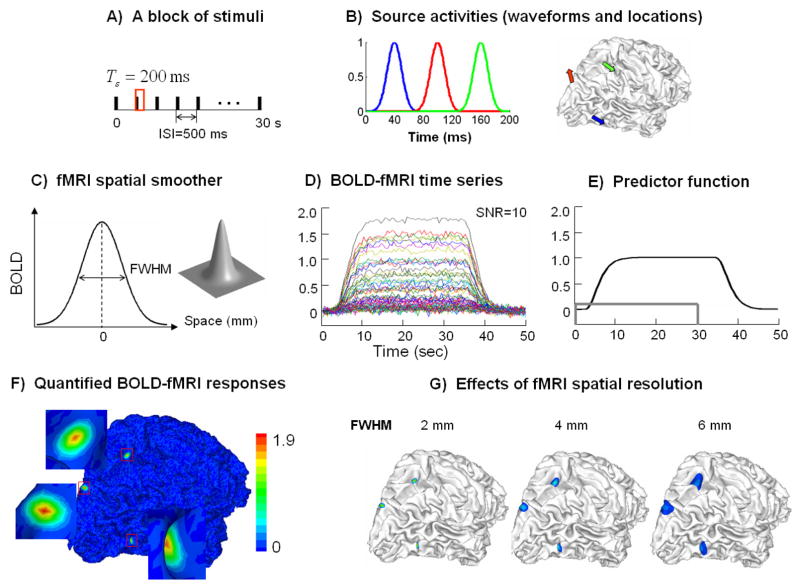
Fig. 4 shows the simulated BOLD fMRI signals and the quantified fMRI maps. The simulated fMRI responses were induced by a 30-sec block of stimuli with an ISI of 500 ms (Fig. 4.A). The electrical current sources were located at the lateral occipital sulcus (blue), the medial occipital dorsal area (red) and the intraparietal sulcus (green) on the right hemisphere (Fig. 4.B, right). Representative source locations were selected to be within the sulcal fundus, the sulcal wall and the gyral crown, respectively. The source waveforms shown in corresponding colors were simulated as 3 temporally uncorrelated gauss functions (Fig. 4.B left). After applying a 2-D spatial gauss smoother with a given FWHM (Fig. 4.C), the simulated BOLD responses emerged within 3 extended regions. The noise-contaminated fMRI signals surrounding the “red” source are plotted in Fig. 4.D). These time courses had a similar shape as the predictor signal (Fig. 4.E) such that they could be fitted with the predictor signal simply after scaling. The quantified fMRI response at each cortical location was precisely the scaling factor that allowed for the best fit between the scaled predictor signal and the measured BOLD response. This scaling factor was also found approximately proportional to the averaged BOLD signal change at the steady state with stimuli relative to the resting state without stimuli.
Figure 4.
A) Stimulation protocol, B) current source waveforms evoked by a single stimulus and the source locations on the cortex; the 3 sources are indicated by different colors, C) a gauss function describing the spatial resolution of fMRI, D) simulated BOLD-fMRI time series at SNR=10, E) the predictor signal (the unfilled gray box indicates the duration of the stimulation block), F) the map of quantified fMRI responses, G) the quantified fMRI map with different fMRI spatial resolutions as described by the FWHM (2, 4, 6 mm).
The map of quantified fMRI responses is shown in Fig. 4.F). Three activated regions were revealed. The extent of these regions depended upon the fMRI spatial resolution (or specificity), which was inversely proportional to FWHM. With an increasingly larger FWHM, the fMRI response extended from a point source to a larger region, in which the quantified values of fMRI responses became gradually smaller than the time integral of corresponding source powers (Fig. 4.G). According to Eq. (33), the time-variant spatial constraint at any specific cortical location is proportional to the quantified fMRI response. Therefore, the observed effect of FWHM also implies that the lower specificity of fMRI give rises to weaker fMRI constraints to the EEG inverse solution.
Time-variant spatial constraints
Fig. 5 illustrates an example of probing the temporal change of source variance based on the segmented EEG epochs. To simplify the illustration, let us look closely at a period of time while a single source is activated.
Figure 5.
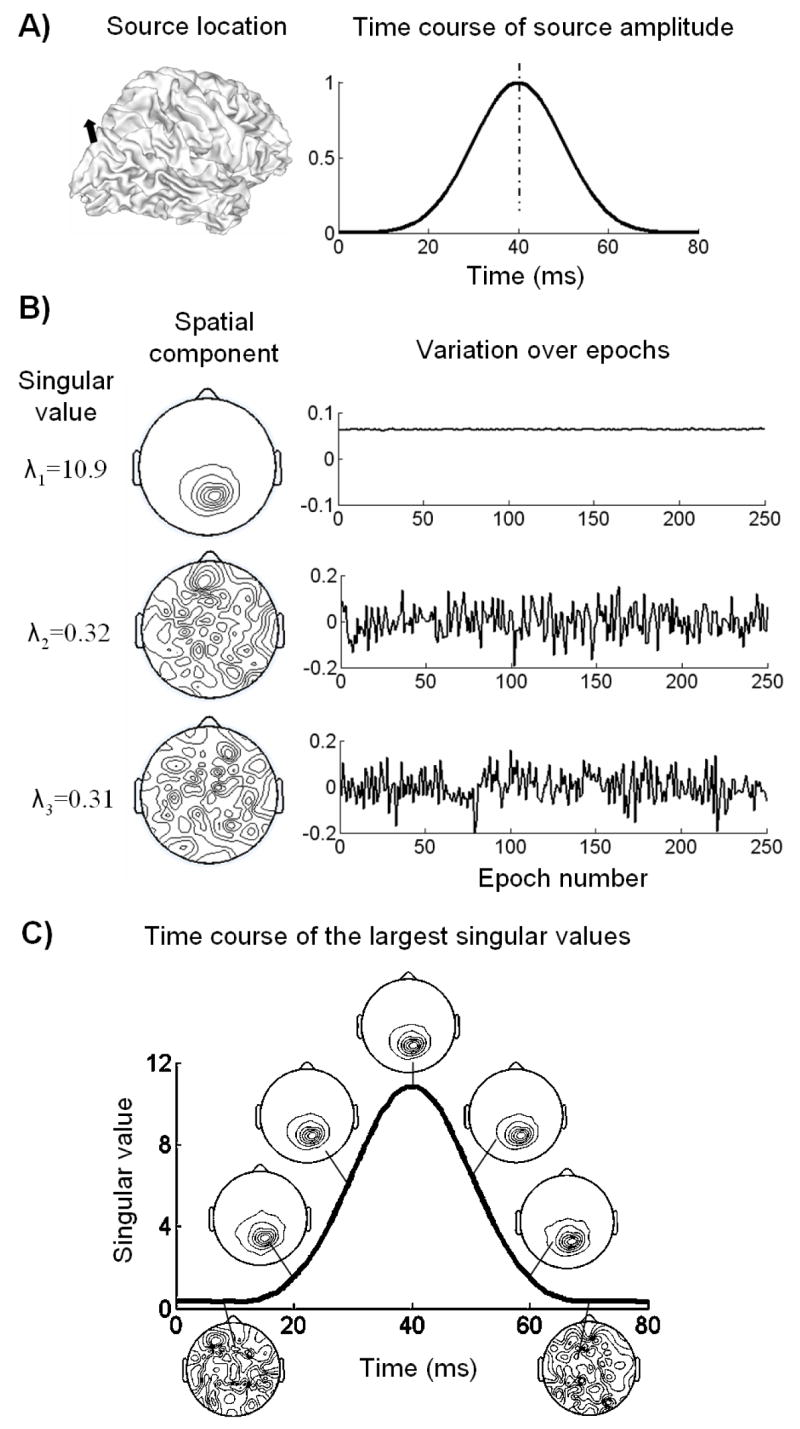
An example of the SVD analysis on the segmented epochs. A) The EEG data was simulated from a single source activity, with the source location on the cortex shown on the left and the source waveform shown on the right; B) the largest 3 SVD components of the data at the peak latency (40 ms) over all the epochs. The singular values are shown in the left column, the decomposed spatial components shown in the middle and the corresponding variations over epochs shown in the right; C) the plot of the largest singular value as a function of time; the spatial components associated with the largest singular value at 7 representative time points are displayed along the plotted time course.
The source location and waveform is displayed in Fig. 5.A). Since the ERP signal after response averaging had a SNR of 10, the EEG data in every epoch had an average SNR of 0.6. Fig. 5.B) shows the SVD components obtained from the data at the 40-ms latency in all the epochs. Only 3 components with largest singular values are shown. The singular value for the first decomposed component was found to be much larger than those for the second and third components. Clearly, the first spatial component1 more likely represented the scalp potential field generated by internal brain sources, whereas the second and third spatial components attributed to external recording noises. The first temporal component2, which reflected the variation of the global field strength over epochs, had a DC offset with small variation. However, dramatic oscillations around 0 were observed in the second and third temporal components. Based on these observations, we inferred that the first SVD component contained the scalp potential field arising from the source activity at 40 ms, as well as its variation over epochs. Applying the discrete Picard condition also ended up with the same conclusion that only the first component at this time instant satisfied the Picard condition while all other components should be truncated.
For a better understanding of this conclusion and its implication, it is worthwhile to mention an important feature of SVD. With the singular value gradually decaying from its maximum value toward zero, both the left and right singular vectors necessarily tend to have more and more oscillations. Therefore, if the signal is less variable over epochs than the noise, which are the case in practical ERP studies, then the SVD component(s) with the largest singular value(s) mostly reflect the variance of source activities instead of that of the noise. On the other hand, these components also tend to be spatially smooth and more likely to satisfy the Picard condition. Accordingly, the DC line shown in Fig. 5.B) indicates that the source signal at 40 ms is repeated over epochs with little variation.
After repeating the SVD analysis to every time instant, we plotted the largest singular value as a function of time shown in Fig. 5.C). For several representative time points (from 10 to 70 ms stepped by 10 ms), the corresponding first spatial component was also displayed along the plotted time course. The source amplitudes at 10 and 70 ms were very small as shown in Fig. 5.A). The decomposed spatial components at these 2 latencies also appeared to be too noisy to satisfy the Picard condition. At other selected time points, the spatial patterns appeared to be similar and the resultant inverse solutions of these spatial patterns should also be spatially consistent to each other. These results demonstrate that the spatial component(s) with largest singular value(s), if satisfying the Picard condition, reflect the potential fields projected from the source space to the sensor space and contain the information on where the source is most likely located at the latency of interest.
By comparing Fig. 5.C) with Fig. 5.A), we also noticed that the temporal change of largest singular values was in general agreement with the time course of the real source amplitude. This finding further supported our previous argument that the principal SVD components nicely isolated the signal from the noise.
While the spatial component(s) with largest singular value(s) indicate the source locations at different latencies, the time course of largest singular values represents the temporal variation of source amplitude. In addition, the decomposed spatial components had the field strength equal to 1 because the singular vectors were always unitary vectors. According to Eq. (27) and Eq. (31), the absolute amplitudes of source estimates for the principal SVD components should be proportional to the largest singular values. Therefore, the similarity between Fig. 5.A) and 5.C) further justify the plausibility of estimating the time-variant source variance from the segmented epochs.
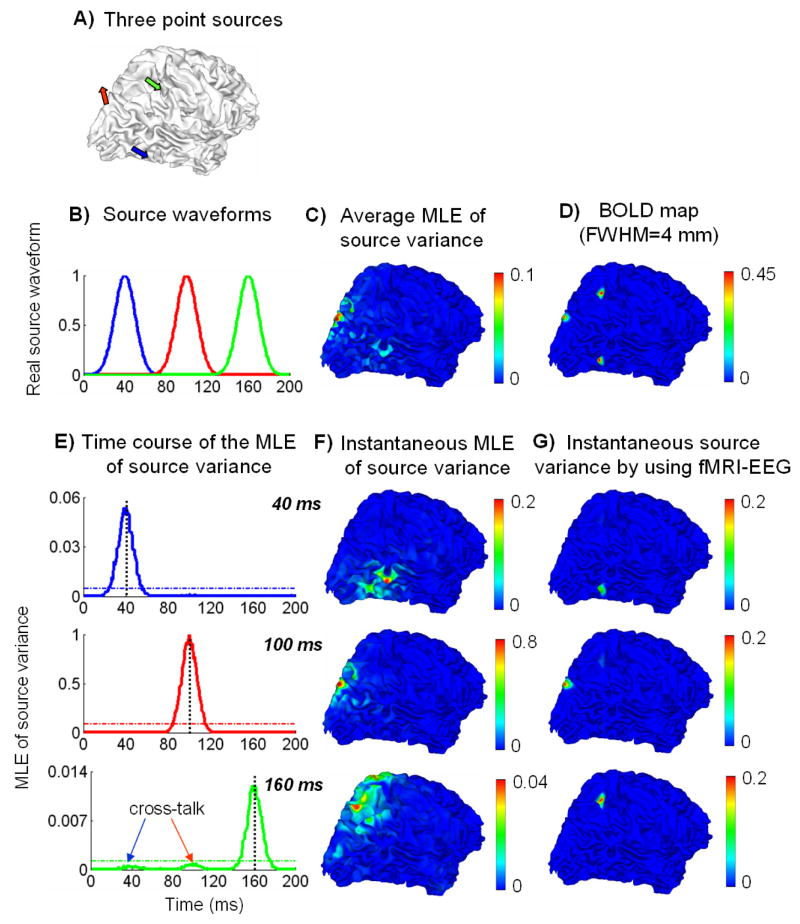
To assess the accuracies of the estimated time-variant source variances in both time and space, Fig. 6 summarizes the results of source variance estimation based on the EEG or the combination of fMRI and EEG. The source configuration and stimulation protocol used here were identical as in Fig. 4. 3 temporally uncorrelated (Fig. 6.B) sources were selected from the cortex (Fig. 6.A) to generate the BOLD fMRI and EEG signals. The quantified fMRI map with a 4-mm FWHM is shown in Fig. 6.D).
Figure 6.
A) Source locations, B) source waveforms, C) the spatial distribution on the cortex of the average MLE of source variance averaged over the entire time period, D) the map of quantified BOLD fMRI responses, E) the time courses of the MLE of source variances at three source locations respectively, F) the instantaneous cortical distributions of the MLE of source variances at 3 peak latencies (40, 100 and 160 ms) identified from E), G) the instantaneous cortical distributions of time-variant source variances derived from combination of fMRI and EEG at the 3 peak latencies.
The MLE of source variances were computed from the segmented epochs. Fig. 6.E) plots the time courses of the source variance MLE at each of 3 source locations respectively. The shape of these time courses agreed with the corresponding source waveforms with mild distinction. The maximal source variance MLE arrived at exactly the same latencies (40, 100 and 160 ms) as the real source activities. 2 “bumps” were observed in the estimated time course of the “green” source, which was caused by the cross-talks in the inverse solution from the “blue” and “red” sources respectively. However, the absolute values of the estimated source variances tended to be much smaller than those of the real source signals, except for the “red” source which was located at the gyral crown.
Fig. 6.F) shows the spatial distribution of the source variance MLE at 3 peak latencies (40, 100 and 160 ms) identified from Fig. 6.E). From the segmented EEG, the estimated map of source variances clearly spread out and the spatial maximum was not correctly localized to the original location of the source that was activated at the corresponding time instant. Fig. 6.C) shows the spatial distribution of the mean MLE of source variance averaged over the entire time period. This spatial distribution is qualitatively consistent with the quantified fMRI map (Fig. 6.D), although Fig. 6.C) exhibits spatial ambiguities and biases.
All these results based on the EEG alone demonstrate that the temporal change of source variances could be well retrieved from the segmented EEG epochs, but the absolute values of source variance were usually underestimated or significantly biased due to the ill-posed nature of the EEG inverse problem.
We further derived a set of time-variant spatial constraints by combining the “static” constraint from the fMRI and the “dynamic” constraint from the EEG based on Eq. (33). Fig. 6.G) shows the spatial distribution of the fMRI-EEG derived source variances at 3 peak latencies. In contrast to Fig. 6.D), Fig. 6.G) provided more accurate spatial prior constraints for each of 3 latencies respectively than the time-invariant spatial constraints based on the fMRI alone. The fMRI false-positives that occurred in the time-invariant fMRI constraints were successfully excluded from affecting the subsequent inverse solution. As opposed to Fig. 6.F), Fig. 6.G) also provided more localized and accurate prior constraints than those based on the EEG alone, by taking advantage of the high-spatial resolution of fMRI.
fMRI-EEG integrated source imaging with fMRI false positives
Following the example used in Fig. 6, we further imaged the cortical current density distribution at 3 peak latencies (40, 100 and 160 ms) using 3 algorithms: the proposed adaptive Wiener filter, the Wiener estimation using a time-invariant fMRI constraint and the minimum-norm estimation based on the EEG alone. Fig. 7.A) shows the reconstructed current density visualized on the cortical surface. Obviously, the use of time-variant spatial constraints in the adaptive Wiener filter algorithm resulted in the most accurate imaging results among all 3 algorithms. As shown in the top row in Fig. 7.A, 3 focal sources were revealed at each of 3 latencies respectively without showing any interference among them, in agreement with the fact that all 3 sources were temporally uncorrelated. The conventional Wiener filter also identified 3 sources with high spatial resolutions, benefiting from the use of fMRI spatial constraints. However, spurious sources were clearly observed at 40 ms and 100 ms. On the other hand, the minimum-norm solution without using any fMRI constraint had a low spatial resolution as often experienced in the EEG (or MEG) source imaging.
Figure 7.
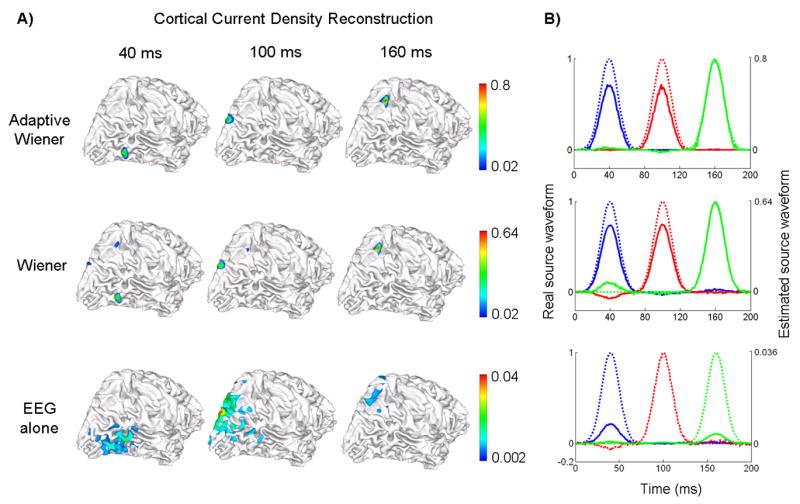
Source distribution reconstruction and source waveform estimation under fMRI false positives. The source locations and simulated source waveforms are the same as used in Fig. 6. A) Reconstructed cortical current density distribution at 3 peak latencies (40, 100 and 160 ms) shown in 3 columns, by using 3 different algorithms: the adaptive Wiener filter (1st row), the conventional Wiener filter using time-invariant spatial constraints (2nd row) and the weighted minimum norm based on the EEG alone (3rd row); B) Estimated source waveforms at each of 3 source locations color-coded as in Fig. 6. The estimated waveforms are shown in solid lines and the simulated original waveforms are shown in dashed lines. The 3 rows also correspond to 3 algorithms as in Fig. 7.A).
The time courses of source estimates at these 3 source locations using different algorithms are plotted (in solid lines) in Fig. 7.B) in comparison with the real source waveforms (in dashed lines). Note that the real and estimated waveforms are plotted in different scales as indicated at the left and right axes respectively. Among all 3 algorithms, the source waveforms reconstructed by using the adaptive Wiener filter were the closest in both shape and absolute amplitude to the real source waveforms. The estimated time courses using the conventional Wiener filter were clearly more accurate than the minimum-norm solution; however compared to the adaptive Wiener filter, obvious positive and negative “bumps” were observed obviously at 40 ms and slightly at 160 ms, which were essentially because of the fMRI false positive priors that amplified the cross-talks among sources in the inverse solution.
fMRI-EEG integrated source imaging with fMRI false negatives
We further investigated the performance of the proposed adaptive Wiener filter approach in dealing with the fMRI missing sources (i.e. fMRI false negatives). Again, 3 sources were selected from the cortical surface (see Fig. 8.A). The source waveforms consisted of 2 gauss functions (for the “red” and “green” sources) that were temporally uncorrelated and a short-duration pulse (for the “blue” source) with smaller peak amplitude (see Fig. 8.C).
Figure 8.
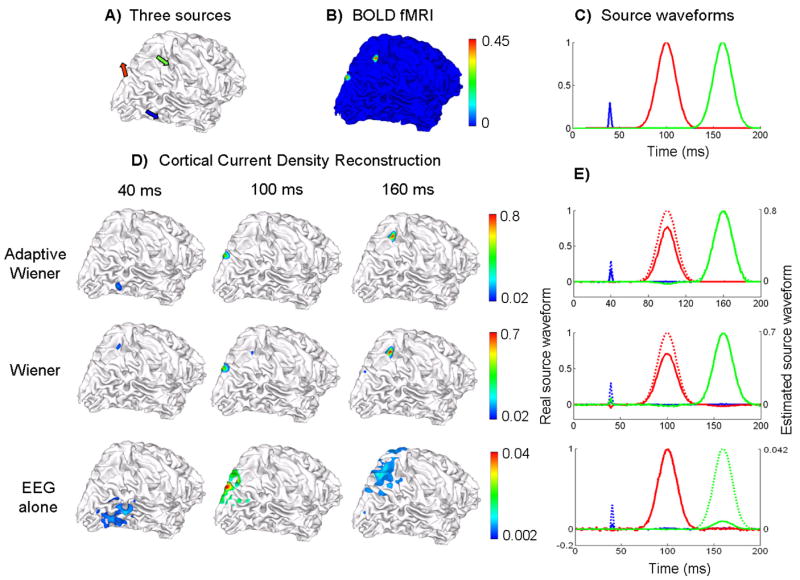
Source distribution reconstruction and source waveform estimation under fMRI false negatives. A) 3 source locations, B) quantified BOLD fMRI map, C) the simulated source waveforms, D) Reconstructed cortical current density distribution at 3 peak latencies (40, 100 and 160 ms) shown in 3 columns, by using 3 different algorithms: the adaptive Wiener filter (1st row), the conventional Wiener filter using time-invariant spatial constraints (2nd row) and the weighted minimum norm based on the EEG alone (3rd row); E) Estimated source waveforms at each of 3 source locations color-coded as in Fig. 8.C). The estimated waveforms are shown in solid lines and the simulated original waveforms are shown in dashed lines. The 3 rows also correspond to 3 algorithms as in Fig. 8.D).
Since the “blue” source had an almost transient and smaller activity that was insufficient to induce a large and sustained BOLD response, we could not identify this source from the map of quantified BOLD responses (Fig. 8.B) and hence the “blue” source behaved as an fMRI invisible source. This fMRI invisible source became problematic in the conventional Wiener estimation of current density. At 40 ms when the “blue” source was activated and reached its peak amplitude, the source activity at (or around) the “blue” source location could not be imaged, as shown in the middle row of Fig. 8.D). Instead, the spurious activity at an instantaneous fMRI false positive region (around the “green” source) was observed. At the other 2 latencies, spurious source activities with small amplitudes still emerged in the estimated current density distribution when the Wiener filter algorithm with a time-invariant spatial constraint was used.
Although the “blue” source was transient, the EEG-based source imaging could still detect this source activity due to the high temporal resolution of EEG. But again, the imaged source distribution had a low spatial specificity. By taking full advantage of the temporal information from the EEG, the adaptive Wiener filter could clearly image and localize the “blue” source activity at 40 ms, as well as the other 2 source activities at 100 ms and 160 ms respectively.
The superiority of the adaptive Wiener filter was further confirmed by its ability to estimate the waveforms of both fMRI visible and invisible sources. As shown in Fig. 8.E), only the adaptive Wiener filter approach could recover the transient source activity in the estimated source time courses, without sacrificing the estimation accuracies to other sustained source activities.
Reconstructing source activities with complicated temporal dynamics
To assess the applicability of the proposed adaptive Wiener filter approach to reconstructing the source activities with complicated temporal dynamics, we simulated 3 source activities with a variety of temporal features. These 3 sources were located at the same locations as in the previous stimulations. Then we compared the source waveforms estimated by using the adaptive Wiener filter approach (in solid lines) with the originally simulated source waveforms (in dashed lines). The results are summarized in Fig. 9.
Figure 9.
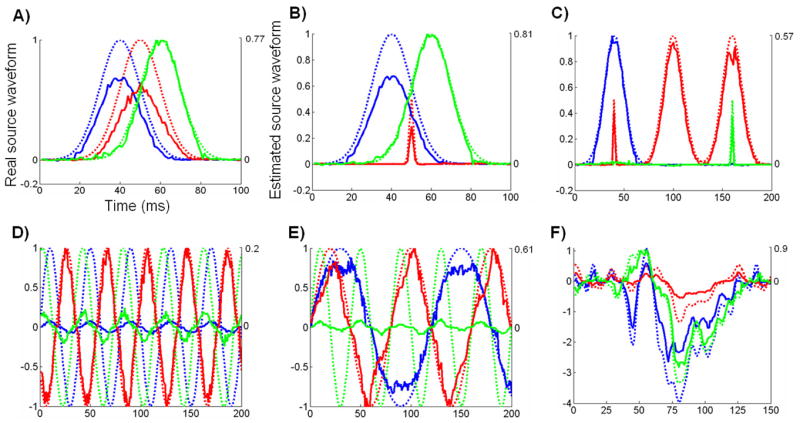
Estimated source waveforms compared to the real source waveforms with different temporal features. 3 sources locations are the same as in Fig. 8. The originally simulated waveforms are shown in dashed lines and the estimated source waveforms are shown in solid lines.
In Fig. 9.A), all 3 sources had gauss-function time courses that were overlapped over time. The shapes of the reconstructed source waveforms were close to gauss functions and the onset and peak latencies were also consistent with the simulated real source activities. However, slightly more fluctuations were observed in the reconstructed waveforms than in the real source waveforms.
In Fig. 9.B), a transient source activity (“red”) was included in addition to two overlapping gauss-function waveforms (“blue” and “green”). The “red” source was also an fMRI invisible source which occurred at the time point when both the other two sources were also active. In this situation, the time courses of both the fMRI visible and invisible sources were also well reconstructed.
In Fig. 9.C), the “green” source was a transient source temporally overlapping with a sustained “red” source. The “red” source also had a short-duration peak around the same time when the sustained “blue” source reached its peak amplitude. Clearly in this situation, both the fMRI false positives and false negatives existed with and without overlaps over time. Nevertheless, we could still estimate the source waveforms that were consistently accurate for both the sustained and transient source activities.
In addition, we simulated 3 rhythmic activities that had the same frequency but different phases (Fig. 9.D) or the same initial phase but different frequencies (Fig. 9.E). In both situations, the frequency and phase information were well reflected in the estimated source waveforms without significant distortion, whereas we also observed distinctions in absolute amplitudes between the estimated and real source waveforms
In Fig. 9.F), we simulated the source activities by using the “realistic” dipole source waveforms estimated from a real ERP data set acquired in a visual experiment. In this case, the source activities had fairly complicated temporal features. The estimated source waveforms were highly correlated with the simulated real source waveforms, without loosing even detailed temporal dynamics.
The results in Fig. 9 all demonstrate good performances of the proposed adaptive Wiener filter algorithm to accurately estimate the source activities with a high temporal resolution, based on simulated fMRI and EEG data.
Experimental results
In response to the unilateral visual stimulation (Fig. 10.A), the activated cortical areas at the contralateral hemisphere were revealed in the fMRI activation map (Fig. 10.B). The fMRI activation map indicated a dorsal visual pathway covering V1, V2, dorsomedial areas (such as V3 and V7), intraparietal sulcus (IPS) as well as medial temporal (MT) area (also known as V5). The top row of Fig. 10.C shows the time course of global field power of VEP, which indicates three VEP peak latencies (76, 112 and 212 ms). The 2nd through 4th rows of Fig. 10.C show the reconstructed contralateral CCD distribution using three imaging algorithms, respectively. From the CCD images reconstructed by only using the VEP data, the dorsal pathway was seen gradually extending from lower-tier visual areas to high-tier visual areas. By using our proposed adaptive Wiener filter to integrate the fMRI and EEG data, a consistent sequence of activities was observed with a much enhanced spatial resolution, showing the pathway starting from V1/V2 and then V3/V3a and finally V5/V7 and IPS. The observed cortical visual pathway was generally in agreement with the well-known hierarchical organization of the visual system (Felleman and Van Essen, 1991). In contrast, the imaging results obtained by using the conventional 90% fMRI-weighted approach also had an improved spatial resolution compared to the EEG-alone source imaging. However, it imposed a false positive source region in and around V1/V2 at the latency of 212 ms, whereas a more likely high-tier EEG source around V5 observable from the EEG data was missed.
Figure 10.
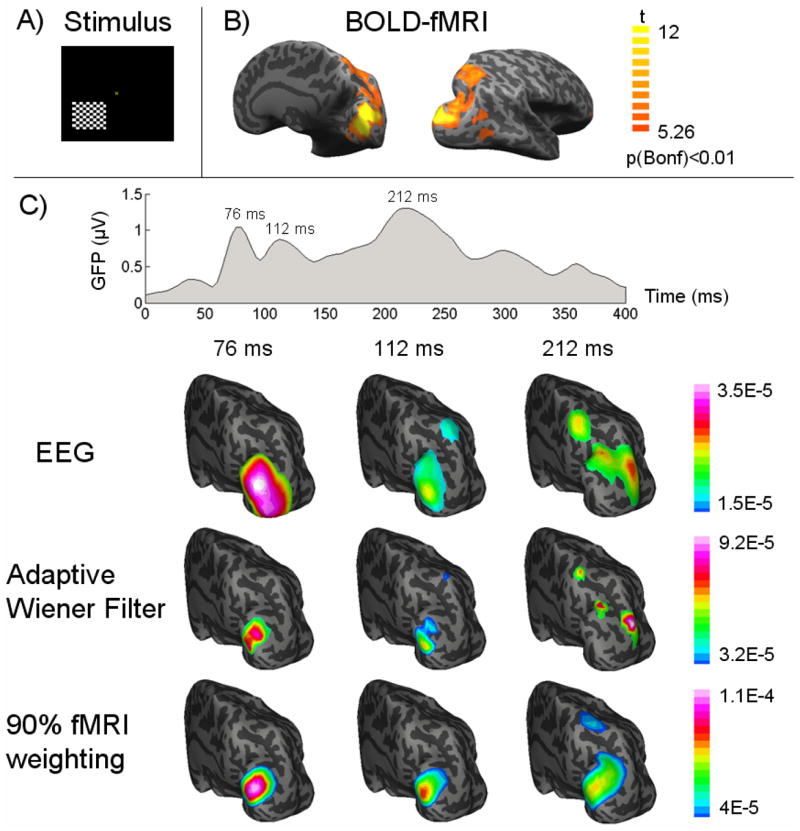
A) The pattern-reversal checkerboard visual stimulation, B) fMRI activation map with a corrected threshold p<0.01, and C) the global field power of VEP and the dynamic cortical source distribution at three VEP latencies (76, 112, 212 ms after the visual onset) imaged from EEG alone (1st row), or fMRI-EEG integration using our proposed adaptive wiener filter (2nd row) and the conventional 90% fMRI weighted algorithm (3rd row). Both the source images and the fMRI activation map are visualized on an inflated representation of cortical surface.
DISCUSSION
The proposed adaptive Wiener filter method on the fMRI-EEG integration significantly differs from the existing methods in two important aspects: 1) quantifying the fMRI response as proportional to the time integral of EEG source power, 2) estimating the time-variant source covariance matrices from both fMRI and EEG data. Our pilot simulation results have demonstrated that the proposed method is capable of handling the mismatches between locations of fMRI activations and EEG source activities at any time instant (including fMRI false positives and false negatives), as well as probing the millisecond temporal dynamics of source activities. Our preliminary experimental application also suggests a robust performance of improved spatial resolution (relative to the EEG-alone inverse estimates) and temporal resolution (relative to the fMRI).
In previously reported fMRI-EEG multimodal neuroimaging studies, the fMRI data analysis yields an fMRI activation map, which is then used to constrain the EEG inverse solutions in a subsequent step; however, the pixel values in the fMRI activation map have not been rigorously given any quantitative interpretation that is also physically relevant to the following step of the fMRI-constrained EEG source imaging or localization. In contrast, the fMRI data in the present study are quantified as well-defined physical constraints to the EEG inverse solutions. The time integral (over the ERP period) of source power is constrained to be proportional to the quantified fMRI response for each source location. In this sense, the proposed fMRI quantification method also represents a more specific inference regarding underlying neural activities. Existing fMRI analysis methods are often used to quantify the level by which the BOLD signal is statistically correlated to the designed protocol of tasks of interests. Based upon such a statistical analysis, inferences are often made voxel by voxel regarding how likely a region in the brain is involved in the neural computation underlying the tasks. Clearly, such an inference is conceptual rather than physical. In the present study, we quantitatively relate the fMRI signal over a time scale of seconds to the averaged electrical signal over a much shorter time scale of tens of milliseconds. In short, we suggest using the proposed fMRI quantification method in all fMRI-EEG multimodal neuroimaging studies, or even in fMRI studies.
The proposed fMRI quantification method relies on an assumption that the relationship between neural activity and fMRI response is linear. Although such an assumption is commonly made in the fMRI analysis and interpretation, the nonlinear aspect of fMRI response has also been observed, such as under repetitive stimulation (Janz et al, 2001). The nonlinearity may arise from the neural and/or hemodynamic adaptation or habituation (Janz et al, 2001), or the vascular refractory effect (Cannestra et al, 1998), or the interplay of multiple factors. However, our recent investigation of neurovascular coupling based on the VEP and CBF data under graded brain suppression shows that the linear model is still a good approximation of neurovascular coupling relationship, although it contains a subtle nonlinear component (Zhang et al, 2007). Furthermore, the nonlinearity of fMRI response is probably less of concern in most experiments combining ERP and fMRI (as discussed in this paper), where the adjacent stimuli (in ERP paradigms) are often required to be sufficiently separated in time to avoid the interference among stimuli.
In most existing fMRI-EEG (or -MEG) integrated source imaging algorithms, the fMRI-derived spatial constraints have to be assumed to be time-invariant within a short time period during which the source imaging is carried out instant by instant. This is essentially because the source temporal information cannot be resolved by fMRI. However, when the “static” fMRI spatial information is taken as a time-invariant weighting matrix (in the fMRI-weighted minimum norm formulation) or source covariance matrix (in the Wiener filter formulation) for every time point, it is almost unavoidable that the imaging results would be affected by the fMRI-EEG mismatches, which may happen at any time and also vary over time. Previous efforts have been mainly focused upon choosing an empirical weighting factor for locations inside the fMRI activation relative to those outside (Liu et al, 1998; Babiloni et al, 2003; Ahlfors and Simpson, 2004). In such a way, fMRI constraints are weakened such that distortions due to fMRI false positives and false negatives may be alleviated but perhaps never removed. However, this type of methods, no matter what the fMRI weighting factor is chosen to be, has a tradeoff between the robustness against invalid fMRI prior constraints and the spatial resolution of the instantaneous inverse solution. If the fMRI weighting factor is chosen to be 1, the inverse solution is effectively the minimum norm solution; if the fMRI weighting factor is chosen to be infinitely large, the inverse solution can be highly biased by the fMRI-EEG mismatches. On the other hand, the proposed adaptive Wiener filter approach is aimed at correcting fMRI-EEG mismatches in a much more fundamental way, in consideration of the fact that the mismatches are essentially caused by the different time scales at which the fMRI and EEG signals are generated and collected respectively. The proposed adaptive Wiener filter method holds the promise to remove the mismatches instead of attempting to alleviate the resulting distortions with a cost of lower spatial resolution.
In addition, the assumption of a time-invariant source covariance matrix is also not technically valid. A time-invariant source covariance matrix implies that the source signal at any specific location is a stationary stochastic process over time and its sampled values at all time points are drawn independently from an identical distribution. Such an assumption is not valid in practice because neural networks in the brain are always carried out by source signals with rapidly and coordinated temporal evolvement that are certainly not exchangeable over time. In contrast, the estimation of time-variant source covariance matrices in the proposed adaptive Wiener filter method relies on the assumption that at any time instant, the scalp potential maps recorded in different epochs are independent observations of a stochastic process with the index set over channels, which is a reasonable assumption when the electrical responses are repeatedly induced over epochs by the same stimulus or task.
There are more factors other than those addressed in this paper that may also give rise to the spatial mismatches between the fMRI activations and instantaneous source activities. The fMRI spatial specificity and the cross-modal co-registration error may lead to a difference between locations of neural activities and those of the detected fMRI activations (Wagner and Fuchs, 2001). However, these factors are probably more technical rather than fundamental, in a sense that they may be resolved (or bypassed) before applying the integrated imaging algorithm. For example, one may use a spin-echo sequence and increase the field strength to eliminate the contribution from large draining veins, such that the collected fMRI signals originate exclusively from the microvasculature (Yacoub et al, 2003), resulting in an improved fMRI specificity. One may also use advanced geometric manipulations with optimization procedures that combine the landmark and surface point fitting procedures to ensure a good enough co-registration of difference coordinate systems respectively for the fMRI and EEG data.
In the present study, we assume a linear transform model to describe the relationship in time between BOLD fMRI signals and the power of electrical responses. However, recent studies also investigated the correlation between BOLD signals and the EEG (and LFP) power spectrum (Mukamel et al, 2005; Niessing et al, 2005; Kilner et al, 2005). It was suggested that the BOLD responses were positively correlated with the high-frequency components of EEG (or LFP) signals and negatively correlated with the low-frequency components. Such an obvious difference between the models described in time and in frequency does not necessarily mean they are contradictory to each other. Instead, we believe that their difference only reflects the different aspects of the hemodynamic-to-electrophysiological coupling addressed in these two types of models. The model in time as used here describes how the BOLD signals relate to the event-related electrical response, whereas a model in frequency describes how the BOLD signals reflect the change of continuous electrical signals. It remains unclear how the fMRI-EEG/MEG multimodal neuroimaging should benefit from these recently reported findings (Mukamel et al, 2005; Niessing et al, 2005) on the correlation of BOLD signals with frequency components of EEG power spectrum, although it is indeed desirable.
Although the singular value decomposition of the recorded EEG over epochs also allows computing the noise covariance matrix in a time-variant manner, it may not be necessary under most circumstances since the noise is not time-locked to the “events” and can be assumed to be time-invariant. Therefore, one can estimate the noise covariance matrix simply from the pre-onset part of EEG epochs. For every pre-onset time point, a covariance matrix can be computed from the multi-channel EEG data over epochs. Then, the noise covariance matrix can be obtained by averaging the computed covariance matrices at all pre-onset time points.
It may also be worthwhile to mention that the information from fMRI and EEG have also been proposed to be fused in a symmetric fashion (Trujillo-Barreto et al, 2001; Daunizeau et al, 2007), in which a common hierarchical Bayesian model are formulated for both fMRI and EEG. These symmetric Bayesian approaches may represent another feasible way that potentially leads to a reliable fMRI-EEG integrated neuroimaging.
Acknowledgments
The authors are very much grateful to Drs. Wei Chen and Nanyin Zhang for their help in collecting the fMRI data, and would like to thank Chenguang Liu, Lin Yang, Xu Li, Han Yuan, Christopher Wilke and Lei Ding for valuable technical discussions. This work was supported in part by NIH RO1 EB007920-01A1, RO1 EB00178, NSF BES-0411480, and a grant from the Institute of Engineering in Medicine of the University of Minnesota.
Footnotes
The spatial components are the left singular vectors in Eq. (26).
The temporal components are the right singular vectors in Eq. (26). Although called “temporal”, they are actually not the signals over time but rather the signals at the same latency over epochs.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Ahlfors SP, Simpson GV, Dale AM, Belliveau JW, Liu AK, Korvenoja A, Virtanen J, Huotilainen M, Tootell RBH, Aronen HJ, Ilmoniemi RJ. Spatiotemporal activity of a cortical network for processing visual motion revealed by MEG and fMRI. J Neurophysiol. 1999;82:2545–2555. doi: 10.1152/jn.1999.82.5.2545. [DOI] [PubMed] [Google Scholar]
- Ahlfors SP, Simpson GV. Geometrical interpretation of fMRI-guided MEG/EEG inverse estimates. NeuroImage. 2004;22:323–332. doi: 10.1016/j.neuroimage.2003.12.044. [DOI] [PubMed] [Google Scholar]
- Allen PJ, Polizzi G, Krakow K, Fish DR, Lemieux L. Identification of EEG events in the MR scanner: the problem of pulse artifact and a method for its subtraction. NeuroImage. 1998;8:229–239. doi: 10.1006/nimg.1998.0361. [DOI] [PubMed] [Google Scholar]
- Allen PJ, Josephs O, Turner R. A method for removing imaging artifact from continuous EEG recorded during functional MRI. NeuroImage. 2000;12:230–239. doi: 10.1006/nimg.2000.0599. [DOI] [PubMed] [Google Scholar]
- Arthurs OJ, Boniface S. How well do we understand the neural origins of the fMRI BOLD signal. Trends Neurosci. 2002;25:27–31. doi: 10.1016/s0166-2236(00)01995-0. [DOI] [PubMed] [Google Scholar]
- Babiloni F, Cincotti F, Babiloni C, Carducci F, Basilisco A, Rossini PM, Mattia D, Astolfi L, Ding L, Ni Y, Cheng K, Christine K, Sweeney J, He B. Estimation of the cortical functional connectivity with the multimodal integration of high resolution EEG and fMRI data by Directed Transfer Function. NeuroImage. 2005;24:118–131. doi: 10.1016/j.neuroimage.2004.09.036. [DOI] [PubMed] [Google Scholar]
- Bandettini PA, Wong EC, Hinks RS, Tikofsky RS, Hyde JS. Time course EPI of human brain function during task activation. Magn Reson Med. 1992;25:390–397. doi: 10.1002/mrm.1910250220. [DOI] [PubMed] [Google Scholar]
- Bonmassar G, Schwartz DP, Liu AK, Kwong KK, Dale AM, Belliveau JW. Spatiotemporal brain imaging of visual-evoked activity using interleaved EEG and fMRI recordings. NeuroImage. 2001;13:1035–1043. doi: 10.1006/nimg.2001.0754. [DOI] [PubMed] [Google Scholar]
- Boynton GM, Engel SA, Glover GH, Heeger DJ. Linear systems analysis of functional magnetic resonance imaging in human V1. J Neurosci. 1996;16:4207–4221. doi: 10.1523/JNEUROSCI.16-13-04207.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cannestra AF, Pouratian N, Shomer MH, Toga AW. Refractory Periods Observed by Intrinsic Signal and Fluorescent Dye Imaging. J Neurophysiol. 1998;80:1522–1532. doi: 10.1152/jn.1998.80.3.1522. [DOI] [PubMed] [Google Scholar]
- Dale AM, Sereno MI. Improved localization of cortical activity by combining EEG and MEG with MRI cortical surface reconstruction: A linear approach. J Cogn Neurosci. 1993;5:162–176. doi: 10.1162/jocn.1993.5.2.162. [DOI] [PubMed] [Google Scholar]
- Dale AM, Buckner RL. Selective averaging of rapidly presented individual trials using fMRI. Hum Brain Mapp. 1997;5:329–340. doi: 10.1002/(SICI)1097-0193(1997)5:5<329::AID-HBM1>3.0.CO;2-5. [DOI] [PubMed] [Google Scholar]
- Dale AM, Liu AK, Fischl BR, Buckner RL, Belliveau JW, Lewine JD, Halgren E. Dynamic statistical parametric mapping: combining fMRI and MEG for high-resolution imaging of cortical activity. Neuron. 2000;26:55–67. doi: 10.1016/s0896-6273(00)81138-1. [DOI] [PubMed] [Google Scholar]
- Dale AM, Halgren E. Spatiotemporal mapping of brain activity by integration of multiple imaging modalities. Curr Opin Neurobiol. 2001;11:202–207. doi: 10.1016/s0959-4388(00)00197-5. [DOI] [PubMed] [Google Scholar]
- Darvas F, Pantazis D, Kucukaltun-Yildirim E, Leahy RM. Mapping human brain function with MEG and EEG: methods and validation. NeuroImage. 2004;23:S289–299. doi: 10.1016/j.neuroimage.2004.07.014. [DOI] [PubMed] [Google Scholar]
- Daunizeau J, Grova C, Marrelec G, Mattout J, Jbabdi S, Pélégrini-Issac M, Lina JM, Benali H. Symmetrical event-related EEG/fMRI information fusion in a variational Bayesian framework. NeuroImage. 2007;36:69–87. doi: 10.1016/j.neuroimage.2007.01.044. [DOI] [PubMed] [Google Scholar]
- Felleman DJ, Van Essen DC. Distributed hierarchical processing in the primate cerebral cortex. Cereb Cortex. 1991;1:1–47. doi: 10.1093/cercor/1.1.1-a. [DOI] [PubMed] [Google Scholar]
- Friston KJ, Jezzard P, Turner R. Analysis of Functional MRI Time-Series. Hum Brain Mapp. 1994;1:153–171. [Google Scholar]
- Friston KJ, Holmes AP, Worsley KJ, Poline JB, Frith CD, Frackowiak RSJ. Statistical parametric maps in functional imaging: A general linear approach. Hum Brain Mapp. 1995;2:189–210. [Google Scholar]
- Fuchs M, Wagner M, Wischmann HA, Kohler T, Theiben A, Drenckhahn R, Buchner H. Improving source reconstructions by combining bioelectric and biomagnetic data. Electroencephalogr Clin Neurophysiol. 1998;107:93–107. doi: 10.1016/s0013-4694(98)00046-7. [DOI] [PubMed] [Google Scholar]
- Fujimaki N, Hayakawa T, Nielsen M, Knosche TR, Miyauchi S. An fMRI-constrained MEG source analysis with procedures for dividing and grouping activation. NeuroImage. 2002;17:324–343. doi: 10.1006/nimg.2002.1160. [DOI] [PubMed] [Google Scholar]
- George J, Mosher JC, Schmidt D, Aine C, Wood C, Lewine J, Sander J, Belliveau JW. Functional neuroimaging by combined MRI, MEG and fMRI. Human Brain Mapp. 1995;S1:89. [Google Scholar]
- Goldman RI, Stern JMJE, Jr, Cohen MS. Acquiring simultaneous EEG and functional MRI. Clin Neurophysiol. 2000;111:1974–1980. doi: 10.1016/s1388-2457(00)00456-9. [DOI] [PubMed] [Google Scholar]
- Gotman J, Benar CG, Dubeau F. Combining EEG and fMRI in epilepsy: methodological challenges and clinical results. J Clin Neurophysiol. 2002;21:229–240. doi: 10.1097/01.wnp.0000139658.92878.2a. [DOI] [PubMed] [Google Scholar]
- Hansen PC. The discrete Picard condition of discrete ill-posed problems. BIT. 1990;30:658–672. [Google Scholar]
- Hansen PC. Review. Vol. 34. 1992. Analysis of discrete ill-posed problems by means of the L-curve, SIAM; pp. 561–580. [Google Scholar]
- Hämäläinen MS, Ilmoniemi J. Interpreting measured magnetic fields of the brain: estimates of current distributions. Helsinki University of Technology. Department of Technical Physics Technical Report TKK-F-A559.1984. [Google Scholar]
- Hämäläinen MS, Sarvas J. Realistic conductivity geometry model of the human head for interpretation of neuromagnetic data IEEE. Trans Biomed Eng. 1989;36:165–171. doi: 10.1109/10.16463. [DOI] [PubMed] [Google Scholar]
- Hämäläinen MS, Hari R, Ilmoniemi RJ, Knuutila J, Lounasmaa OV. Magnetoencephalography - theory, instrumentation, and applications to noninvasive studies of the working hunman brain. Rev Mod Phys. 1993;65:413–497. [Google Scholar]
- Hauk O. Keep it simple: a case for using classical minimum norm estimation in the analysis of EEG and MEG data. NeuroImage. 2004;21:1612–1621. doi: 10.1016/j.neuroimage.2003.12.018. [DOI] [PubMed] [Google Scholar]
- He B, Musha T, Okamoto Y, Homma S, Nakajima Y, Sato T. Electrical dipole tracing in the brain by means of the boundary element method and its accuracy. IEEE Trans Biomed Eng. 1987;34:406–414. doi: 10.1109/tbme.1987.326056. [DOI] [PubMed] [Google Scholar]
- He B. Brain electric source imaging: scalp Laplacian mapping and cortical imaging. Crit Rev Biomed Eng. 1999;27:149–188. [PubMed] [Google Scholar]
- He B. Modeling and Imaging of Bioelectric Activity: Principles and Applications. Kluwer Academic/Plenum Publishers; 2004. [Google Scholar]
- Heeger DJ, Huk AC, Geisler WS, Albrecht DG. Spikes versus BOLD what does neuroimaging tell us about neural activity. Nat Neurosci. 2000;3:631–634. doi: 10.1038/76572. [DOI] [PubMed] [Google Scholar]
- Heeger DJ, Ress D. What does fMRI tell us about neuronal activity? Nat Rev Neurosci. 2002;3:142–151. doi: 10.1038/nrn730. [DOI] [PubMed] [Google Scholar]
- Im CH, Liu Z, Zhang N, Chen W, He B. Functional cortical source imaging from simultaneously recorded ERP and fMRI. J Neurosci Methods. 2006;157:118–123. doi: 10.1016/j.jneumeth.2006.03.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Janz C, Heinrich SP, Kornmayer J, Bach M, Hennig J. Coupling of neuronal activity and BOLD fMRI response: new insights by combination of fMRI and VEP experiments in transition from single events to continuous stimulation. Magn Reson Med. 2001;46:482–486. doi: 10.1002/mrm.1217. [DOI] [PubMed] [Google Scholar]
- Kilner JM, Mattout J, Henson R, Friston KJ. Hemodynamic correlates of EEG: A heuristic. NeuroImage. 2005;28:280–286. doi: 10.1016/j.neuroimage.2005.06.008. [DOI] [PubMed] [Google Scholar]
- Korvenoja A, Huttunen J, Salli E, Pohjonen H, Martinkauppi S, Palva JM, Lauronen L, Virtanen J, Ilmoniemi RJ, Aronen HJ. Activation of multiple cortical areas in response to somatosensory stimulation: combined magnetoencephalographic and functional magnetic resonance imaging. Human Brain Mapp. 1999;8:13–27. doi: 10.1002/(SICI)1097-0193(1999)8:1<13::AID-HBM2>3.0.CO;2-B. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kwong KK, Belliveau JW, Chesler DA, Goldberg IE, Weisskoff RM, Poncelet BP, Kennedy DN, Hoppel BE, Cohen MS, Turner R, Cheng HM, Brady TJ, Rosen BR. Dynamic magnetic resonance imaging of human brain activity during primary sensory stimulation. Proc Natl Acad Sci USA. 1992;89:5675–5679. doi: 10.1073/pnas.89.12.5675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lai Y, van Drongelen W, Ding L, Hecox KE, Towle VL, Frim DM, He B. In vivo human skull conductivity estimation from simultaneous extra- and intracranial electrical potential recordings. Clin Neurophysiol. 2005;116:456–465. doi: 10.1016/j.clinph.2004.08.017. [DOI] [PubMed] [Google Scholar]
- Lauritzen M, Gold L. Brain function and Neurophysiological correlates of signals used in functional neuroimaging. J Neurosci. 2003;23:3972–3980. doi: 10.1523/JNEUROSCI.23-10-03972.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin FH, Belliveau JW, Dale AM, Hämäläinen MS. Distributed current estimates using cortical orientation constraints. Human Brain Mapp. 2006;27:1–13. doi: 10.1002/hbm.20155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu AK, Belliveau JW, Dale AM. Spatiotemporal imaging of human brain activity using functional MRI constrained magnetoencephalography data: Monte Carlo simulations. Proc Natl Acad Sci USA. 1998;95:8945–8950. doi: 10.1073/pnas.95.15.8945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Z, Ding L, He B. Integration of EEG/MEG with MRI and fMRI in Functional Neuroimaging. IEEE Eng Med Biol Mag. 2006a;25:46–53. doi: 10.1109/memb.2006.1657787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Z, Kecman F, He B. Effects of fMRI-EEG mismatches in cortical current density estimation using fMRI and EEG: a simulation study. Clin Neurophysiol. 2006b;117:1610–1622. doi: 10.1016/j.clinph.2006.03.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Logothetis NK, Pauls J, Augath M, Trinath T, Oeltermann A. Neurophysiological investigation of the basis of the fMRI signal. Nature. 2001;412:150–157. doi: 10.1038/35084005. [DOI] [PubMed] [Google Scholar]
- Logothetis NK. The neural basis of the blood-oxygen-level-dependent functional magnetic resonance imaging signal. Phil Trans R Soc Lond B. 2002;357:1003–1037. doi: 10.1098/rstb.2002.1114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martindale J, Mayhew J, Berwick J, Jones M, Martin C, Johnston D, Redgrave P, Zheng Y. The hemodynamic impulse response to a single neural event. J Cereb Blood Flow Metab. 2003;23:546–555. doi: 10.1097/01.WCB.0000058871.46954.2B. [DOI] [PubMed] [Google Scholar]
- Mathiesen C, Caesar K, Akgören N, Lauritzen M. Modification of activity-dependent increases of cerebral blood flow by excitatory synaptic activity and spikes in rat cerebellar cortex. J Physiol. 1998;512:555–566. doi: 10.1111/j.1469-7793.1998.555be.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mattout J, Phillips C, Penny WD, Rugg MD, Friston KJ. MEG source localization under multiple constraints: an extended Bayesian framework. NeuroImage. 2006;30:753–767. doi: 10.1016/j.neuroimage.2005.10.037. [DOI] [PubMed] [Google Scholar]
- Mukamel R, Gelbard H, Arieli A, Hasson U, Fried I, Malach1 R. Coupling between neuronal firing, field potentials, and fMRI in human auditory cortex. Science. 2005;309:951–954. doi: 10.1126/science.1110913. [DOI] [PubMed] [Google Scholar]
- Niessing J, Ebisch B, Schmidt KE, Niessing M, Singer M, Galuske RAW. Hemodynamic signals correlate tightly with synchronized gamma oscillations. Science. 2005;309:948–951. doi: 10.1126/science.1110948. [DOI] [PubMed] [Google Scholar]
- Nunez PL, Srinivasan R. Electrical fields of the brain: the neurophysics of EEG. 2. Oxford University Press; 2005. [Google Scholar]
- Oostendorp TF, Delbeke J, Stegeman DF. The conductivity ratio of the human skull: results of in vivo and in vitro measurement. IEEE Trans Biomed Eng. 2000;47:1487–1492. doi: 10.1109/TBME.2000.880100. [DOI] [PubMed] [Google Scholar]
- Pascual-Marqui RD, Michel CM, Lehmann D. Low resolution electromagnetic tomography: A new method for localizing electrical activity in the brain. Int J Psychophys. 1994;18:49–65. doi: 10.1016/0167-8760(84)90014-x. [DOI] [PubMed] [Google Scholar]
- Pascual-Marqui RD. Review of methods for solving the EEG inverse problem. Intl J Bioelectromagn. 1999;1:75–86. [Google Scholar]
- Phillips C, Mattout J, Rugg MD, Maquet P, Friston KJ. An empirical Bayesian solution to the source reconstruction problem in EEG. NeuroImage. 2005;24:997–1011. doi: 10.1016/j.neuroimage.2004.10.030. [DOI] [PubMed] [Google Scholar]
- Ogawa S, Lee TM, Kay AR, Tank DW. Brain magnetic resonance imaging with contrast dependent on blood oxygenation. Proc Natl Acad Sci USA. 1990;87:9868–9872. doi: 10.1073/pnas.87.24.9868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ogawa S, Tank DW, Menon R, Ellermann JM, Kim S-G, Merkle H, Ugurbil K. Intrinsic signal changes accompanying sensory stimulation: functional brain mapping with magnetic resonance imaging. Proc Natl Acad Sci USA. 1992;89:5951–5955. doi: 10.1073/pnas.89.13.5951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rees G, Friston K, Koch C. A direct quantitative relationship between the functional properties of human and macaque V5. Nat Neurosci. 2000;3:716–723. doi: 10.1038/76673. [DOI] [PubMed] [Google Scholar]
- Sato M, Yoshioka T, Kajihara S, Toyama K, Goda N, Doya K, Kawato M. Hierarchical Bayesian estimation for MEG inverse problem. NeuroImage. 2004;23:806–826. doi: 10.1016/j.neuroimage.2004.06.037. [DOI] [PubMed] [Google Scholar]
- Shulman RG, Rothman DL. Interpreting functional imaging studies in terms of neurotransmitter cycling. Proc Natl Acad Sci USA. 1998;95:11993–11998. doi: 10.1073/pnas.95.20.11993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trujillo-Barreto NJ, Martínez-Monte E, Melie-García L, Valdés-Sosa PA. A symmetrical Bayesian model for fMRI and EEG/MEG neuroimaging fusion. Int J Bioelectromagn. 2001;3(1) [Google Scholar]
- Vanni S, Warnking J, Dojat M, Delon-Martin C, Bullier J, Segebarth C. Sequence of pattern onset responses in the human visual areas: an fMRI constrained VEP source analysis. NeuroImage. 2004;21:801–817. doi: 10.1016/j.neuroimage.2003.10.047. [DOI] [PubMed] [Google Scholar]
- Wagner M, Fuchs M, Kastner J. fMRI-constrained dipole fits and current density reconstructions. Proc 12th Intl Conf Biomag. 2000:785–788. [Google Scholar]
- Wagner M, Fuchs M. Integration of functional MRI, structural MRI, EEG and MEG. Intl J Bioelectromagn. 2001;3(1) [Google Scholar]
- Wan X, Riera J, Iwata K, Takahashi M, Wakabayashi T, Kawashima R. The neural basis of the hemodynamic response nonlinearity in human primary visual cortex: implications for neurovascular coupling mechanism. NeuroImage. 2006;32:616–625. doi: 10.1016/j.neuroimage.2006.03.040. [DOI] [PubMed] [Google Scholar]
- Yacoub E, Duong TQ, Van De Moortele P-F, Lindquist M, Adriany G, Kim K-G, Ugurbil K, Hu X. Spin-echo fMRI in humans using high spatial resolutions and high magnetic fields. Magn Reson Med. 2003;49:655, 664. doi: 10.1002/mrm.10433. [DOI] [PubMed] [Google Scholar]
- Zhang N, Liu Z, He B, Chen W. Non-invasive study of neurovascular coupling during brain suppression. J Cereb Blood Flow Metab. 2007 doi: 10.1038/sj.jcbfm.9600531. in press. [DOI] [PubMed] [Google Scholar]
- Zhang Y, van Drongelen W, He B. Estimation of in vivo human brain-to-skull conductivity ratio with the aid of intracranial electrical simulation. Applied Physics Letters. 2006;89:223903. doi: 10.1063/1.2398883. [DOI] [PMC free article] [PubMed] [Google Scholar]