Water inertial reorientation: Hydrogen bond strength and the angular potential

Abstract

The short-time orientational relaxation of water is studied by ultrafast infrared pump-probe spectroscopy of the hydroxyl stretching mode (OD of dilute HOD in H₂O). The anisotropy decay displays a sharp drop at very short times caused by inertial orientational motion, followed by a much slower decay that fully randomizes the orientation. Investigation of temperatures from 1°C to 65°C shows that the amplitude of the inertial component (extent of inertial angular displacement) depends strongly on the stretching frequency of the OD oscillator at higher temperatures, although the slow component is frequency-independent. The inertial component becomes frequency-independent at low temperatures. At high temperatures there is a correlation between the amplitude of the inertial decay and the strength of the O-DO hydrogen bond, but at low temperatures the correlation disappears, showing that a single hydrogen bond (ODO) is no longer a significant determinant of the inertial angular motion. It is suggested that the loss of correlation at lower temperatures is caused by the increased importance of collective effects of the extended hydrogen bonding network. By using a new harmonic cone model, the experimentally measured amplitudes of the inertial decays yield estimates of the characteristic frequencies of the intermolecular angular potential for various strengths of hydrogen bonds. The frequencies are in the range of ≈400 cm⁻¹. A comparison with recent molecular dynamics simulations employing the simple point charge-extended water model at room temperature shows that the simulations qualitatively reflect the correlation between the inertial decay and the OD stretching frequency.

Although a great deal is known about water's bulk thermodynamic properties, the complex intermolecular forces that govern its nanoscopic structural arrangements and dynamics have made a detailed picture of the instantaneous local structures of water and their evolution elusive. Numerous models for the structure of water have been proposed to account for its anomalous behavior at different temperatures and pressures (1–6). These models all have some degree of success in reproducing the observed radial distribution function and other properties of water.

Here, we present results on the fast, local (inertial) angular motions of dilute HOD molecules in water within their initial hydrogen-bonding structure through a study of how the orientational motions of water depend on the OD stretching frequency and temperature. The short-time orientational motions of the HOD molecule depend on the potential energy surface established by neighboring water molecules. Measurements of the orientational relaxation as a function of OD stretching frequency and temperature provide insight into how the motions of the HOD molecule depend on the strength of the O-DO hydrogen bond (nature of the potential energy surface) and how the local structure of water changes with temperature. The measurements provide a benchmark for theoretical descriptions of the intermolecular interactions in water.

Various aspects of the temperature dependence of orientational relaxation of water have been studied by using NMR (7, 8), dielectric relaxation (9), optical Kerr effect (OKE) (10), and ultrafast infrared (IR) spectroscopy (11). Results emerging from these studies include the observation that the activation energy for reorientation depends on temperature, indicating that the structures of water and the mechanism for orientational relaxation change with temperature. NMR has the potential to measure the single-particle orientational correlation function. However, several assumptions must be made to extract a single orientational relaxation time, τ_r, which is averaged over the entire ensemble (12). Dielectric relaxation and OKE measure different correlation functions, but both are primarily measurements of orientational relaxation for the entire ensemble and thus do not directly provide single-particle orientational information.

Ultrafast IR polarization selective pump-probe spectroscopy of the hydroxyl stretch of dilute HOD in either H₂O or D₂O has several advantages for measuring the short-time orientational motions of water molecules. The OD stretching frequency is correlated with the strength of the O-DO hydrogen bond (13–15). By frequency resolving the IR pump-probe signal, water molecules forming different strengths of hydrogen bonds can be studied. The anisotropy decay of water is a direct time domain measurement of the mechanical motions of water molecules through the single-particle orientational correlation function. The greatest advantage of the IR anisotropy measurement is that information is obtained directly from the data. With accurate measurements of the signal parallel, I_‖(t), and perpendicular, I_⊥(t), to the pump polarization, vibrational excited-state population decay, P(t), is obtained by using

and the orientational relaxation, r(t) (anisotropy decay) is given by

where C₂(t) is the second Legendre polynomial orientational correlation function. In the experiments presented below, we study the OD stretch of dilute HOD in H₂O to prevent vibrational excitation transfer (16). In pure water, vibrational excitation transfer causes an artificial decay of the orientational anisotropy, interfering with the measurement of orientational relaxation (17).

Below we present the results of ultrafast IR pump-probe anisotropy experiments on dilute HOD in H₂O at temperatures ranging from 1°C to 65°C. We find that at most temperatures, the magnitude of the inertial anisotropy decay of the HOD molecule depends on the OD stretching frequency (O-DO hydrogen bond strength) but that the long-time reorientation is frequency-independent. The magnitude of the inertial component of the orientational relaxation describes the range of angles sampled by the OD bond vector as the angular velocity autocorrelation function relaxes.

We estimate the characteristic frequencies of the intermolecular modes responsible for the inertial motion by assuming that the intermolecular potential energy surface is harmonic. We develop a model we call the harmonic cone that is analogous to the wobbling-in-a-cone model of orientational relaxation (18–20). In the wobbling-in-a-cone model, the only potential is a hard wall at the cone boundary. Here, the motion occurs on a harmonic potential. The frequencies extracted from the data are in the range of ≈400 cm⁻¹, and are qualitatively consistent with instantaneous normal mode analyses of water that show a broad band caused by rotational and translational motions extending from 0 cm⁻¹ to >900 cm⁻¹ (21, 22).

An important aspect of the results is that, at lower temperatures, the magnitude of the inertial component becomes frequency-independent; at low temperatures the inertial motion does not depend on the strength of the O-DO hydrogen bond. It is suggested that as the temperature is reduced the inertial orientational motion increasingly depends on the collective nature of the hydrogen-bonding network, and therefore, becomes independent of the strength of the single OD hydrogen bond that is correlated with the observed OD stretch vibrational frequency.

Recently, the simple point charge-extended (SPC/E) model for water has been used extensively in molecular dynamics (MD) simulations to study the dynamics of water (23–27). Simulations of the inertial angular motion of an HOD in D₂O display a dependence on the frequency of the OH stretching mode, which is correlated with the strength of the O-HO hydrogen bond (25, 27). More detailed simulations of the system studied here (the OD stretch of HOD in H₂O) are presented below. Like the simulations of HOD in D₂O, the new results exhibit a dependence of the inertial angular motion on the OD stretch frequency (the strength of the O-DO hydrogen bond). The room temperature experimental results presented here are in general agreement with the room temperature classical MD simulations. However, the SPC/E MD simulations systematically overestimate the amplitude of the inertial decay of the orientational correlation, do not have the correct functional form for the frequency dependence, and the long-time reorientation extracted from the simulations is too fast. Both the previous and current simulations find that the long-time-scale complete orientational randomization is independent of the hydroxyl stretch frequency, in agreement with experimental results. The explanation for the lack of frequency dependence for the long-time reorientation is that complete orientational randomization involves concerted rearrangement (breaking and forming) of a number of hydrogen bonds. The reorientation event occurs by a large-amplitude jump, facilitated by the formation of a bifurcated hydrogen bond involving the old acceptor and the new acceptor (26). The probability of a new hydrogen bond acceptor becoming available is independent of the observed hydroxyl stretch frequency, so the long-time anisotropy decay is hydroxyl stretch frequency independent.

The results presented below provide a systematic experimental examination of the temperature and frequency dependence of the magnitude of the short-time angular motions of water. These results will contribute to understanding the temperature-dependent nature of the local structure of water.

Results and Discussion

Frequency-Dependent Anisotropy Decays.

A great deal is known about the orientational relaxation of HOD in H₂O and D₂O (28–32). In particular, several groups have demonstrated that the long-time anisotropy decay of HOD in H₂O is independent of frequency (30–32). Narrowband two-color pump-probe experiments have observed multiexponential intermediate and long-time anisotropy decays for HOD in D₂O. This result was interpreted as indicating that the global structural rearrangement associated with the long-time anisotropy decay depends on the strength of the O-HO hydrogen bonds, with molecules experiencing stronger bonds reorienting more slowly (11, 31, 33, 34). However, recent IR pump-probe experiments on HOD in D₂O with 45-fs pulses, which have sufficient band width to span the entire OH absorption line, thereby eliminating spectral diffusion from the measurements, observed that the anisotropy decayed as a single exponential after an ultrafast inertial component during the first 100 fs (29). Furthermore, MD simulations on HOD in D₂O do not display a frequency dependence to the anisotropy decay after the first 100 fs, providing additional evidence that the underlying mechanisms for reorientation are the same in H₂O and D₂O (25, 27). Because it is necessary to study an isotopically mixed system to avoid vibrational excitation transport, it is useful to study the OD stretch of HOD in H₂O because the properties of H₂O rather than D₂O are obtained and the OD stretch has a narrower absorption band.

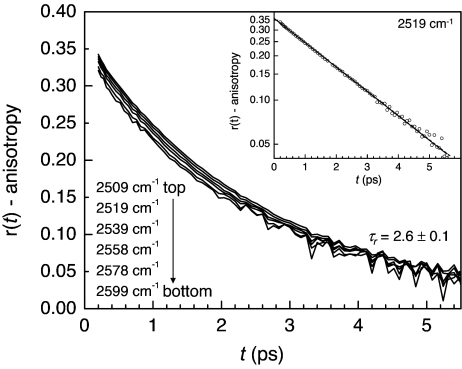
The frequency dependence of the anisotropy decay at 25°C is shown in Fig. 1. The pump-probe data used to compute the anisotropy decays has been corrected for a small, well documented thermal contribution (30, 32). Data for times <200 fs have been omitted because of a strong nonresonant artifact caused by the CaF₂ windows that interferes with the resonant signal. Six anisotropy curves are shown ranging in frequency from 2,509 cm⁻¹ to 2,599 cm⁻¹. Eighteen frequencies for seven independent data runs were analyzed. Within experimental error, all of the decay curves have the same decay constant, τ_r = 2.6 ± 0.1 ps, for times >200 fs. For temperatures near room temperature and above, the long-time-scale orientational relaxation is frequency-independent within experimental error. The temperature dependence of the long-time-scale orientational relaxation will be discussed in more detail subsequently.

Fig. 1.

Plot of long-time anisotropy decay curves for various frequencies at 25°C. The slow component of the orientational relaxation is wavelength-independent. (Inset) A decay curve on a semilog plot with single exponential fit. All decays are exponential within experimental error.

Although the long-time anisotropy decay is frequency-independent, between t = 0 and t = 200 fs, there is an extremely fast decrease in the anisotropy caused by inertial orientational motion. The presence of this inertial component has been noted by several groups (19, 29, 30, 35). The interesting result, which has not been observed previously, is that the amplitude of the inertial component depends on the OD stretching frequency. This can be seen clearly in Fig. 1 as the changing amplitude of the inertial component causes the anisotropy decays to be offset from one another. The higher curves have lower OD stretching frequencies and smaller inertial drops. The lower curves have higher OD stretching frequencies and larger inertial drops. Because the OD stretching frequency is known to depend on the strength of the O-DO hydrogen bond, the magnitude of the inertial decay is correlated with the hydrogen bond strength.

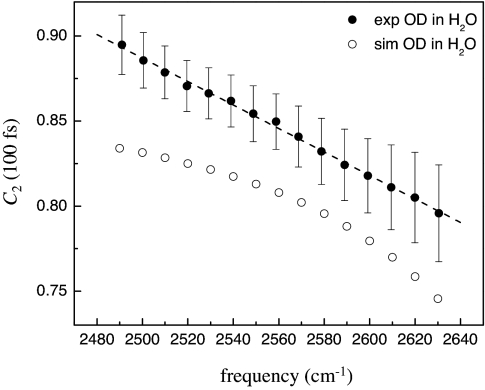
Fig. 2 displays the OD stretch frequency dependence of the amplitude of the orientational correlation function at t = 100 fs for the experiment and simulation. The experimental data in Fig. 2 were measured at 25°C (filled circles). The experimental amplitudes come from extrapolating the best exponential fit to the experimental data back to t = 100 fs. This time point was chosen because previous simulations (25, 27) and experiments (29) suggest that the inertial motion is complete by ≈100 fs. The data presented here are the average of seven datasets; the error bars are the standard deviations. The line through the experimental data is a linear fit to the points. The experimental data show a pronounced frequency dependence. Within experimental error, the amplitude of the inertial drop appears to be linear with frequency. It is important to note that dephasing of the OD oscillators introduces an inherent spread in the measured hydroxyl stretch frequency because of the homogeneous line width (≈60 cm⁻¹) of HOD in H₂O (23, 36, 37). This spread in frequency will cause the inertial drop reported at a particular OD stretch frequency to be the average over a range of frequencies. However, the linear relationship observed in Fig. 2 suggests that the uncertainty in frequency should not have a substantial effect on the results.

Fig. 2.

Amplitudes of the experimentally measured orientational correlation functions at t = 100 fs as a function of the OD stretching frequency (hydrogen bond strength, solid circles). The dashed line is a linear fit to the data. Also, the amplitudes of the orientational correlation function from MD simulations (open circles) are shown.

The open circles in Fig. 2 are the results of an MD simulation of SPC/E HOD in H₂O. The MD simulation results presented here use methods similar to the earlier work of Skinner and coworkers (25), but with an improved method for calculating the hydroxyl stretch frequencies (38) that has been extended to the case of the OD stretch of HOD in H₂O. Previous simulations of HOD in D₂O have reported the amplitude of the inertial drop at several central frequencies but the frequency bin size about these central frequencies was large (80 cm⁻¹) (27). The simulation results presented here use bin sizes of 10 cm⁻¹ to provide a much finer scale for comparing the amplitude of the inertial drop to the experimental data. As can been seen in Fig. 2, the simulations have a trend that is similar to the experimental data but the amplitude of the inertial drop is larger at all frequencies. In addition, the simulation displays a clear curvature whereas the experimental data are linear. The long-time anisotropy decay observed in the MD simulation is significantly faster than the experimentally measured decay indicating that the hydrogen bond network dynamics in the simulation are too fast. In previous simulations (25, 27) the orientational correlation function was reported at only a few OH frequencies but the amplitudes of the inertial drops were similar to the results of the simulation reported here.

The IR anisotropy experiment measures the correlation function of the second Legendre polynomial, 〈P₂(μ̂₀·μ̂_t)〉, where μ̂₀ and μ̂_t are the OD bond unit vectors in the lab frame at times 0 and t, respectively; a change in the angle between μ̂₀ and μ̂_t results in a decrease in the anisotropy. Therefore, the amplitude of the orientational correlation function at t = 100 fs is related to the angular range that the OD bond traverses in the first 100 fs after excitation. From the experimental results presented in Fig. 2, there is a distinct correlation between the strength of the hydrogen bond (OD stretching frequency) and the inertial angular range that the HOD molecule is able to sample. Stronger hydrogen bonds (lower OD stretching frequencies) allow less angular freedom (smaller drop) and weaker hydrogen bonds (higher OD stretching frequencies) allow more angular freedom (larger drop).

The fact that the experimental data show a correlation between the angular range and the OD stretching frequency provides strong evidence that the intermolecular angular potential energy surface, which restricts the angular motion, depends in part on the strength of the O-DO hydrogen bond. It is reasonable to postulate that a smaller angular range will occur for a steeper angular potential energy surface.

Inertial Motion on a Harmonic Potential.

To obtain information on the nature of the intermolecular potential energy surface based on the amplitude of the inertial drop and its dependence on the O-DO hydrogen bond strength, we use a harmonic approximation. We assume that the inertial dynamics can be modeled as occurring on an effective harmonic potential energy surface. This assumption allows us to extract a characteristic oscillator frequency that describes the inertial motion of the HOD molecule. In addition, we take the inertial motion to be complete after ≈100 fs. This time is based on the results of MD simulations (25, 27) and ultrafast IR experiments (29) that show a transition into the exponential decay associated with hydrogen bond network rearrangement after ≈100 fs. We also employ the fact that the inertial motion and its damping occur on a time scale much faster than the hydrogen bond network rearrangement so that the dynamics of the two processes are separable. This assumption is reasonable because the inertial motion occurs on a time scale of tens of femtoseconds, whereas the long-time dynamics have a characteristic time scale of 2.6 ps. The effects of including the contribution from the long-time dynamics will be discussed briefly below.

It is well known that water interacts strongly with its neighbors through the formation of approximately four hydrogen bonds. These interactions set up a potential energy surface that restricts the angular motion of the HOD molecule. The simplest model for this potential energy surface is an effective two-dimensional harmonic potential. The pump-probe anisotropy experiment is sensitive to changes in the polar angle, θ, of the OD bond vector relative to the laboratory frame. The second dimension appears through the azimuthal symmetry of the harmonic potential. The two-dimensional potential can provide information about characteristic changes such as steepening or flattening of the potential energy surface that affects polar angular motion. Hydrogen bonds restrict the motion of the HOD molecule through this effective potential, but fluctuations in the hydrogen-bonding network also constantly provide stochastic forces that apply torques to the HOD molecule within its potential well. The combination of stochastic torques and a confining potential causes the HOD molecule to move ballistically within its potential well for some time (inertial motion) before its angular velocity loses memory of its initial value and direction (decay of the angular velocity autocorrelation function).

A model for the short-time orientational motion of water must calculate the second-rank rotational time correlation function, C₂(t) = 〈P₂(μ̂₀·μ̂_t)〉, where μ̂₀ and μ̂_t are OD bond unit vectors in the lab frame at times t = 0 and t, respectively. The angular “harmonic cone” potential is determined at the molecular level by the hydrogen-bonding interactions between water molecules. Therefore, a natural choice for the z axis in what we call the “molecular level frame” is the intermolecular unit vector connecting the oxygen on the HOD molecule to the neighboring oxygen that participates in the ODO hydrogen bond. This choice of z axis leads to the reasonable result that the minimum of energy for the harmonic potential occurs for a linear hydrogen bond. The OD bond vectors, μ̂₀ and μ̂_t, make polar angles, θ₀ and θ_t, with this axis. By using the addition theorem for spherical harmonics (39), and following the treatment of Lipari and Szabo (18), we can make a connection between the measurement in the lab frame and the dynamics in the molecular level frame.

The assumption that the inertial dynamics are separable from the long-time dynamics means that the inertial motion damps before hydrogen bond network rearrangement occurs. If we further use the assumption that the inertial motion is complete by 100 fs, we can write C₂(100 fs) = C₂^inertial (∞). In this case, the polar angles, θ₀ and θ_∞, are uncorrelated, and so, as discussed by Lipari and Szabo (18),

By using the assumption that the intermolecular potential is harmonic with respect to the polar angle, θ, about the harmonic cone axis, we can write an expression for 〈P₂(cos θ)〉.

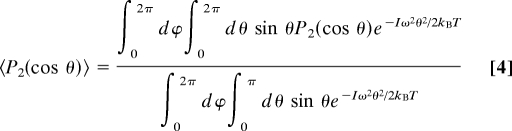Here, I is the average moment of inertia of the HOD molecule (I = 2.847 × 10⁻⁴⁷ kg·m⁻²), ω is the angular frequency of the oscillator, k_B is Boltzmann's constant, and T is the temperature in Kelvin. The denominator is for normalization, and the exponential gives the thermal equilibrium Gaussian distribution of angles allowed by the effective intermolecular harmonic potential about the OO direction. The integration over ϕ comes in because of the azimuthal symmetry of the potential. By using Eq. 4 in Eq. 3 we can write an expression that connects the experimentally measured amplitude of the (normalized) correlation function at 100 fs with the oscillator frequency of the effective harmonic potential, ω.

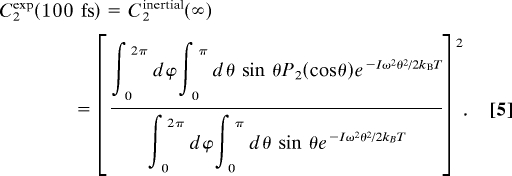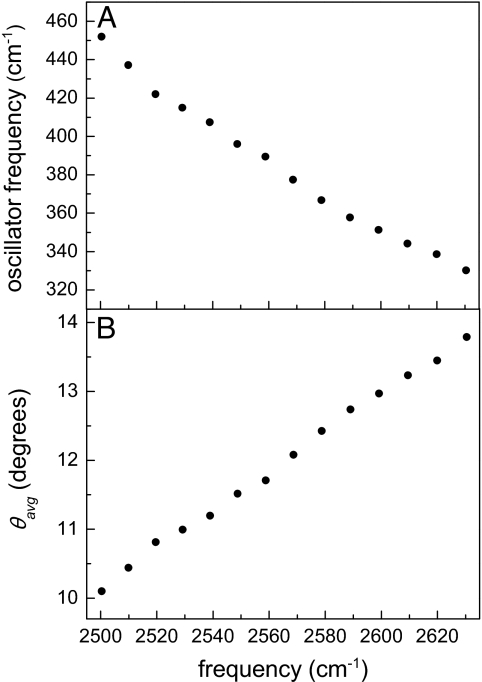
The oscillator frequencies extracted from the experimental data at 25°C based on this model are shown in Fig. 3A. The frequencies range from ≈320 cm⁻¹ for weaker hydrogen bonds (high OD stretching frequency) to ≈450 cm⁻¹ for stronger hydrogen bonds (low OD stretching frequency). With these oscillator frequencies, we can estimate the characteristic amplitude of the angular motion allowed by the intermolecular potential energy surface for each OD stretching frequency.

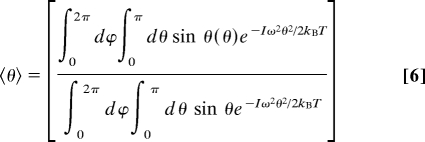〈θ〉 is the average angular range of motion for a given oscillator frequency ω. Fig. 3B gives the values of 〈θ〉 based on the oscillator frequencies in Fig. 3A.

Fig. 3.

Results of the analysis based on the harmonic cone model. (A) Oscillator frequency as a function of OD stretching frequency. (B) Average angular deviations, 〈θ〉 = θ_avg, determined from the oscillator frequencies in A.

Fig. 3 shows that there is a clear correlation between the OD stretching frequency and the nature of the local angular potential energy surface. Larger inertial drops are correlated with higher OD stretching frequencies. The frequency of the OD stretch depends primarily on the strength (length) of the O-DO hydrogen bond. MD simulations have shown that the stretching frequency is much less sensitive to the O-DO angle (24). Weaker hydrogen bonds have larger oxygen–oxygen distances. The results in Fig. 3 based on the harmonic cone model indicate that the increase in OO distance is correlated with a shallower angular potential (lower harmonic oscillator frequency) and a larger amplitude angular motion. Intuitively, this correlation seems reasonable; as the OO distance increases, the attraction pulling the D toward the O is weaker, and therefore the energetic price that is paid for an angular deviation is reduced allowing the HOD more freedom to sample its angular space.

The discussion given above only describes the fastest inertial angular motions of the HOD molecule in its instantaneous local potential. This local potential only exists unchanged on a time scale comparable to the fluctuations of the water molecules surrounding the HOD. On a longer time scale, the evolution of the hydrogen-bonding network will change the local potential and eventually lead to complete orientational randomization. The experimental anisotropy decays (Fig. 1) show that the orientational relaxation occurs with a single time constant for all times >200 fs (see Fig. 1 Inset). It has been proposed that the mechanism for the long-time reorientation of water involves large-amplitude angular jumps (26, 40). The orientational motion of the HOD molecule therefore depends on two processes, the inertial motion that occurs on a fast time scale, and the large-amplitude angular jumps that occur on a longer time scale.

Although it is not possible for a correlation function to have exponential behavior at t = 0, we can qualitatively consider the effect that an exponential decay with a time constant of 2.6 ps would have on the estimated oscillator frequencies. Rather than attributing the anisotropy value at 100 fs solely to the inertial motion, there would also be a contribution to the drop from the exponential decay that would reduce the amplitude caused by the inertial motion. Although this is a small effect, the result would be higher oscillator frequencies and smaller values for 〈θ〉 than the values reported in Fig. 3, but the trends would remain the same.

The inertial motions of the HOD molecule are usually attributed to librations and hindered translations, and the oscillator frequencies in Fig. 3 lend support to that interpretation. The frequencies are somewhat smaller than the central frequency in the librational spectrum of HOD, which peaks at ≈585 cm⁻¹, but are larger than the frequencies attributed to hindered translations that occur at <200 cm⁻¹. The harmonic potential used here provides a qualitative picture of how the potential energy surface may be affected by the changing hydrogen bond strength, but it is not a true representation of the complicated forces and torques acting on the HOD molecule. Each of the ≈4 nearest neighbors constantly executes hindered translational motions, all of which affect the orientation of the central HOD molecule. We have simplified all of these forces into a single harmonic potential. Nonetheless, analysis of the experimental observable (the amplitude of the inertial drop) with the harmonic cone model provides useful information about the effect of hydrogen bond strength on the angular potential.

Temperature Dependence of the Inertial Angular Motion.

The many anomalous properties of water manifest themselves as the temperature and pressure of the system are changed (41). A number of molecular level structural models for water attempt to explain the changes in density of water as a function of temperature and/or pressure (1–6). At low temperatures, most models suggest that the structures in liquid water become extended tetrahedral networks, lending rigidity to the hydrogen-bonding network. At high temperatures, the water network is more flexible, with the hydrogen-bonding structures moving away from well developed tetrahedral geometries. The amplitude of the inertial drop as a function of temperature and OD stretching frequency provides information on the intermolecular potential created by the local hydrogen-bonding structures.

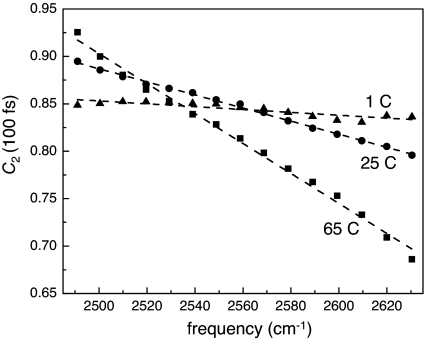
Fig. 4 shows the amplitude of the inertial drop as a function of OD stretching frequency at three temperatures: 1°C, 25°C, and 65°C. These three datasets are representative of the many temperatures that were studied. Several trends are immediately apparent. At high temperature, the inertial drop changes substantially as the strength of the hydrogen bond (OD stretching frequency) changes. Stronger hydrogen bonds (lower frequencies) allow less angular motion; weaker hydrogen bonds (higher frequencies) allow more angular motion. At low temperature the picture changes completely. At sufficiently low temperatures the inertial drop does not depend on the OD stretching frequency within experimental error.

Fig. 4.

Temperature dependence of the experimentally measured orientational correlation function at t = 100 fs as a function of OD stretching frequency. The solid lines are linear fits to the data.

As discussed above, there is an inherent uncertainty in the OD stretch frequency because of homogeneous dephasing. The effect of changing temperature on the homogeneous line width of water is unknown. However, the absorption line shape indicates that the homogeneous width does not dominate the spectrum at low temperature. Therefore, it is unlikely that the homogeneous width is responsible for the lack of frequency dependence at low temperature.

The disappearance of the correlation between the hydrogen bond strength and the inertial angular motion suggests that the collective effects of a more rigid hydrogen-bonding network control the motion of the HOD molecule at low temperatures. Whereas the OD spectroscopic probe is mainly sensitive to the O-DO hydrogen bond, the motion of the HOD molecule depends on the potential energy surface set up by all of its neighbors. For a correlation to exist between the OD stretch frequency and the inertial decay, the angular motion of the HOD must be strongly dependent on the O-DO hydrogen bond. At high temperatures, the structure of water is more open. The density decreases and the interactions between water molecules are weaker. The blue shift of the IR spectrum with increased temperature suggests that the distribution shifts toward weaker hydrogen bonds (5). The wavelength dependence of the inertial decay indicates that the O-DO hydrogen bond is very important in determining the angular potential. At the higher temperatures, the two hydrogen bonds donated by HOD, the O-DO hydrogen bond and the O-HO hydrogen bond, may dominate the angular potential. For a weak O-DO hydrogen bond, the O-HO hydrogen bond can range from strong to weak. In some sense, the interaction responsible for the potential could be thought of as ranging from weak to moderate. For a strong O-DO hydrogen bond, the O-HO hydrogen bond can again range from strong to weak, and the potential can range from moderate to strong. If the potential is dominated by only these two bonds, the result would be a correlation between the OD stretch frequency and the amplitude of the inertial decay. Recent instantaneous normal mode studies provide support for this interpretation, finding that the two donated hydrogen bonds determine the nature of the intermolecular potential energy surface almost entirely (22).

At low temperatures, the density of water increases and the IR spectrum (5) indicates that the equilibrium distribution favors stronger hydrogen bonds, producing a more ordered tetrahedral structure. The lack of wavelength dependence in the amplitude of the inertial component at low temperature (see Fig. 4) suggests that collective effects involving many water molecules determine the angular potential for the HOD molecules under observation. If many hydrogen-bonding interactions participate in determining the angular potential, then the influence of the single O-DO hydrogen bond under investigation is diminished. The result will be a lack of correlation between the OD stretch frequency and the amplitude of the inertial decay. In this picture, the fact that the inertial motion does not depend on the OD stretch frequency is indicative of multiwater molecule collective interactions dominating the angular potential at low temperatures. At high temperatures, however, the potential is more strongly determined by the two hydrogen bond interactions in which the HOD hydroxyls are hydrogen bond donors.

Concluding Remarks.

The short-time inertial motions of water molecules are important indicators of the nature of the local hydrogen-bonding structure and potential energy landscape. The results presented here demonstrate that the strength of the ODO hydrogen bond is correlated with the amplitude of the inertial angular motion. Weaker ODO hydrogen bonds allow more inertial angular motion than stronger hydrogen bonds. However, the correlation disappears at low temperature. The most likely cause of this change is the increase in collective interactions in the hydrogen-bonding network, which decouple the angular potential from a significant dependence on the ODO bond under observation.

A harmonic cone model based on inertial motion in a harmonic potential is used to estimate the characteristic frequencies of the intermolecular potential energy surface. The frequencies corresponding to the effective harmonic potential that restricts the short-time angular motion of the HOD molecule display a well defined trend, with lower frequencies matched with larger-amplitude inertial motions. The values for the oscillator frequencies fall in the range of ≈400 cm⁻¹ indicating that the orientational modes responsible for the short-time inertial motion are probably librations and hindered translations of the HOD. The translational motions of the surrounding water molecules exert torques on the HOD, changing its orientation through translational-rotational coupling.

There are two important trends in the inertial angular motion observed in these experiments: the trend with frequency (see Figs. 2 and 3) and the trend with temperature (see Fig. 4). Both provide new information that is intimately related to the nature of the water hydrogen bond potential energy surface, how it changes with hydrogen bond strength, and how it changes with temperature.

Materials and Methods

D₂O was added to H₂O to make a solution of ≈2.5 mol % D₂O in H₂O. Samples were housed in copper sample cells between 3-mm-thick CaF₂ windows separated by a 25-μm-thick Teflon spacer. The sample temperature was controlled by using a feedback temperature control system and a constant flow liquid N₂ cryostat. Sample temperatures were stable to 0.1°C

A Ti:Sapphire oscillator/regenerative amplifier pumped an OPA and difference frequency mixing stage (AgGaS₂) to produce ≈70 fs mid-IR pulses with ≈4 μJ per pulse. The polarization of an intense pump pulse (≈90%) is set to 45°. Components of the probe parallel and perpendicular to the pump are resolved after the sample by using a single wire grid polarizer in a computer-controlled rotation stage. The pump-probe signal is frequency resolved and detected with a 32-element MCT Array detector.