Scale-dependence of Cope's rule in body size evolution of Paleozoic brachiopods

Abstract

The average body size of brachiopods from a single habitat type increased gradually by more than two orders of magnitude during their initial Cambrian–Devonian radiation. This increase occurred nearly in parallel across all major brachiopod clades (classes and orders) and is consistent with Cope's rule: the tendency for size to increase over geological time. The increase is not observed within small, constituent clades (represented here by families), which underwent random, unbiased size changes. This scale-dependence is caused by the preferential origination of new families possessing initially larger body sizes. However, this increased family body size does not confer advantages in terms of greater geological duration or genus richness over families possessing smaller body sizes. We suggest that the combination of size-biased origination of families and parallel size increases among major, more inclusive brachiopod clades from a single habitat type is best explained by long-term, secular environmental changes during the Paleozoic that provided opportunities for body size increases associated with major morphological evolution.

Increasing body size is a pervasive predictor of population-level selection (1), and although macroevolutionary trends of increasing size, including Cope's rule (2–7), are known for many fossil groups, the mechanisms by which short-term size advantages are manifested at longer time scales remains poorly understood. Macroevolutionary size increases can occur via two distinct pathways: (i) maximum and mean size can increase within a clade because of passive diffusion from an unchanging lower size (sometimes termed “increasing variance”) or (ii) size increase can be driven and accompanied by increases in minimum size (7–10). Here, we confine Cope's rule to this second, driven pathway because it implies that clades with larger body sizes have greater evolutionary fitness than smaller clades. Such advantages can arise in several ways, including from the biological benefits of larger, optimal sizes (1, 4, 7); from size-linkages with changing environmental conditions (11–13); or from preferential sorting of clades associated with larger body size (14, 15). Analyses of size trends have focused on post-Paleozoic groups, limiting our understanding of size evolution during the otherwise well studied Cambrian and Ordovician radiations of animals and during the Paleozoic in general. Brachiopods offer a natural exemplar for such studies because of their fundamental contribution to these Lower Paleozoic radiations, their ecological dominance in most Paleozoic benthic marine communities, and their unrivaled fossil record (16–19). This study uses the largest and temporally most extensive database of fossil brachiopod sizes assembled to date to evaluate the existence and causes of size increases during the Cambrian through Devonian: the 170-million-year (Myr) interval covering the initial ascent of brachiopods to their zenith of Phanerozoic diversity. Recent cladistically based brachiopod classifications (17–20) allow detailed testing of the mechanisms responsible for these trends.

Results and Discussion

Size Trends Within Large Clades (Phylum, Classes, and Orders).

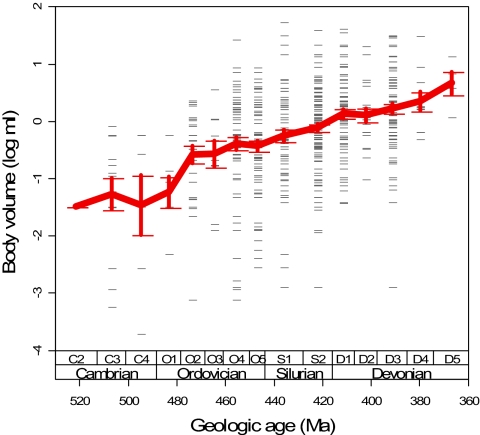
A database of brachiopod body sizes (measured here as shell volume) for 369 adult genera [see supporting information (SI) Appendix, Tables 1 and 2] from deep-subtidal, soft-substrate habitats demonstrates that brachiopod body size increased substantially and gradually during the Early and Mid-Paleozoic (Fig. 1), from a Cambrian mean of 0.04 ml (−1.40 log₁₀ ml ± 0.27 SE, n = 18 genera) to a Devonian mean of 1.55 ml (0.19 log₁₀ ml ± 0.06, n = 150). The magnitude of size increase between periods is statistically significant. We evaluated within-phylum dynamics by using maximum-likelihood comparisons among three evolutionary models: directional (driven, biased, general random walk) change (DRW), unbiased (passive) random walk (URW), and stasis (22), with DRW generally resulting in a pattern of Cope's rule when there is a positive directionality parameter (a maximum-likelihood estimate of the magnitude of the rate of size change). The brachiopod phylum-level size trend is overwhelmingly supported by the directional model (SI Appendix, Table 3), with a constant and positive rate of size increase of 0.013 log₁₀ ml/Myr ± 0.005. This rate of change is small but is sufficient to gradually increase brachiopod size by an order of magnitude every 77 Myr, on average. Sparse sampling during the Cambrian makes it impossible to resolve here whether size increase was continuous throughout the Cambrian–Devonian or was delayed until the Ordovician Radiation. Regardless, the increasing minimum size of brachiopods overall is consistent with Cope's rule, excluding a passive, diffusional trend of increasing variance through time (7–10). These increases are not the result of sampling heterogeneities because they are observed when sampling is standardized by rarefaction (SI Appendix, Fig. 5).

Fig. 1.

Increasing size trend in Cambrian–Devonian brachiopod genera from deep-subtidal, soft-substrate habitats. Time scale from ref. 21 with 11-Myr bins used in the Paleobiology Database. Each data point is the observed body volume for a single genus plotted at its bin midpoint age; several points overlap. Simultaneously increasing minimum, mean, and maximum sizes through most durations are consistent with Cope's rule. SE bars around means are 1 SD from the distribution of 2,000 bootstrap replicates. Trend in median sizes (data not shown) is nearly identical to mean trends. Ma, megaannum (millions of years ago).

Such a phylum-wide increase can result from the accumulation of within-clade processes where constituent clades are all tending toward larger size or from among-clade processes where constituent clades remain at a constant size throughout each of their histories but clades with small body-sized genera are replaced over time by clades with larger-sized genera (14, 15). Because recent brachiopod classifications use cladistically informed standards and recognize many monophyletic groups (17–20), we treated classes, orders, and families as representative clades of varying levels of hierarchical nestedness. Although many of these clades, especially families, are likely paraphyletic, our results remain adequate summaries of the evolutionary relationship between morphological and body size evolution in Paleozoic brachiopods because these taxonomic groups are defined by morphological similarity.

We evaluated the underlying mechanism for this trend by using two distinct tests. The first test applies the maximum-likelihood approach used above to differentiate DRW, URW, and stasis dynamics manifested in all genus occurrences within these clades of varying nestedness. Although this test is robust to errors in bin ages and sampling heterogeneities and does not require explicit genus-level phylogenies within each clade (22), it loses resolving power for shorter time series, and model selection can only be conducted on clades spanning a minimum of five time intervals. In addition to estimation of the directionality parameter for each clade, this method also allows estimation of the joint directionality parameter: the maximum-likelihood estimate of a single directionality parameter held constant across all constituent clades (22). The second test assesses the magnitudes and directions of change in the minimum and maximum sizes from the first to the last interval within clades (10) and can be conducted on clades spanning as few as two intervals. Unlike the first test, however, this test can be sensitive to outliers and may overlook important short-term dynamics between first and last occurrences.

Here, these two tests are concordant at the among-class and among-order levels, with both levels of largely monophyletic clades displaying independent, broadly parallel body size increases throughout the study interval (Fig. 2). Trends in these clades are best supported by the URW models (see SI Appendix, Table 3), although DRW and stasis models have substantial support in many instances. Nonetheless, among-class and among-order distributions of directionality parameters are significantly positive and of similar magnitude (Fig. 3 and SI Appendix, Table 5), with no clade best fit by a negative parameter. Although model selection is not powerful enough at these sample sizes to definitively rule out the parametrically simpler URW model (22), these results suggest a shared, but weak, tendency for size to increase within each of these clades when considered in aggregate.

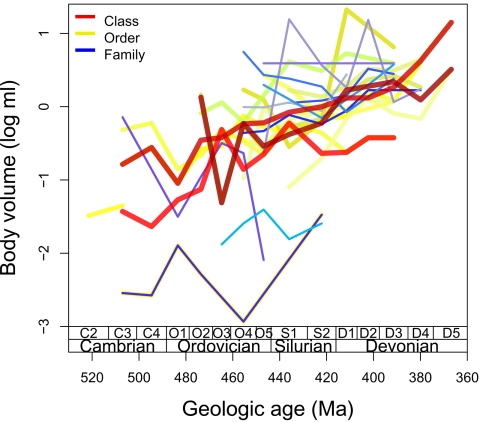
Fig. 2.

Mean size trends among brachiopod clades (classes, orders, and families). Different clades are distinguished by different shades of color, with line width corresponding to level of hierarchical nestedness. Large clades display parallel trends of increasing size (i.e., classes parallel other classes, orders parallel other orders), whereas trends within small, constituent clades (families) display more stochastic dynamics. Only clades with a minimum of 10 occurrences over five intervals are colored, except for the addition of order Paterinida, included to allow additional documentation of Cambrian trends, and the omission of class Craniata, which suffers from inconsistent sampling. The greenish trend represents the overlaying of a thick yellow order trend and a thin blue family trend because order Acrotretida here includes a single family. See SI Appendix, Fig. 6 for identities of these and additional taxa. SE bars are comparable in magnitude to those for the Brachiopoda as a whole, as shown in Fig. 1. Time scale details also are as in Fig. 1. Ma, megaannum (millions of years ago).

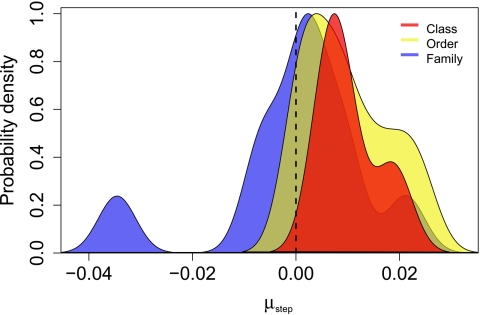
Fig. 3.

Within-clade directionality parameter distributions within three hierarchical clade levels. The directionality parameter, μ_step, is the maximum-likelihood estimate for the mean rate of directional size change (log₁₀ ml/Myr) within a brachiopod clade. Large clades [classes (n = 4) and orders (n = 11)] all have statistically positive distributions consistent with Cope's rule, whereas small, constituent clades (families, n = 10) are indistinguishable statistically from zero tendency (SI Appendix, Table 5). Distributions were estimated by using Gaussian kernel density estimation with shared bandwidth (0.00361); maximum-likelihood estimates are available in SI Appendix, Table 3. Similarly distinct distributions occur in the joint directionality parameters for each clade level and when the parameters for DRW, URW, and stasis models are combined by using multimodel inference (23, 24).

The tendency for widespread size increases is also supported statistically by the second test (Fig. 4 and SI Appendix, Table 4), where only two orders display a net decrease in maximum size and both decreases are of small magnitude. Seven orders are represented by few genera or include extremely large or small genera persisting for the duration of each order, and these orders potentially bias evaluation of the net behavior of minimum and maximum size. After removal of these 7 orders, 8 of 10 orders still display increases in maximum size, and the magnitude of increases is significantly positive. Although the majority of these ordinal increases are consistent with Cope's rule (increasing minimum and maximum, occurring in quadrant 1), the two orders with concurrent minimum size decreases are sufficient at this sample size to exclude Cope's rule as the sole mode of size change among orders (10).

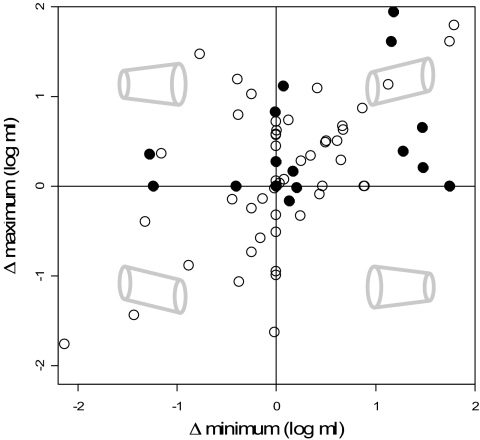
Fig. 4.

Net behavior of minimum and maximum size transitions within individual brachiopod orders (filled circles, n = 17) and families (open circles, n = 86). Axes note the change in the minimum (on abscissa) and maximum sizes, measured in log₁₀ ml, from oldest to youngest occurrences in each taxon (10); this overall behavior is portrayed by gray images, with time progressing to the right. For example, the upper right quadrant (quadrant 1) represents increases in the minimum and maximum (i.e., Cope's rule), while the upper left quadrant (quadrant 2) represents an increase in the overall size range (i.e., increased variance) caused by increasing maximum and decreasing minimum sizes. Several points overlap on origin (values provided in SI Appendix, Table 4).

This parallelism for increases in size among independent clades reduces the likelihood that the trends are an artifact of methodological or taphonomical biases. There is no reason to suspect that changes occurred in the field practices used to collect fossils from these periods, making it unlikely that small brachiopods were overlooked by systematists in Mid-Paleozoic collections. Indeed, the brachiopod order with the consistently smallest sizes, Acrotredida, also displays simultaneously increasing minimum and maximum size trends (SI Appendix, Fig. 6B and Tables 3 and 4). The increases also transcend differences in shell structure and mineralogy, decreasing the likelihood that the trends are simple artifacts of taphonomical biases. Classes Lingulata and Paterinata have organophosphatic shells, and the remaining classes share calcitic shells that have a variety of structural fabrics (17–20). Finally, the trends are also unlikely to be an artifact of taxonomic practice because of the cladistic basis for high-level brachiopod classification (20) and standardized taxonomic practices for families and lower levels (17–19). Improbably large degrees of bias—not simply error—would have to exist to eliminate these broadly congruent trends.

Size Trends Within Smaller Constituent Clades (Families).

The same tendency toward size increase is not observed within smaller constituent clades, represented here by families. Trends at this level are more variable (Fig. 2), and individual clades are best fit by the URW model (SI Appendix, Table 3), with much less support for the DRW and stasis models compared with their more-inclusive clades (classes and orders). This random, unbiased behavior across families is most clearly visible in the distribution of directionality parameters (Fig. 3), which is indistinguishable from zero tendency (SI Appendix, Table 5) and displays greater variation compared with their more-inclusive clades (orders and classes). This lack of an overall tendency is also evident in the behavior of maximum and minimum sizes in these families (Fig. 4 and SI Appendix, Table 4). Substantial numbers of families plot in all four quadrants, with most displaying either mutual increases in minimum and maximum size (i.e., Cope's rule) or mutual decreases. The rarity of changes in variance (quadrants 2 and 4) might be expected here because these smallest clades have short durations and few genera per interval. However, maximum size increases are neither significantly more frequent than decreases (12 vs. 8) nor of greater magnitude when analyses are restricted to the 20 best-sampled families. There is also no statistical support for Cope's rule in the families displaying increasing maximum size, with only eight of these plotting in quadrant 1.

It might be argued that the decreasing tendency for size increases within smaller clades is an artifact of diminishing sample sizes (25, 26). This is unlikely here for two reasons. In the second test (Fig. 4), those families not demonstrating size trends were the ones with the most occurrences and longest durations; poorly sampled families were removed to preclude such biases. Also, although sampling can decrease the precision of parameter estimates and the power of model discrimination in the maximum-likelihood tests (Fig. 3), it does not affect the accuracy of these parameters (22). It is notable, in this light, that the joint directionality parameter calculated across all families (a measure less prone to sample-size effects because it estimates a shared size tendency across all clades simultaneously) remains negligibly positive (4.7 × 10⁻⁷ log₁₀ ml/Myr ± 9.6 × 10⁻⁶) and substantially below that for classes (0.007 log₁₀ ml/Myr ± 0.004) and orders (0.007 log₁₀ ml/Myr ± 0.003). Thus, the dynamics in clades of varying hierarchical nestedness are distinct and consistent within each level of nestedness, with dynamics within the smallest constituent clades insufficient to ratchet up to those observed within larger, more inclusive clades.

Macroevolutionary Selection Among Families.

One way to reconcile such discrepancies would be if size-related macroevolutionary processes within constituent clades (e.g., those represented here by families) are different from those within their more inclusive clades (14, 15, 27, 28). Three possibilities—none mutually exclusive but each capable of creating the observed trends (27)—include (i) positive bias in the mean size of originating families, (ii) positive correlation between family mean body size and geological duration, and (iii) positive correlation between family mean body size and genus richness (a proxy for speciation rate). The first hypothesis implies that size-biased selection acts only during speciation events, coincident with major morphological changes of an extent that a systematist would define a new family. The latter two hypotheses imply that larger size preferentially connotes greater family-level fitness. Because family-level brachiopod phylogenies are not available, we tested these three hypotheses for the 87 best-sampled families by computationally resampling candidate ancestor–descendent pairs at random on the basis of order of stratigraphic occurrence and evaluating how frequently each hypothesis was demonstrated as statistically significant. This technique essentially evaluates the sensitivity of each hypothesis to changing phylogenetic structure (29) and has been used in other analyses of Cope's rule in fossil taxa where phylogenies were unavailable (4). Such stratigraphically based phylogenies are also reasonable given the exceptionally complete fossil record of brachiopods (16, 20, 30, 31).

Newly originating brachiopod families here have significantly larger body sizes—on average 0.238 log₁₀ ml (±0.072 SD), more so per origination event—than their ancestors in ≈75% of candidate phylogenies (SI Appendix, Fig. 7 and Tables 6 and 7). These few increases alone are nearly sufficient to account for the magnitude of the overall phylum-level size trend (Fig. 2). This result is unlikely to be caused by taxonomic practice because body size is not a basis for brachiopod classification (17). In contrast, significant size-biased relationships for family duration or genus richness occur in fewer than 17% and 3% of phylogenies, respectively. These results are upheld when restricted to families whose last occurrences here predate the final D5 bin, where artificial truncation might bias results. Taken together, these results suggest that major morphological changes resulting n the origin of new families also are associated with significant increases in body size. The origination of new clades with large body sizes from smaller, and potentially less specialized, ancestors bolsters a longstanding, but previously poorly documented, explanation for Cope's rule (7).

The pervasive Cambrian–Devonian brachiopod size increases reported here, encompassing the critical Cambrian and Ordovician radiations, conform to Cope's rule at multiple hierarchical levels, with strong support at the level of phylum and substantial, but not exclusive, support at the levels of class and order, where increasing size range (variance) plays a subsidiary role. These net increases are caused not by the accumulation of trends within smaller constituent clades (families) but instead by the preferential origination of new families of initially large body size, implying that size has little long-term impact within families once they originate. This result is consistent with other size analyses questioning whether microevolutionary dynamics can be extrapolated to larger scales (10). Any proximate explanation for these trends must reconcile the parallel driven increases among independent classes and independent orders, the more stochastic dynamics within families, and the size-biased origination of families. Given that these trends are expressed in multiple, independent brachiopod clades from deep-subtidal, soft-substrate habitats, a secular environmental explanation—perhaps related to changes in energetics, trophic complexity, productivity, nutrient availability, or oceanographic or substrate characteristics (32–35)—seems most likely and facilitated the correlated evolution of both major morphological change and increased body size.

Materials and Methods

Characteristics of the Brachiopod Size Database.

The database used here includes 1,655 brachiopod occurrences of 369 genera from 239 collections (vetted from 97 publications in the global literature) representing deep-subtidal, soft-substrate habitats (SI Appendix, Table 1, and the Paleobiology Database accessed August 2006 at http://paleodb.org/cgi-bin/bridge.pl). We dated collections by using the Paleobiology Database binning scheme with subequal stage-level durations (11.4 Myr ± 2.8 SD) and boundary dates taken from ref. 21. For additional details, see SI Appendix, Materials and Methods.

Size Measurement and Conversion to Body Volume.

To obtain adult brachiopod genus body sizes, we used calipers to obtain anteroposterior, transverse, and dorsoventral (ATD) measurements (in millimeters) on one specimen per genus from monographic illustrations, primarily those in the brachiopod volumes of the Treatise on Invertebrate Paleontology (17–19). Methodological analyses (36–38) have demonstrated that such measurements provide accurate estimates of body size. Analyses were conducted at the level of genus (or genus-equivalents: members of indeterminate taxa), using a randomly chosen species to represent each genus.

Body volume was used as a common measure of body size to mitigate against biases caused by shape changes during the Cambrian–Devonian and because volume is strongly correlated with body mass. Use of any raw ATD measurement alone resulted in essentially identical results. Body volume was estimated allometrically from the product of the three ATD measurements (converted to centimeters): log₁₀ (volume, ml) = 0.896 log₁₀ (ATD, cm³) − 0.265 (equation 5 in ref. 38). This equation is applicable for a wide range of Paleozoic benthic invertebrates and provides an unbiased estimate of shell volume (<1 log₁₀ ml) (38). Size was transformed to base-10 logarithmic units for all analyses.

Maximum-Likelihood Time-Series Analyses of Size Evolution.

Trends were assembled from the series of size distributions of all unique genera (or genus-equivalents) within each bin, with mean size (log₁₀ volume) and SE calculated from 2,000 replicates (with replacement) (39). Maximum likelihood was used to evaluate the model support of each time series for three evolutionary models: DRW, URW, and stasis (R library, paleoTS; refs. 22 and 40). DRW with a positive directionality parameter will generally result in a trend of Cope's rule. DRW was modeled as a general random walk in which parameters were estimated from the normal distribution (mean and variance parameters) of size transitions best supported by each time series. The URW model is similar, but the distribution mean is set to zero. The stasis model also has a normal distribution (mean and variance), but it is optimized across all time bins independent of size transitions; in other words, it assumes that size is not autocorrelated through time. In this manner, stasis models no net temporal trend (22, 26). Model selection used small-sample, unbiased Akaike's information criterion (AIC_c) (23, 41) to rank the fit of the observed time series to these three models given differences in their number of parameters. Size variance within each clade was not pooled across bins because of significant heterogeneity. Relative support for each model was assessed by using Akaike's weight (23, 24).