Testing evolutionary theories of menopause

Abstract

Why do women cease fertility rather abruptly through menopause at an age well before generalized senescence renders child rearing biologically impossible? The two main evolutionary hypotheses are that menopause serves either (i) to protect mothers from rising age-specific maternal mortality risks, thereby protecting their highly dependent younger children from death if the mother dies or (ii) to provide post-reproductive grandmothers who enhance their inclusive fitness by helping to care and provide for their daughters' children. Recent theoretical work indicates that both factors together are necessary if menopause is to provide an evolutionary advantage. However, these ideas need to be tested using detailed data from actual human life histories lived under reasonably ‘natural’ conditions; for obvious reasons, such data are extremely scarce. We here describe a study based on a remarkably complete dataset from The Gambia. The data provided quantitative estimates for key parameters for the theoretical model, which were then used to assess the actual effects on fitness. Empirically based numerical analysis of this nature is essential if the enigma of menopause is to be explained satisfactorily in evolutionary terms. Our results point to the distinctive (and perhaps unique) role of menopause in human evolution and provide important support for the hypothesized evolutionary significance of grandmothers.

1. Introduction

Menopause marks the end of the human female reproductive capacity life and occurs at age approximately 50 years in all populations (Gosden 1985). The preceding 10–15 years are characterized by declining fertility, so most of a woman's reproductive potential is compressed into only approximately 20 years of a longer biological lifespan. By contrast, other female primates retain fertility almost to the end of the lifespan (Pavelka & Fedigan 1991; Caro et al. 1995). This difference between the life-history patterns of human and non-human primates has prompted interest in the evolutionary factors that might explain menopause (Williams 1957, 1999; Kirkwood & Holliday 1986; Hill & Hurtado 1991, 1996; Rogers 1993; Peccei 1995, 2001; Hawkes et al. 1997, 1998; Kirkwood 1997; Turke 1997; Packer et al. 1998; Mace 2000; Perls & Fretts 2001; Shanley & Kirkwood 2001; Hawkes 2003, 2004; Cohen 2004).

If menopause does have an evolutionary basis, it is necessary that any fitness advantage offsets the obvious disadvantage of curtailed childbearing. The age of menopause is at least partly genetically determined (Snieder et al. 1998; Peccei 1999; Kirk et al. 2001; Pettay et al. 2005), which supports the idea that selection may have acted to optimize the length of the fertile portion of the life cycle.

The two major hypotheses to explain the evolution of menopause are based on (i) the extremely protracted dependency of human infants on protection and provisioning by adults, particularly the mother, and (ii) the opportunities for intergenerational cooperation within kin groups. The high dependency of human offspring appears to be due to the combination of a large brain and the pelvic constraint on the birth canal. Babies are born with brain sizes near to the limit compatible with safe delivery, resulting in significant risk in case of complications (Abitbol et al. 1996), yet even so the newborn infant still requires its brain to grow for a considerable period before becoming capable of independent survival. Maternal mortality increases with age (Yerushalmy et al. 1940; Grimes 1994), so it may make sense to cease having more children when the risks outweigh the benefits. This argument alone can account for a post-reproductive life equivalent to the time it takes to raise the last born successfully to independence. On the other hand, humans are unique in the extent to which kin assist in care and provisioning of young. Thus, the alternative theory is that menopause enhances fitness by producing post-reproductive grandmothers who can assist their adult offspring by sharing the burden of provisioning and protecting their grandchildren (Hawkes et al. 1998; Hawkes 2004). Human infants are unable to provision themselves to any realistic degree before age 5, and even then the period of nutritional dependency may last until puberty (Kaplan 1996; Bogin 1997). This high dependency seems at odds with the comparatively early age of human weaning, unless people other than the mother also participate in the care and provision of a child. The prime candidate for such participation is the maternal grandmother. Not only is she the person with the greatest assured genetic interest in her daughter's reproductive success, but also there is growing empirical evidence for her involvement in this role. The presence of a grandmother results in children being larger (Hawkes et al. 1998) and having reduced mortality (Sear et al. 2000, 2002; Voland & Beise 2002; Lahdenperä et al. 2004), and in mothers having higher fertility (Bereczkei 1998; Lahdenperä et al. 2004).

An essential test for any evolutionary theory is that it makes quantitative sense, i.e. the proposed adaptation actually results in an increase in fitness. In a recent quantitative study, we showed that neither of the two major hypotheses can account for evolution of menopause by itself, but that in combination they can readily do so (Shanley & Kirkwood 2001). Ultimately, theories must be tested with empirical data. This requires access to populations in which individual records are sufficiently detailed and living conditions sufficiently representative of those under which ‘natural fertility’ might be observed. Such populations are rare but comprehensive life-history data were gathered in four villages in The Gambia, beginning in 1950 (McGregor 1991). In 1975, a medical centre was established, which resulted in a rapid improvement in child survival. We gained access to the data of 1950–1975 comprising detailed records of over 5500 individuals. Multi-level statistical analysis of the data has shown that child survival in the first year of age depends strongly on the presence of the mother, with no significant contribution from grandmothers. Beyond the first year, particularly between first and second years, the presence of a maternal grandmother also exerts a significant protective effect (Sear et al. 2000, 2002).

The Gambian data provided us with an opportunity to test the competing hypotheses for the evolution of menopause, making use of the theoretical life-history model developed by Shanley & Kirkwood (2001). By quantifying the measurable benefits to children receiving maternal and grandmaternal care, we use the model to determine whether menopause actually enhances fitness, as compared to the situation where fertility is continued for longer. In view of the exhaustive efforts required to collect data of sufficient quality, and the pervasive effects of social and economic development on populations around the world, we believe that this opportunity may be unique.

2. Material and methods

(a) Data

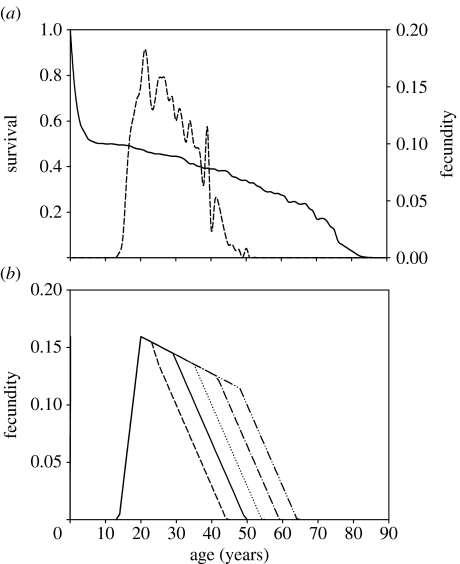
The data for this study come from the two most accurately documented villages, Keneba and Manduar, in the West Kiang district of The Gambia. The data were collected beginning in 1950 and provide sufficient detail to produce complete genealogical trees of the population (McGregor 1991). In 1975, the British Medical Research Council established a medical centre in the largest village of Keneba. This substantially improved the healthcare and had a strong impact on demographic parameters such as child survival. The data used in this analysis were therefore restricted to the period before 1975. Figure 1a shows the composite survival and fecundity patterns for the female population in Keneba during this period. Throughout this paper, fertility is used as a descriptive term and fecundity as a quantitative measure representing female births.

Figure 1.

(a) Age-specific survival and fecundity patterns within the study population. Fecundity is represented by the dashed line. (b) Linearized representation of the observed fecundity pattern (solid line) and its modification for hypothetical ages of menopause between 45 and 65 years.

The data have been analysed using multi-level regression analysis to identify the influence of kin on mortality (Sear et al. 2000) and fecundity (Sear et al. 2003). Table 1 summarizes the results for Keneba together with the neighbouring village of Manduar. The mortality of children in the ranges 0–12 and 12–24 months was increased dramatically by the death of the mother. The mortality of children aged 12–24 months was reduced by the presence of the maternal grandmother. Fathers, siblings, grandfathers and paternal grandmothers had no statistically significant impact on child mortality. Adult fecundity was largely independent of maternal kin (Sear et al. 2003), which is surprising, given the assistance that mothers may provide their adult daughters both in direct care for their existing children and in helping with farming tasks. Mothers-in-law had, however, a slight positive effect on the probability of giving birth, but this was not included in the analysis.

Table 1.

Statistically significant effects of maternal and grandmaternal survival on child mortality within the Gambian dataset shown with an estimated 95% CI. (See Sear et al. 2000, 2002.)

child's age	0–1 years	1–2 years
surviving mother effect	13.4-fold decrease (4.0–44.2)	11.7-fold decrease (2.5–54)
surviving grandmother effect	—	2.0-fold decrease (1.2–3.5)

(b) Theoretical model

The model (Shanley & Kirkwood 2001) is based on the schedules of adult and juvenile mortality and fecundity, and it groups the female population into different classes with respect to life-history state. Total annual mortality at age x is partitioned into separate components μ_i(x) associated with specific features, such as childbearing. The probability ϕ_i(x) of being exposed to individual components of mortality is also calculated as a function of age. The predicted survival and fecundity curves are obtained and the free parameters of the model estimated by least-squares fit of the predicted survival and fecundity for the raw data. Each class experiences reproduction and mortality appropriate to its state, which may be affected by the giving or receiving of intergenerational support.

For infants, there are four possible states defined by the presence or absence of mother and grandmother. The probability that an infant of age x has a living mother is given by

$${\varphi }_{\text{mother}}(x)=\sum _{y=x_{\text{maturity}}}^{x_{\text{menopause}}}{\text{e}}^{-ry}{b}_y{l}_{y+x},$$

where l_x and b_x represent the survival and fecundity (number of female births), respectively, at age x, and x_maturity and x_menopause refer to the minimum and maximum ages of reproduction, respectively. The factor e^−ry is required to take account of non-stationary populations, where r is the intrinsic rate of natural increase. The probability that an infant that was born to a mother (age y) has a living grandmother is

$${\varphi }_{\text{grandmother}}(x)=\sum _{y=x_{\text{maturity}}}^{x_{\text{menopause}}}{\text{e}}^{-ry}{b}_y{l}_y{\varphi }_{\text{assist}}(y+x),$$

where ϕ_assist(x), the probability that a female (age x) has a living mother who does not have dependent children of her own, is given by

$${\varphi }_{\text{assist}}(x)=\sum _{y=x+x_{\text{maturity}}}^{x+x_{\text{menopause}}}{\text{e}}^{-r(y-x)}{b}_{y-x}{l}_y(1-{\varphi }_{\text{depchild}}(y)),$$

the factor (1−ϕ_depchild(x)) accounting for the loss in assistance due to the presence of dependent children (0–3 years), where

$${\varphi }_{\text{depchild}}(x)=2(b_x+l_1{b}_{x-1}+l_2{b}_{x-2}).$$

See Keyfitz (1977) for further details regarding the derivation of demographic probabilities.

The associated mortality components μ_mother(x), μ_orphan(x), μ_grandmother(x) and μ_{nograndmother}(x) are deduced from μ(x) calculated from the survival data shown in figure 1 along with the information from table 1 that μ_mother(1)=13.4 μ_orphan(1), μ_mother(2)=11.7μ_orphan(2) and μ_grandmother(2)=2.0μ_{nograndmother}(2).

Young adults have high fecundity and are exposed to mortality risks linked with childbirth and childcare. The probability of childbirth ϕ_birth(x) is 2b_x, and a two-component model of the associated exponentially increasing mortality rate μ_birth(x) is assumed

$${\mu }_{\text{birth}}(x)=({\mu }_{\text{birth}}(x_{\text{maturity}})-{\alpha }_{\text{birth}})+{\alpha }_{\text{birth}}\text{exp}({\beta }_{\text{birth}}(x-x_{\text{maturity}})).$$

We use four sets of values for the parameters α_birth and β_birth: none, (0.0, 0.0); low, (0.002928, 0.1); medium, (0.000485, 0.181221); and high, (0.0000001, 0.5) and a value of 0.05 for the initial risk of childbirth mortality μ_birth(x_maturity). The values of α_birth and β_birth were chosen to explore a range of age-related increase in mortality above the age of 50 years, which in the absence of data is hypothetical, while for each set retaining a similar profile below this age. The probability of having dependent children ϕ_depchild(x) is given above and a value of 0.05 for the associated mortality rate μ_depchild was found by least-squares fit to the survival data. Middle-aged adults experience declining fecundity and an age-related increase in the risk of childbirth. Older adults show a senescence-related increase in mortality μ_senescence(x) described by the standard Gompertz–Makeham equation,

$${\mu }_{\text{senesence}}(x)={\mu }_0\text{exp}(\beta (x-x_{\text{maturity}})).$$

We use a value of 0.005 for μ₀ and 0.085 for β.

The probability of belonging in each state class is calculated from the survival and fecundity data. Predicted survival l_calc at age x+1 is calculated by exposing the cohort of survivors at age x to components of mortality μ_i with probability ϕ_i as follows:

$$l_{\text{calc}}(x+1)=l_{\text{calc}}(x)\sum \Phi (x)\text{exp}\left(-\sum \mu (x)\right),$$

where Φ(x) is the probability of being in any given state as a function of the product of the probabilities ϕ_i(x) and (1−ϕ_i(x)), and ∑μ(x) is the total mortality associated with that state. For example, for an infant age x,

$$\begin{array}{l}{l}_{\text{calc}}(x+1)=l_{\text{calc}}(x)({\varphi }_{\text{mother}}(x){\varphi }_{\text{grandmother}}(x)\text{exp}(-{\mu }_{\text{mother}}(x)-{\mu }_{\text{grandmother}}(x)))\\ +((1-{\varphi }_{\text{mother}}(x)){\varphi }_{\text{grandmother}}(x)\text{exp}(-{\mu }_{\text{orphan}}(x)-{\mu }_{\text{grandmother}}(x)))+({\varphi }_{\text{mother}}(x)(1-{\varphi }_{\text{grandmother}}(x))\text{exp}(-{\mu }_{\text{mother}}(x)-{\mu }_{\text{nograndmother}}(x)))+((1-{\varphi }_{\text{mother}}(x))(1-{\varphi }_{\text{grandmother}}(x))\text{exp}(-{\mu }_{\text{orphan}}(x)-{\mu }_{\text{nograndmother}}(x)))\end{array}$$

(c) Analysis

Life-history data are used to compute the intrinsic rate of natural increase, r, of the population, which we take as a measure of evolutionary fitness. Simulations were obtained by varying the fecundity schedule, replacing the fecundity curve shown as the solid line (figure 1b) with the hypothetical curves, and using the mortality and fecundity costs and benefits determined from the data and model to converge iteratively on a stable population. Using this procedure we explore how selection might influence the age at which fecundity ceases. If for a given set of model parameters, which in turn we derive from the multi-level statistical analysis (Sear et al. 2000), there is a fitness optimum (a peak in the fitness curve) associated with ceasing reproduction early; this indicates that the hypothesis on which the model is based can explain evolution of menopause. If there is no optimum (i.e. if r continues to increase as fecundity is extended to later ages), this suggests that the model cannot account for the evolution of menopause. (N.B. In interpreting the figures, it is important to note that fitness can be meaningfully compared only within the same curve for the different assumed ages of menopause. Each individual curve is based on its particular assumptions about the structure of the relationships among kin of the factors affecting survival and fertility; the curves pass through a common point for menopause at age 50 because each has been constrained by the actual data. Comparisons of fitness levels between curves have no meaning in this context.)

3. Results

The Gambian population has a growth rate of r=0.013, as determined directly from the survival and fecundity data in figure 1a. We then calculated how r would vary if we imposed menopause at different ages between 45 and 65 years, the other life-history parameters being estimated from the data. This permits the possible evolutionary advantage of menopause to be revealed. Next by varying, within this framework, some of the characteristics affecting the population, we could examine the effect of these characteristics on the strength of the basis for the evolution of menopause.

We first considered the contribution from age-related maternal mortality. Between 1950 and 1975 total annual maternal mortality was approximately 0.01. There were too few maternal deaths to establish the relationship with age with any reliability, but other data suggest an exponential increase in age-related maternal mortality in this population prior to the age of menopause (Yerushalmy et al. 1940; Grimes 1994). Since our model required us to extrapolate for hypothetical ages of menopause above 50 years, we assumed that in the absence of menopause the exponential rise would continue above age 50 and used a series of exponential curves with slope parameters denoted as low, medium and high (figure 2). The absence of a clear maximum in the fitness curve even at the highest level of exponential age-related increase in maternal mortality indicates, as found in Rogers (1993) and later in Shanley & Kirkwood (2001), that the increasing mortality risk of giving birth at older ages was not sufficient on its own to select for menopause.

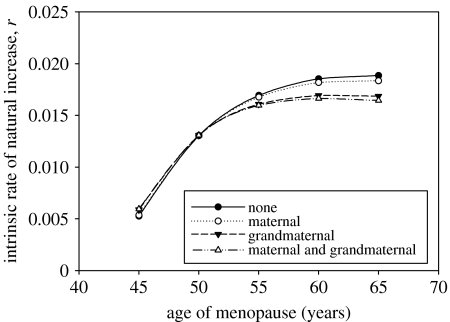
Figure 2.

Estimated relationship between intrinsic rate of natural increase, r, and age at menopause for three levels (zero, medium and high) of age-related exponential increase in the risk of mortality during childbirth. The medium level corresponds to a doubling of risk every 3.8 years. The high level corresponds to a doubling of risk every 1.4 years.

We next included the effects of the presence of surviving mothers and/or grandmothers on child survival, using parameters from the ‘high’ level of maternal mortality shown in figure 2. The maternal influence alone had little effect on producing a fitness maximum for menopause (figure 3; compare top with second curve), even though the impact of maternal survival on infant mortality was shown by statistical analysis of the data to be clearly important. The absence of a fitness effect associated with menopause was due to the fact that although the magnitude of the effect (13.4-fold from 0 to 1 year; 11.7-fold from 1 to 2 years; see table 1) was large, the probability of being orphaned was actually quite small. Less than 2% of 0–2-year-olds were affected. This figure was predicted to rise to 3.5% in the hypothetical case that the age of menopause was delayed to 65 years, but even at this level the effect was not critical. On the other hand, we found that the observed influence of grandmothers on child survival from 1 to 2 years was of greater importance for the fitness curve (figure 3; compare top with third curve), even though the magnitude of the protective effect (2.0-fold increased survival; table 1) was smaller than that for mothers. This was due to the fact that varying the age of menopause had a significant impact on the probability that a child might benefit from the presence of a surviving grandmother without dependent offspring of her own. For example in the curve shown, the survival of 50-year-old females is reduced from 35 to 20% when the age of menopause is increased to 65 years. The probability of being encumbered with dependent offspring increases from 1 to approximately 50%. The net result in the population as a whole is that a 2-year-old child has only a 16% chance of receiving grandmaternal care compared with 58% with an age of menopause of 50. These figures are obtained from ϕ_grandmother(2) which is used to compute the total probability that an infant 1–2 years old is born to a mother aged between 15 and the age of menopause (50 and a hypothetical 65 years in the preceding case) who herself has a living mother available to provide assistance (§2). An interesting point revealed by the model is that although the dependent-offspring effect appears as more important for this age class, the population growth rate is far more sensitive to the reduction in survival. This is explained by the fact that the mortality burden that older females suffer by giving birth removes them permanently from the population, which alters the entire population structure. The combined effect of maternal and grandmaternal influences was sufficient to produce a clear fitness maximum for menopause (figure 3, bottom curve), albeit at an age between 55 and 60 years instead of approximately 50.

Figure 3.

Estimated relationship between the intrinsic rate of natural increase, r, and age at menopause for four cases: (i) no effect of mother or grandmother on child survival; (ii) death of mother assumed to result in 13.4-fold increase in mortality of children aged 0–1 years and 11.7-fold increase in mortality of children aged 1–2 years; (iii) death of grandmother assumed to result in 2.0-fold increase in mortality of grandchildren aged 1–2 years; and (iv) both (ii) and (iii). In all cases, the age-related exponential increase in the risk of mortality during childbirth is assumed to be at the high level from figure 2.

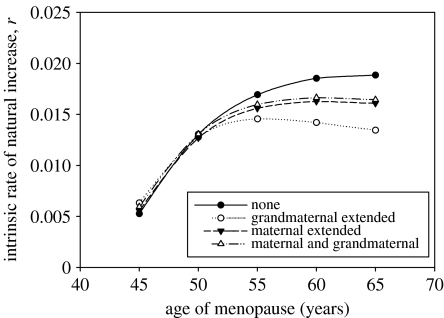
Although orphaned 3-year-olds can and do survive, they are certainly not self-sufficient and in some populations this dependency extends to puberty (Kaplan 1996). To test the importance of this factor in our analyses, we also performed calculations for two extreme assumptions that: (i) the orphan-mortality disadvantage continued, at a linearly declining rate, from ages 2 to 15, when it became zero and (ii) a similarly extended effect was encountered for the disadvantage of not having a grandmother (note that in all cases a grandmother is assumed to become available to provide assistance when her last-born child reaches 3 years of age; i.e. the calculation of ϕ_depchild(x) in ϕ_assist(x) is unaltered). Figure 4 shows the predicted relationships between fitness and age of menopause in these cases. As a point of reference, the two upper curves correspond to the upper and lower curves in figure 3. The effect of the assumption with regard to the maternal contribution was not notably different from the combined maternal and grandmaternal effect that was seen in figure 3(iv). This is unsurprising because few children lose their mothers in the first 2 years, and those that do are not represented at older ages owing to the high levels of mortality. However, when the grandmaternal effect was extended, the fitness benefit of menopause became more sharply defined. This differential impact on fitness can be explained by the greater probability of a child experiencing the grandmaternal than the maternal effect.

Figure 4.

Estimated relationship between the intrinsic rate of natural increase, r, and age at menopause for four cases: (i) no effect of mother or grandmother on child survival; (ii) death of mother assumed to result in 13.4-fold increase in mortality of children aged 0–1 years and 11.7-fold increase in mortality of children aged 1–2 years and death of grandmother assumed to result in 2.0-fold increase in mortality of grandchildren aged 1–2 years; (iii) as (ii) where the 11.7-fold increase in mortality of children aged 1–2 years following the death of the mother is assumed to decrease linearly between ages 2 and 15 years; (iv) as in (ii) where the the 2.0-fold increase in mortality of grandchildren aged 1–2 years following the death of the grandmother is assumed to decrease linearly between ages 2 and 15 years.

An important aspect not yet discussed is the sensitivity of the model predictions to the range of values given in table 1. The range corresponds to an estimated 95% CI derived from standard errors presented in Sear et al. (2000). The model predictions are relatively insensitive to the surviving mother effects on child mortality for 0–1 and 1–2 years even at the upper limits of the fold differences. The model is far more sensitive to the surviving grandmother effect. One extreme of the 95% interval approaches a fold difference of 1, and not surprisingly the model predictions are close to those presented for ‘none’ in figures 3 and 4. The fitness curve predicted with the other extreme, a fold difference of 3.5, corresponds very closely with the grandmaternal extended-care curve shown in figure 4, which again highlights the dramatic effect that a grandmother can have. We have presented the results in detail only for the high age-related increase in maternal morality and care parameter set. The results for the medium and low age-related increase show a similar pattern, with the conditions for a maximum becoming increasingly severe. In the case of no age-related increase there was no evidence of a maximum under any of the conditions considered.

4. Discussion

Not only is it intriguing to try and resolve the evolutionary puzzle of menopause but also, at a time when assisted-fertility techniques offer new opportunities to overcome the biological limits on human fertility, the advisability of such approaches might be better informed if we knew why menopause occurs. The Gambian data are a highly valuable resource for this purpose. To perform this test requires, we assume at least initially, that the circumstances under which the people lived, gave birth and died in the two Gambian villages during the period 1950–1975 were representative of those under which menopause might have evolved. We will return to this assumption later.

The strongest influence on child survival detected in the statistical analysis of the Gambian dataset was the effect of maternal survival (table 1). However, even this was only statistically significant during the first 2 years of life. Since the probability of a child losing its mother during this time was small, there was little support from these data for the hypothesis that the age-related increase in maternal mortality, together with the potential loss of maternal care, might be sufficient to cause menopause (Peccei 1995; Packer et al. 1998). The only other kin found to have a significant influence on child survival was the maternal grandmother. The grandmother's influence was significant during a short window of time (1–2 years of a grandchild's age) and it is probably significant that this corresponds quite closely with the age of weaning. This fits with the grandmother hypothesis for the evolution of the menopause (Hawkes et al. 1997, 1998; Hawkes 2003), and with similar proposals for the evolution of human childhood (Bogin 1997). We might have expected that the benefit gained by having a grandmother during this critical stage of development would also result in earlier reproductive maturation or higher levels of subsequent fertility. However, these effects were not statistically significant within the data.

Overall, our results highlight the importance of the grandmaternal contribution. Nevertheless, the absence of a clear optimum, which would be revealed by declining fitness for ages of menopause above 50, shows that the reduction of grandchild mortality is only just sufficient to offset the fitness benefits that might otherwise accrue from continued reproduction of the grandmother herself. Two possibilities exist which, when added to those represented in our analysis, would reinforce the optimality of menopause at 50. Firstly, some of the effects not statistically significant in the data might still be real. For example, although the significant effects of a mother's and/or grandmother's presence were limited to short windows in a child's development, it seems highly likely that smaller effects would operate outside these windows. We chose conservatively to include only those factors whose magnitude exceeded the threshold for significance. This will have lessened the power of our model to reveal the optimality of menopause. Secondly, it is probable that in order to maintain reproductive viability beyond age 50 would require significantly greater physiological investments in the maintenance and repair of not only the ovaries but also the female soma. Grandmothers enhance the survival of their grandchildren through protection and/or provisioning. Thus, they lift some of the burden from adult daughters, enabling higher levels of fertility and an earlier age of weaning. Bearing in mind that one of the primary factors in life-history evolution is the trade-off between resources invested in body maintenance (survival) and fecundity, it is easy to see how the physiological outcomes of investments in a daughter's reproductive success may be self-reinforcing, by drawing upon the concept forming the core of the disposable soma theory of ageing (Kirkwood & Holliday 1986; Kirkwood 1996). We know of no data that would permit these effects to be quantified so we did not include them in our work, but it is clear that they would tend to depress the fitness of a life-history strategy in which menopause was postponed. Along similar lines, Hawkes et al. (1998) also suggested that a lower lifetime cost of reproduction resulting from early menopause might free resources for increased maintenance of somatic tissues, which they interpreted as a possible driver in the process of evolving extended human longevity.

In all studies that attempt to draw evolutionary conclusions about features of the human life history, we need to consider whether the population in question might have been too much perturbed by recent development for such inferences to be possible. In other words, are the Gambian data sufficiently ‘natural’? It is reassuring that, at least for child mortality, the Gambian data correspond closely with other data from hunter–gatherer populations (Gurven & Kaplan 2007). When comparing results from the Gambian data, however, with previous analysis (Shanley & Kirkwood 2001) of a (much less detailed) 1906 Taiwanese dataset (Hamilton 1966), we find some difference in the importance of the fertility enhancement due to grandmothers. Whereas in the Taiwanese life history, the fitness effects associated with menopause were more sensitive to grandmaternal effects on daughters' fertility than on grandchild mortality, the Gambian data showed no significant fertility enhancement. Even if we assumed a real effect (but one which did not attain statistical significance), we did not find its impact on selection for menopause emerging as strongly as in the Taiwanese data. In spite of these caveats, our results help throw light on the possible evolutionary foundations of menopause. For menopause to be adaptive there must be a combination of factors, and we have shown that the most important are a dramatic increase in maternal mortality with age and a benefit to grandchildren provided by the maternal grandmother. We believe such a detailed quantitative analysis of the actual fitness effects of varying age at menopause, based on real data, to be without precedent. It should be noted that without such an analysis, even the best evidence that grandmothers promote grandchild survival, enhance daughter's fertility and so on cannot confirm whether or not such benefits might actually explain evolution of menopause.