Target concentration intervention is needed for tobramycin dosing in paediatric patients with cystic fibrosis – a population pharmacokinetic study

Abstract

Aim

The primary aim was to estimate the population pharmacokinetic parameters of once-daily intravenous (i.v.) tobramycin in paediatric cystic fibrosis (CF) patients and to investigate the influence of covariates. The second aim was to assess the need for target concentration intervention (TCI) for tobramycin in this patient group.

Methods

Retrospective demographic, dosing and concentration data were collected from 35 CF patients (21 female, 14 male) aged 0.5–17.8 years, from whom 318 tobramycin plasma concentrations were available. NONMEM was used to estimate the population pharmacokinetics of tobramycin. Simulations were performed using weight-based dosing with a weight from a covariate distribution model to evaluated current dosing schedules and monitoring practices.

Results

A two-compartment model best described the data with population parameter estimates for clearance of central compartment (CL) of 6.37 l h⁻¹ per 70 kg; volume of central compartment (V_c) of 18.7 l per 70 kg; intercompartmental clearance (Q) of 0.393 l h⁻¹; and volume of peripheral compartment (V_per) of 1.32 l. The inclusion of total body weight as covariate reduced the random component of between-subject variability in CL from 50.1% to 11.7% and in V_c from 62.2% to 11.6%. The between-occasion variability on CL was estimated in the final model as 6.5%. Simulations show that one dose does not fit all and TCI and dose adjustment are required.

Conclusions

This study provides the first pharmacokinetic model of once-daily i.v. tobramycin for the use of target concentration intervention in paediatric CF patients.

What is already known about this subject

• Two recent papers have been published which have attempted to build a full population pharmacokinetic model for tobramycin in children with cystic fibrosis.

• However, neither study was able to provide any information about between-subject variability (BSV) and between-occasion variability (BOV), which is necessary to justify and draw conclusions about the use of target concentration intervention (TCI).

• In the publications no simulations were provided to show any new directions or evaluate current therapy.

What this study adds

• This study provides sound evidence that TCI must be undertaken in this patient group, as the BOV is significantly less than the BSV.

• The simulations from this model clearly show that current dosing and monitoring methods will not achieve the necessary targets to maximize the pharmacokinetic–pharmacodynamic relationships of aminoglycosides in this patient group.

• The model presented is able to be easily incorporated into Bayesian dose individualization software, e.g. Abbottbase or TCIworks, to achieve dosing targets more accurately.

Introduction

Young children with cystic fibrosis (CF) are at risk of pulmonary infection from a number of pathogens, especially Pseudomonas aeruginosa (PA). Once this organism becomes established in the lungs of CF patients it becomes increasingly difficult to eradicate, and is associated with increased morbidity [1, 2]. Intravenous tobramycin is a mainstay in the treatment of PA infections in CF patients [3].

The pharmacokinetics (PK) of tobramycin and other aminoglycoside antibiotics are well known and have been described in several patient populations [4–6]. Tobramycin is mainly cleared unchanged via the kidney, and again relationships between renal elimination and serum creatinine concentrations have been described to predict tobramycin concentration from renal function [4, 5, 7]. The PK of aminoglycosides has also been linked with the pharmacodynamic properties. The once-daily (OD) aminoglycoside dosing approach was introduced over 10 years ago after evidence that high peak plasma concentrations lead to a more successful therapeutic outcome [8]. Aminoglycosides show a significant postantibiotic effect, which persists for some time after the concentrations have fallen below the minimal inhibitory concentration (MIC), and efficacy has been linked with the ratio of peak concentration to the MIC, and toxicity with high trough concentrations, which relates to long and high exposure. It has also been demonstrated that OD administration has advantages in terms of efficacy and perhaps reduced risk for nephrotoxicity compared with the traditional 8-hourly administrations [9, 10] and reduced development of adaptive resistance. Numerous guidelines for therapeutic drug monitoring have been suggested either using area under the curve (AUC) calculations [11–13], a Bayesian approach [13] or monitoring for concentrations of <1 mg l⁻¹ before the next dose (at 24 h postdose) [9]. Monitoring is necessary not only to achieve therapeutic success, but also to prevent excessive exposure, which has been associated with a higher incidence of adverse events [14]. The various monitoring methods have made the application of the OD approach in clinical cases much easier, and it is the more common practice throughout most countries today [11, 15–17]. However, to our knowledge no appropriate guidelines for the optimal dosing and monitoring of aminoglycosides have been established for CF patients, in particular in the paediatric group, where it is important to eradicate PA as early and intensively as possible to prevent early colonization of resistant forms.

Therefore, the aims of this study were to (i) develop a population PK model for tobramycin in paediatric CF patients, (ii) evaluate the influence of covariates, in particular serum creatinine, and (iii) test whether tobramycin in CF patients is a candidate for the use of target concentration intervention (TCI) [18].

Methods

Patients and sampling

The data were collected retrospectively from July 2005 until September 2006 from all paediatric CF patients admitted as inpatients at Mater Health Services, Brisbane, Australia. Ethics approval for this data collection was obtained from the Mater Health Services Human Research and Ethics Committee.

Tobramycin was administered as an OD infusion with a duration (D) of 30 min with an additional time difference [lag time (t_lag)] between the time of hanging the infusion and the time when the drug reached the patient. As per the hospital protocol, either the initial tobramycin dose was 10 mg kg⁻¹ based on total body weight or the tobramycin dose from the last hospital admission was used as a start dose. Furthermore, as per protocol this dose was subsequently adjusted as per TCI to achieve an AUC between 80 and 100 mg l h⁻¹ according to a suggested AUC for adult patients by Begg et al.[11]. The first blood sample was collected 1–1.5 h after the commencement of the infusion and the second at 8–14 h after commencement of the infusion. The exact times were recorded as part of routine drug monitoring. If dose adjustment was required, the same monitoring process was repeated after the patient commenced the new dose. Otherwise, monitoring was repeated 7 days later depending on the length of the patient's admission. For the purpose of estimating between-occasion variability (BOV), an occasion was defined as one dosing interval with subsequent drug concentrations.

Drug assay

The tobramycin serum concentrations were analysed with an automated fluorescence polarization immunoassay (Abbott Axsym; Abbott Laboratories, North Ryde, Australia) by the Chemical Pathology Department, Mater Pathology Service, Brisbane, Australia. The lower limit of quantification of the assay has been set at 0.3 mg l⁻¹. The coefficient of variation for the tobramycin assay was 5.98% at 16.7 mg l⁻¹ and 3.36% at 0.89 mg l⁻¹.

Population analysis

Modelling was performed using the first order conditional estimation (FOCE) method with interaction in NONMEM, version 5.1.1 (GloboMax LLC, Hanover, MD, USA) [19] in conjunction with a G77 FORTRAN compiler and Wings for NONMEM (http://wfn.sourceforge.net). One-, two- and three- compartmental models with first- or zero-order input and linear elimination were evaluated. The PK parameters of the model were parameterized so that clearance and volume of distribution were estimated.

The overall variability in the parameters, e.g. clearance (CL) between all individuals was estimated as population parameter variability (PPV). The PPV contained the between-subject variability (BSV) and BOV (see Equation 1), which was modelled using an exponential error model. Both of these can be divided into random and predictable variability, where the predictable component is the amount of variability which can be explained by the influence of covariates on the parameter estimate. BSV and BOV are described as the approximate coefficients of variation (%) from the standard deviation of a log-normal distribution with mean zero (see Equation 2).

(1)

(2)

BSV_CLij and BOV_CLij are the BSV and BOV of CL for the i^th patient at the j^th occasion, respectively, and CL_pop is the population predicted value of CL. The predictable component of BSV can be calculated from the difference in BSV after the addition of a covariate to the base model.

The residual unexplained variability (RUV) was described using an exponential error model:

(3)

where ε_ik is the deviation of the k^th observed drug concentration for the i^th individual (C_ik) from the respective model-predicted concentration (C_{pred, ik}). ε_ik is a randomly distributed variable with mean of 0 and variance σ². A full omega block structure was used to allow for covariance between the parameters.

A stepwise approach was used to analyse the data, and exploratory graphical analysis was first carried out before separately introducing each covariate into the structural model to find possible relationships between parameters, e.g. CL, and patient characteristics such as total weight, lean body weight [20], serum creatinine, creatinine clearance, renal function calculated from the creatinine production rate [5] and creatinine clearance predicted from serum creatinine concentrations with the Cockroft and Gault formula [21]. Low serum creatinine concentrations were also accounted for with previously suggested cut-off procedures [6, 13]. The pattern of weighted residuals, changes in the BSV, RUV and the objective function value (OFV) were examined.

Model validation

Nested models were hypothesis-tested using the likelihood ratio test in which the change in OFV approximates the χ² distribution (χ²_1,0.01 > 6.6). Other modelling diagnostics included an assessment of the ‘goodness-of-fit’ (GOF) plots, precision of the parameter estimates, change in the OFV and a visual predictive check (VPC) on the final model using S-Plus. The VPC involved generation of 1000 simulated concentration sets from the final population model parameters. The observed concentrations were dose-normalized to the average prescribed dose of 350 mg, given as an OD dose. The 10th and 90th percentiles as well as the 50th (median) percentiles were plotted against postdose time, and the dose-normalized study data were superimposed.

The stability and performance of the final model were assessed via an internal validation method which involved nonparametric bootstrapping with re-sampling and replacement. The $Covariance function in NONMEM, to describe the precision of the parameters with the asymptotic standard errors, was not successful for most models, therefore the empirical posterior distribution of the fixed and random estimates from 1000 bootstrap replicates was calculated by obtaining the 95% confidence interval of the parameter estimate distribution.

Dosing guidelines

As already shown, OD dosing regimens of tobramycin generate concentration–time profiles with high peak concentrations (C_max) for the effective killing of PA[9]. This study's aim was to consider the relevance of TCI to improving tobramycin treatment, in particular with regard to side-effects, which are related to exposure to the drug. Therefore AUC, calculated as Dose/CL_ij, was chosen as the target with a variability range of 80–125%, which was chosen arbitrarily, but is in accordance with the bioequivalence criteria used by regulatory agencies. However, additionally we have still summarized the simulation in regards to C_max. For the assessment of the current and other suggested dosing regimens with regard to this target the parameter estimates from the final model were used for 1000 Monte Carlo simulations. The simulations were performed with NONMEM and analysed with S-Plus. For all the tested mg kg⁻¹ dosing regimens the dose was calculated during the simulation with a weight from a covariate distribution model, where the population weight and the variance were equal to the average weight and range found in this study. The 10–90th percentiles were determined, which allows for an 80% success rate, and assessed compared with the current target ranges used in the clinic.

Results

Patients

A total of 318 tobramycin concentrations were recorded from 35 CF patients (21 female/14 male), whose demographic data are shown in Table 1. Only one of the patients appeared to have reduced renal function with a creatinine clearance <50 ml min⁻¹. However, the serum creatinine concentrations of all patients were within the normal laboratory range (20.0–73.0 μmol l⁻¹). Further patient demographics and characteristics were obtained from the clinical notes and are summarized in Table 1.

Table 1.

Patients' demographic data

Characteristics	Mean (range)
Age (years)	9.5 (0.5–17.9)
Total body weight (kg)	34.0 (6.0–72.6)
Height (cm)	131.0 (60.0–178.0)
Serum creatinine (μmol l−1)	44.0 (20.0–73.0)
Creatinine clearance (ml min−1) [21]	105.7 (23.0–194.7)
Observations/patient	9.1 (2.0–26.0)
Occasions/patient	4.6 (1.0–14.0)
Dose (mg)	311.7 (70.0–560.0)
Dose (mg kg−1)	9.6 (6.9–15.2)

The data history obtained contained on average nine samples per patient from an average four to five occasions. The individual tobramycin doses ranged from 70 to 560 mg with an average dose of 9.6 mg kg⁻¹ OD (311 mg). The sampling times ranged from 0.6 to 14 h postdose, with most samples taken 1–2 h and 7–12 h after the start of the infusion. None of the measured tobramycin concentrations was below the limit of quantifications (<0.3 mg l⁻¹) of the assay used.

Population pharmacokinetics

A two-compartment model best described the observed concentration–time relationship for tobramycin in this population compared with a one-compartment model (ΔOFV = 20.58). The exponential error model was superior compared with both the additive and the combined residual error model. The infusion time was fixed to 30 min as per hospital protocol and then an observed ‘lag-time’ between the hanging of the infusion bag and the time when the drug entered the patient's vein was estimated as 24 min. This corresponded to the usual observed time for the drug to travel though the burette system. The BSV was estimated for CL and volume of distribution of the central compartment (V_c) and of the peripheral compartment (V_per) as well as covariance between these parameters. The inclusion of BOV on CL resulted in a further reduction of the OFV by 17.56 units, which was estimated in the final model as 6.47%. However, the inclusion of BOV on V_c also did not improve the model any further based on OFV values and GOF plots and was estimated to be <2% if included.

The final model included total body weight (WT), scaled allometrically with a 3/4 exponent for CL and 1 for V_c and both standardized for 70 kg, as a covariate. This model had a 104.7 point reduction OFV compared to the base model and showed a reduction of the BSV on CL from 55.2% to 11.7%, on V_c from 59.8% to 11.66 and on V_per from 182.7% to 41.95%. The predictive performance and also the GOF plots improved compared with the base model. Other covariates, such as body composition descriptors and covariates used to predict the renal clearance of tobramycin, were tested and included into the base model. However, these showed either no further improvement of the model than WT or no influence at all, and were therefore not retained in the model.

The estimates of the final model were 6.37 l h⁻¹ per 70 kg and 18.70 l per 70 kg for CL and V_c and 0.39 l h⁻¹ and 1.32 l for the intercompartmental clearance (Q) and V_per. The results of the base and final (covariate) PK model are summarized in Table 2. The population value of 6.3 l h⁻¹ per 70 kg for CL can be used to calculate an individual value (with the individual's weight) and from that the maintenance dose.

Table 2.

Parameter estimates of the base model, the covariate model and the 1000 bootstrap runs [median and 95% confidence interval (CI)]

Parameter	Base model	Covariate model	1000 bootstrap replicates Median (95% CI)
Objective function value	636.194	531.507	513.29 (355.93, 702.08)
Fixed parameters
CL (l h−1)	2.98	6.37†	6.26† (5.37, 6.98)
Vc (l)	8.22	18.70†	18.60† (16.00, 20.56)
Q (l h−1)	0.12	0.39	0.40 (0.25, 0.79)
Vper (l)	9.93	1.32	1.57 (1.00, 4.90)
tlag (h)	0.39	0.40	0.40 (0, 0.60)
Dc (h)	0.5‡	0.5‡	0.5‡
Random parameters (CV %)
BSV CL	55.23	11.70	11.45 (6.74, 15.94)
BSV Vc	61.97	11.66	10.63 (3.19, 18.80)
BSV Vper	182.76	41.95	53.29 (17.43, 109.20)
BOV CL	6.44	6.47	6.60 (3.06, 8.98)
Correlations between BSVs
R (CL, Vc)	0.98	0.73	0.74 (0.34, 1.04)
R (CL, Vper)	0.39	0.49	0.97 (−1.00, 1,01)
R (Vc, Vper)	0.52	0.27	0.52 (−0.98, 1.00)
Residual variability (CV %)	18.65	19.00	18.55 (15.42, 21.91)

^†The typical value of clearance and volume refer to a patient with a total body weight of 70 kg for comparison with adult values. Typical value = Typical parameter estimate × (total body weight/70)^∧f, f = 3/4 for clearance, f = 1 for volume.

^‡Fixed. CL, Typical clearance from central compartment; V_c, typical volume of central compartment; Q, typical intercompartmental clearance; V_per, typical volume of peripheral compartment; t_lag, typical lag-time between time of hanging infusion and drug entering the patient's vein; D_c, duration of infusion into the central compartment; BSV, between-subject variability; BOV, between-occasion variability; R, correlation coefficient between BSVs.

Model evaluation

The GOF plots for the final model are shown in Figures 1 and 2. The weighted residual graphs show no visual or statistical bias for the prediction. In Figure 3 the visual predictive check confirms the good fit of the model to the observed data. About 16% of the data lie outside the 10th and 90th percentile, with most of the observed concentrations evenly distributed around the median.

Figure 1.

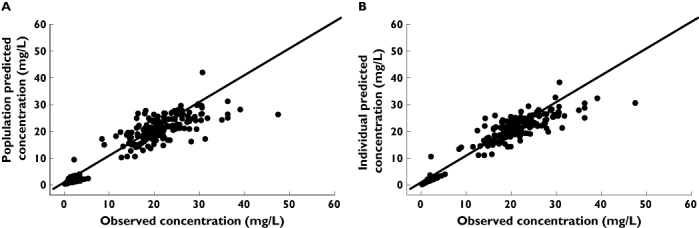
(A) Population and (B) individual predicted tobramycin concentrations vs. observed tobramycin concentrations (mg l⁻¹)

Figure 2.

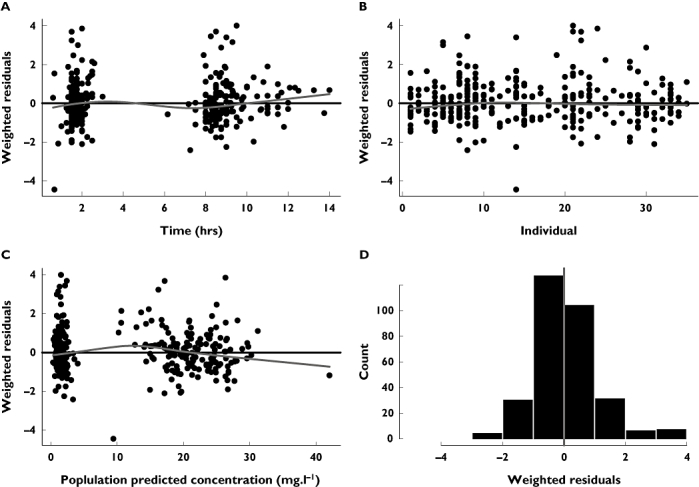
(A) Weighted residuals vs. time (h) after dose (B) individual and vs. (C) population predicted concentrations (mg l⁻¹) including a loess fit (grey) and (D) histogram of the weighted residuals

Figure 3.

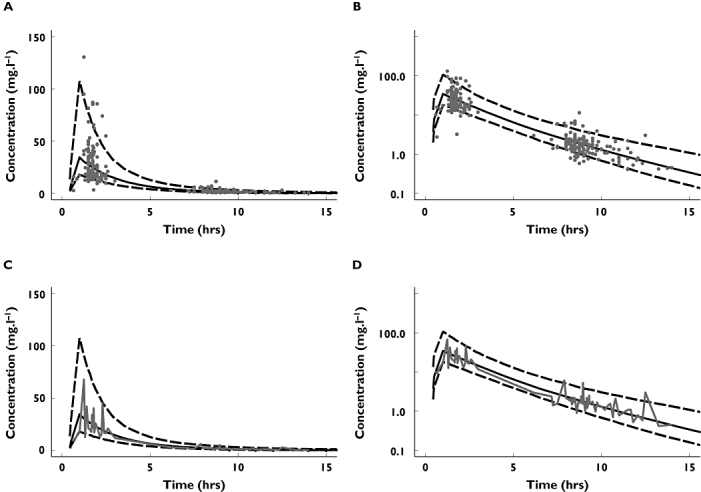
Visual predictive check showing the observed concentrations as grey points (A,B) or as grey 50th percentile line of the observed concentrations (C,D) with a logarithmic scale on the ordinate (B,D) and a nonlogarithmic scale (A,C)

Dosing guidelines

The aim of the simulations was to assess the dosing regimens in regards to the percentage of patients achieving an AUC of 100 mg l h⁻¹ to evaluate the exposure of patients to the drug. Comparing the percentage of patients who achieved target success, it is shown that with a ‘one dose fits all’ approach only a 1/3 of patients were within the range, 1/3 below and about 1/3 at risk of overexposure. When evaluating the dosing regimens which were based on the weight of the patients, a low mg kg⁻¹ dose of 7.5 mg kg⁻¹ will show the smallest number of patients within the AUC target range. On the other hand, increasing the dose above 10 mg kg⁻¹ does not greatly increase the percentage of patients in the target range, but rather increases the risk of higher exposure. A OD dose of 10 mg kg⁻¹ (WT) tobramycin was found to provide the best compromise between success and overexposure (see Table 3). These results are also confirmed when looking at the aim of achieving 30 mg l⁻¹ (24–38 mg l⁻¹) for C_max concentration, with an safe and effective variability (SEV) of, again, 80–125%. A high C_max concentration, approximately 10 times the MIC for PA in this population, is desirable [22]. It was not possible to obtain these specific MIC values in retrospect from the study patients, and therefore a previously suggested C_max concentration was adopted here. Table 3 shows the results of the simulation for C_max concentration; with a ‘one dose fits all’ approach and a lower mg kg⁻¹ dosing regimen, not many patients achieve a high peak, but a 10 mg kg⁻¹ dose again proves the most efficient.

Table 3.

Results from simulations of several once-daily dosing regimens

	Percentage of patients
Dosing regimen	350 mg	7.5 mg kg−1	8.5 mg kg−1	10 mg kg−1	11 mg kg−1	12 mg kg−1
Within AUC range (80–125 mg l h−1)	37.9	21.7	44.2	72.1	76.9	69.4
Outside AUC range (80–125 mg l h−1)	62.1	78.3	55.8	27.9	23.2	30.6
Below AUC 80 mg l h−1	36.6	78.1	55.0	22.2	10.3	4.4
Above AUC 125 mg l h−1	25.5	0.2	0.8	5.7	12.9	26.2
Below 1 mg l−1 at 24 h	100	100	100	100	100	100
Below 0.3 mg l−1 at 24 h	97.2	100	99.8	99.7	99.6	99.6
Within Cmax range (24–38 mg l−1)	29.8	17.3	55.8	91.6	92.5	80.2
Below Cmax of 24 mg l−1	39.0	82.7	44.2	7.1	1.3	0.4
Above Cmax of 38 mg l−1	31.2	0	0	1.3	6.2	19.4

Furthermore, Table 3 shows that monitoring for trough concentrations of 1 mg l⁻¹ at 24 h after the last dose should not be done, because with any of the OD dosing regimens 100% of the patients will have tobramycin concentrations <1 mg l⁻¹, or 0.3 mg l⁻¹, which is the limit of quantification of the assay. Tobramycin trough concentrations after OD dosing do not reflect C_max concentrations or AUC values over the dosing interval.

These results can be used only in patients with normal serum creatinine concentrations, due to the characteristics of our study population.

Discussion

Several population PK models for aminoglycosides have been developed [4–6, 13, 23], but there was no model to assist TCI in a paediatric population of CF patients. For clinic purposes the PK of tobramycin are often described by a one-compartment model, but several studies have reported that the PK profile of tobramycin corresponds to a two-compartment model [4, 5, 24]. The data in this study were obtained solely from clinic routine data, and most observations were within two sampling windows around 1.5 and 7 h after the last dose. However, the data still supported a two-compartment model with a significant drop in the OFV. The population PK parameters found in this study are very similar to those reported by others. When scaled to 70 kg, the estimate for CL was 6.37 l h⁻¹ per 70 kg and for V_c 18.70 l per 70 kg compared with 4.7 l h⁻¹ per 70 kg and 19.5 l per 70 kg in a study by Matthews et al.[5].

Tobramycin is cleared renally and the clearance of the drug should correlate with the glomerular filtration rate, based on its molecular characteristics (low molecular weight, highly polar molecule). We tried to establish a model in this patient group which could predict the clearance of tobramycin as a function of serum creatinine concentration and/or other patient characteristics. However, only one study patient showed reduced estimated creatinine clearance as a sign of reduced renal function, which is more common in older rather than younger CF patients, or CF patients after transplantation. Creatinine clearance was estimated using the Cockcroft and Gault equation, which is not validated in the paediatric population. Although no relationship between serum creatinine concentration and CL was identified from scatter plots, there was a correlation between creatinine clearance and individual predicted values of CL. Despite this visual correlation, and even after the use of several different cut-off methods for low creatinine concentrations [4, 6], the relationship between creatinine clearance and tobramycin CL did not improve. Neither the addition of serum creatinine nor of creatinine clearance to the model provided improvement of the overall model or reduced the OFV significantly to be included. This is probably due to the lack of patients with reduced estimated creatinine clearance in our study, and may well reflect a general absence of renal impairment in this patient group. As a consequence, we are uncertain how our model will behave in CF patients with renal impairment. It was observed that the Cockcroft and Gault equation in CF children dramatically overpredicts glomerular filtration, as the predicted values of creatinine clearance appear to be double that of tobramycin clearance, e.g. 100 ml min⁻¹ (6 l h⁻¹) creatinine clearance ∼3 l h⁻¹ tobramycin clearance. On this basis, we would conclude that the Cockcroft and Gault equation should not be used to predict the likely renal clearance of tobramycin in CF children.

Even though the PK of a number of drugs are known to be different in patients with CF compared with non-CF subjects, it has recently been shown that some of these differences are due to differences in body composition, e.g. less adipose tissue as a result of malnutrition in CF patients [25]. This, in turn, would affect the volume of distribution of hydrophilic drugs, which distribute mainly into lean tissues, e.g. β-lactam antibiotics, aminoglycoside. A meta-analysis of population PK studies with seven β-lactam antibiotics and ciprofloxacin in patients with CF has recently shown that the average total clearance and average volume of distribution is within 80–125% for all eight drugs compared with healthy volunteers after allometric scaling of clearance and volume by lean body mass [25]. In this study, scaling of these two parameter estimates by lean body weight (LBW) (calculated using the equation by Janmahasatian et al.[20]) did not improve the prediction over CL and V_c scaled allometrically [26] by WT. The newly proposed equation for the prediction of LBW from total body weight, sex and body mass index did not include paediatric data and might therefore not be suitable for use in a paediatric population.

The results obtained from our model with regard to PK variability suggest that WT does not account for all of the variability to be used alone to predict individual doses. To justify and gain information for subsequent dosing from TCI, the following conditions need to be shown for a drug: (i) variability of concentrations in the target population cannot be explained by patient characteristics alone; (ii) the BSV should be greater than the BOV and the overall PPV greater than the safe and effective variability; and (iii) the BOV should be smaller than the SEV [5, 18]. The SEV of a drug is a subjective definition of the upper and lower boundaries of the effectiveness of this drug. We have used a SEV for tobramycin of 0.135, as previously suggested and calculated from the variability range of 80–125% [5], to compare this with the variability estimated in our study. Because the BOV estimated for CL (0.0042) is smaller than the SEV, TCI will be useful to individualize therapy, for an efficient and safe therapy with tobramycin. A large amount of the random variability, however, is explained by the influence of total body weight, and doses should be based on the WT of each patient. All three criteria mentioned above for the justification of TCI are satisfied with the model provided here.

Furthermore, we have been able to show that even when using the safest and most effective dose (10 mg kg⁻¹) as the initial treatment dose, only a maximum of 72% of patients will achieve AUCs within 80–125% of the target. With any other dose, either fewer patients will be within this range or more patients will be at risk of toxicity. To increase the number of patients within the safe target range further, concentration monitoring with appropriate dose adjustment is required. Table 3 also shows the results of using an average dose for all paediatric CF patients, with the results demonstrating that only 37% of patients achieved the target. Therefore, this dosing approach should no longer be used. The simulations undertaken were aimed to reduce overexposure to tobramycin using the OD dosing regimen. The target range chosen here could have been tighter based on the characteristics of the drug.

Two recently published papers using a population PK approach have suggested the use of a one-compartment PK model for tobramycin in paediatric CF patients [27, 28]. However, the authors were unable to provide any information about BSV and BOV, which is necessary to justify and draw conclusions about the use of TCI. In the publications no simulations were provided to show any new directions or to evaluate current therapy. A nomogram was provided by Massie et al. for the use of dose individualization, but the accuracy of nomograms is limited by the precision with which graphs can be drawn, reproduced and viewed. Although it has previously been shown that the use of nomograms might be helpful, they should be used only in applications where an approximate answer is appropriate. Use in other circumstances could result in inaccurate dosing [29]. Monitoring of tobramycin concentrations linked with the use of a Bayesian TCI approach is a more effective way to ensure successful treatment [13]. Indeed, recent comparisons of nomogram methods vs. Bayesian TCI [30, 31] with aminoglycosides in adult patients with normal and impaired renal function have shown poor performance, with either significant under- or overdosing with the nomogram method. Both authors concluded that nomogram methods should not be used in this patient group. Given that similar population PK parameters and variability parameters have been described for this CF population to those seen in adults receiving gentamicin [5], a comparable result would be expected if a nomogram test were to be repeated.

This study has provided an appropriate model describing the PK of tobramycin, which can be used for TCI purposes. In addition, it includes the necessary information about the PK variability in this population to draw conclusions regarding TCI, and has clearly demonstrated that TCI provides substantial therapeutic benefits over the ‘one dose fits all’ approach.

Competing interests: None to declare.

The authors would like to acknowledge Mr Andrew Barron for his support with the data collection, Dr Bruce Green for his advice during the modelling process and David Cowley, the Director of Chemical Pathology at Mater Pathology Services, for providing the assay. Furthermore, the authors are indebted to the staff and patients of the Cystic Fibrosis unit at the Mater Hospital, Brisbane for their support with the blood sampling.