Motor step size and ATP coupling efficiency of the dsDNA translocase EcoR124I

Abstract

The Type I restriction-modification enzyme EcoR124I is an archetypical helicase-based dsDNA translocase that moves unidirectionally along the 3′–5′ strand of intact duplex DNA. Using a combination of ensemble and single-molecule measurements, we provide estimates of two physicochemical constants that are fundamental to a full description of motor protein activity—the ATP coupling efficiency (the number of ATP consumed per base pair) and the step size (the number of base pairs transported per motor step). Our data indicate that EcoR124I makes small steps along the DNA of 1 bp in length with 1 ATP consumed per step, but with some uncoupling of the ATPase and translocase cycles occurring so that the average number of ATP consumed per base pair slightly exceeds unity. Our observations form a framework for understanding energy coupling in a great many other motors that translocate along dsDNA rather than ssDNA.

Introduction

Molecular motor proteins have numerous roles in DNA metabolism and are central to replication, recombination and repair. An important class of nucleic acid motors are the helicases, which can be classified on the basis of homologous amino-acid motifs into superfamilies (SF) 1–5 (Singleton et al, 2007). For many helicases—all those characterized thus far from SF1 for example—directional translocation takes place on a single-stranded polynucleotide. Accordingly, a duplex DNA (or RNA) must be melted to gain access to the linear track. This structural transition in a nucleic acid is the classical role for which helicases are known, and indeed named. However, there are also a great many enzymes—a large proportion of those found in SF2 for example—that, although classified as helicases, are actually dsDNA translocases that move along intact duplex polynucleotides (Hopfner and Michaelis, 2007; Seidel and Dekker, 2007; Singleton et al, 2007). These enzymes do not directly unwind DNA and are thus not helicases in the eponymous sense. One such example is the chromatin-remodelling factors (Lia et al, 2006; Zhang et al, 2006; Seidel and Dekker, 2007). Compared to the ssDNA motors, very little is known about dsDNA translocation. A key piece of information in developing a mechanistic framework for understanding these enzymes is how efficiently the motor couples ATP hydrolysis to protein stepping on dsDNA: how much energy in the form of ATP is required to move a step along DNA and how big is that step? Knowing this information puts a physical constraint on how domain motions of the helicase motor core are coupled to the nucleic acid.

To solve this fundamental puzzle for the dsDNA translocases, we have examined the motor activity of an archetype dsDNA motor (Singleton et al, 2007), the ATP-dependent Type I restriction-modification (RM) enzyme EcoR124I. The extensive characterization of the dynamics of initiation, translocation and termination of this enzyme (Seidel et al, 2005), alongside extensive kinetic analysis of translocation (Firman and Szczelkun, 2000; Seidel et al, 2004; McClelland et al, 2005; Stanley et al, 2006), means that EcoR124I is the best test system for addressing this question.

The Type I RM enzymes are widely distributed in both bacteria and archaea, and have a beneficial role in protecting a host cell from invasion by foreign DNA such as bacteriophages and plasmids (Murray, 2000). Type I RM enzymes comprise three protein subunits: HsdS, HsdM and HsdR. HsdS and HsdM (HsdS₁HsdM₂) form independently active methyltransferases (MTase) that recognize specific, bipartite sequences (e.g., GAAnnnnnnRTCG for EcoR124I) (Janscak et al, 1996). The HsdR subunits are fusions of PDE(x)K nuclease and SF2 helicase domains (McClelland and Szczelkun, 2004). To cleave DNA, HsdR must bind the MTase and use its helicase motor to translocate along intact dsDNA using ATP hydrolysis (Stanley et al, 2006). As the HsdR motor remains bound to the MTase during translocation, a growing loop of DNA is extruded (van Noort et al, 2004). The MTase core can recruit two HsdRs to form an HsdS₁HsdM₂HsdR₂ complex where each HsdR acts independently (Janscak et al, 1996; Seidel et al, 2004, 2005). As a consequence, translocation by both HsdRs in a complex results in the extrusion of two DNA loops, one on each side of the site (van Noort et al, 2004). We have shown previously that EcoR124I moves on intact dsDNA without unwinding, using principal motor contacts to the 3′–5′ strand (Stanley et al, 2006). The motor can still translocate on 3′–5′ ssDNA if loaded via dsDNA, although the processivity is greatly reduced (Stanley et al, 2006). The polar motion of EcoR124I on dsDNA has been highlighted as a paradigm for many other dsDNA translocases (Hopfner and Michaelis, 2007), for example, the chromatin-remodelling enzymes (Durr et al, 2006). Using a combination of fast-mixing ensemble and single-molecule techniques, we have now extended the understanding of this enzyme to include the ATP coupling efficiency and motor step size. Our data are consistent with structural models for dsDNA translocation and support the proposal that dsDNA and ssDNA translocases share a similar gross mechanism for motion along different polynucleotide tracks (Hopfner and Michaelis, 2007).

Results

Measurement of the temperature dependence of ATP hydrolysis by stopped-flow fluorimetry

The ratiometric ATP coupling efficiency (ATP hydrolysed per base pair moved) can be determined simply by comparing the rates of ATP hydrolysis and dsDNA translocation. To ensure that our observations are not biased by a particular set of experimental conditions, we carried out our ATPase and translocase measurements at a range of ATP concentrations and temperatures. Any change in the mechanism that in turn changes the coupling can then be identified (Lucius and Lohman, 2004). Previous studies of Type I enzymes reported a large range of different ATP couplings of ∼1–3.1 ATP/bp (Endlich and Linn, 1985; Davies et al, 1999; Bianco and Hurley, 2005). The principle caveat of these measurements was that while measuring the ATPase activity, the translocase activity was typically not measured but inferred indirectly from cleavage experiments or from published data, taken under different experimental conditions. For example, a recent and rather extensive ATPase study reported an inefficient coupling of 3.1 ATP/bp (Bianco and Hurley, 2005). One way that the coupling was calculated was by dividing an ATPase rate (in units of ATP/min) by a processivity parameter (in units of bp). However, this actually gives a value in units of ATP/bp/min, which does not represent a true coupling constant. Another way that the coupling was calculated was by dividing the maximum ATPase rate measured at 37°C by a maximum translocation rate measured at 20°C in a separate study. However, as shown below, over such a temperature difference, the translocation rate changes by a factor of ∼3. Therefore, to obtain a precise coupling efficiency, it is crucial to measure both activities directly under the same experimental conditions, which even for SF1 helicases has only been accomplished very recently (Tomko et al, 2007).

To measure both activities with the best accuracy, we utilized a rapid-mix stopped-flow fluorimeter. We were thus able to initiate our reactions under reproducible conditions, that is, identical mixing times, identical mixing conditions, etc. To measure the EcoR124I ATPase activity, we utilized a coumarin-labelled phosphate binding protein (PBP) sensor developed by Martin Webb (Figure 1A; Materials and methods; Supplementary Figures S1–S3; Supplementary data) (Webb, 2003, 2007). The binding of phosphate to the sensor is both fast and tight, allowing rapid ATPase kinetics on a millisecond timescale to be followed. Unlike enzyme-coupled ATPase assays (e.g., the LDH-coupled assays used in other EcoR124I studies; Bianco and Hurley, 2005), the sensor does not have a time lag and the kinetics observed can be related directly to the ATPase kinetics immediately upon starting the reaction (see Supplementary Figure S3). Using the stopped-flow fluorimeter, we preincubated EcoR124I with linear DNA substrates, initiated the reaction by rapid mixing with ATP and then followed the increase in free phosphate released during ATP hydrolysis from the increase in fluorescence of the sensor (Figure 1A and B; Materials and methods; Webb, 2003). Because of the considerable site-independent ATPase activity of EcoR124I (Zinkevich et al, 1997), all data were corrected for background activity measured using a non-specific DNA that is the parental vector for all our specific substrates (Figure 1B, inset; Materials and methods). Hydrolysis of the specific DNA does not occur because on linear substrates collision with a second translocating enzyme is required to activate the nuclease activity (Szczelkun et al, 1996).

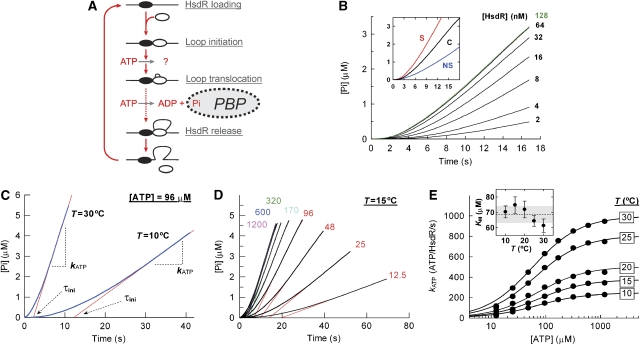
Figure 1.

The temperature dependence of ATP hydrolysis during steady-state loop extrusion. (A) Cartoon showing the cycle of initiation, translocation and termination of DNA translocation by an EcoR124I HsdR subunit (white oval). For clarity, translocation on one side of the MTase only is shown. DNA is shown as a black line and the EcoR124I MTase as a black oval. The binding of free inorganic phosphate by PBP is indicated. (B) Dependence of phosphate release on the availability of free HsdR (concentrations indicated). One-site linearized pLKS5 was at 0.5 nM, MTase at 60 nM and ATP at 80 μM. (inset) Example of background correction at 128 nM HsdR. The phosphate release measured using the specific linear pLKS5 (S) was corrected by the background level using non-specific linear pTYB11 (NS) to generate the corrected profile (C). (C) Example kinetic profiles at 10 and 30°C. The steady-state phase of the reaction was fitted to equation (3) to give k_ATP; the x-axis intercept gives the initiation time (data not shown; Frieden, 1979). (D) Example of an ATP titration (μM concentrations of ATP indicated), with each profile fitted to equation (3). (E) Hyperbolic dependence of k_ATP on [ATP] as a function of temperature. Solid lines show fits to equation (4). Statistical error bars are smaller than the scatter of the data points. Fitting to equation (4) was not weighted to either the statistical or systematic errors (discussed in Supplementary data). (inset) Dependence of K_M on temperature. Error bars are the standard error of the mean (s.e.m.) of the fitted values. The dotted line shows the average K_M across the temperature range and the grey box the associated standard deviation (s.d.). V_max,calc and s.e.m. (bp/s) calculated from the fits were 246±3 (10°C), 376±7 (15°C), 503±23 (20°C), 807±11 (25°C) and 998±7 (30°C).

The ATPase kinetics recorded under a large variety of conditions (Figure 1B–D) is always characterized by very low initial rate, followed by a acceleration phase until finally a constant steady-state rate is achieved. This behaviour can actually be understood on a quantitative level, as the dynamics of initiation, termination and reinitiation of EcoR124I translocation have been previously quantitatively defined using rigorous kinetic analysis (Figure 1A; Seidel et al, 2005): the MTase forms a stable, long-lived complex on the DNA (t_1/2>30 min) that, in a second-order process, recruits free HsdR onto the adjacent DNA; the loaded HsdR then starts to translocate a DNA loop, preceded by initiation step(s); at any stage during translocation, the HsdR may detach from the DNA and MTase, terminating the loop; a second HsdR can then be recruited from solution by the MTase to repeat the cycle. Knowing this cycle on a quantitative level allows us to correctly model our ATPase kinetics by numeric integration (Supplementary Figure S4; Seidel et al, 2005). Consistent with the empirical data, the resulting profiles are characterized by a slow exponential lag in the kinetics until a linear steady-state phase is reached, during which the majority of MTase–DNA complexes have HsdRs attached, which are occupied in loop translocation (Supplementary Figures S4 and S6; Frieden, 1979). The lag represents slow loop initiation and recycling of dissociated motors.

Overall, our experimental profiles match those expected from the model (Figure 1B and C) and can be almost completely described by a single exponential approach to a linear steady state (Supplementary Figure S5). But we note that there are small but nonetheless systematic deviations from the fit during the initiation stages, and the reasons are discussed in Supplementary data (see Supplementary Figure S5). Irrespective of the exact details of the initiation pathway, we can use linear regression to fit the steady-state segment of the data to give the global steady-state k_ATP (Figure 1C; Materials and methods; Frieden, 1979); this is a macroscopic constant that averages over all the motors translocating but also over the various rates during one stepping cycle—ATP binding, hydrolysis and product release steps—and is typically governed by one step, which is rate limiting in the cycle.

To determine accurately the rate of ATP hydrolysis per HsdR molecule, we need to know the concentration of motors that contribute to the observed steady-state rate. As two HsdR molecules can be loaded by each DNA-bound MTase (Seidel et al, 2005), the maximum concentration of translocating HsdR molecules is equal to twice the concentration of DNA sites (i.e., 0.5 nM DNA sites saturated with MTase correspond to 1 nM HsdR binding sites; Materials and methods). Consequently, there are two sources of systematic error that can contribute to the accuracy of the ATPase rate (see Supplementary data): firstly, uncertainty in the DNA concentration gives an error in the concentration of HsdR loading sites of ±6%; secondly, although we ensured that the reaction rate was saturated with respect to the HsdR (Figure 1B), motor turnover during translocation leads to subsaturation of the steady state (Seidel et al, 2005). Under the conditions used here and based on the kinetic parameters determined previously (Seidel et al, 2005), there is an additional 5% uncertainty in the concentration of the steady-state population (Supplementary Figure S6). These errors become important when we consider the coupling ratios below (see Figure 3C; Supplementary data).

ATPase rates were examined at five temperatures (10, 15, 20, 25 and 30°C) and across a range of ATP concentrations above and below the K_M,app. An example of ATP titration taken at 15°C is shown (Figure 1D). k_ATP values were determined from the linear phases of the profiles. The dependence of k_ATP on the ATP concentration and temperature is shown in Figure 1E. At all temperatures, the rates increase hyperbolically with increasing ATP, to reach a saturated maximum. The temperature dependence gives a Q₁₀=∼2.0 (where Q₁₀ is the temperature coefficient, defined as the change in rate when the temperature is increased by 10°C; data not shown). The data could be fitted to equation (4) (see Materials and methods) to give apparent K_M values that were, within error, invariant of temperature (Figure 1E, inset).

Measurement of the temperature dependence of DNA translocation by stopped-flow fluorimetry

DNA translocation can be measured in bulk solution by the triplex displacement assay (Firman and Szczelkun, 2000; McClelland et al, 2005), which allows variation in both temperature and ATP concentration. Using the stopped-flow fluorimeter, we preincubated our enzyme with specific linear DNA substrates containing a fluorescent triplex bound at varying distances downstream of the recognition site, initiated the reaction by rapid mixing with ATP and then followed the increase in the fluorescence of the triplex probe as it was displaced following collision of the HsdR (Figure 2A; Materials and methods). By following this protocol, we could measure translocation under exactly the same conditions used above for the ATPase measurements. Data from five different triplex spacings were fitted to the global kinetic model considered above in the ATPase data to obtain k_step (Materials and methods; Seidel et al, 2005). As with k_ATP, this is a macroscopic constant that averages over ATP binding/hydrolysis/release and motor steps in one stepping cycle.

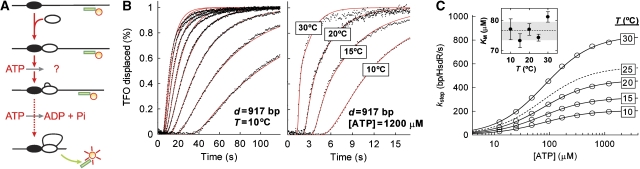
Figure 2.

The temperature dependence of translocation rate measured using ensemble triplex displacement assays. (A) Cartoon as in Figure 1A showing displacement of a fluorescent triplex (green line) during translocation of EcoR124I. The triplex assay returns the translocation rate for one HsdR, regardless of whether it is part of an R₁ or R₂ complex (McClelland et al, 2005). (B) Representative fluorescent triplex displacement profiles. Final reaction conditions were 1 nM linear pMDS44a (of which 0.5 nM carries the triplex), 30 nM MTase and 120 nM HsdR. Red lines are fits to the kinetic traces based on the model in Figure 1A and as described in Materials and methods to give k_step. (Left panel) Displacement profiles at 10°C at ATP concentrations (right to left) 12.5, 25, 48, 96, 170, 320, 600 and 1200 μM. (right panel) Displacement profiles at a range of temperatures as indicated. (C) Hyperbolic dependence of k_step on [ATP] as a function of temperature. Solid lines show fits to equation (4). The dotted line represents the fitted trace from data obtained previously (Seidel et al, 2005). Statistical error bars are smaller than the scatter of the data points. Fitting to equation (4) was not weighted to the statistical errors (discussed in Supplementary data). (inset) Dependence of the K_M on temperature. Error bars are the s.e.m. of the fitted values. The dotted line shows the average K_M across the temperature range and the grey box the associated s.d. V_max,calc and s.e.m. (bp/s) calculated from the fits or those described previously (Seidel et al, 2005) were 208±5 (10°C), 316±5 (15°C), 463±5 (20°C), 576±2 (25°C; Seidel et al, 2005) and 840±5 (30°C).

Translocation rates were examined at four temperatures (10, 15, 20 and 30°C) and across a range of ATP concentrations above and below the K_M,app. Similar measurements at 25°C were obtained previously (Seidel et al, 2005). Examples of displacement profiles are shown in Figure 2B. The dependence of k_step on the ATP concentration and temperature is shown in Figure 2C. At all temperatures, the data show that the rates increase hyperbolically with increasing ATP. As above, the temperature dependence gives a Q₁₀=∼2.0 (data not shown). The apparent K_M values obtained from fits to equation (4) are, within error, equal to the values obtained in the ATPase assays (Figure 2C, inset)

ATP coupling efficiency of EcoR124I

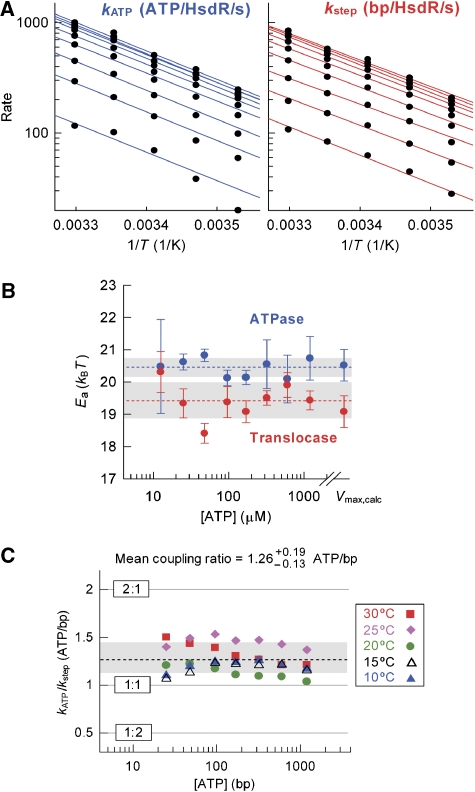
To compare directly the ATPase and translocation rates obtained above, we must ensure that changes in ATP concentration and/or temperature do not result in changes in the kinetic pathway (Lucius and Lohman, 2004; Tomko et al, 2007). If this were to occur such that the ATPase and translocase reactions were rate-limited by different steps in the pathway, then the coupling ratio observed would be specific to a particular solution condition. The experimental k_ATP and k_step values presented in Figures 1E and 2C and the V_max,calc values obtained from the corresponding fits were compared using the Arrhenius relationship: where v is the observed rate, v₀ is the pre-exponential factor, E_a is the activation energy barrier height and k_BT is the energy of the surrounding heat bath. ATPase and translocase data at each ATP concentration were fitted to equation (1) independently (Figure 3A; Supplementary Figures S7 and S8). No significant deviations from equation (1) were observed over the temperature ranges examined, indicating that the same kinetic pathway exists under all conditions. Within experimental error, the E_a values obtained for the ATPase and translocase activities were similar and invariant with ATP concentration (Figure 3B). These observations can be justified as follows.

Figure 3.

Coupling efficiency of ATP hydrolysis to DNA translocation. (A) Temperature dependence of the rate of ATP hydrolysis (left panel) and translocation (right panel) at ATP concentrations (bottom to top in both panels) 12.5, 25, 48, 96, 170, 320, 600 and 1200 μM. The topmost line in each panel represents the V_max,calc data obtained from the hyperbolic fits in Figures 1E and 2C, and Seidel et al (2005). Solid lines represent independent fits to equation (1). Statistical error bars are smaller than the scatter of the data points. Fitting to equation (1) was not weighted to the statistical errors (discussed in Supplementary data). Each individual fit is shown in Supplementary Figures S7 and S8. (B) Dependence of the activation energies (E_a) obtained in (A) on [ATP]. Error bars are the s.e.m. V_max,calc values are arbitrarily plotted at 8 mM ATP. Dotted lines represent the average E_a values and the grey boxes the associated s.d. values. (C) The effect of temperature and [ATP] on the ATP coupling ratio (k_ATP/k_step). Grey lines show the ratios of ATP hydrolysed to base pairs translocated, as indicated. The dotted line shows the mean coupling ratio, 1.26 ATP/bp. The s.d. of the sample mean is ±0.14 (N=35). The grey box represents the precision of the mean (^+0.19_−0.13) and is calculated by error propagation as the sum of the 95% confidence interval of the sample and the systematic error in k_ATP (discussed in Supplementary data).

For our measurements, the translocation pathway can be described in a simplified manner by the kinetic scheme below: 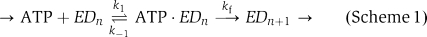where ED_n and ED_n+1 represent the motor (E) bound to the DNA (D) at positions n and n+1, respectively, k₁ and k₋₁ represent the reversible ATP association and k_f represents a subsequent rate-limiting step that could reflect any part of the cycle thereafter (ATP hydrolysis, protein domain motions, ADP/P_i release, etc.; Lucius and Lohman, 2004). We assume that there is only one rate-limiting step per cycle (i.e., there is no other step with a similar rate to the slowest step). Our data are consistent with Scheme 1 only if ATP binding is in rapid equilibrium (i.e., k₋₁≫k_f; Lucius and Lohman, 2004). Under these conditions, the same repeated step (k_f) will remain rate limiting at all ATP concentrations. Consequently, we would expect that, as observed, varying the ATP concentration will vary the rate in a hyperbolic manner but that the same energetic barrier (that for the k_f step) will exist at all concentrations.

Because of the invariant Arrhenius relationship for both ATPase and translocase rates over a range of ATP concentrations, we are confident that the kinetic mechanism does not vary appreciably across the conditions examined. Consequently, we are also confident in directly comparing the ATPase and translocase rates to obtain an apparent coupling efficiency that is valid over a wide range of solution conditions. The k_ATP:k_step ratios at each temperature and ATP concentration are shown in Figure 3C. The values obtained do not show any systematic relationship with either ATP or temperature. The scatter is most likely due to statistical experimental error (Supplementary data). We therefore calculated an average coupling constant from the sample of 1.26 ATP/bp with an s.d. of ±0.14 (N=35). However, an important source of error in this value comes from the systematic errors in the k_ATP values (see above and Supplementary data). To quantify the precision of the sample mean, we calculated the error propagation from the sum of the 95% confidence interval (±4%) and the additive systematic errors in k_ATP (+11 and −6%; Supplementary data), to give a coupling constant of 1.26_−0.13^+0.19 ATP/bp. Given the wide range of solution conditions explored and the error range in our measurements, we can assert that EcoR124I hydrolyses between 1.1 and 1.5 ATPs for every base pair of dsDNA translocated.

Measurement of the temperature dependence of DNA translocation by single-molecule measurements

One of the most compelling reasons to use EcoR124I as an archetype dsDNA translocase in these studies is that we can measure the activity of single enzyme molecules using a well-established magnetic tweezers set-up (Figure 4A; Seidel et al, 2004, 2005; Stanley et al, 2006). Motor events can be observed as a transient decrease in the end-to-end length of the DNA due to the formation of DNA loops. Both the rate and lifetime of a translocation event can be scored. As the reported rates correspond to the total velocity of shortening of the end-to-end length of the DNA, events with only one motor running (R₁) can be distinguished from those with two motors running (R₂), as the latter cause a temporary doubling of the rate. As in the ensemble experiments, the use of a one-site linear DNA substrate significantly reduces the chance of DNA cleavage occurring (Szczelkun et al, 1996; Seidel et al, 2004).

Figure 4.

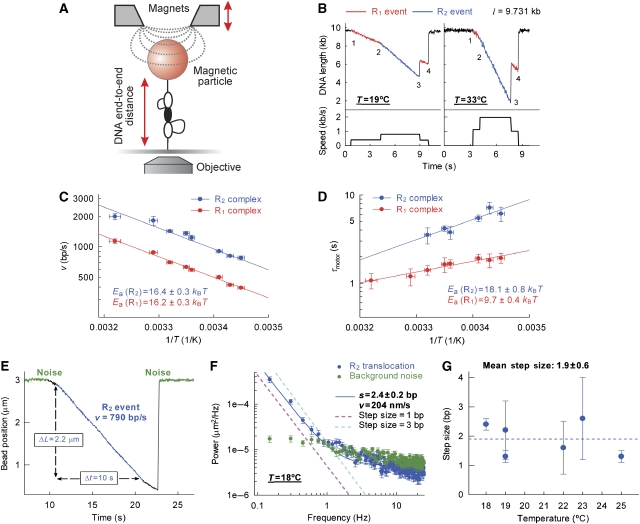
Temperature dependence of EcoR124I step size measured using single-molecule magnetic tweezers assays. (A) Magnetic tweezers set-up (Seidel et al, 2004). A DNA molecule with a single EcoR124I site is anchored between a glass coverslip and a magnetic bead. Magnets are used to maintain the DNA in a stretched conformation. Translocation of one (not shown) or two (shown) HsdR results in the formation of expanding DNA loops, which reduce the apparent end-to-end DNA length and this is monitored by video microscopy. (B) Example time traces recorded at two different temperatures with MTase at 20 nM, HsdR at 160 nM, ATP at 4 mM and the applied stretching force at 3 pN. Each trace shows a similar profile, with the initiation of the first motor to form an R₁ event (1), the initiation of the second motor to form an R₂ event (2), the dissociation of one or other motor with the concomitant release of a trapped DNA loop to return to an R₁ event (3) and finally the dissociation of the remaining motor (4). The graphs below the time traces show the development of the translocation rate, which has been determined from a straight line fit to the data (data not shown) and calculating its derivative. R₂ events have a rate that is twice that of R₁ events (Seidel et al, 2004). (C) Temperature dependence of the R₁ or combined R₂ translocation velocity from the magnetic tweezers. Solid lines represent independent fits to equation (1). Error bars in the y-axis represent s.e.m. and errors bars in the x-axis represent the systematic error in the temperature. (D) Temperature dependence of the motor lifetime (τ_motor) for single HsdR within an R₁ or R₂ complex. Solid lines represent independent fits to equation (1) where v=1/τ_motor. Error bars as in (C). (E) Example of a long-duration R₂ translocation event recorded at 18°C and 3 pN. The average spectral density of such events was examined to obtain estimates of the step size. (F) Power spectrum averaged over 14 translocation events at 18°C. The blue line represents the fit to equation (2). The two dotted lines indicate step sizes of precisely 1 or 3 bp. The green data are the power spectrum of the noise during periods of inactivity. Error bars represent s.e.m. (G) The temperature dependence of the step size. The dotted line represents the mean across the temperature range. Error bars represent the s.e. returned from the fit (see (F)).

To assess the physical step size of the enzyme, which is required to obtain the ATP coupling efficiency, it would be ideal if one could resolve individual steps directly from the tracking profiles. However, EcoR124I motor events can only be observed for forces <5 pN (Seidel et al, 2004), conditions where large Brownian fluctuations of the DNA in combination with the high motor velocity limit the spatial resolution of individual steps to step sizes of >10 bp at 10 Hz. But it is possible to calculate a smaller step size from a noise analysis of a measured translocation profile following many thousands of steps (Charvin et al, 2002; Neuman et al, 2005). When the motor cycle is governed by a single rate-limiting step (i.e., as in Scheme 1), the stochastic nature of stepping produces a random deviation from a straight line in the position–time relationship. This stepping noise, which is proportional to the step size, has distinct spectral characteristics at low frequencies compared to the approximately Gaussian noise of the magnetic bead fluctuations (Charvin et al, 2002; Neuman et al, 2005). Consequently, it is possible to extract the step size from a Fourier analysis of multiple steps during a translocation run in the magnetic tweezers. For example, this method has been used to determine an unwinding step size for the UvrD helicase of 6 bp (Dessinges et al, 2004).

To carry out this analysis on EcoR124I, we assume that Scheme 1 holds, that is, each enzymatic cycle is governed by a single rate-limiting step. (Multiple rate-limiting steps would lead to a decrease in the stepping randomness and thus a lower stepping signal compared to background noise.) To validate this under the single-molecule conditions, tweezers experiments were performed at different temperatures with a fixed, saturating concentration of ATP (Materials and methods); example profiles at two temperatures are shown in Figure 4B.

For each temperature examined, data were collated for the translocation velocity and lifetime for both R₁ and R₂ events and fitted to equation (1) (Figure 4C and D). In agreement with the stopped-flow measurements, linear Arrhenius relationships were obtained, which supports the assumption that speed is limited by a single rate (modelling additional temperature-dependent and temperature-independent rates causes significant deviations from the data; Supplementary Figure S9). The activation energies for the R₁ and R₂ events are similar, whereas the absolute speeds are two-fold different across the temperature range examined (Figure 4C). These results are consistent with previous independent observations that the R₂ rate is simply the sum of translocation rates for each of the divergent HsdR motors (Seidel et al, 2004). Comparison of the data from the tweezers assay with that from the triplex assay shows that there is excellent agreement in the HsdR translocation rates (Supplementary Figure S10). The duration of both R₁ and R₂ motor events (τ_motor) decreased with increasing temperature. Linear Arrhenius relationships were again obtained, with activation energies for the R₁ and R₂ species, which are two-fold different (Figure 4D). These results are also consistent with previous work, which showed that translocation termination (defined as the dissociation of a single HsdR from the MTase loader complex) is governed by a single rate (Seidel et al, 2004, 2005).

Step size of EcoR124I measured by magnetic tweezers

To determine the step size, we examined long-lived R₂ translocation events at different temperatures (Materials and methods). The activity of each motor in an R₂ complex is statistically independent (Figure 4C; Szczelkun, 2002; Seidel et al, 2004, 2005), and the resulting stepping profiles will be indistinguishable from those of one motor in an R₁ complex (except for a doubling in the overall rate). To provide the best balance between decreasing instrumental noise (by minimizing Brownian motion of the bead) while increasing the run length (which in turn maximizes the occurrence of low-frequency noise), we chose to examine R₂ tweezers data for conditions of [ATP]=4 mM and F=3 pN. Note that we can neglect any influence of the applied force on the apparent step size, as the stepping rate is independent of force up to 5 pN, most likely because the force-producing step never becomes rate limiting before the complex collapses (Seidel et al, 2004). A typical profile under these conditions is shown (Figure 4E). Under the assumption, validated above, of a single rate-limiting step per stepping cycle, the power spectrum of a translocation run can be analysed by 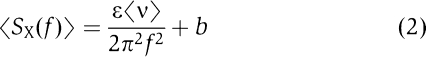where f is the frequency, ɛ the step size, ν the speed and b the experimental background noise (Charvin et al, 2002; Neuman et al, 2005). To improve precision further, the power spectra of multiple translocation events were averaged (Figure 4F). The power spectrum of instrumental noise (i.e., during periods of motor inactivity) is shown for comparison. For this example, a step size of 2.4 bp can be estimated from a fit to equation (2). The dashed lines in Figure 4F show the relationship expected for steps of 1 or 3 bp. Clearly, these do not describe the data well.

Step sizes estimated in this way were determined at a range of temperatures (Figure 4G). Although enzyme speed changes considerably over the temperature range (Figure 4C), the step sizes are, within experimental limits, constant. From this, we can estimate a temperature-independent mean step size of 1.9±0.6 bp. We note that any additional source of error—nonlinearities in the length measurements—increase the low-frequency noise (additional deviation from a straight line in the position–time relationship) and therefore might lead to a slight overestimation of the real step size. Moreover, if EcoR124I occasionally makes short pauses during translocation (see discussion about uncoupling below) or exhibits a slight sequence dependence of its translocation rate, then again the step size would be somewhat overestimated. Our data thus clearly exclude step sizes exceeding 2. EcoR124I most likely makes steps of 2 bp or perhaps 1 bp at a time along the dsDNA track.

Discussion

We have shown above that motion of the dsDNA motor EcoR124I along intact dsDNA can occur in steps of 1–2 bp, with ∼1 ATP consumed for each base pair moved. Most notably, both results are consistent with a model in which the motor makes small steps on DNA of ⩽2 bp. Much larger differences between the coupling ratio and the apparent step size have been found for other helicase motors (see below).

A small step size explains a number of features of the EcoR124I mechanism: (1) DNA translocation produces changes in DNA twist, with one supercoil induced every 11±2 bp (Seidel et al, 2004). This is consistent with a small step size where the motor will track closely the helical pitch of the DNA. (2) The translocation rate is independent of force up to ∼5 pN (above which DNA tension significantly reduces the lifetime of translocation; Seidel et al, 2004). This is consistent with a small step size, which would only slow down any force-producing step by a factor of ∼1.4 (calculated assuming a force-dependent Arrhenius relationship (Seidel et al, 2004), a step size of 1 bp and a force of 4 pN). (3) DNA translocation is sensitive to changes in the DNA backbone as minor as a single missing phosphate group at a nick (Stanley et al, 2006). This is consistent with the enzyme tracking the DNA backbone closely. (4) EcoR124I is a true dsDNA translocase (Stanley et al, 2006). Any transient DNA unwinding during translocation would most likely lead to a strong sequence-dependent translocation rate, as seen for some true helicases (Johnson et al, 2007), which in turn should significantly increase the observed stepping noise. However, our small step size is inconsistent with large sequence-dependent effects.

Despite a rather close match between ATPase coupling and apparent physical step size, both measured values are, however, not entirely in agreement with a simple uniform stepping model in which 1 or 2 bp steps are made by the enzyme with precisely 1 ATP hydrolysed per step. On the one hand, the ATPase coupling is significantly larger than 1:1 (Figure 3C) and, on the other hand, the apparent step size is close to 2 and thus larger than the coupling ratio (Figure 4G). In the following discussion, we will therefore consider several models, each of which can explain this.

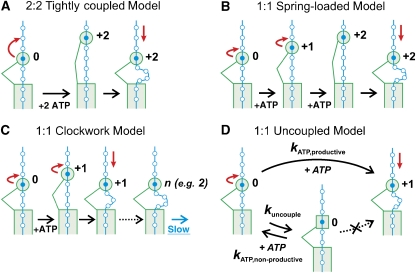
2:2 Tightly coupled Model

The motor makes a 2 bp step along the DNA lattice after hydrolysis of 2 ATP (Figure 5A). Within this model, two sequential ATP-binding–hydrolysis–release cycles must occur; simultaneous, cooperative ATP binding at two independent ATP binding sites is not supported by the strictly hyperbolic ATP dependence of k_step and k_ATP (Figures 1E and 2C). This in turn implies that the energy of the first hydrolysis event must be stored (e.g., within a strained conformational intermediate state of the motor) to be made available following the second hydrolysis event. Note that this model can only give rise to an apparent step size of 2 bp from a Fourier analysis if one allows the rates of the two ATP hydrolysis events to be different. Otherwise, a step size of 1 bp would be obtained (this corresponds to the Clockwork Model with k_fast/k_slow=1, which is discussed below and in Figure 6A).

Figure 5.

Models for different stepping modes of EcoR124I. EcoR124I MTase (M) is represented as a rectangle, HsdR (R) as a circle or square (with the protein–protein connection to the MTase as a line) and the DNA as beads-on-a-string with each base pair as a separate bead. (A) 2:2 Tightly-coupled Model. Starting at position 0, HsdR consumes 2 ATP before making a step of 2 bp, so pumping 2 bp into the expanding DNA loop at each step. (B) 1:1 Spring-loaded Model (Myong et al, 2007), with an elastic linkage between the HsdR and MTase. HsdR consumes 1 ATP for each step on the DNA, partitioning 1 bp at a time into the expanding loop. Forward stepping causes the linkage between the HsdR and MTase to stretch until, at a threshold (here, 2 bp), recoil causes the HsdR to be pulled back. (C) 1:1 Clockwork Model (Tomko et al, 2007). HsdR consumes 1 ATP for each step on the DNA, partitioning 1 bp at a time into the expanding loop. After a set number of steps (n), a slow step occurs before stepping restarts. The pause most likely represents a conformational resetting of the HsdR. (D) 1:1 Uncoupled Model. HsdR consumes 1 ATP for each step on the DNA, pumping 1 bp into the expanding loop at each step with a rate k_{ATP,productive}. Alternatively, HsdR can enter a cycle of ATP hydrolysis that does not move the HsdR forward (or backward): HsdR can stall at its current position with a rate k_uncouple, before returning to a translocation competent state with a rate k_{ATP,non-productive}.

Figure 6.

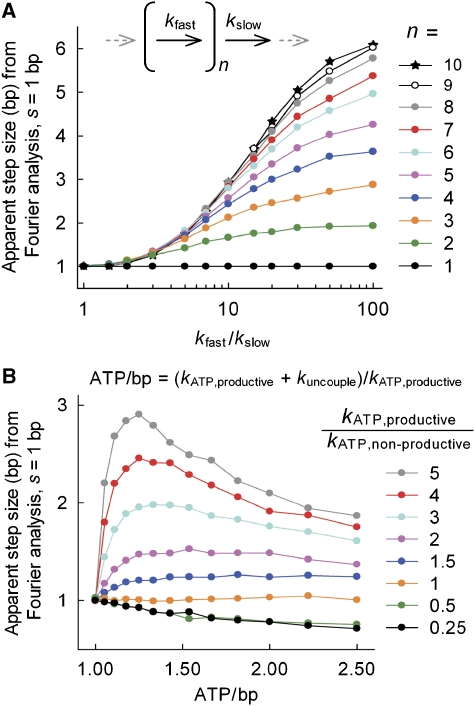
The effect of different translocation modes on the apparent step size of a motor with a true step size of 1 bp. Using the models in Figure 5, Poisson stepping profiles were simulated using the parameters shown. Apparent step sizes were then estimated from a Fourier analysis of the simulated traces (see Supplementary data for further details). (A) The effect of a pause every n steps (the Clockwork Model in Figure 5C). 1 bp steps are made at the rate k_fast. After completing n steps, the motor undergoes a conformational change at the rate k_slow during which no stepping occurs. The effect of the number of steps before pausing and the relative rates of the fast and slow steps are shown. Increasing the number of steps before the pause and decreasing the rate of the pause step cause an overestimation of the step size. (B) The effect of uncoupled steps (the Uncoupled Model in Figure 5D). The effect of changes in the coupling ratio (ATP/bp) and the rate ratio of the two ATPase steps are shown. Uncoupled steps can lead to occasional slow cycles that can result in an over- or underestimation of the apparent step size. Similar uncoupling events could account for the large kinetic step sizes seen in some other helicase studies (see main text).

1:1 Spring-loaded Model

The motor makes 1 bp steps along the DNA lattice with 1 ATP hydrolysed per step, but with an elastic linkage between the HsdR and, for example, the MTase, such that measurable DNA shortening is observed only after a threshold strain has accumulated. This model has been adapted from the recently proposed mechanism of HCV NS3 helicase (Myong et al, 2007). The threshold could be reached every 2 bp, as depicted in Figure 5B. As noted above, this model only returns an apparent step size >1 bp from a Fourier analysis if there are rate differences within the cycle before DNA shortening.

1:1 Clockwork Model

The motor makes 1 bp steps along the DNA lattice with 1 ATP hydrolysed per step, but with a pause every n steps (Figure 5C). This model has been recently proposed for the translocation of UvrD along ssDNA to explain the difference between an apparent kinetic step size of 4.6 nt and an ATPase coupling of 1 ATP/nt (Tomko et al, 2007). Depending on the ratio between the fast stepping rate and the slow pausing rate, one could obtain an apparent step size anywhere between 1 and n from a Fourier analysis (Figure 6A).

1:1 Uncoupled Model

Based on the coupling of >1 ATP/bp observed here, we propose a new model that has not been discussed previously. It assumes 1 bp steps along the DNA lattice with 1 ATP hydrolysed per step, but additionally allows non-productive (uncoupled) steps. In the latter case, the motor enters a cycle of ATP hydrolysis that does not lead to movement of the enzyme (Figure 5D). Consequently, a coupling of >1 ATP/bp is observed. If one allows the rate of the uncoupled cycle to be slower than the stepping rate, an apparent step size significantly larger than 1 can also be observed (Figure 6B).

Based on the data presented here, we cannot absolutely rule out any of these models, as, under particular conditions, all can return an apparent step size of ∼2 bp. Although there is some value in attempting to discuss the plausibility of the different models, one has to keep in mind that our current knowledge about the dynamics and mechanisms of SF2 helicases, and helicases in general, is rather limited. Although there are now a large number of structural and biochemical studies of SF1 and SF2 helicases that provide strong support for a coupling ratio of 1 ATP/bp (Roman and Kowalczykowski, 1989; Dillingham et al, 2000; Soultanas and Wigley, 2001; Lee and Yang, 2006; Büttner et al, 2007, Hopfner and Michaelis, 2007), model-based step size determinations (Dessinges et al, 2004; Tomko et al, 2007) and single-molecule experiments resolving individual steps (Dumont et al, 2006; Myong et al, 2007) have provided evidence that are not in agreement with a simple uniform stepping model with a step size of 1 bp. Our study of dsDNA translocation also provides support for a non-uniform stepping mechanism. However, in addition to the previously suggested mechanisms, that is, the Spring-loaded and Clockwork Models (see above), we propose that one should also consider models in which uncoupling between hydrolysis and forward stepping is allowed.

From the examination of SF1 and SF2 structures, it has been proposed that helicases have evolved to use the same underlying inchworm-like motion of two RecA domains for motion on both ssDNA and dsDNA (Hopfner and Michaelis, 2007; Singleton et al, 2007). Given that the magnitude of domain motions between ATP-bound and nucleotide-free conformations has been determined to be ∼0.34 nm (Büttner et al, 2007; Hopfner and Michaelis, 2007), we favour mechanisms where the smallest step taken on DNA is 1 bp. The 1:1 Uncoupled Model (Figure 5D) is the only one considered here that can also accommodate a coupling of >1 ATP/bp, as depicted in Figure 3C (even higher errors of up to 10% in the DNA concentration would still return a coupling >1). However, there is no reason why uncoupled ATPase activity could not occur within the context of a Spring-loaded and/or Clockwork mechanism. What could be the structural rationale for uncoupling? Comparison of processive and non-processive SF2 helicases has revealed that duplex unwinding is powered by very similar RecA domain motions in both systems (Sengoku et al, 2006; Büttner et al, 2007). The additional structural element that assists processive motion has been identified as a so-called ratchet domain, which clamps the nucleic acid template during forward movement (Büttner et al, 2007). Potentially, this clamping may not be 100% efficient, leading to occasional ATP binding and hydrolysis without forward motion. A definitive view of the stepping mechanism(s) of dsDNA translocases such as EcoR124I will probably be achieved only by simultaneously resolving the base-pair-sized motor steps and ATPase cycle in single-molecule experiments, where, in particular, the latter measurements are challenging.

Materials and methods

Preparation of proteins and DNA

EcoR124I was purified, reconstituted and tested as previously described (Stanley et al, 2006). For magnetic tweezers experiments, DNA substrates were prepared from pRSgap (Stanley et al, 2006) into which a 1.4 kbp PCR fragment from pSFVI (3780–5140 bp) carrying a single EcoR124I site was cloned between the XhoI and the HindIII sites. DNA tails with biotin- and digoxigen-modified bases were ligated as described previously (Stanley et al, 2006) at the SacI and PciI sites of the plasmid. This provides a 9.7 kbp DNA construct with the EcoR124I site close to the centre of the molecule. For phosphate release experiments, ApaI-linearized versions of single-site specific (pLKS5; Stanley and Szczelkun, 2006) and non-specific (pTYB11; New England Biolabs) plasmids were prepared as described (Seidel et al, 2005). For the triplex assays, ApaI-linearized versions of the single-site specific plasmids pMDS43a, -44a, -45a, -46a and -47a were prepared as described (McClelland et al, 2005). Both this family of plasmids and pLKS5 are based on the parental vector pTYB11 and show >98% sequence identity. DNA for the ensemble experiments was highly purified by density gradient centrifugation in CsCl–ethidium bromide (Vipond et al, 1995). DNA concentrations were measured by absorbance at 260 nm in a Perkin Elmer Lambda 14 spectrophotometer using an average extinction coefficient for dsDNA of 0.02 ml/μg/cm (Sambrook and Russell, 2001). The specific DNA and non-specific DNA were checked by ethidium bromide fluorescence following agarose gel electrophoresis to ensure that the concentrations matched. The errors associated with the determination of DNA concentration are discussed in Supplementary data.

Phosphate release assay

Coumarin-labelled PBP was prepared, characterized, calibrated and tested according to Webb (2003) (Supplementary data; Supplementary Figures S1–S3). Rapid mixing fluorescence was performed using an SF61-DX2 stopped-flow fluorimeter (TgK Scientific Limited, Bradford-on-Avon, UK) with λ_ex=435 nm (∼2 nm bandwidth) with a 455 nm band pass filter placed between the sample housing and photomultiplier tube (PMT). Temperature was maintained between 10 and 30°C by a waterbath connected to the chamber housing the syringes and flow cell. Pre-equilibrated samples in reaction buffer (50 mM Tris–HCl, pH 8.0, 10 mM MgCl₂, 1 mM DTT) containing 1 nM linear DNA, 120 nM MTase, 0–400 nM HsdR, 12 μM PBP, 30 mM 7-methylguanosine (Sigma) and 0.05–0.005 U/ml purine nucleoside phosphorylase (Sigma) were loaded into syringe ‘C' of the SF61-DX2. Pre-equilibrated samples in reaction buffer containing 0–2400 μM ATP, 12 μM PBP, 30 mM 7-methylguanosine and 0.05–0.005 U/ml purine nucleoside phosphorylase were loaded into syringe ‘D'. (Mg²⁺ ions are required for both the ATPase (and thus translocase) and nuclease activities. The Mg²⁺ ion concentration was chosen to be saturating with respect to the in vitro nucleotide concentration, which parallels cellular conditions in Escherichia coli (Kuzminov, 1999).) Equal volumes (50 μl) of C and D were mixed and the progress of the reaction was monitored using default hardware settings. For the standard reactions, the final conditions were 0.5 nM linear DNA, 60 nM MTase, 200 nM HsdR and 0–1200 μM ATP. The PMT response was calibrated using titration of a P_i standard according to Webb (2003) and was shown to be linear at all temperatures (Supplementary data; Supplementary Figure S2; Supplementary Table S1). The accuracy of the assay was validated by comparison to a radioactive ATPase assay (Supplementary Figure S3).

Triplex displacement assay

Triplex displacement measurements were carried out in the SF61-DX2 stopped-flow fluorimeter as described (McClelland et al, 2005; Seidel et al, 2005). Temperature was maintained between 10 and 30°C by a waterbath connected to the chamber housing the syringes and flow cell. Final reaction conditions were 1 nM linear DNA (0.5 nM tetramethylrhodamine triplex), 60 nM MTase, 200 nM HsdR, 12 mM phosphocreatine, 10 U/ml creatine phosphokinase and 0–1200 μM ATP in reaction buffer. k_step values were determined from reactions at each of five different triplex spacings (484, 917, 1414, 2054 and 2774 bp).

Magnetic tweezers assays

Magnetic tweezers experiments have been carried out as previously described using M-280 dynabeads (Invitrogen) (Seidel et al, 2004). Enzyme reactions have been carried out in reaction buffer using 20 nM MTase, 160 nM HsdR and a DNA stretching force of 3±0.3 pN in all experiments. Under these conditions, the translocation rate is independent of the force (Seidel et al, 2004). The temperature during the measurements was varied by controlling the temperature of the surrounding room or by simultaneously controlling the temperature of the objective using an objective heater (Bioptechs) and the temperature of the flow cell system using transparent heating elements (Alflex) placed on top of the cell.

Data analysis

Previously described methods were used to analyse the triplex displacement profiles (McClelland et al, 2005; Seidel et al, 2005) and the time traces from the magnetic tweezers (Seidel et al, 2004, 2005; Stanley et al, 2006). Linear steady-state phases of the ATPase rate profiles were fitted to where C_p is the phosphate concentration, k_ATP is the macroscopic steady-state ATPase rate, τ_ini is the macroscopic initiation delay time and t is the reaction time. ATP dependence data were fit to a Michaelis–Menten relationship: Fits to equations (1) and (4) were not weighted to statistical or systematic errors (the statistical and systematic errors associated with the ensemble experiments are discussed in Supplementary data). Systematic errors associated with k_ATP were incorporated in the analysis of the average coupling ratio (see above and Figure 3C).

Single-molecule translocation events were analysed as described previously (Seidel et al, 2004). Segments of constant enzyme velocity were fitted with straight lines to extract translocation rates and processivities. For step size estimation by noise analysis, we recorded at each temperature typically 10–20 translocation events containing a segment of constant R₂ velocity of more than 6.7 s (or 400 data points at 60 Hz sampling rate). From each segment, the constant slope was subtracted and the resulting data were subdivided into 6.7 s subsegments that were slightly overlapping. For each subsegment, the power spectrum was calculated and all power spectra from all subsegments at a given temperature were averaged to reduce the statistical error. For power spectrum calculations, a Hanning window was applied, but similar results were obtained if no window was applied (data not shown). The averaged power spectrum was subsequently fit by equation (2) to extract the step size. Background noise was treated the same way by analysing segments where no enzymatic activity has been observed.

Supplementary Material

Supplementary Data