REVIEW OF SIGNAL DISTORTION THROUGH METAL MICROELECTRODE RECORDING CIRCUITS AND FILTERS

Abstract

Interest in local field potentials (LFPs) and action potential shape has increased markedly. The present work describes distortions of these signals that occur for two reasons. First, the microelectrode recording circuit operates as a voltage divider producing frequency-dependent attenuation and phase-shifts when electrode impedance is not negligible relative to amplifier input impedance. Because of the much higher electrode impedance at low frequencies, this occurred over frequency ranges of LFPs measured by neurophysiologists for one head-stage tested. Second, frequency-dependent phase shifts are induced by subsequent filters. Thus, we report these effects and the resulting amplitude envelope delays and distortion of waveforms recorded through a commercial data acquisition system and a range of tungsten microelectrodes. These distortions can be corrected, but must be accounted for when interpreting field potential and spike shape data.

Various metal microelectrodes have been designed to isolate spikes (Green 1958; Hubel 1957; Levick and Cleland 1974; Merrill and Ainsworth 1972; Wolbarsht et al. 1960; reviewed by Lemon 1984), and different metals and insulations are in use today. An equivalent circuit model of a metal microelectrode in tissue has been proposed that has important theoretical implications about frequency-dependent amplitude attenuation (Lemon 1984; Robinson 1968) and phase shifts (Geddes 1972) of recorded signals. Such consideration in past neurophysiological literature has been primarily given only to the recording of spiking activity. Filtering applied during data acquisition or offline further distorts recorded signals (Oppenheim and Schaefer 1998). If not prevented or accounted for, such distortions can introduce uncertainty into analyses of LFPs or spike shapes. Many recent studies have described LFP phase (Bragin et al. 1995; Haslinger et al. 2006; Lee et al. 2005; Lin et al. 2006; Murthy and Fetz 1996; O’Keefe and Recce 1993; Skaggs et al. 1996), spike-field phase relationships (Haslinger et al. 2006; Lee et al. 2005; Lin et al. 2006; Murthy and Fetz 1996; O’Keefe and Recce 1993; Skaggs et al. 1996), event-triggered potentials (Kreiman et al. 2006; Fries et al. 2001a,b) and LFP power or coherence comparisons across frequencies (Fries et al. 2001a,b; Liu and Newsome 2006; Rickert et al. 2005; Womelsdorf et al. 2006). However, phase distortion caused by the recording system is rarely considered (but see O’Keefe and Recce 1993) and electrode-induced effects have been overlooked. Therefore, we performed systematic measurements to verify that the equivalent circuit model applies to commercial electrodes (FHC) and a data acquisition system (Plexon) in common use by neurophysiologists, and to demonstrate the signal distortions that can occur.

MATERIALS AND METHODS

Equivalent circuit model

Figure 1 illustrates a modified version of a commonly cited equivalent circuit model of a metal microelectrode recording in the brain (Robinson 1968). The effective electrode impedance (Z_e’) is the sum of impedances due to the resistance of the electrolyte (R_s), the resistance of the electrode metal (R_m) and, most importantly, the resistance and capacitance at the double layer that forms at the electrode/electrolyte interface at the uninsulated electrode tip (R_e and C_e). The effective amplifier input impedance (Z_a’) is the total impedance to ground past the electrode; this includes a path through the first amplifier, or head-stage (Z_a), and shunting routes to ground outside the amplifier (R_sh and C_sh) which are typically capacitive. This shunt capacitance arises mainly from the capacitance across the insulation between the electrode shaft and the surrounding electrolyte as well as the cumulative capacitance along cables and connectors between the electrode and head-stage amplifier (Robinson 1968). These routes to ground parallel to the amplifier reduce the effective amplifier impedance, and being capacitive, this effect increases with signal frequency.

Figure 1.

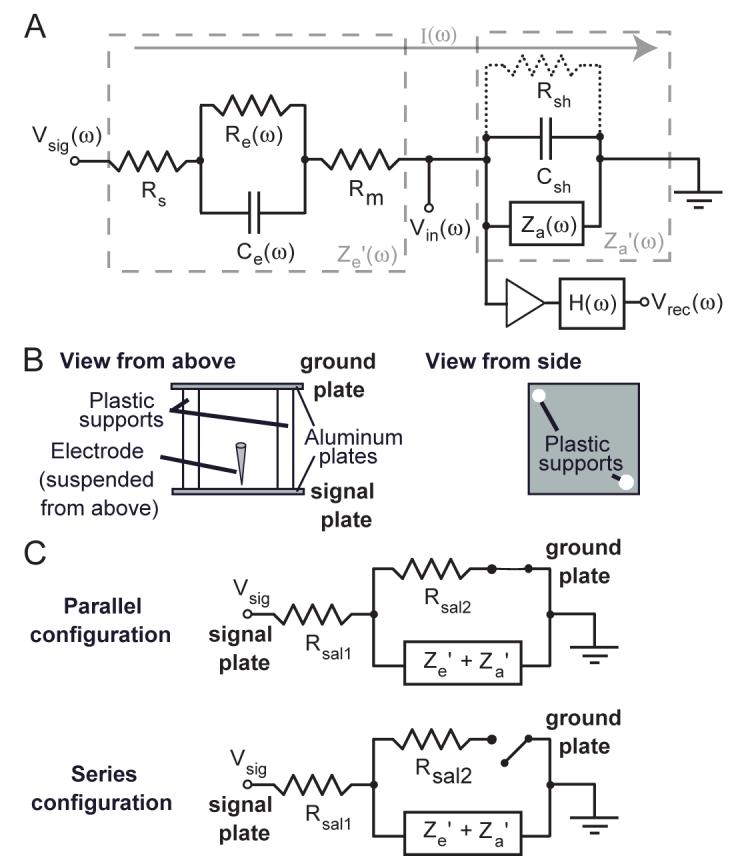
Equivalent circuit model and methods. A: equivalent circuit model of a metal microelectrode in the brain adapted from Robinson 1968. The entire circuit is comprised of the electrode in the brain and the amplifier with a filter. The effective impedance of the electrode (Z_e’) is comprised of the resistance of the electrolyte solution (R_s), the resistance and capacitance at the double layer interface of the electrolyte and the uninsulated electrode tip (R_e and C_e) and the (negligible) resistance of the metal electrode (R_m). The effective input impedance of the amplifier (Z_a’) is comprised of the input impedance of the head-stage amplifier (Z_a) and the shunt resistance and capacitance to ground from the tip of the electrode to the input of the amplifier (R_sh and C_sh). The triangle represents an ideal amplifier that draws no current. The non-ideal aspects of the amplifier have been accounted for in Z_a. Given the frequency-dependent potential at the electrode tip (V_sig(ω)), a current (I(w)) is drawn towards ground through the electrode and effective amplifier circuit, creating the potential (V_in(ω)) at the input of the amplifier which is subject to the frequency response of analog filters (H(w)) before being recorded (V_rec(ω)), all according to the equation: V_rec(ω) = H(ω)[(V_sig(ω)· Z_a’(ω))/(Z_e’(ω) + Z_a’(ω))]. Thus, the microelectrode recording circuit corresponds to a voltage divider with a frequency-dependent gain due to the filtering of H(ω) and the frequency dependence of the impedances Z_e’ and Z_a’. B: diagram of microelectrode testing apparatus. Two aluminum plates were connected and separated from each by non-conducting plastic supports, shown here from a top and side view. The apparatus was immersed in dilute saline with voltage signals applied to the signal plate with an electrode suspended from above 3 mm away. See the Methods section for more details. C: equivalent circuits for the parallel and series configuration. R_sal1 is the resistance for current to travel from the signal plate to the electrode tip in the saline, and R_sal2 is the remaining resistance for current to reach the ground plate.

Signals at the tip of the electrode (V_sig) generate currents (I) that flow to ground through the series combination of the effective electrode impedance and the effective amplifier input impedance:

$$\mathrm{I}\left(\omega \right)=\frac{{\mathrm{V}}_{\mathrm{sig}}\left(\omega \right)}{{{\mathrm{Z}}_{\mathrm{a}}}^{\prime }\left(\omega \right)+{{\mathrm{Z}}_{\mathrm{e}}}^{\prime }\left(\omega \right)}$$ (1)

The voltage at the input of the amplifier (V_in) is given by

$${\mathrm{V}}_{\mathrm{in}}\left(\omega \right)={\mathrm{V}}_{\mathrm{sig}}\left(\omega \right)-\mathrm{I}\left(\omega \right)\cdot {\mathrm{Z}}_{\mathrm{e}}’\left(\omega \right)=\frac{{\mathrm{V}}_{\mathrm{sig}}\left(\omega \right)\cdot {{\mathrm{Z}}_{\mathrm{a}}}^{\prime }\left(\omega \right)}{{{\mathrm{Z}}_{\mathrm{a}}}^{\prime }\left(\omega \right)+{{\mathrm{Z}}_{\mathrm{e}}}^{\prime }\left(\omega \right)}$$ (2)

Equation 2 shows that Z_a’ and Z_e’ form a voltage divider so that when Z_a’ is not substantially larger than Z_e’, V_in will be less than V_sig. This signal attenuation will be accompanied by a phase shift between V_sig and V_in because Z_a’ and Z_e’ are complex values with phases and magnitudes. When multiplying and dividing complex numbers, phases are respectively added and subtracted independently of the numbers’ magnitudes, while the phase of a complex sum is the phase of the separately summed real and imaginary fractions weighted by the magnitudes of each number, so that larger numbers contribute more to the phase of the resulting sum. Therefore the phase difference between V_sig and V_in equals the phase of the effective input impedance Z_a’ minus the phase of the combined impedance Z_a’ + Z_e’. When Z_a’ is much larger than Z_e’ the phase of the combined impedance is dominated by the phase of Z_a’, so the resulting phase shift will be negligible. When this is not the case, potentially noticeable phase shifts will occur and will increase in size as both the relative magnitude of Z_e’ to Z_a’ increases and the overall phase difference between Z_e’ and Z_a’ increases. The direction of the phase shift will depend on whether Z_e’ is more or less capacitive than Z_a’, resulting in positive or negative going phase shifts respectively. For example, if Z_e’ were purely capacitive (phase = -90) and Z_a’ were purely resistive (phase = 0), then when the magnitudes of Z_a’ and Z_e’ are approximately equal, the phase of V_in relative to V_sig would be about 45 degrees, indicating that V_in would lead V_sig by this amount. This phase shift would increase towards an asymptote of 90 degrees as Z_e’ becomes larger than Z_a’. Note that because Z_a’ and Z_e’ are functions of frequency, the magnitude and phase relationship between V_sig and V_in will be frequency dependent.

It is worth noting that only the first amplifier’s input impedance is critical for the measurement, as this is the only amplifier that interacts with the electrode and affects the possibly considerable voltage drop that may occur across it. At this stage, the initial amplifier sets its voltage using its electrical power source based on its gain and the signal input to it, with the limitation that it cannot set a voltage larger than the voltage of its power source. That signal is then sent to following amplifiers and/or recording equipment, and at each stage an additional possible voltage divider is created involving the output impedance of the preceding stage and the input impedance of the following stage. However, no further signal distortion typically occurs at these stages as the input impedance of these stages can usually easily be set well above the output impedance of the preceding stage.

Filtering effects

Physiological data acquisition systems include filters that will affect signals in a manner described by the transfer function of the system (H(ω)) such that:

$${\mathrm{V}}_{\mathrm{rec}}\left(\omega \right)=\mathrm{H}\left(\omega \right)\cdot {\mathrm{V}}_{\text{in}}\left(\omega \right)=\mathrm{H}\left(\omega \right)\cdot \frac{{\mathrm{V}}_{\mathrm{sig}}\left(\omega \right)\cdot {{\mathrm{Z}}_{\mathrm{a}}}^{\prime }\left(\omega \right)}{{{\mathrm{Z}}_{\mathrm{a}}}^{\prime }\left(\omega \right)+{{\mathrm{Z}}_{\mathrm{e}}}^{\prime }\left(\omega \right)}$$ (3)

Any filter, analog or digital, that could be applied in real time during data acquisition would necessarily introduce some frequency dependent phase shifts that become large near the filter’s passband edges. However, once data acquisition has stopped it becomes possible to re-apply the same filter to time reversed data which imposes exactly the same phase shifts introduced during acquisition but in the opposite direction, thus correcting the phase shifts applied during acquisition. This forms the basis for phase-shift free filters that may be applied in post acquisition processing (Mitra 2001).

Data collection procedures

Signals were recorded using a MAP system (Plexon Inc., Dallas, TX) in which signals were passed through a first and second amplifier, which we refer to as a head-stage and a preamplifier, respectively, following the convention of the company that constructed it. After the amplifiers, signals are passed to a Multichannel Acquisition Processor (MAP) for A to D conversion and recording. At the stage of the preamplifier, each input channel is separated into two output channels that undergo different analog filtering, with one channel designed to record higher frequency spikes and one designed to record lower frequency field potentials, which we refer to as the spike and LFP channels, respectively. In this article, when the outputs from both channels are not overlayed, values shown in plots at and below 175 Hz were obtained from the LFP channel data, and values at and above that were obtained from spike channel data as indicated on the plots. Taken together, the two outputs enabled us to perform measurements across the entire frequency range of interest, and for those frequencies that could be measured through either channel (∼80 Hz to 300 Hz), the results from each channel were the same.

Most of the data presented in this study was recorded with a HST/8 o50-G20 (Rev 3.0) head-stage (Plexon Inc., Dallas, TX) with a gain of 20, which we refer to as the low input impedance head-stage (38 MΩ input resistance with 3 pF of parallel capacitance and 10 pF of series capacitance acting on the input before amplification). This was used with a following preamplifier with a gain of 50 (Plexon Inc., Dallas, TX). The preamplifier was configured as a PBX2/16sp/16fp preamplifier with two cascaded 1-pole low-cut Butterworth filters and a 4-pole high-cut Butterworth filter for each of 16 spike channels (100 Hz - 8 kHz) and 16 field potential channels (0.7 Hz - 170 Hz). Additional filtering by the MAP system’s SIG board causes the effective low-cut frequency of the recorded spike channels to be ∼250 Hz. Unless otherwise specified, all data presented in this study was recorded with this equipment.

Different head-stages and preamps were used in some recordings to determine the effects of different equipment. We tested a second head-stage (Plexon Inc., Dallas, TX) with a gain of 1, HST/8o50-G1-GR, which we refer to as the high input impedance head-stage (>1 GΩ input resistance with ∼2 pF of parallel input capacitance and no series capacitance). This was primarily used with a PBX2/16sp/16fp preamplifier (Plexon Inc., Dallas, TX) with a gain of 1000 but with the same LFP and spike channel filters as the primary preamplifier mentioned above. We also obtained the phase response of the LFP channel of a second preamplifier for signals up to 300 Hz passed directly to the high input impedance head-stage across no resistance. This preamplifier was configured as a PBX/16sp-r-G50/16fp-G50 preamplifier (Plexon Inc., Dallas, TX) with 16 spike channels (spike data not shown) and 16 field potential channels (1-pole Butterworth filters, cutoffs of 3.3 - 88 Hz). Because this configuration resulted in an overall gain of 50 between the head-stage and preamp instead of an overall gain of 1000 that occurred with all other recordings, larger voltage signals were tested with this combination of equipment to compensate, though all other equipment and procedures were kept the same. The resulting data from this test is shown in the grey line in Figure 7.

Figure 7.

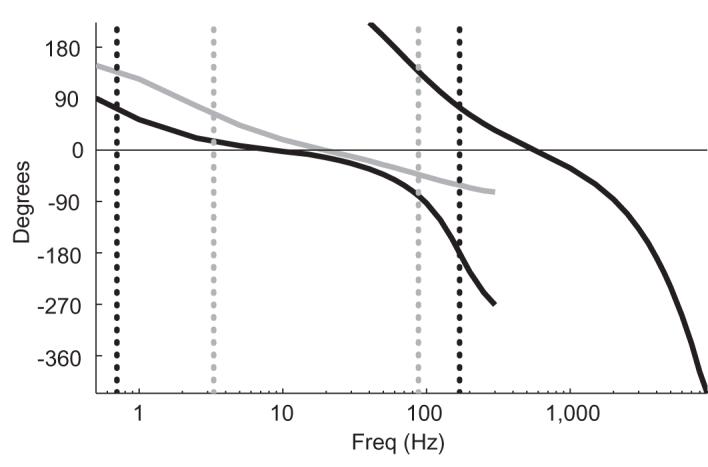
Filter-induced phase shifts. The recorded phase shifts of signals sent directly into head-stages used with different analog filters are shown, with spike and LFP channel data overlapping. A positive phase means that the recorded signal leads the actual signal. Frequency is shown on a log scale. For a list of the exact frequencies tested, please see the Signals used subsection in the Methods section. Both head-stages were used through-out this study with following preamplifiers with identical specified filter properties, which had resulting phase shifts shown here in black. The data above 10 Hz were recorded using the low input impedance head-stage, and the data at and below 10 Hz were recorded with the high input impedance head-stage which has no series capacitance that introduces additional phase shifts in this frequency band. (see Figure 10) This black line was used as the purely filter-induced reference phase and subtracted from other data recorded with this equipment to determine the phase shifts introduced by other sources. The grey line shows the LFP channel phase shifts recorded for a second preamplifier with the high input impedance head-stage. The dotted vertical lines show the cut-off frequencies for the LFP channel filter with its phase response shown in the corresponding color.

The MAP unit can also record additional analog signals via BNC inputs on a separate card (National Instruments, TX). This was used to record the actual non-attenuated voltage signal as well as the spike channel data as a continuous signal using the OUT board of the MAP unit. The LFP channel was automatically recorded by this same equipment, and thus all three signals for analysis in this study (actual signal, spike channel, and LFP channel) were time-stamped and recorded simultaneously by the same equipment. The sampling rate used for all recordings was 20kHz. Channel 1 was used for all recordings, and the inputs to unused channels were grounded.

Most voltage signals used in this study were generated by clipping onto the audio output pin of a computer playing matlab generated .wav files. This allowed us to present arbitrary signals to the system and to reproduce with ease precisely the same signal at many frequencies across different conditions. Distortions introduced by the audio card of the computer qualitatively seemed small for most signals, and were unimportant to the conclusions of the study as we were able to record the actual output signal in all cases. In order to generate signals of the appropriate amplitudes for use with the neural recording equipment, signals were first attenuated by a factor of about 100 by being passed through a voltage divider constructed by connecting a 100 Ω and 1 Ω resistor in series, with the exception of the few tests that were performed with the secondary preamplifier using larger and unattenuated voltages. Some later tests were performed using sinusoidal signals created by a function generator (33220A function/arbitrary waveform generator, Agilent Technologies, Santa Clara, CA). Output signals from this were still initially routed through the same voltage divider.

To verify amplifier input impedance, the attenuated signal was passed directly to the head-stage connector or passed across resistors with impedances varying from 11.5 to 88 MΩ for the low input impedance head-stage. For the high input impedance head-stage, low frequency signals were passed across very high metallic resistances ranging from .5 to 2.5 GΩ, while moderate to higher frequency signals were passed across moderate resistances ranging from 1.2 to 66.0 MΩ. See the impedance calculations subsection in this methods section for a description of how the amplifier input impedance was assessed using this data.

For the electrode data, an apparatus was constructed consisting of two square 7 × 7 inch aluminum plates connected together by two plastic supporting rods causing a plate separation of 7 inches. A coarse schematic of the apparatus can be seen in Figure 1B. The plates were connected with their broad sides facing each other and they stood on their thin edge in a large plastic tub filled with either dilute saline with a concentration of 0.225% by weight or physiological saline with a concentration of 0.9% by weight. By passing current between the plates, a one-dimensional voltage gradient was created in the dimension normal to the plates’ broad sides. Voltage changed with the horizontal position between the two plates but was approximately uniform in the two directions orthogonal to this: the vertical direction and the horizontal direction parallel to the plates. The dilute saline was initially chosen as its higher resistivity allowed for a better control of this gradient. Later recordings were made with both saline concentrations to investigate potential effects of saline concentration on the electrode tip impedance.

To provide a verification of the equivalent circuit model, data was collected under two configurations. In the parallel configuration, the attenuated signal was connected to one plate, which we define as the signal plate, with the other plate connected to ground, which we call the ground plate. In this case, when the electrode tip is immersed in the saline it provides a high impedance route to ground from the signal plate that is parallel to a lower impedance route through the ground plate. The actual voltage gradient in the saline will primarily be unaffected by the presence or the position of the electrode. This is generally analogous to the case of neural recording. In the series configuration, the ground plate is disconnected from everything, so that the electrode would be the only series connection between the signal plate and ground and thus all current in the signal passing through the aluminum plate must pass through the electrode and amplifier circuit as well. Resistance between the two plates was measured before and after each recording session and found to be around 100 to 200 Ω. At the start of a session the resistance was occasionally larger than this, in which case we sanded down both plates’ surfaces which served to lower the impedance to the appropriate level, most likely by removing aluminum oxide or possibly solid sodium chloride that had formed on the plates.

The electrodes used for data collection solely in the dilute saline with the low input impedance head-stage were 5 tungsten microelectrodes, (FHC, Bowdoinham, ME) 3 insulated with glass and 2 with epoxylite, with varying impedances ranging from .5 to 9.8 MΩ at 1 kHz per the manufacturer specifications. We tested an additional epoxylite insulated electrode with a manufacturer specified impedance of 8.4 MΩ at 1 kHz using only the high input impedance head-stage in dilute saline. The FHC catalog numbers for the 5 electrodes used with the low input impedance head-stage were: UEWLGASEBN1E, UEWLGASEFN1E, UEWLGASGBN4E, UEWLGASGDN4E, and UEWLGASGFN4E, and the catalog number for the electrode used with only the high input impedance head-stage in dilute saline was UEWLGASEFN1E. We later tested 3 additional epoxylite insulated electrodes with manufacturer specified 1 kHz impedances ranging from .5 to 10 MΩ with both head-stages and in dilute and/or physiological saline. The catalog numbers for these electrodes are: UEWLGASEBN1E, UEWLGASEDN1E and UEWLGASEFN1E. The order in which the tests were performed for both head-stages and saline concentrations was varied for each of these electrodes. Through the course of the experiment the impedance of each electrode was independently measured (see Figures 3C, 4C, and 6B), and the tests conducted in physiological saline matched reasonably well with the manufacturer specified values (see Figure 6B). The tip geometry was not varied across electrodes.

Figure 3.

Measurement of effective electrode impedance for one electrode. Plots show amplitude data from signals recorded with one high impedance glass-insulated electrode in dilute saline using different manipulated values of Z_a’ with the low input impedance head-stage. Line colors are coded from grey to blue based on the value of Z_a’ at 10 Hz, with the precise values for each line indicated in A. Parallel configuration data is shown with solid lines, series configuration data is shown with dashed lines. Spike and LFP channel data (see Methods) are shown overlapping in A, but in B and C the vertical dashed line denotes the point where data to the left corresponds to the LFP channel data only, and data to the right corresponds to the spike channel data only. Frequency is shown on a log scale. For a list of the exact frequencies tested, please see the Signals used subsection in the Methods section. A: raw gain of the recorded over the actual signal. B: normalized gain showing the voltage attenuation across the electrode, given by the value in A for each recording divided by the raw gain of the reference recording, which was done with a steel pin with negligible impedance. C: effective electrode impedance (Z_e’) calculations derived from the above data for each trace. Z_e’ is shown on a log scale.

Figure 4.

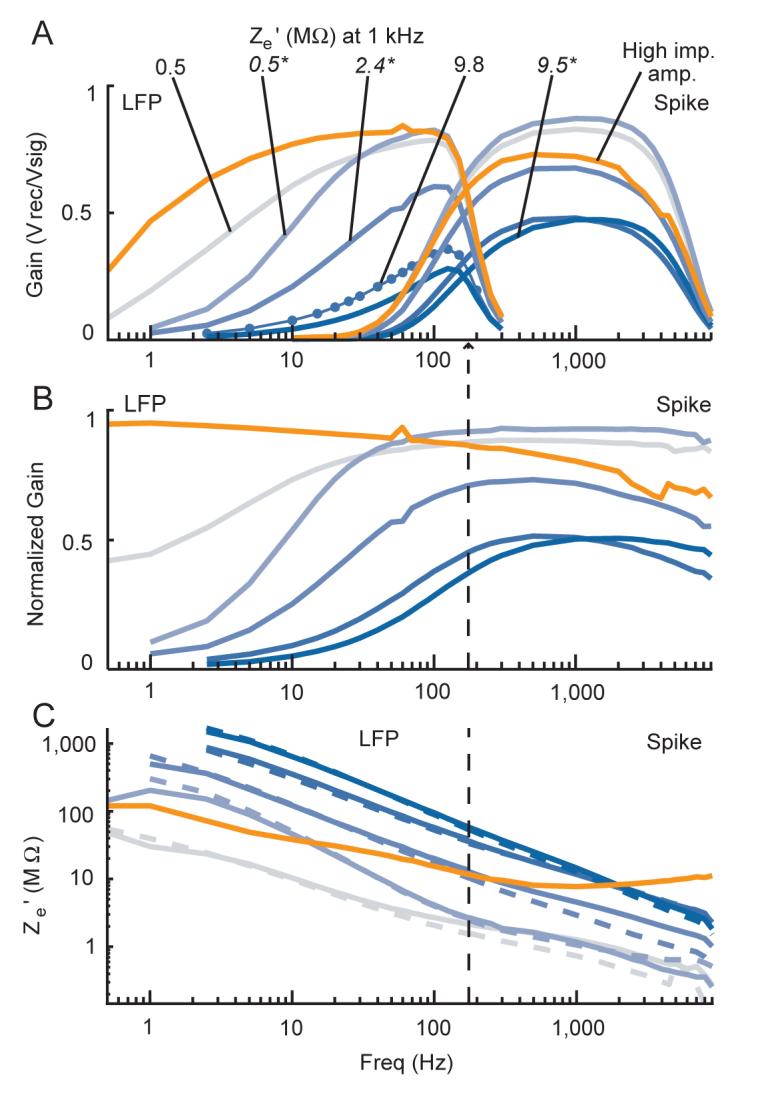
Voltage attenuation and impedance measurements for several electrodes. Plots show amplitude data from signals recorded with electrodes in dilute saline. Grey-to-blue lines show data recorded using the low input impedance head-stage for electrodes with low-to-high measured impedance values at 10 Hz. The manufacturer specified 1 kHz impedance value for each electrode is indicated in A. Values in italics and followed by an asterisk denote data from a glass insulated electrode. Orange lines show data recorded with the higher input impedance head-stage for one electrode with a large specified 1 kHz impedance of 8.4 MΩ. Parallel configuration data is shown with solid lines, series configuration data is shown with dashed lines. A and B denote parallel confugration recordings with no Z_a’ manipulations, and C shows the average parallel and series configuration values across 4 different values of Z_a’. Spike and LFP channel data (see Methods) are shown overlapping in A, but in B and C the vertical dashed line denotes the point where data to the left corresponds to the LFP channel data only, and data to the right corresponds to the spike channel data only. Frequency is shown on a log scale. For a list of the exact frequencies tested, please see the Signals used subsection in the Methods section. A: raw gain of the recorded over the actual signal. B normalized gain showing voltage attenuation across the electrode, given by the value in A for each recording divided by the raw gain of the reference recording, which was done with a steel pin with negligible impedance. C: Effective electrode impedance (Z_e’) calculations derived from the above data for each trace. Z_e’ is shown on a log scale.

Figure 6.

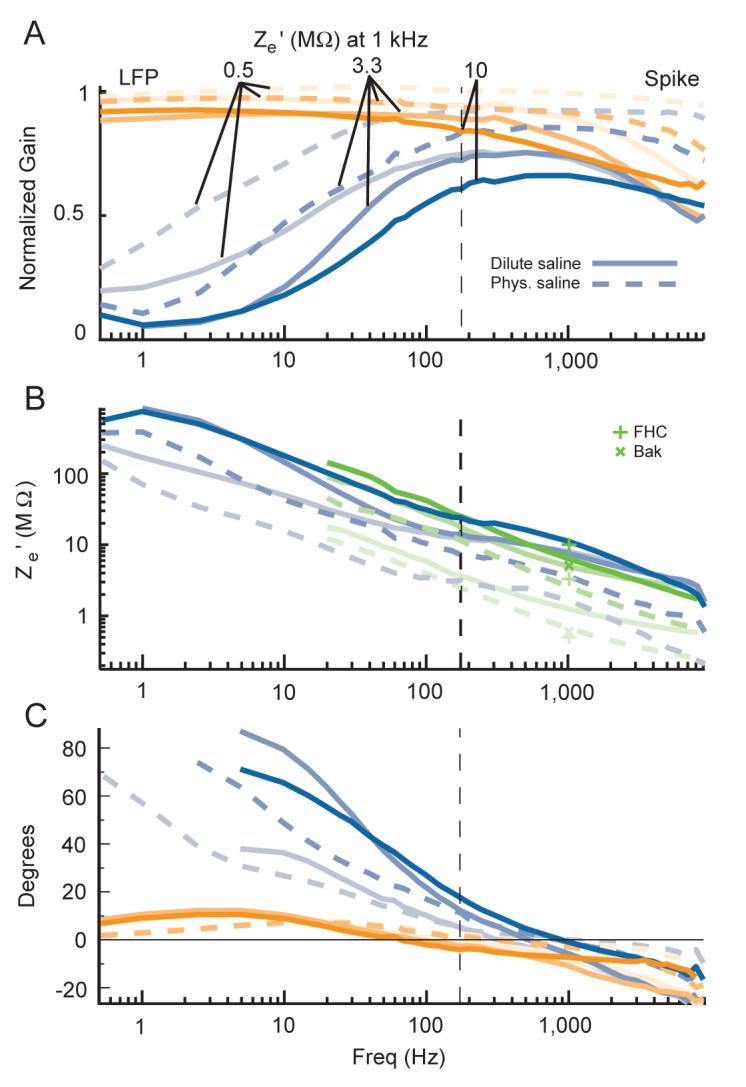
Voltage attenuation, phase shifts and impedance measurements with different saline concentrations. In all plots and colors, data recorded in physiological saline is shown with dashed lines, and data recorded in dilute saline is shown in solid lines. The saturation level of all colors reflects electrode impedance, with the strongest colors showing data collected with the highest impedance electrodes. The manufacturer specified 1 kHz impedance value for each electrode is indicated in A. All electrodes were epoxylite insulated. Blue lines show data recorded with the low input impedance head-stage in the parallel configuration, orange lines show data recorded with the high input impedance head-stage in the parallel configuration, and green lines show impedance measurements made with the Agilent LCR meter. Frequency is shown on a log scale for all plots. For a list of the exact frequencies tested, please see the Signals used subsection in the Methods section. A: the normalized gain showing voltage attenuation across the electrode, as in figures 3B and 4B. B: the effective electrode impedance (Z_e’) calculations, derived from the low input impedance head-stage data only in A as well as the measurements made by the Agilent LCR meter. A + denotes an electrode’s manufacturer specified value at 1 kHz, and a x denotes the value from the Bak metal electrode impedance tester at 1 kHz made in dilute saline. Measurements with the Bak tester in physiological saline were always somewhat lower than the dilute saline values, but these are not shown for clarity. Z_e’ is shown on a log scale. C: electrode-amplifier circuit induced phase shifts.

Using a surgical micromanipulator clamping onto a single channel microdrive, (FHC, Bowdoinham, ME) electrodes were suspended from above and lowered to a vertical position 100 microns below the saline surface at a horizontal position between the two plates 3 mm away from the signal plate. The horizontal distance from the signal plate was set by using the surgical micromanipulator to very carefully touch the side of the electrode to the plate as determined by careful visual inspection, then advancing it 3 mm away from the plate. The depth of the saline surface was determined through online viewing of the signals recorded by the amplifier while adjusting the electrode depth with the microdrive to determine when electrical contact was consistently first made between the electrode and the saline. The electrode was then lowered with the microdrive 100 microns beyond that point for data collection. We compared the data recorded from each electrode to data recorded from a specially constructed steel pin reference electrode with 0.5 mms of un-insulated tip and negligible tip impedance. This reference electrode was suspended 600 microns below the saline surface, with the horizontal position and other conditions kept the same to obtain an estimate of the actual voltage presented to each electrode, accounting for any effects of the aluminum plates and saline. Data was collected close to the signal plate so that the recorded voltages would be as large as possible while maintaining a small voltage gradient which resulted from the small output voltages used along with the large horizontal separation between the plates. The small voltage gradients were desired to help diminish the effects of variables that could not be reproduced between electrodes with exact precision, such as the orientation and horizontal position of the electrode. Recordings of sinusoidal voltages at a few frequencies were conducted after each recording session for each electrode to ensure that the electrode’s impedance was not affected by the signals applied during the session. Only small apparent impedance drops were noticed on occasion.

During data collection with the electrodes and the low impedance head-stage, Z_a’ was manipulated by clipping onto the connection between the electrode and the head-stage and connecting that to ground through different metallic resistors with known impedances (R_sh in Figure 1A). This created an additional parallel route to ground downstream of the electrode tip and lowered Z_a’ by a known amount. This was done in both the parallel and series configurations to create the additional 10 Hz Z_a’ values of approximately 2, 8, and 14 MΩ in addition to the un-manipulated value of 38 MΩ.

For the electrodes tested in both concentrations of saline, additional impedance measurements were made using a commercially available LCR meter (E4980A, Agilent Technologies, Santa Clara, CA), which is an instrument that can measure inductance (L), capacitance (C) and resistance (R). Measurements were made in the 4 terminal paired configuration with the high potential and current leads ultimately connected to the plate near the electrode, and the low potential and current leads ultimately connected to the top of the electrode. All other leads to the aluminum plates were disconnected while this measurement was made. In addition to these tests, a corroborating impedance measurement at 1 kHz was made using a 1 kHz metal electrode impedance tester (Model Imp-1, Bak Electronics, Mount Airy, MD)

Signals used

The bulk of the data for this study was gathered using sinusoidal voltages with frequencies varying from 0.5 Hz to 9 kHz. The exact frequencies (in Hz) tested that underly the data shown in each figure are: .5, 1, 2.5, 5, 10, 15, 20, 25, 30, 40, 50, 60, 70, 80, 90, 100, 125, 150, 175, 200, 250, 300, 500, 1000, 1500, 2000, 2500, 3000, 3500, 4000, 4500, 5000, 6000, 7000, 8000 and 9000. The amplitudes of most of the un-attenuated signals were kept approximately constant with a peak amplitude of ∼320 mV for the metallic resistor data and ∼200 mV for the electrode data. For situations in which the resulting signals were too small to record reliably because of the combined effects of filters and resistors or electrodes, signal amplitudes were increased to improve the signal to noise ratio in order to better determine the recorded phases and amplitudes. Every data point analyzed however was considered only in terms of the gain relative to the applied voltage which was also recorded, so the absolute voltage of the signals was unimportant.

The amplitudes used to record electrode data thus corresponded to voltages of less than 2 mV at the electrode tip. Evoked potentials recorded in cortex with microelectrodes have been published with maxima that exceed this (Kandel and Buzsaki 1997), although physiological values at higher frequencies resulting from action potentials typically do not reach this level. Current density is known to affect electrode impedance when the current density exceeds a certain level (Geddes et al. 1971), but our estimations suggest that with the equipment and signals we used, current densities were well below this level. Additionally, we verified at a few frequencies that electrode and amplifier impedance do not appreciably change with current amplitude for the signals and equipment we used (data not shown). This suggests that for physiological recordings with any reasonable equipment, any distortions that occur will not depend on signal amplitude appreciably.

The amplitude and phase of the digitized recorded signals were measured in two ways, each using 50 cycles of the data. For most recordings, the nlinfit function in Matlab (Mathworks, vs 2007b) was used to find the best sine-wave fit given the known frequency of the sinusoid. In some cases the Hilbert transform was used instead, defining the amplitude as the average magnitude of the Hilbert transform and defining the phase as the phase of the first sample resulting from a linear fit of the complex phase of the Hilbert transform. The code used for each method is provided in the Supplementary Materials. Amplitude ratios and phase comparisons between the recorded and actual signals were always made using the same method for each signal. For more details, see the Supplementary Methods online.

For the verification of group delay with data, passband filtered pulse signals with different center frequencies were used, similar to what is shown in example 5.1 of (Oppenheim and Schaefer 1998). A few examples of signals used are shown in Figure 9 (see Supplementary Materials online). The center frequencies of the filters used also varied from 0.5 to 9 kHz while the duration of the signal itself decreased with frequency to allow for more precise temporal localization of the smaller group delays at higher frequencies. The filter and duration specifications were determined to provide the best frequency localization for each signal, given that the amplitude envelope varied sharply enough over time to determine the delay between the two envelopes at each frequency. The filtered pulses used were obtained by windowing sinusoids of the given carrier frequency with the first of the discrete prolate spheroidal sequences with a time-bandwidth product of 1 for a given duration. The maximum voltages of the filtered pulses used for each recording session approximately matched the voltage amplitude of the sinusoidal signal used for each frequency in the same session. For these signals, we used the magnitude of the Hilbert transform, which can be thought of as the instantaneous amplitude of a time series (Marple 1999a), as an estimation of the amplitude envelope for both the recorded and actual signal. We then determined the amplitude envelope delay to be the time delay at which the cross-correlation between the actual and recorded envelope estimates was maximal. For our data this gave the exact same results to a previously published method of estimating group delay that we later found (Marple 1999b) in which the order in which the cross-correlation and Hilbert transform were applied was reversed from what we have presented here.

Figure 9.

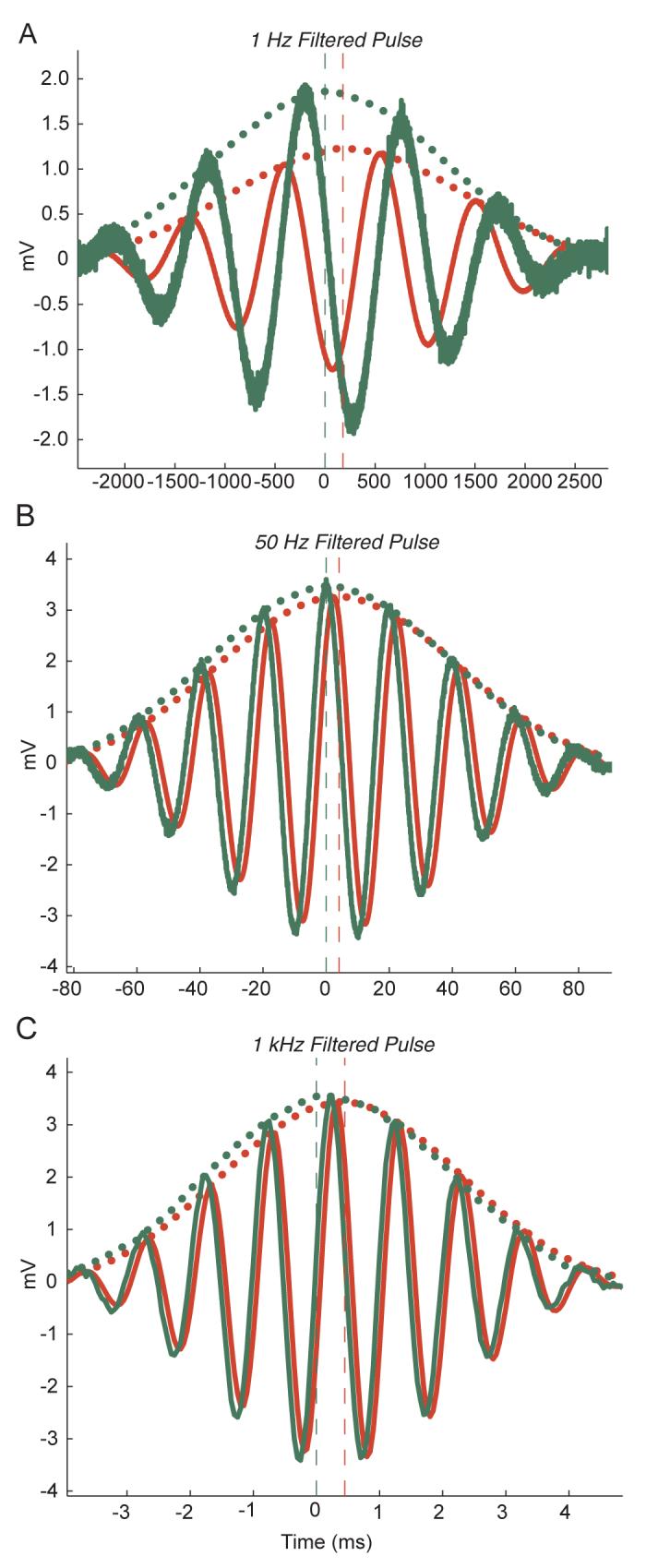
Examples of filtered frequency pulses used for amplitude envelope and group delay measurements. Actual signals presented directly to the head-stage are shown in green, recorded signals are shown in red. For each signal, the raw values are shown with solid lines and the Hilbert-magnitude estimations of the amplitude envelope with local average smoothing applied are shown with dotted lines. The maximum point of each estimated envelope is shown with vertical dashed lines. Data are presented for bandpass filtered pulses centered around frequencies of A: 1 Hz, B: 50 Hz, and C: 1kHz. LFP channel data are shown in A and B, spike channel are data shown in C.

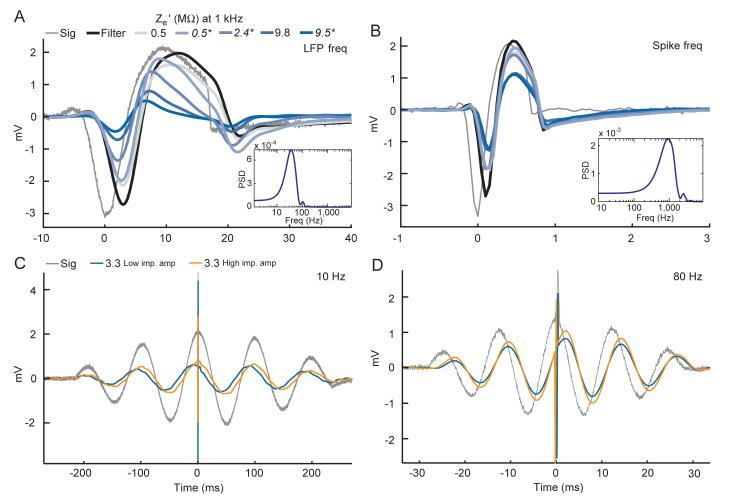
For the shape distortion data, we used a voltage shape obtained from a single neuron’s recorded waveform, as well as a frequency-modulated version of the same waveform with signal power concentrated in the LFP frequency ranges. The original waveform had a duration of 1 ms, which was temporally modulated to have a duration of about 25 ms in the lower frequency version. Properties of the computer’s audio card did distort the lower frequency waveform somewhat, but, again, because we were able to record the actual voltage applied this was unimportant as to our purpose of demonstrating shape distortion by the recording equipment. The insets of Figure 10 A and B show an estimate of the power spectral density of the actual signals sent using a Fourier Transform windowed with the first of the discrete prolate spheroidal sequences with a time-bandwidth product of 1 for the duration of the signal. Also, to demonstrate a recording of high frequency spikes recorded simultaneously with lower frequency field potentials, we also used the same passband filtered pulse signals that were used to verify the group delay, but with the high frequency spike waveform added at the highest central peak of the signal. These signals were recorded using one electrode with a 1 kHz impedance verified to be 3.3 MΩ using the 1 kHz metal electrode impedance tester. For the presentation of this recorded data, the system’s LFP channel output is displayed with the Spike channel added to it around the time of the spike.

Figure 10.

Recorded waveform shapes. Grey-to-blue lines show waveforms recorded in the parallel configuration in the low input impedance head-stage for electrodes with low-to-high measured impedance values at 10 Hz. The manufacturer specified value at 1kHz indicated in the color legend above the plot. Values in italics and followed by an asterisk denote data from a glass insulated electrode. The thin grey line shows the actual voltage presented, and the thick black line shows the voltage recorded with the signal voltage applied directly to the same head-stage. Dilute saline was used for the electrode recordings in A and B, and physiological saline was used for the data in C and D. A: LFP channel data only for a lower-frequency version of the waveform. B: Spike channel data only for a higher-frequency version of the waveform. Beneath each plot is a power-spectral density (PSD) estimation of the actual voltage waveform in each plot, obtained with a windowed Fourier transform. C and D: 10 and 80 Hz frequency pulse waveforms additively combined with the high frequency spike from B. LFP channel data is displayed with the Spike channel data additively combined to it at the time of the recorded spike.

The variance of all the measurements performed in this study was negligible, provided that all electrical connections were adequately made and left undisturbed between measurements and that the signal amplitudes used for measurements with electrodes were kept sufficiently low to avoid affecting electrode impedance. To estimate the variance that occurs while changing electrical connections, we performed measurements with one low impedance electrode at 50 Hz several times while alternating connections between the low and high input impedance head-stages and the corresponding following amplifiers between each measurement. There was somewhat more variance in the high input impedance head-stage measurements than the low input impedance head-stage. High input impedance head-stage measurements had a range of the raw gain spanning 5.3% of the maximal value, while the low input impedance head-stage measurements had a range of the raw gain spanning only .3% of the maximal value. There was no systematic trend in the value of the impedance across these measurements, suggesting the electrode impedance was not altered by them.

Impedance calculations

To determine the effective amplifier input impedance, calculations were made using the amplitude ratio (V_rec/V_sig), which we refer to as the gain, observed in the metallic resistor data across all frequencies. To remove the effects of analog filters, the gain for each recording was divided by the same signal’s gain in the reference recording where the signal was applied directly to the head-stage using no resistors at all. We refer to this value as the normalized gain, or here as V_rat’. V_rat’ along with the magnitude of the known metallic resistance the signal was sent across, which in this case is Z_e’, can be used to calculate the effective input impedance of the head-stage as Z_a’ = (V_rat’ · Z_e’)/(1- V_rat’). This is a rewritten version of equation 2 using V_rat’ in place of V_rec/V_sig, and considering V_rec and V_sig to be the raw gain of the metallic resistor and reference recording respectively.

To determine the effective electrode impedance, this same procedure was followed with electrode recordings to obtain V_rat’, using the gain of the steel pin recordings as the reference recording to remove any effects caused by the saline or aluminum plates in addition to removing effects caused by the analog filtering. This along with the known magnitude of Z_a’ was used to calculate the effective electrode impedance at each frequency as Z_e’ = Z_a’ · (1/V_rat’ - 1), which is again a rewritten version of equation 2 and the equation above.

We report the value calculated for all the individual Z_a’ values tested for one electrode, (Figure 3) in addition to the averages for the parallel and series configurations across the 4 tested values of Z_a’ for several electrodes (Figure 4). In reporting averages of electrode impedance measurements in each configuration, a few outlying recordings were discounted for some electrodes.

Phase calculations

The measured phase shift for each recording was defined as the phase of the recorded signal minus the phase of the actual signal, so that a positive phase referred to the recorded signal leading the actual signal. The phases were plotted using the unwrap function in matlab to provide a seemingly continuous phase response across frequencies. Since the precise value of the phase is ambiguous since a phase curve is equivalent to the same curve shifted by any multiple of 360 degrees, 0 degrees was defined so that the phases for the most frequencies within the passband of each channel’s filters were closest to 0 degrees. For the presentation of electrode-amplifier circuit induced phase shifts in Figure 5 and 6, the filter-induced reference phase shown in black in Figure 7 was subtracted from the raw recorded phase shift with each electrode to remove the common filter-induced phase effects and leave only the phase shifts resulting from the electrode-amplifier circuit. The filter-induced reference phase was obtained from the recorded phase shifts of signals sent directly into the head-stage and was comprised of data collected from both the low and high input impedance head-stages as both were used with following preamplifiers with identical specified filter properties. The data above 10 Hz were recorded using the low-impedance head-stage, and the data at and below 10 Hz were recorded with the high impedance head-stage which has no series capacitance acting before amplification that introduces additional phase shifts in this frequency band. For the electrode data collected with the high input impedance head-stage, the high input impedance reference phase data was subtracted over the entire frequency range recorded to produce the orange curves in Figure 5.

Figure 5.

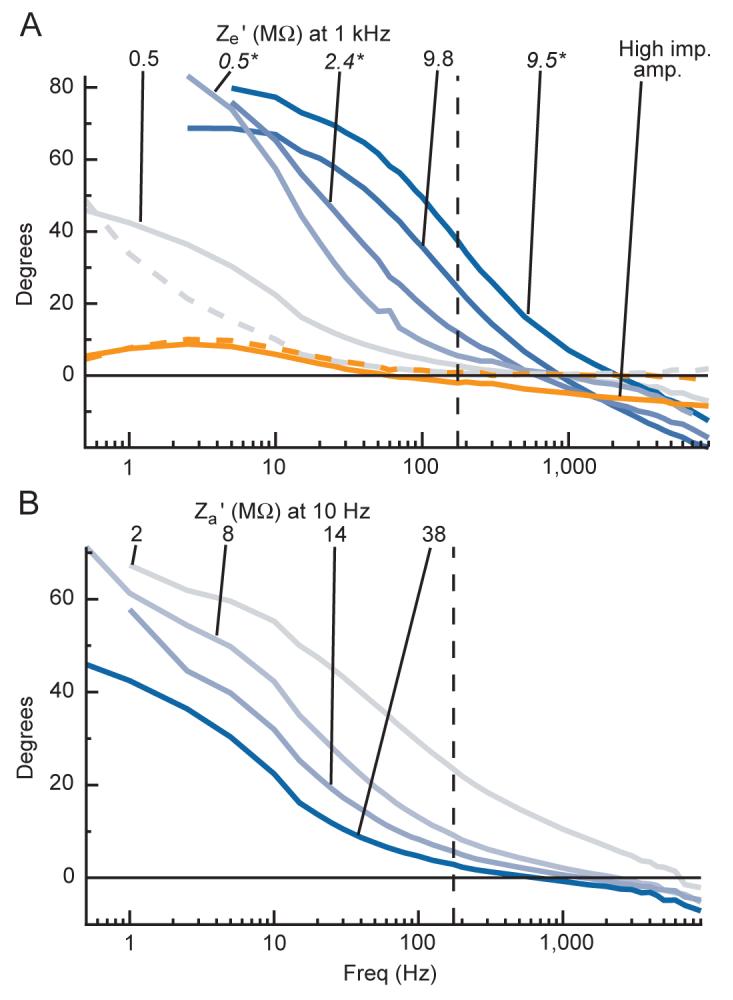
Electrode-amplifier circuit induced phase shifts using electrodes. All phase shifts are shown after subtracting the phase shifts induced by the system filters (see Figure 8). A positive phase means that the recorded signal leads the actual signal. Frequency is shown on a log scale. For a list of the exact frequencies tested, please see the Signals used subsection in the Methods section. The vertical dashed lines denote the points on each plot where data to the left corresponds to the LFP channel data and data to the right corresponds to the spike channel data. A: phase shifts for signals recorded using different electrodes in the parallel configuration in dilute saline. Grey-to-blue lines show data recorded using the low input impedance head-stage for electrodes with low-to-high measured impedance values at 10 Hz. The manufacturer specified 1 kHz impedance value for each electrode is indicated. Values in italics and followed by an asterisk denote data from a glass insulated electrode. Orange lines show data recorded with the higher input impedance head-stage for one electrode with large high-frequency impedance. The dashed lines in grey and orange show the phase shifts for the steel pin reference electrode used with the low and high impedance head-stages respectively. B: phase shifts for signals recorded with a low impedance epoxylite-insulated electrode in the parallel configuration in dilute saline with the low impedance head-stage while manipulating Z_a’. Line colors are coded from grey to blue based on the manipulated value of Z_a’ at 10 Hz, with the precise values indicated.

To calculate group delay, the derivative of the phase with respect to frequency is approximated using the change in phase and frequency between each pair of consecutive frequency points explicitly measured. Group delay was then calculated according to the equation below:

$$\text{Group Delay}\left(\frac{f_1+f_2}{2}\right)=-\left[\frac{\Delta Ph}{360}\right]∕\Delta f$$ (4)

ΔPh is the difference in phase between adjacent frequencies measured in units of degrees, Δf is the difference in frequency in units of Hz, f1 and f2 are the frequencies of the consecutive measurements used in the calculation, and Group Delay is given in units of seconds. The group delay measurement using each pair of consecutive frequencies is defined as pertaining to the group delay observed at the mean of the two frequencies.

RESULTS

Determination of amplifier input impedance

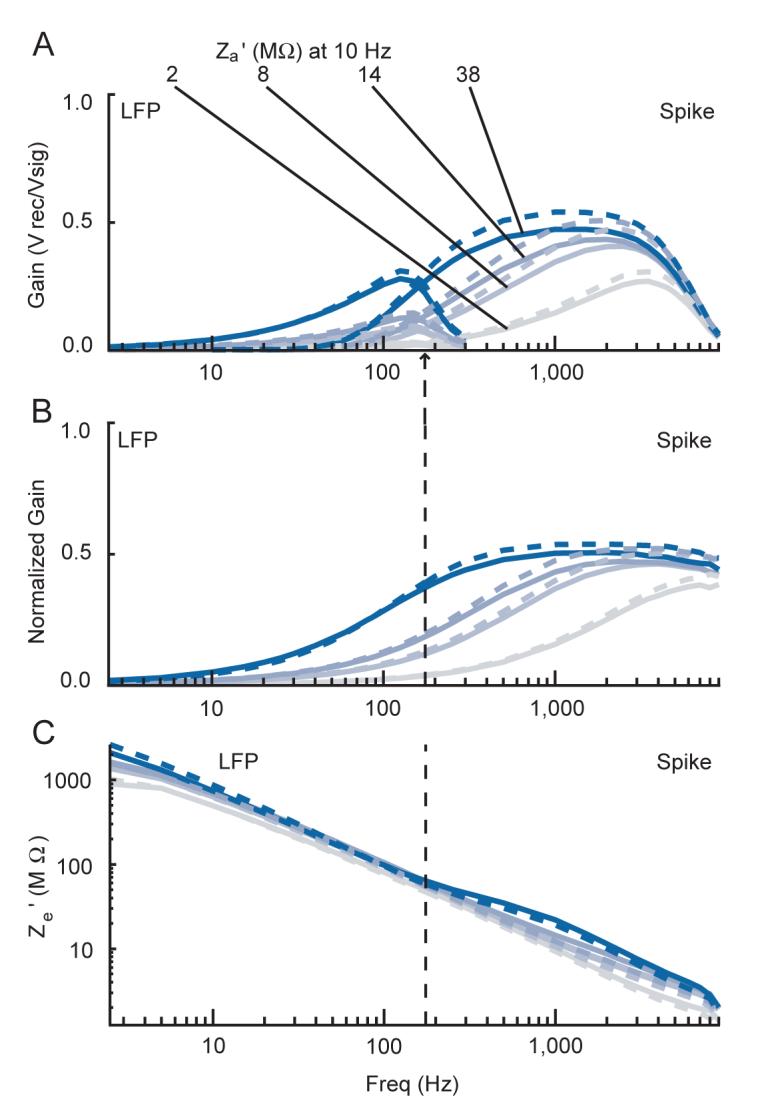
To verify that the equivalent circuit model applies to microelectrode recordings, we measured the input impedance for two head-stages, one with lower and one with higher input impedance. To do this we measured V_rec with V_sig consisting of sine wave voltages (0.5 to 9 kHz) applied to the head-stage across different metallic resistances. Figure 2 plots measurements made with the lower input impedance head-stage through a range of metallic resistors. The variation of gain (V_rec/V_sig) through the LFP and spike channels as a function of frequency and resistance is clear (Figure 2A). By normalizing the gain for each resistor by the gain for signals applied directly to the head-stage, the filter properties of the system were removed (Figure 2B). The normalized gain allows us to calculate the effective input impedance of the head-stage for each resistor (Figure 2C). The input impedance we measured corresponds to the specifications of this head-stage. The parallel input capacitance of the head-stage causes the input impedance to decrease at high frequencies; the series capacitance causes it to rise at very low frequencies. The impedance measurements are largely independent of the resistive load and match well with the specified values, except at high frequencies where our measurements are consistently low, suggesting an added voltage drop across these resistors. However, this is expected given the presence of the capacitance shunting the amplifier, C_sh. These deviations from the specified input impedance at high frequency permit an estimation of C_sh which measured ∼2.7 pF in our recording setup. It is important to note that this value can change for the same equipment according to its physical arrangement.

Figure 2.

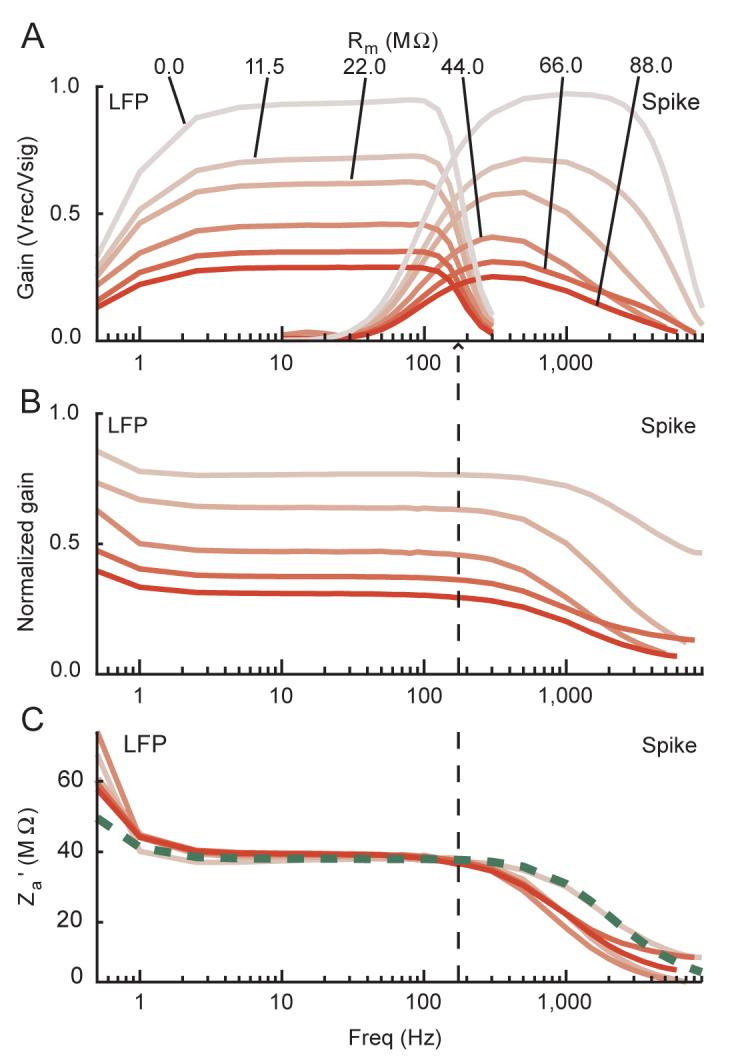
Measurement of effective amplifier input impedance. Plots show amplitude data from signals sent directly to the low input impedance head-stage across different metallic resistors (R_m). Line colors are coded from grey to red based on the magnitude of R_m, with the precise values for each line indicated in A. Spike and LFP channel data (see Methods) are shown overlapping in A, but in B and C the vertical dashed line denotes the point where data to the left corresponds to the LFP channel data only, and data to the right corresponds to the spike channel data only. Frequency is shown on a log scale. For a list of the exact frequencies tested, please see the Signals used subsection in the Methods section. A: raw gain of the recorded over the actual signal. B: normalized gain showing the voltage attenuation across the resistor. This plot shows the raw gains in A for each recording with a greater than zero resistance divided by the raw gain of the reference recording, which was the recording in which R_m was zero. C: effective amplifier input impedance calculations derived from the above data for each trace. The green dashed line represents the reported value of the amplifier alone.

We also tested a head-stage with a higher input impedance which we empirically verified in a similar fashion. Due to the very high input resistance, the effective input impedance for this head-stage was largely determined by the capacitance within and outside the amplifier for most frequencies. For low frequencies, we verified there was little voltage drop over very high metallic resistances, while for moderate to higher frequencies we verified that there was little voltage drop over moderate resistances.

Equivalent circuit verification and signal attenuation

After determining the input impedance of the amplifier (Z_a’), we determined whether the equivalent circuit describes signals recorded through metal microelectrodes immersed in dilute saline, using the apparatus depicted in Figure 1B. This was done in a parallel configuration and a series configuration (Figure 1C, see Methods). If the equivalent circuit model is correct, then measurements of electrode impedance should be independent of both the configuration and the value of Z_a’.

Figure 3 plots measurements made with the lower input impedance head-stage through a representative high impedance, glass-insulated electrode. Systematic variation of raw (Figure 3A) and normalized (Figure 3b) gain (V_rec/V_sig) through the LFP and spike channels was observed as a function of frequency and Z_a’ with slightly higher gain in the series than in the parallel configuration. This is to be expected because more total current travels through the saline in the parallel configuration, resulting in a larger voltage drop from the signal plate to the electrode tip. The normalized gain at the various values of Z_a’ afforded calculation of the effective electrode impedance as a function of frequency (Figure 3c). Electrode impedance measured across signal frequencies did not vary with Z_a’ for either parallel or series configurations. This constancy was found for all electrodes tested. Thus, the equivalent circuit was verified.

The same pattern of results was obtained for electrodes spanning impedance values from .5 to 9.8 MΩ (manufacturer specified at 1 kHz) (Figure 4). Beyond extending the verification of the equivalent circuit, it is also clear that electrode impedance increased substantially with decreasing frequency, and was 10 to 45 times higher at 10 Hz than 1 KHz, consistent with previous reports (Merrill and Ainsworth 1972; Lemon 1984). Note that the rise in electrode impedance at low frequencies is not just a result of a constant capacitance across frequencies since R_e and C_e are generally considered to be frequency dependent themselves (Robinson 1968; Ferris 1974), which is supported by our calculations of R_e and C_e (Figure S1, see Supplementary Results online) that rely on the recorded amplitudes and phase shifts with each electrode and our estimation of Z_a’. As a consequence of the frequency dependence of the electrode impedance, the effective amplifier gain was much less at the lower frequencies. We have also confirmed this in the brain with simultaneous recordings of electrodes with different impedances in the same approximate brain location (Nelson et al. 2006). Tungsten microelectrodes commonly used for isolating single spikes are typically 2 to 3 MΩ at 1 KHz. Thus, considerable attenuation of LFP frequency signals can occur when such electrodes are used with this lower impedance head-stage.

The orange lines in Figure 4 show results using the higher impedance head-stage with one high impedance electrode, with a manufacturer specified impedance of 8.4 MΩ. We can see that no considerable attenuation occurs with this electrode, as the normalized gain (Figure 4B) is close to one over the entire frequency range tested.

Electrode-amplifier circuit induced phase shifts

Besides amplitude attenuation, the equivalent circuit of microelectrode recordings shows that signals will also be distorted through frequency-dependent phase shifts. We measured the phase of V_in relative to the phase of V_sig as a function of frequency for signals sent across electrodes of different impedances by subtracting the phase-shifts induced by the acquisition system’s filters alone from the phase shifts of the same sinusoidal signals recorded with electrodes (Figure 5A). Marked phase shifts occurred when using the lower impedance head-stage for signals below 100 Hz where electrode impedance was higher, and were greater overall for higher impedance electrodes. These phase shifts are positive in direction at lower frequencies and exceed 80 degrees in our data, which in conjunction with the estimated electrode impedance magnitudes suggest that the phase angle of the electrode impedances are nearly a full -90 degrees over these frequencies for some electrodes (Figure S1). At higher frequencies the phase shifts shown in Figure 5 reverse in direction, becoming slightly negative, suggesting that Z_a’ is more capacitive than Z_e’ at these frequencies because of the shunt and parallel amplifier input capacitance. The phase shifts recorded with the steel pin reference electrode shown by the dashed grey line for this head-stage are sizeable below 10 Hz, primarily resulting from the series capacitance within the head-stage acting on the input before amplification. This would thus partly contribute to the phase shifts recorded with other electrodes at those frequencies, though for most electrodes these phase shifts would be large even without this contribution. The phase shifts also increase in magnitude as Z_a’ decreases (Figure 6B) as described above, following the predictions of the equivalent circuit.

The orange lines in Figure 5A again shows results using the higher impedance head-stage with one high impedance electrode, demonstrating that like the attenuation, no electrode-amplifier circuit induced phase shifts occur with this head-stage.

Saline concentration effects

After recording data in dilute saline, we were interested in determining if the effects we have shown are qualitatively or quantitatively different in physiological (0.9 % by weight) saline. From a careful inspection of Figures 3 and 4, it is apparent that though our measurements are consistent with each other, they are noticeably higher than the manufacturer specified impedance values. To reconcile this, we made independent impedance measurements using a commercially available LCR meter and a 1kHz metal electrode impedance tester (see Methods) for several electrodes in both saline concentrations. This was done in addition to performing the same sinusoidal recordings with both head-stages as we had done before, but without the additional manipulations of the value of Z_a’.

The results are shown in Figure 6. The resulting normalized gains (Figure 6A) show that there was less voltage attenuation in the physiological saline for both head-stages, though considerable low frequency voltage drops still occurred with the low impedance head-stage for all tests performed. Interestingly, at high frequencies some attenuation does consistently occur for the high input impedance head-stage, and the gains are similar to what is observed with the low input impedance head-stage for the same electrodes and saline conditions. This suggests that effects from shunt capacitance (C_sh) in this recording setup dominate the value of Z_a’ over this frequency range and demonstrates that even when using a high input impedance head-stage, investigators may want to take care to minimize this capacitance to avoid minor to moderate spiking signal loss and shape distortion. The electrode-amplifier circuit induced phase shifts for the same conditions are shown in Figure 6C. This again shows that the phase shifts co-occur with amplitude attenuation which can both be quite large at low frequencies with the low impedance head-stage in either saline concentration. This also shows high frequency phase shifts that are largely independent of the head-stage, as was found with the high frequency amplitude effects.

Figure 6B shows the resulting electrode impedances predicted by the model based on the low impedance amplifier data in addition to other corroborating measurements. As before, we see that the impedance values resulting from the normalized gains in dilute saline are consistently larger than the value specified by the manufacturer. However, when performed in physiological saline, we see that there is a decrease in impedance measurements that is roughly two-fold across all frequencies. This occurred in both the sinusoidal recordings and the measurements of the Agilent LCR meter. The resulting impedance measurements in physiological saline values match well with the manufacturer specified impedances, suggesting the saline concentration was the primary cause of the mismatch between the manufacturer specified impedance values and our earlier recordings.

It is important to note that this change in impedance across different saline concentrations is not a result of the changed resistance through the solution itself, but instead reflects an effect on the impedance across the electrode/electrolyte interface at the electrode tip. First, the data in each case is compared to the steel pin reference electrode data recorded under the same conditions to account for changes in the actual voltage at the tip between conditions. The change in saline concentration would however affect the value of R_s resulting from the resistance encountered to reach the small electrode tip. This has been estimated before to be largely negligible in physiological saline compared to the impedance across the electrode tip (Robinson 1968). The dilute saline would be expected to have a four-fold increase in resistivity compared to physiological saline (Grimnes and Martinsen 2000), but the value of R_s would still remain largely neglible. Finally, the value of R_s would not change with frequency. Since the absolute impedance differences between saline concentrations are clearly frequency dependent, it further suggests that this results from a change in the impedance across the electrode tip (R_e and C_e).

Filter-induced phase shifts

Filters used in the data acquisition system (H(ω)) can cause substantial phase shifts between V_in and V_rec that would add to the phase shifts induced by the electrode-amplifier circuit. To isolate this, we measured directly the phase of V_rec relative to the phase of V_sig as a function of frequency for signals sent directly to the head-stage (V_in = V_sig), shown in black (Figure 7) for the filters used in the rest of this study with both head-stages. These phase shifts become large near the edges of the filters’ passbands, although the raw phase shift within the passbands of these filters is considerable as well.

Figure 7 shows another characteristic of filter-induced phase shifts. Over the narrow frequency range where a given signal can be recorded simultaneously through both the spike and the LFP channels, the outputs of the two channels are out of phase with each other. While expected, this result clearly demonstrates that different phase shifts arise from the different filter properties of the two channels. To further illustrate this, we used a second LFP preamplifier with different filter properties to record signals up to 300 Hz, with results shown in grey on Figure 7. Even in the region where the passbands of the two LFP amplifiers overlap, considerable differences in the phase response occurs, with each LFP preamplifier inducing characteristic shifts from the phase of the input signal. We have also found that phase shifts near the filter passband edges can vary from channel to channel for a given preamplifier (Figure S2). Thus, equipment-specific filtering properties must be accounted for to report accurately the phase of LFP data, especially at frequencies near the passband edges of analog filters.

Group delay

The phase shift at a given frequency can be translated into a time delay for a pure sinusoid at that frequency. If the phase shift were constant across frequencies, this would correspond to a progressively decreasing time shift as the frequency increases. On the other hand, if the phase shifts of a system were the result of a pure time delay of the signal, then the phase response would be a linear function of frequency, with the magnitude of the slope reflecting the magnitude of the delay. The negative derivative of the phase with respect to frequency, called the group delay, is a useful measure of delay even when the phase response is non-linear. For a narrow bandwidth around a given frequency where the variation of phase with frequency is approximately linear, the group delay measures the delay of the amplitude envelope for all components of signals within this narrowband “group” of sinusoids (Oppenheim and Schaefer 1998; Smith 2006). Note that at any particular frequency, the group delay need not equal the time shift calculated directly from the phase shift (i.e., the phase shift in fractions of a cycle divided by the frequency), which is called the phase delay. The two delays will differ over at least some part of the spectrum if the system’s phase response is not entirely linear. When the group delay and phase delay are not equal, the system will necessarily distort the shapes of signals in the time-domain (Smith 2006).

Figure 8A shows the group delay for the electrode data; this is just the negative derivative of the low input impedance head-stage phase data from Figure 5 (in units of cycles) with respect to frequency (see Equation 4, Methods) without the subtraction of the filter-induced reference phase. Group delay varies modestly with electrode impedance and generally decreases with increasing frequency. For comparison, the group delay calculated from the filter-induced phase shifts of the black line in Figure 7 is shown here, and the group delay for the metallic resistor data is shown in Figure 8B. The filter-induced group delay through the LFP channel is relatively constant from 25 to 85 Hz at ∼3 ms, and the group delay through the spike channel above 1 kHz is constant at ∼0.15 ms. The electrode-amplifier circuit induced phase shifts in the microelectrode data resulted in added delays in the LFP frequency range that varied on average from an additional 0.35 ms at 85 Hz to 1.10 ms at 35 Hz. Over lower frequencies, the additional delays were even larger for some electrodes, with the series capacitance within the low impedance head-stage partly contributing to this. Recall that the purely filter-induced group delays from either head-stage will be the same as both use the same filters with the same phase response. To summarize, the group delay in the spike-related frequency range will not distort spike timing appreciably, but the group delay in the LFP frequency range will introduce a systematic delay that can become quite large at lower frequencies.

Figure 8.

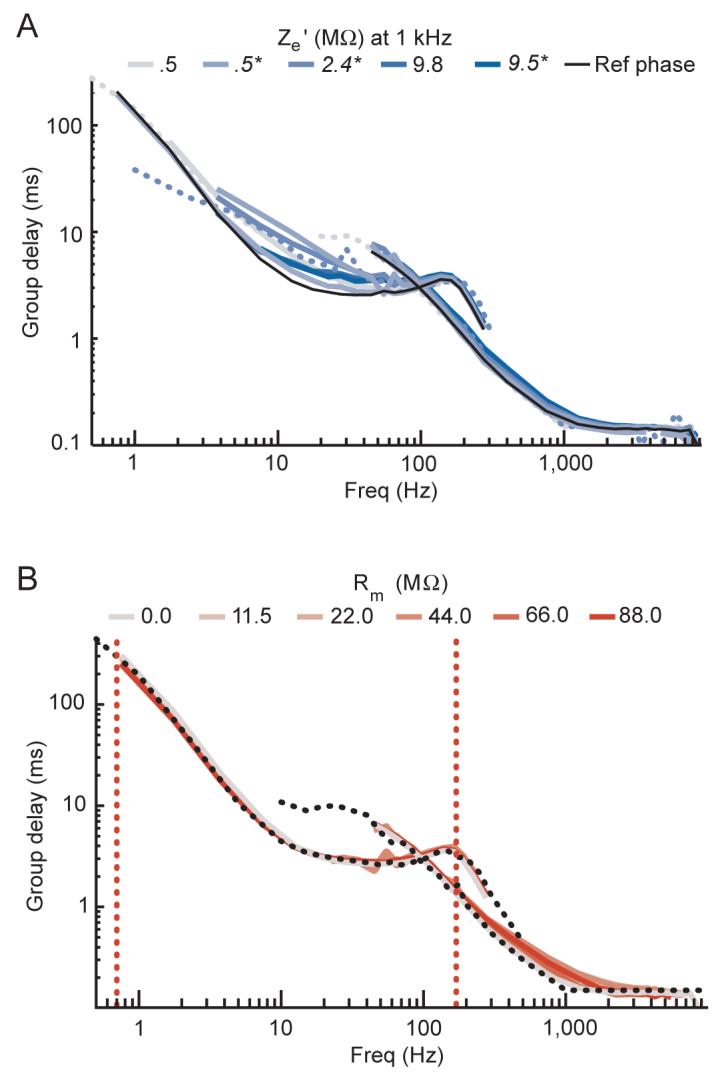
Group delays. Spike and LFP channel data are shown overlapping. Frequency is shown on a log scale. For a list of the exact frequencies tested, please see the Signals used subsection in the Methods section. The filter-induced phase shifts were not subtracted from any data shown here. A: group delay for electrode data. Grey-to-blue lines show data recorded in dilute saline in the parallel configuration using the low input impedance head-stage for electrodes with low-to-high measured impedance values at 10 Hz. Solid lines show group delays calculated from equation 4 (see methods) using the recorded phase shifts of sine waves at different frequencies, while dotted lines show the measured amplitude envelope delay using narrowband filtered pulse signals recorded with two electrodes. The manufacturer specified values at 1 kHz are indicated in the color legend above the plot. Values in italics and followed by an asterisk denote data from a glass insulated electrode. The group delays from the filter-induced reference phase response (the black lines from Figure 8) are shown by the black line for comparison. B: group delay for metallic resistor data. Line colors are coded from grey to red based on the value of R_m, with the precise values for each line indicated above the plot. The dotted black line shows the measured amplitude envelope delay using narrowband filtered pulse signals sent directly to the head-stage with no resistors, which corresponds well with the calculated group delay. The dotted vertical lines show the cut-off frequencies for the LFP channel filter used.

These conclusions depend on the quality of the group delay function derived from the phase shift measurements. To obtain a more direct measurement of group delay, we sent narrowband filtered pulses (see Methods for description, Figure 9 for examples) and measured the time delay at which the cross-correlation between the actual and recorded envelope estimates was maximal. The dotted traces in Figure 8A show the results for two of the electrodes color-coded for the electrode’s impedance. Each of these traces matches very well the electrode’s calculated group delay. Other electrodes tested in this manner also showed good matches with their group delays, as did the metallic resistor data (Figure 8B). This confirms that the group delay measured for this system actually measures the delay of the amplitude envelope of a signal at a given frequency, which differs from the phase delay of the signal directly calculated from the phase shift of the carrier frequency.

Distortion of field potential and spike waveforms

Because the group delay and phase delay are not equal over many frequencies, and because of the amplitude attenuation by analog filters and the electrode itself, we expect distortion of recorded waveform shapes in the time domain to occur. To view this, we recorded with and without microelectrodes a voltage shape obtained from a single neuron’s recorded waveform as well as a frequency-modulated version of the same waveform with the signal power concentrated in the LFP frequency ranges (Figure 10). Figure 10A shows the results for the LFP frequency range waveform, in which the delay in the recorded signal of about 3 to 4 ms can be clearly seen, matching the group delay for the relevant frequency ranges comprising this waveform. Electrode impedance dependent distortion of the recorded shapes can also clearly be seen, probably resulting largely from the amplitude attenuation properties of the electrode, with more of the lower frequencies of the signal being filtered out as electrode impedance increases.

Figure 10B shows the results for the raw waveform in the spike frequency range, in which the shorter (∼0.1 ms) delay can also clearly be seen. The effect of electrode impedance can be seen in the progressive attenuation of the amplitude of the recorded waveform, with a tendency for both the electrode and non-electrode data to attenuate the first large negative trough more so than the following large positive peak. The most conspicuous shape distortion though, is the phantom after-hyperpolarization that is not present in the input signal. Of course the sub-ms delay in the overall timing of the spike will have little appreciable impact since the precision of spike timing is rarely important to that degree. However, the amplitude attenuation of the spikes could potentially make it more difficult to record and isolate spikes among noise, particularly with higher impedance electrodes. As we showed earlier, this cannot be avoided with higher impedance amplifiers since Z_a’ in this frequency range is dominated by the shunt capacitance, at least for our experimental setup. The filter-induced phantom after-hyperpolarization suggests that any inferences made about this portion of the action potential in particular without adjusting for the distortion would be misleading.

Finally, to demonstrate the effects of these distortions on simultaneously recorded spikes and LFPs, we used frequency pulses with the high frequency spike from Figure 13B added to the signal at the maximum of the highest central peak. The results from one medium impedance electrode in physiological saline using either head-stage are shown in Figure 13C and D. For the 10 Hz signal, the filter-induced phase shift happens to be near zero at this frequency (see Figure 8), resulting in a near-zero phase shift observed with the high impedance head-stage. However, electrode-amplifier circuit induced phase shifts with the low impedance amplifier cause the carrier wave of the recorded signal to lead the actual signal causing the recorded spike to appear on the falling edge of the recorded LFP oscillation instead of at its true position at the peak. For the 80 Hz signal, the direction of the filter-induced and electrode-amplifier circuit induced phase shifts counteract each other, with the filter-induced phase shifts dominating and causing the recorded spike to appear well on the rising edge of the recorded LFP oscillation instead of at its true position at the peak. It is worth noting that this considerable filter-induced phase shift occurs at this frequency even though based solely on the high frequency cutoff of 170 Hz one might superficially expect the phase shift to be negligible at 80 Hz.

DISCUSSION

Summary

We have shown that signals recorded with tungsten micro-electrodes and an acquisition system commonly used in neurophysiology can be distorted substantially from the actual signals at the electrode tip. This distortion consists of frequency-dependent phase shifts and amplitude attenuation. The system filters imposed noticeable phase shifts even within their passbands. The observed phase shifts were dependent on the exact specifications of the pre-amplifier selected for use in a given system. When the electrode impedance was high with respect to the effective input impedance of the head-stage amplifier, both attenuation and additional phase shifts of the recorded signal occurred. Of the two head-stages we tested, this occurred with the lower input impedance head-stage and primarily at lower frequencies because of the oft-overlooked fact that micro-electrode impedance becomes much higher as frequency decreases. As such, equipment designed primarily to record spiking activity may not be able to record LFP activity without distorting the signal. We demonstrated that the distortions decrease with increasing saline concentration, but are still considerable with the low input impedance head-stage in physiological saline. Thus, these effects are of particular importance when gathering and interpreting LFP data. We showed that phase effects from both sources lead to amplitude envelope delays that differ from the direct time equivalent of the phase shift at a given frequency. We have also demonstrated shape distortion effects on recorded lower frequency event-triggered potentials and spike shapes.

Impact of distortions

If the distortions demonstrated in this study occur and are not accounted for, any analysis using such LFP or spike shape data would be affected, and in certain cases this may lead to incorrect conclusions. Negative results at lower frequencies in LFP power or coherence (Fries et al. 2001a; Liu and Newsome 2006), particularly at sub-gamma frequencies (<40 Hz) become difficult to interpret as are direct comparisons of these measures across frequencies (Fries et al. 2001b; Rickert et al. 2005; Womelsdorf et al. 2006). Measures of absolute LFP phase in relation to an event or spikes will be shifted (Bragin et al. 1995; Haslinger et al. 2006; Lee et al. 2005; Lin et al. 2006; Murthy and Fetz 1996; Skaggs et al. 1996) meaning that any mappings of potentials onto the times when neurons locally are excited and inhibited (Fries et al. 2001a; Haslinger et al. 2006; Lin et al. 2006) will be incorrect. Because of the amplitude envelope delays, there will be subtle delays imposed on the timing of changes in frequency power or coherence (Womelsdorf et al. 2006). And finally, theoretical interpretations of spike shapes (Barthó et al 2004; Gold et al. 2006; Nowak et al. 2003, Mitchell et. al. 2007) and event-triggered LFPs (Fries et al. 2001a,b; Krieman et al. 2006) may be incorrect, and techniques using waveforms as classification data (Fries et al. 2001a, Krieman et al. 2006) will be affected as well.

We would like to clearly indicate that we are not claiming that the results of any of the articles we mention above are necessarily distorted or that all of their conclusions should be questioned even if some signal distortion did occur. Indeed different equipment than what we have tested was often used, and such studies may or may not be susceptible to such distortions to a similar degree. However, due to past and current standards in the literature regarding methodological documentation it is not possible for a reader to determine the extent to which LFP data in a given publication may have been affected or to be certain that such distortions are negligible. In a qualitative review of the LFP literature, we found that though cutoff frequencies for filter passbands are usually mentioned, the filter phase response is rarely mentioned. The filter specifications that are given are typically insufficient for the reader to be sure that the phase response will be near zero for the frequency ranges in question, even in cases where this would affect some of the conclusions of the article. Electrode impedance ranges measured at 1 kHz are only occasionally mentioned. The names of companies providing the amplification and recording equipment are also occasionally mentioned, but importantly, specific model numbers or relevant input impedances of amplifiers are never mentioned. This additional information should be included as well, as we have shown that different products provided by the same company can be susceptible to different levels of distortions. Indication of accounting for all the signal distortions we have shown is also never given.

Additionally, though some conclusions from analyses we have mentioned may be rendered incorrect as result of distortions that were not considered, this will not be true of conclusions from all analyses of such data. Most notably, comparisons within a given frequency band across different conditions using the same equipment should remain valid, though such comparisons at lower frequencies may be subject to a lower signal to noise ratio. While it is possible that rigorous statistical testing like bootstrapping and other methods could alleviate this to a certain extent, if potential distortions are a problem for a given data set, uncertainty regarding negative results at low frequencies would inevitably remain regardless of the statistical procedures employed on the distorted data. If the signal is analyzed in the time domain which combines LFP activity from all frequencies, then if the underlying neural activity between the two conditions differs at all then their frequency content must differ and the distortions will affect the recorded activity under each condition differently. As we have shown, the time-domain waveform shape of the signal can be distorted, which would thus affect such comparisons across conditions, most notably for results involving the precise timing of activity.

However, an impact of unaccounted signal distortion that is much more important than whether or not it may render a given specific analysis to be strictly wrong is that it leads to an overall distorted view of the underlying neural activity and the state of the brain during experiments. With LFPs in particular, though some progress can be made using recorded activity merely as an arbitrary signal with which to determine when activity in a brain area generally differs between conditions, of critical importance to truly understanding the brain will be to determine what the underlying brain states are that give rise to the recorded neural activity. Signal distortions that are not accounted for will lead such mappings to be incorrect. For example, in one recent study (Lin et. al 2006) the authors note that basal forebrain tonic neurons (BFTNs) synchronize spiking activity just before the troughs of recorded prefrontal cortex (PFC) LFP theta oscillations of about 10 Hz. They interpret this as suggesting that the BFTN synchronization leads and probably contributes to a cortical activity increase that results in the LFP trough. Inferences like these are potentially the most fruitful uses of LFP activity to improve our understanding of the brain. However, if their recordings were distorted, which a reader cannot ascertain, then their general finding that BFTN synchronization occurs phase locked with PFC theta activity would likely still be true, but the reported phase at which this occurs and the theoretical interpretation of this relative to the timing of cortical excitation may need to be adjusted.

Because the distortions we have shown can implicate different underlying neural activity as giving rise to recorded data and can also potentially alter certain direct conclusions, they should be kept in mind when interpreting any LFP result, though we cannot quantify their extent in any given existing article. Our results also emphasize the importance of including methodological details in publications. Of course not every trivial detail of an experiment can be mentioned so a proper balance must be found, but our work illustrates some of the problems that can result from reporting too little. In particular, the mindset that a reader should assume that methodological details not mentioned in the article were done correctly by the experimenters without any verification of that has obvious negative consequences for the advancement of science. Particularly with the advent of web-based supplemental materials there is ample room to put full details of the experimental apparatus in publications. We also encourage instrument providers to post more complete information on their web sites. However, we feel it is most appropriate for the specific equipment used in a study to be documented in the article text or supplemental information, rather than solely in an external source like a lab website. This avoids confusion as the equipment used often varies between projects in a lab and it allows the reader to more easily find the information they need.

While we hope that our results will lead readers to view existing LFP literature in a somewhat different light, our primary concern is that those performing future neurophysiology experiments will be more aware of these distortions and either avoid them entirely or account for them properly. Additionally, it is important for authors themselves to understand how this recording circuit works, which reveals in what instances and in what ways electrode characteristics like impedance will affect recorded signals. Investigators should not solely rely on equipment providers to ensure that their recordings are done correctly. Among other reasons, the way that equipment is arranged in a particular experiment independently of how it is built affects the shunt capacitance. We have shown that even with the best of equipment, this could lead to degradation of recorded spiking activity, making isolating single cell activity in the brain more difficult.

With regards to electrode-amplifier circuit induced distortions, while our results indicate that this will be a problem for a low-impedance head-stage that has been in use by some for recording LFPs, this is not true of all available amplifiers as we have demonstrated with a higher-impedance head-stage. Indeed, amplifiers with very high input impedances have been easily obtainable for some time (Purves, 1981). It cannot be our place to test all the equipment used in neurophysiology today, but we hope that in light of what we have shown, prudent labs will determine what distortions arise in their experiments, particularly if their work involves recording LFPs. We cannot say exactly how widely used the 38 MΩ head-stage that we tested in this study is, but we do know that some other labs have been using it for recording LFPs with microelectrodes. Additionally, it seems likely to us that other equipment providers may have additionally distributed equipment that results in at least some degree of low-frequency signal distortion, as problems could easily result from overlooking or being unaware of the large increases in electrode impedance at low frequencies. Considering electrode impedances at 1 kHz as they are often labeled, amplifier input impedances of several tens of MΩ easily seem sufficiently high, though we have shown that indeed they are not for the recording of LFPs.

With regards to filter-induced distortions, provided that analog filters are used before digitizing and recording potentials, which is for all practical purposes a requirement for most recording systems, phase distortions will necessarily occur as they are a property of any causal filter. These distortions are therefore far more prevalent, though they are seldom accounted for in existing LFP studies. Sensitivity to this issue should also be present when considering the use of post-recording digital filters, as many of these may introduce phase shifts as well but carefully implemented ones may not. Potential filter-induced phase shifts should always be kept in mind when interpreting existing and future results reporting the absolute phases of field potentials (Bragin et al. 1995; Haslinger et al. 2006; Lee et al. 2005; Lin et al. 2006; Murthy and Fetz 1996; Skaggs et al. 1996), shapes of spikes (Barthó et al 2004; Gold et al. 2006; Nowak et al. 2003, Mitchell et al. 2007) and evoked potentials (Fries et al. 2001a,b; Krieman et al. 2006).

Correction techniques

An easy way to avoid the electrode-amplifier circuit induced portion of the effects that we have shown is through hardware adjustments with the use of a head-stage with a much higher input impedance than the 38 MΩ head-stage tested for most of this study. As we have shown, amplifiers with low frequency input impedances of 1 GΩ are sufficient to eliminate this distortion for all practical purposes with the use of most metal microelectrodes under reasonable conditions. It should also be noted that shunt capacitance can compromise even the highest amplifier input impedances, so care must always be taken to minimize this, for example with the use of minimal-length cables between the electrode and head-stage, negative capacitance injection, driven shield arrangements or other techniques (Purves, 1981 pp. 45-49).

Care should also be taken to select filter properties appropriate for the intended analyses, another useful hardware adjustment. Passband edges should be placed as far off as possible from the frequency ranges of interest since the region of negligible phase shift is somewhat narrower than the region of negligible amplitude attenuation. The number of poles and type of filter can be selected to achieve the proper balance between phase distortions and amplitude response fluctuations in the passband, both of which form tradeoffs with each other.

For any of the effects we have shown that could not be avoided during data acquisition, software adjustments involving ex post facto correction routines using de-convolutions are possible to account for them once the transfer function of all the elements in the circuit are known. This is easily obtainable for the recording system itself by recording sine wave voltages spanning the frequency spectrum of interest with a desired resolution as we have done in this study, though other techniques like the use of a chirp signal may be possible, which would only require the use of one test signal. Signals can be generated using a function generator or a computer’s audio output as was done in this study. If additional electrode-amplifier circuit induced effects could not be sufficiently mitigated with an appropriate head-stage, measurements of the system transfer function including the electrode would need to be performed as well. Preferably, this should be done within the brain before and after a recording session to get the best estimate of the transfer function resulting from the electrode’s impedance at the time of recording. Available online in the Supplementary Note is a text file containing Matlab code to generate .wav files for signal generation, interpret the recorded data to obtain the transfer function, and apply the correction techniques given the empirically obtained transfer function. For Plexon users, a software tool provided by Plexon for correcting preamplifier phase distortions can be downloaded from www.plexoninc.com/support/phase.html.

Other electrode variables

There is no indication that the nature of the equivalent circuit described in this article will depend on electrode characteristics, though the value of specific model parameters may. For example, insulation material may affect the shunt capacitance to ground, as glass insulation for example has been known to be more capacitive than epoxylite (Robinson 1968), but with recordings at a negligible depth we found that results with different insulation materials were not qualitatively different. The physical properties of an electrode, which we have not investigated here, may also considerably affect the signals recorded by an electrode in a complicated physical environment like the brain (Lemon 1984).

The basic equivalent circuit we present applies to other types of micro-electrodes as well, including glass micropipette, carbon fiber and microwire electrodes. These typically have much higher impedances than metal microelectrodes and it has been suggested that with such electrodes experimenters have typically used appropriately high input impedance amplifiers (Geddes et al. 1967), though we feel documentation of this is still warranted in articles presenting such data.