Predicting Thymine Dimerization Yields from Molecular Dynamics Simulations

Abstract

It was recently shown that thymine dimers in the all-thymine oligonucleotide (dT)₁₈ are fully formed in <1 ps after ultraviolet excitation. The speed and low quantum yield of this reaction suggest that only a small fraction of the conformers of this structurally disordered oligonucleotide are in a position to react at the instant of photon absorption. In this work, we explore the hypothesis that conventional molecular dynamics simulations can be used to predict the yield of cyclobutane pyrimidine dimers in DNA. Conformations obtained from simulations of thymidylyl-(3′-5′)-thymidine in various cosolvents were classified as dimerizable or nondimerizable depending on the distance between the C5-C6 double bonds of the adjacent thymine bases and the torsion angle between them. The quantum yield of cyclobutane pyrimidine dimer formation was calculated as the number of dimerizable conformations divided by the total number of conformations. The experimental quantum yields measured in the different solvents were satisfactorily reproduced using physically reasonable values for the two parameters. The mean dimerizable structure computed by averaging all of the dimerizable cis-syn conformations is structurally similar to the actual cis-syn dimer. Compared to the canonical B-form TT step, the most important structural property of a dimerizable conformation is its reduced helical twist angle of 22°.

INTRODUCTION

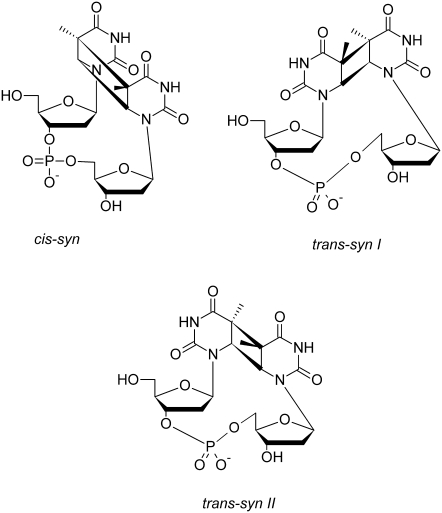
Cyclobutane pyrimidine dimers (CPDs) (Fig. 1) are the major carcinogenic photolesions created in DNA by ultraviolet (UV) irradiation. CPDs are formed in a [2 + 2] photocycloaddition reaction, which fuses the C5-C6 double bonds of adjacent bases in a cyclobutane ring. Despite decades of study, the mechanism of CPD formation has remained elusive, and there is no microscopic theory for the pronounced effects of structure and base sequence on this important photoreaction. Recently, ultrafast spectroscopic techniques, which have had great success in elucidating photophysical decay pathways of excited electronic states in DNA (1,2), were used to study thymine dimerization (3). Using femtosecond time-resolved infrared spectroscopy, it was shown that dimer formation in (dT)₁₈ occurs within 1 ps of photoexcitation (3). Because most conformational motions take place on slower timescales and because many conformers are thermally populated at any instant of time, it was argued that the initial conformation of the dimer in its ground electronic state controls whether reaction takes place. The quantum yield of CPD formation in DNA is less than a few percent, suggesting that CPDs are formed when rare conformers absorb UV light (3–5).

FIGURE 1.

The most abundant stereoisomers of the thymine photodimer.

Past experiments support the paradigm that ground-state conformation controls photoreactivity. In the technique known as UV photofootprinting, photodamage sites in DNA are determined by sequencing and used to make structural inferences based on the assumption that damage probabilities are modulated by structure (6,7). Dimerization quantum yields close to unity have been observed in solid-state model systems (8–11), suggesting that favorably aligned thymine residues can react with high efficiency. In addition, recent comparative molecular dynamics (MD) simulation and photochemical studies (5) have shown that conformational differences lead to altered quantum yields. These results all suggest that in genomic DNA, the ensemble of thermally accessible structures is critically important for determining CPD yields. Pehrson suggested that bending the DNA double helix toward the major groove at the site immediately 5′ to the dimer site promotes dimer formation based on crystal structures of photodimers (12). However, there is uncertainty about the precise conformations that are prone to CPD formation.

We report here a combined experimental and computational study designed to test the hypothesis that ground-state conformations determine thymine dimerization. MD simulations were conducted to sample conformations of thymidylyl-(3′-5′)-thymidine (dTpdT) in aqueous solution in the presence of varying amounts of organic cosolvents. Base destacking by addition of an organic cosolvent reduces the quantum yields of thymine dimer formation in dTpdT (13,14), (dT)₁₈ (15), and calf thymus DNA (16). dTpdT was chosen because its small size facilitates the calculation of multinanosecond MD trajectories. It has also been shown to be a good model for dimerization in DNA (17).

In our approach, we assume that whether dimerization occurs is completely determined by the ground-state conformation at the instant when a dTpdT molecule absorbs a UV photon. We classify conformations sampled from MD trajectories of at least 95 ns for each solvent system into dimerizable and nondimerizable subsets using a simple two-parameter model described below. The dimerization quantum yield is then equated to the fraction of all conformers in the dimerizable set. As will be shown below, this simple model successfully reproduces experimental quantum yields in a variety of solvent systems. To have a consistent set of experimental quantum yields to compare with our simulations, CPD yields were first measured in several cosolvents as described in the next section.

METHODS

Quantum yield measurements

The sodium salt of dTpdT and 1,3-dimethyluracil (DMU) were obtained from Sigma-Aldrich (St. Louis, MO) and used as received. Solutions were prepared with ethanol (HPLC/spectrophotometric grade, Sigma-Aldrich), 1,4-dioxane (spectrophotometric grade, Sigma-Aldrich), and 50 mM phosphate buffer at pH 7. No additional salt was added because it has been shown that CPD quantum yields in dinucleosides are approximately the same for salt concentrations between 0 and 0.1 M (18). Samples for irradiation contained 3 mL of dTpdT solution in a mixture of phosphate buffer and organic cosolvent. The initial absorbance of this solution was between 0.7 and 1.0 at 260 nm.

Solutions of dTpdT were placed in a 1-cm-pathlength fused silica cuvette in a photochemical reactor (RPR-200, Southern New England Ultraviolet, Branford, CT) and stirred continuously during UV irradiation with a mercury germicidal lamp emitting at 254 nm (Ushio America, Cypress, CA). Irradiation was interrupted every few minutes to record an absorption spectrum using a Lambda 25 UV-vis spectrometer (PerkinElmer, Waltham, MA).

Absorbed photon fluxes were measured by chemical actinometry using the photohydration reaction of 1,3-dimethyluracil (19,20). A 10⁻⁴ M aqueous solution of 1,3-dimethyluracil was irradiated for a precise time interval of between 10 and 15 min before and after each experiment. The absorbed flux per unit time was calculated from the measured absorbance of 1,3-dimethyluracil at 267 nm before and after irradiation, assuming that the photohydrate does not absorb at 267 nm. The absorption coefficient of 1,3-dimethyluracil at 267 nm (8.9 × 10³ M⁻¹ cm⁻¹) was used (21). The photon flux, I₀, in einsteins/s was calculated as (22)

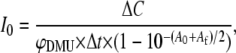(1)

where ΔC is the change in concentration of 1,3-dimethyluracil during irradiation, Δt is the total irradiation time, φ_DMU is the quantum yield of photohydration of 1,3-dimethyluracil (1.30 × 10⁻² (20)) and A₀ and A_f are the initial and final absorbance of the irradiated sample.

Correction for other photoproducts

It was assumed that only thymine CPDs (T〈〉T) and (6-4) thymine-thymine photoadducts are formed. Other photoproducts including the thymine photohydrate are known to be formed in negligible yields (23). The concentration of dTpdT versus time was calculated from the absorbance of the irradiated solution at 260 nm using an absorption coefficient of 17,200 M⁻¹ cm⁻¹ for dTpdT (24). T〈〉T absorption (ɛ₂₆₀ = 200 M⁻¹ s⁻¹ (25)) is only 2% as large as dTpdT, and was neglected. The change in absorption at 260 nm after irradiation was used to calculate a quantum yield of photodegradation from the initial slope of a graph of dTpdT concentration versus the absorbed photon flux. The concentration of the thymine-thymine (6-4) photoadduct was estimated from the change in absorbance at 325 nm, using an absorption coefficient of 4,600 M⁻¹ cm⁻¹ (26). Finally, the quantum yield of dimerization was calculated by subtracting the quantum yield of formation of the (6-4) photoadduct from the quantum yield of photodegradation. This procedure measures the total yield for all thymine photodimers regardless of stereochemistry.

Molecular dynamics simulations

Initial structures and equilibration

The starting structure for dTpdT was built using the Hyperchem 7.1 program (Hypercube, Gainesville, FL) from crystallographic data (27). This structure was energy-minimized using Hyperchem's implementation of the Cornell et al. force field (28), and used with a single explicit Na⁺ ion as the starting structure for MD runs.

MD simulations were done using the GROMACS 3.2.1 (29–31) package (double precision) with the FFAMBER (32) implementation of the Cornell et al. force field. All bond lengths were constrained using the SHAKE algorithm (33) with a relative tolerance of 10⁻⁸. Bond lengths and angles of water molecules were constrained using the SETTLE algorithm (34). A step size of 1 fs was used for simulations at 400 K, and a step size of 2 fs was used for all other simulations. The particle mesh Ewald method (35) was used to model long-range electrostatic forces, and a cut-off of 9 Å was used in the evaluation of van der Waals forces. The pairs list contained atoms separated by up to 9 Å and was updated every 20 fs.

All MD simulations were carried out with explicit solvent molecules in a cubic box with an edge length of 25 Å subject to periodic boundary conditions. The number of added solvent molecules was calculated from reported densities of dioxane/water and ethanol/water mixtures (36). Water molecules were modeled with the TIP3P model compound (37). All-atom ethanol or dioxane molecules were built and energy minimized, in the latter case starting from the chair conformer. Charge assignments for ethanol and dioxane were made as described in the Supplementary Material.

The energy of the entire solute-solvent system (hereafter referred to as the “system”) was minimized iteratively using the steepest-descent method followed by the limited memory BFGS (L-BFGS) method (38). A 3 ps molecular dynamics simulation at 400 K was performed each time after L-BFGS energy minimization and the procedure was repeated until no further decrease in energy was observed. For simulations in binary solvents, the positions of the atoms in the dTpdT molecule were constrained during a 10-ns molecular dynamics simulation at 800 K by applying harmonic positional restraints each with a force constant of 10⁵ kJ mol⁻¹ nm⁻² and directed in the x, y, and z directions of the periodic solvent box. This procedure froze the conformation of the solute, but allowed the two types of solvent molecules to mix completely. These structures were then used as the starting point for simulated annealing.

Simulated annealing

High-temperature molecular dynamics (39,40) was used to sample conformational space in each of the solvent mixtures studied. The system was heated gradually from 0 to 400 K in 10 ps, followed by a 50-ps equilibration period. Next, a 3-ns molecular dynamics simulation was conducted, and a snapshot of the system was taken every 100 ps. Each sampled snapshot of the system was then energy minimized using steepest descent followed by the limited memory BFGS algorithm (38).

Production simulations and convergence analysis

Production simulations for conformational sampling were performed by heating the solute-solvent system from 0 to 300 K in 10 ps, increasing the temperature after every picosecond, followed by a 110-ps minimum equilibration period. A total of 25 production runs, each lasting 6 ns, were conducted for each system studied. Better structural sampling was achieved by combining these individual production runs, each of which used a different starting structure produced by high-temperature molecular dynamics, as discussed above. Conformations were sampled every picosecond, resulting in 150,025 conformations for each solvent, which were stored and used for subsequent analysis. The reverse cumulative average (41) of the separation between C5-C6 double bonds was evaluated as a means of judging equilibration and convergence as described in Supplementary Materials. Based on this analysis, the equilibration period was extended as necessary by removing an initial segment of the production trajectory (see Table S2). Quantum yields calculated using either half of the remaining trajectory were the same within the limits of experimental error.

Analysis of geometrical parameters

Bond distances and torsion angles were measured using routines in GROMACS 3.2.1 (29–31) and 3DNA 1.5 (42). Statistical analyses were performed using IGOR Pro 5.0.4.8 (Wavemetrics, Lake Oswego, OR) and SPSS 15.0 (SPSS, Chicago, IL). The mean dimerizable structure was fitted and constructed in MOLMOL 2K.2 (43) and molecular visualization was performed using the University of California at San Francisco Chimera version 1 build 2304 (44).

RESULTS AND DISCUSSION

Experimental quantum yields

The quantum yields of 6-4 photoadduct and CPD formation measured in this study are listed in Table 1. The results in aqueous solution compare well with literature values (18,23,45). The observed decrease in dimer formation with increasing ethanol concentrations agrees well with results of Tramer et al. (13). The results are also in agreement with a study by Dellweg and Wacker (46), in which it was argued that reduced base stacking of dTpdT in organic solvents attenuates the efficiency of dimerization.

TABLE 1.

Experimental quantum yields of dTpdT photodegradation (φ_deg), (6-4) photoadduct formation (φ_6-4), and thymine dimerization (φ_T〈〉T) for dTpdT in various solvents

Cosolvent in 50 mM phosphate buffer	φdeg (× 102)	φ6-4 (× 103)	φT〈〉T*(× 102)
None	1.8 ± 0.3	2.0 ± 0.7	1.6 ± 0.3
	2.0 ± 0.2†	1.1 ± 0.1†	1.7 ± 0.1†
40% (v/v) ethanol	1.2 ± 0.1	1.8 ± 0.3	1.1 ± 0.1
50% (v/v) dioxane	0.8 ± 0.2	1.3 ± 0.2	0.7 ± 0.2
60% (v/v) ethanol	0.81 ± 0.09	1.2 ± 0.1	0.7 ± 0.1

^*Sum of all stereoisomers.

^†From Douki (18).

Molecular dynamics studies

Two-parameter model for dimerizable conformations

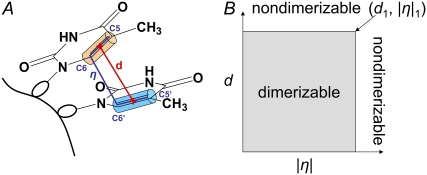
Our hypothesis is that the fraction of reactive conformations (hereafter referred to as “dimerizable conformers”) is equal to the quantum yield of dimerization. For this proof-of-principle study, we adopt the simplest binary model and assume that dimerizable conformers react with unit quantum yield upon UV absorption, whereas nondimerizable conformers have zero probability of reaction. The central issue is thus the classification of conformations as dimerizable or nondimerizable. Although there are limitless ways to do this, we settled on a simple approach that uses a minimal set of geometrical parameters. A short interbase distance is clearly a necessary condition for reaction as discussed by many workers (8,10,13,47). There is, however, evidence that additional conformational constraints are needed. For example, Santini et al. (5) found that the 2′-O-methyl derivative of rTprT have similar vertical separations from each other, despite a difference in CPD quantum yields of nearly a factor of 3 (48). It has been suggested that the C5-C6 bonds of the thymines must be approximately parallel for photoreaction to occur (3,49). We therefore explored whether the two parameters illustrated in Fig. 2 A can identify conformations that result in thymine dimers. The two parameters are the distance, d, between the midpoints of the C5-C6 double bonds, and the absolute value of the improper torsion angle, η, defined as C5-C6-C6*-C5*, where the asterisk denotes atoms on the 3′ base. These two conformational parameters were sampled at every picosecond of the MD simulations.

FIGURE 2.

(A) Two-parameter model for identification of dimerizable conformations in dTpdT. At each time step during the molecular dynamics simulation, the separation between the midpoints of the C5-C6 double bonds, d, and the improper torsion angle between the same bonds, η, are calculated. (B) A conformer is assumed to dimerize when photoexcited if these parameters satisfy the inequalities 0 < d ≤ d₁ and 0 ≤ |η| ≤ η₁, corresponding to the shaded area in the graph.

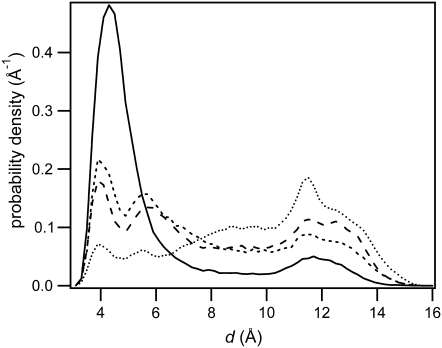
Fig. 3 shows a histogram of the distance, d, evaluated from the MD trajectories in the various solvent systems. The fraction of dTpdT conformers with d ≤ 5 Å decreases with an increase in organic cosolvent concentration, consistent with earlier experimental results (13,50) and MD simulations (51). Small values of d (<3 Å) are forbidden by steric and electrostatic repulsion, and the smallest value of d observed in water is 3.00 Å. Further discussion of base stacking in dTpdT is found in Supplementary Material. The probability density of the absolute value of the improper torsion angle, η, is shown in the Supplementary Material, Fig. S3.

FIGURE 3.

Probability density of the C5-C6 bond separation (d) for all conformers of dTpdT in water (solid line), 40% (v/v) ethanol (short-dashed line), 60% (v/v) ethanol (long-dashed line), and 50% (v/v) dioxane (dotted line).

It was impossible to use d or η by itself to predict quantum yields. Many instances of short d distances have excessively high η values. In addition, it was found that d is distributed very differently in 50% (v/v) dioxane and in 60% (v/v) ethanol, despite their similar quantum yields (Table 1). The inability to predict quantum yields using only η is understandable inasmuch as many extended, destacked conformations are encountered in which the C5-C6 bonds of the bases are approximately parallel even though the bases are quite distant.

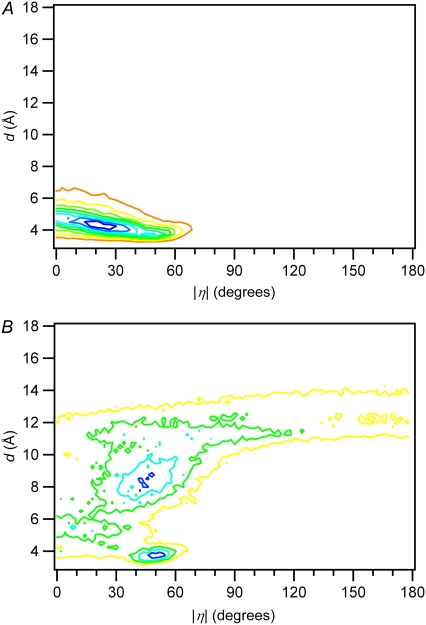
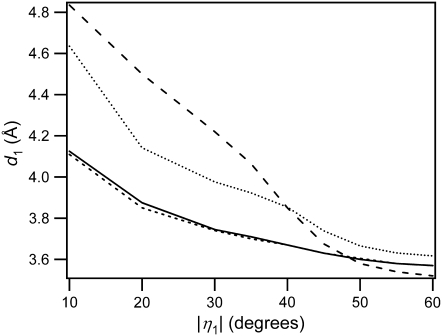
We therefore sought a model that uses both d and η to identify dimerizable conformations. The joint probability density of d and |η| is shown for water and 50% dioxane in Fig. 4, A and B, respectively, and for the other solvents in Fig. S4. As the cosolvent concentration is increased, the fraction of closely stacked conformers decreases, and the proportion of conformers with large η values increases. For relatively closely stacked conformers (d < 5 Å), |η| tends to decrease as d increases due to steric hindrance. There are countless ways to construct constraints with these two parameters for identifying dimerizable conformers. We adopted the arguably simplest two-parameter model illustrated in Fig. 2 B. In this model, a point (d₁, |η|₁) is chosen and all conformers falling in the shaded rectangular region are counted and divided by the total number of conformers to obtain a theoretical quantum yield. It is motivated by the notion that the C5-C6 double bonds must be close and in nearly parallel alignment for the reaction to occur. The point (d₁, |η|₁) is not unique for a given solvent, as shown in Fig. 5 and by the cumulative distributions in Fig. S5. Fig. 5 shows that for each possible value of d, a value of |η| can always be found that reproduces the experimental quantum yield in each solvent. The d versus η curves are generally different in each solvent, but all cross approximately in the vicinity of d = 3.7 Å and η = 50°. The finding that there is a small region of d-|η| space that yields parameters that predict quantum yields in all solvents validates this approach, as discussed in more detail below.

FIGURE 4.

Distribution of conformers at different values of d and |η| for (A) dTpdT in water and (B) dTpdT in 50% (v/v) dioxane. The axes on the graphs are scaled the same for comparison.

FIGURE 5.

Loci of points d₁, η₁ (defined in Fig. 2) such that the fraction of dimerizable conformers is equal to the experimental thymine dimer quantum yield (Table 1) in each solvent. The errors in the d values are ±0.03 Å. Line styles are the same as in Fig. 3.

Because the curves do not cross exactly at the same point, we selected several (d₁, |η|₁) pairs for calculating quantum yields for comparison with experiment (Table 2). The |η|₁ values in Table 2 were chosen to lie at the intersection of pairs of curves in Fig. 5. Then, the d values for each solvent obtained from the curves in Fig. 5 at the chosen value of |η|₁ were averaged to give d₁. The second parameter set in Table 2 (d < 3.63 Å and |η| < 48.2°) yields the best agreement with the experimental quantum yields in all four solvents. Conformers with d < 3.63 Å and |η| < 48.2° will be referred to hereafter as “dimerizable conformers”. The value d = 3.63 Å is just slightly greater than that found for solid crystals of Thy-(CH₂)₃-Thy, which dimerize with high efficiency (49). In the crystal, the separations between the C5 and C6 atoms of the two bases are 3.549 Å and 3.452 Å, respectively (49).

TABLE 2.

Calculated thymine dimer quantum yields (φ_T〈〉T) using different parameter sets for d₁ and η₁

		Calculated φT〈〉T (× 102)
d1 (Å)	η1 (°)	water	40% (v/v) ethanol	50% (v/v) dioxane	60% (v/v) ethanol
3.76	40.0	2.8	1.9	0.47	0.49
3.63	48.2	1.9	1.3	0.51	0.79
3.58	55.0	1.6	1.1	0.50	0.96
3.57	60.0	1.6	1.1	0.57	1.1

Relative orientation of the bases and dimer stereochemistry

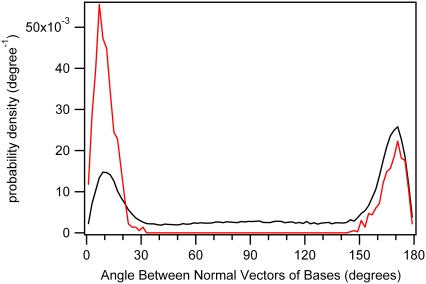
The relative alignment of the C5-C6 double bonds has important stereochemical consequences for dimer formation. Studies indicate that only the cis-syn and trans-syn dimers (Fig. 1) are formed in appreciable yields in DNA (17,18). To explore thymine dimer stereochemistry, a unit vector normal to each thymine base plane was calculated for every conformer from the cross product of unit vectors directed along the N1-C2 and N1-C6 bonds. The angle between the two normal vectors for all dTpdT molecules is distributed as shown in Fig. 6 (black curve). This curve shows an excess of antiparallel versus parallel alignments. In addition, there is a broad continuum of intermediate alignments with angles between 30° and 150°. In contrast, the dimerizable conformers in water exhibit only parallel and antiparallel alignments, with no intermediate structures (Fig. 6, red curve). This is because the small value of d in the dimerizable set of conformers is only compatible with parallel and antiparallel alignments.

FIGURE 6.

Distribution of the angle between the normal vectors of the two bases of dTpdT in water. The black line is for all conformers, and the red line represents the subset of dimerizable conformers.

Fig. 6 shows that dimerizable conformers that produce cis-syn dimers can be unambiguously identified by the requirement that the base plane normal vectors make an angle <90°. Because dimerizable conformers with antiparallel base alignment yield trans-syn dimers, Fig. 6 and Table 3 suggest that 32% of all dimers in water will have trans-syn geometry. Experiments suggest that the percentage of trans-syn stereoisomers is ∼10% (17,18). This difference may be due to electronic factors not accounted for in our model, which considers only ground-state geometry. Parallel alignment of the C5-C6 double bonds leads to a much lower degree of base-base overlap in the trans-syn than in the cis-syn case (Fig. S6). The smaller overlap could reduce any electronic interaction necessary for reaction. Eisinger and Lamola observed a larger exciton splitting for broken thymine dimers in which the thymines were positioned nearer to each other than is the case for an average TT step (47). Thus, the trans-syn geometry with its reduced base-base overlap could attenuate the electronic coupling necessary for reaction.

TABLE 3.

Calculated trans-syn yields for dTpdT from MD simulations

Solvent conditions	trans-syn quantum yield (× 10−3)	trans-syn yield (% of total dimer yield)
Water only	5.9	32
40% (v/v) ethanol	4.2	33
50% (v/v) dioxane	3.5	69
60% (v/v) ethanol	5.6	70

Structural characteristics of the dimerizable conformers

We have shown to this point that simple geometrical criteria exist for identifying “reactive” conformers sampled from MD trajectories such that the fraction of these conformers is numerically equal to the dimerization quantum yield. Furthermore, the same two criteria predict the extent of dimer formation in different solvent systems having widely different conformational populations. This suggests that the chosen criteria have correctly identified the primary conformational factors in the actual reaction pathways. We now examine this issue in detail by comparing structural characteristics of the dimerizable conformers selected by our criteria with the canonical B-form structure of a TT step and with published cis-syn T〈〉T structures.

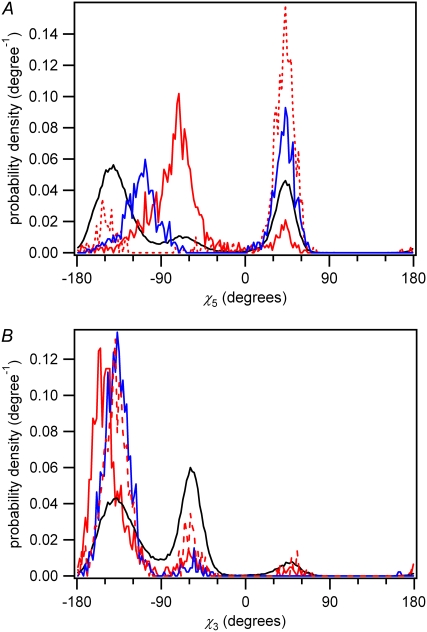
Fig. 7 A displays the probability density for the glycosidic torsion angle of the 5′ base (χ₅) of dTpdT for various conformer subpopulations. The cis-syn dimerizable conformers have an average χ₅ value in the syn conformational range (χ₅ ≈ −67°) in contrast to the set of all conformers, dimerizable and nondimerizable, which prefers the anti conformation (χ₅ ≈ −140°) normally found in B-DNA. Park et al. showed in their crystal structure analysis of a thymine dimer-containing dodecamer that χ₅ adopts a unique syn value of −52.2° (52). Our value is in good agreement with theirs and with NMR measurements (53). The trans-syn dimerizable population also displays a syn conformation for χ₅, but in the +synclinal range (χ ≈ +60°), in agreement with results from an NMR study of the trans-syn CPD of dUpdT (54).

FIGURE 7.

Distribution of the glycosidic torsion angle (χ) of the (A) 5′ base and (B) 3′ base of dTpdT for various conformer sets in water. Black line, all conformers; solid red line, cis-syn dimerizable conformers; dashed red line, trans-syn dimerizable conformers; blue line, nondimerizable conformations with d < 3.66 Å.

The glycosidic torsion angle of the 3′ base (χ₃) is shown in Fig. 7 B. It can be seen from Fig. 7 that the N-glycosidic bonds of the vast majority (87%) of cis-syn dimerizable conformers have 5′-syn and 3′-anti conformation, as seen in the NMR study of McAteer et al. (53). On the other hand, the trans-syn dimerizable conformers have mostly 5′-syn and 3′-anti conformation (71%), corresponding to the trans-syn I dimer (55,56), or 5′-anti and 3′-syn conformation (20%), corresponding to the trans-syn II diastereomer (57). The N-glycosidic bond of the 3′ base of both cis-syn and trans-syn dimerizable conformers is primarily anti, but a higher percentage of syn conformers is observed in the trans-syn case, in agreement with experiment (53,54,56,57).

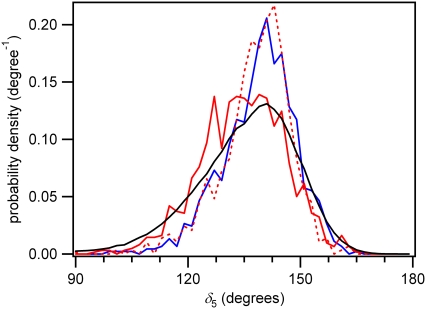
The δ dihedral angle is an indicator of sugar puckering in DNA (58). For the 5′ base, it assumes a value of ∼130° for the cis-syn (corresponding to C1′-exo) and ∼140° (corresponding to C3′-endo) for trans-syn dimerizable conformers (Fig. 8). Similar values are found in actual cis-syn (53) and trans-syn (54,56) dimers studied using NMR spectroscopy. We fail to find evidence that specific minor conformers with a C3′-endo sugar pucker at the 5′ base are responsible for dimerization as suggested by Moriou et al. (4). Our modeling may fail to reproduce the C3′-endo pucker preference because of the bias in the Cornell et al. (28) force field for B-DNA structure (59).

FIGURE 8.

Probability distribution for the δ dihedral angle of the 5′ base of dTpdT in water for different conformer populations. Line styles are the same as in Fig. 7.

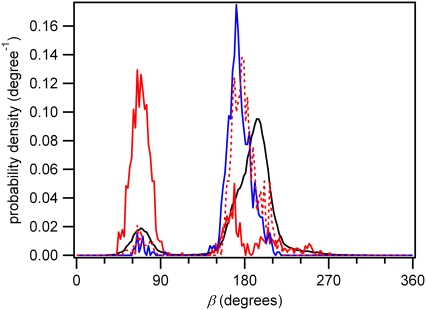
The distribution of the backbone torsion angle β for the 3′ base of dTpdT is graphed for various conformer sets in Fig. 9. The trans-syn dimerizable conformers closely mirror the distribution of all conformers, which are primarily in the antiperiplanar range typical of B-DNA. NMR measurements of trans-syn dimers of dUpdT show that most of the population (84%) is in the antiperiplanar domain (54,56). On the other hand, the cis-syn dimerizable structures overwhelmingly have an unusual +synclinal (∼+70°) β angle not found in B-DNA. This value is considerably smaller than the one in the authentic cis-syn dimer (β ≈ 150° (52,53)). Fig. S7, A and B, shows the distribution of the backbone dihedral angles ɛ and ζ, respectively.

FIGURE 9.

Distribution of the dihedral angle β of the 3′ base of dTpdT in water. Line styles are the same as in Fig. 7.

In general, the dimerizable conformers adopt backbone dihedral angles that are similar to those of the actual cis-syn dimer. The overall good agreement shows that selection of conformers that have close and parallel double bonds results in conformational properties for the entire TT step that closely resemble those in the photodimer. In other words, many of the characteristic conformational properties of the thymine dimer are the automatic result of bringing the C5-C6 double bonds into close and nearly parallel alignment.

The γ dihedral angle of the dimerizable population agrees poorly with that found in the authentic cis-syn dimer, as described in more detail in the Supplementary Material discussion. This may be due to the presence of excursions into the antiperiplanar torsion angle range, and away from the +synclinal range. This is a well documented limitation of the Cornell et al. force field (28) for long MD simulations (60,61). The shift toward the +synclinal region of the α dihedral angle reported by Pérez and others was not observed in the dimerizable population. However, such a shift was observed for the population as a whole (Supplementary Material, Fig. S8 A). This is attributed to a preponderance of −synclinal values of α for conformers with small interbond separation (Fig. S9).

Mean structure of the cis-syn dimerizable conformers

The preceding discussion has highlighted the many conformational similarities between the dimerizable conformers and the actual dimer photoproduct. These similarities can be further appreciated by examination of the mean dimerizable structure (MDS). The cis-syn MDS was calculated from all dimerizable conformers with parallel base alignment in aqueous solution using a randomly selected conformer to align all remaining dimerizable conformers such that the root mean-square deviation was minimized. The coordinates of all conformers so aligned were then averaged. Dihedral angles for the cis-syn MDS in aqueous solution are listed in Table 4. The cis-syn MDS is nearly the same in each cosolvent mixture, with the exception of 60% (v/v) ethanol, as discussed in Supplementary Material. The fact that a common MDS is found in most solvents suggests that the modeling has succeeded in capturing reactive conformations along the reaction coordinate and not arbitrary, solvent-dependent ones that happen to reproduce the experimental quantum yields.

TABLE 4.

Backbone dihedral angles of the mean dimerizable structure (MDS), the cis-syn thymine dimer, and canonical A- and B-type DNA structures

Dihedral angle	MDS	cis-syn dimer*	A-DNA†	B-DNA†
5′ base
χ	−66	−77	−161	−119
δ	+130	+126	+81	+128
ɛ	−167	−169	−157	−176
ζ	−91	−81	−71	−95
3′ base
χ	−144	−111	−161	−119
α	−90	−78	−67	—
β	+79	+163	+174	+176
γ	+174	+37	+56	—
δ	+123	+122	+81	+128

^*From McAteer et al. (53).

^†From Schneider et al. (71).

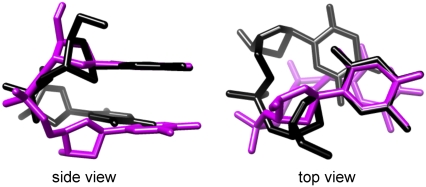
Although the separation between the two base planes is similar in the B-form TT step and in the MDS (Fig. 10), the base-base overlap is much greater in the latter structure. The cis-syn MDS has a base-base overlap area of 3.6 Ų compared to minimal overlap in A- and B-form DNA. This overlap produces a high degree of alignment between the reactive C5-C6 bonds and ensures that the corresponding π orbitals can interact in a manner that is not possible in the canonical DNA structures. Greater base overlap is due to the smaller helical twist angle of 22° for the MDS compared to values of ∼30° and 36° for A- and B-form DNA, respectively. The need for reduced twist angles explains why the quantum yield of dimerization in double-stranded DNA is still on the order of just a few percent per excited TT step despite short vertical base-base distances due to base stacking (3).

FIGURE 10.

cis-syn mean dimerizable structure (magenta) compared with the canonical B-form dTpdT structure (black).

Further support for the hypothesis that the rare dimerizable TT conformers have reduced twist angles comes from a theoretical study of the energies of stacked base pairs as a function of several conformational parameters (62). According to this analysis, decreasing the twist angle of a TT step from the value of ∼36° found in B-form DNA to the value of ∼22° of the dimerizable conformers identified here results in an increase in conformational free energy of ∼1.5 kcal mol⁻¹. Such a state should be populated no more than 7% of the time at room temperature—a value that compares favorably with the experimental dimerization quantum yield of 3%.

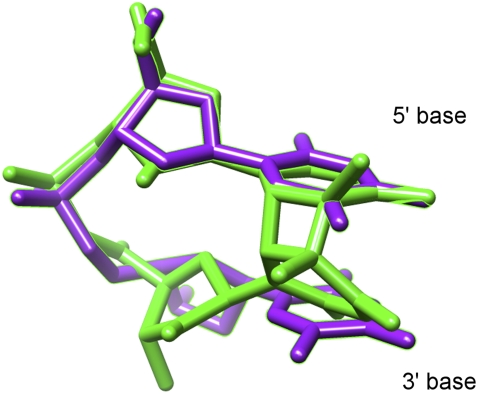
As expected, the cis-syn MDS calculated from MD trajectories in aqueous solution is very similar to the actual cis-syn dimer (Fig. 11). The 5′ base of the former structure exhibits the distinctive high anti value for the glycosidic torsion angle χ reported by multiple investigators for the 5′ base of the dimer (53,55,63,64). On the other hand, the conformation of the 3′ base of the cis-syn MDS has less in common with the 3′ base of the dimer. In the MDS, significant rotation about the O5′-C5′ bonds is observed, as seen from the distribution of the β dihedral angle (Fig. 9). This can also be seen in Fig. 11, where the 5′ base of the MDS is conformationally very similar to its counterpart in the cis-syn dimer structure reported by McAteer et al. (53). Bond rotation about the O5′-C5′ of the 3′ nucleotide is postulated to occur at a later stage along the reaction coordinate.

FIGURE 11.

cis-syn mean dimerizable structure (magenta) compared with the actual cis-syn dimer structure (green) from McAteer et al. (53).

Possible model limitations

The model presented assumes complete steric control and ignores electronic effects on reactivity. It neglects the possibility that a molecule located at a particular point in nuclear coordinate space on the excited state potential energy surface (i.e., with a given conformation) may possibly branch to different final states. This will reduce the quantum yield of reaction below unity even when the two thymine bases are favorably oriented for photoreaction. This could be the result of a potential energy barrier on the excited-state surface, but this is unlikely given the ultrafast timescale of dimerization (3). Even if dimerization occurs in a barrierless process, electronic effects could still be important. Photocycloaddition reactions like that of ethylene with itself occur via conical intersections between two electronic states (65). The topology of the conical intersection plays a central role in the mechanism and affects whether the excited molecule reaches the product well or decays back to reactants (65,66).

We have tacitly assumed that passage through the putative conical intersection responsible for dimerization always leads to the photodimer product. This is supported by dimerization quantum yields of approximately unity in some solid-state crystals of thymine derivatives (49,67,68). However, it is possible that electronic effects could be important at other bipyrimidine sites such as CC, where reactions are observed less frequently than at TT sites. By design, we have varied the solvent, but not the solute, thereby minimizing such electronic effects. It has also been shown previously that the ¹ππ* state, which is believed to be the photodimer precursor state, does not depend significantly on solvent properties. In this case, the solvent-dependent quantum yields should be understandable in terms of conformational differences of dTpdT, as demonstrated in this study.

CONCLUSIONS

We have presented a simple two-parameter model that predicts thymine dimer yields from molecular dynamics simulations of dTpdT in aqueous cosolvent mixtures. The results agree well with experimental quantum yields, suggesting that the model has succeeded in capturing conformational characteristics necessary for dimerization. Quantum yields for CPD formation are low because the conformational states necessary for this [2 + 2] cycloaddition are encountered infrequently. Our study has suggested that a number of these conformational properties are similar to ones found in the final photoproduct structure. The N-glycosidic torsion angle and sugar pucker angles appear to be conserved between the mean dimerizable structure and the final product. Although dimerizable conformers were identified using heuristic criteria, these criteria successfully predict dimerization yields under different solvent conditions, strengthening the case that minor conformers are responsible for CPD formation in DNA (3,4).

Our model can easily be applied to other systems to test how base pairing and base sequence affect the occurrence of dimerizable conformations. It will be important to examine whether variation in dimerization yields seen for the various bipyrimidine sites are due to conformational differences or reflect electronic effects not included in the model presented here. In this respect, quantum chemical calculations of the excited state pathways responsible for reaction will be invaluable.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.