Effects of Surface Water on Protein Dynamics Studied by a Novel Coarse-Grained Normal Mode Approach

Abstract

Normal mode analysis (NMA) has received much attention as a direct approach to extract the collective motions of macromolecules. However, the stringent requirement of computational resources by classical all-atom NMA limits the size of the macromolecules to which the method is normally applied. We implemented a novel coarse-grained normal mode approach based on partitioning the all-atom Hessian matrix into relevant and nonrelevant parts. It is interesting to note that, using classical all-atom NMA results as a reference, we found that this method generates more accurate results than do other coarse-grained approaches, including elastic network model and block normal mode approaches. Moreover, this new method is effective in incorporating the energetic contributions from the nonrelevant atoms, including surface water molecules, into the coarse-grained protein motions. The importance of such improvements is demonstrated by the effect of surface water to shift vibrational modes to higher frequencies and by an increase in overlap of the coarse-grained eigenvector space (the motion directions) with that obtained from molecular dynamics simulations of solvated protein in a water box. These results not only confirm the quality of our method but also point out the importance of incorporating surface structural water in studying protein dynamics.

INTRODUCTION

One major goal of studies of protein structure-function relationships is to identify their macroscopic correlated motions, and how these motions change in response to various external perturbations, such as ligand-binding. A variety of experimental approaches, including x-ray crystallography, NMR spectroscopy, and single-molecule biophysical techniques, have provided insights into macroscopic protein motions by monitoring the structural alterations of the same protein under different conditions. On the other hand, theoretical studies, such as molecular dynamics (MD) simulations and normal mode analysis (NMA), can also provide valuable information about internal protein motions (1,2).

Standard MD simulations sample the conformational space of a protein using the definitions for atomic interactions from various force fields and usually include explicitly treated water to reproduce solvent effects (3,4). Correlated protein motions can then be extracted from the MD simulations through diagonalizing the covariance matrix obtained from a section of the MD trajectory. This is also referred to as essential dynamics (5), principal component analysis (PCA) (6), or quasiharmonic analysis (7,8), due to the complex and anharmonic nature of protein dynamics. However, the size of the system, especially with explicitly treated water molecules, has provided a great computational challenge, generally limiting the timescale of MD simulations for large macromolecules to the nanosecond range, significantly shorter than the biologically relevant timescale of conformational changes that may require milliseconds or longer. Therefore, inefficient sampling is still a significant obstacle to extracting meaningful correlated motions from MD simulations (9,10).

Classical all-atom normal mode analysis (AANM) offers the ability to overcome some of the computational cost of MD simulations. AANM makes the simplifying assumption that protein motions can be described by harmonic motions around a local minimum on the protein energy surface. Starting with an initial protein structure, standard AANM requires an extensive minimization of the system's potential energy followed by the calculation of the Hessian matrix, whose 3N × 3N (N = the number of atoms) elements represent the second derivative of the potential energy function along the Cartesian coordinates. Diagonalization of the mass-weighted Hessian matrix can then be used to generate the eigenvectors and eigenvalues of the matrix, which provide, respectively, information about the directions of the various correlated motions within the protein and their amplitudes at a given frequency (11–14).

However, the application of AANM to biological macromolecules has been limited by the requirements of physical memory to store the all-atom Hessian matrix and the significant CPU time to diagonalize the very large matrix. Therefore, in practice, AANM is normally applied to protein systems containing at most a few hundred residues, in most cases without explicitly treated water molecules. However, since solvent has important and complex interactions with the solute molecule, the explicit treatment of solvents is thought to be essential to faithfully reproduce protein dynamics. For MD simulations, it has been a standard practice to simulate a protein molecule in a box filled with explicitly treated water molecules and use periodic boundary conditions. However, performing AANM on such a system to extract protein motions is usually beyond the capabilities of currently available computational hardware and software.

To date, there have been only a few published AANM studies involving explicitly treated water molecules within a distance of several Angstroms of the protein surface (15–17). These studies showed that incorporating surface water is helpful to reproduce experimental observations, including the B-factors determined by x-ray crystallography. However, given the scarcity of these studies, novel techniques, with the ability to efficiently incorporate solvent effects and provide a complete survey of the vibrational spectrum, are still needed to improve the efficiency of AANM for large systems.

Technically, even though the storage of a Hessian matrix has become less of an obstacle due to the introduction of sparse matrix techniques, the diagonalization of the all-atom matrix is still a challenge and new algorithms are being continuously added to various linear algebra packages. These include the method of diagonalization in a mixed basis (18,19) implemented in CHARMM (20) and the iterative Lanczos/Arnoldi factorization method (21) implemented in GROMACS (22), two widely used simulation packages. Nevertheless, these iterative numerical methods are still very time consuming and can only yield a small fraction of the total eigenvectors, usually those corresponding to the lowest vibrational frequencies.

Fortunately, the low-frequency vibrational modes are closely related to large-amplitude correlated protein motions with minimum energy costs, which usually reflect the conformational changes relevant to protein function (1,23). Indeed, the collective motions represented by these eigenvectors are in good agreement with independent experimental measurements (24–26). However, pinpointing the most functionally relevant individual mode is not a trivial task. In addition, it has been suggested that a combination of modes is required for a reasonable mapping of the correlated motions (1,13,27). Moreover, recent studies showed that the modes of higher frequencies are also important, because energy input from external perturbations can shift the distribution of different modes to higher frequencies (13,28). Thus, a complete survey of the eigenvector space and corresponding eigenvalues is important for various theoretical applications, such as the calculation of thermodynamic configuration entropy and heat capacity.

As an alternative to classical AANM, coarse-grained approaches have been pursued to reduce the size of the system and improve computational efficiency (14,29–31). The block normal mode method (BNM) is an effective coarse-grained NMA approach that treats proteins as a system of rigid blocks (32–34). However, BNM still relies on a complex all-atom representation and starts from the same all-atom Hessian matrix as AANM. An important breakthrough came with the introduction of the elastic network model (ENM), which simplifies the complex atomic interactions to potential energy functions with only a single parameter (1 kcal/mol/Ų) for C-α atoms, thus bypassing the time-consuming energy minimization steps (35,36). ENM (or isotropic Gaussian network model) reflects the intrinsic protein dynamics embedded in the overall molecular topology and effectively reproduces certain aspects of the atomic fluctuations determined by NMR and x-ray crystallography (37–39). The corresponding model used in NMA is referred to as the anisotropic network model (ANM) (40). Despite the dramatic simplifications, ENM is widely applied to large macromolecules and assemblies beyond the reach of traditional methods (41–45).

However, there is a trade-off between accuracy and speed in these coarse-grained methods. Much effort has gone into comparing results from these approximate methods with the results of classical AANM, the parent method, or the results of MD simulations, as a reference (32,33,42,46). Based on the degree of similarity between the low-frequency eigenvectors of AANM and the corresponding eigenvectors of coarse-grained methods, BNM has been found to produce more accurate results than ENM (32,33,45). This is not surprising because BNM starts from an extensively energy-minimized system described by an all-atom force field and then projects the all-atom Hessian matrix to the space of predefined blocks. In the limit, this method allocates only one residue in each block, providing the highest possible resolution in the implementation of the BNM method (however, at the greatest computational cost). Such an approach is implemented in the most recent version of CHARMM. Nonetheless, even BNM results show significant deviations from the AANM approach. Moreover, no coarse-grained method is able to incorporate the contributions from explicitly treated water molecules.

Here we implemented a novel coarse-grained normal mode method (CGNM) based on a partition scheme of the all-atom Hessian matrix to extract the correlated motions in the subspace of C-α atoms. We carried out our initial analysis on the 120-amino-acid cyclic nucleotide-binding domain (CNBD) and adjacent upstream 90-amino-acid cytoplasmic C-linker region from the HCN2 hyperpolarization-activated cyclic nucleotide-regulated cation channel (47). High resolution x-ray crystallography has shown that in the presence of cyclic nucleotides, this isolated soluble protein domain forms a fourfold symmetric tetrameric assembly with one cyclic nucleotide bound in the CNBD of each of the four subunits (48).

In this study, we report that CGNM provides a more accurate description of the motions of the HCN2 CNBD, as well as that of four other proteins, compared to two other coarse-grained methods, ENM and BNM, based on the degree of similarity of the results from the three coarse-grained approaches with the results of a full AANM analysis. It is important to note that we found that CGNM also allowed us to incorporate explicitly treated surface water molecules into protein motions projected in the subspace of the relevant atoms (C-α atoms in this study). Furthermore, a comparison of our CGNM results containing a layer of surface water with MD results on the same protein in a water-filled box demonstrates the importance of incorporating such surface structural water in studying protein dynamics.

METHODS

Classical AANM and coarse-grained CGNM analyses

We used a representative snapshot from MD simulations based on the x-ray crystal structure of the HCN2 channel C-terminus protein (PDB ID 1Q5O) (48) as the starting structure for the NMA described here. Briefly, the MD simulations, which we described in detail elsewhere (49), were performed as follows. We used the GROMOS96 force field from the GROMACS package (22,50). The whole system contains four subunits and each subunit contains 8636 protein atoms, 4 cAMP molecules, 23,654 water molecules, and 12 chloride ions to balance the charge in the system. For the bound ligand, cAMP, we used the topology generated by the PRODRG server and the partial charges defined in the GROMOS96 force field (50). We used the flexible SP3 water model in the simulation (51). The distance between the protein and each side of the rectangle box was set at 10 Å. The particle mesh Ewald method (52), with a cutoff distance of 10 Å, was used for the electrostatic potential energy. Before MD simulations, we applied basic energy minimization steps (steepest descent (SD) and conjugate gradient (CG)) to optimize the starting system and remove any nonphysical contacts. During the first 500 ps of the MD simulation, the positions of the heavy atoms in the protein were fixed so that the system, especially the explicit water molecules, can be further optimized. After these steps, we carried out a normal MD simulation with a time step of 2 fs and collected the trajectory every 0.5 ps.

To carry out the normal mode calculations based on the all-atom force fields, we first performed an extensive energy minimization to ensure that the starting structure represents a local minimum on the energy surface. To achieve this, we applied SD and CG followed by the limited-memory Broyden-Fletcher-Goldfarb-Shanno method (22) at double precision numerical accuracy to the representative snapshot structure from the MD simulations obtained above. During these energy minimization steps, the electrostatic energy was described by a switch function with the distance for normal treatment set at 15 Å and the cut-off distance set at 18 Å (53).

The key step in the analysis was then to calculate the Hessian matrix for the entire system, containing the second derivatives of the potential energy functions (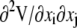). The matrix was then partitioned into four sections to extract the C-α components according to the equation

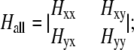(1)

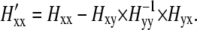(2)

Here, H_xx, H_yy, H_xy, and H_yx submatrices contain the elements representing the interactions of, respectively, relevant to relevant atoms, nonrelevant to nonrelevant atoms, relevant to nonrelevant atoms, and nonrelevant to relevant atoms. In the CGNM method, the energetic contributions of all interactions with and between nonrelevant atoms (the non-C-α atoms here) are incorporated into a simplified Hessian matrix for the relevant-atom subspace, H′_xx, using Eq. 2. The theoretical basis for deriving the C-α atom motions based on the atomic fluctuations from classical AANM was published by Berendsen and colleagues (54). A similar equation was used to extract the effective force constant matrix for C-α atoms (55) and discussed in the GROMACS discussion board (www.gromacs.org) in 2005 for the purpose of comparing AANM and MD-based PCA in the C-α subspace. Moreover, a recent study by Eom et al. (56) used a very similar method to obtain a coarse-grained approximation to ENM. After basic matrix manipulations, we found that our partitioning approach (Eqs. 1 and 2) is identical to that of Eom et al. The major difference between our study and that of Eom et al. is that we have applied a coarse-grained approximation to classical NMA based on all-atom force fields, whereas Eom et al. aimed to improve the efficiency of ENM (which they referred to as the Gaussian network model).

To sort the Hessian into relevant and nonrelevant parts, we first converted the sparsely-stored mass-weighted Hessian matrix into a double precision ASCII file. We then generated an index file in which the indices for all C-α atoms (relevant atoms) were arranged at the beginning followed by non-C-α atoms. Each entry in the sparse Hessian matrix was read into the program and allocated to a new position, using the index file as a key for sorting. The C-α component (xx part) was stored in a dense matrix format. The symmetrical xy and yx parts were stored in a coordinate format for a sparse matrix. Non-C-α components (yy) were stored in a row-major format for a sparse matrix. We used a direct solving routine from the PARDISO package (57) and standard LAPACK and BLAS routines for matrix calculations.

Based on the eigenvectors and the corresponding eigenvalues, the following equation was used to calculate the mean-square fluctuation (MSF) (Ų):

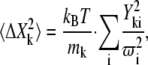(3)

where k is the atom index, i is the eigenvector index, m_k is the atom mass, and ω is vibrational frequency.

The following equation was used to calculate the configurational entropy based on the eigenvalues from ENM, CGNM, or PCA (58,59):

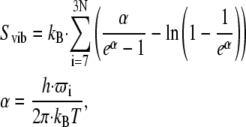(4)

where h is Planck's constant, k_B is Boltzmann's constant, and ω is the vibrational frequency.

Normal mode analysis based on elastic network model (ENM)

C-α atom coordinates from the energy minimized structures were directly used in the NMA based on the potential energy function defined by the elastic network model (ENM or anisotropic network model (ANM)) (40). For ENM, we used the default settings of the force constant (1 kcal/mol/Ų) and cutoff distance (13 Å).

Block normal mode analysis

The same all-atom Hessian matrix was projected onto a subspace of rigid blocks, each of which contained a single residue for the protein or a single cAMP molecule for the bound ligand, to pursue the highest resolution possible with this method. The degrees of freedom equal six times the number of blocks. The Fortran code of DIAGRTB (v2.52) was used in this research with a modification of the size of the array, LRWORK, from 32,000,000 to 200,000,000, so that larger systems could be accommodated (32,33).

PCA based on MD simulations

We used g_covar from GROMACS to perform PCA on a section of the MD trajectory. Overall rotational and translational motions were removed by fitting the protein structure of each time frame to a reference structure (starting frame). For the MD simulations at low temperatures, we reduced the system temperature with a simulated annealing protocol and then collected the MD trajectories after a 200-ps equilibration at the corresponding temperature. For each PCA, we used a 2-ns-long MD trajectory containing 4000 frames. The eigenvalue outputs from the PCA analysis represent the vibrational amplitude and were converted into the square of angular velocity by the equation

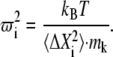(5)

The anharmonic factor for each eigenvector from PCA was calculated by the equation

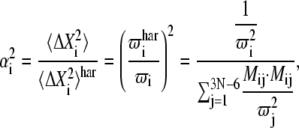(6)

where i is the index for PCA eigenvectors, j is the index for NMA eigenvectors, 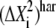is the harmonic mean-square fluctuation as described by the NMA eigenvectors, and M_ij is the dot product between the ith PCA eigenvector and jth NMA eigenvector (60).

Alignment of correlated coordinate systems

The reference structures from two eigenvector systems were first aligned to the mass center of the molecule. A rotation matrix was then calculated based on two aligned reference structures. The second set of eigenvectors was rotated by the equation

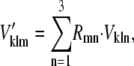(7)

where k is the eigenvector index, l is the atom index, and m and n are the indices of xyz dimension (12). The following parameters for the overlap analysis, including dot product (Eq. 8), spanning coefficient (Eq. 9) (33,46), and cumulative overlap factor (COF) (Eq. 10) (54), were calculated based on these aligned eigenvector sets.

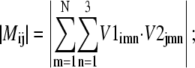(8)

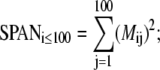(9)

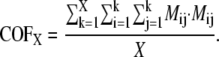(10)

Unit conversion among different simulation packages

AANM, CGNM, and BNM use the same mass-weighted Hessian matrix; therefore, the corresponding orthogonal eigenvector output should still be mass-weighted. However, the default output of eigenvectors is not mass-weighted in the GROMACS program and not strictly orthogonal. We modified the source code of GROMACS to generate mass-weighted orthogonal eigenvectors for AANM analysis. We converted the GROMACS eigenvalues (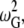 based on the mass-weighted Hessian matrix, in units of kJ/mol/nm²/amu) into the square of angular velocity (in units of s⁻²) by multiplying the Gromacs eigenvalues by the conversion factor of 10⁻²⁴, based on the relation

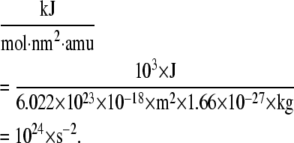(11)

The following equation was used for calculating the MSF (Ų):

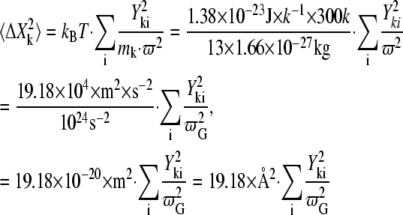(12)

where 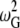is the eigenvalue of the Gromacs unit, k is the atom index, and i is the eigenvector index.

Since we compared the results of different methods in the subspace of C-α atoms, mass-weighting will not affect the eigenvector results of ENM. However, a mass factor is needed for the calculation of vibrational frequencies and atomic fluctuation amplitudes. To our knowledge, there is no standard method for converting the units to compare the ENM results directly with other calculations (e.g., AANM, BNM, etc.) without scaling. Here, we tentatively added a mass factor corresponding to the mass of C-α atom so that the angular velocity in units of s⁻¹ and MSF in units of Ų can be generated using a force constant of 1 kcal/mol/Ų. The eigenvalues were converted into the square of the angular velocity by multiplying by the factor

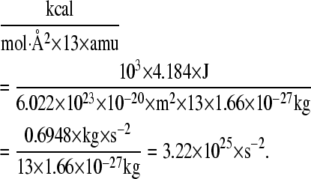(13)

The eigenvalue output from PCA analysis (default GROMACS in units of nm²; no mass weighting; C-α only) was converted into the square of angular velocity by the equation

(14)

The experimental B-factor obtained through x-ray crystallography can be directly converted to atomic fluctuation (MSF, in Ų) using the equation (61)

(15)

RESULTS

Comparison of AANM with coarse-grained ENM, BNM, and CGNM approaches

Our goal in this study was to develop a coarse-grained approximation to classical all-atom normal mode (AANM) analysis (11,12). We have implemented a novel coarse-grained normal mode analysis (CGNM) that decreases the computational cost associated with AANM by partitioning the all-atom Hessian matrix containing the second derivative of the potential energy function into relevant and nonrelevant components, here focusing on the C-α atoms (see Methods, Eq. 2). To assess the accuracy of our method, we first compared the results of AANM, the standard for these comparisons, with those of CGNM, as well as with results from two other coarse-grained approaches, ENM and BNM (32,40). As ENM and BNM treat proteins in a vacuum in the absence of water, we first compared the four methods under these dehydrated conditions. In the following section, we consider the effects on CGNM results of adding surface water.

As NMA is based on a harmonic approximation of the protein energy surface near an ideally global minimum, it first requires an extensive minimization of the potential energy of the starting protein structure. Here we used a representative structure of the HCN2 C-terminus protein obtained from a 20-ns-long MD trajectory based on the original crystal structure (48). This procedure allows the protein structure to be efficiently equilibrated in the same force field used by subsequent NMA (GROMOS96) (50), as reasonably long MD simulations should optimize the loop conformations and allow for small-scale rearrangement of secondary structures (62,63).

We first removed all water molecules from the representative MD snapshot structure. After an extensive minimization of the system, the final structure containing only the protein and cAMP atoms was used to generate the all-atom Hessian matrix, which was then iteratively diagonalized to produce the AANM result, providing the reference for comparison with the coarse-grained methods. Due to the limitation of computational resources, only a small fraction of the total eigenvectors and corresponding eigenvalues were calculated (2000, or 8% of 26,232). All technical details are given in Methods and Table 1. Briefly, ENM starts from the C-α atom coordinates and generates a complete set of orthogonal eigenvectors. BNM and CGNM methods started from the same all-atom Hessian matrix used by AANM. Whereas BNM simplifies the calculation through projecting the all-atom Hessian matrix into predefined rigid blocks, CGNM relies on a matrix-partitioning scheme to integrate the energetic contributions from non-C-α atoms into the motions of C-α atoms. Since the eigenvector outputs of BNM are in the all-atom space, they were projected to the C-α atom subspace for comparison purposes. This was followed by a normalization step that makes each eigenvector unitary (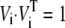) but not strictly orthogonal (V_i · V_j = 0, i ≠ j). The eigenvector outputs of CGNM are naturally orthogonal in the C-α subspace and thus were directly used in the overlap analysis.

TABLE 1.

Comparison of parameters used in different NMA approaches

	AANM	ENM	BNM	CGNM
Residues	804	804	804	804
Atoms	8636	804	8636	8636
Starting Hessian matrix size	25,9082	24122	25,9082	25,9082
Working Hessian matrix size	25,9082	24122	48242	24122
Practical/theoretical eigenvector set	2000/25,908	2412/2412	4824/4824	2412/2412
Eigenvector dimension	25,908	2412	25,908	2412
C-α only component extraction	Yes	No	Yes	No
Orthogonality of C-α component	No, but normalized	Yes	No, but normalized	Yes
CPU time (3.4 Ghz Xeon, sequential implementation)	∼67 h	∼1 h	∼5 h	∼7 h
Peak physical memory (Mbyte)	∼1577	44	∼1400	∼1900

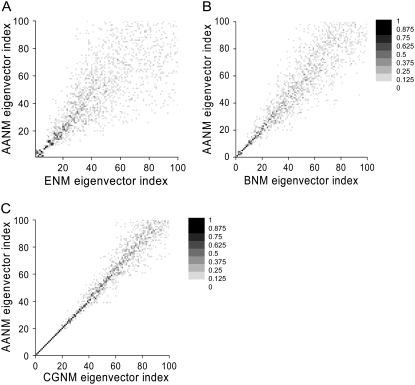
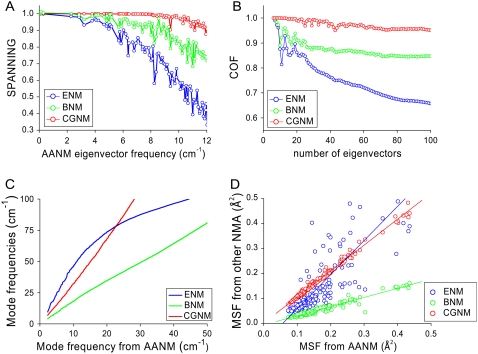
The results of ENM, BNM, and CGNM were compared to the results of AANM in terms of the overlap of the resulting eigenvectors, representing the direction of correlated motion, and eigenvalues, representing the amplitude or the frequency of each motion. Three different methods were used to check the overlap between the eigenvectors from AANM versus a given coarse-grained method. First, a direct view of overlap was obtained from a plot of the inner product between each pair of eigenvectors (Eq. 8). Such plots confirm previous studies that BNM generates results closer to those of AANM than does ENM; this is shown by the tighter clustering of points near the ideal diagonal relationship for the BNM versus AANM plot (33,46) (Fig. 1, A and B). It is important to note that CGNM provides an even better match (tighter diagonal clustering) with the AANM results than does BNM (Fig. 1 C). Second, we quantified the overlap between two sets of eigenvectors using the spanning coefficient (Eq. 9), representing the overlap between each AANM eigenvector with a group of eigenvectors from each coarse-grained analysis (33,45,54). The nearly straight line of the spanning coefficient curve of CGNM up to a frequency of 10 cm⁻¹ indicated that the 70 or so lowest-frequency AANM eigenvectors can be almost completely mapped by the first 100 eigenvectors of CGNM (Fig. 2 A). However, this close mapping only extends as far as the first ∼10 or ∼15 AANM eigenvectors for ENM or BNM, respectively (Fig. 2 A).

FIGURE 1.

Grayscale plot showing the absolute value of the dot product between each pair of eigenvectors. (A) Gray scale plot showing the absolute value of the dot product between the eigenvectors from ENM analyses (x axis) versus AANM analyses (y axis). The quality of correspondence between eigenvectors is indicated by the darkness of the symbol and its proximity to the diagonal. (B) Results for BNM (x) versus AANM (y). (C) Results for CGNM (x) versus AANM (y).

FIGURE 2.

Quantification of the similarity of results between AANM and three coarse-grained NMA methods. (A) Spanning coefficients for each eigenvector of AANM analysis were calculated based on the first 100 eigenvectors of ENM (blue), BNM (green), and CGNM (red). The index for AANM eigenvector was converted to vibrational frequency. (B) COF of eigenvectors from AANM versus coarse-grained methods. (C) Cross plots of eigenvalues from coarse-grained versus AANM results. (D) Cross plot of MSF values from coarse-grained versus AANM results for each C-α atom. The linear equation Y = A + B × X was used to fit comparisons between different methods. CGNM: B = 1.04, R = 0.996; BNM: B = 0.37, R = 0.969; and ENM: B = 1.36, R = 0.838, where R is the correlation coefficient.

A potential bias of using spanning coefficients is that an arbitrary number (100 here) of eigenvectors needs to be predefined, because the spanning coefficient involving all eigenvectors is theoretically equal to 1. This makes the spanning coefficient less meaningful when comparing systems of different dimensions of freedom. To circumvent this difficulty, we calculated COF, a factor for the overlap between two pools of eigenvectors as a function of pool size (54) (Eq. 10, Fig. 2 B). Consistent with the other methods of comparison, the COF results show that CGNM significantly outperforms the other two methods: the space represented by the first 100 eigenvectors from AANM overlaps 95% of that of CGNM versus 85% of BNM and only 65% of ENM.

Based on the results shown above, it is clear that the CGNM method generates a more accurate set of eigenvectors than does BNM or ENM. Next, we checked the accuracy of different coarse-grained methods through calculating the atomic fluctuations based on the eigenvalues and eigenvectors of the Hessian matrices, still using the results from AANM as a reference. MSF or root mean-square fluctuation (RMSF) was used to provide a direct measure of the atomic vibrational amplitude. Both MSF and RMSF values can be used to compare computational results with experimental measures of motion, such as B-factors (see Methods, Eq.15).

To gain insight into atomic fluctuations we first plotted the eigenvalues from individual coarse-grained methods against the corresponding values from AANM (Fig. 2 C). Over a large range of eigenvalues, there is a nearly linear relationship between the results of AANM and those of CGNM or BNM, suggesting a close relationship. In contrast, such ENM results did not show a close agreement with those of AANM. Next, we used the eigenvalues and the eigenvectors of the vibrational modes to calculate the atomic fluctuations for each atom (Eq. 3) (Fig. 2 D). As predicted from the eigenvalues, the ENM fluctuation results (blue circles) deviate significantly from the other results. Both the CGNM (red circles) and BNM results (green circles) are in good agreement with the results from AANM on a residue-by-residue basis. Based on the correlation coefficient R values, the CGNM results (0.996) show a slightly better agreement with AANM compared to BNM (0.969). In contrast, both CGNM and BNM correlations are significantly better than that of ENM (0.838). To exclude possible errors introduced by the extraction of C-α components and the normalization step associated with AANM and BNM, we performed independent calculations using the original all-atom eigenvectors, which yielded identical results (Supplementary Material, Fig. S1).

NMA results incorporating a layer of explicit water on the protein surface

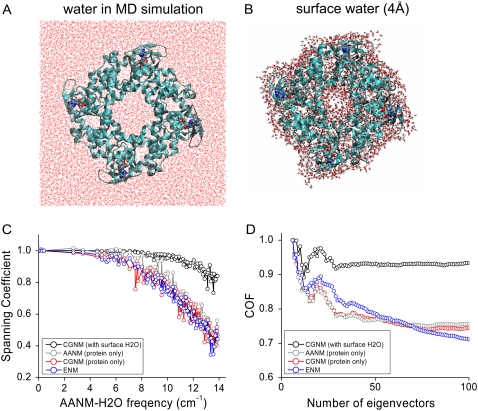
Next, we expanded CGNM to incorporate the effect of explicitly treated surface water molecules on protein dynamics, an area that to date has not been addressed by other coarse-grained normal mode methods and is computationally expensive for classical AANM. Previous experimental studies showed that the thickness of the surface structural water layer ranged from 3 Å for lysozyme, determined by x-ray and neutron scattering (64,65), to 5 Å for lactose, determined by terahertz spectroscopy (66). Here, we treated the case of a 4-Å-thick layer of explicit water on the protein surface, a compromise that enables the calculations to stay within the limits of currently available computational resources (Fig. 3, A and B). The all-atom Hessian matrix used in the CGNM calculations incorporated the interactions among all protein atoms, cAMP ligands, and explicitly treated water molecules. The corresponding hydration level is 0.56 (water mass/protein mass) and the system is of significant size (8636 protein atoms, 108 cAMP atoms, and 8817 water atoms). As a result, we could solve for <0.5% (250) of a total of over 52,683 AANM eigenvectors and eigenvalues using local computational resources. The BNM method could not be tested under these conditions because it does not currently include a method for allocating surface water molecules to specific blocks.

FIGURE 3.

Spanning coefficient and cumulative overlap factor curves for different NMA methods with and without surface water molecules. (A) In the MD simulation system, the tetrameric HCN2 CNBD/C-linker domain was put in the center of a box containing explicitly treated water (n = 23,658; red lines). (B) Energy-minimized structure of protein with a surface layer of explicitly treated water molecules (n = 2939). (C) Spanning coefficient for each AANM (with water) eigenvector was calculated using the first 100 eigenvectors of CGNM with water (black), AANM without water (gray), CGNM (protein only, red), and ENM (protein only, blue). (D) COF curves showing the overlap between two pools of eigenvectors as a function of the number of eigenvectors involved.

Inclusion of surface water led to a significant difference in AANM results compared to those obtained using AANM in the absence of water (Fig. 3, C and D). It was not surprising that AANM results with water also diverged from those obtained with CGNM or ENM in the absence of water. We were impressed that CGNM results in the presence of surface water showed a good agreement with those obtained using AANM in the presence of surface water, with an increased overlap of eigenvectors indicated by a twofold increase in spanning coefficients (∼80%) compared to values obtained with the other methods in the absence of water (∼40% (Fig. 3 C)). Improvement was also observed in the larger COF values with CGNM (∼93%) versus those with the other methods (∼75% using the first 100 eigenvectors (Fig. 3 D)).

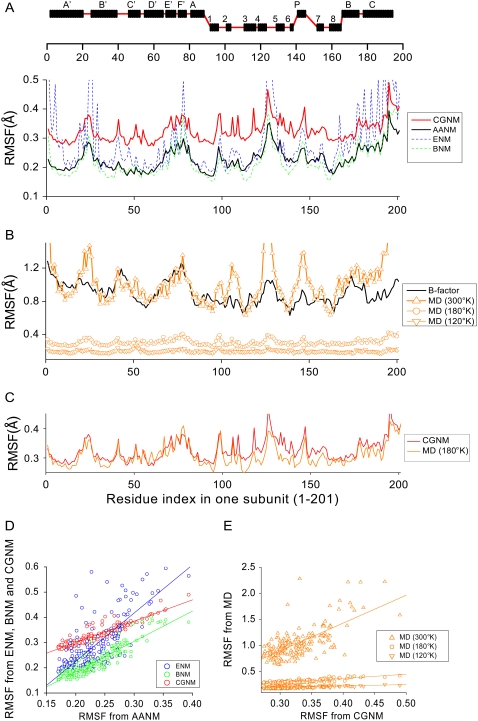
Using AANM with surface water results as a standard, we next checked the accuracy of the RMSF values for each C-α atom using ENM, BNM, or CGNM (Fig. 4). CGNM with water (red curve) faithfully reproduced the pattern of the corresponding AANM results (black curve, Fig. 4 A). The shift in absolute amplitude is due to the different number of eigenvectors used (2406, or 99.7%, for CGNM; 244 modes, or 0.5%, for AANM). The striking similarity is reflected in the high R-factor of the CGNM data versus the AANM data (0.925 (Fig. 4 D, left)), which is much greater than that for ENM (0.780) and slightly greater than BNM (0.915, limited to calculations without water).

FIGURE 4.

Comparison of RMSF values from various NMA approaches, MD simulations, and values converted from crystallographic B-factors. (A, top) Secondary structure along the primary sequence of a single subunit. (A, bottom) Comparison of RMSF values based on the first 244 of 52,683 eigenvectors from AANM with surface water (black line) with RMSF values based on the complete set of eigenvectors (2406) from CGNM with surface water (red line). The RMSF values for ENM (blue) and BNM (green) are also shown for comparison purposes. (B) Comparison of RMSF values converted from crystallographic B-factors (black line) with values determined from MD trajectories (orange) collected at 300 K (triangles), 180 K (circles), and 120 K (inverted triangles). (C) RMSF values from CGNM with water (red) are in good agreement with those from MD simulations at 180 K (orange). (D) Cross plots of RMSF results based on AANM with surface water versus RMSF results from ENM (blue), BNM (green), and CGNM (red). Results were fit with the linear equation Y = A + B × X, where R is the correlation coefficient: ENM: B = 1.91, R = 0.780; BNM: B = 1.20, R = 0.915; CGNM: B = 0.84, R = 0.925. (E) Cross plots of RMSF results based on CGNM with surface water and RMSF results based on MD simulations at different temperatures. Linear least-squares fit results: 300 K: B = 5.33, R = 0.70; 180 K: B = 0.82, R = 0.85; 120 K: B = 0.30, R = 0.69).

The effect of solvent molecules on protein dynamics is an important issue that has been addressed by experimental and computational approaches. Previous studies using AANM revealed that inclusion of surface water dampened the amplitude of atomic fluctuations (16,67). We found a similar effect of surface water using CGNM, in which the average fluctuations of C-α atoms with surface water (0.11 Ų) is significantly smaller than that of protein alone (0.16 Ų), providing further support for the ability of CGNM to incorporate surface water in protein dynamics.

Are the CGNM results with a 4-Å layer of surface water molecules comparable to results based on MD simulations, in which the protein is fully embedded in a 102 × 102 × 81 ų box filled with both surface and bulk water (Fig. 3 A)? MD simulations of the protein at 300 K did a reasonably good job of reproducing the absolute amplitude and overall pattern of RMSF values from x-ray crystallographic B-factors (Fig. 4 B). However, the RMSF values from MD simulations at 300 K are approximately three times larger than the CGNM results (Fig. 4 A). Moreover, the R factor between MD results and CGNM results with surface water is only 0.70 (Fig. 4 E). This deviation is likely caused by the contribution of random, diffusive motions that are included in the MD simulations but are ignored by the harmonic treatment of motions in all NMA approaches.

Since diffusive motions are greater at higher temperatures, we examined the ability of NMA to more accurately correspond to MD simulation results at lower temperatures. We first collected MD trajectories at 120 K and 180 K, respectively. The RMSF based on the MD simulation at 120 K was much smaller than that at 300 K; however, the convergence with CGNM results was not improved (0.69) (Fig. 4 B). Interestingly, the agreement between CGNM and MD simulation results at 180 K was much improved, in terms of both the absolute value of fluctuations and overall pattern, with the R-factor increased to 0.85 with a slope factor of 0.82 (Fig. 4 C). These results indicate that at certain low temperatures (180 K), the atomic fluctuations can be largely accounted for by harmonic motions involving the protein plus surface water but do not necessarily involve the bulk solvent that is also present in the MD simulations.

Comparing MD simulations with CGNM, with and without water, at different temperatures

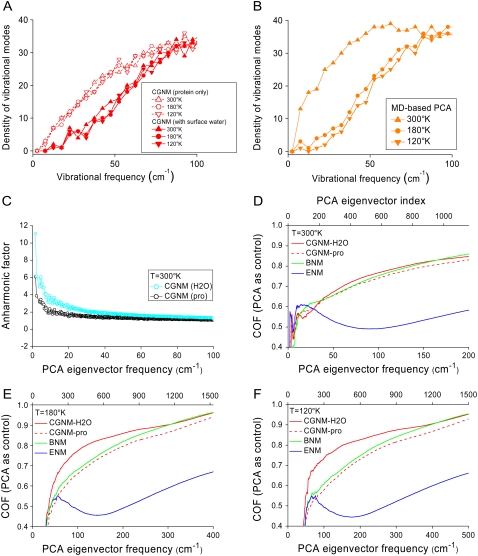
To further examine the effect of surface water on protein dynamics, the distribution of vibrational-mode frequencies was plotted for both CGNM and MD simulations at the three different temperatures. Previous studies have shown that explicit water has a complex influence on protein dynamics, including temperature-dependent frictional dampening and temperature-independent shifting of the vibrational modes to higher frequencies (68–70). However, it is not clear whether these effects are due to an interaction of the protein with surface structural water versus an interaction that also requires the presence of bulk solvent (71). Here, using CGNM, we find that surface water alone is sufficient to shift fluctuations to higher frequencies (Fig. 5 A), an effect that is observed at all three temperatures, thus confirming its temperature-independent character. It is most likely that this effect represents a static interaction of a cagelike structure formed by the interaction of surface water with exposed residues on the protein surface (65).

FIGURE 5.

Effects of solvent on protein dynamics determined by CGNM and MD approaches. (A) Distributions of the vibrational mode densities for CGNM without water (open symbols) and CGNM with water (solid symbols) at three temperatures, 300 K (triangles), 180 K (open circles), and 120 K (inverted triangles). (B) Distributions of the vibrational mode densities for MD simulations at 300 K (triangles), 180 K (circles), and 120 K (inverted triangles). All plots are shown in brown to be consistent with Fig. 4. (C) Anharmonic factor for the PCA modes from MD simulations at 300 K based on harmonic CGNM modes without (black) or with (blue) surface water. (D) COF curves showing the overlap between the eigenvectors from MD simulations at 300 K and CGNM with water (red solid line), CGNM without water (red dashed line), BNM (green), or ENM (blue). (E) COF results showing the overlap between MD results and CGNM, BNM, and ENM results at 180 K. (F) COF results showing the overlap between MD results and CGNM, BNM, and ENM results at 120 K.

To isolate the potential influence of the anharmonic, diffusive protein motions captured by MD simulations but not by CGNM, we compared the frequency distributions of vibrational modes between CGNM with 4 Å surface water and the MD simulations with bulk solvent (∼10 Å from protein surface plus periodic boundary condition). The distribution of vibrational modes from MD simulations at low temperatures (180 K and 120 K) was quite similar to those from CGNM with water (Fig. 5 B). However, MD simulations, but not CGNM, revealed a significant shift to lower frequencies upon raising the temperature to 300 K. This is in good agreement with previous studies suggesting that the shift to low frequencies is related to the anharmonic nature of protein dynamics (Fig. 5 C) and that the contributions from bulk solvent are more prominent at high temperatures (300 K) and for low-frequency modes (69,70).

As a final test of the various NMA approaches, we compared the orthogonal sets of eigenvectors in the subspace of C-α atoms derived from the three coarse-grained methods (ENM, BNM, and CGNM) versus the eigenvectors based on PCA of MD simulation trajectories (Fig. 5 D). At 300 K, the COF curves show a poor overlap between the eigenvectors at frequencies <25 cm⁻¹ from the MD simulations versus those obtained from all three NMA methods. At increasing frequencies, there is a gradual increase in the overlap of the NMA results with the PCA modes, consistent with the idea that frequencies >40–50 cm⁻¹ correspond to more “harmonic” protein vibrations (60).

Does the use of CGNM with a layer of water molecules on the protein surface make any significant difference in the overlap of eigenvectors with MD simulations? Careful examination of the COF curve suggests that indeed the results from CGNM with water are slightly but consistently better than the CGNM results without water at 300°K. An even greater improvement in overlap with the MD simulations was observed when using CGNM with water at lower temperatures (180 K (Fig. 5 E) and 120 K (Fig. 5 F)). The increased overlap between CGNM with surface water and the MD simulations at the two lower temperatures (but especially at 120 K) suggests not only that CGNM is able to incorporate, at least partially, the contributions from explicit surface water, but also that surface water makes a significant contribution to protein vibrational modes with frequencies >50 cm⁻¹.

DISCUSSION

In this article, we implemented a matrix-partitioning scheme to extract the C-α components from the all-atom Hessian matrix, thus providing a novel coarse-grained NMA approach, which we termed CGNM. This method generated more accurate results than did other coarse-grained NMA methods, including ENM and BNM, based on a comparison with results obtained using classical AANM. However, CGNM retained the benefits of a great reduction in computational cost with the two other coarse-grained approaches. The flexibility in partitioning the all-atom Hessian matrix into relevant versus nonrelevant groups makes it straightforward to scale the scope of analysis, for example, from C-α atoms only to inclusion of all backbone atoms, depending on the size of the system and the available computational resources. In this manner, we were able to model the contributions from explicitly treated surface water to protein motion, which is beyond the reach of other coarse-grained NMA methods. Thus, the CGNM method represents a novel coarse-grained NMA approach that can be used to obtain more accurate results for systems of significant size.

Multiple lines of evidence indicate that CGNM produces more accurate results than ENM or BNM, using AANM results as a reference. Overlap plots and spanning coefficients clearly show that CGNM outperformed the other coarse-grained methods for the first 100 or so individual eigenvectors, which are of great functional significance because they represent the directions of protein conformational changes with highest amplitude, slowest frequency, and least energetic cost. COF, which has the advantage of representing the overlap of two groups of eigenvectors, confirmed that CGNM more closely reproduces classical AANM results than do ENM or BNM methods. We also confirmed that CGNM outperforms ENM or BNM on dozens of other proteins, with a range in size from 200 to 1300 amino acids (results of four other sample proteins are shown in Figs. S2 and S3).

A comparison of eigenvalues and related atomic fluctuations among different NMA methods also revealed differences among the three coarse-grained methods. ENM generated a surprisingly good match to the AANM results given the dramatic simplifications in its potential energy functions. However, the results from BNM and CGNM were in much better agreement with the AANM results compared to ENM, indicating that the detailed chemical information embedded in the all-atom Hessian matrix used for AANM, BNM, and CGNM makes an important contribution. These results are in good agreement with a recent comprehensive comparison among NMA approaches of different complexity (41). Moreover, CGNM performed slightly better than BNM, as shown by the correlation coefficient (R) between their MSF values and the values obtained by AANM.

Why does CGNM yield more accurate results than BNM, even though both methods are derived from the same all-atom Hessian matrix? BNM is rooted in the rotation-translation block model, which projects the all-atom Hessian matrix into a subspace of rigid blocks. Even though BNM fully takes into account the coupled motions between different blocks, the method ignores the small high-frequency vibrations related to the intrinsic flexibility within each block (72). Moreover, during analysis, the intermediate BNM results in the subspace of rigid blocks must be projected first back onto the space for all atoms and then onto the subspace of C-α atoms. However, the center of mass for each block is different from the position of the C-α atoms and varies among different amino acid residues. In contrast, CGNM is based on partitioning the all-atom Hessian matrix through a simple but theoretically rigorous scheme, which is then used to derive the motions for the C-α atoms (55). The fact that CGNM implicitly incorporates energetic contributions from non-C-α atoms into C-α atoms may contribute to the greater accuracy of this method.

A key advantage of CGNM is its ability to incorporate the detailed chemical information imbedded in the protein structure, including explicitly treated structural water molecules on the protein surface. For most MD applications, it has been relatively standard to treat solvent molecules explicitly, which is required to reproduce the electrical and dynamic properties of solvents (70,73–76). Indeed, experimental and theoretical studies have found that the surface water molecules within a radial distance of 3–5 Å from the protein surface have very different physical-chemical properties from those in bulk solvent and play important roles in modulating protein motions. For example, the experimental observation that the density of the first hydration shell is ∼5% higher than that of bulk water has been successfully reproduced by MD simulations (65,77,78). Ideally, classical AANM should be performed on the same protein-water system used in MD simulations. However, the size of the system limits the AANM method so that bulk solvent and surface water must often be omitted for proteins of significant size. Here, we applied CGNM to systems containing a layer of explicitly treated water molecules and found that it not only reproduced results based on classical AANM with explicit surface water, but also helped delineate some features of complex solvent effects.

The choice of a surface water layer of 4 Å in this study represents a balance that places a modest demand on computational resources but is consistent with experimental observations on protein surface water thickness, ranging from 3 Å for lysozyme (64,65) to 5 Å for lactose (66). We found that CGNM, which is based on a harmonic approximation to the energy surface, in the presence of surface water is able to reproduce MD results for atomic fluctuations of a fully solvated protein at 180 K. Interestingly, this temperature (180 K) is near the glass-transition point where diffusion starts to contribute significantly more to protein dynamics than does harmonic vibration (17,71,79–81). Moreover, spectroscopic experiments on bovine serum albumin showed that there is a significant dynamic change (glass transition) at around 170 K to 180 K, which might be due to formation of a rigid structure formed by water molecules covering the protein surface (79,82). These results corroborate this study, in which only the surface water is treated explicitly.

However, it is noticeable that even though CGNM results with water show an improved match with the atomic fluctuations from MD simulations compared to CGNM results on the dehydrated protein, the results from CGNM differ in important respects from those obtained using MD simulations or from experimentally determined crystallographic B-factors. This might be due to the complex nature of the protein energy surface and complex interactions between protein and solvent. The good agreement between the B-factors and the MD results at 300 K confirms the advantages of MD, a method that does not involve a harmonic approximation of the protein energy surface and explicitly treats all water molecules (Fig. 4 B).

The CGNM results are successful in reproducing previous observations that solvation increases protein vibrational frequencies and point to the role of surface water in this phenomenon (24,69,83). Moreover, these effects are likely to reflect temperature-independent interactions in which surface water molecules serve to fill in protein surface irregularities and stabilize polar side chains, forming a cagelike structure around the protein surface (83). In contrast, a comparison of CGNM with surface water to MD simulations including bulk water indicate that bulk water molecules behave more like free water, acting to decrease the vibrational frequency of protein dynamics in a temperature-dependent manner (70). A recent experimental study of the influence of hydration on protein dynamics gives direct support to our results. Quasielastic neutron and light-scattering experiments show that adding an initial hydration layer (h ≈ 0.2) increases the fast vibrational modes. Interestingly, further increasing the hydration level (h > 0.2) significantly activates slower processes (78). Therefore, these experimental observations are in good agreement with our simulation results showing the different contributions of solvent molecules to protein dynamics (70,84,85).

The poor overlap in the eigenvectors from various NMA approaches (no water or surface water only) with the MD simulation results (surface water and bulk water), especially for the low-frequency modes (25 cm⁻¹), is not surprising. A previous study using a jump-among-minima model, which divides protein motions into intra-substate motions and inter-substate jumps based on a multiple local minima model of the energy surface, generated a much better overlap with MD results than does NMA (86). Moreover, a mixture of harmonic NMA plus diffusive Brownian dynamics has been proven to be effective in reproducing the results of MD simulations and experimental observations (55,87). These studies suggest that the harmonic approximation of the protein energy surface and the neglect of solvent limits the ability of NMA approaches, including AANM, BNM, and CGNM, to reproduce the directionality of intrinsic anharmonic protein dynamics in the native state (54,84). However, for modes beyond 25 cm⁻¹, there is a gradual increase in the fidelity of CGNM and BNM, especially for CGNM with a layer of surface water. It is interesting that this frequency region is the same spectrum covered by terahertz absorption spectroscopy (1 THz = 33 cm⁻¹), where experimental results showed that solvation tends to enhance protein dynamics (88–90). Therefore, CGNM provides a convenient tool for modeling the contributions of surface water into protein dynamics at these higher frequencies. In principle, CGNM could be expanded to incorporate the effect of bulk solvent molecules in conjunction with other methods, such as the Langevin Model (71).

Thus far, the results presented for the HCN2 CNBD are for the cyclic-nucleotide bound state of the protein. However, we obtained similar results for the unliganded protein, using a representative snapshot from a 20-ns-long MD simulation with cAMP removed as the starting structure (Fig. S4–S6). One theoretical application of a complete set of eigenvectors and eigenvalues from NMA is the estimation of the configurational entropy (58,59). Taking advantage of the CGNM results for the unliganded protein versus the cAMP-bound protein in the subspace of C-α atoms, we estimated the entropy change of C-α atoms upon cAMP binding to be −127.8 J/mol without water or −174.3 J/mol with surface water (Table 2). Both values should be smaller than the estimate involving all atoms. However, the direction of the changes from the two independent calculations is consistent with previous MD results and the concept that ligand binding for hydrophilic or charged ligands (cAMP carries a negative charge) usually involves a reduction in the configurational entropy of the protein (91–93). Further improvements of the computational routine will focus on reducing the memory cost and use of more efficient routines for sparse matrix manipulation. With advances in computational algorithms, more memory-efficient and high-performance (sequential or parallel) routines could further improve this method and thus widen its application to more complex systems.

TABLE 2.

Configurational entropy of C-α atoms based on NMA and PCA (300 K)

	Unliganded protein (8.31 J/mol/K)	cAMP-bound protein (8.31 J/mol/K)	Difference (8.31 J/mol/K)
ENM-protein	4103.92	4126.26	22.34
ENM-water	4154.64	4156.63	1.99
CGNM-protein	2555.63	2540.23	−15.40
CGNM-water	2390.10	2369.13	−20.97
PCA (10 ns)	3051.79	2957.70	−97.09
PCA (4 ns)	2756.74	2680.41	−76.33

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.