Abstract
The mechanosensitive channel of large conductance (MscL) belongs to a family of transmembrane channel proteins in bacteria and functions as a safety valve that relieves the turgor pressure produced by osmotic downshock. MscL gating can be triggered solely by stretching of the membrane. This work reports an effort to understand this mechanotransduction by means of molecular dynamics (MD) simulation on the MscL of mycobacterium tuberculosis embedded in a palmitoyloleoylphosphatidylethanolamine membrane. Equilibrium MD under zero membrane tension produced a more compact protein structure, as measured by its radii of gyration, compared to the crystal structure, in agreement with previous experimental findings. Even under a large applied tension up to 1000 dyn/cm, the MscL lateral dimension largely remained unchanged after up to 20 ns of simulation. A nonequilibrium MD simulation of 3% membrane expansion showed a significant increase in membrane rigidity upon MscL inclusion, which can contribute to efficient mechanotransduction. Direct observation of channel opening was possible only when an explicit lateral bias force was applied to each of the five subunits of MscL in the radially outward direction. Using this force, open structures with a large pore of radius 10 Å could be obtained. The channel opening takes place in a stepwise manner and concurrently with the water chain formation across the channel, which occurs without direct involvement of protein hydrophilic residues. The N-terminal S1 helices stabilize the open structure, and the membrane asymmetry (different lipid density on the two leaflets of membrane) promotes channel opening.
INTRODUCTION
Mechanical stimuli generated in cellular environments are converted by a class of membrane proteins, known as mechanosensitive (MS) channels, into a variety of electrical or chemical signals. This provides a basic mechanism of, e.g., hearing, touch, and osmotic regulation (1–3). The mechanosensitive channel of large conductance (MscL), found in bacteria, detects and responds to forces from the lipid bilayer membranes and forms a large nonselective channel (diameter 30–40 Å) for osmolites across the membrane (4), relieving the acute turgor pressure generated by osmotic downshock. MscL has been reconstituted in liposomes and shown to be activated directly by membrane tension (5). Because of its large unitary conductance (∼3 nS) and relative ease of manipulation, bacterial MscL has been studied extensively and serves as a representative model system to understand mechanotransduction and, more generally, the relation between the lipid-protein interaction and the membrane protein function (6).
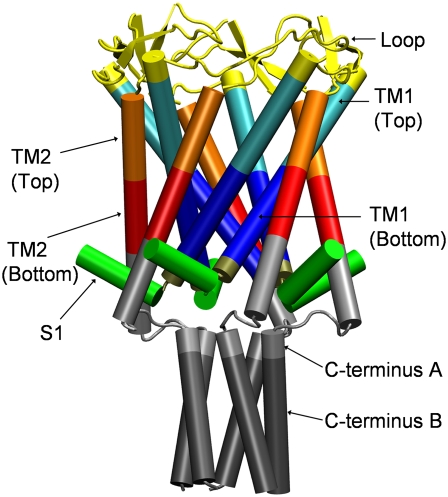
MscL from Escherichia coli (Eco-MscL) is the best characterized MS channel, with 136 amino acids in each of five identical subunits. Although the crystal structure of Eco-MscL has not been resolved, the solved structure of its homolog from Mycobacterium tuberculosis (Tb-MscL) (7,8) shows a pentameric assembly of subunits with two transmembrane (TM) domains near its closed state (Fig. 1). The Tb-MscL subunit has both its N- and C-termini in the cytoplasmic side and traverses the membrane twice in the form of TM1 and TM2 α-helices with a periplasmic loop region in between, and ends as a third helical domain (S3) inside the cytoplasm. From the N-terminus, the structural components are arranged in the order S1-TM1-Loop-TM2-S3. According to the recent crystal structure 2OAR (8), the N-terminal S1 helices stem from TM1 near the bottom of the transmembrane region and point outward between TM2 helices of two other monomeric units of MscL. The pore is lined with five TM1 helices and constricted near the cytoplasmic side by the Ile14 and Val21 residues of the TM1 domain, and has a diameter of ∼3 Å. Despite their close sequence homology, Eco-MscL gates at a significantly lower tension (∼12 dyn/cm) (9) than Tb-MscL (>20 dyn/cm) (10). These tension values are near or beyond the lytic limit of many phospholipid bilayer membranes (11).
FIGURE 1.
Structure of MscL in the crystalline state. The crystal structure (PDB code 2OAR) is shown with structural components rendered in different colors. All components shown were included in the full MscL simulations, whereas C-terminus B was excised in truncated MscL simulations. The components, with their residues, were: the whole protein (Met1–Asn125), S1 (Met1–Arg11), TM1 top (Leu30–Ile43), TM1 bottom (Val15–Ala29), TM2 top (Leu69–Phe79), TM2 bottom (Phe80–Leu89), the loop region (Asn44–Asp68), C-terminus A (Val90–Asp108), and C-terminus B (Thr109–Asn125). Note that the definition of TM2 (bottom) does not include some residues of the helix to make it consistent with the old 1MSL analysis where TM2 helix is much shorter. The image was prepared with the software package VMD (57).
Based on experiments on the spin-labeled (12,13) and cysteine-substituted (14,15) Eco-MscL and computer modeling, the open state was suggested to have some 45–70° tilts in the TM1 and TM2 helices relative to the pore axis, the pore still being lined with TM1 helices, and the membrane-normal-projected length of TM2 reduced from 35 to 25 Å. Thus, the identity and composition of the lipids influences the gating behavior of MscL as a result of the hydrophobic mismatch and modified lateral pressure profile (16,17). In particular, the asymmetric incorporation of lysophosphatidylcholine (LPC) into either leaflet of the bilayer membrane has induced a spontaneous opening of Eco-MscL (12,13), indicating the crucial effect of asymmetric lateral pressure distribution on gating. On the other hand, reduction of the lipid chain length from 18 to 16 or 14 carbons did induce protein structural changes, but this state was still nonconducting (12,13). Between the closed and open states, several states with intermediate conductance have also been identified (9) whose transition to the fully open state is largely tension-independent. The gating of MscL is generally believed to progress in a smooth irislike fashion (15). However, the importance of asymmetric movements of the five subunits in MscL gating has also been noted (18).
There have been numerous efforts to understand mechanotransduction using theoretical modeling and atomistic simulations. Early molecular dynamics (MD) simulation studies employing the crystal structure of Tb-MscL (7) explored the equilibrium structure in the membrane environment (19,20), the behavior of gain-of-function mutants (20), and limited channel gating under tension or external force (19,21). Kong et al. (22) applied targeted MD on model structures of Eco-MscL (23). Elmore and Dougherty looked at the effects of lipid headgroup identity and lipid chain length (24) on the equilibrium behavior of Tb-MscL. Using a similar atomistic model of Tb-MscL in explicit membrane, Colombo et al. (25) observed a deformation and partial opening of the protein under a large negative lateral pressure corresponding to a tension of 500 dyn/cm. Gullingsrud and Schulten (26) studied the gating of a homology model of Eco-MscL with and without membrane by applying steering forces on a few specific residues and noted the largest effect when residues on the cytoplasmic side were pulled. Meyer et al. (27) observed a restructuring of the loop region of Eco-MscL placed in a curved membrane. The effect of electric field has also been studied on the mechanosensitive small-conductance (MscS) channel (28). The equilibrium MD studies and a normal-mode analysis (29) generally indicate the smallest fluctuations near the channel constriction region. However, among the TM2 helices, the cytoplasmic side exhibits larger amplitude of the slow modes than the periplasmic end (29). At the continuum mechanics level (30–32), the MscL-protein interaction has been usually formulated in terms of three major components: 1), the membrane lateral tension coupled to the in-plane area of MscL; 2), the bending mode of the membrane coupled to the shape change of the protein; and 3), the hydrophobic mismatch, that is, the thickness of membrane coupled to the height of the protein. This approach provides a theoretical framework with which experimental or simulation results can be interpreted, although it usually omits the hydration effect, and the relative contribution of energetic components is difficult to quantify due to insufficient information on the material properties of the relevant system. Recently, an intermediate approach was reported (33) that employs finite element models of the MscL membrane system with parameters gleaned from atomistic simulations.
In this article, MD simulation methods are applied to the problem of MscL mechanotransduction with a focus on the effect of the membrane under several different physical conditions. Three different methods are applied to the atomistic models of Tb-MscL embedded in a palmitoyloleoylphosphatidylethanolamine (POPE) bilayer membrane. First, the MscL structural changes in equilibrium with and without lateral tension are studied by equilibrium MD under different lateral pressures. The effect of membrane asymmetry on the structure is also investigated by employing membranes with different numbers of lipid molecules in the upper and lower leaflets of the bilayer. Second, the modification of the in-plane elastic properties of the membrane due to the presence of MscL is investigated by nonequilibrium MD (NEMD) simulation of the membrane area expansion (34). Third, large-scale structural changes during gating are directly monitored by applying a radially outward bias force to MscL with applied tension, and in both symmetric and asymmetric membranes. This approach is distinguished from existing studies of a similar nature (22,26) in that 1), the applied force is uniformly distributed to all atoms of each subunit in a mass-weighted way; and 2), the incremental effects of membrane configuration are investigated as well. Although a uniform bias force does not reflect the membrane pressure profile or specific lipid-protein interaction, it is the simplest possible protocol and can reveal which parts of MscL are expanded easily and which parts resist opening. This provides an insight into MscL expansion that is complementary to steered MD studies (26) where only a small number of atoms are pulled. The effect of membrane is partly accounted for in the radial bias force simulations because the membrane always interacts with the MscL during force application and modulates its response.
The results presented here suggest a close interplay between the membrane physical state and MscL opening. For example, the membrane elasticity is enhanced by MscL and, in turn, the partial opening and wetting of MscL is facilitated by asymmetric configurations of the membrane where one leaflet is denser than the other one. Thus, the asymmetric lateral pressure profile is shown to be an important factor in MscL gating, consistent with a similar effect from LPC incorporated in the upper leaflet of the otherwise symmetric membrane (12,13). In addition, during an equilibrium MD simulation under zero and negative lateral pressures (0 to −1000 bar), MscL contracted to a conformation with a smaller radius of gyration about the membrane normal axis, confirming a previous experimental finding that the crystal structure of Tb-MscL is in a partially expanded state (35–37). Finally, these MD results include the first such results obtained with the new 2OAR MscL structure.
METHODS
Computational models and system preparation
A single POPE lipid structure was obtained from Tieleman and Berendsen (38) and replicated to form a bilayer composed of 392 lipids. Although the presence of phosphatidylethanolamine (PE) lipid is known to increase the tension threshold of MscL gating in membranes composed of phosphatidylcholine (PC) (39), POPE was chosen because PE is a predominant lipid headgroup of the bacterial membrane. The structure was hydrated with ∼10,000 simple-point-charge (SPC) water molecules (40), subjected to energy minimization, and equilibrated at 308 K and 1 bar for >10 ns (see Supplementary Material for further details). The resulting configurations (PWE1-PWE4; see Supplementary Material) were used in the NEMD simulations of the membrane-water (POPE) system. The Tb-MscL crystal structure was obtained from the PDB file 2OAR (8) and placed in a cylindrical membrane hole generated by removing ∼100 lipids from an equilibrated membrane PWM0 (cf. Supplementary Material). Residues 126–151 were not resolved in 2OAR, leaving 125 residues (Met-1 to Asn-125) per monomer in the simulated MscL. Residues were in a standard charged state and terminal groups were modeled as uncharged. This makes the modeled protein neutral. This structure was then energy-minimized and a short 0.05-ns constant NVT simulation was performed with the protein heavy atoms restrained. This initial configuration of the MscL-POPE system will be referred to as MPW0. System MPW0 had one MscL pentamer, 284 POPE lipids, and ∼20,000 SPC water molecules (∼80,000 atoms in total). This system was then equilibrated for ∼6 ns (Table 1, E1R, E2, and E3) under constant NPT conditions. The system size at the end of the E3 simulation was 94.7 × 93.8 × 115.2 Å3. To examine the protein-lipid interaction in the long timescale, a separate series of equilibrium simulations (Table 1, F1R–F4B) was performed with 5 or 10 ns of simulation with restraints on protein followed by 30 or 20 ns of unrestrained dynamics. To reduce computational cost, a truncated MscL system was also prepared by removing C-terminal residues 109–125 (Fig. 1) and ∼5000 water molecules from the output of the E3 simulation, leaving ∼64,000 atoms in a box of size 95.6 × 93.5 × 94.3 Å3 after 1 ns equilibration (Table 1, SE). Residues in the truncated MscL have the same charges as in the whole protein, except for the C-terminal carboxyl group, which was modeled as deprotonated to make the protein neutral. Experimental studies indicate that partial deletion of C-terminal residues does not affect MscL conductance significantly (41). Asymmetric membranes were prepared by removing four lipids at a time from one of the two leaflets of the bilayer accommodating MscL with multinanosecond equilibrations in between (Table 1, SEC–SEF). The bias potential runs (see below) were performed on a symmetric (142/142 lipids in the upper/lower monolayer (see Table 3, RS)) and two asymmetric membranes (134/142 and 142/134 lipids (see Table 3, RSE and RSF)).
TABLE 1.
Summary of equilibrium MD simulations performed
| Label | Starting configuration (lipid number in the upper/lower leaflet) | Duration (ns) | Barostat* ( τp) τp) |
|---|---|---|---|
| Full MscL + symmetric membrane | |||
| E1R†‡ | MPW0 (142/142) | 0.05 | B (1 bar, 1 ps) |
| E2 | E1R output | 0.9 | B (1 bar, 1 ps) |
| E3 | E2 output | 5 | B (1 bar, 1 ps) |
| F1R†‡ | MPW0 (142/142) | 0.05 | B (1 bar, 10 ps) |
| F2R‡ | F1R output | 2.95 | B (1 bar, 1 ps) |
| F3R§ | F2R output | 7 | B (1 bar, 1 ps) |
| F4 | 2 ns F3R | 30 | B (1 bar, 1 ps) |
| F4B | 7 ns F3R | 20 | B (1 bar, 1 ps) |
| Full MscL + symmetric membrane with negative lateral pressure¶ | |||
| NE | E3 output | 5 | B (−1000 bar, 500 ps) |
| NF | 15 ns F4 | 5 | B (−1000 bar, 500 ps) |
| Truncated MscL + membrane | |||
| SE‖ | E3 output (142/142) | 1 | B (1 bar, 1 ps) |
| SEC** | SE output (138/142) | 2.1 | |
| SED** | SE output (142/138) | 2.1 | |
| SEE** | SEC output (134/142) | 2.1 | |
| SEF** | SED output (142/134) | 2.1 | |
| SF1†† | F4B output (142/142) | 0.05 | |
| SF2 | SF1 output (142/142) | 20 | |
| Truncated MscL + membrane with negative lateral pressure¶ | |||
| NS | SE output (142/142) | 7 | B (−1000 bar, 500 ps) |
| NSE | SEE output (134/142) | 6 | B (−1000 bar, 500 ps) |
| NSF | SEF output (142/134) | 6 | B (−1000 bar, 500 ps) |
| NSB1 | 5 ns SF2 (142/142) | 20 | B (−100 bar, 50 ps) |
| NSB2 | 5 ns NSB1 (142/142) | 13 | B (−100 bar, 1 ps) |
All simulations were based on the new 2OAR crystal structure (8). In addition, simulations E1R–E3, NE, SE–SF1, and NS–NSF also were carried out with the old 1MSL structure (8). If necessary, these simulations will be referred to with the extra letter “Z” (e.g., “ZE3” for the 1MSL equivalent of E3). Temperature was maintained at 308 K by the Nose-Hoover thermostat (τp = 0.5 ps) in all cases except for E1R, E2, and F1R–F4B, which used the Berendsen thermostat (τp = 1 ps).
Normal pressure was maintained at 1 bar, with τp = 1 ps in all cases. B, Berendsen barostat.
The starting configuration MPW0 was prepared from the crystal structure (2oar.pdb), as described in text, via energy minimization and 0.05 ns of dynamics.
Protein heavy atoms were restrained to the crystal structure with force constant 1000 kJ mol−1 nm−2.
The protein alpha carbons were restrained to the crystal structure with force constant 1000 kJ mol−1 nm−2.
The normal pressure was effectively controlled with τp = 1 ps by increasing the normal component of the barostat compressibility parameter.
Residues 109–118 were removed in the starting configuration and then energy minimization was carried out before running the MD simulation.
After removal of four lipid molecules, 0.1 ns of the simulation was run with the protein heavy atoms restrained to the initial coordinates, followed by 2 ns without restraints.
The system was prepared as in the SE run. During the energy minimization and dynamics, the protein heavy atoms were restrained to the starting configuration with force constant 1000 kJ mol−1 nm−2.
TABLE 3.
Summary of simulations with the radial bias force
| Label | Starting configuration* (lipid number upper/lower leaflet) | Duration | Barostat parameters (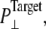 τp) τp) |
|---|---|---|---|
| RS | NS output (142/142) | 10 ns | |
| RSE | NSE output (134/142) | 9 ns | B (−200 bar, 100 ps) |
| RSF | NSF output (142/134) | 9 ns |
In all cases, five virtual sites are harmonically connected to the centers of mass of five subunits of MscL (force constant 1.0 × 105 kJ mol−1 nm−2). The sites were pulled in radially outward directions on the xy plane at the rate of 1.0 Å/ns. The normal pressure was kept at 1 bar. Temperature was maintained at 308 K by the Nose-Hoover thermostat (τp = 0.5 ps) in all cases. B, Berendsen barostat.
See Table 1 for descriptions of simulations NS, NSE, and NSF.
Parts of the simulations presented above were also performed starting with the older PDB structure 1MSL (Ala10–Arg118 (7)). Since the results with the 1MSL structure are not much different from those obtained with the 2OAR structure, only the 2OAR structure results will be presented in most cases. However, comparison of the radial bias force simulations with the two structures provides insight into the role of S1 helices in the gating of MscL. Also, the NEMD and constant NPAT simulations in Table 2 were carried out only with the 1MSL structure, since the focus there is the protein-induced modification of membrane rigidity and the two crystal structures are similar in the outer TM2 region in contact with the membrane.
TABLE 2.
Summary of the NEMD and constant NPAT simulations performed
| Label | Starting configuration | Duration | Method |
|---|---|---|---|
| POPE (192/192 lipids) | |||
| SP1-SP4 | PWE1-PWE4* | 10 ns each | NEMD |
| AP1-AP4 | PWE1-PWE4* | 5 ns each | NPAT |
| MscL(1MSL)†-POPE (142/142 lipids) | |||
| SM1-SM3 | 1-2 ns ZE3† | 10 ns each | NEMD |
| AM1-AM3 | 1-2 ns ZE3† | 5 ns each | NPAT |
The system area was kept constant in the NPAT runs, whereas it was expanded instantaneously by 3% in the NEMD runs. All simulations used the Nose-Hoover thermostat at 308 K and the Berendsen barostat to control the normal pressure at 1 bar with τp = 1 ps. The lateral component of compressibility was set to zero in all cases to prevent area changes due to the barostat.
Systems PWE1–PWE4 were prepared as described in Supplementary Material.
Force-field parameters for POPE were those of Berger et al. (42) (lipid.itp) available at GROMACS website (http://www.gromacs.org). For MscL, the GROMACS force field (ffgmx.itp) was employed. All bonds were constrained to their equilibrium lengths with the LINCS algorithm. For the rigid SPC water, the SETTLE algorithm was used. All simulations used the periodic boundary condition, and the closest distance between MscL images was at least 20 Å at equilibrium.
Computational methods
MD simulations were performed with GROMACS 3.3.1 in most production runs and partly with 3.2 or 3.3b (43,44), with modifications for the NEMD and radial bias force runs. For temperature and pressure controls, the Nose-Hoover (45,46) and Berendsen (47) algorithms, respectively, were used as implemented in the GROMACS program, with relaxation times of 0.5 and 1.0 ps, respectively, in most cases. Equilibrium simulations with zero tension were performed using the anisotropic pressure control with target pressure of 1 bar in all directions. Simulations under negative lateral pressure were also carried out using the same algorithm. The employed target pressures were 1 bar in the membrane normal (z) direction and −100 or −1000 bar in the lateral (in-plane; x and y) direction. The corresponding tension values are ∼100 or 1000 dyn/cm. Thus, in the initial stages of simulation, the system was generally in a nonequilibrium state. To see how the barostat parameters affect the pressure relaxation from these initial states, several different barostat relaxation times and compressibility parameters have been used. The employed values are given in Tables 1–3. The Lennard-Jones (LJ) interactions were cut off at 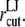 The POPE membrane simulations with
The POPE membrane simulations with 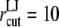 Å resulted in the separation of two monolayers. Thus,
Å resulted in the separation of two monolayers. Thus, 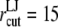 Å was used in the early stages of the POPE membrane simulation (Supplementary Material) and was reduced to 12 Å in the majority of production simulations. The particle-mesh Ewald method (48) was used to treat long-range electrostatic interactions with a real-space cutoff radius of 10 Å and grid spacing of 1.2 Å. The time step size was 2 fs in all cases and trajectories were saved every 2 ps for analysis in most cases.
Å was used in the early stages of the POPE membrane simulation (Supplementary Material) and was reduced to 12 Å in the majority of production simulations. The particle-mesh Ewald method (48) was used to treat long-range electrostatic interactions with a real-space cutoff radius of 10 Å and grid spacing of 1.2 Å. The time step size was 2 fs in all cases and trajectories were saved every 2 ps for analysis in most cases.
For membrane channel proteins, the radius of gyration about the channel symmetry axis, 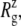 provides a useful measure of the lateral size of the protein. It is calculated as
provides a useful measure of the lateral size of the protein. It is calculated as
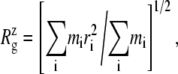 |
(1) |
where 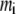 is the mass of atom i and
is the mass of atom i and 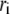 is the distance of atom i from the symmetry (z) axis. For simplicity, the channel symmetry axis is taken as the z axis, which is normal to the membrane in the initial configuration. The root mean-square deviation (RMSD) of the MscL from a reference structure provides additional information on the structural change. RMSDs of all atoms in MscL were computed after least-square fit of each MD structure to the crystal structure.
is the distance of atom i from the symmetry (z) axis. For simplicity, the channel symmetry axis is taken as the z axis, which is normal to the membrane in the initial configuration. The root mean-square deviation (RMSD) of the MscL from a reference structure provides additional information on the structural change. RMSDs of all atoms in MscL were computed after least-square fit of each MD structure to the crystal structure.
The membrane thickness was determined as the mean distance along the z axis between the phosphorus atoms belonging to each leaflet of the bilayer. In MscL-POPE systems, the thickness was also calculated for lipids located within ∼10 Å of MscL (33 lipids in each monolayer) and the rest. The lipid order parameter was determined as described in Supplementary Material and its values for the lipids near and far away from MscL were separately calculated. The two groups of lipids were prepared with the initial configuration and not updated again because the lipid diffusion was not large on the MD timescale. Pore radius of MscL was calculated with the HOLE program (49). The deuterium order parameter SCD of the palmitoyl chains of the POPE bilayer was determined from the orientation of C-C bonds assuming tetrahedral configuration (50), since the united atom model was used.
The NEMD simulation for the area change was carried out by instantaneously expanding the area of equilibrium systems at 1 bar pressure and then monitoring the lateral stress response while keeping the normal pressure at 1 bar, as described in Jeon and Voth (34). For a stepwise strain of the form,
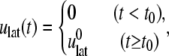 |
(2) |
the apparent lateral relaxation function G2D(t) is obtained from
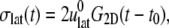 |
(3) |
where 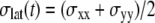 is the observed lateral stress and the condition of constant normal pressure of 1 bar is implicitly assumed. G2D(t) is related to the area compressibility (or expansibility, depending on the sign of
is the observed lateral stress and the condition of constant normal pressure of 1 bar is implicitly assumed. G2D(t) is related to the area compressibility (or expansibility, depending on the sign of 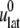 ) modulus KA via a Fourier transform,
) modulus KA via a Fourier transform,
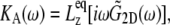 |
(4) |
where 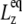 is the equilibrium size of the system along the membrane normal (including the water layers) and “∼” denotes a half Fourier transform. Note that
is the equilibrium size of the system along the membrane normal (including the water layers) and “∼” denotes a half Fourier transform. Note that 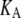 relates the areal strain to the tension, whereas
relates the areal strain to the tension, whereas 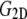 specifies the stress response. Thus,
specifies the stress response. Thus, 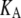 remains largely constant regardless of the water content of the system, whereas
remains largely constant regardless of the water content of the system, whereas 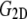 will be roughly inversely proportional to the thickness of the water layer, which cannot produce an elastic response and “dilutes” the total elastic response of the system. (In this study, the POPE system has a thickness
will be roughly inversely proportional to the thickness of the water layer, which cannot produce an elastic response and “dilutes” the total elastic response of the system. (In this study, the POPE system has a thickness 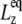 of ∼76 Å and the MscL-POPE system has
of ∼76 Å and the MscL-POPE system has 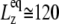 Å) (see Jeon and Voth (34) and Evans and Needham (51) for details). The experimentally determined static limit (
Å) (see Jeon and Voth (34) and Evans and Needham (51) for details). The experimentally determined static limit (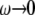 ) of
) of 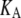 is reported in Rawicz et al. (52) for membranes of various lipid compositions. The application of the stepwise strain in Eq. 2 was accomplished by a modification of the GROMACS routine “deform”. The Berendsen barostat was used to maintain the normal pressure at 1 bar. Further details on the employed NEMD algorithm are provided in Supplementary Material. For a summary of NEMD simulations performed, see Table 2. The equilibrium lateral pressure
is reported in Rawicz et al. (52) for membranes of various lipid compositions. The application of the stepwise strain in Eq. 2 was accomplished by a modification of the GROMACS routine “deform”. The Berendsen barostat was used to maintain the normal pressure at 1 bar. Further details on the employed NEMD algorithm are provided in Supplementary Material. For a summary of NEMD simulations performed, see Table 2. The equilibrium lateral pressure 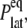 required to obtain
required to obtain 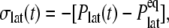 was determined from a separate equilibrium constant-area (NPAT) simulation with the same area as the initial (equilibrium) value of the NEMD run and a normal pressure of 1 bar. In the evaluation of σlat(t), average data from three to four independent trajectories were used. The amplitude of strain was
was determined from a separate equilibrium constant-area (NPAT) simulation with the same area as the initial (equilibrium) value of the NEMD run and a normal pressure of 1 bar. In the evaluation of σlat(t), average data from three to four independent trajectories were used. The amplitude of strain was 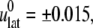 representing expansion (+) or compression (–) of the membrane area. The resulting G2D(t) was then fit to a multiexponential function of the form
representing expansion (+) or compression (–) of the membrane area. The resulting G2D(t) was then fit to a multiexponential function of the form
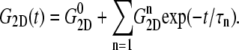 |
(5) |
Using this function, the area expansibility modulus in Eq. 4 becomes
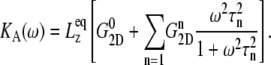 |
(6) |
The static value 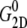 is not easy to determine reliably from a finite-length simulation, mainly because of its small magnitude comparable to
is not easy to determine reliably from a finite-length simulation, mainly because of its small magnitude comparable to 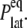 According to our previous study (34), it was obtained from
According to our previous study (34), it was obtained from 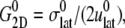 where the static limit
where the static limit 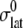 is replaced by the average of the lateral stress over the last 2.5 ns of 10-ns-long NEMD trajectories.
is replaced by the average of the lateral stress over the last 2.5 ns of 10-ns-long NEMD trajectories.
The radial bias potential was applied to induce lateral expansion of MscL. The potential had the harmonic form
 |
(7) |
where the reaction coordinate, ξ, is the average lateral distance between centers of mass of each pulled group, to which the bias force was applied, and the reference group, i.e.,
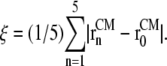 |
(8) |
Here, 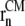 and
and 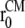 are the in-plane projections of the centers of mass of the nth pulled group and the reference group, respectively. The pulled groups were chosen here as five subunits of MscL and the reference group was the collection of five pulled groups. The force on a pulled group was distributed to every atom of the group in a mass-weighted fashion. Because the pulled group is part of the reference group, the reaction force was not applied to the reference group, unlike in the original GROMACS implementation. The forces due to
are the in-plane projections of the centers of mass of the nth pulled group and the reference group, respectively. The pulled groups were chosen here as five subunits of MscL and the reference group was the collection of five pulled groups. The force on a pulled group was distributed to every atom of the group in a mass-weighted fashion. Because the pulled group is part of the reference group, the reaction force was not applied to the reference group, unlike in the original GROMACS implementation. The forces due to 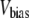 were implemented in the “AFM pulling” and “umbrella sampling” routines of GROMACS. In the AFM pulling method, a simpler scheme was used in which five distances between pulled groups and the reference group are treated independently (instead of averaged, as in Eq. 8) and the center of bias potential,
were implemented in the “AFM pulling” and “umbrella sampling” routines of GROMACS. In the AFM pulling method, a simpler scheme was used in which five distances between pulled groups and the reference group are treated independently (instead of averaged, as in Eq. 8) and the center of bias potential, 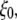 in Eq. 7 was increased linearly in time to expand five MscL subunits in the radially outward direction in the plane of the membrane. The bias potential did not affect the motion in the z direction. This method was used on the three MscL-POPE systems defined in Table 3 to obtain an expanded structure. The free-energy profile along the channel expansion coordinate based on the umbrella sampling method described above will be the subject of future work. The modified GROMACS source codes for the NEMD and bias force simulations are available from the authors upon request.
in Eq. 7 was increased linearly in time to expand five MscL subunits in the radially outward direction in the plane of the membrane. The bias potential did not affect the motion in the z direction. This method was used on the three MscL-POPE systems defined in Table 3 to obtain an expanded structure. The free-energy profile along the channel expansion coordinate based on the umbrella sampling method described above will be the subject of future work. The modified GROMACS source codes for the NEMD and bias force simulations are available from the authors upon request.
RESULTS
Contraction of MscL during equilibrium simulations without tension
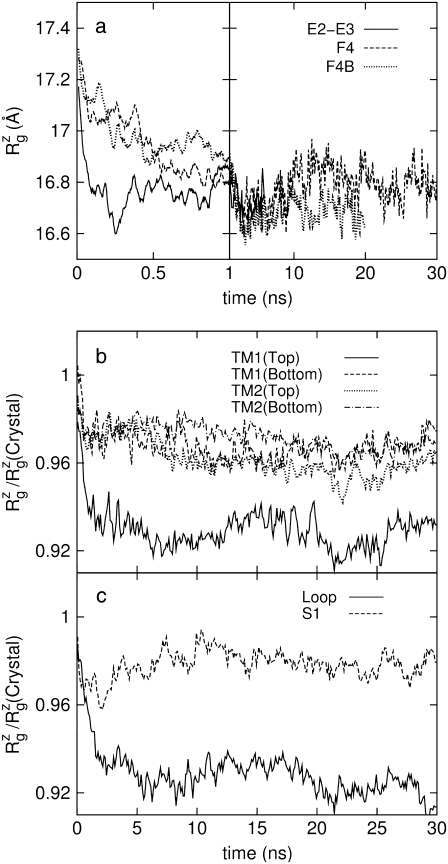
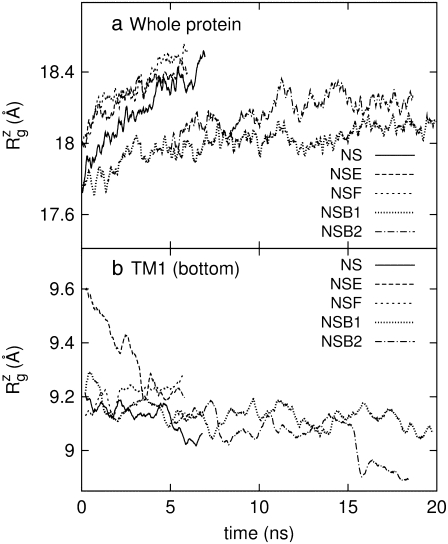
The crystal structure of MscL (2OAR) has an 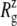 of 17.4 Å. Table 4 shows the
of 17.4 Å. Table 4 shows the 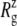 of the crystal structure and three equilibrium trajectories in Table 1. The three trajectories are different in their lengths of simulation and, more importantly, in the amount of equilibration with restraints on the protein. Simulation E2-E3 followed only 0.05 ns of equilibration with restraints (E1R in Table 1), whereas F4 and F4B were started from 5 and 10 ns of restrained simulations (F1R–F3R in Table 1). Despite these differences, the
of the crystal structure and three equilibrium trajectories in Table 1. The three trajectories are different in their lengths of simulation and, more importantly, in the amount of equilibration with restraints on the protein. Simulation E2-E3 followed only 0.05 ns of equilibration with restraints (E1R in Table 1), whereas F4 and F4B were started from 5 and 10 ns of restrained simulations (F1R–F3R in Table 1). Despite these differences, the 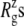 of the three trajectories over the last 5 ns are similar, and they all exhibit a contraction of MscL from the crystal structure by 0.6–0.7 Å. Individual components showed different degrees of contraction. A large change of more than 1 Å was observed in the top half of TM1 and loop regions. On the other hand, the bottom half of TM1, which contains the constriction point of the channel, showed a <0.3-Å decrease in
of the three trajectories over the last 5 ns are similar, and they all exhibit a contraction of MscL from the crystal structure by 0.6–0.7 Å. Individual components showed different degrees of contraction. A large change of more than 1 Å was observed in the top half of TM1 and loop regions. On the other hand, the bottom half of TM1, which contains the constriction point of the channel, showed a <0.3-Å decrease in 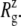 Fig. 2 a shows the
Fig. 2 a shows the 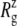 of the whole protein as a function of time for the three simulations. This clearly shows that the contraction of MscL took place within 1 ns after release of MscL restraints. The structural relaxation is much faster in E2-E3 than in F4 and F4B. This indicates that in simulations F4 and F4B, the lipids are better stabilizing the starting crystal structure thanks to longer simulation time with restraints on the protein. The short-range protein-lipid interactions are also stronger in F4 and F4B than in E3. The average of short-range LJ plus Coulomb interactions between POPE lipids and MscL are −2970, −3601, and −3802 kcal/mol for the last 5 ns of simulations E3, F4, and F4B, respectively. Despite this, the protein lateral dimensions in three simulations tend to converge with the nanosecond timescale as can be seen in the long-time behavior of Fig. 2 a. Fig. 2, b and c, shows relative
of the whole protein as a function of time for the three simulations. This clearly shows that the contraction of MscL took place within 1 ns after release of MscL restraints. The structural relaxation is much faster in E2-E3 than in F4 and F4B. This indicates that in simulations F4 and F4B, the lipids are better stabilizing the starting crystal structure thanks to longer simulation time with restraints on the protein. The short-range protein-lipid interactions are also stronger in F4 and F4B than in E3. The average of short-range LJ plus Coulomb interactions between POPE lipids and MscL are −2970, −3601, and −3802 kcal/mol for the last 5 ns of simulations E3, F4, and F4B, respectively. Despite this, the protein lateral dimensions in three simulations tend to converge with the nanosecond timescale as can be seen in the long-time behavior of Fig. 2 a. Fig. 2, b and c, shows relative 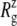 changes of MscL components from the crystal structure (2OAR) during 30 ns of simulation F4. The top half of TM1 and the loop region are easily identified as having the largest contraction, of ∼8%, whereas the rest of the components show only a 2–4% decrease in
changes of MscL components from the crystal structure (2OAR) during 30 ns of simulation F4. The top half of TM1 and the loop region are easily identified as having the largest contraction, of ∼8%, whereas the rest of the components show only a 2–4% decrease in 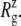 Similar analysis of all three simulations puts the relative lateral contraction in the following order, from smallest to largest: bottom TM1 < S1 ≈ TM2 < top TM1 ≈ loop. Although not shown here, equilibrium simulations on the older 1MSL structure also result in somewhat larger contraction.
Similar analysis of all three simulations puts the relative lateral contraction in the following order, from smallest to largest: bottom TM1 < S1 ≈ TM2 < top TM1 ≈ loop. Although not shown here, equilibrium simulations on the older 1MSL structure also result in somewhat larger contraction.
TABLE 4.
Lateral dimensions of MscL and its components in the crystal structure and averages over equilibrium simulations
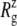 (Å) (Å)
|
|||||
|---|---|---|---|---|---|
| 1MSL | 2OAR | E3 | F4 | F4B | |
| Whole protein | 15.37 | 17.39* | 16.73 (0.07) | 16.80 (0.07) | 16.69 (0.06) |
| S1 | — | 20.46 | 19.46 (0.13) | 20.02 (0.12) | 19.23 (0.16) |
| TM1 (top half) | 16.95 | 17.14 | 16.17 (0.17) | 15.93 (0.13) | 16.32 (0.13) |
| TM1 (bottom half) | 9.51 | 9.41 | 9.30 (0.10) | 9.12 (0.07) | 9.21 (0.08) |
| TM2 (top half) | 18.16 | 18.01 | 17.32 (0.11) | 17.27 (0.10) | 17.24 (0.12) |
| TM2 (bottom half) | 19.36 | 20.14 | 18.88 (0.11) | 19.47 (0.10) | 19.41 (0.13) |
| Loop | 17.22 | 21.75 | 20.27 (0.20) | 20.04 (0.15) | 20.50 (0.12) |
The radii of gyration about the MscL symmetry axis, 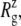 for the crystal structures (1MSL and 2OAR) and three equilibrium simulations (E3, F4, and F4B (see Table 1)), employing the 2OAR structure. The averages over the last 5 ns are presented for each simulation result. SD is given in parentheses. For a definition of each component, see Fig. 1.
for the crystal structures (1MSL and 2OAR) and three equilibrium simulations (E3, F4, and F4B (see Table 1)), employing the 2OAR structure. The averages over the last 5 ns are presented for each simulation result. SD is given in parentheses. For a definition of each component, see Fig. 1.
Truncated MscL (residues Met1–Asp108) has a 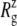 of 17.10.
of 17.10.
FIGURE 2.
Change of MscL lateral dimensions during equilibrium MD under zero tension measured by the radius of gyration about the symmetry axis 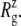 (a)
(a) 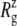 of the whole protein for the three trajectories—E2-E3, F4, and F4B—described in Table 1. (b and c) Relative changes in
of the whole protein for the three trajectories—E2-E3, F4, and F4B—described in Table 1. (b and c) Relative changes in 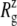 from the crystal structure (2OAR) for the six components defined in Fig. 1. The data is from trajectory F4.
from the crystal structure (2OAR) for the six components defined in Fig. 1. The data is from trajectory F4.
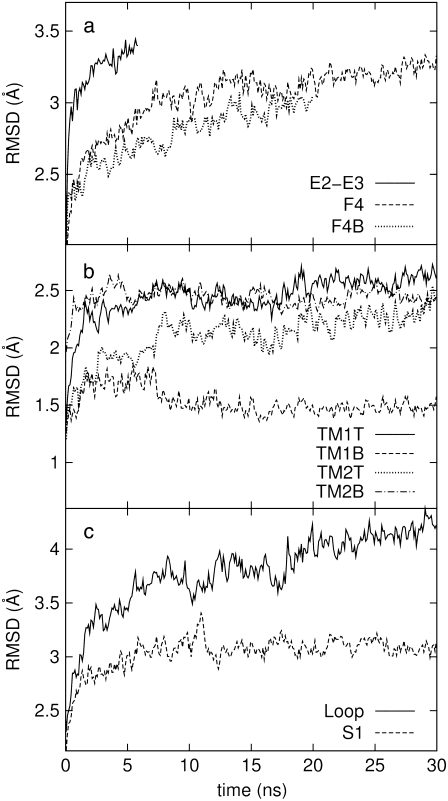
Fig. 3 a shows the RMSD of the whole protein from the crystal structure for the three equilibrium trajectories E2-E3, F4, and F4B. The whole-protein RMSD is in the 3–3.5 Å range and it might not have fully converged after 30 ns (F4). The sharp initial increase in RMSD for trajectory E2-E3 is consistent with the rapid contraction observed in Fig. 2 a. In contrast, the RMSDs for trajectories F4 and F4B show a slower rise and have lower value (3–3.3 Å) at the end of simulation than in E2-E3 (3.5 Å). Fig. 3, b and c, displays the RMSD of individual components calculated from trajectory F4. Fig. 3 b shows that the transmembrane parts of MscL (TM1 and TM2) have RMSDs of <2.6 Å. In particular, the bottom half of TM1 (TM1B) shows the smallest RMSD, only 1.5 Å, consistent with the small 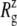 observed in Fig. 2 b. The largest RMSD, >4 Å, is found in the loops (Fig. 3 c), whereas all the other components in Fig. 3, b and c, show RMSD smaller than the whole protein value of 3.3 Å. Thus, the water-exposed regions of MscL, the loops and the C-terminal S3 helices, are the most mobile parts of MscL.
observed in Fig. 2 b. The largest RMSD, >4 Å, is found in the loops (Fig. 3 c), whereas all the other components in Fig. 3, b and c, show RMSD smaller than the whole protein value of 3.3 Å. Thus, the water-exposed regions of MscL, the loops and the C-terminal S3 helices, are the most mobile parts of MscL.
FIGURE 3.
RMSD of MscL from the crystal structure during equilibrium MD under zero tension. (a) RMSD of the whole protein for the three trajectories, E2-E3, F4, and F4B, described in Table 1. (b and c) RMSDs of individual components from trajectory F4. The six components are defined in Fig. 1.
These equilibrium MD trajectories clearly show that the MscL embedded in membrane has a smaller lateral dimension than the crystal structure (both 1MSL and 2OAR). This supports previous experiments by Blount and co-workers indicating that the 1MSL crystal structure is not in a fully closed, but in a partially closed, state (35–37).
Effects of membrane asymmetry and lateral tension on the MscL structure
The opening of MscL requires an external driving force either from tension on the membrane or asymmetric incorporation of single-chain lipids such as LPC. To simulate such external driving forces, MD simulations were performed with negative lateral pressure and/or asymmetric membranes with different numbers of lipids in the two monolayers, the latter mimicking the effect of incorporating amphipath (12,13) by producing an asymmetric pressure profile across the membrane.
Simulations with negative lateral pressure are summarized in Table 1. Simulations with full MscL (NE and NF) used target pressure 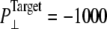 bar with barostat relaxation time, τP, of 500 ps. The large τP value was employed to expand the area slowly and allow the system to equilibrate to the increased area. In all cases, the target pressure in the membrane normal,
bar with barostat relaxation time, τP, of 500 ps. The large τP value was employed to expand the area slowly and allow the system to equilibrate to the increased area. In all cases, the target pressure in the membrane normal, 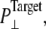 was kept at 1 bar. Since the system thickness,
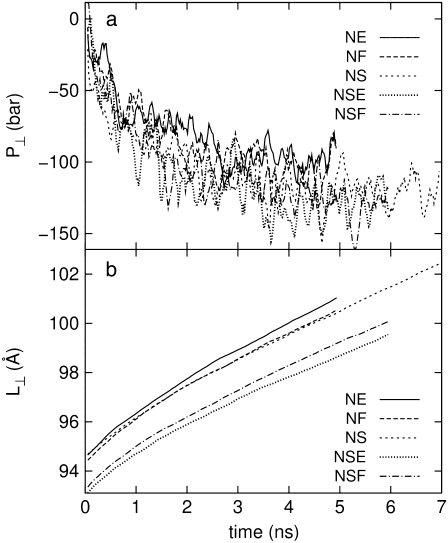
was kept at 1 bar. Since the system thickness, 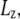 is ∼10 nm, the employed target pressure corresponds to a lateral tension, γ (Lz(Pz − P⊥)), of ∼1000 dyn/cm. However, the actual lateral pressure never came close to the target and it reached a steady value of about −100 bar after 3 ns (Fig. 4 a). During this time, the system area continued to increase (Fig. 4 b). Thus, the system approaches a nonequilibrium steady state in 3 ns. The average lateral pressure between 3 and 5 ns is −96.9 bar for NE and −103.8 bar for NF. Trajectory NF was started from the 15-ns configuration of run F4 (Table 1) and therefore better equilibrated than NE. This explains the slightly lower lateral pressure for NF in the steady state. As also shown in Fig. 4, a similar behavior is observed in the systems with truncated MscL and symmetric or asymmetric membrane configurations (simulations NS, NSE, and NSF in Table 1). The steady-state lateral pressures of NS, NSE, and NSF are −118.3, −130.2, and −126.8 bar, respectively. These values cannot be compared directly with the full MscL results because the truncated system has a thinner water layer and smaller system thickness, Lz, than the full MscL systems. Instead, the effective tension in the steady state (calculated from actual system pressure and size) should be used for comparison. The average tension values over the last 2 ns are 99.1 (NE), 107.0 (NF), 97.7 (NS), 112.0 (NSE), and 107.5 (NSF) dyn/cm. This shows that the MscL-POPE system can sustain lateral tension of ∼100 dyn/cm in the MD timescale, but not much more. Also, it can be seen that better equilibration (NF) can yield somewhat larger tension in the nonequilibrium steady state when compared with results from shorter equilibration (NE and NS). In addition, asymmetric membranes (NSE and NSF) can achieve similarly larger tension because there are eight fewer lipids in the system.
is ∼10 nm, the employed target pressure corresponds to a lateral tension, γ (Lz(Pz − P⊥)), of ∼1000 dyn/cm. However, the actual lateral pressure never came close to the target and it reached a steady value of about −100 bar after 3 ns (Fig. 4 a). During this time, the system area continued to increase (Fig. 4 b). Thus, the system approaches a nonequilibrium steady state in 3 ns. The average lateral pressure between 3 and 5 ns is −96.9 bar for NE and −103.8 bar for NF. Trajectory NF was started from the 15-ns configuration of run F4 (Table 1) and therefore better equilibrated than NE. This explains the slightly lower lateral pressure for NF in the steady state. As also shown in Fig. 4, a similar behavior is observed in the systems with truncated MscL and symmetric or asymmetric membrane configurations (simulations NS, NSE, and NSF in Table 1). The steady-state lateral pressures of NS, NSE, and NSF are −118.3, −130.2, and −126.8 bar, respectively. These values cannot be compared directly with the full MscL results because the truncated system has a thinner water layer and smaller system thickness, Lz, than the full MscL systems. Instead, the effective tension in the steady state (calculated from actual system pressure and size) should be used for comparison. The average tension values over the last 2 ns are 99.1 (NE), 107.0 (NF), 97.7 (NS), 112.0 (NSE), and 107.5 (NSF) dyn/cm. This shows that the MscL-POPE system can sustain lateral tension of ∼100 dyn/cm in the MD timescale, but not much more. Also, it can be seen that better equilibration (NF) can yield somewhat larger tension in the nonequilibrium steady state when compared with results from shorter equilibration (NE and NS). In addition, asymmetric membranes (NSE and NSF) can achieve similarly larger tension because there are eight fewer lipids in the system.
FIGURE 4.
Changes in (a) the lateral pressure 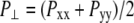 and (b) the lateral dimension
and (b) the lateral dimension  during the simulations with negative lateral pressure. Trajectories NE and NF are for the whole MscL, and NS, NSE, and NSF are for the truncated MscL. The target lateral pressures are −1000 bar in all cases. See Table 1 for further details.
during the simulations with negative lateral pressure. Trajectories NE and NF are for the whole MscL, and NS, NSE, and NSF are for the truncated MscL. The target lateral pressures are −1000 bar in all cases. See Table 1 for further details.
To further study the long-time system behavior under sustainable lateral pressure, longer simulations, with 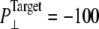 bar, were performed (NSB1 and NSB2) starting from a truncated system prepared with longer equilibration totaling >35 ns (F1R-F3R, F4B, SF1, and 5-ns SF2). In NSB1, the τP was 50 ps, and this was reduced to 1 ps in the NSB2 run that starts from the 5-ns configuration of NSB1. As shown in Supplementary Material, Fig. S3, these trajectories, which do not seem to have converged even after 10 ns, exhibit much slower area expansion. The lateral pressures for these trajectories in Fig. S3 show that due to slow area expansion trajectory NSB1 did not reach the target pressure of −100 bar. However, trajectory NSB2 lateral pressure reached the target value immediately, due to faster barostat relaxation. Since the system area was still expanding, NSB2 also can be regarded as being in a nonequilibrium steady state rather than in full equilibrium. This indicates that achieving a full equilibrium state of a protein-membrane system with the largest sustainable tension can take at least tens of nanoseconds.
bar, were performed (NSB1 and NSB2) starting from a truncated system prepared with longer equilibration totaling >35 ns (F1R-F3R, F4B, SF1, and 5-ns SF2). In NSB1, the τP was 50 ps, and this was reduced to 1 ps in the NSB2 run that starts from the 5-ns configuration of NSB1. As shown in Supplementary Material, Fig. S3, these trajectories, which do not seem to have converged even after 10 ns, exhibit much slower area expansion. The lateral pressures for these trajectories in Fig. S3 show that due to slow area expansion trajectory NSB1 did not reach the target pressure of −100 bar. However, trajectory NSB2 lateral pressure reached the target value immediately, due to faster barostat relaxation. Since the system area was still expanding, NSB2 also can be regarded as being in a nonequilibrium steady state rather than in full equilibrium. This indicates that achieving a full equilibrium state of a protein-membrane system with the largest sustainable tension can take at least tens of nanoseconds.
The MscL structural changes under negative lateral pressure are shown in Fig. 5 for five systems with truncated MscL (NS–NSB2 in Table 1). The radius of gyration, 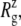 for the whole protein increases in all five trajectories (Fig. 5 a). With a
for the whole protein increases in all five trajectories (Fig. 5 a). With a 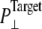 of −1000 bar (NS, NSE, and NSF),
of −1000 bar (NS, NSE, and NSF), 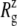 increases much faster than with a
increases much faster than with a 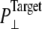 of −100 bar (NSB1 and NSB2). The unconverged values of
of −100 bar (NSB1 and NSB2). The unconverged values of 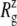 at the end of simulations are between 18.1 and 18.4 Å, well above the crystal structure value (17.10 Å for the truncated 2OAR, as seen in Table 4) but not enough to produce large structural changes in MscL. In fact, the
at the end of simulations are between 18.1 and 18.4 Å, well above the crystal structure value (17.10 Å for the truncated 2OAR, as seen in Table 4) but not enough to produce large structural changes in MscL. In fact, the 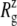 of MscL components (Fig. S4) shows that none of the components are more expanded than in the crystal structure. Thus, the expansion of the whole protein is mainly attributed to the C-terminal regions not included in the component analysis. The truncation of C-terminal S3 helices must have caused some fraying of C-terminal residues, giving a large
of MscL components (Fig. S4) shows that none of the components are more expanded than in the crystal structure. Thus, the expansion of the whole protein is mainly attributed to the C-terminal regions not included in the component analysis. The truncation of C-terminal S3 helices must have caused some fraying of C-terminal residues, giving a large  for the whole protein. Most importantly, the constricted TM1 bottom half does not expand and even contracts somewhat, as observed in Fig. 5 b for all simulations except NSF. Pore radius profiles of MscL in Fig. S5 also show that the constriction region is narrower under tension than in the crystal structure. This indicates that the constriction region is not directly coupled to the applied tension in the initial stage of gating and its lateral expansion needs to be triggered by the structural changes of the protein outer region.
for the whole protein. Most importantly, the constricted TM1 bottom half does not expand and even contracts somewhat, as observed in Fig. 5 b for all simulations except NSF. Pore radius profiles of MscL in Fig. S5 also show that the constriction region is narrower under tension than in the crystal structure. This indicates that the constriction region is not directly coupled to the applied tension in the initial stage of gating and its lateral expansion needs to be triggered by the structural changes of the protein outer region.
FIGURE 5.
Changes in the MscL radius of gyration 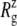 during the simulations with negative lateral pressure. (a)
during the simulations with negative lateral pressure. (a) 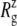 of the whole protein. (b)
of the whole protein. (b) 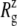 of the constricted bottom half of TM1. Trajectories NS–NSF have target pressure
of the constricted bottom half of TM1. Trajectories NS–NSF have target pressure 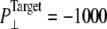 bar. NSB1 and NSB2 have
bar. NSB1 and NSB2 have 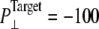 bar. The trajectories are described in Table 1. Note that NSB2 starts at 5 ns of NSB1.
bar. The trajectories are described in Table 1. Note that NSB2 starts at 5 ns of NSB1.
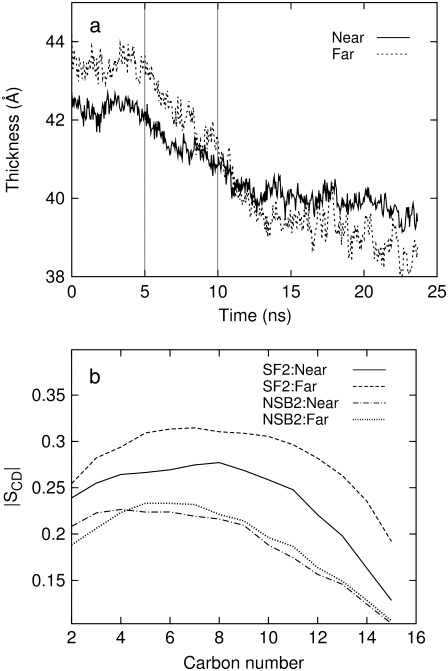
Thickness and lipid order parameter of the membrane surrounding MscL are displayed in Fig. 6 for SF2 (zero tension) and NSB1/NSB2 (negative lateral pressure) trajectories (cf. Table 1). It shows that the membrane thickness is smaller and the lipid more disordered in the vicinity of MscL than in the remote region. Also, by comparing Fig. 6 with Table S1 and Fig. S2, it can be seen that the POPE membrane with embedded MscL is thinner and more disordered than pure POPE membrane, even in the remote region. This indicates that POPE lipid is compressed in the normal direction to accommodate MscL. Under negative lateral pressure, however, the lipids adjacent to MscL maintain their thickness and order much better than the remote lipids (Fig. 6). Thus, the membrane near MscL can be more resistant to expansion despite being less ordered than in bulk, due to protein-lipid interactions. This is consistent with a recent study suggesting the effective buffering of bulk lipid properties by the lipids in direct contact with MscL (53).
FIGURE 6.
Membrane thickness and lipid order parameter of the palmitoyl chain for lipids within ∼10 Å of MscL (Near) and the rest of the lipids (Far). (a) The normal distance between phosphorus atoms from the two leaflets of the bilayer is displayed for simulations under zero tension (0–5 ns, trajectory SF2) and negative lateral pressure of −100 bar (5–10 ns, NSB1; 10–23 ns, NSB2). The vertical lines at 5 and 10 ns mark the beginning of NSB1 and NSB2 simulations, respectively. (b) The lipid order parameters. The tension is zero in simulation SF2 and about 100 dyn/cm in NSB1/NSB2. The order parameters were calculated from the 4–5 ns (SF2) and 22–23 ns (NSB2) parts of the trajectory shown in a. See Table 1 for other details of simulations SF2, NSB1, and NSB2.
The insensitivity of MscL to the large applied tension is a puzzling result. First of all, it should be noted that the system never exhibited the prescribed pressure and was still expanding when the simulation was terminated. Even under a relatively mild condition with 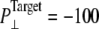 bar, the system size did not fully converge in 20 ns (Fig. S3). This clearly indicates that the simulation time is not long enough to cover the intrinsic response time of the MscL membrane to applied tension. Under applied tension, the membrane needs time to equilibrate to the increased area/lipid to fully exhibit the intended negative internal pressure. Failure to do this means that the protein never feels the stretching force prescribed by the target lateral pressure. Moreover, the overall path from the closed to the open state of MscL may be downhill under adiabatically applied tension, but it can still have many local barriers due to the ruggedness of the free-energy landscape. Thus, even under full stretching force from the membrane, MscL must overcome many small barriers, which takes time. In addition, the strength of the protein-lipid interaction increases with longer equilibration and in turn yields larger tension under stretching conditions, as was observed in the comparison of trajectories NE and NF above. There are other issues, such as the quality of the force field, but the most critical issue seems to be the mismatch in timescales between the simulation and the system response. Quantifying the latter time and reproducing adiabatic MscL gating from membrane tension will be an important computational challenge for the future, as is true with the sampling of the conformational states of many biomolecular systems.
bar, the system size did not fully converge in 20 ns (Fig. S3). This clearly indicates that the simulation time is not long enough to cover the intrinsic response time of the MscL membrane to applied tension. Under applied tension, the membrane needs time to equilibrate to the increased area/lipid to fully exhibit the intended negative internal pressure. Failure to do this means that the protein never feels the stretching force prescribed by the target lateral pressure. Moreover, the overall path from the closed to the open state of MscL may be downhill under adiabatically applied tension, but it can still have many local barriers due to the ruggedness of the free-energy landscape. Thus, even under full stretching force from the membrane, MscL must overcome many small barriers, which takes time. In addition, the strength of the protein-lipid interaction increases with longer equilibration and in turn yields larger tension under stretching conditions, as was observed in the comparison of trajectories NE and NF above. There are other issues, such as the quality of the force field, but the most critical issue seems to be the mismatch in timescales between the simulation and the system response. Quantifying the latter time and reproducing adiabatic MscL gating from membrane tension will be an important computational challenge for the future, as is true with the sampling of the conformational states of many biomolecular systems.
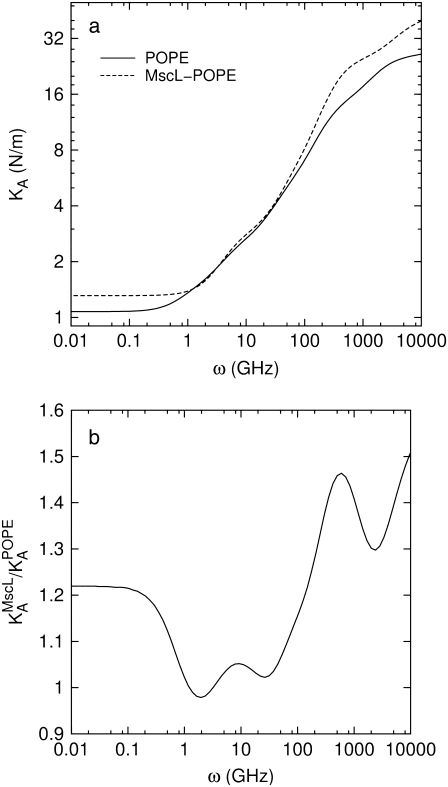
Elastic modulus of the MscL-membrane system
The results in the preceding section demonstrate that the membrane tension and/or the structural asymmetry of the membrane is rather ineffective in inducing MscL structural changes on the timescale of tens of nanoseconds. To better understand the system response to these driving forces, the dynamic elastic modulus of the hydrated POPE membrane and MscL membrane systems were calculated with NEMD. For each system, the lateral stress was calculated by averaging results of three to four independent 10-ns NEMD simulations with the stepwise strain, as described in Methods and Table 2. From these calculations, the relaxation function, G2D(t), was determined using Eq. 3. In this process, the equilibrium pressure, 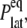 −4.035 (POPE) and −11.803 bar (MscL-POPE) as determined from separate NPAT runs (see Methods), was subtracted from the NEMD lateral pressure to obtain the lateral stress, according to
−4.035 (POPE) and −11.803 bar (MscL-POPE) as determined from separate NPAT runs (see Methods), was subtracted from the NEMD lateral pressure to obtain the lateral stress, according to 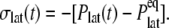 Table 5 summarizes the results of a multiexponential fit of the G2D(t) according to Eq. 5. It shows relaxation modes spanning the subpicosecond to nanosecond timescale, with some difference between the POPE and MscL-POPE systems. This difference comes from the different thickness of the water layer in the two systems, as well as the intrinsic changes arising from MscL-lipid interactions (34). In particular, the static modes, with
Table 5 summarizes the results of a multiexponential fit of the G2D(t) according to Eq. 5. It shows relaxation modes spanning the subpicosecond to nanosecond timescale, with some difference between the POPE and MscL-POPE systems. This difference comes from the different thickness of the water layer in the two systems, as well as the intrinsic changes arising from MscL-lipid interactions (34). In particular, the static modes, with 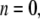 have similar amplitude
have similar amplitude 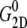 of ∼1.5 kbar despite the fact that the water layer is much thicker in the MscL-POPE system than in the POPE system (see Methods). The difference due to material property changes can be isolated by considering the area expansibility modulus KA(ω). Using the system thickness (
of ∼1.5 kbar despite the fact that the water layer is much thicker in the MscL-POPE system than in the POPE system (see Methods). The difference due to material property changes can be isolated by considering the area expansibility modulus KA(ω). Using the system thickness (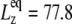 and 118.6 Å, respectively, for the POPE and MscL-POPE systems) determined from the aforementioned NPAT simulations, Eq. 6 yields the frequency-dependent KA(ω), as shown in Fig. 7. It is evident that MscL inclusion noticeably enhances the rigidity of membrane against area expansion at the frequency range considered. In particular, the static limit at small ω (KA(0) = 1.08 ± 0.28 N/m for the POPE and 1.31 ± 0.25 N/m for the MscL-POPE system) shows that the MscL-POPE system is 22% more difficult to expand than pure POPE membrane. Although the absolute value of KA(ω) for the POPE system is around four times larger than the experimental values for many phosphatidylcholine membranes (52), the observed relative difference between the POPE and MscL-POPE systems should have a much smaller uncertainty. The area fraction of MscL in the MscL-POPE system is estimated to be 0.16 by comparing the areas of the two systems. Assuming that the rigidity of MscL is much larger than the membrane region, this area fraction accounts for the majority, but not all, of the 22% enhancement in KA(ω).
and 118.6 Å, respectively, for the POPE and MscL-POPE systems) determined from the aforementioned NPAT simulations, Eq. 6 yields the frequency-dependent KA(ω), as shown in Fig. 7. It is evident that MscL inclusion noticeably enhances the rigidity of membrane against area expansion at the frequency range considered. In particular, the static limit at small ω (KA(0) = 1.08 ± 0.28 N/m for the POPE and 1.31 ± 0.25 N/m for the MscL-POPE system) shows that the MscL-POPE system is 22% more difficult to expand than pure POPE membrane. Although the absolute value of KA(ω) for the POPE system is around four times larger than the experimental values for many phosphatidylcholine membranes (52), the observed relative difference between the POPE and MscL-POPE systems should have a much smaller uncertainty. The area fraction of MscL in the MscL-POPE system is estimated to be 0.16 by comparing the areas of the two systems. Assuming that the rigidity of MscL is much larger than the membrane region, this area fraction accounts for the majority, but not all, of the 22% enhancement in KA(ω).
TABLE 5.
Multiexponential decomposition of G2D(t) after expansion of the system area by 3% ( ) obtained with NEMD
) obtained with NEMD
| POPE
|
MscL-POPE
|
|||
|---|---|---|---|---|
| n | 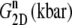 |
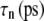 |
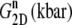 |
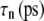 |
| 1 | 71.87 | 0.0107 | 73.82 | 0.0114 |
| 2 | 14.29 | 0.618 | 0.5615 | 0.123 |
| 3 | 12.27 | 5.06 | 12.80 | 0.261 |
| 4 | 3.528 | 28.6 | 15.65 | 3.81 |
| 5 | 1.463 | 221 | 3.030 | 20.4 |
| 6 | 0.5349 | 1100 | 1.336 | 223 |
| 0 | 1.517 | ∞ | 1.500 | ∞ |
“POPE” is from the hydrated POPE membrane and “MscL-POPE” is from the system with embedded MscL.  and
and 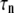 are, respectively, the amplitude and relaxation time of the nth mode of the relaxation function (Eq. 5).
are, respectively, the amplitude and relaxation time of the nth mode of the relaxation function (Eq. 5).
FIGURE 7.
(a) Frequency-dependent area expansibility modulus, KA(ω), of hydrated POPE membrane and POPE membrane with embedded MscL protein. (b) The change in KA(ω) of MscL-embedded membrane relative to the POPE membrane system.
In Fig. 6, the lipids in the vicinity of MscL were observed to be thinner and more disordered than remote ones under zero tension, whereas they maintained their thickness and order much better when the membrane was stretched. The observed enhancement of the membrane elastic response upon incorporation of MscL can be partly attributed to these lipids near MscL that exhibit the unusual property of being more resistant to expansion despite being less ordered.
Opening of MscL channel by the application of radial bias force
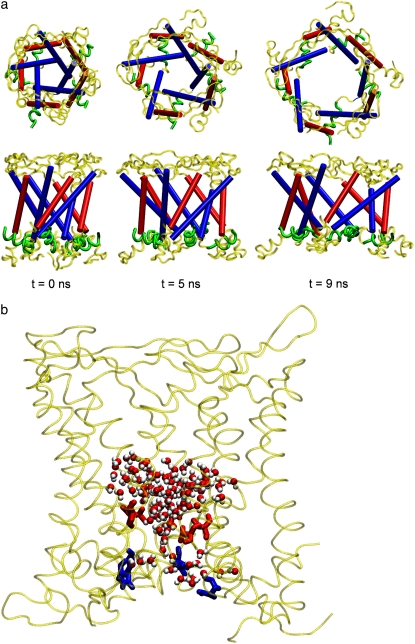
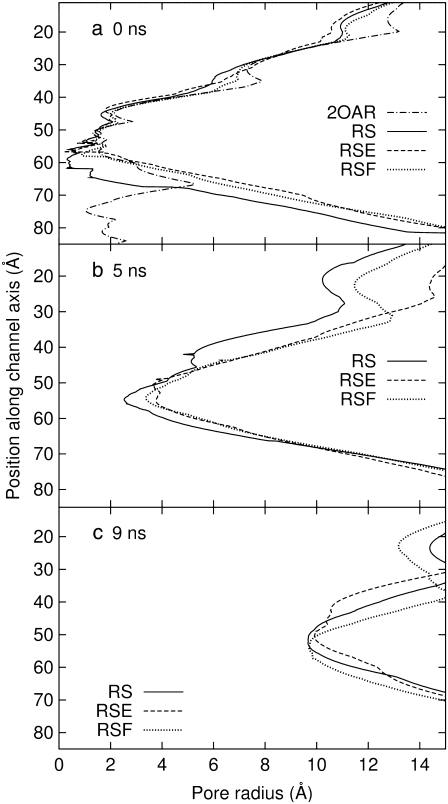
The three bias force simulations described in Methods and Table 3 all yielded open MscL structures in 9–10 ns of expansion at the rate of 1.0 Å /ns. Fig. 8 a shows MscL at 0, 5, and 9 ns of simulation RS in symmetric membrane. The initially constricted channel is partially opened and a chain of water forms across the channel at 5 ns. (The formed water channel resembles the one in Fig. 8 b, taken from simulation RSE.) Further expansion results in a wide channel with radius∼10 Å at 9 ns, as shown in Fig. 9. During the expansion, the transmembrane α-helices maintain their structure quite well except for a few breakages of long helices into two to three smaller ones.
FIGURE 8.
Structural changes of MscL during channel opening. (a) Top view (upper row) and side view (lower row) of structures in a symmetric membrane at 0, 5, and 9 ns of simulation RS, from left to right, respectively. Blue tubes represent TM1, red tubes TM2, and green ribbons S1 helices; the remainder of MscL is shown in yellow. (b) The initially formed water chain at 4.08 ns of simulation RSE. Water molecules near the constriction region are shown as red and white spheres, red licorice represents hydrophobic Val21 residues, and blue licorice represents hydrophilic Asn13 and Asp16 residues that stabilize the water chain from below the constriction region. See Table 3 for details of simulations RS and RSE. The images were prepared with the software package VMD (57).
FIGURE 9.
Pore-radius profiles of MscL under radial bias force. (a) Radii of the crystal structure and three configurations at 0 ns of radial bias force simulations in symmetric and asymmetric membranes. (b and c) Radii of the three configurations at 5 and 9 ns of their trajectory. Simulations RS, RSE, and RSF are described in Table 3. Note that RS–RSF used truncated MscL and thus no radius is defined beyond 80 Å in the vertical axis.
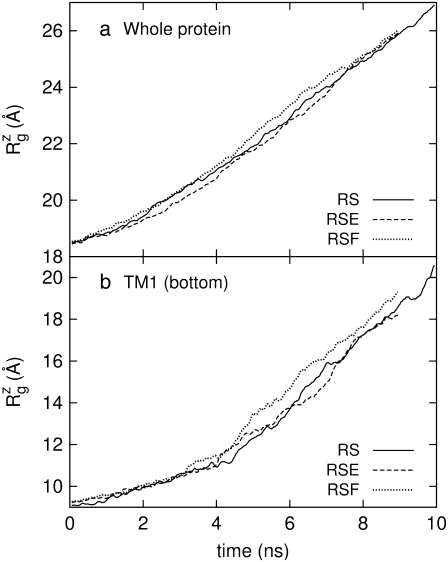
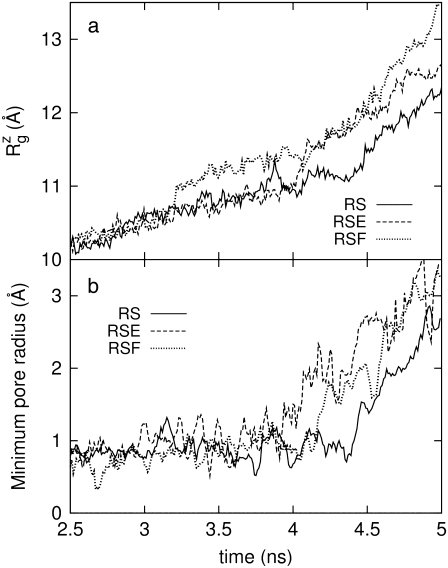
Fig. 10 displays the changes in 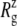 from trajectories RS-RSF for (a) the whole protein and (b) the constricted bottom half of TM1. The whole protein
from trajectories RS-RSF for (a) the whole protein and (b) the constricted bottom half of TM1. The whole protein  shows an almost linear increase but the TM1 bottom shows two stages of expansion, with an initially slow expansion followed by a fast increase in
shows an almost linear increase but the TM1 bottom shows two stages of expansion, with an initially slow expansion followed by a fast increase in 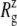 beginning at ∼4 ns (Fig. 10 b). The evolution of the minimum pore radius in Fig. 11 shows that this accelerated expansion coincides with a sudden increase in minimum pore radius at 4–4.5 ns. Inspection of each trajectory at 2-ps intervals reveals that the formation of a persistent water chain takes place at 4.56, 4.07, and 4.45 ns in RS, RSE, and RSF, respectively. One such water chain from simulation RSE is shown in Fig. 8 b. Thus, three important events in the MscL gating, i.e., the increase in channel expansion rate, the sudden jump in minimum pore radius, and the water chain formation across the channel, all take place at the same time. It is difficult to discuss the cause-effect relations among them, but it is expected that they will provide positive feedback to each other. For example, the increased pore radius will facilitate water chain formation, and vice versa. This in turn will lead to stabilization of the open structure and accelerated expansion. It is worthy of note that the channel opening proceeds in an almost stepwise manner. As Figs. 9 and 10 show, the pore remained closed for the initial 4 ns and then expanded steadily for the rest of the simulation, whereas the average lateral dimension of the whole protein increased at a fairly uniform rate over the entire simulation.
beginning at ∼4 ns (Fig. 10 b). The evolution of the minimum pore radius in Fig. 11 shows that this accelerated expansion coincides with a sudden increase in minimum pore radius at 4–4.5 ns. Inspection of each trajectory at 2-ps intervals reveals that the formation of a persistent water chain takes place at 4.56, 4.07, and 4.45 ns in RS, RSE, and RSF, respectively. One such water chain from simulation RSE is shown in Fig. 8 b. Thus, three important events in the MscL gating, i.e., the increase in channel expansion rate, the sudden jump in minimum pore radius, and the water chain formation across the channel, all take place at the same time. It is difficult to discuss the cause-effect relations among them, but it is expected that they will provide positive feedback to each other. For example, the increased pore radius will facilitate water chain formation, and vice versa. This in turn will lead to stabilization of the open structure and accelerated expansion. It is worthy of note that the channel opening proceeds in an almost stepwise manner. As Figs. 9 and 10 show, the pore remained closed for the initial 4 ns and then expanded steadily for the rest of the simulation, whereas the average lateral dimension of the whole protein increased at a fairly uniform rate over the entire simulation.
FIGURE 10.
Radial expansion of MscL by the application of radial bias force under negative lateral pressure of −200 bar (tension of ∼200 dyn/cm). (a) Radii of gyration, 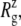 for the whole protein. (b)
for the whole protein. (b) 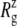 for the constricted TM1 bottom. The system in RS has a symmetric membrane, whereas systems in RSE and RSF have asymmetric membrane configurations (Table 3). The center of radial bias force,
for the constricted TM1 bottom. The system in RS has a symmetric membrane, whereas systems in RSE and RSF have asymmetric membrane configurations (Table 3). The center of radial bias force, 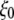 (see text), moved at a rate of 1 Å/ns.
(see text), moved at a rate of 1 Å/ns.
FIGURE 11.
Radii of gyration, 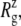 and pore size of the MscL constriction region (TM1 bottom) during the channel opening period by the application of radial bias force under negative lateral pressure of −200 bar (tension of ∼200 dyn/cm). (a) Radii of gyration,
and pore size of the MscL constriction region (TM1 bottom) during the channel opening period by the application of radial bias force under negative lateral pressure of −200 bar (tension of ∼200 dyn/cm). (a) Radii of gyration, 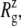 for TM1 bottom. (b) Minimum pore radius of the channel. The system in RS has a symmetric membrane, whereas systems in RSE and RSF have asymmetric membrane configurations (Table 3). The center of radial bias force
for TM1 bottom. (b) Minimum pore radius of the channel. The system in RS has a symmetric membrane, whereas systems in RSE and RSF have asymmetric membrane configurations (Table 3). The center of radial bias force 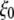 (see text) moved at a rate of 1 Å/ns.
(see text) moved at a rate of 1 Å/ns.
The S1 helix plays an important role in MscL opening. To illustrate this, the old 1MSL structure, which has no S1 helix, was used in the radial bias force simulations with almost identical conditions. These resulted in a pore of ∼3-Å radius for 4 ns of radial bias force simulation but at longer times the MscL structure became distorted and the fivefold symmetry was lost. In contrast, simulations using the 2OAR structure preserved the protein symmetry and structure up to the end, with a pore of radius 10 Å. Fig. 8 a shows that the S1 helices initially point outward radially and make contact with two TM2 helices from other monomeric units that are ahead of it in a clockwise direction. This presumably provides a better contact and stability among monomeric units. In the highly expanded state (t = 9 ns in Fig. 8 a), however, the S1 parts rotate so that it is aligned in the tangential direction on the cytoplasmic periphery of the protein. This enables the S1 units to maintain their interaction with other TM2 helices even with a wider gap between the latter helices. In addition, the loop region seems to contribute to the stability of MscL during the opening. It makes contact with the TM1 and loop from an adjacent monomeric unit in the counterclockwise direction. This contact was preserved during the expansion. The fact that the loop and S1 are directed oppositely and make contact with other monomers in the opposite directions would contribute to stabilizing the open structure, because transmembrane helices tilt significantly. Had they been aligned in the same direction, the structure would be more prone to falling apart. The behavior of individual components during the MscL opening is summarized in Fig. S6. Most of the components show a steady increase in lateral dimension. In particular, the top half of TM1 (Fig. S6 a) expands faster than the top half of TM2 (Fig. S6 c), and they have a comparable lateral dimension at the end of simulations. It is also interesting to note that the S1 helices (Fig. S6 f) do not expand much initially but exhibit rapid increase in lateral dimension after 4 ns, coincident with the channel opening. A similar transitional behavior around 4 ns can be identified in TM2 bottom (Fig. S6 d) and in the loop region (Fig. S6 e). This indicates that the channel opening involves a concerted motion of these subunits. The plateau found at 7–8 ns in S1 helices (Fig. S6 f) can be explained by the aforementioned rearrangement of S1 from radial to tangential directions.
Simulations RSE and RSF with asymmetric membranes exhibit interesting differences from simulation RS, which has a symmetric membrane. According to Fig. 11, the channel opening in RSE and RSF is initiated earlier by ∼0.5 ns than in RS. Also, Fig. 9 b shows that the minimum pore radii in RSE and RSF are ∼1 Å larger than in RS at 5 ns. Thus, the membrane asymmetry can lower the threshold tension for channel opening significantly. This can be caused by the protein structural changes induced by membrane asymmetry or higher lateral tension arising from the fewer number of lipids in the asymmetric membrane. The relative importance of the two is difficult to gauge at this point. The membrane asymmetry is also reflected in the 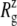 of individual components shown in Fig. S6. For example, RSE has a larger lateral dimension than RS or RSF in the loop region (Fig. S6 e), because its upper leaflet has low density. On the other hand, the TM2 bottom half (Fig. S6 d) is generally more expanded in RSF, which has fewer lipids on the lower leaflet.
of individual components shown in Fig. S6. For example, RSE has a larger lateral dimension than RS or RSF in the loop region (Fig. S6 e), because its upper leaflet has low density. On the other hand, the TM2 bottom half (Fig. S6 d) is generally more expanded in RSF, which has fewer lipids on the lower leaflet.
It is remarkable that the partially open state of MscL in Fig. 8 b shows little interaction between water molecules at the bottleneck region of the channel and nearby hydrophilic residues. As shown in the figure, the only hydrophilic assistance comes from Asn13 and Asp16 on the cytoplasmic side of TM1. These residues make contact with water molecules on the lower side of the channel and can possibly stabilize the water chain once one is formed. However, these residues are distant from the Val21 that forms the hydrophobic lock and cannot move into the constriction region to directly induce water chain formation. Inspection of trajectories around the initial channel opening at 2-ps intervals revealed that intermittent water chains keep appearing and disappearing for a few tens of picoseconds without direct involvement of protein hydrophilic residues before a persistent chain is formed. This suggests that the driving force for water chain formation does not come from the movement of hydrophilic residues to the constriction region. Instead, the connection of the water channel and its subsequent growth may be driven by the hydrophobic interaction between the channel water and the pore residues that makes the disconnected channel water clusters increasingly unstable as their size grows. With no available hydrophilic residues to stabilize the surfaces of water clusters facing the constriction region, this force can be relieved only by the connection of the clusters. The importance of hydrophobic interactions in channel gating has been demonstrated previously by hydrophilic mutations of the MscL and MscS constriction regions (54,55) and a dewetting transition in melittin tetramer (56). However, a more quantitative study of the hydrophobic effect over a wider range of gating behaviors would be necessary to resolve this issue.
We note that the bias potential used in the radial bias force simulations can be used as an umbrella sampling potential in the calculation of a free-energy profile along the channel expansion coordinate. A full investigation of the quantitative free-energy profile of MscL gating will be the subject of future work. Several other issues to be explored in the future include the possible roles of both long-wavelength membrane motions (not captured in an atomistic MD simulation box) and lipid rafts in stabilizing the proposed open-channel state.
CONCLUSIONS
In this article, the gating of the mechanosensitive channel protein MscL has been studied using equilibrium and nonequilibrium MD simulations. The equilibrium MD on the crystal structure of MscL resulted in even further contraction and supported the notion that the crystal structure is in a partially open state. Through the NEMD simulation of membrane area expansion, the inclusion of MscL is found to increase the rigidity of the membrane by 22% against area expansion, larger than the area fraction of MscL (0.16) indicates. This could be attributed to lipids adjacent to the protein which maintain their structure and order under tension due to protein-lipid interaction. Channel opening and large water column formation across the protein could be observed by applying radial bias forces on the MscL-membrane system under large negative lateral pressure. It was shown that the channel pore expansion is concurrent with the water chain formation across the channel. Also, consistent with previous experimental studies on the asymmetric LPC incorporation (12,13), the asymmetric membrane is shown to facilitate channel opening significantly. A recent study (53) showed that the lipid chain length dependence of MscL-lipid binding constant differs on the two sides of the membrane, again pointing to the importance of membrane asymmetry in MscL-lipid interaction. Finally, the water chain formation across MscL was found to take place without direct involvement of hydrophilic residues of MscL. This indicates an important role of hydrophobic forces on the MscL gating. Although not pursued in detail here, a direct computation of the free-energy profile along the channel gating pathways may become a viable approach in a large class of membrane channel proteins with the proper refinement of the current method in terms of the choice of parameters and application of bias potentials.
SUPPLEMENTARY MATERIAL
To view all of the supplemental files associated with this article, visit www.biophysj.org.
Acknowledgments
Computer resources were provided by the National Science Foundation, under the NSF Teragrid program, and by the Center for High Performance Computing at the University of Utah.
This work was supported by a grant from the National Institutes of Health (RO1-GM63796).
Jonggu Jeon's present address is Department of Chemistry, Korea University, Seoul 136-701, Republic of Korea.
Editor: Eduardo Perozo.
References
- 1.Hamill, O. P., and B. Martinac. 2001. Molecular basis of mechanotransduction in living cells. Physiol. Rev. 81:685–740. [DOI] [PubMed] [Google Scholar]
- 2.Sukharev, S., and D. P. Corey. 2004. Mechanosensitive channels: multiplicity of families and gating paradigms. Sci. STKE. 219:re4. [DOI] [PubMed] [Google Scholar]
- 3.Kung, C. 2005. A possible unifying principle for mechanosensation. Nature. 436:647–654. [DOI] [PubMed] [Google Scholar]
- 4.Cruickshank, C. C., R. F. Minchin, A. C. Le Dain, and B. Martinac. 1997. Estimation of the pore size of the large-conductance mechanosensitive ion channel of Escherichia coli. Biophys. J. 73:1925–1931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Sukharev, S. I., B. Martinac, V. Y. Arshavsky, and C. Kung. 1993. Two types of mechanosensitive channels in the Escherichia coli cell envelope: solubilization and functional reconstitution. Biophys. J. 65:177–183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Perozo, E., and D. C. Rees. 2003. Structure and mechanism in prokaryotic mechanosensitive channels. Curr. Opin. Struct. Biol. 13:432–442. [DOI] [PubMed] [Google Scholar]
- 7.Chang, G., R. H. Spencer, A. T. Lee, M. T. Barclay, and D. C. Rees. 1998. Structure of the MscL homolog from Mycobacterium tuberculosis: a gated mechanosensitive ion channel. Science. 282:2220–2226. [DOI] [PubMed] [Google Scholar]
- 8.Steinbacher, S., R. Bass, P. Strop, and D. C. Rees. 2007. Structures of the prokaryotic mechanosensitive channels MscL and MscS. Curr. Top. Membranes. 58:1–24. [Google Scholar]
- 9.Sukharev, S., W. J. Sigurdson, C. Kung, and F. Sachs. 1999. Energetic and spatial parameters for gating of he bacterial large conductance mechanosensitive channel, MscL. J. Gen. Physiol. 113:525–539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Moe, P. C., G. Levin, and P. Blount. 2000. Correlating a protein structure with function of a bacterial mechanosensitive channel. J. Biol. Chem. 275:31121–31127. [DOI] [PubMed] [Google Scholar]
- 11.Evans, E., V. Heinrich, F. Ludwig, and W. Rawicz. 2003. Dynamic tension spectroscopy and strength of biomembranes. Biophys. J. 85:2342–2350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Perozo, E., D. M. Cortes, P. Sompornpisut, A. Kloda, and B. Martinac. 2002. Open channel structure of MscL and the gating mechanism of mechanosensitive channels. Nature. 418:942–948. [DOI] [PubMed] [Google Scholar]
- 13.Perozo, E., A. Kloda, D. M. Cortes, and B. Martinac. 2002. Physical principles underlying the transduction of bilayer deformation forces during mechanosensitive channel gating. Nat. Struct. Biol. 9:696–703. [DOI] [PubMed] [Google Scholar]
- 14.Sukharev, S., M. Betanzos, C.-S. Chiang, and H. R. Guy. 2001. The gating mechanism of the large mechanosensitive channel MscL. Nature. 409:720–724. [DOI] [PubMed] [Google Scholar]
- 15.Betanzos, M., C.-S. Chiang, H. R. Guy, and S. Sukharev. 2002. A large iris-like expansion of a mechanosensitive channel protein induced by membrane tension. Nat. Struct. Biol. 9:704–710. [DOI] [PubMed] [Google Scholar]
- 16.Cantor, R. S. 1997. Lateral pressures in cell membranes: a mechanism for modulation of protein function. J. Phys. Chem. B. 101:1723–1725. [Google Scholar]
- 17.Gullingsrud, J., and K. Schulten. 2004. Lipid bilayer pressure profiles and mechanosensitive channel gating. Biophys. J. 86:3496–3509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Iscla, I., G. Levin, R. Wray, and P. Blount. 2007. Disulfide trapping the mechanosensitive channel MscL into a gating-transition state. Biophys. J. 92:1224–1232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Gullingsrud, J., D. Kosztin, and K. Schulten. 2001. Structural determinants of MscL gating studied by molecular dynamics simulations. Biophys. J. 80:2074–2081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Elmore, D. E., and D. A. Dougherty. 2001. Molecular dynamics simulations of wild-type and mutant forms of the Mycobacterium tuberculosis MscL channel. Biophys. J. 81:1345–1359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Bilston, L. E., and K. Mylvaganam. 2002. Molecular simulations of the large conductance mechanosensitive (MscL) channel under mechanical loading. FEBS Lett. 512:185–190. [DOI] [PubMed] [Google Scholar]
- 22.Kong, Y., Y. Shen, T. E. Warth, and J. Ma. 2002. Conformational pathways in the gating of Escherichia coli mechanosensitive channel. Proc. Natl. Acad. Sci. USA. 99:5999–6004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Sukharev, S., S. R. Durell, and H. R. Guy. 2001. Structural models of the MscL gating mechanism. Biophys. J. 81:917–936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Elmore, D. E., and D. A. Dougherty. 2003. Investigating lipid composition effects on the mechanosensitive channel of large conductance (MscL). Using molecular dynamics simulations. Biophys. J. 85:1512–1524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Colombo, G., S. J. Marrink, and A. E. Mark. 2003. Simulation of MscL gating in a bilayer under stress. Biophys. J. 84:2331–2337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Gullingsrud, J., and K. Schulten. 2003. Gating of MscL studied by steered molecular dynamics. Biophys. J. 85:2087–2099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Meyer, G. R., J. Gullingsrud, K. Schulten, and B. Martinac. 2006. Molecular dynamics study of MscL interactions with a curved lipid bilayer. Biophys. J. 91:1630–1637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Sotomayor, M., V. Vasquez, E. Perozo, and K. Schulten. 2007. Ion conduction through MscS as determined by electrophysiology and simulation. Biophys. J. 92:886–902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Valadié, H., J. J. Lacapčre, Y.-H. Sanejouand, and C. Etchebest. 2003. Dynamical properties of the MscL of Escherichia coli: a normal mode analysis. J. Mol. Biol. 332:657–674. [DOI] [PubMed] [Google Scholar]
- 30.Markin, V. S., and F. Sachs. 2004. Thermodynamics of mechanosensitivity. Phys. Biol. 1:110–124. [DOI] [PubMed] [Google Scholar]
- 31.Wiggins, P., and R. Phillips. 2004. Analytic models for mechanotransduction: Gating a mechanosensitive channel. Proc. Natl. Acad. Sci. USA. 101:4071–4076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Wiggins, P., and R. Phillips. 2005. Membrane-protein interactions in mechanosensitive channels. Biophys. J. 88:880–902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Tang, Y., G. Cao, X. Chen, J. Yoo, A. Yethiraj, and Q. Cui. 2006. A finite element framework for studying the mechanical response of macromolecules: application to the gating of the mechanosensitive channel MscL. Biophys. J. 91:1248–1263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Jeon, J., and G. A. Voth. 2005. The dynamic stress responses to area change in planar lipid bilayer membranes. Biophys. J. 88:1104–1119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Levin, G., and P. Blount. 2004. Cysteine scanning of MscL transmembrane domains reveals residues critical for mechanosensitive channel gating. Biophys. J. 86:2862–2870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Bartlett, J. L., G. Levin, and P. Blount. 2004. An in vivo assay identifies changes in residue accessibility on mechanosensitive channel gating. Proc. Natl. Acad. Sci. USA. 101:10161–10165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Iscla, I., G. Levin, R. Wray, R. Reynolds, and P. Blount. 2004. Defining the physical gate of a mechanosensitive channel, MscL, by engineering metal-binding sites. Biophys. J. 87:3172–3180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Tieleman, D. P., and H. J. C. Berendsen. 1998. A molecular dynamics study of the pores formed by Escherichia coli OmpF porin in a fully hydrated palmitoyloleoylphosphatidylcholine bilayer. Biophys. J. 74:2786–2801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Moe, P., and P. Blount. 2005. Assessment of potential stimuli for mechano-dependent gating of MscL: effects of pressure, tension, and lipid headgroups. Biochemistry. 44:12239–12244. [DOI] [PubMed] [Google Scholar]
- 40.Berendsen, H. J. C., J. P. M. Postma, W. F. van Gunsteren, and J. Hermans. 1981. Interaction models for water in relation to protein hydration. In Intermolecular Forces. B. Pullman, editor. Reidel, Dordrecht. 331–342.
- 41.Ajouz, B., C. Berrier, M. Besnard, B. Martinac, and A. Ghazi. 2000. Contributions of the different extramembranous domains of the mechanosensitive ion channel MscL to its response to membrane tension. J. Biol. Chem. 275:1015–1022. [DOI] [PubMed] [Google Scholar]
- 42.Berger, O., O. Edholm, and F. Jahnig. 1997. Molecular dynamics simulations of a fluid bilayer of dipalmitoylphosphatidylcholine at full hydration, constant pressure, and constant temperature. Biophys. J. 72:2002–2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Lindahl, E., B. Hess, and D. van der Spoel. 2001. GROMACS 3.0: a package for molecular simulation and trajectory analysis. J. Mol. Model. 7:306–317. [Google Scholar]
- 44.Spoel, D. V. D., E. Lindahl, B. Hess, G. Groenhof, A. E. Mark, and H. J. C. Berendsen. 2005. GROMACS: fast, flexible, and free. J. Comput. Chem. 26:1701–1718. [DOI] [PubMed] [Google Scholar]
- 45.Nosé, S. 1984. A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 52:255–268. [Google Scholar]
- 46.Hoover, W. G. 1985. Canonical dynamics: equilibrium phase-space distributions. Phys. Rev. A. 31:1695–1697. [DOI] [PubMed] [Google Scholar]
- 47.Berendsen, H. J. C., J. P. M. Postma, W. F. van Gunsteren, A. DiNola, and J. R. Haak. 1984. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 81:3684–3690. [Google Scholar]
- 48.Darden, T., D. York, and L. Pedersen. 1993. Particle mesh Ewald: An N-log(N) method for Ewald sums in large systems. J. Chem. Phys. 98:10089–10092. [Google Scholar]
- 49.Smart, O. S., J. G. Neduvelila, X. Wanga, B. A. Wallacea, and M. S. P. Sansom. 1996. HOLE: a program for the analysis of the pore dimensions of ion channel structural models. J. Mol. Graph. 14:354–360. [DOI] [PubMed] [Google Scholar]
- 50.Egberts, E., and H. J. C. Berendsen. 1988. Molecular dynamics simulation of a smectic liquid crystal with atomic detail. J. Chem. Phys. 89:3718–3732. [Google Scholar]
- 51.Evans, E., and D. Needham. 1987. Physical properties of surfactant bilayer membranes: thermal transitions, elasticity, rigidity, cohesion, and colloidal interactions. J. Phys. Chem. 91:4219–4228. [Google Scholar]
- 52.Rawicz, W., K. C. Olbrich, T. McIntosh, D. Needham, and E. Evans. 2000. Effect of chain length and unsaturation on elasticity of lipid bilayers. Biophys. J. 79:328–339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Powl, A. M., J. M. East, and A. G. Lee. 2007. Different effects of lipid chain length on the two sides of a membrane and the lipid annulus of MscL. Biophys. J. 93:113–122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Anishkin, A., C.-S. Chiang, and S. Sukharev. 2005. Gain-of-function mutations reveal expanded intermediate states and a sequential action of two gates in MscL. J. Gen. Physiol. 125:155–170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Anishkin, A., and S. Sukharev. 2004. Water dynamics and dewetting transitions in the small mechanosensitive channel MscS. Biophys. J. 86:2883–2895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Liu, P., X. Huang, R. Zhou, and B. J. Berne. 2005. Observation of a dewetting transition in the collapse of the melittin tetramer. Nature. 437:159–162. [DOI] [PubMed] [Google Scholar]
- 57.Humphrey, W., A. Dalke, and K. Schulten. 1996. VMD: visual molecular dynamics. J. Mol. Graph. 14:33–38. [DOI] [PubMed] [Google Scholar]