Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2008 Jan 22;94(9):3393–3404. doi: 10.1529/biophysj.107.112805

Distribution of Amino Acids in a Lipid Bilayer from Computer Simulations

Justin L MacCallum 1, W F Drew Bennett 1, D Peter Tieleman 1
PMCID: PMC2292383  PMID: 18212019

Abstract

We have calculated the distribution in a lipid bilayer of small molecules mimicking 17 natural amino acids in atomistic detail by molecular dynamics simulation. We considered both charged and uncharged forms for Lys, Arg, Glu, and Asp. The results give detailed insight in the molecular basis of the preferred location and orientation of each side chain as well the preferred charge state for ionizable residues. Partitioning of charged and polar side chains is accompanied by water defects connecting the side chains to bulk water. These water defects dominate the energetic of partitioning, rather than simple partitioning between water and a hydrophobic phase. Lys, Glu, and Asp become uncharged well before reaching the center of the membrane, but Arg may be either charged or uncharged at the center of the membrane. Phe has a broad distribution in the membrane but Trp and Tyr localize strongly to the interfacial region. The distributions are useful for the development of coarse-grained and implicit membrane potentials for simulation and structure prediction. We discuss the relationship between the distribution in membranes, bulk partitioning to cyclohexane, and several amino acid hydrophobicity scales.

INTRODUCTION

Integral membrane proteins are responsible for a range of important cellular processes, including transport and signaling, and are targeted by a substantial fraction of current drugs. However, our current understanding of membrane protein structure and membrane protein interactions with lipids is still rather limited due to the difficulties in obtaining high-resolution structures of membrane proteins and the disordered nature of the lipid environment with its strong gradients in density, chain order, and polarity.

The thermodynamics of lipid side chain interactions is a major and general determinant of membrane protein structure and behavior. The lipid-exposed outside of integral membrane proteins is largely hydrophobic, matching the hydrophobic nature of the lipid tails that make up ∼40% of the thickness of the bilayer. However, for simple hydrophobic side chains partitioning is likely nontrivial, because the structure of the lipid chains enhances the role that the shape of hydrophobic side chains is expected to play.

The behavior of polar and charged residues when they are moved into the hydrocarbon core is governed by large and opposing tendencies, including hydrogen bonding, hydrophobic effects, and the energetic costs of membrane deformation and transfer of charges and dipoles into a low dielectric environment.

Two recent crystal structures of voltage gated potassium channels present a particularly striking example of the difficulty of predicting the behavior of lipid-exposed charged residues (1,2). Both structures contain arginine residues that appear to be lipid exposed, leading to at least one model in which the arginine residues remain lipid exposed during channel gating (3,4). This model has provoked considerable controversy for a number of reasons, including arguments based on the energetics of having an arginine residue exposed to the lipid core (5,6). Interestingly, the small conductance mechanosensitive channel MscS, which although not voltage-gated is voltage-sensitive (7), also appeared to have lipid-exposed arginine residues in the crystal structure. However, the arginine residues reside at the interface in a more recent structure (8).

Understanding the partitioning of amino acid side chains into lipid bilayers is thus a critical step for understanding the thermodynamics of membrane protein structure and stability (9). Numerous experimental studies have addressed this question with significant success (10–12). However, the results of most experiments have limited spatial resolution. In particular, it is difficult to control the local environment of a side chain in experiments due to the inhomogeneous nature and the deformability of the bilayer. These factors also make the behavior of side chains difficult to predict.

Atomistic computer simulations may overcome these limitations and provide a level of detail that is not accessible to experiment, whereas at the same time they can be validated against experimental macroscopic measurements. Qualitatively, simulations of a systematic series of designed pentapeptides (13,14) have provided a molecular interpretation of the thermodynamic measurements that form the basis of the widely used hydrophobicity scale of White et al. (15,16). More quantitatively, the partitioning of side chain analogs between water and hydrophobic solvents in particular has been used to test and parameterize molecular dynamics force fields (17–23). Several computational studies have also addressed the distribution of specific small molecules in lipid bilayers (24–33). We combine the two approaches and calculate the position dependent free energy of analogs of the amino acid side chains with sub-ångström resolution in a dioleoylphosphatidylcholine (DOPC) bilayer, using umbrella sampling. The side chains were truncated at the β-carbon, yielding small molecule analogs. For example, valine becomes propane, and serine becomes methanol. For simplicity, the chemical analogs are referred to by the three-letter code of the corresponding amino acid.

Our calculated potentials of mean force (PMF) show large gradients in free energy as the side chains move across the membrane, with distinct behavior depending on hydrophobicity, shape, polar and charged character. We discuss the different classes of amino acids and compare the results to experimental partition coefficients for small molecules and a number of existing hydrophobicity scales based on host-guest peptides. We have compared the current results to several experimental scales in detail in a previous publication (33).

Our results may also be useful for the development of simpler potentials to describe membranes. We have used the PMFs to parameterize a coarse-grained model for proteins (67) that is consistent with the coarse-grained lipid force field of Marrink et al. (34,35) in which ∼4 nonhydrogen atoms are combined and described by a single interaction site. The PMFs could also be used as implicit potentials or as part of implicit potentials, such as the statistical potential of Ulmschneider et al. (36), the generalized Born-based potentials of Im et al. (37) and Feig et al. (38,39), in combination with Rosetta (40,41), and the free energy-based potential of Lazarides (42).

METHODS

The partitioning of all amino acid side chains excluding His, Gly, and Pro, but including both the charged and neutral forms of Glu, Asp, Lys, and Arg, were calculated by molecular dynamics simulations. The side chains were truncated at the β-carbon; the α-carbon was replaced by a proton and the charge on the β-carbon was adjusted appropriately. Gly, Pro, and His were not modeled as Gly and Pro do not have suitable small molecule equivalents of their side chains, and His is difficult to treat accurately due to its multiple possible protonation states.

Each simulation contained two copies of the same side chain, one in either leaflet of the DOPC bilayer, to increase computational efficiency. The system contained 2807 water molecules, 64 DOPC molecules, and 2 side chains. Depending on the side chain there were ∼11,900 atoms in total. All simulations were run with the GROMACS 3.3.1 software package (43). The Berger et al. force field was used for the DOPC molecules (44), the OPLS all-atom force field for the side chains (45,46), and the Simple Point Charge water model (47). This combination has been tested previously and found to yield relatively accurate water-cyclohexane transfer free energies (21). The system was maintained at a constant temperature of 298 K using the weak coupling algorithm (48) to lipids and solvent separately, with a coupling constant of 0.1 ps. The pressure was held constant at 1 bar using the semi-isotropic weak coupling algorithm, with a coupling constant of 1 ps. The SETTLE algorithm (49) was used to constrain water bond lengths and angles. All other bond lengths were constrained with the LINCS algorithm (50), allowing for a 2-fs time step. Electrostatic interactions were evaluated using the smooth particle mesh Ewald method (51,52), with a real space cutoff of 1.0 nm, grid spacing of 0.12 nm, and a fourth-order spline interpretation. Lennard-Jones interactions were truncated at 1.0 nm.

Umbrella sampling was used to calculate free energy profiles for partitioning of the side chains. A harmonic restraint with a force constant of 3000 kJ mol−1 nm−2 was applied to the distance between the side chain's center of mass and the center of mass of the bilayer, in the direction normal to the bilayer, to ensure sampling of the entire system occurred. There was a 0.1 nm spacing between biasing potentials, with a total of 38 simulations for each side chain. The two side chains were offset, so that when the first side chain was in the center of the bilayer, the other side chain was in bulk water. Carrying out the simulations in this way allows additional statistics to be gathered at essentially no cost, whereas at the same time ensuring that the two side chains are always at least 3.7 nm apart. Each simulation was run for at least ∼30 ns for a total of ∼20 μs of simulation time for all the side chains. The charged and polar residues, as well as Trp, were run for up to 80 ns as required to obtain acceptable error margins. The weighted histogram analysis method (53) was used to calculate the PMFs for the side chains from the biased distributions. As two side chains were simulated for each window, the error could be estimated by the difference between the two PMFs, which should be zero in the limit of infinite sampling. We treat the two halves of the PMFs as independent samples and report the standard error. As the free energy profiles are relative, they were shifted to be zero in bulk water in all cases.

RESULTS

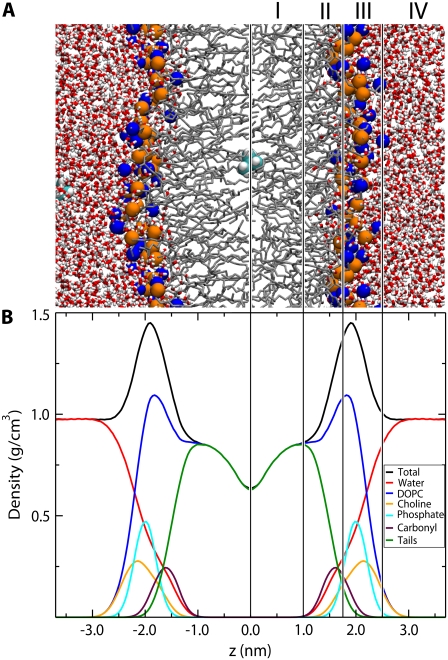
A snapshot and partial density profile of the simulated bilayer system are shown in Fig. 1. To aid in the description of the PMFs below we have adopted a four-region model of the bilayer based on the density profile, similar to that of Marrink et al. (34). Starting from the center of the bilayer, Region I contains only the hydrophobic lipid tails, and has the lowest density of the entire system. Region II contains both hydrophobic tails and the initial portion of the polar headgroup density and begins at the minimum depth of the carbonyls, where the lipid tail density falls drastically. Region II ends where the lipid tail density intersects the choline density. Throughout this region, the total system density increases dramatically. It is chemically the most diverse region, containing both hydrophobic and hydrophilic components as well as limited water penetration. The total system density peaks at the start of Region III, and then falls to the density of bulk water. Region III contains most of the charged phosphate and choline density. Region IV is comprised primarily of bulk water with a small portion of the DOPC headgroup density.

FIGURE 1.

FIGURE 1

Open in a new tab

Snapshot and partial density profiles of the simulated system. The lines and roman numerals divide the system into four regions as described in the text. (A) Snapshot of the simulated system. The lipid nitrogen and phosphate atoms are shown as blue and orange spheres respectively. Water is shown as red (oxygen) and white (hydrogen) cylinders. The lipid tails are shown as thin gray lines. Two valine side chains are shown as cyan (carbon) and white (hydrogen) spheres. (B) Partial density profile for the system.

Distribution of Ala, Val, Ile, Leu

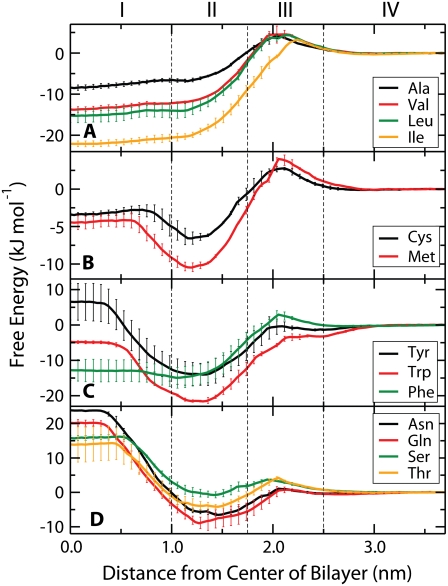
The PMFs for the aliphatic side chains (Ala, Val, Ile, Leu) are shown in Fig. 2 A. The energetic minimum for all four aliphatic residues is at the center of the bilayer. Ile has the lowest free energy (−22 kJ/mol) at the center of the bilayer and Ala has the highest (−8 kJ/mol). The profile is generally smooth with a barrier of up to 5 kJ/mol between bulk water and the beginning of the lipid chains.

FIGURE 2.

FIGURE 2

Open in a new tab

PMFs for uncharged amino acids: (A) aliphatic, (B) Cys and Met, (C) aromatic, (D) polar. All PMFs are set to zero in the water phase. The system is divided into the same four regions as in Fig. 1. Error bars indicate the SE based on the asymmetry between the two leaflets of the bilayer.

Distribution of Cys, Met

Fig. 2 B shows the PMFs for Cys and Met. Transfer to the center of the membrane is slightly favorable for both residues, in agreement with measurements of the transfer of these compounds from water into cyclohexane (54). The minima for both PMFs are near the center of Region II, consistent with the slightly amphipathic nature of these molecules.

Distribution and orientation of Trp, Tyr, Phe

The PMFs for the aromatic side chains (Trp, Tyr, Phe) are shown in Fig. 2 C. Tyrosine has a positive free energy in Region I (7 kJ/mol), whereas phenylalanine and tryptophan both have negative free energies of −5 kJ/mol and −13 kJ/mol, respectively. Trp and Tyr have deep global minima in the center of Region II, which seems due to their amphipathic nature. Trp has the deepest interfacial minimum of any residue at −22 kJ/mol, whereas Tyr has the next deepest at −14 kJ/mol.

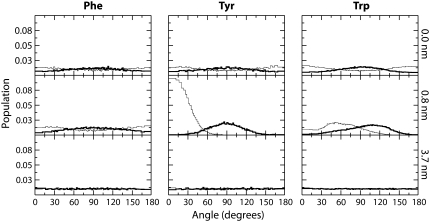
The orientation of the aromatic rings as a function of location in the bilayer is of interest in the context of membrane protein structure and the use of fluorescence probes, which often contain aromatic ring systems. We calculated the orientation of the rings by defining two vectors. The first vector θ1, is normal to the plane of the aromatic ring. The second vector, θ2, is between C1 and C3 of the benzene ring of both Tyr and Phe, whereas for Trp the vector was between CD1 and CH2. The distribution of angles between these vectors and the bilayer normal are shown in Fig. 3 for three locations in the bilayer.

FIGURE 3.

FIGURE 3

Open in a new tab

Orientation of aromatic residues as a function of depth in the membrane. The panels show the orientations when the aromatic residue is at the center of the membrane (top), at 0.8 nm from the center (middle), and in bulk water (bottom). The thick lines represent the distribution of θ1, which is the angle between the normal of the aromatic ring and the bilayer normal. Thin lines represent the distribution of θ2, which represents the angle between the long axis of the molecule and the bilayer normal. For Phe and Tyr, θ2 represents the angle between the vector defined by C1 and C3 of the benzene ring and the bilayer normal. For Trp, θ2 represents the angle between the vector defined by CD1 and CH2 and the bilayer normal.

All residues display a uniform distribution in Region IV, which is expected as there should be no preferential alignment of the molecule in bulk water. At the center of the bilayer, all of the molecules have a slight tendency to align the plane of the ring with the bilayer normal, an effect most apparent for Trp. At 0.8 nm from the center of the bilayer, in the dense, ordered portion of the lipid tails, all three molecules display a strong tendency to align their ring structures with the lipid tails. For Trp and Tyr there is a clear trend for the polar portion of the molecule to face out of the bilayer toward the water phase.

Distribution of Thr, Ser, Gln, Asn

The PMFs for the four polar residues (Asn, Gln, Ser, Thr) are all similar (Fig. 2 D). They have large positive free energies at the bilayer center, with Asn the highest (24 kJ/mol) and Thr the lowest (13 kJ/mol). There is an interfacial minimum for all four residues in the center of Region II, consistent with the amphipathic nature of these molecules. The free energy increases rapidly as the side chain moves closer to the center of the membrane. Near the center of Region I, the free energy plateaus and remains essentially constant through the center of the bilayer.

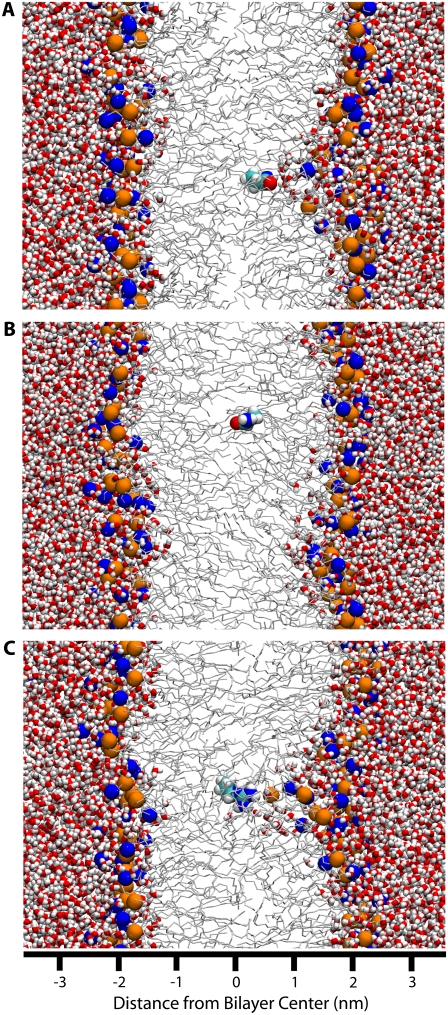
The plateau in the center of Region II correlates strongly with local defects in bilayer structure (see Water Defects below). At distances between the interfacial minimum and the plateau, large water defects in the bilayer are observed, which hydrate the polar side chains (Fig. 4 A). At the edge of the plateau the water defects suddenly dissipate, leaving an isolated side chain (Fig. 4 B).

FIGURE 4.

FIGURE 4

Open in a new tab

Snapshots of polar and charged residues near the center of the bilayer. The system is presented using the same colors and representations as Fig. 1. (A) Asn at 0.4 nm from the center of the bilayer. A large, partially lipid-lined water defect is present. (B) Asn at 0.3 nm from the center of the bilayer. Moving the Asn 0.1 nm further from the center of the bilayer has led to the dissipation of the water defect. (C) A positively charged Arg at the center of the bilayer, with associated water defect.

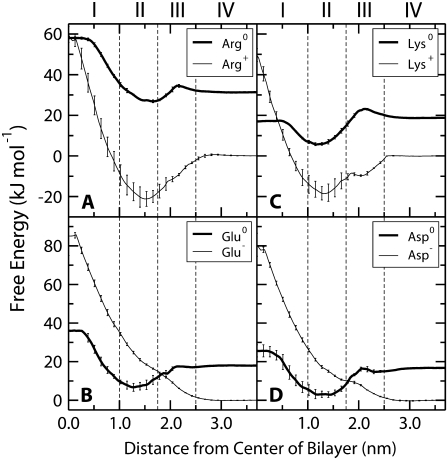
Distribution of Arg, Lys, Glu, Asp

The PMFs for the charged and neutral forms of Lys, Arg, Asp, and Glu are shown in Fig. 5. The neutral PMFs have been shifted by the free energy of neutralizing the residues in bulk water at pH 7. The partitioning of the neutral forms is comparable to the polar residues, with similar PMFs and a consistent pattern of water defect formation and dissipation. For the ionized forms, there is a large difference between the PMFs for positively and negatively charged side chains. For Arg and Lys, there is a decrease in free energy from bulk water to the center of Region II, after which the PMFs rise steeply to the bilayer center. In contrast, for Glu and Asp there is a steady increase in energy from bulk water to the center of the bilayer without a local minimum in Region II. The PMFs for all of the charged forms continue to increase until the center of the bilayer, which correlates with the presence of a large water defect that penetrates all the way to the center of the bilayer (Fig. 4 C).

FIGURE 5.

FIGURE 5

Open in a new tab

PMFs for the ionizable residues: (A) Arg, (B) Lys, (C) Glu, (D) Asp. The PMFs for the ionized forms have been set to zero in the water phase. The neutral PMFs have been offset by the free energy to neutralize the residue in bulk water at pH 7.0. Error bars indicate the SE based on the asymmetry between the two leaflets of the bilayer.

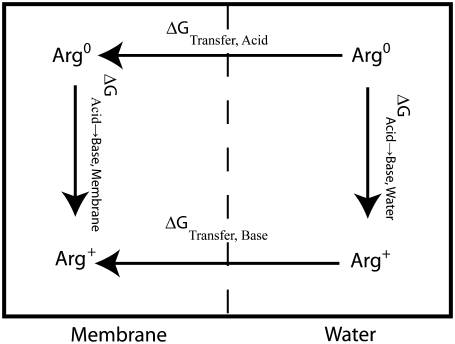
The distribution of Arg, Lys, Glu, and Asp is complicated by the fact that the free energy for changing their ionization state may outweigh the free energy cost of burying a charge in the membrane. Although we cannot directly simulate the protonation/deprotonation reactions, we can calculate the free energy difference between the charged and uncharged state of each amino acid as a function of the depth inside the membrane. We use a thermodynamic cycle (Fig. 6) that includes protonation/deprotonation in bulk water (not calculated from the simulation but taken from the pKa of each side chain) and calculating the PMFs for each charged or neutral side chain in the membrane. These three calculations form three sides of the square in Fig. 6 and are sufficient to calculate the fourth: the free energy of protonation/deprotonation as function of depth in the membrane. This way, we do not have to assume a charge state, and in fact we can calculate for each depth and each side chain what the preferred charge state is.

FIGURE 6.

FIGURE 6

Open in a new tab

Thermodynamic cycle for calculation the pKa as function of depth in the membrane. The two ΔGTransfer values are calculated by umbrella sampling and ΔGAcid→Base,Water is calculated based on the pKa as described in the text. Calculation of these three terms allows the fourth term, ΔGAcid→Base,Membrane to be determined.

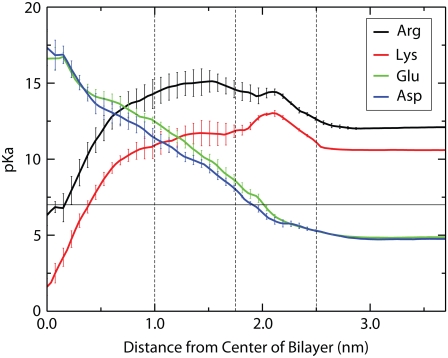
The calculated depth-dependent pKa values are shown in Fig. 7. The pKa is calculated from the free energy difference between the charged and neutral forms at a given depth using 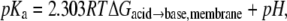Inline graphic where R is the gas constant, T is the temperature, and the pH is 7.0. For Asp and Glu, large positive shifts of up to ∼11 units are observed, consistent with the molecules becoming overwhelmingly likely to be protonated and thus neutral. The pKa reaches a value of 7 at ∼2.2 nm from the center of the bilayer, indicating that this is the crossover point between the ionized and neutral forms. For Lys, there is a large negative pKa shift, with the pKa reaching the crossover value of 7 at ∼0.4 nm from the center of the bilayer. There is also a large negative shift in pKa for Arg, however, it only reaches a pKa of 7 at the very center of the bilayer, indicating that the charged and neutral forms are nearly equal in free energy, and thus equal in population at this point.

FIGURE 7.

FIGURE 7

Open in a new tab

Side chain pKa as a function of depth in the membrane. The pKa is calculated from the free energy difference between the acidic and basic species as described in the text. Error bars indicate the SE error based on the asymmetry between the two leaflets of the bilayer.

Water defects

Large water defects accompany the partitioning of polar and charged residues into the hydrocarbon core (Fig. 4). The defects are very broad at the base on the surface of the bilayer, becoming narrow with only a few molecules surrounding the polar portion of the side chain. Lipid headgroups partially line the water defect, as seen in Fig. 4, A and C.

These water defects are extremely stable and repeatable. For example, for Asn at 0.4 nm from the center of the bilayer, once a defect has formed it is present for the remainder of the simulation (Fig. 4 A). In contrast, when Asn is 0.3 nm from the center of the bilayer, a water defect does not form on the 80 ns time scale of our simulations (Fig. 4 B). When a charged Arg molecule is placed at the center of the membrane, initially with no water defect, a water defect rapidly forms in the first few nanoseconds and is stable for the entire simulation (Fig. 4 C).

DISCUSSION

The primary results of our calculations are simply the distributions of the different amino acid analogs in a model bilayer. However, these distributions are nontrivial, and have significant biological implications because the thermodynamics of lipid–protein interactions is a fundamental driving force for processes involving membrane proteins and peptides. We will discuss the properties of the different classes of amino acids and specifically address the importance of water defects, the ionization behavior of ionizable residues, the relevance of our side chain results for hydrophobicity scales, and limitations of the classical simulations.

Most of the side chains have small energetic barriers at the middle of Region III. In addition, all of the side chains, except the totally hydrophobic aliphatic residues and phenylalanine, have local minima at the middle of Region II. One might expect that the energetic barriers in Region III are due to the disruption of favorable interactions between the zwitterionic headgroups. However, in a recent study of the partitioning of hexane where the PMFs were resolved into entropic and enthalpic components, we showed that partitioning to Region III is entropically very unfavorable, and enthalpically favorable (27). The local minimum at the center of Region II can be explained by the chemical diversity of this region. Most of the side chain analogs are at least somewhat amphipathic, and this region of the bilayer provides an optimum environment for an amphipathic molecule as it contains the interface between the hydrophobic lipid tails, and the polar carbonyl and phosphate groups, as well as significant water penetration.

Hydrophobic residues

The hydrophobic residues have distributions similar to that of hexane, but modulated by changes in size and, interestingly, shape. Surprisingly, the free energy for Ile is much more favorable than Ile. This can be explained by the fact that the side chains were truncated at the β-carbon. Thus Leu is a branched molecule (isobutane), whereas Ile is linear (butane), allowing it to pack into the lipid tails more effectively. The partitioning of Ile is slightly less favorable (−22 kJ/mol vs. −25 kJ/mol) than for hexane (27) as expected for a shorter linear alkane, however a different force field was used to model hexane in that study, making direct comparison difficult.

The aliphatic residues partition primarily to Region I, as would be expected for small hydrophobic molecules, in agreement with previous studies (24,27,55). The free energy increases as the side chain moves from the center toward the carbonyl groups because of an unfavorable entropy change due to the increasing order in the lipid tails (27). The free energy increases sharply from the center of Region II as the side chain moves into an increasingly polar and dense environment.

Polar residues

There is a delicate balance between the energetic cost of forming a water defect and the energetic benefit of hydrating the polar side chain. For short water defects, the free energy of hydrating the side chain compensates for the cost of forming the defect. As the defect becomes longer, the cost of forming the defect eventually becomes so large that it is no longer compensated by the gain in energy from hydration and the defect dissipates. The exact balance appears to be determined by the charge or polarity of the side chain and the physical properties of the lipid bilayer, such as the area per lipid and chain ordering. The more polar residues generally have longer water defects. In particular, the ionized forms of Asp, Glu, Lys, and Arg have water defects that are stable even when the side chain is in the center of the membrane. Water defects in the membrane due to the presence of polar or charged moieties are an emerging trend from several recent simulation studies in the context of lipid flip-flop (21), potassium channel voltage sensors (56), and in simulations of peptides containing polar or charged transmembrane peptides (5,57).

Recently, Johansson and Lindahl (57) have observed large water defects in simulations of transmembrane peptides containing polar or charged residues at various positions. They found a strong correlation between the amount of water hydrating the residue in the membrane and two commonly used hydrophobicity scales (15,58). They speculate that the free energy for partitioning a side chain may be determined by the entropic cost of maintaining hydration of the side chain, rather than the enthalpic loss due to loss of hydration, if one assumes that the cost of forming a defect is primarily entropic in nature. In our simulations, however, for all of the polar residues the water defect dissipates near the center of the bilayer, leaving the molecule with no hydrating water. Thus, we feel that the free energy for transfer to the center of the membrane is likely determined simply by the free energy of transfer between water and bulk hydrocarbon, whereas closer to the interface, the free energy of forming a water defect is a dominant factor.

Aromatic residues

Although all three residues (Trp, Tyr, Phe) are aromatic, they each have different chemical properties leading to distinct PMFs. Factors such as shape, hydrogen-bonding potential, and nonspecific electrostatic interactions may all play a role in the distribution of aromatic residues (31,59,60). Tryptophan in particular has attracted significant attention due its prevalence in membrane proteins in locations where it seems to “anchor” the protein in a lipid bilayer (31,59–61). Striking examples include the peptide gramicidin A (62) and OmpF porin (59), but the phenomenon is widespread. We calculate the distribution of Trp, Phe, and Tyr analogs within a consistent framework with the other amino acid analogs.

Loss of hydrogen bonding to the polar hydroxyl group of tyrosine makes partitioning to the center of the bilayer unfavorable. Based on the difference between Tyr and Phe at the center of the bilayer, we can estimate the cost of burying a hydroxyl group in the hydrocarbon core at ∼19 kJ/mol. Phenylalanine is purely hydrophobic, leading to a large favorable free energy for transfer to the lipid tails. Although tryptophan is primarily hydrophobic, it has enough polar character that transfer to the center of the bilayer is not as favorable as one might expect. Based on our calculations, Trp is the sixth most hydrophobic residue behind Ile, Leu, Val, Phe, and Ala, in good agreement with experiments measuring the partitioning between water and cyclohexane (54).

These results are consistent with the observation of aromatic belts in the interfacial region of integral membrane proteins (60). Interestingly, Trp is often considered to be the most hydrophobic residue based on partitioning into octanol (15) or model membranes (16). Instead, we feel Trp should be regarded as the most interfacially active side chain. Partitioning into model membranes actually reflects the interfacial preference for tryptophan, whereas water saturated octanol is known to form a heterogeneous environment with regions composed of hydrophobic alkane chains and hydrophilic hydroxyl groups and water (63) that may mimic the interfacial region of lipid bilayers more than their center.

A recent simulation study (31) examined the partitioning of analogs of Trp (indole) and Phe (benzene), and found that the interfacial preference of Trp was due to a combination of weak electrostatic factors and the otherwise hydrophobic nature of Trp. The hydrogen bonding ability of Trp and its small dipole moment tend to drive the molecule into polar environments, while at the same time Trp is very hydrophobic, which drives it into apolar environments. The membrane interface provides the optimum environment, with the apolar ring structure buried in the lipid tails, while there is still opportunity for electrostatic interactions with the carbonyl, glycerol, and headgroup moieties. Similar arguments can explain the interfacial preference of Tyr, although the electrostatic interactions for Tyr are much less subtle due to the presence of the highly polar hydroxyl group.

Fig. 3 shows the orientation of the aromatic residues at three different locations in the bilayer. As expected, none of the aromatic residues displays any preferential orientation in bulk water (lower panels). At the center of the membrane (upper panels), there is a slight tendency for all three residues to align with the plane of the ring structure aligned with the lipid tails (θ1 ≈ 90°). This effect is strongest for Trp, likely due to the larger size of its double ring structure. For Tyr, and especially Trp, there is a tendency to point the polar portion of the molecule toward the membrane interface (θ2 ≈ 0° or 180°). In the more dense portion of the lipid tails (middle panel), Trp and Tyr display a strong tendency to align the plane of the ring with the lipid tails (θ1 ≈ 90°), whereas this effect is much less pronounced for Phe. Additionally, both Trp and Tyr display a very strong tendency to point the polar portion of the molecule toward the lipid–water interface (θ2 ≈ 0°). This effect is very strong for Tyr, consistent with the highly polar nature of the hydroxyl group. Overall, the observed orientations in the center of the membrane and near the interface are in good agreement with previous MD simulations (61).

Ionizable residues

We can predict the ionization state of the charged residues based on the free energy difference between the charged and neutral forms. Fig. 7 shows the pKa values for the charged residues as a function of depth in the bilayer. The pKa values of both Asp and Glu move above 7.0 at distances less than ∼2.2 nm from the center of the bilayer, indicating that lipid exposed Asp and Glu residues will be protonated in Regions I and II. For lysine, the pKa does not fall below 7.0 until around 0.4 nm from the center of the bilayer, meaning that a lipid exposed lysine residue would remain charged well into Region I, accompanied by large water defects. In contrast, for Arg the pKa reaches a value of 7.0 only very near the center of the bilayer, raising the possibility that a lipid exposed arginine may still remain charged even at the center of a DOPC bilayer, stabilized (relative to a bulk hydrocarbon environment) by a large water defect (Fig. 4 C).

Dorairaj and Allen have determined recently the PMF of a poly-Leu helix containing a single positively charged Arg residue, in a DPPC membrane (5). They obtain a free energy of ∼70 kJ/mol for transferring the arginine from water to the center of the membrane, which is slightly higher than the 57 kJ/mol we calculate. However, because they are simulating an Arg residue in the context of a poly-Leu helix, the relevant quantity to compare is cost of transferring an Arg from water to the center of the membrane plus the cost of moving a Leu from the center of the membrane to water. Using our PMFs we obtain a value of 58 + 15 = 73 kJ/mol, which compares very favorably with their results. They also observe the formation of a large defect reaching all the way to the center of the bilayer and maintaining the hydration of the Arg residue. Water that has penetrated the hydrocarbon core of the bilayer stabilizes the Arg by as much as 145 kJ/mol, although that is not enough to overcome the electrostatic and deformation barrier presented by the membrane. In their study, they did not determine the protonation state of the arginine residue at the center of the membrane because they simulated the positively charged state only. In our simulations, however, we have simulated both the charged and neutral forms of arginine and find that the pKa shifts by ∼5.5 units so that it is very close to 7.0 at the center of a DOPC bilayer - indicating that the charged and neutral forms are approximately equally likely. Dorairaj and Allen additionally carried out continuum electrostatics calculations on the same system and found that the results depended heavily on the rotameric state of the arginine side chain and the dielectric constant of the protein. They obtained a wide range of values from ∼60 to 170 kJ/mol, depending on the exact choices made in the calculation. The extreme variability of the results points to the difficulty in performing continuum electrostatics calculations on systems of this type. Additionally, the favorable agreement observed in some cases is likely fortuitous, as continuum electrostatics models do not allow for flexibility of the bilayer as would be required for the formation of a water defect.

Relevance for hydrophobicity scales

We have chosen to compare our calculated partitioning data to three sets of experimental data: partitioning of the side chain analogs from water to cyclohexane (54); partitioning of a series of small peptides (Ace-WLxLL) between water and a POPC membrane (16); and partitioning of the same peptides between water and water-saturated octanol (15).

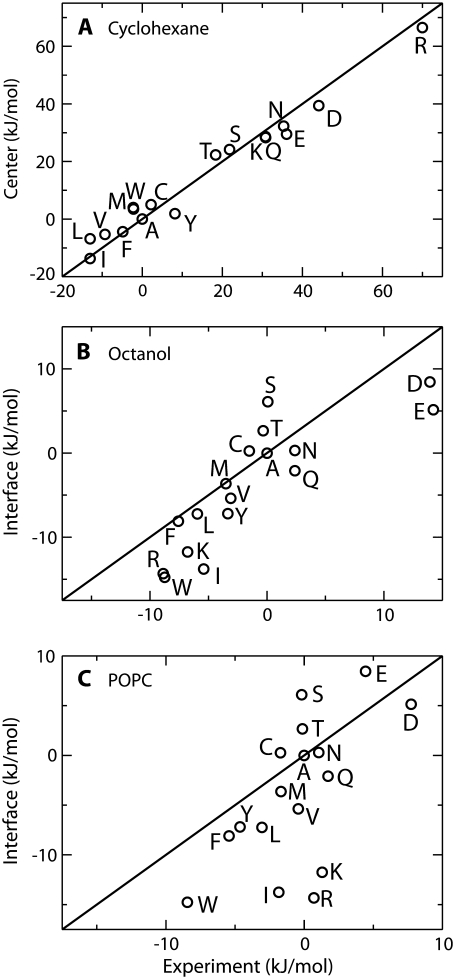
Fig. 8 A compares the free energy calculated for transferring the side chain from water to the center of the membrane, with the experimentally measured free energy for transferring the side chain from water to cyclohexane (54). Overall, the agreement with experiment is very good across a wide range of transfer free energies (approximately −20 kJ/mol to +60 kJ/mol). The strong correlation observed indicates that for partitioning the center of the membrane behaves similarly to a bulk alkane. However, this observation only applies near the center of the membrane as at other positions water defects may form, leading to large changes in free energy.

FIGURE 8.

FIGURE 8

Open in a new tab

Comparison of calculated transfer free energies with several interfacial scales. All scales have been shifted so that the free energy for Ala is zero. Solid lines indicate perfect agreement between calculation and experiment and are not best-fit lines. (A) Comparison between calculated free energy for transferring the side chain from water to the center of the bilayer, and the experimental water to cyclohexane transfer free energy (54). (B) Relationship between the calculated water to membrane interface transfer free energy, and the experimental partitioning of Ace-WLLxL peptides between water and water saturated 1-octanol (15). (C) Comparison between the calculated transfer free energy between water and the membrane interface and the experimental partitioning of Ace-WLLxL peptides between water and a POPC bilayer (16).

A comparison of the calculated water to lipid interface free energy with the partitioning of a series of Ace–WLxLL peptides between water and octanol (15) is shown in Fig. 8 B. Again, the overall agreement between the calculated and experimental values is good, with a correlation coefficient of 0.84. A least-squares fit (not shown) yields a slope of ∼0.9, indicating that the variation across residues is slightly higher for the experimental values than in calculation. The agreement between the calculated and experimental scales is expected as octanol is thought to mimic the membrane interface.

Fig. 8 C compares the calculated results with the partitioning of a series of pentapeptides between water and the interface of a POPC bilayer (16). The agreement between the calculated and experimental values is not as good as in the previous two cases, with a correlation coefficient of 0.61. A least squares fit (not shown) yields a slope of 1.2 indicating that the variation among residues is stronger in the calculated results than in experiment. In particular, Arg, Lys, and Ile are too favorable on the calculated scale compared to experiment. Leaving these three residues out of the fit leads to an increased slope of 1.3 and improves the correlation coefficient to 0.85.

We do not expect that the calculated results should exactly match the experimental results as we are dealing with two different systems: one system dealing with small molecule analogs of the side chains, and the other system dealing with side chains in the context of a pentapeptide. In our simulations, both Arg and Lys are strongly oriented at the minimum in Region II, such that the aliphatic tail is buried in the lipid chains, while the charged moiety is partitioned into the carbonyl region. This orientation is not possible in the pentapeptide due to the presence of the charged C terminus. Thus, we expect that the Arg and Lys side chains studied here should be more favorable than in experiment because they are able to adopt a more favorable orientation. This effect likely applies to all residues to some degree, although we expect it to be strongest for Lys and Arg as they are the most amphipathic residues. The calculated free energy for transferring Ile into the membrane interface is also too favorable compared to experiment. We believe that this is because both Ile and Leu are branched amino acids, whereas because of truncation at the β-carbon, only Leu (isobutane) is branched in the current study, and Ile (butane) is not.

The differences discussed above highlight the need for further study on the effects the peptide environment on partitioning. These results provide a baseline for side chains in the absence of a peptide, allowing for comparison with further studies on the effects of the peptide backbone and neighboring residues.

Implications for voltage gated channels

We feel that our results have important implications for understanding membrane proteins that may have lipid exposed charges, such as voltage gated ion channels (1–4) and MscS (7). Although we do not directly study K+ channel gating here, we attempt to answer the broader question of what happens when a charged residue is placed in the membrane. What is the energetic cost of placing a charge in the membrane? Would there be a change in protonation state? Is there any change in the structure of the bilayer?

From the available evidence, it is unclear if a mostly hydrophobic helix containing several charges, such as the S4 segment of voltage gated K+ channels, could be inserted as a stable transmembrane helix with the charges exposed. Experimentally, it has been shown that the transmembrane and nontransmembrane orientations of S4 are nearly equal in energy (64). However, the experimental system used is complex and it is not clear what the local environment of the charges is; they may buried in protein–protein contacts rather than lipid exposed. Computer simulations of S4 have shown it to be stable as a transmembrane helix over 10 ns, with the formation of large water defects to maintain hydration of the charges (56). However, these simulations do not show the thermodynamic stability of the transmembrane orientation. Our simulations could be used to argue the thermodynamic stability of this arrangement, as the transfer of ∼4 Leu residues from water to the bilayer interior is enough to balance the transfer of a single Arg. However, this argument is far too simplistic and misses important backbone contributions, and does not consider the possibility of surface bound orientations.

There are two main conclusions that can be drawn from the available data. First, placing a charged residue in the center of the membrane costs significantly less than would be predicted from continuum theories or bulk solvation measurements. Second, given the first conclusion, we feel that one must be very cautious about making energetic arguments in such systems. There simply is not enough data available to make definitive conclusions. Although it may turn out that the charges on S4 are not lipid exposed during gating (65), models that due include lipid exposure cannot currently be ruled out based on energetic arguments.

Interestingly, the gating charges on the N-terminal end of the S4 segment in voltage gated potassium channels are almost always Arg rather than Lys (1). If the gating charges are lipid exposed, as suggested by one model (3,4), Arg would naturally be favored over Lys, as Lys would be deprotonated near the center of the membrane, rendering it useless as a gating charge.

Finally, it seems that the cost of burying a positively charged Arg or Lys residue near the center of the membrane is at least partially determined by the cost of forming a water defect. This raises the interesting possibility that the partitioning of charged and polar residues may be nonadditive. For example, the energetic cost of partitioning the arginine residues in S4 may be determined mostly by the free energy of partitioning the deepest Arg. The remaining Args are spatially close and may be able to “piggyback” on the existing water defect. Such an arrangement could lead to a nonadditive free energy for the remaining residues. Further study is needed to determine the exact mechanism and magnitude of this effect.

Limitations

The side chains used in our study are truncated at the β-carbon, a situation different than experienced by the side chain in the context of a transmembrane helix. This truncation changes the available orientations of the side chains and even changes the chemical nature of Ile, making it linear rather than branched. Our scale is also completely missing backbone contributions, which may play an important role in determining partitioning. Finally, the truncated side chains do not experience any shielding or occlusion as they would in a transmembrane helix.

In our simulations, two side chain analogs are present per simulation box to improve sampling. The two analogs are always separated by 3.7 nm in the z-dimension to minimize the interactions between them. The distance between the two molecules is usually higher as the analogs are offset in the xy-plane. To assess the interaction between the two analogs we have recalculated the PMF for Arg with only a single analog in the simulation box (40 ns simulation). There is little difference between the results obtained using 1 or 2 molecules per simulation (Supplementary Material, Fig. S1). The minimum shifts slightly toward the center of the membrane when only one Arg is present and the interfacial minimum is slightly less deep in the headgroup region, with a maximum difference of ∼4 kJ/mol. These differences are comparable to the uncertainty in our calculations. Thus, the use of two Arg molecules per simulation box, separated by at least 3.7 nm, leads only to very small changes in the PMF and no changes in our conclusions. We expect that the charged residues represent a worst case scenario and that the errors for the other residues are likely even smaller.

We used the OPLS-AA force field for these calculations. We have calculated previously the partitioning of the side chain analogs between water and cyclohexane, using either OPLS-AA (17) or the Berger lipid tail parameters (21) to model the cyclohexane. The results are in good agreement with experiment. However, the agreement is not perfect and the force field represents a source of error. We have shown that changing the partial charges on some residues can significantly improve the water-cyclohexane partition free energies (21), but those modifications have not been used here. Additionally, the interactions between lipids and side chains have not been explicitly parameterized or validated, instead the models have been parameterized based on experimentally measured quantities, such as water-cyclohexane transfer free energy, hydration free energy, and area per lipid. The underlying assumption is that if such models are parameterized to reproduce certain properties of a system, they can be used to make predictions of other properties on which they have not been parameterized. The close agreement between our results and those of Dorairaj and Allen (5), which were carried out using a completely different force field, suggests that both force fields do a reasonable job of representing the interactions between the side chains, lipids, and water.

Polarization is not included explicitly in the OPLS-AA, or in any other widely used biomolecular force fields. This is an interesting conundrum for the type of problem studied here, because we are explicitly transferring charged and polar residues from water to a hydrophobic environment. Based on purely electrostatic arguments (the Born equation), the free energy of transfer for an ion from a dielectric constant of 80 to 2 would almost be cut in half compared to transferring the same ion from a dielectric constant from 80 to 1. The dielectric constant for an alkane based on our lipid tail parameters is 1, whereas experimentally liquid alkanes have a dielectric constant of ∼2. Using an all-atom lipid model does not significantly improve the situation, yielding a dielectric constant virtually indistinguishable from 1 (66), as the main factor missing is electronic polarization. The situation is not as clear as this however, because the force field is parameterized to implicitly include the average effects of polarization. This is clearly shown by the excellent agreement of the water/cyclohexane partitioning data from the simulations compared to experiment. Our simulations and others also show that the cost of forming water defects in a 3-nm thick membrane is less than burying naked charges. As soon as these water defects appear, or water is bound to buried charges, the effective dielectric constant is much higher than 1 or 2, and the error in the calculations much less than in the pure continuum approximation, but difficult to estimate. In principle, it might be possible to calculate a correction based on continuum electrostatics. However, in practice, such calculations are extremely sensitive to the exact parameters chosen. The presence of water defects in the lipid tails likely dominates the electrostatic interactions such that a change in the dielectric constant of the tails from 1 to 2 would lead to only very small changes in free energy.

CONCLUSIONS

We have calculated the free energy for partitioning into a DOPC bilayer for 17 of 20 amino acids. The calculated values are in good agreement with experiment, especially at the center of the bilayer. The most striking finding is formation of large water defects that hydrate the polar and charged residues on penetration into the acyl chains. The stability of these defects is determined by a balance between the cost of forming a water defect, and the energy gained by hydrating the polar side chain. Lys, Glu, and Asp are all likely neutral when partitioned to the center of the membrane as the cost of forming a water defect in the center of the membrane outweighs the cost of protonating or deprotonating the residue. For Arg, it seems energetically feasible that the residue could remain ionized at the center of the membrane remaining stabilized by a large water defect. Overall, the presence of these water defects should reinforce the idea that biological membranes are very fluid, elastic, and deformable structures. These results should also dispel the notion that the membrane can be regarded as a generic low dielectric slab.

SUPPLEMENTARY MATERIAL

All PMFs discussed in this article are available in numerical form as Supplementary Material.

To view all of the supplemental files associated with this article, visit www.biophysj.org.

Acknowledgments

This work is supported by the National Science and Engineering Research Council (NSERC). J.L.M. is supported by studentships from National Science and Engineering Research Council, Alberta Ingenuity, and the Killam Trust. D.P.T. is an Alberta Heritage Foundation for Medical Research Senior Scholar and Canadian Institutes of Health Research New Investigator.

Editor: Eduardo Perozo.

References

  • 1.Jiang, Y. X., A. Lee, J. Y. Chen, V. Ruta, B. T. Chait, and R. MacKinnon. 2003. X-ray structure of a voltage-dependent K+ channel. Nature. 423:33–41. [DOI] [PubMed] [Google Scholar]
  • 2.Long, S. B., E. B. Campbell, and R. MacKinnon. 2005. Crystal structure of a mammalian voltage-dependent Shaker family K+ channel. Science. 309:897–903. [DOI] [PubMed] [Google Scholar]
  • 3.Jiang, Y. X., V. Ruta, J. Y. Chen, A. Lee, and R. MacKinnon. 2003. The principle of gating charge movement in a voltage-dependent K+ channel. Nature. 423:42–48. [DOI] [PubMed] [Google Scholar]
  • 4.Long, S. B., E. B. Campbell, and R. MacKinnon. 2005. Voltage sensor of kv1.2: structural basis of electromechanical coupling. Science. 309:903–908. [DOI] [PubMed] [Google Scholar]
  • 5.Dorairaj, S., and T. W. Allen. 2007. On the thermodynamic stability of a charged arginine sidechain in a transmembrane helix. Proc. Natl. Acad. Sci. USA. 104:4943–4948. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Grabe, M., H. Lecar, Y. N. Jan, and L. Y. Jan. 2004. A quantitative assessment of models for voltage-dependent gating of ion channels. Proc. Natl. Acad. Sci. USA. 101:17640–17645. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Perozo, E., and D. C. Rees. 2003. Structure and mechanism in prokaryotic mechanosensitive channels. Curr. Opin. Struct. Biol. 13:432–442. [DOI] [PubMed] [Google Scholar]
  • 8.Anishkin, A., B. Akitake, and S. Sukharev. 2007. Characterization of the resting MscS: modeling and analysis of the closed bacterial mechanosensitive channel of small conductance. Biophys. J. 94:1252–1266. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.White, S. H., and W. C. Wimley. 1999. Membrane protein folding and stability: physical principles. Annu. Rev. Biophys. Biomol. Struct. 28:319–365. [DOI] [PubMed] [Google Scholar]
  • 10.von Heijne, G. 2007. Formation of transmembrane helices in vivo—is hydrophobicity all that matters? J. Gen. Physiol. 129:353–356. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.White, S. H. 2007. Membrane protein insertion: the biology–physics nexus. J. Gen. Physiol. 129:363–369. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Wolfenden, R. 2007. Experimental measures of amino acid hydrophobicity and the topology of transmembrane and globular proteins. J. Gen. Physiol. 129:357–362. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Aliste, M. P., and D. P. Tieleman. 2005. Computer simulation of partitioning of ten pentapeptides Ace-WLXLL at the cyclohexane/water and phospholipid/water interfaces. BMC Biochem. 6:30. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Aliste, M. P., J. L. MacCallum, and D. P. Tieleman. 2003. Molecular dynamics simulations of pentapeptides at interfaces: salt bridge and cation-pi interactions. Biochemistry. 42:8976–8987. [DOI] [PubMed] [Google Scholar]
  • 15.Wimley, W. C., T. P. Creamer, and S. H. White. 1996. Solvation energies of amino acid side chains and backbone in a family of host-guest pentapeptides. Biochemistry. 35:5109–5124. [DOI] [PubMed] [Google Scholar]
  • 16.Wimley, W. C., and S. H. White. 1996. Experimentally determined hydrophobicity scale for proteins at membrane interfaces. Nat. Struct. Biol. 3:842–848. [DOI] [PubMed] [Google Scholar]
  • 17.MacCallum, J. L., and D. P. Tieleman. 2003. Calculation of the water-cyclohexane transfer free energies of neutral amino acid side-chain analogs using the OPLS all-atom force field. J. Comput. Chem. 24:1930–1935. [DOI] [PubMed] [Google Scholar]
  • 18.Oostenbrink, C., A. Villa, A. E. Mark, and W. F. Van Gunsteren. 2004. A biomolecular force field based on the free enthalpy of hydration and solvation: the GROMOS force-field parameter sets 53A5 and 53A6. J. Comput. Chem. 25:1656–1676. [DOI] [PubMed] [Google Scholar]
  • 19.Shirts, M. R., and V. S. Pande. 2005. Solvation free energies of amino acid side chain analogs for common molecular mechanics water models. J. Chem. Phys. 122:134508. [DOI] [PubMed] [Google Scholar]
  • 20.Shirts, M. R., J. W. Pitera, W. C. Swope, and V. S. Pande. 2003. Extremely precise free energy calculations of amino acid side chain analogs: comparison of common molecular mechanics force fields for proteins. J. Chem. Phys. 119:5740–5761. [Google Scholar]
  • 21.Tieleman, D. P., J. L. MacCallum, W. L. Ash, C. Kandt, Z. Xu, and L. M. Monticelli. 2006. Membrane protein simulations with a united atom lipid and all atom protein model: side chain transfer free energies and model proteins. J. Phys. Condens. Matter. 18:S1221–S1234. [DOI] [PubMed] [Google Scholar]
  • 22.Villa, A., and A. E. Mark. 2002. Calculation of the free energy of solvation for neutral analogs of amino acid side chains. J. Comput. Chem. 23:548–553. [DOI] [PubMed] [Google Scholar]
  • 23.Xu, Z., H. H. Luo, and D. P. Tieleman. 2007. Modifying the OPLS-AA force field to improve hydration free energies for several amino acid side chains using new atomic charges and an off-plane charge model for aromatic residues. J. Comput. Chem. 28:689–697. [DOI] [PubMed] [Google Scholar]
  • 24.Bemporad, D., J. W. Essex, and C. Luttmann. 2004. Permeation of small molecules through a lipid bilayer: a computer simulation study. J. Phys. Chem. B. 108:4875–4884. [Google Scholar]
  • 25.Bemporad, D., C. Luttmann, and J. W. Essex. 2004. Computer simulation of small molecule permeation across a lipid bilayer: dependence on bilayer properties and solute volume, size, and cross-sectional area. Biophys. J. 87:1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Feller, S. E., C. A. Brown, D. T. Nizza, and K. Gawrisch. 2002. Nuclear Overhauser enhancement spectroscopy cross-relaxation rates and ethanol distribution across membranes. Biophys. J. 82:1396–1404. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.MacCallum, J. L., and D. P. Tieleman. 2006. Computer simulation of the distribution of hexane in a lipid bilayer: spatially resolved free energy, entropy, and enthalpy profiles. J. Am. Chem. Soc. 128:125–130. [DOI] [PubMed] [Google Scholar]
  • 28.Marrink, S. J., and H. J. C. Berendsen. 1994. Simulation of water transport through a lipid-membrane. J. Phys. Chem. 98:4155–4168. [Google Scholar]
  • 29.Marrink, S. J., and H. J. C. Berendsen. 1996. Permeation process of small molecules across lipid membranes studied by molecular dynamics simulations. J. Phys. Chem. 100:16729–16738. [Google Scholar]
  • 30.Marrink, S. J., F. Jahnig, and H. J. C. Berendsen. 1996. Proton transport across transient single-file water pores in a lipid membrane studied by molecular dynamics simulations. Biophys. J. 71:632–647. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Norman, K. E., and H. Nymeyer. 2006. Indole localization in lipid membranes revealed by molecular simulation. Biophys. J. 91:2046–2054. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Vemparala, S., L. Saiz, R. G. Eckenhoff, and M. L. Klein. 2006. Partitioning of anesthetics into a lipid bilayer and their interaction with membrane-bound peptide bundles. Biophys. J. 91:2815–2825. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.MacCallum, J. L., W. F. D. Bennett, and D. P. Tieleman. 2007. Partitioning of amino acid side chains into lipid bilayers: results from computer simulations and comparison to experiment. J. Gen. Physiol. 129:371–377. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 34.Marrink, S. J., A. H. de Vries, and A. E. Mark. 2004. Coarse grained model for semiquantitative lipid simulations. J. Phys. Chem. B. 108:750–760. [Google Scholar]
  • 35.Marrink, S. J., S. Risselada, S. Yefimov, D. P. Tieleman, and A. H. de Vries. 2007. The MARTINI forcefield: coarse grained model for biomolecular simulations. J. Phys. Chem. B. 111:7812–7824. [DOI] [PubMed] [Google Scholar]
  • 36.Ulmschneider, M. B., M. S. P. Sansom, and A. Di Nola. 2005. Properties of integral membrane protein structures: derivation of an implicit membrane potential. Proteins. 59:252–265. [DOI] [PubMed] [Google Scholar]
  • 37.Im, W., M. Feig, and C. L. Brooks. 2003. An implicit membrane generalized born theory for the study of structure, stability, and interactions of membrane proteins. Biophys. J. 85:2900–2918. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 38.Tanizaki, S., and M. Feig. 2006. Molecular dynamics simulations of large integral membrane proteins with an implicit membrane model. J. Phys. Chem. B. 110:548–556. [DOI] [PubMed] [Google Scholar]
  • 39.Tanizaki, S., and M. Feig. 2005. A generalized Born formalism for heterogeneous dielectric environments: application to the implicit modeling of biological membranes. J. Chem. Phys. 122:124706. [DOI] [PubMed] [Google Scholar]
  • 40.Yarov-Yarovoy, V., D. Baker, and W. A. Catterall. 2006. Voltage sensor conformations in the open and closed states in ROSETTA structural models of K+ channels. Proc. Natl. Acad. Sci. USA. 103:7292–7297. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 41.Yarov-Yarovoy, V., J. Schonbrun, and D. Baker. 2006. Multipass membrane protein structure prediction using Rosetta. Proteins. 62:1010–1025. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 42.Lazaridis, T. 2003. Effective energy function for proteins in lipid membranes. Proteins Struct. Funct. Genet. 52:176–192. [DOI] [PubMed] [Google Scholar]
  • 43.Lindahl, E., B. Hess, and D. van der Spoel. 2001. GROMACS 3.0: a package for molecular simulation and trajectory analysis. J. Mol. Model. 7:306–317. [Google Scholar]
  • 44.Berger, O., O. Edholm, and F. Jahnig. 1997. Molecular dynamics simulations of a fluid bilayer of dipalmitoylphosphatidylcholine at full hydration, constant pressure, and constant temperature. Biophys. J. 72:2002–2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 45.Jorgensen, W. L., D. S. Maxwell, and J. Tirado-Rives. 1996. Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. J. Am. Chem. Soc. 118:11225–11236. [Google Scholar]
  • 46.Kaminski, G. A., R. A. Friesner, J. Tirado-Rives, and W. L. Jorgensen. 2001. Evaluation and reparametrization of the OPLS-AA force field for proteins via comparison with accurate quantum chemical calculations on peptides. J. Phys. Chem. B. 105:6474–6487. [Google Scholar]
  • 47.Berendsen, H. J. C., J. P. M. Postma, W. F. van Gunsteren, and J. Hermans. 1981. Interaction models for water in relation to protein hydration. In Intermolecular Forces. B. Pullman, editor. D. Reidel, Dordrecht, The Netherlands. 331–342.
  • 48.Berendsen, H. J. C., J. P. M. Postma, A. DiNola, and J. R. Haak. 1984. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 52:1695–1697. [Google Scholar]
  • 49.Miyamoto, S., and P. A. Kollman. 1992. SETTLE. J. Comput. Chem. 13:952–962. [Google Scholar]
  • 50.Hess, B., H. Bekker, H. J. C. Berendsen, and J. G. E. M. Fraaije. 1997. LINCS: a linear constraint solver for molecular simulations. J. Comput. Chem. 18:1463–1472. [Google Scholar]
  • 51.Darden, T., D. York, and L. Pedersen. 1993. Particle mesh Ewald: an N-log(N) method for Ewald sums in large systems. J. Chem. Phys. 98:10089–10092. [Google Scholar]
  • 52.Essmann, U., L. Perera, M. L. Berkowitz, T. Darden, H. Lee, and L. G. Pedersen. 1995. A smooth particle mesh Ewald potential. J. Chem. Phys. 103:8577–8592. [Google Scholar]
  • 53.Kumar, S., D. Bouzida, R. H. Swendsen, P. A. Kollman, and J. M. Rosenberg. 1992. The weighted histogram analysis method for free-energy calculations of biomolecules: I. The method. J. Comput. Chem. 13:1011–1021. [Google Scholar]
  • 54.Radzicka, A., and R. Wolfenden. 1988. Comparing the polarities of the amino acids: side-chain distribution coefficients between the vapor phase, cyclohexane, 1-octanol, and neutral aqueous solution. Biochemistry. 27:1664–1670. [Google Scholar]
  • 55.White, S. H., G. I. King, and J. E. Cain. 1981. Location of hexane in lipid bilayers determined by neutron diffraction. Nature. 290:161–163. [Google Scholar]
  • 56.Freites, J. A., D. J. Tobias, G. von Heijne, and S. H. White. 2005. Interface connections of a transmembrane voltage sensor. Proc. Natl. Acad. Sci. USA. 102:15059–15064. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 57.Johansson, A. C. V., and E. Lindahl. 2006. Amino-acid solvation structure in transmembrane helices from molecular dynamics simulations. Biophys. J. 91:4450–4463. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 58.Hessa, T., H. Kim, K. Bihlmaler, C. Lundin, J. Boekel, H. Andersson, I. Nilsson, S. H. White, and G. von Heijne. 2005. Recognition of transmembrane helices by the endoplasmic reticulum translocon. Nature. 433:377–381. [DOI] [PubMed] [Google Scholar]
  • 59.Killian, J. A., and G. von Heijne. 2000. How proteins adapt to a membrane-water interface. Trends Biochem. Sci. 25:429–434. [DOI] [PubMed] [Google Scholar]
  • 60.Yau, W. M., W. C. Wimley, K. Gawrisch, and S. H. White. 1998. The preference of tryptophan for membrane interfaces. Biochemistry. 37:14713–14718. [DOI] [PubMed] [Google Scholar]
  • 61.Tieleman, D. P., L. R. Forrest, M. S. P. Sansom, and H. J. C. Berendsen. 1998. Lipid properties and the orientation of aromatic residues in OmpF, influenza M2, and alamethicin systems: molecular dynamics simulations. Biochemistry. 37:17554–17561. [DOI] [PubMed] [Google Scholar]
  • 62.Killian, J. A. 1992. Gramicidin and gramicidin lipid interactions. Biochim. Biophys. Acta. 1113:391–425. [DOI] [PubMed] [Google Scholar]
  • 63.MacCallum, J. L., and D. P. Tieleman. 2002. Structure of neat and hydrated 1-octanol from computer simulations. J. Am. Chem. Soc. 124:15085–15093. [DOI] [PubMed] [Google Scholar]
  • 64.Hessa, T., S. H. White, and G. von Heijne. 2005. Membrane insertion of a potassium-channel voltage sensor. Science. 307:1427. [DOI] [PubMed] [Google Scholar]
  • 65.Campos, F. V., B. Chanda, B. Roux, and F. Bezanilla. 2007. Two atomic constraints unambiguously position the S4 segment relative to S1 and S2 segments in the closed state of Shaker K channel. Proc. Natl. Acad. Sci. USA. 104:7904–7909. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 66.Stern, H. A., and S. E. Feller. 2003. Calculation of the dielectric permitivity profile for a nonuniform system: application to a lipid bilayer simulation. J. Chem. Phys. 118:3401–3412. [Google Scholar]
  • 67.Monticelli, L., S. Kandasamy, X. Periole, R. Larson, D. P. Tieleman, S. J. Marrink. The MARTINI coarse grained force field: extension to proteins. J. Chem. Theory Comput. In press. [DOI] [PubMed]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES